EN中文

地球信息科学学报 >

2014 , Vol. 16 >Issue 6: 839 - 845

DOI: https://doi.org/10.3724/SP.J.1047.2014.00839

复杂线-线对象的拓扑关系描述与计算方法

  • 吴长彬 ,
  • 闾国年
展开
  • 1. 南京师范大学 虚拟地理环境教育部重点实验室,南京 210023;2. 江苏省地理信息资源开发与利用协同创新中心,南京 210023

作者简介：吴长彬(1977-),男,博士,副教授,研究方向为GIS、空间关系、时空数据模型。E-mail:

收稿日期: 2014-01-07

  要求修回日期: 2014-02-07

  网络出版日期: 2014-11-01

基金资助

国家自然科学基金项目(41101350,41471318)

江苏高校优势学科建设工程资助项目

收起

Representation and Calculation Method of Topological Relationships for Complex Line Objects

  • WU Changbin ,
  • LV Guonian
Expand
  • 1. Key Laboratory of Virtual Geographic Environment, Ministry of Education, Nanjing Normal University, Nanjing 210023, China;2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
*Corresponding author: WU Changbin, E-mail:

Received date: 2014-01-07

  Request revised date: 2014-02-07

  Online published: 2014-11-01

Copyright

《地球信息科学学报》编辑部 所有
Fold

摘要

空间拓扑关系是GIS中空间查询和分析的基础。针对当前空间拓扑关系模型在表达较复杂对象间拓扑关系存在局限性的突出问题,以线对象为实例,根据点集拓扑理论,重新定义和区分线对象的复杂性;以9I模型为基础,提出一种适合二维复杂线对象的拓扑关系的线性序列描述模型,将复杂线-线的拓扑关系表示成基本拓扑关系的组合。分析不同情形下线之间拓扑关系不同的计算方法。为实现复杂线-线拓扑关系的计算,提高扫描线算法的效率,探讨包络矩形粗滤、线节点重合或共线的斜率坐标判断法等改进方法,提出判断线-线是否相交的矢量叉乘法,具有快速高效的特点。最后,通过实验系统导入线坐标串,进行图形绘制、拓扑关系计算并输出结果,从而验证该模型和算法的可行性。

关键词： 拓扑关系; 线性序列; 9I模型; 扫描线算法; 矢量叉乘

本文引用格式

吴长彬 , 闾国年 . 复杂线-线对象的拓扑关系描述与计算方法[J]. 地球信息科学学报, 2014 , 16(6) : 839 -845 . DOI: 10.3724/SP.J.1047.2014.00839

Abstract

Topological relationship is one of the basic topics of geographic information systems (GISs), and it has been widely applied to data organization and spatial analysis. Many scholars have studied the models of topological relationship and achieved some progresses, among which the 9-Intersections Model (9IM) is well known. This paper aims at finding a method to solve the prominent issue that current models of spatial topological relationships could not represent complex objects. Taking the line object as an example, according to the concepts of point set topology, the complexity of the line object is redefined and distinguished. A linear sequence model of topological relationships, which is based on 9-Intersections Model (9IM) for complex line objects, is proposed and it is represented by some composite basic 9IM matrices. To calculate and distinguish these topological relationships, we applied different methods according to the different relationships between the lines, e.g. some of the lines intersect, some overlap, and others may disjoint. Our main works are stated as follows: we designed an improved sweep-line algorithm to increase the efficiency of the program; we took rectangular envelope algorithm to reduce the execution times, and used vector cross product to determine whether there are any intersections between lines; and we also used coordinates and slopes to deal with some special situations. The test system is developed to prove the capability and efficiency of the model and the calculation method. The procedure is: firstly, the coordinates of two polylines are input; secondly, the polylines are drawn and displayed on the screen, and then the algorithm is executed; finally, the results of topological expressions are produced and shown. As a result, our model can successfully calculate most special relationships between complex polylines, but without the involvement of arc or self-intersection. Generally, this model is still incomplete at present and needs to be improved in future.

Key words： topological relationships; linear sequence; 9I model; sweep-line algorithm; vector cross product

1 引言

目前,空间拓扑关系的研究主要集中在简单目标和2个对象间拓扑关系的描述和推理问题上面,比较典型的是Egenhofer等[1]提出的9I模型（9-Intersection Model）。虽然9I模型在表达简单对象（如单点、直线段、不带洞的凸面）的拓扑关系是比较完备的,但缺乏对复杂目标（多个简单目标组成的复杂目标）空间关系描述和推理的研究[2]。随着应用的不断深入,人们发现4I[3]、9I、及V9I[4]模型适于目标间只有一次相交的简单拓扑关系的描述和计算,在表达目标间存在的复杂拓扑关系上则非常有限。而在现实中,空间对象往往都是比较复杂的,例如,错综复杂的道路交通网、道路与公园复杂的空间语义、含岛的地籍宗地等,这类对象间的拓扑关系很难笼统地用“相交”或“相邻”等词汇表达。因而可以认为,交叉模型的基础理论已基本建立,以后的工作是用这种方法研究更复杂对象间更细致的关系[5]。
近几年,针对复杂对象间的拓扑关系的描述有：Duboisset等[6]、Egenhofer[7]在9I模型的基础上讨论了组合面之间拓扑关系的表达方法;Schneider 等[8-9],Praing等[10],Mckenney等[11],吴长彬等[12-13]对复杂对象的区分和表达方法;Kurata[14-15]提出的9+-Intersection扩展模型,将九元组中的任一维元素进一步细分,以表示有向线、三维球体等复杂的对象;Li等[16],邓敏等[17]提出的复杂线之间的关系,表示为组成序号、特征点序号、环类型号、联结序号的组成;Kimfung等[18],邓敏等[19]扩展了4I模型,用Ao∩Bo、Ao\B、Bo\A、 ∂ A∩ ∂ B 4个元组分别表示A和B内部相交的个数、A内部去除B之后剩余部分的个数、A内部去除B之后剩余部分的个数、A与B边界相交的个数。
关于拓扑关系的计算问题,属于计算机图形学或计算几何的范畴。但目前相关的研究多集中在点在面内及线求交等基本的运算方法,而未考虑地理对象的复杂性和特殊性;对于对象之间的复杂空间拓扑关系的计算也缺乏有效的方法,研究尚需加强。一些成熟的商业软件如ArcGIS、Oracle Spatial等也只能进行intersect、contain、within等简单空间拓扑关系（基于9I模型）的运算,尚无法较好地实现复杂空间拓扑关系的计算和分析。
本文通过对线的复杂性进行重新区分,提出复杂对象的线性序列表达模型,将线对象间的复杂拓扑关系表示成基本拓扑关系的组合,模型表达比较简单,容易通过算法实现;同时,又提出了一种矢量叉乘的线-线拓扑关系快速判断方法。

2 复杂线-线对象拓扑关系的描述

2.1 线复杂性的区分

按照点集拓扑的理论,线的内部（L°）指的是不包含节点的线本身,线的边界（ ∂ L）指的是线的节点。为了便于研究,我们重新给出复杂线的定义。
定义1 设X是R2下一个连通的拓扑空间,X中的一条线L定义为：
L = ⋃ i = 1 n f i ( [ 0,1 ] ) ,其中 ∀ 1 ≤ i ≤ n ： f i : [ 0,1 ] → R 2 是一个连续函数。
f 0 和 f 1 表示的是线的2个节点。则当 n = 1 ,且 ∀ a , b ∈ [ 0,1 ] , a ≠ b : f ( a ) ≠ f ( b ) ， L 是条简单线,否则为复杂线;当 a , b ∈ ( 0,1 ) , a ≠ b : f ( a ) = f ( b ) ,L是条自相交的线;当 ∃ a ∈ { 0,1 } , b ∈ [ 0,1 ] : f ( a ) = f ( b ) ,L是条自相接的线;当f(0)=f(1),L是条闭合的线。
如图1所示,（a）是一条简单线,两个节点之间只有一个单一的线性函数（即1维单纯形）,用SL表示,其余都是复杂线,用CL表示;（b）是具有多个节点的普通线;（c）是条自相交的线;（d）是自相接的线;（e）是闭合的线。若线是曲线的情况,则函数为非线性函数。
Fig. 1 Different shapes of line

图1 线的几种情况

2.2 线-线的复杂拓扑关系的线性序列描述方法

复杂对象之间存在着无限种拓扑关系,无法穷举,这是一种客观存在,跟所采用的模型无关。本文提出一种新的线性序列扩展模型：即将对象间的复杂空间拓扑关系表示为N个基本空间拓扑关系的线性组合（图2）,其按一定的次序排列,便可解决对象间复杂空间拓扑关系的表达问题,且模型比较简单,容易通过算法实现。该基本空间拓扑关系可采用4I、9I、V9I等表示,也可以是基于本体的拓扑关系描述。
Fig. 2 Representation of topological relationships between complex object

图2 复杂对象的拓扑关系表达方法示意图

定义2 存在这样的一组拓扑关系,其描述的是简单点、线、面（符合定义1）之间的拓扑关系,则称为基本拓扑关系（Basic Topological Relationship）。
定义3 对于复杂的点、线、面之间的拓扑关系可分解为若干基本拓扑关系的组合,称为复杂拓扑关系（Complex Topological Relationship）。
本文以9I模型为例进行说明,图3表示了9I模型能区分的33种线拓扑关系[20],按照简单线与复杂线的定义,其中的第LL1、LL2、LL4、LL5、LL9、LL15、LL20、LL22、LL24、LL27、LL30（共11种）是简单线,它们之间的拓扑关系为基本拓扑关系,其余则是复杂拓扑关系。
Fig. 3 33 different topological relationships between two lines[20]

图3 2条线-线之间的33种拓扑关系[20]

假设线CL不带弧,也不存在自相交的情况,CL可表示为若干直线段的组成,CL=L1+L2+…+Ln。
但对于线存在以下的两种情形时,难以分解和表示：（1）线为曲线的情况时,由于线的形态难以控制,所以无法分解;（2）线本身存在部分重叠或自相交时,这种情况将变得非常复杂难以表示,故本文也暂不考虑。
下面以具体的实例来说明。设有折线L1与L2,为了将复杂线间的复杂拓扑关系分拆成基本拓扑关系的组合,按照基本拓扑关系的要求,其表示的必须是两两简单线（直线段）之间的拓扑关系。假设,有一条扫描线从最左侧往右扫描,当碰到任意一条折线的节点时（不包括折线本身的起始和终止端点）就停留一次,如果两条折线的端点重合时不重复记录,这样两条扫描线间所包含的L1与L2的部分必然是直线段。设一共有n条扫描线,则L1与L2之间的复杂拓扑关系可以表示成n+1个基本拓扑关系的组合。但当出现线段与扫描线重合的特殊情况时,必须加1。
图4中L1由5个节点组成（不包括起始端点）,L2由4个节点组成（不包括起始端点）,扫描线从左往右依次记录了位置,由于其中L1的第4个节点与L2的第4个节点重合,故建立了8条扫描线。因此,L1与L2之间的复杂拓扑关系可表示成9个基本拓扑关系的组合,即CR(L1,L2)=LL1+LL2+LL24+LL22+LL24+LL2+LL24+LL22+LL24,根据每类基本拓扑关系出现的次数和秩序,可进一步表示为：
CR ( L 1 , L 2 ) = ( 1 ) LL 1 + ( 2,6 ) LL 2 + ( 3,5 , 7,9 ) LL 24 + ( 4,8 ) LL 22
或记为：
CR ( L 1 , L 2 ) = ( 1 ) φ φ ¬ φ φ φ ¬ φ ¬ φ ¬ φ ¬ φ + ( 2,6 ) ¬ φ φ ¬ φ φ φ ¬ φ ¬ φ ¬ φ ¬ φ + ( 3,5 , 7,9 ) φ φ ¬ φ φ ¬ φ ¬ φ ¬ φ ¬ φ ¬ φ + ( 4,8 ) ¬ φ φ φ φ ¬ φ φ φ φ ¬ φ
Fig. 4 An example of complex topological relationship between lines

图4 复杂的线-线拓扑关系实例

考虑到线的起始点可以任意假设,若扫描线从右往左扫描,则上式等价于： CR ( L 1 , L 2 ) = LL 24 + LL 22 + LL 24 + LL 2 + LL 24 + LL 22 + LL 24 + LL 2 + LL 1 ,即：
CR ( L 1 , L 2 ) = ( 9 ) LL 1 + ( 4,8 ) LL 2 + ( 1,3 , 5,7 ) LL 24 + ( 2,6 ) LL 22
或记为：
CR ( L 1 , L 2 ) = ( 9 ) φ φ ¬ φ φ φ ¬ φ ¬ φ ¬ φ ¬ φ + ( 4,8 ) φ φ ¬ φ φ ¬ φ ¬ φ ¬ φ ¬ φ ¬ φ ( 1,3 , 5 , 7 ) ¬ φ φ ¬ φ φ φ ¬ φ ¬ φ ¬ φ ¬ φ + ( 2,6 ) ¬ φ φ φ φ ¬ φ φ φ φ ¬ φ
当基本拓扑关系连续出现多次时,为了节省存储空间,可以简单记为[m..n]。

3 线-线复杂拓扑关系的计算方法

空间拓扑关系的算法设计,要考虑到算法的可行性、解决问题的全面性、执行的效率等。目前在GIS基础研究和计算机图形学等研究领域,虽然已建立了相关的计算几何算法基础,如线与线之间的交点算法,但要实现复杂线-线空间拓扑关系计算,还需对算法进行改进。
交点算法是计算几何的一个基本算法,也是实现拓扑关系的一个基础。若直接对线段两两比较求交,即所谓的“暴力求交”法,效率很低(时间复杂性O(n2))。当前效率较高的线段求交方法是平面扫描算法。它假设二维平面上的一个集合S,用一条垂直于X轴的扫描线SL经过集合S从左向右进行扫描。扫描线只有遇到线或面的节点时,才停留,这种引起STA中内容改变的平面要素称为状态变迁点（或者事件点）。实质上就是把一个二维的、静态的计算几何问题转化为一个一维的、动态的求解问题。只比较相邻线段,以减少计算,提高效率,时间复杂性是O(k+nlogn)。
复杂线-线拓扑关系的计算可基于扫描线法,但为了提高效率,对算法可作进一步的改进。在判断是否进入堆栈时,可采用包络矩形判断法,即分别计算两条折线的最小和最大x, y值（xmin, ymin, xmax, ymax）,得出各自的包络矩形MBR（包围盒）。这只需要对两个包络矩形MBR的重叠部分进行求交运算即可,从而减少了扫描线包络矩形外节点不必要的停留。
判别两条线是否相交,是线-线拓扑关系计算的关键问题。由于拓扑关系是定性而不是定量的,不需要精确地求得2条线的交点,只要判别两条线是否相交即可。因而,可以对线-线求交的算法进行改进。
（1）线-线是否相交的矢量叉乘法
在高等数学里矢量运算包含矢量加减、矢量点乘、矢量叉乘;在物理中常有2个相互垂直的矢量作用,叉乘是描述这类效应的矢量运算。叉乘用“×”表示,其积仍为矢量。若A、B是交角为 θ 的2个矢量,则叉乘定义为：
矢量积方向垂直于包含A、B平面,用右手判断。
假设平面上有两条线,分别为mimi+1和nini+1,为了判断mimi+1和nini+1是否有交点,若以线段mimi+1为参考,则我们只要判断ni和ni+1两个端点是否在mimi+1的同侧,若在同侧,则说明两线段不相交;在异侧,则说明相交。
设向量p=mi+1-mi,方向由mi指向mi+1;设向量q1=ni-mi,方向由mi指向ni;设向量q2=ni+1-mi,方向由mi指向ni+1。然后,判断向量p和q1的叉乘值,即z1=p×q1,其按照右手大拇指法则,手掌由p扫向q1,大拇指的方向就是z1所在的方向;同样判断向量p和q2的叉乘值,即z2=p×q2。则有：
①当z1与z2的符号或方向相同时,ni和ni+1在mimi+1的同侧,线段不相交,如图5（a）所示;
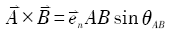
Fig. 5 Vector cross multiplication to determine the intersection between two lines

图5 根据矢量叉乘判断两线段是否相交

②当z1与z2的符号或方向相反时,ni和ni+1在mimi+1的异侧,线段相交,如图5（b）所示。
（2）线节点重合或共线的斜率坐标判断法
矢量叉乘只能判断两条线是否相离或相交的情况,但对于线-线至少有一个节点重合或者共线的情况,必须进行特殊处理,可采用坐标和斜率判断的方法,具体处理的方法如表1所示。
Tab. 1 Different methods by different topological relationships between lines

表1 不同情况下线拓扑关系计算的不同方法

序号 平面上的两条线 语义 拓扑关系的判断方法
1 线-线相离 采用矢量叉乘的判断法
2 线-线相交 采用矢量叉乘的判断法
3 线-线外相接 采用坐标和斜率判断的方法,当斜率k不等,但有一个端点坐标相等
4 线-线内相接 采用坐标和斜率判断的方法,当斜率k不等,但有一个端点在另一直线上
5 线-线相等 采用坐标和斜率判断的方法,当斜率k相等,且两条线段的两个端点都相等时
6 线-线部分包含 采用坐标和斜率判断的方法,当斜率k相等,且两条线段的有一个端点坐标相等时
7 线-线完全包含 采用坐标和斜率判断的方法,当斜率k相等,且两条线段的两个端点都不相等,但都在另一直线上时
8 线-线部分重叠 采用坐标和斜率判断的方法,当斜率k相等,且两条线段的两个端点都不相等,但有一个端点在另一直线上时
如果两条直线共线,如图3中LL5、LL20、LL22、LL27的4种情形,且两条直线的斜率k都相等,则根据另外2个端点坐标值的不同情况,较容易将4种情形区分开来;点在线上可以通过矢量叉乘值为0进行判断。而对于LL4、LL24两种相接的情况,两条直线的斜率k不相等,根据2个端点坐标值的不同情况也可以区分开来。

4 线-线复杂拓扑关系的实验与结果分析

我们对多种线-线之间的复杂拓扑关系情况进行了实验分析,如图6所示,在下方的信息框里显示了利用所设计算法计算的线性序列模型表达结果,与预想的完全一致,证明了采用的模型与算法切实有效。
Fig. 6 Interface of complex topological calculation between lines

图6 线-线的复杂拓扑关系情况计算界面

实验步骤如图7所示：（1）导入自定义的两个对象的坐标串文件,以文本的方式,记录的格式为（点号,x坐标,y坐标）,对象的坐标及编号显示在程序界面左边的列表中;利用绘笔（pen）工具在屏幕上绘出该图形;（2）运行程序代码,通过执行扫描动作,在程序运行过程中,动态地记录并输出堆栈值的变化过程,以分析算法的执行过程是否正确;（3）程序自动分析出两个被扫描对象各部分的局部拓扑关系,并将分析的结果显示在程序界面下方的文本框中。
Fig. 7 Test processes of computing topological relationships between complex lines

图7 复杂线对象的拓扑关系计算的实验步骤

程序运行过程中动态地输出事件点和STA栈的状态,及拓扑关系计算的结果,如图8所示。
Fig. 8 The result of topological computing

图8 线-线复杂拓扑关系计算输出结果

通过对一组不同线段数量的折线之间拓扑关系计算的算法效率测试,得出如图9所示的曲线。分析得出,随着扫描线数量的增加,算法的耗时也不断增加。算法的时间主要受线段的数量（n）和交个数（k）的影响,另外,由于需要处理一些拓扑关系的特殊情况,也消耗了一部分时间。
Fig. 9 The efficiency analysis of the improved sweep-line algorithm

图9 改进的扫描线算法效率分析图

5 结论与讨论

拓扑关系表达是空间认知的一个重要内容,人类对地理空间认知的有限性,加上空间数据本身的多尺度性、表现形式的多样性等特点,导致模型在表达上存在的不确定性和不完备性。地理对象既存在简单的对象也存在复杂的对象,利用点集拓扑理论可以区分对象的复杂性。4I、9I等模型对简单对象的拓扑关系表达是比较完备的,但其在表达复杂对象的拓扑关系上是有限的。本文以二维线对象为实例,提出了复杂拓扑关系的线性序列表达模型,将复杂对象的复杂拓扑关系表示成基本拓扑关系的有序组合是合理的,易于理解和程序实现,可有效地解决复杂线对象的拓扑关系的表达问题。

The authors have declared that no competing interests exist.

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Egenhofer M J, Sharma J, Mark D M.A critical comparison of the 4-intersection and 9-intersection models for spatial relations: Formal Analysis[J]. AutoCarto, 1993,11:1-11.

[2]
杜世宏,秦其明,王桥.空间关系及其应用[J].地学前缘,2006,13(3):69-80.

[3]
Egenhofer M J, Franzosa R D.Point-set topological spatial relations[J]. Int. J. Geographical Information Systems, 1991,5(2):161-176.

[4]
Chen J, Li C M, Li Z L, et al.Improving 9-Intersection Model by replacing the complement with voronoi region[J]. Geo-spatial Information Science, 2000,3(1):1-10.

[5]
吴建新,方裕,陈斌.拓扑空间关系描述理论研究现状与发展[J].地理与地理信息科学,2005,21(3):1-4.

[6]
Duboisset M, Pinet F, Kang M, et al.A general framework to implement topological relations on composite regions[C]. LNCS, 2007,4653:823-833.

[7]
Egenhofer M J.A reference system for topological relations between compound spatial objects[C]. ER 2009 Workshops, LNCS, 2009,5833:307-316.

[8]
Schneider M.Computing the Topological Relationship of Complex Regions[C]. Database and Expert Systems Applications, Lecture Notes in Computer Science, 2004,3180:844-853.

[9]
Schneider M, Behr T.Topological relationships between complex spatial objects[J]. ACM Trans.on Database Systems, 2006,31:39-81.

[10]
Praing R, Schneider M.Efficient implementation techniques for topological predicates on complex spatial objects[J]. Geoinformatica, 2008,12(3):313-356.

[11]
Mckenney M, Pauly A, Praing R, et al.Local topological relationships for complex regions[C]. In 10th Int. Symp. on Spatial and Temporal Databases, 2007,4605:203-220.

[12]
吴长彬,闾国年.空间拓扑关系若干问题研究现状的评析[J].地球信息科学学报,2010,12(4):524-531.

[13]
吴长彬,闾国年.线面拓扑和度量关系的细分描述和计算方法[J].计算机辅助设计与图形学学报,2009,21(11):1551-1557.

[14]
Kurata Y. The 9+-Intersection: A universal framework for modeling topological relations[C]. GIScience,LNCS,2008(5266):181-198.

[15]
Kurata Y.Three-valued 9-intersection for deriving possible topological relations from incomplete observations[R]. Lecture Notes in Geoinformation and Cartography, Advances in GIScience, 2009:289-308.

[16]
Li Z L, Deng M.A hierarchical approach to the line-line topological relations[C]. Progress in Spatial Data Handling, 2006:365-382.

[17]
邓敏,李志林,祁华斌.GIS线目标间空间关系的集成表达方法[J].测绘学报,2007,36(4):421-427.

[18]
Liu K F, Shi W Z.Extended model of topological relations between spatial objects in geographic information systems[J]. International Journal of Applied Earth Observation and Geoinformation, 2007,9:264-275.

[19]
邓敏,李志林,李永礼,等.GIS线目标间拓扑关系描述的4交差模型[J].武汉大学学报(信息科学版),2006,31(11):945-948

[20]
Egenhofer M J, Herring J R. Categorizing binary topological relationships between regions, lines and points in geographic databases[A]. A Framework for the Definition of Topological Relationships and An Approach to Spatial Reasoning within this Framework[C], 1991:1-28.

Options
文章导航

/

〈 〉