EN中文

地球信息科学学报 >

2014 , Vol. 16 >Issue 6: 874 - 881

DOI: https://doi.org/10.3724/SP.J.1047.2014.00874

基于MapReduce的空间敏感性分析并行算法设计

  • 李帆 , 1, 2 ,
  • 何洪林 , 1, * ,
  • 任小丽 1, 2 ,
  • 张黎 1 ,
  • 路倩倩 1, 2 ,
  • 于贵瑞 1
展开
  • 1. 中国科学院地理科学与资源研究所 生态系统网络观测与模拟重点实验室,北京 100101
  • 2. 中国科学院大学,北京 100049
*通讯作者：何洪林(1971-),男,研究员,研究方向为生态信息学。E-mail:

作者简介：李 帆(1987-),男,山西太原人,硕士生,研究方向为生态信息学。E-mail:

收稿日期: 2013-12-28

  要求修回日期: 2014-02-24

  网络出版日期: 2014-11-01

基金资助

科学院先导专项“应对气候变化的碳收支认证及相关问题”(XDA05050600)

国家生态系统观测评估技术系统集成研究与示范(2013BAC03B00)

MSR-CNIC Windows Azure 合作计划项目“基于Windows Azure的陆地生态系统碳水通量估算与不确定性研究”

国家科技部环保公益性行业科研专项(gyh5031103)

收起

Research on Spatial Sensitivity Analysis Using Parallel Algorithm Based on MapReduce

  • LI Fan , 1, 2 ,
  • HE Honglin , 1, * ,
  • REN Xiaoli 1, 2 ,
  • ZHANG Li 1 ,
  • LU Qianqian 1, 2 ,
  • YU Guirui 1
Expand
  • 1. Key Laboratory of Ecosystem Network Observation and Modeling, Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China
  • 2. University of Chinese Academy of Sciences, Beijing 100049, China
*Corresponding author: HE Honglin, E-mail:

Received date: 2013-12-28

  Request revised date: 2014-02-24

  Online published: 2014-11-01

Copyright

《地球信息科学学报》编辑部 所有
Fold

摘要

近年来,随着遥感空间数据广泛应用于生态系统,推动了区域尺度生态遥感参数模型的发展。敏感性分析对识别模型关键参数,降低模型不确定性和完善模型具有重要作用。区域尺度的生态遥感参数模型,在进行模型参数敏感性分析时,由于涉及到空间数据的复杂运算,单机环境无法满足快速分析的要求。为了提高生态遥感参数模型空间敏感性分析效率,本文以青藏高原为研究区域,利用植被光合模型VPM(Vegetation Photosynthesis Model)和开源云计算平台Hadoop,设计和实现了基于Sobol′的生态遥感参数模型空间敏感性分析并行算法,并在实验室集群环境下进行算法分析,验证了算法的有效性和适用性。该算法的核心是利用MapReduce并行编程技术,对空间敏感性分析中的地图抽样和模型迭代过程进行任务分割,将分割后的子任务分配至不同的计算节点进行并行计算。实验表明,本文提出的并行策略,能有效缩短地图抽样和模型迭代计算时间,相比于单机算法,并行算法的运行速度提高了14倍左右。

关键词： 遥感参数模型; 空间敏感性分析; Sobol′; MapReduce

本文引用格式

李帆 , 何洪林 , 任小丽 , 张黎 , 路倩倩 , 于贵瑞 . 基于MapReduce的空间敏感性分析并行算法设计[J]. 地球信息科学学报, 2014 , 16(6) : 874 -881 . DOI: 10.3724/SP.J.1047.2014.00874

Abstract

In recent years, with the rapid development of remote sensing technology, the spatial data represented by remote sensing images is widely used in ecosystem modeling, which promoted the development of ecological remote sensing parametric model in the regional scale. Sensitivity analysis is a key step for ecosystem model uncertainty quantification. It can identify the dominant parameters, reduce the model calibration uncertainty, and enhance the model optimization efficiency. Due to the intensive computation of spatial data during the sensitivity analysis, the traditional stand-alone environment cannot meet the requirements of rapid analysis for the regional scale remote sensing parametric model. This study designed and realized a parallel algorithm of Sobol′ spatial sensitivity analysis utilizing Hadoop, which is an open source cloud computing platform, based on VPM (Vegetation Photosynthesis Model). In order to verify the efficiency of the algorithm, we designed a comparison experiment to compare the efficiency differences of the traditional serial algorithm and the parallel algorithm. The parallel programming technology we used in this research was MapReduce, which divided the processes of map sampling and the iterative calculation during the spatial sensitivity analysis into subtasks, and assigned them to multiple computing nodes for parallel computing. The numerical experiment showed that the parallel strategy proposed in this study effectively shortened the time of model iterative calculations and significantly improved the efficiency of spatial sensitivity analysis for ecological remote sensing parametric model. Compared with the serial algorithm, the computing efficiency of the parallel algorithm was enhanced by 14 times.

Key words： remote sensing parametric model; spatial sensitivity analysis; Sobol′; MapReduce

1 引言

生态模型是模拟生态系统结构、功能和变化过程及其调控机理的重要手段,采用数学公式和物理方程对生态现象和生态过程进行简化、抽象,主要包括经验模型、过程模型和遥感参数模型。在实际的建模过程中,观测误差的存在和对机理过程的有限认识使模型参数存在很大的不确定性,进而给模型模拟结果带来误差[1]。通过敏感性分析(Sensitivity Analysis)可有效评价模型参数的不确定性对模拟结果的影响,增强模型的有效性和稳定性。
敏感性分析就是假设模型表示为 y = f ( x 1 , x 2 , … , x n ) (xi为模型的第i个参数),令每个参数在一定的取值范围内变动,研究和评价这些参数的变动对模拟结果的影响程度[2]。通常敏感性分析包括局部敏感性分析(Local Sensitivity Analysis)和全局敏感性分析(Global Sensitivity Analysis),局部敏感性分析只检验单个参数的变化对模型结果的影响程度,具有原理简单、可操作性强的特点,但是由于忽略了参数间的相互作用,致使分析结果存在一定的片面性;全局敏感性分析同时检验多个参数的变化对模拟结果的影响,可以分析各参数间的相互作用对模拟结果的影响[3]。目前,全局敏感性分析方法广泛应用于生态模型参数敏感性评价中[1],如以多元回归法、Morris方法、傅里叶幅度灵敏度检验法为主的定性分析方法和以方差分解理论为主的扩展傅里叶幅度灵敏度检验法、Sobol′方法为主的定量分析方法。其中,定量Sobol′方法[4]不仅能够给出模型各参数敏感性大小的排序,还能对模型结果的不确定性进行拆分,量化各参数的不确定性对模型结果不确定性的贡献率大小。该方法适用于站点尺度,应用于区域尺度遥感参数模型时,还需要考虑空间数据的变异性和自相关性,因此,Lilburne等[5-7]提出了基于地图抽样和模型迭代的空间Sobol′方法,但需要大量的运算,计算成本高昂,单机环境无法满足参数敏感性快速分析的要求。随着以Hadoop[8]为代表的开源云计算平台逐渐应用于科学计算领域,为降低计算成本提供了可能。
Hadoop是Apache软件基金会发起的开源项目,实现了包括分布式文件系统(Hadoop Distributed File System, HDFS[9-10])和并行编程模型(MapReduce[11-12])在内的云计算平台,已成为工业界和学术界进行云计算应用和研究的标准平台。其中,MapReduce是Google提出的分布式并行编程模型,其核心思想是任务的分解和结果的合并。将计算作业拆分成若干个Map任务,并分配到不同的节点执行,不同Map任务的执行结果再通过Reduce任务进行合并,得到最终的计算结果。MapReduce分布式处理框架的出现极大简化了并行程序的编写,将数据分发、进程调度等细节交由底层框架来管理,使用户集中精力于计算任务本身的实现[13],被广泛应用到地学、生态学等领域。冯敏等[14]以山影分析模型为例,探讨了地形分析模型的MapReduce并行化计算方法,在3个计算节点的情况下,相比于相同配置的单机环境,地形数据的计算效率提升了1.3倍。赵青松等[15]提出了基于MapReduce的作物生长模型并行算法实现方案,提升了作物生长模型模拟的效率。但是,运用MapReduce并行编程模型,对生态遥感参数模型空间敏感性分析效率进行提升的研究方案仍然较少。因此,本文提出了基于MapReduce的空间Sobol′方法并行化实现方案,将其应用到青藏高原区域的植被光合模型(Vegetation Photosynthesis Model, VPM)参数敏感性分析中,并在相同的计算机硬件配置条件下,与空间Sobol′的串行算法进行效率对比分析,验证并行化方案的有效性和实用性。

2 基于Sobol′的空间敏感性分析算法及并行化设计

2.1 Sobol′方法

Sobol′方法[4]是I. M. Sobol′于1993年基于方差分解理论提出的全局敏感性分析方法,该方法的核心是把模型分解为单个参数及参数之间相互组合的函数[16]。假设模型 y = f x , x = ( x 1 , x 2 , … , x k ) , xi服从[0,1]均匀分布,f(x)平方可积,模型可分解为：
式(1)中, f i ( x i ) 表示包含单个参数 x i 的分解项; f ij ( x i , x j ) 表示同时包含参数xi和 xj的分解项; f1,2,k(x1, x2, xk)表示包含所有参数的分解项。依此类推,函数总的方差可分解为：
式(2)中, V 为总方差; Vi为xi的单因子方差;Vij为xi和xi的双因子交互作用的方差。依此类推, V 1,2 , … , k 为所有因子的方差,对上式进行归一化处理,并令
S i 1 , … , i s = V i 1 , … , i s V (3)
得到：
式(4)中, S i 为一阶敏感度, S ij 为二阶敏感度,依此类推, S 1,2 , … , k 为k阶敏感度。引入参数xi的总敏感度 S Ti = ∑ S ( i ) , S ( i ) 指所有包含参数xi的敏感度。

2.2 空间Sobol′方法

Lilburne等[5-7]于2009年提出了基于Sobol'的空间敏感性分析方法。该方法的核心思想是根据各参数的概率分布对其逐像元进行抽样,并将抽样结果组成一幅具有编号的栅格地图。需要注意的是,抽样次数要足够充分才能反映出该参数的空间变异性。在模型迭代计算时,根据编号值将对应的栅格地图代入模型进行模拟。最后,将栅格化的模型结果转换为标量化的目标函数值,再运用传统的Sobol′方法计算各参数的敏感性系数。其串行算法流程如图1所示。
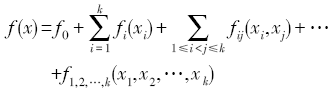
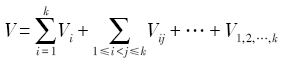
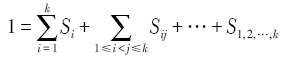
Fig. 1 Flow chart of serial spatial sensitivity analysis algorithm based on Sobol′

图1 基于Sobol′的空间敏感性分析串行算法流程

2.3 空间Sobol′算法并行化设计

在空间Sobol′串行算法流程中,有2个关键阶段制约了整体的运行效率：(1)地图抽样阶段。为了充分反映驱动变量的空间变异性,需要有足够的抽样次数,且随着抽样次数的增加,所需的计算时间也越长;(2)模型迭代阶段。受到模型结构复杂度、栅格图像文件大小及其读写速率的限制,成千上万次模型迭代所需的时间无法接受。这2个阶段的处理过程并不复杂,主要是针对海量数据的重复性循环迭代,所以,本研究采用适于数据密集型计算的并行编程模型MapReduce对这2个阶段分别进行并行化处理,充分利用集群的存储与计算资源,大幅提升遥感参数模型的空间敏感性分析效率。
2.3.1 地图抽样并行化
遥感参数模型各驱动变量的地图抽样都是彼此独立完成的,因此,可将单个驱动变量的单次抽样作为Map任务分割的最小粒度,将不同驱动变量的各次抽样分配到不同的TaskTracker节点上并行执行,任务的动态分配和调度由Hadoop底层框架来完成,其并行抽样过程如图2所示。
Fig. 2 Schematic diagram of map sampling parallelization for driving variables

图2 驱动变量地图抽样任务并行示意图

其中,Map任务对读取到的抽样记录进行解析,获得待抽样的驱动变量名及其抽样结果编号,根据驱动变量名读取栅格图像文件并执行抽样程序。抽样结果根据驱动变量名和抽样结果编号命名,以二进制文件格式保存到HDFS中,为后期模型迭代计算做准备。整个Map过程涉及的输入输出数据项如表1所示。
Tab. 1 The input and output data of Map phase

表1 Map阶段输入输出数据项

数据项 键(key) 值(value)
输入 驱动变量名 抽样结果编号
输出 空值(NullValue) 二进制抽样结果文件
Map任务结束时,直接将抽样结果以文件形式保存至分布式文件系统,不涉及对Map任务的处理结果进行Reduce归约操作。整个地图抽样阶段的并行算法流程如图3所示。
Fig. 3 Flow chart of map sampling parallel algorithm for driving variables

图3 驱动变量地图抽样并行算法流程图

2.3.2 模型迭代并行化
为使敏感性分析结果能够收敛,需要进行上万次,甚至数十万次模型模拟。每次模拟计算都可以动态分配给不同的Map任务并行执行,每个Map任务计算所得的模拟结果通过进程间通讯的方式传递给Reduce任务进行合并,如图4所示。
Fig. 4 Schematic diagram of the parallel algorithm of model iterative simulation

图4 模型并行迭代计算示意图

在进行模型模拟时,模型输入是一组随机的驱动变量抽样编号,例如,模型有5个驱动变量分别为A、B、C、D和E,405、804、385、706和242分别为这5个驱动变量对应的抽样编号,根据编号可以找到地图抽样阶段生成的抽样结果,将其代入模型进行运算得到模拟结果。最后,将模拟结果传递给Reduce任务合并成一个模拟结果矩阵,根据这一矩阵计算各驱动变量的敏感性系数。整个算法流程如图5所示,涉及的输入输出数据项如表2所示。
Fig. 5 Flow chart of parallel algorithm of model iterative simulation

图5 模型迭代计算并行算法流程图

Tab. 2 The input and output data of Map and Reduce phases

表2 Map和Reduce阶段输入输出数据项

数据项 键(Key) 值(Value)
Map输入 矩阵行索引 各驱动变量抽样编号列表
Map输出 矩阵行索引 模拟结果Y
Reduce输入 矩阵行索引 模拟结果Y
Reduce输出 空值(NullValue) 模拟结果矩阵

3 算法实验与结果分析

3.1 植被光合模型(VPM)

VPM(Vegetation Photosynthesis Model)模型是一个以植被光合作用为原理、涡度相关碳通量观测资料为基础,以及遥感和气象资料为驱动变量,模拟生态系统总初级生产力(Gross Primary Productivity, GPP)的光能利用率模型[17-21]。主要公式如下：
GPP = ε g × FPA R c h l × PAR (5)
FPA R c h l = a × EVI (6)
ε g = ε 0 × T sc alar × W sc alar × P sc alar (7)
式中,GPP为总初级生产力;FPARchl是冠层中叶绿素吸收的光合有效辐射比例,通过增强型植被指数(Enhance Vegetation Index, EVI)估算;本文a取值为1.0[17-18];PAR是光合有效辐射;ε0表示最大光能利用率; ε g 表示受温度、水分和物候状态约束下的实际光能利用率;Tscalar、Wscalar、Pscalar分别是温度、水分和物候状态对光能利用效率ε0的影响系数。Tscalar通过陆地生态系统模型(Terrestrial Ecosystem Model, TEM)中的温度控制方程进行计算[22-23]。
T scalar = ( T - T min ) ( T - T max ) ( T - T min ) ( T - T max ) - ( T - T opt ) 2 (8)
式(8)中,Tmax、Tmin和Topt分别是进行光合作用的最高、最小和最适温度,本研究中Topt取值为一年中EVI达到最大时所对应的空气温度[22-23],Tmin取值为0,Tmax取值为Topt+(Topt-Tmin)。冠层水分含量指标Wscalar的计算表达式为：
W scalar = 1 + LSWI 1 + LSW I max (9)
式(9)中,LSWI是陆地表面水分指数(Land Surface Water Index),LSWImax是植被生长季LSWI的最大值。在VPM模型中,Pscalar表征冠层水平叶物候对光合作用的影响。对于草地生态系统来说,由于整个生长季都有新的叶子出现,可将Pscalar取值为1.0[24]。

3.2 研究区背景与数据

本文的研究区域为青藏高原,范围是26.0°N~39.39°N,73.32°E~104.79°E,总面积达2.57×106 km2,占我国陆地总面积的26.8%[25]。青藏高原的高海拔决定了它的自然条件显著区别于同纬度的平原和低地地区,形成寒冷、少雨、干燥的高原气候,植被类型以高寒草地为主,是我国面积最广的天然草地分布区。
VPM模型的原始输入数据包括遥感数据和气象数据,其中遥感植被指数(EVI、LSWI)数据利用2004年第27个8天(2004.7.27-2004.8.3)的MODIS 8天合成地表反射率产品进行波段计算获得,所采用的这一时间序列是全年植被生长最旺盛的时期[21]。气象要素(T、PAR)空间分布数据是基于青藏高原地区2004年有效常规气象观测台站(共88个)的观测站点数据,采用ANUSPLIN[26-29]插值方法进行空间插值得到。最大光能利用率(ε0)是利用国家1:100万草地植被类型图,根据涡度相关通量观测数据,采用蒙特卡罗马尔科夫链(MCMC)[30]参数估计方法获得。上述栅格数据的空间分辨率均为1 km× 1 km,行数为1926,列数为2547。
本实验所用的集群由11台机架式服务器组成,其中,1台Dell R710服务器作为管理节点(NameNode),10台Dell R710服务器作为计算节点(DataNode)。其中,每台服务器配置两颗Inter(R) Xeon(R) E5620 2.40GHz的4核CPU,内存大小为16GB。机器间通过Dell PowerConnect 6224千兆交换机相连。实验中,空间敏感性分析串行算法的运行环境是10个计算节点中的第一台服务器,这样可以保证单机与并行环境下,效率的差异不是由于硬件性能的不同而引起的。

3.3 结果分析

(1) 空间敏感性分析结果
模型输入数据准备完成后,执行空间Sobol′并行算法对模型参数进行全局敏感性评价(表3)。从表3的敏感性分析结果看出,VPM模型的5个输入变量敏感性排序为ε0>T>EVI>PAR>LSWI,其中,ε0对于模型结果不确定性的贡献率达到90%以上,远大于其他4个变量。另外,各参数的一阶敏感度之和小于1,说明参数之前存在一定的交互作用,但与总敏感度之和相差不大,说明输入变量之间的交互作用对于模型结果的影响较小。
Tab. 3 First order sensitivity indices and total order sensitivity indices of VPM model inputs

表3 VPM模型参数的一阶敏感度系数和总敏感度系数

输入变量 一阶敏感度系数(Si) 总敏感度系数(STi)
ε0 0.92270 1.00414
T 0.00508 0.04957
PAR 0.00042 0.00563
EVI 0.00184 0.02241
LSWI 0.00005 0.00070
总和 0.93009 1.08245
(2) 地图抽样阶段并行效率分析
为简化对地图抽样阶段算法效率的讨论,只针对温度变量进行分析,比较其在不同抽样次数条件下,串行抽样算法与并行抽样算法的性能差异。本次实验中,并行算法共启动了10个Map任务参与抽样。实验结果如图6所示,串行算法与并行算法抽样次数的临界点在250次左右：小于临界点,并行算法的执行效率要低于串行算法;大于临界点,并行抽样的效率明显提升。随着抽样次数的大幅增加,串行算法的执行时间呈指数级增长,并行算法的执行时间缓慢地呈线性增长。抽样次数越多,并行算法的加速比就越大;当抽样次数为5000时,加速比可达3.47。
Fig. 6 Efficiency comparison between serial and parallel sampling algorithm

图6 单机和并行抽样算法的运行效率对比图

如图7所示,对温度变量进行5000次地图抽样时,当Map任务的数量小于20,随着Map任务数量增加,并行抽样的时间迅速减少。在25到30的区间内,增加Map任务的个数无法继续提高并行算法的效率,甚至会降低执行效率;这是由于增加的Map任务虽然能分担部分抽样,但额外增加的系统框架开销会降低总体的执行效率。当Map数目大于30,相比于启动、释放Map所需的时间来说,在总体上仍然可以提高整个并行抽样的效率,但是效率提升的速度相对缓慢。
Fig. 7 Sampling efficiency comparison chart of 5000 samples using different amounts of Maps

图7 抽样次数为5000时不同Map任务数目抽样效率对比图

(3) 模型迭代阶段并行效率分析
在模型迭代计算阶段,比较了不同迭代次数条件下,串行算法和并行算法的效率差异。算法的运行时间如图8所示,无论对于串行还是并行迭代,每一次迭代所执行的计算过程都一样,总的迭代时间取决于迭代次数,都呈线性增长趋势;对于不同的迭代次数,并行算法的加速比基本保持不变,能达到14左右。
Fig. 8 Efficiency comparison chart of serial and parallel algorithms for model iterative simulation

图8 单机和并行模型迭代算法的运行效率对比图

4 结论

以空间数据为驱动变量的生态模型,在进行参数敏感性分析时面临海量的数据处理与计算任务,本文在Hadoop数据密集型计算框架下,运用MapReduce并行编程模型,实现了基于Sobol′的空间敏感性分析并行算法,有效提高了生态遥感模型的参数敏感性分析效率,且本算法的并行实现策略可为其他空间敏感性分析算法的并行化设计提供参考。然而,对于计算复杂度较高的过程机理模型,模型前后两次迭代之间往往存在数据的传递,而本算法没有考虑Map任务之间的数据传递,以及执行的先后顺序,这些问题将有待下一步深化研究。

The authors have declared that no competing interests exist.

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
徐崇刚,胡远满,常禹,等.生态模型的灵敏度分析[J].应用生态学报,2004,15(6):1056-1062.

[2]
蔡毅,邢岩,胡丹,等.敏感性分析综述[J].北京师范大学学报(自然科学版),2008,44(1):9-16.

[3]
孔凡哲,宋晓猛,占车生,等.水文模型参数敏感性快速定量评估的RSMSobol方法[J].地理学报,2011,66(9):1270-1280.

[4]
Sobol I M.Sensitivity analysis for non-linear mathematical models[J]. Mathematical modeling & Computational Experiment, 1993,1:407-414.

[5]
Lilburne L, Tarantola S.Sensitivity analysis of spatial models[J]. International Journal of Geographical Information Science, 2009,23(2):151-168.

[6]
Saltelli A.Making best use of model evaluations to compute sensitivity indices[J]. Computer Physics Communications, 2002,145(2):280-297.

[7]
Tarantola S, Nardo M, Saisana M, et al.A new estimator for sensitivity analysis of model output: An application to the e-business readiness composite indicator[J]. Reliability Engineering & System Safety, 2006,91(10-11):1135-1141.

[8]
Apache Hadoop. Hadoop[EB/OL].

[9]
Ghemawat S, Gobioff H, Leung S, et al.The Google file system[C]. Symposium on Operating Systems Principles, 2003.

[10]
Chang F, Dean J, Ghemawat S, et al.A distributed storage system for structured data[J]. ACM Transactions on Computer Systems, 2008,26(2):205-218.

[11]
Dean J, Ghemawat S.MapReduce: Simplified data processing on large cluster[J]. Communications of the ACM, 2008,51(1):107-113.

[12]
Dean J, Ghemawat S.MapReduce: A flexible data processing tool[J]. Communications of the ACM, 2010,53(1):72-77.

[13]
康超. 面向时空分析的海量日志处理关键技术研究及应用[D].北京:中国科学院计算机网络信息中心,2012.

[14]
冯敏,尹芳,诸云强,等.基于MapReduce的分布式地形数据计算研究[J].华中科技大学学报(自然科学版),2011,39(1):24-27.

[15]
赵青松,陈林,孙波,等.基于Hadoop的云环境下作物生长模型算法的实现与测试[J].农业工程学报, 2013,29(8):179-186.

[16]
任启伟,陈洋波,周浩澜,等.基于Sobol法的TOPMODEL[J].人民长江,2010,41(19):91-94.

[17]
Xiao X M, Hollinger D, Aber J D, et al.Satellite-based modeling of gross primary production in an evergreen needle leaf forest[J]. Remote Sensing of Environment, 2004,89:519-534.

[18]
Xiao X M, Zhang Q Y, Braswell B, et al.Modeling gross primary production of temperate deciduous broadleaf forest using satellite image and climate data[J]. Remote Sensing of Environment, 2004,91:256-270.

[19]
Xiao X M, Zhang Q Y, Hollinger D, et al.Modeling gross primary production of an evergreen needleaf forest using MODIS and climate data[J]. Ecological Applications, 2005,15:954-969.

[20]
Xiao X M, Zhang Q Y, Saleska S, et al.Satellite-based modeling of gross primary production in a seasonally moist tropical evergreen forest[J]. Remote Sensing of Environment, 2005,94:105-122.

[21]
刘敏. 基于RS和GIS的陆地生态系统生产力估算及不确定性研究[D].南京: 南京师范大学硕士学位论文, 2008.

[22]
Potter C S, Randerson J T, Field C B, et al.Terrestrial ecosystem production —— a process model-based on global satellite and surface data[J]. Global Biogeochemical Cycles, 1993,7(4), 811-841.

[23]
Wang H S, Jia G S, Fu C B, et al.Deriving maximal light use efficiency from coordinated flux measurements and satellite data for regional gross primary production modeling[J]. Remote Sens. Environ, 2010,114(10):2248-2258.

[24]
Li Z Q, Yu G R, Xiao X M, et al.Modeling gross primary production of alpine ecosystems in the Tibetan Plateau using MODIS images and climate data[J]. Remote Sens. Environ, 2007,107(3):510-519.

[25]
张镱锂,李炳元,郑度,等.论青藏高原范围与面积[J].地理研究, 2002,21(1):1-8.

[26]
Hutchinson M F. ANUSPLIN Version 4.2 User Guide[R]. Canberra: Centre for Resource and Environmental Studies, Australian National University, 2002.

[27]
于贵瑞,何洪林,刘新安,等.中国陆地生态信息空间化技术研究(Ⅰ)——气象/气候信息的空间化途径[J].自然资源学报,2004,19(4):537-544.

[28]
何洪林,于贵瑞,刘新安,等.陆地生态信息空间化技术研究(Ⅱ)——太阳辐射要素[J].自然资源学报,2004,19(5):679-687.

[29]
刘新安,于贵瑞,范辽生,等.陆地生态信息空间化技术研究(Ⅲ) ——温度、降水等气候要素[J].自然资源学报,2004,19(6):818-825.

[30]
曹晨. 基于MCMC方法的统计模型的参数估计[D].南京:南京航空航天大学,2007.

Options
文章导航

/

〈 〉