EN中文

地球信息科学学报 >

2015 , Vol. 17 >Issue 10: 1143 - 1151

DOI: https://doi.org/10.3724/SP.J.1047.2015.01143

一种面向海量浮动车数据的地图匹配方法

  • 王晓蒙 , 1, 2 ,
  • 池天河 , 2*, * ,
  • 林晖 1, 2 ,
  • 邵静 1, 2 ,
  • 姚晓婧 1, 2 ,
  • 杨丽娜 2
展开
  • 1. 中国科学院大学,北京 100049
  • 2. 中国科学院遥感与数字地球研究所,北京 100101
*通讯作者：池天河(1961-),男,研究员,研究方向为遥感空间信息系统、智慧城市。E-mail:

作者简介：王晓蒙(1986-),男,博士生,研究方向为地图学与地理信息系统、智慧城市。E-mail:

收稿日期: 2015-04-15

  要求修回日期: 2015-05-15

  网络出版日期: 2015-10-10

基金资助

国家科技支撑计划项目(2015BAJ02B00);国家科技部政策引导类项目(2011FU125Z24)

收起

A Research of Map-Matching Method for Massive Floating Car Data

  • WANG Xiaomeng , 1, 2 ,
  • CHI Tianhe , 2, * ,
  • LIN Hui 1, 2 ,
  • SHAO Jing 1, 2 ,
  • YAO Xiaojing 1, 2 ,
  • YANG Lina 2
Expand
  • 1. University of Chinese Academy of Sciences, Beijing 100049, China
  • 2. Institute of Remote Sensing and Digital Earth, CAS, Beijing 100101, China
*Corresponding author: CHI Tianhe, E-mail:

Received date: 2015-04-15

  Request revised date: 2015-05-15

  Online published: 2015-10-10

Copyright

《地球信息科学学报》编辑部 所有
Fold

摘要

浮动车数据已广泛应用于交通监管、智能出行、城市规划等领域,地图匹配是浮动车数据关键技术之一,保障匹配算法精度的同时提高匹配效率,是面向海量浮动车数据地图匹配方法的难点。本文提出一种基于HMM（Hidden Markov Model）的地图匹配模型,相对传统模型尝试了多个方面的改进：在发射概率计算中引入航向角变量,并探讨了该变量对模型精度的影响;以格网对路网进行划分,构建哈希索引,实现候选路段快速查找;采用路径无权距离替代路径实际距离,并对路网进行预处理,根据浮动车有限时间内的活动范围构建路段转移矩阵,实现路段转移概率快速计算,以减小路径匹配算法时间复杂度。将模型应用于北京出租车轨迹数据匹配结果表明,对于采样时间间隔在1~120 s的浮动车数据模型切实可行。在满足匹配精度应用需求的前提下,模型效率有了较大幅度提升,能有效应用于海量浮动车数据地图匹配。

关键词： 浮动车; 地图匹配; 隐马尔可夫模型; 网格; 路段转移矩阵

本文引用格式

王晓蒙 , 池天河 , 林晖 , 邵静 , 姚晓婧 , 杨丽娜 . 一种面向海量浮动车数据的地图匹配方法[J]. 地球信息科学学报, 2015 , 17(10) : 1143 -1151 . DOI: 10.3724/SP.J.1047.2015.01143

Abstract

Floating Car Data (FCD) has been widely applied into traffic supervision, smart travelling, urban planning and so forth. Map-matching is one of the key technologies of FCD, for current map-matching algorithms, it is difficult to improve their map-matching efficiency considerably with a guaranteed accuracy. To solve this problem, our research proposes a map-matching model based on Hidden Markov Model (HMM), and makes a variety of improvements compared with the traditional model: (1) in addition to the position information, it introduces the heading angle variable to emission probability calculation, and discusses its influences on model accuracy and how to set a reasonable weight; (2) it divides road network according to a square grid, constructs candidate road segments searching algorithm based on hash index, and then discusses the optimization approach of the candidate road segment collection; (3) the numbers of segments in the path is used as the measurement for transition probability computation instead of the practical length, which simplifies the calculation procedure; (4) by preprocessing the road net, it constructs a road segment transition matrix according to the characteristic that floating cars have a limited scope of space activities in a given time, which realizes the fast calculation of road segment transition probability and reduces the time complexity of road matching calculation to a significant extent. We have applied this map-matching model in analyzing Beijing taxis’ trajectory data, in which the sampling time interval varies from 1 s to 120 s. The result demonstrates that this model is practicable, the required road segment transition matrix can be constructed in affordable space cost, and its efficiency is improved significantly with the condition that the accuracy meets the application requirements, which makes the model more applicable for massive FCD map-matching. As a conclusion, the proposed model has a high application value for multiple cases.

Key words： FCD; map matching; HMM; grid; road segment transition matrix

1 引言

交通信息采集是智能交通系统的基础,传统的信息采集技术包括感应线圈、摄像头、地磁等,随着移动传感器技术的发展,浮动车（Floating Car Data,FCD）技术逐渐成为国内外研究的热点。浮动车数据具备实时性强、采集成本低、覆盖范围广等优点,主要基于大规模实时运行的交通工具（如公交车、出租车等）,通过GPS、加速度器、陀螺仪等车载传感器收集交通信息。目前,浮动车技术已应用于多个领域,包括交通监管[1]、路径推荐[2]、行程时间估计与预测[3]、城市规划[4]等。
由于数据采集、地图数据处理等过程存在误差,浮动车数据应用前需进行地图匹配（Map-Matching,MM）,将轨迹数据匹配到路网上。目前,地图匹配主要应用几何分析、拓扑分析、概率理论、模糊逻辑、卡尔曼滤波等[5]方法。传统的几何分析方法（如“点-线”邻近分析）实现简单、效率高,但面对复杂路网时,无法保障匹配精度及匹配路段的连续 性[6]。为提高匹配精度,Pyo等[7]提出了基于多假设跟踪技术（Multiple Hypothesis Technique,MHT）和贝叶斯定理的最优路径匹配算法,然而,由于匹配过程中候选路径数量以几何倍数增长,算法效率较低。此后,学者主要从候选路段筛选和路径匹配2个关键步骤,对地图匹配算法进行改进提升匹配效率。为提高候选路段查找效率,Raymond[8]以道路交点替代候选路段,将点与线的邻域分析转换为点与点,降低了几何分析复杂度,缺点是道路交点难以反映浮动车的真实位置;章威和李宇光分别基于格网划分[9]和路网栅格化技术[10]构建索引,通过折半算法实现了候选路段快速查找,时间复杂度为 O lnm ,m为索引规模。为提高路径匹配算法效率,一方面需控制匹配过程中候选路径数量的增长速度,另一方面需提高路径分析效率。基于隐马尔可夫模型（Hidden Markov Model, HMM）的地图匹配算法[11-13],根据马尔可夫链特性有效控制了候选路径数量。此外,还有学者通过最大路径距离[9,12]、误差椭圆[14]、多准则动态编程[15]等方法,动态地排除路径匹配中不合理的路径或对轨迹进行分段增量处理[16-18],从而达到控制候选路径规模的目的,然而路径匹配过程中难以避免大量的路径分析,为提高最短路径分析效率,Gutierrez构建了以交通规则约束的Dijkstra算法[19],也有学者建议采用A*算法进行最短路径分析[11,13],但仍难以满足大规模数据轨迹数据匹配的需求。
Fig. 1 HMM-MM process

图1 基于HMM的地图匹配过程

综上所述,兼顾精度和效率仍然是地图匹配算法的难点,是面向海量浮动车数据应用亟待解决的关键问题。本文提出一种基于HMM的地图匹配模型,相对之前的匹配模型尝试了4个方面的改进策略,在发射概率的计算中增加航向角变量,并探讨航向角对模型精度的影响;在状态转移概率的计算中采用路径无权距离替代实际距离,简化路段转移概率计算过程;候选路段筛选过程中,构建基于格网划分和哈希索引的路段快速查找算法,以进一步减小算法时间复杂度;路径匹配过程中,根据浮动车数据特点对路网进行预处理,构建路段转移矩阵,并以哈希索引实现最短路径快速分析,将单次分析的时间复杂度减小为 O 1 ,大幅降低路径匹配过程中递推计算所消耗的时间,以突破HMM在面向海量浮动车数据地图匹配应用中的瓶颈。

2 地图匹配模型

2.1 基于HMM的地图匹配

浮动车轨迹 T t n | n = 1,2 … , N ,是由 N 条浮动车状态记录组成的序列,每条记录 t n 包含了车辆的位置、速度、航向角及时间戳等信息。轨迹数据地图匹配是从路网 G 找到与每个轨迹记录对应的路段,使路段相连而成的路径更符合真实轨迹。匹配过程中,不仅要考虑浮动车位置与路段距离、航向夹角等因素,还需考虑匹配路段之间的连接关系。基于HMM的地图匹配（HMM-MM）能综合考虑以上因素,使匹配结果具有较高的精度。
在HMM-MM过程中,浮动车轨迹点所在路段为隐性状态（Hidden State）,记为 s ,一般根据轨迹点观测值确定一个候选路段集合 S n ;浮动车观测值 t n 主要考虑航向角和位置;发射概率（Emission Probability）代表特定隐性状态下,得到某观测值的概率,记为 Pr t n | s ;状态转移概率（Transition Probability）是隐性状态 s n 转移到下一个隐性状态 s n + 1 的概率,本文称路段转移概率,记为 Pr s n , s n + 1 。HMM-MM主要思路是确定轨迹 T 对应的最大似然路径 Pa th s n ∈ S n | n = 1,2 … , N ,使得该路径在马尔可夫链中的联合概率最大,联合概率通过递推公式求解（式（1））。
J n = Pr t n | s max s n - 1 ∈ S n - 1 Pr s n - 1 , s n J n - 1 （1）
式中, J n 为前n个路段的联合概率, J 1 = Pr t 1 | s 。最后一个路段为候选路段中使得联合概率最大的路段,即 s N = argma x s N ∈ S N J N 。通过向前递推求得sN-1,…,s1,得到最大似然路径,如图1所示。
HMM-MM分为候选路段筛选和路径匹配2个关键步骤,候选路段筛选包括邻近路段查找、初次筛选、发射概率计算和候选集优化等内容,得到候选路段集合后根据路径匹配算法递推得到最优路径,期间路段转移概率通过预先处理的路段转移矩阵得到,模型工作流程如图2所示。
Fig. 2 Map-matching model based on HMM

图2 基于HMM的地图匹配模型

2.2 候选路段筛选

候选路段筛选的目的是查找轨迹点 t n 附近具备一定匹配条件的路段集合,本文主要根据浮动车航向角与道路方向的夹角 α （图3(a)）和浮动车到路段的最短距离 d （图3(b)）来判断路段,是否符合候选路段匹配条件。路段在计算机中表现为多段线,在折点处将其分割为多个子路段（Sub-Segment）,有利于简化计算,并提高求解夹角 α 、距离 d 的精度（图3(c)）,因此,在邻近路段查找、初次筛选、发射概率计算等步骤中都以子路段为基础。最后,在候选集优化步骤中将子路段转换为路段,并删除冗余路段,以降低路径匹配算法的时间复杂度。
Fig. 3 Road segment selecting by included angles and distances

图3 轨迹点与路段的方向夹角和距离

本文以格网划分和哈希索引的方式,实现邻近路段快速查找,将目标区域划分为 N × N 个正方形网格,并从西南到东北方向对网格顺序编码,将格网与路网叠加分析得到网格与子路段之间的相交关系,并构建哈希索引。通过轨迹点位置坐标计算网格编码,进而根据对应的哈希值获取与网格相交的子路段集合,坐标转换为网格编码的计算公式如式（2）所示。
f grid x , y = Int y - Y min L cell × N ew + Int x - X min L cell + 1 （2）
式中, Int 为取整运算;( x , y )为当前位置的坐标; X min 和 Y min 为格网西南边界坐标值; N ew 为网格东西方向的单元格数量。 L cell 为单元格边长,根据GPS位置最大偏移误差设置,为提高计算效率,格网边界坐标取整数,将 L cell 设置为 2 m 形式,使网格数量为 2 n × 2 n ,这样可将乘除法转换为位运算。
通过网格查找到轨迹点对应的子路段集合后,根据最大航向夹角 α max 和最大偏移误差 d max 进行初次筛选,排除方向不一致或距离较远的子路段。如图4中,轨迹点 t 1 根据网格g4查找到5条子路段,根据初次筛选规则可排除2条方向不一致或距离较远的子路段。
发射概率 Pr t n | s 为条件概率,为方便计算,将观测状态中的位置和航向角转换为与路段 s 的距离 d 和夹角 α ,则发射概率可表示为式（3）。
Fig. 4 Candidate road segments searching by grids

图4 基于网格的邻近子路段查找

Pr t n | s = Pr d n , α n | s = w d f d d n s + w α f α α n s （3）
式中, d n s 为第n个轨迹点到子路段的最短距离; α n s 为第n个轨迹点航向角与子路段的方向夹角; w d 、 w α 分别为距离和夹角权重,且 w d + w α = 1 ; f d 和 f α 分别为距离和夹角概率分布函数。
发射概率 Pr t n | s 的值域为 0 , 1 ,当距离和夹角为0时达到最大值1,距离和夹角越大则越接近0,一般情况下GPS位置偏移符合正态分布,通过对实际数据分析,夹角更符合指数分布,结合式（3）得到发射概率公式（式（4））。
Pr t n | s = w d 1 2 π σ exp - d n s 2 2 σ 2 + w α λ e - λ α n s （4）
式中, σ 为距离概率分布参数; λ 为夹角指数分布参数。当浮动车停止无法从记录中获取准确的航向角信息时,可根据 t 与 t - 1 时刻的坐标计算浮动车轨迹方向,或将距离权重 w d 设置为1,确保观测值相对准确。另外,当浮动车位置坐标位于网格边缘时,可能遗漏部分候选子路段,例如,图4中的 t 2 位于网格g2中,而与其较匹配的2个子路段位于相邻网格g3和g5中。本文通过设置发射概率阀值 p min ,用于判断是否有必要搜索相邻网格,将轨迹点 t n 对应的候选子路段集合表示为式（5）。
CS S n = s , p | p = Pr t n | s , s ∈ S S n , 且满足 d max 和 α max 约束条件 (5)
式中, S S n 为轨迹点 t n 所在网格对应的候选子路段集合。当 CS S n 中发射概率都小于 p min ,则有必要在相邻网格查找候选子路段。将网格等分为4个子网格,相邻网格为目标点所在子网格紧邻的3个网格,如图4中 t n 对应的相邻网格为 g 3 、 g 5 和 g 6 ,将相邻网格对应的子路段集合记为 N S n ,则此时候选子路段集合为：
CS S n = s , p | p = Pr t n | s , s ∈ S S n ⋃ N S n , 且满足 d max 和 α max 约束条件 (6)
根据“子路段-路段”映射关系将候选子路段集合 CS S n 转换为候选路段集合 CR S n ,并对候选路段集合进行优化,删除 CR S n 中的重复路段和冗余路段。重复路段是由路段分割造成,重复路段中只需选取发射概率最大的项,冗余路段是在候选路段集合中发射概率较低,且删除后不影响候选路段集合和上下文之间的拓扑关系的路段。
针对候选路段集合中的路段 s ,假设 s 的邻接路段集合与候选路段集合存在交集 NextS ,若 s 的发射概率大于 NextS 中所有路段的发射概率,则将 NextS 中的所有路段作为冗余路段删除;若 s 的发射概率小于 NextS 中任意路段的发射概率,则将 s 作为冗余路段删除（图5）。候选路段筛选的具体算法见算法1。

2.3 路段转移矩阵

根据递推式(1)求解最佳匹配路径时,需选取合适的变量计算相邻轨迹点候选路段之间的转移概率。在时间间隔较短时,浮动车更倾向于选择距离较短的路径,因此,一般将最短路径距离应用于计算路段转移概率[15,17,20]。由于路径匹配过程中需进行大量路段转移概率计算（图1）,最短路径算法（如Dijkstra）难以满足海量数据地图匹配的需求。本文根据浮动车在较短时间内活动范围具有一定局限性的特点,提出一种预处理的路段转移概率分析方法,预先对路网进行拓扑分析,计算全局范围内路段间最短距离,并生成路段转移矩阵（式（7））。
D = d 1 1 ⋯ d 1 n ⋮ d i j ⋮ d n 1 ⋯ d n n (7)
根据预先生成的路段转移矩阵,能直接计算出路段转移概率,而不需进行最短路径分析,极大程度降低了算法时间复杂度。实际路网中,路段间路段数量（即路径无权距离）与路径实际距离呈正相关,因此,将矩阵 D 中 d i j 设置为第 i 个路段到第 j 个路段的无权最短路径距离,以便简化计算。构建路段转移矩阵时,只需根据浮动车采样时间间隔内的活动范围计算有限个路段转移距离,浮动车活动范围由最大路段转移距离 S D max 表示, S D max 取值由采样时间间隔、浮动车速度和路段平均长度确定,例如,针对采样间隔为120 s的样本,假设浮动车平均速度峰值为45 m/s,路段平均长度为400 m,则 S D max 设置为13或14比较合理。通过对路网分析,筛选出符合约束条件的路段转移项,形成路段转移集合（式（8））。
SD = s i , s j , d i j , p i j | s i , s i ∈ S , 且 d i j ≤ S D max (8)
式中, s i 为起始路段; s j 为终止路段。集合范围受最大转移距离 S D max 约束; p i j 为路段转移概率。根据指数分布函数计算：
Pr s i , s j = β e - β d i j d i j ≤ S D max （9）
遍历路网 G 中的所有路段,从任意路段 s i 出发,采用广度优先算法搜索与 s i 连通的路段,遍历深度即为路段间的距离,当深度达到 S D max 时停止搜索,以此类推最终生成路段转移集合,具体算法见算法2。
虽然路段转移集合空间成本随着 S D max 呈倍数增长,但面对实际浮动车数据,通过设置合理的 S D max ,既能保证路段转移集合的完整性,又能将空间成本控制在合理的区间内。
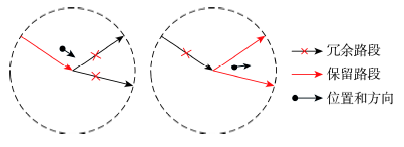
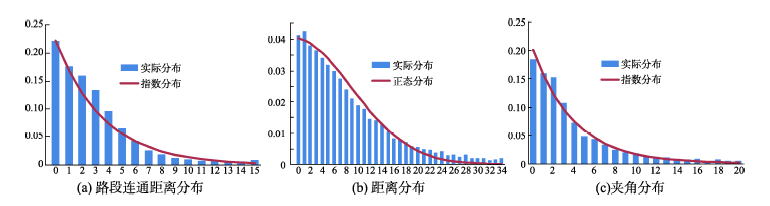
Fig. 5 Eliminate redundant segments

图5 删除冗余路段

2.4 路径匹配算法

根据式(1)递推求解最大似然路径,对于轨迹点 t i ,若当前已匹配的候选路径集合为 PList ,针对 t i 中任意候选路段 r ,查找 PList 中转移到 r 概率最大的路径,将 r 加入到该路径中,并计算联合概率,形成 t i 时的候选路径集合,以此类推直到求解出最终的候选路径集合,根据联合概率选出最大似然路径,对于第1个轨迹点,初始联合概率设置为候选路段对应的发射概率。具体算法见算法3。

3 模型应用

3.1 数据特征

本文研究范围为北京市六环以内区域,总面积约4295 km2,根据2012年北京路网数据,区域覆盖路段12.48万条,分割后产生子路段25.71万条,总里程约20 000 km。根据GPS定位误差和区域面积选择合适的格网范围和单元格大小（64 m×64 m）,将格网与路网叠加分析得到与路网相交网格28.85万个。对格网和路网相交结果统计分析,99%的网格包含子路段数量少于10个,其中,90%少于4个,50.23%的网格只包含1个子路段,由此估计,路段分割不会对模型效率产生较大影响。
浮动车数据为北京市2012年出租车轨迹数据,记录了1.26万辆出租车一个月内的运行状态,包括时间、位置、航向角、车速等信息,样本总量约8亿条。浮动车活动范围覆盖了大部分路网,采样时间间隔为1~120 s。

3.2 模型实现

模型包括静态数据和算法实现2部分。静态数据包括路网拓扑关系（邻接矩阵）;子路段、路段、网格三者间映射关系;路段转移集合。对格网和路网进行叠加分析,遍历路网、“路网-格网”叠加图层生成路网邻接矩阵、“网格-子路段”映射表、“子路段-路段”映射表。采用哈希表的方式存储各类映射关系,路网邻接矩阵以 rs , NS 的形式组织,路段 rs 为键值, NS 为其对应的邻接路段集合;“网格-子路段”映射表以 grid , SS 的形式组织,网格 grid 为键值, SS 为与其相交的子路段集合;“子路段-路段”以 ss , rs 的形式组织,子路段 ss 为键值, rs 为其所属的路段。对样本数据进行统计分析后确定最大转移距离 S D max 为15,遍历路网邻接矩阵,生成路段转移集合。路网邻接矩阵、“网格-子路段”映射表,以及“子路段-路段”映射表数据规模较小（表1）,能快速装载到内存中,而路段转移集合数据规模较大,对内存有较高的要求,装载也需要一定时间。由于哈希索引对内存要求较高,模型基于64位Java平台实现,由于开发平台间性能存在差异,算法性能分析中的时间只作为参考。
Tab. 1 Static data scale

表1 模型静态数据规模

名称 键值对组织方式 规模（万条） 占用空间（MB）
路网邻接矩阵 rs,NS 12.48 2.7
网格-子路段关系 grid,SS 28.84 5.8
子路段-路段关系 ss,rs 58.39 7.9
有限路段转移集合 si,sj,dij,pij 4000 847
距离参数 σ 根据标准差公式进行估计,夹角参数 λ 根据夹角期望的倒数进行估计, β 根据路径转移距离期望倒数进行估计。随机抽取一部分样本,人工匹配,估计参数初始值 σ * 、 λ * 和 β * 。对模型设置初始值,再随机抽取规模较大的样本,通过迭代分析对参数进行学习,直到参数收敛于较稳定的估计值,得到夹角参数估计 λ ^ 为0.25,距离参数估计 σ ^ 为9.46,以及路段连通距离参数估计 β ^ 为0.27。分布曲线与实际数据的拟合如图6所示。
Fig. 6 Floating car data distributions

图6 浮动车数据分布情况

3.3 精度与效率分析

本文中匹配精度为匹配正确的轨迹点个数与轨迹点总数的比值。为明确距离和夹角的权重关系,选择多组不同的权重策略进行发射概率计算,对匹配结果进行人工检验并进行对比分析得到权重与匹配精度的关系（图7）。
Fig. 7 Comparison of model accuracies under different weight strategies

图7 不同权重策略的模型精度比较

当距离权重大于0.2时,模型匹配精度大于90%,且距离权重越大匹配精度越高,在距离权重为0.9时达到最大匹配精度,这主要是由于夹角采用指数分布,概率随夹角下降的较快,使模型对夹角的变化过于敏感,细微的夹角差别也可能造成差异较大的结果（图8(a)）。但在一些特殊情况下,角度能作为关键的判断依据,如在点到2个路段的距离差别较小时,夹角较小的路段更加符合匹配原则（图8(b)）。综合考虑后,本文将距离权重 w d 设置为0.9,夹角 w α 权重设置为0.1。
Fig. 8 Comparison of matching results under different weight strategies

图8 不同权重策略匹配结果对比

除了模型参数,匹配精度还会受到路网拓扑错误的影响,如匹配结果中原始轨迹被“切断”613次,其中,83.6%是由路网拓扑问题所致。路网拓扑错误主要包括路段缺失和顶点缺失两类,路段缺失是2条路段间缺少使二者相连的中间路段（图9(a)）,顶点缺失是2条路段间无法转移到正确的邻接路段。缺少顶点相连,使二者处于“悬挂”状态（图9(b)）,2种拓扑错误均会导致路段针对1~120 s采样时间间隔的样本,超出路径转移分析范围的数据仅占样本总量的0.13%,多数由于采样时间间隔较大（超过120 s）,此类情况出现的概率极小,几乎不影响模型的总体精度,这进一步说明以路段转移矩阵实现路段转移快速分析的可行性和应用价值。将样本按采样时间间隔进行划分,分别进行匹配,并将本文模型与Newson[12]提出的模型进行对比,去除路网拓扑错误对精度的影响,总体上本文提出的模型精度较高,二者平均精度差为0.85%（图10）,这说明发射概率计算中增加了角度变量有利于提高模型精度,同时也说明采用路径无权距离替代路径实际距离切实可行。
Fig. 9 Road net topology errors

图9 路网拓扑错误

Fig. 10 Comparison of accuracies of map-matching

图10 地图匹配精度对比

在确保模型精度的同时,提升匹配效率是该模型是否能面向海量浮动车数据地图匹配应用的关键。传统模型中候选路段查找以邻域空间搜索为基础,路径匹配中的路段转移概率计算采用最短路径分析算法实现,而本文通过网格实现候选路段快速查找,根据预处理的路段转移矩阵直接计算路段转移概率。随机抽取2365条轨迹,共40 548个浮动车数据作为实验样本,进行地图匹配实验,结果表明,相比传统模型,本文所提出的模型效率明显较高（表2）。
Tab. 2 Computational performance of the model without I/O cost

表2 模型运行效率（除去I/O耗时）

算法类型 路段查找(s) 路径匹配(s) 总耗时(s) 平均(点/s)
传统模型 20.73 43.69 64.42 817.83
本文模型 5.89 0.63 6.52 6219.11

4 结论

浮动车数据已成为智能交通系统的重要数据来源,面对海量浮动车数据,地图匹配模型需在保障匹配精度的同时注重效率的提升,而传统模型难以兼顾匹配精度和效率。本文提出的基于HMM的地图匹配模型,在发射概率计算、路段转移概率计算、路段查找和路径分析等方面进行了改进。实验结果表明,增加航向角变量并设置合理的权重,能有效提高模型精度,相对路径有权距离,路径无权距离同样适用于计算路段转移概率,并能简化计算,基于格网划分的候选路段查找,以及基于路段转移距离预处理的路径分析方法极大程度降低了算法时间复杂度,使HMM-MM能更有效地应用于海量浮动车数据的地图匹配。在实际应用中,浮动车数据采样时间间隔大多数在1~120 s之间,因此,模型适用于大多数浮动车数据地图匹配 应用。后续研究中,需对浮动车活动的时空特征进行深入分析,对路段转移集合空间占用和覆盖率方面进一步优化,以适用于更多地图匹配应用场景。

The authors have declared that no competing interests exist.

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Yuan Y F, Van Lint H, Van Wageningen-Kessels F, et al. Network-wide traffic state estimation using loop detector and floating car data[J]. Journal of Intelligent Transportation Systems, 2014,18(1):41-50.

[2]
Yuan J, ZhengY, Xie X, et al. T-Drive: Enhancing driving directions with taxi drivers' intelligence[J]. IEEE Transactions on Knowledge and Data Engineering, 2013,26(1):220-232.

[3]
Mori U, Mendiburu A, Álvarez M, et al.A review of travel time estimation and forecasting for advanced traveller information systems[J]. Transportmetrica a-Transport Science, 2015,11(2):119-157.

[4]
Yuan N J, Zheng Y, Xie X, et al.Discovering urban functional zones using latent activity trajectories[J]. IEEE Transactions on Knowledge and Data Engineering, 2015,27(3):712-725.

[5]
Quddus M A, Ochieng W Y, Noland R B.Current map-matching algorithms for transport applications: State-of-the art and future research directions[J]. Transportation Research Part C:Emerging Technologies, 2007,15(5):312-328.

[6]
Marchal F, Hackney J, Axhausen K.Efficient map matching of large global positioning system data sets: Tests on speed-monitoring experiment in zürich[J]. Transportation Research Record: Journal of the Transportation Research Board, 2005,1935:93-100.

[7]
Pyo J S, Shin D H, Sung T K.Development of a map matching method using the multiple hypothesis technique[C]. Proceedings of IEEE Intelligent Transportation Systems, 2001:23-27.

[8]
Raymond R, Morimura T, Osogami T.Map matching with Hidden Markov Model on sampled road network[C]. Pattern Recognition (ICPR), IEEE, 2012:2242-2245.

[9]
章威,徐建闽,林绵峰.基于大规模浮动车数据的地图匹配算法[J].交通运输系统工程与信息,2007,7(2):39-45.

[10]
李宇光,李清泉.利用地图栅格化的海量浮动车数据道路匹配快速算法[J].武汉大学学报(信息科学版),2014,39(6):724-728,733.

[11]
Lou Y, Zhang C Y, Zheng Y, et al.Map-matching for low-sampling-rate GPS trajectories[C]. ACM SIGSPATIAL GIS, 2009:352-361.

[12]
Newson P, Krumm J.Hidden Markov map matching through noise and sparseness[C]. Workshop on Advances in Geographic Information Systems, 2009:336-343.

[13]
Goh C Y, Dauwels J, Mitrovic N, et al.Online map-matching based on Hidden Markov model for real-time traffic sensing applications[C]. 15th International IEEE Conference on Intelligent Transportation Systems (ITSC), 2012:776-781.

[14]
李清泉,黄练.基于GPS轨迹数据的地图匹配算法[J].测绘学报,2010,39(2):207-212.

[15]
Chen B Y, Yuan H, Li Q Q.Map-matching algorithm for large-scale low-frequency floating car data[J]. International Journal of Geographical Information Science, 2014,28(1):22-38.

[16]
Brakatsoulas S, Pfoser D, Salas R, et al.On map-matching vehicle tracking data[C]. In Proc. 31st VLDB Conference, 2005:853-864.

[17]
Wang W, Jin J, Ran B, et al.Large-scale freeway network traffic monitoring: A map-matching algorithm based on low-logging frequency GPS probe data[J]. Journal of Intelligent Transportation Systems, 2011,15(2):63-74.

[18]
He Z C, She X W, Zhuang L J, et al.On-line map-matching framework for floating car data with low sampling rate in urban road networks[J]. IET Intelligent Transport Systems, 2013,7(4):404-414.

[19]
Gutierrez E, Medaglia A L.Labeling algorithm for the shortest path problem with turn prohibitions with application to large-scale road networks[J]. Annals of Operations Research, 2008,157(1):169-182.

[20]
Miwa T, Kiuchi D, Yamamoto T, et al.Development of map matching algorithm for low frequency probe data[J]. Transportation Research Part C: Emerging Technologies, 2012,22:132-145.

Options
文章导航

/

〈 〉