EN中文

地球信息科学学报 >

2020 , Vol. 22 >Issue 1: 30 - 40

DOI: https://doi.org/10.12082/dqxxkx.2020.190736

专辑：地理智能

地理流的空间模式：概念与分类

  • 裴韬 , 1, 2, 3, * ,
  • 舒华 1, 2 ,
  • 郭思慧 1, 2 ,
  • 宋辞 1 ,
  • 陈洁 1 ,
  • 刘亚溪 1, 2 ,
  • 王席 1, 2
展开
  • 1. 中国科学院地理科学与资源研究所 资源与环境信息系统国家重点实验室,北京 100101
  • 2. 中国科学院大学,北京 100049
  • 3. 江苏省地理信息资源开发与利用协同创新中心,南京 210023

裴 韬（1972— ）,男,江苏扬州人,研究员,研究方向为地理大数据挖掘。

收稿日期: 2019-12-01

  要求修回日期: 2019-12-31

  网络出版日期: 2020-04-08

基金资助

国家自然科学基金项目(41525004)

国家自然科学基金项目(41421001)

版权

版权所有，未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
收起

The Concept and Classification of Spatial Patterns of Geographical Flow

  • PEI Tao , 1, 2, 3, * ,
  • SHU Hua 1, 2 ,
  • GUO Sihui 1, 2 ,
  • SONG Ci 1 ,
  • CHEN Jie 1 ,
  • LIU Yaxi 1, 2 ,
  • WANG Xi 1, 2
Expand
  • 1. State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
  • 2. University of Chinese Academy of Sciences, Beijing 100049, China
  • 3. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
* PEI Tao, E-mail:

Received date: 2019-12-01

  Request revised date: 2019-12-31

  Online published: 2020-04-08

Supported by

National Natural Science Foundation of China(41525004)

National Natural Science Foundation of China(41421001)

Copyright

Copyright reserved © 2020
Fold

摘要

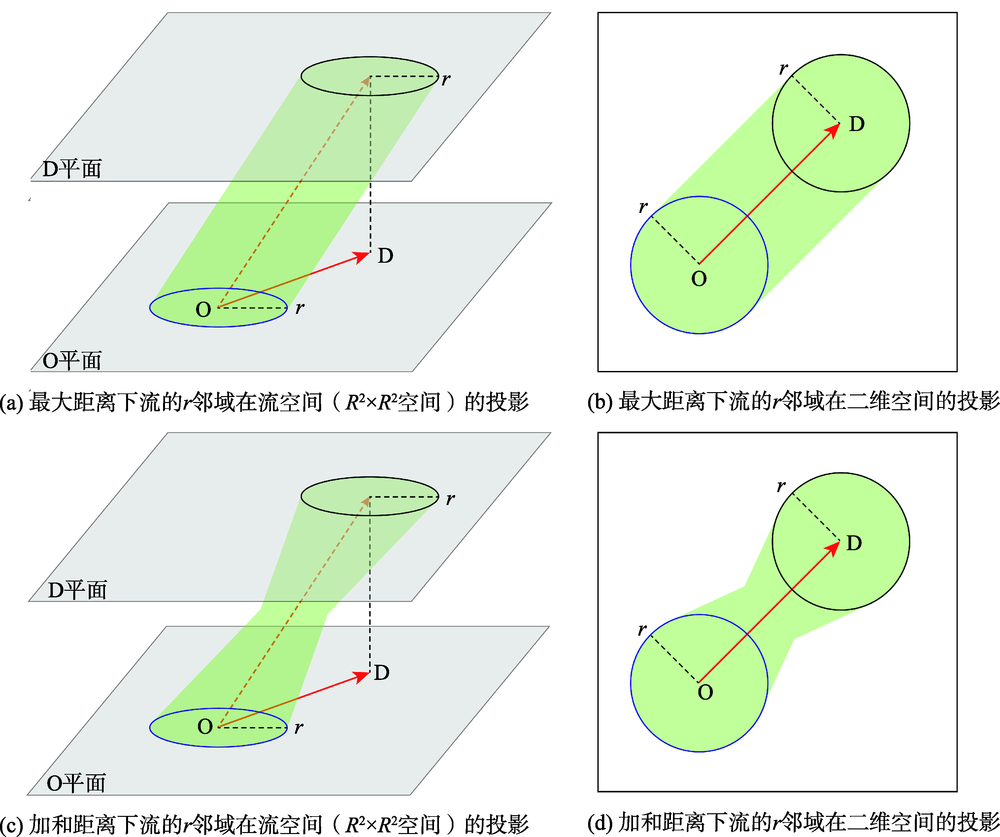
地理流被定义为地理对象在不同空间位置间的流动,而地理流通常涵盖了物质、信息、资金、能量等的空间转移。位置之间各种流的出现与强化,改变了以距离衰减效应为基本规律的传统认知。因此,针对地理流的研究将有助于从新的角度理解地理格局及其形成机理。本文认为可采用2种模型对地理流进行表达：① 将地理流抽象为包含起点和终点坐标的四元组（又称地理流正交模型）;② 将其抽象为包含起点坐标、流长度与流方向的模型（又称地理流极坐标模型）。在地理流表达模型的基础上,流空间可以定义为由两个二维空间通过笛卡尔积形成的四维空间。本文给出了流空间中4种距离（最大距离、加和距离、平均距离和加权距离）、不同距离下地理流的r邻域体积以及地理流密度等测度的定义。根据地理流极坐标模型中不同要素随机性的组合方式,将地理流模式分为随机、丛集、聚散、社区、并行与等长6种常见的单一模式,并梳理了不同模式的识别方法。单一模式之间的组合可以形成混合模式,而多类流数据之间可以形成多元流模式。在未来的研究中,地理流的基础统计理论、地理流模式的挖掘方法以及在实际问题中的应用将是其重要的发展方向。

关键词： 流聚类; 流随机性; 流异质性; 流丛集模式; 流聚散模式; 流社区模式; 流等长模式; 流并行模式

本文引用格式

裴韬 , 舒华 , 郭思慧 , 宋辞 , 陈洁 , 刘亚溪 , 王席 . 地理流的空间模式：概念与分类[J]. 地球信息科学学报, 2020 , 22(1) : 30 -40 . DOI: 10.12082/dqxxkx.2020.190736

Abstract

Geographical flow can be defined as the movements of geographical objects between different locations, which are usually displayed as the movement of matter, information, energy and funds, e.g. the jobs-housing flow in a city, communications between different mobile phone holders and the fund transferred between different business entities. Due to the existence of the various flows, the link strength between different locations may not depend on distance only, say one may strongly related to a store faraway through express delivery rather than a store nearby. The traditional knowledge of distance-decay law may be changed. As a result, research on the geographical flow may help to understand geographical patterns and their mechanism from a new point of view. Two conceptual models are introduced for the expression of geographical flows in this paper. In the first model, a flow is abstracted as a coordinate quaternion composed of the origin point and the destination point (called the orthonormal flow model). Thus, the flow space can be defined as a 4-D space which is formed by the Cartesian product of two 2-D spaces. In the second model, a flow is composed of the origin point coordinates, the flow length and the flow angle (called the polar coordinate model). Based on the expression models, four distances are defined, specifically, maximum distance, additive distance, average distance and weighted distance. In addition, this paper defines some other flow measurements, including flow direction, the volume of a flow's r -neighborhood and the flow density. According to the combination of different statistical features (i.e. heterogeneity, homogeneity and randomness) between variables in the polar coordinate model, the spatial patterns of geographical flows are divided into six single patterns including random, clustering, convergent and divergent, community, parallel (angle-clustered) and equilong (length-clustered). The methods for identifying different flow patterns are also analyzed and summarized. Besides the single patterns, the combination of different single patterns will generate mixed patterns, and if more than one type of flows coexists, multi-flow patterns can be produced. Regarding research directions of geographical flow in the future, three aspects should be given more attentions: the basic statistical theory of flow, the mining method of flow pattern and its application in practical problems.

Key words： flow clustering; flow randomness; flow heterogeneity; flow clustering pattern; flow convergent and divergent pattern; flow community pattern; flow equilong pattern; flow parallel pattern

1 引言

对于一个系统,不同部分之间、要素之间,以及系统与外部环境之间都存在着物质、信息、能量等的移动或交换,从而形成各种形式的流（flow）[1],如全球的人口流动、动物体内的血液流、金融机构中的资金流、网站之间的链接等等。如果流的两端连接的是不同的空间位置,则可称之为地理流。地理流被定义为地理对象在不同位置间的流动,如城市区域之间的职住流、手机用户之间通话的信息流以及不同位置商业实体之间的资金流等。网络时代的到来,位置之间各种流的出现与强化,改变了以距离衰减效应为基本规律的传统认知[2,3],并在人文领域中表现得更为突出[4]。距离不再是解释空间相关的唯一测度（例如,因为轨道交通,与某人住处关系更紧密的可能是远处的工作地,而非周围的场所;而互联网的出现,使得顾客与其他城市卖家的联系经由物流远远强于本地附近的商店）。空间的传统认知正在被改变,各种流的存在重新塑造着地理空间格局,并成为推动地理系统演化的关键因素[5,6,7,8,9]。因此,针对地理流的研究不仅有益于理解地理系统的格局与功能,而且有助于弄清地理系统演化的动力学机制,故而将成为地理格局与机理分析的新视角。
随着大数据时代传感器、网络和定位技术的发展,不同位置之间的多种流被记录下来形成了地理流大数据,而针对地理流大数据的研究的首要任务就是要揭示其中的模式。为了定量描述地理流,已有研究将其定义为包含起点和终点的概念模型[10]（后文将地理流简称为流）。目前针对流的模式分析主要集中在2个方面。① 关于流的总体性质的分析,主要包括流的相关性与异质性判别。流的相关性是指起点或者终点在空间上相近的现象,而异质性是指流的起点和终点的不均匀性。其中,用于衡量流的相关性指标包括流的Moran's I统计量[11];而异质性的指标则包括：流的K函数、局部K函数以及局部Getis-Ord Gi统计量等[12]。② 关于流模式的识别,已有进展主要集中在丛集模式的提取。丛集模式定义为流的起点和终点都丛聚的模式,相关研究可分为2类：① 将流看作为整体的对象,利用时空扫描方法、层次聚类方法和基于密度的聚类方法[13,14,15,16]提取丛聚模式;② 将流看作点对,通过起点和终点丛聚特征的组合定义不同模式的流丛聚,这类丛聚的识别和提取主要依赖于统计判别方法[17]。
已有研究多从空间统计的角度对流的模式展开讨论,但仍然局限于以位置为基础、欧氏距离为测度的位空间中（即位置空间,位空间的基础单元是点。具体讲,二维位置空间中的基础单元就是二维点）,其研究的劣势主要体现在：首先,流在研究中仍然被当作是欧氏空间的点对,因而在计算中难以形成统一的计算体系;其次,针对流的模式仅有异质性与随机性的讨论,而由于流的多维属性、时空耦合等特征,其模式种类较点更为复杂,应该进行详细的分类,形成系统的研究体系。为了克服上述不足,本文突破传统的理论框架,试图构建新的流空间概念与分析框架,并对流模式分类进行较为系统的探讨。流的定义与分析不仅将成为地理信息科学新的分支,同时还可为交通、规划、公共设施服务等问题的解决提供理论工具。

2 流空间定义及其测度

在本文的定义中,流不仅包含起点和终点的位置信息,还包含它们各自的属性信息,且因起、终点之间隐含各种联系,需要耦合在一起考虑。例如,描述一次出行的流不仅包括起点和终点的时空位置信息,还应附带起、终点的土地利用信息;而AB两地之间的交通流量大是指拥有相同起、终点（即AB两点）的交通流形成聚集,而并非只是起点聚集或终点聚集或二者之和,故必须将流作为整体对象进行研究。现有的空间统计模型大多基于欧氏空间及其概念,难以直接用于流数据的分析与计算。在下文中,首先给出流空间的定义,再对流模式的概念进行阐述,并对其进行分类与描述。

2.1 流及流空间的定义

流可以用由起点（O）、终点（D）以及流的属性组成的有序点对多元组表达。令O点时空坐标为 ( x O , y O , z O , t O ) ,D点时空坐标为 ( x D , y D , z D , t D ) ,则流 F 可表示为： ( ( x O , y O , z O , t O ) , ( x D , y D , z D , t D ) , s ) ,其中, x O , y O 为O点的二维平面坐标, z O 为高程, t O 为流从起点开始的时刻,D点的变量类似,不再赘述;s为流的属性,可以是流的类别、状态、形态等特征,或为地理对象之间的物质、信息和能量流的量等。而如果仅考虑O点和D点的二维空间信息,则流F可表示为： ( ( x O , y O ) , ( x D , y D ) ) ,在此情况下,流可看作为一个四维对象,而以流作为基本元素构成的空间则称为流空间。流空间是一个四维空间,在其中,一条流可以视为流事件,流的O点和D点有明确的地理含义,即流事件发生的起点和终点,因而不能简单把流空间看成四维欧氏空间。为了方便对流空间的四维特征进行刻画,同时又不割裂流的地理内涵,可用2个二维平面的笛卡尔积（R2×R2）的形式定义流空间[16]。这2个平面称为O平面和D平面,其中O平面为O点所在的二维平面,D平面为D点所在的二维平面。需要注意的是,这里只是为了数学表达的需要,从逻辑上将O平面和D平面作为2个独立的平面区别对待,但在物理空间中,它们实际上处在同一个二维平面,O点和D点所在的范围可以是2个相邻、相交或相离的区域,甚至是同一个区域（图1）。
图1 流空间中流及其邻域

Fig. 1 Flow and its neighborhood in flow space

需要说明的是,根据流产生的空间范围的不同,又可将流分为自由流和受限流。如以四维流空间为例,自由流是指流的起点和终点的范围分别为二维区域,如台风的起点和终点可以分布在相关海域的任意位置;而受限流的起点和终点只能分布在二维区域的子空间上,如城市中出租车的起点和终点只可能分布在城市的道路上。
除了采用O、D点对表示流的方式之外,只考虑空间属性的流还可以通过点、角度、长度的三元组进行表达,即 ( ( x O , y O ) , θ , l ) ,其中, ( x O , y O ) 为起点O的坐标, θ 为流的方向（以正东为0度）,l为流的长度。或者采用 ( ( x D , y D ) , θ , l ) 的方式表达,其中, ( x D , y D ) 为终点的坐标。上述表达方式也都将流视为四维对象。本文将第1种表达方式称为正交模型,而第2种称为极坐标模型。

2.2 流的距离

为了度量流和流之间的邻近程度,需要定义流之间的距离。本文给出流的4种距离：最大距离、加和距离、平均距离和加权距离（图2）。
图2 流之间的距离

注：最大距离： d ij max = max ( d ij O , d ij ( D ) ) ;加和距离： d ij add = d ij O + d ij ( D ) ）;平均距离： d ij aver = ( d ij O + d ij D ) 2 ）;加权距离： d ij ( weuc ) = α ( d ij ( O ) ) 2 + β ( d ij ( D ) ) 2 。

Fig. 2 Distance between flows

2.2.1 最大距离
2条流Fi和Fj之间的最大距离为2条流O点之间欧氏距离和D点之间欧氏距离的较大者：
d ij max = max ( d ij O , d ij ( D ) )
其中, d ij ( O ) 为2条流Fi和Fj的O点之间的欧氏距离：
d ij ( O ) = ( x i O - x j O ) 2 + ( y i O - y j O ) 2
而 d ij ( D ) 为Fi和Fj的D点之间的距离：
d ij ( D ) = ( x i D - x j D ) 2 + ( y i D - y j D ) 2
2.2.2 加和距离
流Fi和Fj之间的加和距离为2条流O点之间欧氏距离和D点之间欧氏距离之和：
d ij add = d ij O + d ij ( D )
2.2.3 平均距离
2条流Fi和Fj之间的平均距离为2条流O点之间欧氏距离和D点之间欧氏距离的平均值：
d ij aver = ( d ij O + d ij D ) 2
2.2.4 加权距离
2条流Fi和Fj之间的加权距离定义为：
d ij ( weuc ) = α ( d ij ( O ) ) 2 + β ( d ij ( D ) ) 2
式中：α和β为权重参数, α + β = 2 。α和β的引入是为了区分流O点和D点对流之间距离的影响[18]。当 α = β = 1 时,此距离等同于四维欧氏空间的距离。如果将流的长度的影响也考虑在内,则加权距离则可以表达为以下的形式：
d ij ( dissim ) = α ( d ij ( O ) ) 2 + β ( d ij ( D ) ) 2 L i L j
式中：Li和Lj分别为流Fi和Fj的长度[18-19] 。虽然式（6）和（7）中的2种距离在进行流模式提取时具有较好的灵活性,但由于偏离了所能感知的地理空间中距离的物理内涵,因而在相关统计分布的推导方面存在困难。

2.3 流的方向

流的方向定义为起点到终点的有向连线的方向。令流Fi为 ( ( x i O , y i O ) , ( x i D , y i D ) ) ,如果以二维平面x轴正方向为参照,则流Fi的方向为：
θ i = ta n - 1 y i D - y i O x i D - x i O
而如果以另外一条流Fj为参照的话,则流Fi和Fj之间的夹角为：
θ ij = co s - 1 F i → ∙ F j → F i → ∙ F j →
式中： F i → = ( x i D - x i O , y i D - y i O ) , F j → = ( x j D - x j O , y j D - y j O ) 为流Fi和Fj对应的向量。
在城市研究中,流的方向特征可以揭示城市的空间结构。例如,流向呈单个中心汇聚的模式通常表示城市具有单中心结构,而流向呈多个中心汇聚的模式往往指示了城市的多中心结构。

2.4 流邻域的体积

根据前述流空间的定义,如果O点的邻域面积为SO,D点的邻域面积为SD,则由这2个区域的笛卡尔积得到的流空间的体积为 V = ∬ Ω d S o d S D = S O S D 。流空间中某条流的邻域的体积是计算流空间密度及推导流空间统计量的重要指标。令流 F c = ( ( x c O , y c O ) , ( x c D , y c D ) ) 为流空间中的一条流,定义流空间中距离流Fc小于等于r的区域为流的r邻域,则流的r邻域可看作集合 Ω = { F | dis t ( F , F c ) ≤ r } 所占空间（图1）,其中,F为流空间中的任意一条流, dist ( F , F c ) 表示流F和流Fc之间的距离。不同流距离定义下流的r邻域的体积公式如下。
最大距离流r邻域体积：
V Ω = π 2 r 4
加和距离流r邻域体积：
V Ω = 1 6 π 2 r 4
平均距离流r邻域体积：
V Ω = 8 3 π 2 r 4
其中,最大距离和加和距离定义下的流的r邻域在 R 2 × R 2 的流空间以及二维空间中的投影如图1（a）和（c）所示。流邻域可用于确定某条流附近的流的数目,而流邻域体积可以用于估计该流附近流的密度。

2.5 流的密度

二维欧氏空间中,点的密度可定义为单位面积内点的数目。类似地,可定义流空间中流的密度,即单位流空间体积内流的数目。令流空间中某一区域A内部流的密度为 λ ,则 λ ˆ = n V A ,其中n为区域A内流的数目,VA为区域A的体积。然而,当流 的分布范围未知或者流的分布范围明显小于区域 A范围时,上述密度算法则会低估流的密度。此时可借鉴相同情况下点密度的计算方式[20],使用流的二阶特征估计流的密度,以最大距离为例,流的密度为：
λ ˆ = 1 π 2 E d i , 1 4 = n π 2 ∑ i = 1 n d i , 1 4
式中： d i , 1 表示流Fi的一阶邻近距离（即Fi与距其最近的一条流之间的距离）。流的密度可反映位置之间联系的强度。例如,城市中交通OD流的局部密度可以表示不同区域之间的联系强度,这种联系强度在不同区域之间的分布可以为交通规划提供参考。

3 地理流模式分类

空间点的分布模式主要可分为3种：丛集、随机和排斥。一个空间点集必定是上述3种模式的组合。如果采用起点、角度、长度的方式表达流,则其中3个因子也同理分别可以表现为以上3种模式,而3个因子的3个模式组合可以得到27种流模式。在这27种模式中,具有地理意义且较为常见的模式有以下6种：随机（起点随机、方向随机、长度随机）、丛集（起点丛集、方向丛集、长度丛集）、聚散（终点或起点丛集、方向随机或排斥、长度任意）、社区（起点丛集、方向任意、长度丛集）、并行（起点随机、角度丛集、长度任意）与等长模式（起点随机、角度随机、长度丛集）等（图3）。流的模式分类为流的空间分析提供了理论框架,在流模式挖掘时,可以这6种模式为目标进行模型的设计。
图3 流空间模式分类

Fig. 3 The classification of spatial patterns of geographical flows

3.1 随机模式及判别方法

在正交表达模型中,流的随机模式是指流的O点和D点呈随机分布,且OD点之间的连接随机（图3（a））;而在极坐标模型中,随机模式是指起点、角度以及长度都呈随机分布。流的随机模式表示流的产生不存在明显规律,自由流的随机模式可见海洋Argo浮标下沉和上浮的周期过程,而受限流随机模式以路网上的出租车行程等较为多见[16,19]。
目前针对流的随机性的判别方法包括K函数和矢量相关性等方法,其中,流的K函数定义为[18]：
K = λ - 1 ∑ i ∑ j σ ij h n
式中：h为距离,n表示流的数目;λ为研究区中流的密度;当流Fi和Fj之间的距离不超过h时, σ ij h = 1 ,而当流Fi和Fj之间的距离大于h时, σ ij t = 0 。
而流的相关性可由式（15）进行表述[11]：
I = n ∑ i ∑ j w ij ∑ i ∑ j w ij F → i - F → ¯ ∙ F → j - F → ¯ ∑ i F → i - F → ¯ ∙ F → i - F → ¯
式中：n为流的数目; F → i = x i D - x i O , y i D - y i O 为流Fi对应的向量; F → ̅ = x ̅ D - x ̅ O , y ̅ D - y ̅ ( O ) = ∑ x i D - x i ( O ) n , ∑ y i D - y i O n 为n个向量的平均; wij为矢量对象的空间权重矩阵。
实际上,针对时空点数据,许多指标可以用于判断其随机性,如规则单元统计、基于邻近距离的统计以及Ripley's K函数和L函数等[21]。这些指标经过改造可应用于流的随机性判别。当流不满足随机性时,则表现为异质性,而异质性的模式较多,具体描述见下文。

3.2 丛集模式及判别方法

流的丛集模式是流异质性模式中一种常见的情形,可定义为流在流空间上的聚集。如以流的极坐标模型为框架,流丛集模式表现为起点或终点的聚集,同时流的长度以及角度也聚集;如以正交表达模型为基础,丛集模式表现为O点和D点同时聚集（图3（b））。通过识别流的丛集模式可以发现地理对象共同的移动特征以及地理位置之间的密切交互关系,典型的例子包括：城市中不同功能区之间的通勤流[22]、城市之间的人口迁移[23]、城市之间的物资运输[24]以及贸易联系[25]等。
流的丛集模式可以通过流聚类方法发现。流聚类方法的思想是对传统点过程数据聚类方法的扩展。通过重定义流的距离、密度等指标,实现流的聚类。目前流的聚类方法大体可以分为以下 3种：流的层次聚类、流的密度聚类以及流的时空统计聚类方法[26]。流的层次聚类以流距离作为流的相似性度量实现自下而上的流对象逐级合并。这类方法主要用于流簇的识别、归并以及可视化[27,28,29]。流密度聚类方法的主要思路是从流要素集合中识别出具有相对高密度的子集,针对传统点集数据的密度聚类方法,如DBSCAN,OPTICS等,都可以扩展应用到流的聚类中[30]。流的时空统计聚类方法则通过空间关联指数（或其他时空统计量）识别具有局部最优值的流簇子集,该流簇子集被认为是具有统计显著性的丛集模式。这些统计量通常包括Moran's I[11],Getis-Ord G[12,31],Ripley's K-function[31,32]以及最大似然统计量[26]等。这类方法的特点在于将模式的显著性判别引入挖掘算法中,弥补了其他方法缺乏结果显著性检验的不足。

3.3 聚散模式及识别方法

聚散模式包括汇聚模式和发散模式。汇聚模式可定义为流的终点丛集而角度随机或排斥;而发散模式则相反,如图3（c）所示。在现实世界中,这种模式通常对应着人流、物流、信息流、资金流等向某一区域集中流入或者从某一区域溢出。挖掘这种模式有助于发现局部城市中心、交通异常区域、公共资源服务范围等模式,从而为城市规划、公共设施选址等应用提供支撑。
流聚散模式的挖掘方法主要可以分为2大类：① 将流聚合到一定节点单元（如栅格、小区）中,然后根据其流入、流出量进行判断;② 将流作为独立的个体,然后根据其O点和D点的分布特征判断其模式。对于前者而言,相关研究已较为成熟,例如Guo等[33]基于出租车轨迹数据,首先对OD点进行聚类识别出城市热点区域,然后计算各热点区域的净流入/出率,进而分析其客流汇聚和发散情况;Hong等[34]将城市出租车流和共享单车骑行流聚合到路网小区,构建时空交互网络,进而对城市交通的“黑洞”（汇聚）和“火山”（发散）进行实时监测和预警,为城市公共安全提供保障;高楹等[35]对北京市共享单车OD流形成的骑行网络进行分析,通过计算节点净流入/出量,提取强“源”（发散）和强“汇”（汇聚）点,并结合土地利用对共享单车空间调度进行优化。对于后者而言,Lu等[17]根据O点和D点的分布,分类讨论了O点和D点聚集与排斥情况。但总体上针对聚散模式挖掘方法的研究仍较为薄弱。

3.4 社区模式及识别方法

流的社区模式是指,流集中分布在不同的局部区域内,不同局部区域之间无交互或交互较少的规律性空间分布。社区流模式可以体现在不同的尺度上,在大尺度上,通常表现为人口的流动,其社区通常与行政边界吻合度较高[36];在小尺度上,城市内部出租车的OD分布也会表现出一定的社区特点,出租车司机的运营范围通常会与其住址密切相关[37]。
目前流社区模式的挖掘主要采用复杂网络的分析方法：即先将流的位置点（O点和D点）按照一定的空间单元（如行政区划,格网等）进行聚合形成节点,节点之间个体流的叠加形成空间网络的边,在空间网络的基础上采用各种社区划分方法进行模式的提取。根据空间因素在社区划分方法中体现方式的不同,可将其分为以下3类：
（1）不考虑空间位置的通用社区划分方法。此类方法仅考虑流位置间的交互关系,通常采用模块度[38]、边比率[39]、信息熵[40]等作为目标函数,使用不同的优化策略（如层次聚类[41],谱聚类[42]等）获得目标函数最优的节点分区,最终映射到地理空间上形成社区模式。相关的成果如Zhong等[43]使用公交刷卡数据构建了以公交站点为节点,交通流量为边权重的空间网络,通过基于信息熵的Infomap算法划分出城市中人群的活动范围,并发现其与行政边界存在一定差异。该类方法虽然能够识别出一些有趣的社区模式,但由于未考虑空间因素,时常会产出空间上不连续的社区。
（2）考虑空间位置的社区划分方法。此类方法在设计目标函数时融入了节点空间位置的影响,体现了地理学中普遍存在的相关性。如Chen[44]将节点之间空间距离的n次幂的倒数作为边的权重,修改了传统模块度的计算方法。改进后的算法用于中国国内航线网络,并识别出了航线集中分布的社区,与中国七大经济区域的划分大致吻合。
（3）顾及空间邻近性的社区划分方法。此类方法在目标函数的优化过程中增加了节点空间邻近性的限制,缩小了搜索空间,旨在挖掘既交互紧密又在地理空间上相互邻近的流社区。如Guo[45]采用空间受限的禁忌搜索策略,以模块度为优化目标,识别出了不同种群动物在空间中连续的活动范围,体现了不同种群动物的习性。

3.5 其他模式

除了上述较为明显的4种流模式之外,不同指标的组合还会形成若干模式：流起随机与长度任意,而角度丛集的并行模式（图3（e））;流起点与角度随机,而长度丛集的等长模式（图3（f））等。前者可见动物的迁徙流,同种动物的迁徙方向均一致;而后者则以城市内部共享单车流为典型实例,共享单车流的长度大多介于500~3000 m之间。目前针对并行模式与等长模式的挖掘方法还处于空白,未来将是流模式挖掘不可忽视的方向。上文已述及流模式有27种之多,但由于所剩的部分模式在现实世界中出现的概率较小,本文就不再赘述。

3.6 流的混合模式

前述均为流的单一模式,而单一模式相互组合还可以产生混合模式。具体地,丛集模式与聚散模式组合,形成丛集-聚集模式或者丛集—扩散模式（图4（a））。这种模式的典型例子是交通枢纽及不同枢纽之间的出租车OD流（丛集模式由交通枢纽之间的出租车OD流形成,而聚散模式又由交通枢纽与周边区域的客流形成）;社区模式与聚散模式可以形成社区—聚散模式（图4（b））,这种模式可以表现为学区内的学生产生的家庭—学校的上下学流;丛集模式也可以和社区模式结合,形成丛集-社区模式（图4（c））,该模式可以表现为城市功能区内部热点之间的出租车流。除此之外,流的混合模式还有很多,篇幅所限不再一一列举。对于混合模式的挖掘,可以采用针对不同单一模式的挖掘方法,然后再对挖掘的结果进行组合与分析。
图4 流的混合模式

Fig. 4 The mixed flow patterns

3.7 多元流模式

当不同类型的流共存时,就可能形成多元流模式。以数据中存在2种类型的流为例,它们之间的模式主要表现为3种：相关模式、排斥模式和独立模式。相关模式是指在一定空间邻域范围内2种流频繁成组出现的现象。进一步考虑流的O点或D点的邻近组合的不同,可判断流呈正相关还是负相关。其中,流的正相关是指成对出现的流的O点与O点邻近、D点与D点邻近（图5（a））;而流的负相关则相反（图5（b））。排斥模式是指一种流的局部范围内不存在或者较少存在另一种流的模式（图5（c））;而独立模式是指两种流之间的分布独立,即任意一种流在局部范围内的出现不以另一种流的出现为先决条件（图5（d））。
图5 多元流模式

注：不同颜色代表不同类型的流。

Fig. 5 Multi-flow patterns

针对流的相关模式的识别可以由点的相关方法扩展得到。点模式中不同类型点事件的成对邻近被称为点的共位置模式（co-location pattern）,即空间数据集中满足一定邻域关系、频繁出现的对象集合[46]。对于流的相关模式,Tao和Thill等[19]将点的cross-K函数进行扩展,提出流的cross K函数用于评估两类流事件的空间依赖性,并以纽约市不同出租车公司出租车OD流进行验证。而多元流的随机模式与排斥模式同样可以采用cross K函数进行判别。总体来看,有关多元流模式,尤其是相关模式的研究仍存在较大空间,例如,将流抽象为向量进行自相关性分析时,如何考虑空间异质性的影响;在对流的相关模式提取中如何进一步判断相关流丛聚的尺度等都是非常值得探讨的问题。

4 结论及展望

4.1 结论

地理流已经成为研究地理对象移动特征和位置之间交互作用的重要概念模型和分析工具。本文提出四元组正交模型以及极坐标模型对流进行表达,并在此基础上定义了流的最大、加和、平均和加权4种距离,推导出了流的邻域体积、流的密度等测度表达式。针对流可能出现的各种空间模式,本文根据流的极坐标模型中不同变量之间随机性、排斥性与异质性的组合将其进行系统划分,并给出了随机、丛集、聚散、社区、并行以及等长6种常见模式的表达形式与主要特征。相对于时空点集,由于流具有时空高维、特殊时空结构的特点,其模式远比点模式复杂,且类型更多,从而衍生出一系列多元模式和复合模式。也正基于此,流的模式挖掘也才具有较大的空间。

4.2 展望

目前,国内外关于流模式的研究已经逐渐成为地理信息科学的热点,也取得一定的进展。然而,流模式的理论方法及应用仍面临许多机遇与挑战,具体表现在以下3个方面。
（1）流的空间统计理论亟需完善
流空间的统计描述是研究流时空模式的核心。然而,关于流空间随机性的定量研究还不充分。一方面,流空间与位空间由于距离测度的不同、维数的增加以及空间拓扑性质的差异,流的随机分布模型难以直接套用点模式的理论;另一方面,流的异质性判别以及丛聚尺度等特征同样无法直接通过对点的相关理论进行推广得到。流的空间统计理论仍不成熟,许多基础问题仍未得到解决。
（2）流的模式挖掘方法尚处于初步阶段
现有的以空间分布为基础的流模式挖掘方法还主要集中于流的丛集和社区模式的提取,对于随机模式、聚散模式以及混合模式、多元模式关注较少。不仅如此,流中包含或暗含了长度、路径、方向、时间、速度等变量,甚至还可能带有地理对象间的物质、信息、能量流动等属性,这些属性与空间位置信息的结合将导致更多的模式;同时,空间信息与属性信息的耦合分析也有助于更深入理解流模式背后的地理内涵;如果考虑流的时间要素,将会产生更高维度的流的演化模式。另一个不容忽视的问题就是流的可视化。由于流空间的四维和时空耦合特征,目前针对流的可视化大多以二维欧氏空间为基础,当数据量较多时,流的密度、趋势、热点、边缘等特征难以展现,因此,针对大量流数据的可视化研究亟待突破。
（3）与流相关的应用研究有待加强
过去的应用研究对地理对象的空间分布与格局已足够重视,而反映位置之间交互的流尚未在应用中得到应有的关注,从流空间视角分析问题的研究尚待加强。例如,在城市功能的相关研究中,已有基于城市大数据的成果多以位置上的地理要素分布（如POI、手机通话量等）作为功能识别的依据,较少考虑位置间的交互,而实际上,城市功能与流密不可分,流同样是划分城市功能区的重要因素;在公共安全领域,流空间视角的引入有助于理解疾病传播流与人群移动流之间的耦合关系,为传染病的预防和控制提供支撑;在交通规划领域,流空间的视角可以更好地评价公共交通设施的效率。流空间的框架为考察空间交互关系提供了全新的视角,在更好地理解人的行为模式及其动力学机制的同时,可为城市交通、城乡规划、公共卫生、社会公平、公共安全等诸多领域提供理论支撑。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Batty M. The new science of cities[M]. Cambridge: MIT Press, 2013.

[2]
Castells M . The rise of the network society, the information age: Economy, society and culture[M]. Cambridge: Blackwell, 1996.

[3]
修春亮, 魏冶 . 流空间视角的城市与区域结构[M]. 北京: 科学出版社, 2015.

[ Xiu C L, Wei Y. City and regional structure from the view of “space of flows”[M]. Beijing: Science Press, 2015. ]

[4]
刘瑜 . 社会感知视角下的若干人文地理学基本问题再思考[J]. 地理学报, 2016,71(4):564-575.

[ Liu Y . Revisiting several basic geographical concepts: A social sensing perspective[J]. Acta Geographica Sinica, 2016,71(4):564-575. ]

[5]
周一星, 杨家文 . 九十年代我国区际货流联系的变动趋势[J]. 中国软科学, 2001(6):85-89.

[ Zhou Y X, Yang J W . The tendency of freight flow in the 1990's China[J]. China Soft Science, 2001(6):85-89. ]

[6]
金凤君 . 我国航空客流网络发展及其地域系统研究[J]. 地理研究, 2001,20(1):31-39.

[ Jin F J . A study on network of domestic air passenger flow in China[J]. Geographical Research, 2001,20(1):31-39. ]

[7]
修春亮, 孙平军, 王绮 . 沈阳市居住就业结构的地理空间和流空间分析[J]. 地理学报, 2013,68(8):1110-1118.

[ Xiu C L, Sun P J, Wang Q . Residence-employment structure analysis on spaces of geography and flows in Shenyang city[J]. Acta Geographica Sinica, 2013,68(8):1110-1118. ]

[8]
董超, 修春亮, 魏冶 . 基于通信流的吉林省流空间网络格局[J]. 地理学报, 2014,69(4):510-519.

[ Chao D, Chunliang X, Wei Y . Network structure of space of flows' in Jilin Province based on telecommunication flows[J]. Acta Geographica Sinica, 2014,69(4):510-519. ]

[9]
高鑫, 修春亮, 魏冶 , 等. 基于高速公路货流数据的重庆市区县关联网络格局研究[J]. 人文地理, 2016,31(1):73-80.

[ Gao X, Xiu C L, Wei Y , et al. Study on the network of districts and counties in Chongqing based on the date of the highway cargo flows[J]. Human Geography, 2016,31(1):73-80. ]

[10]
Fotheringham A S . Spatial flows and spatial patterns[J]. Environment and planning A, 1984,16(4):529-543.

[11]
Liu Y, Tong D, Liu X . Measuring spatial autocorrelation of vectors[J]. Geographical Analysis, 2015,47(3):300-319.

[12]
Berglund S, Karlström A . Identifying local spatial association in flow data[J]. Journal of Geographical Systems, 1999,1(3):219-236.

[13]
Zhu X, Guo D . Mapping large spatial flow data with hierarchical clustering[J]. Transactions in GIS, 2014,18(3):421-435.

[14]
Tao R, Thill J C . A density-based spatial flow cluster detection method[C]// International Conference on GIScience Short Paper Proceedings, 2016.

[15]
Tao R, Thill J C, Depken II C , et al. flow HDBSCAN: A hierarchical and density-based spatial flow clustering method[C]// Proceedings of the 3rd ACM SIGSPATIAL workshop on smart cities and urban analytics, ACM , 2017: 11.

[16]
Gao Y, Li T, Wang S , et al. A multidimensional spatial scan statistics approach to movement pattern comparison[J]. International Journal of Geographical Information Science, 2018,32(7):1304-1325.

[17]
Lu Y, Thill J C . Assessing the cluster correspondence between paired point locations[J]. Geographical Analysis, 2003,35(4):290-309.

[18]
Tao R, Thill J C . Spatial cluster detection in spatial flow data[J]. Geographical Analysis, 2016,48(4):355-372.

[19]
Tao R, Thill J C. Flow Cross K-function: A bivariate flow analytical method[J]. International Journal of Geographical Information Science 2019:1-17 Http://doi.org/10.1080/13658816.2019.160836

[20]
Pei T, Zhu A X, Zhou C H , et al. Delineation of support domain of feature in the presence of noise[J]. Computers & geosciences, 2007,33(7):952-965.

[21]
Cressie N . Statistics for spatial data[M]. New York: John Wiley & Sons, 1993.

[22]
Liu Y, Wang F, Xiao Y , et al. Urban land uses and traffic ‘source-sink areas': Evidence from GPS-enabled taxi data in Shanghai[J]. Landscape and Urban Planning, 2012,106(1):73-87.

[23]
Chun Y, Griffith D A . Modeling network autocorrelation in space-time migration flow data: an eigenvector spatial filtering approach[J]. Annals of the Association of American Geographers, 2011,101(3):523-536.

[24]
Ducret R, Lemarié B, Roset A . Cluster analysis and spatial modeling for urban freight. Identifying homogeneous urban zones based on urban form and logistics characteristics[J]. Transportation Research Procedia, 2016,12:301-313.

[25]
Castells M . Grassrooting the space of flows[J]. Urban Geography, 1999,20(4):294-302.

[26]
Song C, Pei T, Ma T , et al. Detecting arbitrarily shaped clusters in origin-destination flows using ant colony optimization[J]. International Journal of Geographical Information Science, 2018, 1-21.

[27]
Phan D, Xiao L, Yeh R , et al. Flow map layout[C]. Minneapolis, MN, USA: Proceedings of the IEEE Symposium on Information Visualization, 2005: 219-224

[28]
Boyandin I, Bertini E, Lalanne D . Using flow maps to explore migrations over time[C]. Proceedings of Geospatial Visual Analytics Workshop in conjunction with The 13th AGILE International Conference on Geographic Information Science (GeoVA), 2010.

[29]
Andrienko G, Andrienko N, Fuchs G , et al. Revealing patterns and trends of mass mobility through spatial and temporal abstraction of origin-destination movement data[J]. IEEE Transactions on Visualization and Computer Graphics, 2017,23(9):2120-2136.

[30]
Nanni M, Pedreschi D . Time-focused clustering of trajectories of moving objects[J]. Journal of Intelligent Information Systems, 2006,27(3):267-289.

[31]
Tao R, Thill J-C . FlowAMOEBA: Identifying regions of anomalous spatial interactions[J]. Geographical Analysis, 2019,51(1):111-130.

[32]
Shu H, Pei T, Song C , et al. Quantifying the spatial heterogeneity of points[J]. International Journal of Geographical Information Science, 2019,33(7):1355-1376.

[33]
Guo D, Zhu X, Jin H , et al. Discovering spatial patterns in origin-destination mobility data[J]. Transactions in GIS, 2012,16(3):411-429.

[34]
Hong L, Zheng Y, Yung D , et al. Detecting urban black holes based on human mobility data[C]// Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems. ACM, 2015: 35.

[35]
高楹, 宋辞, 舒华 , 等. 北京市摩拜共享单车源汇时空特征分析及空间调度[J]. 地球信息科学学报, 2018,20(8):1123-1138.

[ Gao Y, Song C, Shu H , et al. Spatial-temporal characteristics of source and sink points of Mobikes in Beijing and its scheduling strategy[J]. Journal of Geo-information Science, 2018,20(8):1123-1138. ]

[36]
Xu J, Li A, Li D , et al. Difference of urban development in China from the perspective of passenger transport around Spring Festival[J]. Applied geography, 2017,87:85-96.

[37]
Kang C, Qin K . Understanding operation behaviors of taxicabs in cities by matrix factorization[J]. Computers, Environment and Urban Systems, 2016,60:79-88.

[38]
Newman M E J, Girvan M . Finding and evaluating community structure in networks[J]. Physical review E, 2004,69(2):026113.

[39]
Cafieri S, Hansen P, Liberti L . Edge ratio and community structure in networks[J]. Physical Review E, 2010,81(2):026105.

[40]
Rosvall M, Bergstrom C T . Maps of random walks on complex networks reveal community structure[J]. Proceedings of the National Academy of Sciences, 2008,105(4):1118-1123.

[41]
Clauset A, Newman M E J, Moore C . Finding community structure in very large networks[J]. Physical review E, 2004,70(6):066111.

[42]
Newman M E J . Modularity and community structure in networks[J]. Proceedings of the national academy of sciences, 2006,103(23):8577-8582.

[43]
Zhong C, Arisona S M, Huang X , et al. Detecting the dynamics of urban structure through spatial network analysis[J]. International Journal of Geographical Information Science, 2014,28(11):2178-2199.

[44]
Chen Y, Xu J, Xu M . Finding community structure in spatially constrained complex networks[J]. International Journal of Geographical Information Science, 2015,29(6):889-911.

[45]
Guo D, Jin H, Gao P , et al. Detecting spatial community structure in movements[J]. International Journal of Geographical Information Science, 2018,32(7):1326-1347.

[46]
Shekhar S, Huang Y . Discovering spatial co-location patterns: A summary of results[C]. Berlin: International symposium on spatial and temporal databases, 2001: 236-256.

Options
文章导航

/

〈 〉