EN中文

地球信息科学学报 >

2020 , Vol. 22 >Issue 3: 474 - 481

DOI: https://doi.org/10.12082/dqxxkx.2020.190381

“数字地形分析”专栏

面向复杂地形的坡位K-means聚类划分研究

  • 高海峰 1 ,
  • 葛莹 , 1, * ,
  • 张杰 2 ,
  • 肖胜昌 2 ,
  • 陈科 2
展开
  • 1. 河海大学地球科学与工程学院,南京 211100
  • 2. 中国电建集团昆明勘测设计研究院有限公司,昆明 650051
* 葛 莹（1963— ）,女,浙江慈溪人,博士,教授,主要从事云计算、空间大数据挖掘、GIS应用等研究。E-mail:

高海峰（1995— ）,男,江苏盐城人,硕士生,主要从事人工智能算法、空间数据挖掘和并行计算等研究。E-mail:gaohaifeng@hhu.edu.cn

收稿日期: 2019-07-17

  要求修回日期: 2019-09-13

  网络出版日期: 2020-05-18

基金资助

云南省重大科技专项——新能源(2013ZB006)

国家自然科学基金项目(41071347)

版权

版权所有，未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
收起

K-means Classifier for Automatic Slope Position Detection in Mountainous Areas

  • GAO Haifeng 1 ,
  • GE Ying , 1, * ,
  • ZHANG Jie 2 ,
  • XIAO Shengchang 2 ,
  • CHEN Ke 2
Expand
  • 1. School of Earth Sciences and Engineering, Hohai University, Nanjing 211100, China
  • 2. Hydrochina Kunming Engineering Corporation LTD, Kunming 650051, China
* GE Ying, E-mail:

Received date: 2019-07-17

  Request revised date: 2019-09-13

  Online published: 2020-05-18

Supported by

Major Science and Technology Projects of Yunnan Province: New Energy(2013ZB006)

National Natural Science Foundation of China(41071347)

Copyright

Copyright reserved © 2020
Fold

摘要

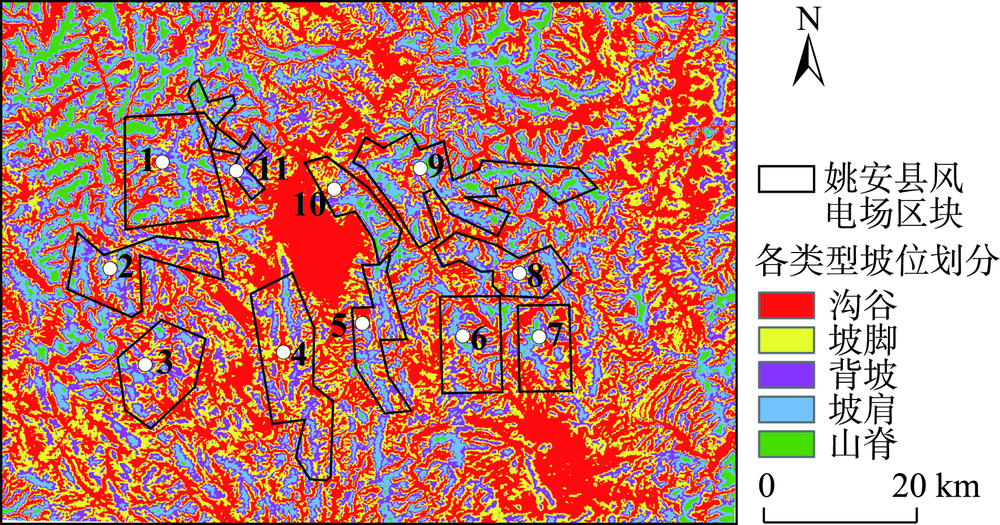
土壤植被研究建立在精准坡位划分的基础上。但现有的坡位大多采用手工划分的方式,存在着自动化程度低、划分精度不高且耗时较长等问题。本文提出一种顾及复杂地形的坡位自动划分算法,尝试采用机器学习K-means方法解决高海拔山区坡位划分的问题,并在山峰区域提取、聚类数确定、以及初始聚类中心选取等关键技术进行了算法的优化。为了验证算法的有效性,以云南省姚安县为研究区,运用提出的算法对研究区坡位进行自动划分,再采用Calinski-Harabasz聚类评价指标、调整兰德系数ARI和误差平方和SSE等一系列方法对坡位K-means聚类划分实验进行分析和评价。研究结果表明,利用该算法所生成的复杂地形坡位与研究区实测等高线相匹配。其次,再从姚安县规划风电场任选4个场址,比较13×13、25×25、37×37三种适宜窗口下坡位自动划分结果,结果表明选取25×25适宜窗口进行坡位划分可靠性最强。再者,计算的规划风电场内山脊、坡肩及背坡比例高达57.13%,也从一个侧面证实了利用该算法划分的坡位结果良好。

关键词： 坡位; 聚类划分; K-means方法; 复杂地形; 云南省姚安县

本文引用格式

高海峰 , 葛莹 , 张杰 , 肖胜昌 , 陈科 . 面向复杂地形的坡位K-means聚类划分研究[J]. 地球信息科学学报, 2020 , 22(3) : 474 -481 . DOI: 10.12082/dqxxkx.2020.190381

Abstract

The slope position has generally been applied in a wide range of soil and vegetation studies. The slope position is manually classified in a long history into five types such as valley, footslope, backslope, slope shoulder, and ridge. It leads to issues of low automation, low precision and time consuming. This paper proposed a K-means algorithm of Machine Learning for clustering classification of slope position in mountainous areas. The performance improvements for the conventional K-means algorithm can be achieved by clustering number selection using the Calinski-Harabasz clustering evaluation index and by initial clustering centers finding using K-means++ in the context of slope position detection. The optimized K-means algorithm of a combination of peak area identification through the morphological white top hat transform function was applied into the automatic detection of slope position in Yao'an County, Yunnan Province based on 90 m×90 m SRTM DEM data. In order to validate this algorithm, a series of replicated experiments were carried out with different threshold values. Three accuracy measures of this algorithm such as Calinski-Harabasz clustering evaluation index, Adjusted Rand index and SSE can be estimated for these experiments. The results show that: (1) the best performance of this K-means algorithm is achieved with a clustering number k = 5; (2) this K-means algorithm is significantly better by using K-means++ to select the initial clustering centers than unoptimized selection; (3) the convergence of this K-means algorithm is the best if the iterations iter = 10,000. Furthermore, these results were obtained in a particular suitable window i.e. 25×25, and the window was compared to other two windows, that is, 13×13 and 37×37. An alternative statistical approach is the direct estimation of classification proportions of slope position for the study area, which can be achieved by evaluating point samples of backslope, slope shoulder, and ridge. Automatic mapping results in the planned wind farms are obtained up to 57.13%, which also indicates that the use of the proposed K-means algorithm may further enhance the potential of slope position detection. The advantages of our algorithm seem to lie in the help it gives for the development of automatic clustering classification of slope position as well as simple manipulation in spatial databases. Further improvements are needed in better performances by integrating fuzzy theory into this algorithm, suitable window selection by using the abruptshift analysis approach, as well as more topographic attributions such as slope, profile curvature and plan curvature, which will lead to the development of our algorithm.

Key words： slope position detection; clustering classification; K-means classifier; mountainous areas; Yao'an County; Yunnan Province

1 引言

坡位是指坡面沿地貌延伸、自上而下切开的纵剖面地形元素,具有典型的层级特征[1]。它构成自坡顶至坡底的坡面,在地理格局上具有明显的空间差异性。许多研究与应用往往需要将坡位划分为不同类型,通常划分为沟谷、坡脚、背坡、坡肩和山脊5类[2]。土壤植被研究通常建立在精准坡位划分的基础上。Schmidt等[3]表示在建立土壤—景观模型中,精准坡位划分是推演土壤类型空间分布的前提。靳甜甜等[4]通过探讨不同坡位的沙棘光合特征,说明坡位是影响沙棘光合作用主要的地形因子。高雪松等[5]在研究不同类型坡位下土壤物理性质和养分的分异时,证实土壤养分在不同坡位呈现不同的特征。
传统的坡位划分是按坡度、曲率等地貌属性进行人工勾画,提取目标区域地貌特征,实现目标区域的坡位划分。这种定性划分方式往往自动化程度较低[6]。Speight[7]根据坡度、剖面曲率和平面曲率等属性通过手工勾画地貌特征来划分坡位。Dikau[8]通过平面、轮廓曲率和曲率半径的组合对坡位进行手工划分。Irvin等[8]提出了基于ISODATA分类的坡位划分自动算法,并将该算法生成的坡位与手工方式进行比较,认为该算法大大减少了人工方法的主观性和繁琐性。尤其是面对复杂地形时,采用人工方式进行坡位划分工作量更大,所以本文尝试采用机器学习K-means方法对DEM数据进行聚类来实现坡位自动划分。
目前,关于坡位自动划分算法研究包括离散硬性坡位划分算法和连续模糊坡位划分算法2种[9]。离散硬性坡位划分算法是指通过布尔集来描述坡位确定边界[10]。史同广等[11]利用窗口移动法通过坡位高程变化来找出布尔集类边界以实现坡位划分。田瑞云等[12]利用地形位置指数（TPI）和坡度来确定DEM与各坡位类别的隶属关系完成坡位划分。然而,Heuvelink和Burrough[10,13]认为离散硬性坡位划分算法因其划分主观,容易产生破碎的坡位划分结果和有用划分信息的丢失。
连续模糊坡位划分算法是指通过模糊集替代布尔集描述坡位模糊边界[14]。它又包括基于模糊聚类的坡位划分算法、基于模糊规则的坡位划分算法和基于相似度的模糊坡位划分算法3类。 Irvin等[8]提出基于模糊聚类的坡位划分算法,通过聚类的方式利用模糊值表示坡位的模糊边界。基于模糊聚类的坡位划分算法在坡位划分时往往会忽略坡位的地理位置信息,所以MacMillan等[15]提出了基于模糊规则的坡位划分算法。该算法在坡位划分过程中使用了30余个地形属性并设置了100余个参数,复杂且实用性不强。为了提高坡位划分算法的实用性,Qin等[16]提出了基于相似度的模糊坡位划分算法,引入相似度以减少地形属性和参数的需求量,但该算法仍旧较为复杂。
本文以复杂地形坡位为研究对象,针对坡位手工划分存在的自动化程度较低、精度不高和操作复杂等问题,提出了一种基于机器学习K-means方法的坡位自动划分算法。具体地说,先采用形态学白色顶帽变换函数自动生成山峰区域,并根据Calinski-Harabasz聚类评价指标确定K-means方法的最优聚类数,再基于K-means++方法优选K-means方法的初始聚类中心,最后运用优化的K-means方法对山峰区域DEM数据进行坡位聚类划分和坡位重分类。在此基础上,对坡位聚类划分结果进行分析评价以验证算法的可靠性。

2 复杂地形坡位K-means聚类划分算法

1967年,MacQueen[17]首次提出K-means方法来解决聚类问题。目前该方法广泛应用于数据挖掘、决策支持、图像分割及机器学习等领域[18]。本文提出一种基于K-means方法的复杂地形坡位自动划分算法,首次采用K-means方法解决坡位划分问题。该算法包括基于白色顶帽变换函数的山峰区域提取和基于K-means方法的坡位聚类划分2个部分。

2.1 基于白色顶帽变换函数的山峰区域提取

白色顶帽变换函数是一种数学形态学的方法,可用于提取DEM山峰和沟谷[19],优点是提取的山峰区域较为显著,能直观反映原始DEM的地形特征,有利于后续运用K-means方法进行坡位聚类划分。具体算法如算法1所示。
Erosion : E λ f X = inf f u : u ∈ λ x Dilation : D λ f X = sup f u : u ∈ λ x
Opening : O λ X = D λ ( E λ f ( X ) )
WTH = x : f x - O λ X
算法 1 运用白色顶帽变化函数提取山峰区域算法
输入：原始DEM数据;设定的山峰区域提取适宜窗口大小t×t。
输出：山峰区域图K
（1）对原始DEM按式（1）进行腐蚀和膨胀变换。式中,λx为正方形结构元素,本文为适宜窗口,窗口大小t×t是设定的形态学处理阈值;
（2）根据腐蚀变化图像Eλƒ(X)和膨胀变化图像Dλƒ(X)按式（2）进行开操作,生成除山峰区域之外的其它区域;
（3）计算式（3）,将原始DEM和Oλƒ(X)相减,生成山峰区域。
算法步骤（3）生成的山峰区域WTH取决于适宜窗口大小t×t,它决定了图中山峰区域是否清晰和高程特征是否明显。经过反复试验,本文最终设定适宜窗口大小为25×25。

2.2 基于K-means方法的坡位聚类划分

随着K-means方法应用深入,它的不足之处也逐步显露。例如,采用K-means方法进行坡位聚类划分需要预先确定聚类数,而随机确定的聚类数会影响聚类结果[20];随机选取的初始聚类中心会导致聚类结果仅收敛至局部最优解而使得聚类结果不稳定[21];聚类收敛条件也会影响聚类结果[22]。为了提高坡位聚类划分精度,本文针对上述问题将K-means方法优化分为5个部分：最优聚类数确定、初始聚类中心优选、坡位聚类划分、聚类收敛条件优化和坡位重分类。
（1）最优聚类数确定
聚类数取值范围通常在2至N之间,N为样本数。大多数应用都是根据实际情况在取值范围内随机选取聚类数[22]。为了克服聚类数随机选取带来的弊端,本文采用Calinski-Harabasz聚类评价指标来确定最优聚类数,其计算公式如下：
s k = tr B k tr W k ∙ m - k k - 1
式中：m为山峰区域格点数;k为聚类数;Bk为类别间协方差矩阵;Wk为类别内协方差矩阵;tr为矩阵的迹。Calinski-Harabasz聚类评价指标s(k)值越大,说明坡位聚类结果越好。经过反复测试,本文确定最优聚类数K为5。
（2）初始聚类中心优选
确定最优聚类数K后,K-means方法还需解决初始聚类中心优选的问题。本文采用K-means++方法选取彼此间相距尽可能远的格点作为初始聚类中心,以提高坡位聚类划分精度[23]。初始聚类中心优选算法如算法2所示。
算法 2 基于K-means++方法的初始聚类中心优选算法
输入：山峰区域图,最优聚类数K
输出：优选的K个初始聚类中心μ1,μ2,… μK
（1）从山峰区域图中随机选择一个格点作为初始聚类中心μ1;
（2）计算各个格点到其最近聚类中心的距离D(xi),再将所有距离相加得到Sum(D(xi));
（3）生成随机数Random ≤ total,计算total=Sum(D(xi))×Random和total-=D(xi),直至total≤ 0。此时的格点就是一个初始聚类中心;
（4）重复(2)和(3),直至选出K个初始聚类中心。
（3）坡位聚类划分
基于K-means方法进行坡位聚类划分如算法3所示。
J C k = ∑ x i - μ k 2
式中：i∈[1, m], m为山峰区域格点数;k∈[1, K],K为最优聚类数;Ck为坡位聚类类别。
算法 3 基于K-means方法进行坡位聚类划分算法
输入：山峰区域图;最优聚类数K;优选的山峰区域初始聚类中心μ1,μ2…μK;前后2次聚类中心的限差tol;聚类迭代次数iter
输出：坡位划分结果（1）按式（5）计算格点xi与初始聚类中心μk之间的欧式距离J(Ck);J(Ck)计算公式如式（5）所示。
（2）设最小欧式距离minDist对应的k为minIndex,判断J(Ck)<minDist,如果是,则minDist=J(Ck),minIndex=k。否则,继续循环k;
（3）将xi的最小欧式距离及其对应的k存入列表[minDist, minIndex];
（4）遍历格点xi,重复执行（2）和（3）,直至i=m;
（5）按各聚类中心计算每一坡位聚类类别Ck的栅格单元均值作为新的初始聚类中心;
（6）反复执行（1）~（5）步骤,直至聚类迭代次数达到iter或新的初始聚类中心与前一次初始聚类中心误差达到限差tol;
（7）按minIndex生成坡位矩阵,确定划分结果。
（4）聚类收敛条件优化
聚类收敛条件是当前后两次聚类中心的误差满足限差或迭代达到一定次数时K-means方法停止迭代的条件。为了确保各聚类中心收敛达到最优解,本文还规定Wn收敛。Wn是DEM格点到其所属聚类中心距离的平方和,其计算公式如下：
W n = J C = ∑ K = 1 K J C k = ∑ K = 1 K ∑ x i - μ k 2
式中：xi是山峰区域格点;Ck是坡位聚类类别;μk是聚类中心。
（5）坡位重分类
由坡位矩阵生成坡位划分专题图,各类型坡位在坡位矩阵中的排列是无序的。为了达到每次生成的坡位图中各类型坡位排列顺序固定的目的,本文借助坡位重分类方法生成坡位图,按各类型坡位的格点数,以沟谷、坡脚、背坡、坡肩和山脊的顺序重新排序后,生成坡位划分专题图。

3 实验与结果

3.1 实验数据

本文选取云南省姚安县为研究区。姚安县位于云南省中北部,地形为四周崇山峻岭,中部平畴广川。海拔最高处3028 m,最低处1135 m,岭谷高差大部分在500 m以上,平均坡度27.01°。该研究区地表起伏悬殊,完全能验证本文提出的算法。本文的数据源是地理空间数据云网站（http://www.gscloud.cn/）下载的90 m分辨率SRTM DEM,如图1所示。
图1 云南省姚安县地形

Fig. 1 DEM of Yao'an County, Yunnan Province

3.2 坡位划分

本文所有实验在ArcGIS平台上借助Python自编程序实现,具体步骤是：
（1）山峰区域提取。按式（1）和（2）对DEM进行数学形态学处理,再根据式（3）生成山峰区域WTH,适宜窗口为25×25,生成的山峰区域图如图2所示。
图2 研究区山峰区域

Fig. 2 Map of peak area in the study area

（2）K-means方法的优化。运用式（4）Calinski-Harabasz聚类评价指标确定最优聚类数K,处理原则是类别间高程值协方差越大越好,类别内高程值协方差越小越好。图3是通过改变聚类数k计算得到Calinski-Harabasz聚类评价指标s(k)值。
图3 s(k)值随聚类数k变化

Fig. 3 s(k)value varies with clustering number k

由图3可知,s(k)值随聚类数k变大显著增加,表明坡位聚类划分结果越来越好。但考虑到坡位划分类别继续增加缺乏实际应用,所以将坡位划分为5类[2]。
根据算法2运用K-means++方法选取彼此相距较远的格点作为初始聚类中心。本文采用误差平方和SSE和调整兰德系数ARI 2种方法来评价随机和K-means++优选的初始聚类中心结果。SSE是指所有格点与对应聚类中心距离的平方和,在迭代次数相同的条件下,SSE越小说明聚类效果越好,坡位划分精度也越高,如图4所示。调整兰德系数ARI度量了训练样本与真实值间的吻合程度。ARI取值为[-1,1],值越大说明聚类结果与真实情况越符合,聚类效果也越好,如图5所示。为了说明起见,将计算所得的SSE×10-8,ARI×102。
图4 2种方法SSE随聚类数k变化

Fig. 4 SSE calculated by the two methods varies with clustering number k

图5 2种方法ARI随聚类数k变化

Fig. 5 ARI calculated by the two methods varies with clustering number k

由图4和图5可知,K-means++优选初始聚类中心明显优于随机初始聚类中心。但从SSE和ARI随聚类数k的变化趋势来看,其变化更加显著,不难看出对K-means方法最优聚类数确定比初始聚类中心优选更加可靠。
聚类收敛条件的优化主要体现在算法迭代次数iter。采用Calinski-Harabasz聚类评价指标来选取迭代次数,该评价指标度量了各坡位类别内集聚程度以及类别间离散程度。计算相同聚类数（k=5）下不同迭代次数s(k)值,如图6所示。
图6 同一聚类数k下s(k)值随迭代次数iter变化

Fig. 6 s(k) value varies with iterations based on a clustering number k

由图6可知,当k=5时,Calinski-Harabasz聚类评价指标s(k)值随迭代次数递增明显变大,说明聚类效果越来越好。当iter=10 000时,s(k)趋于饱和,继续增加迭代次数聚类效果反而变差,所以选择迭代次数iter为10 000。
（3）根据优化的K-means方法实现复杂地形坡位的聚类划分以及坡位图的生成。坡位划分完成后,借助坡位重分类按照各类型坡位格点数,以沟谷、坡脚、背坡、坡肩和山脊的顺序进行坡位排序,生成坡位图,如图7所示。
图7 坡位划分

Fig. 7 Map of slope position automatic classification

4 分析与讨论

对图1姚安县DEM运用GIS空间分析工具生成等高线,等高线间隔设为300 m,再将生成的等高线与坡位划分图进行叠置,如图8所示。
图8 坡位分布与地形等高线叠置

Fig. 8 Overlay map of slope position distribution and topographic contour

由图8可知,西北地区地势起伏较大,中部地区地势平坦,属于盆地地形,坡位划分结果很好反映了研究区地貌形态特征。该算法可以从宏观上揭示地形复杂区域分异特征与地形规律。
高海拔山区如姚安县通过风电场建设可有效利用风能资源。风电场选址会确定在风能资源较为丰富的区域,如图9所示。
图9 坡位分布与姚安县风电场叠置

Fig. 9 Overlay map of slope position distribution and planned wind farms in Yao'an County

图9黑色加粗方框为1—11姚安县规划风电场,本文对每个规划风电场内坡位划分结果进行统计,并选取3个风电场进行坡位划分结果比较,如表1所示。
表1 不同适宜窗口下各类型坡位格点所占比率统计
风电场 适宜
窗口		 沟谷 坡脚 背坡 坡肩 山脊 总计
格点数 占比 格点数 占比 格点数 占比 格点数 占比 格点数 占比 格点数 占比
3 13×13 5531 42.84 3674 28.45 2652 20.54 1025 7.94 30 0.23 12 912 100
25×25 3864 29.93 3916 30.33 3556 27.54 1494 11.57 82 0.64 12 912 100
37×37 3350 25.94 4300 33.30 4102 31.77 1110 8.60 50 0.39 19 635 100
4 13×13 7925 40.36 6193 31.54 4110 20.93 1383 7.04 24 0.12 19 635 100
25×25 5758 29.33 6856 34.92 5493 27.98 1499 7.63 29 0.15 19 635 100
37×37 5684 28.95 7587 38.64 5543 28.23 821 4.18 0 0.00 22 841 100
9 13×13 8518 37.29 5518 24.16 4703 20.59 3396 14.87 706 3.09 22 841 100
25×25 4914 21.51 4879 21.36 5635 24.67 5899 25.83 1514 6.63 22 841 100
37×37 3839 16.81 4864 21.30 6496 28.44 6760 29.60 882 3.86 22 841 100
本文选取13×13、25×25和37×37不同的适宜窗口进行算法验证。由表1可知,适宜窗口25×25下山脊和坡肩所占比率均大于13×13及37×37适宜窗口下的结果。这说明了本算法选取适宜窗口大小25×25进行坡位划分较为可靠。
就适宜窗口25×25而言,在风电场3中,背坡区域占比27.54%,坡肩区域占比11.57%,山脊区域占比0.64%,风电场可建设区域达到39.75%;在风电场4中,背坡区域占比27.98%,坡肩区域占比7.63%,山脊区域占比0.15%,风电场可建设区域达到35.76%;在风电场9中,背坡区域占比24.67%,坡肩区域占比25.83%,山脊区域占比6.63%,风电场可建设区域达到57.13%。可以看出,风电场9的坡位划分结果最好。一般来说,风电场风机位置布设在地势较高、面积较大且地形起伏度较小的地方。从图9可以看出风电场区域内山脊、坡肩符合地形条件。从另一侧面来讲,规划风电场选址间接证明了本文的坡位划分结果良好。
从图10实验结果统计可以看出适宜窗口25×25下各类型坡位分布较为均匀,坡位划分结果良好。风电场项目集中建设在山脊和坡肩上,说明这2个坡位类型风能资源丰富。所以,采用本算法在一定程度上可以提高风电场智能选址的精度。
图10 风电场6不同适宜窗口下坡位分布统计

Fig. 10 Slope position distribution of wind farm 6 based on different suitable windows

5 结论

本文以复杂地形坡位为研究对象,针对坡位划分自动化程度低、精度不高和操作复杂等问题,提出一种面向复杂地形的坡位K-means聚类划分算法。该算法尝试运用机器学习K-means方法实现复杂地形坡位的聚类划分,并应用于云南省姚安县坡位划分实例中,主要研究结论如下：
（1）首先,K-means方法采用Calinski-Harabasz聚类评价指标确定最优聚类数,当聚类数k=5时聚类效果最好,因此将坡位划分为5类;其次,通过 K-means++方法选取初始聚类中心明显优于随机选取的方法;最后,聚类收敛条件在迭代次数iter= 10 000时聚类效果最好。
（2）将生成的坡位图与实测的等高线图进行叠置分析,由图8不难看出二者匹配结果良好,说明坡位划分结果很好地反映了地形复杂地区地貌特征和地形规律。
（3）通过对姚安县规划风电场4个场址内坡位划分结果进行比较分析,选取适宜窗口13×13、 25×25和37×37统计各类型坡位格点所占比率,结果表明适宜窗口25×25下山脊和坡肩所占比率均大于13×13及37×37适宜窗口下的结果,验证了算法选取适宜窗口大小25×25生成山峰区域并实现后续坡位划分的可靠性。
（4）就适宜窗口25×25而言,由表1可知风电场9中背坡区域占比24.67%,坡肩区域占比25.83%,山脊区域占比6.63%,风电场可建设区域达到57.13%。通常在风电场选址建设中山脊、坡肩等区域符合布机的地形条件,因此从一个侧面来讲,姚安县规划风电场选址间接证明了本文的坡位划分结果良好,说明采用本算法在一定程度上可以提高风电场智能选址的精度。
与现有研究相比,本文首次采用机器学习 K-means方法解决复杂地形坡位自动划分的问题,提出的算法旨在推动坡位聚类划分研究进展尝试定义坡位自动划分在空间数据工具库中的简单操作。为确保坡位划分结果精度,本文在算法的关键技术上进行了优化。本算法的优点在于自动划分坡位,且操作智能易行,具有一定的普适性。需要进一步改进的地方有：未考虑到影响坡位划分的坡度、轮廓曲率和平面曲率等地形属性,导致坡位划分结果与实地地貌特征有一定偏差;未引入模糊度的概念,若尝试采用模糊C-means方法实现坡位聚类划分,坡位划分精度可能会更高;适宜窗口未能通过合理的变点分析方法获取,设定上还存在着主观性,坡位划分结果评价有待加强。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
王彦文, 秦承志 . 地貌形态类型的自动分类方法综述[J]. 地理与地理信息科学, 2017,33(4):16-21.

[ Wang Y W, Qin C Z . Rewiew of methods for landform automatic classification[J]. Geography and Geo-information Science, 2017,33(4):16-21. ]

[2]
Ruhe R V. Quaternary landscapes in Iowa[M]. Iowa: Iowa State University Press, 1969.

[3]
Schmidt J, Hewitt A . Fuzzy land element classification from DTMs based on geometry and terrain position[J]. Geoderma, 2004,121(3-4):243-256.

[4]
靳甜甜, 傅伯杰, 刘国华 , 等. 不同坡位沙棘光合日变化及其主要环境因子[J]. 生态学报, 2011,31(7):1783-1793.

[ Jin T T, Fu B J, Liu G H , et al. Diurnal changes of photosynthetic characteristics of Hippophae rhamnoides and the relevant environment factors at different slope locations[J]. Acta Ecologica Sinica, 2011,31(7):1783-1793. ]

[5]
高雪松, 邓良基, 张世熔 . 不同利用方式与坡位土壤物理性质及养分特征分析[J]. 水土保持学报, 2005,19(2):53-56.

[ Gao X S, Deng L J, Zhang S R . Soil physical properties and nutrient properties under different utilization styles and slope position[J]. Journal of Soil and Water Conservation, 2005,19(2):53-56. ]

[6]
秦承志, 朱阿兴, 施迅 , 等. 坡位渐变信息的模糊推理[J]. 地理研究, 2007,26(6):1165-1174.

[ Qin C Z, Zhu A X, Shi X , et al. Fuzzy inference of spatial gradation of slope positions[J]. Geographical Research, 2007,26(6):1165-1174. ]

[7]
Speight J G . Landform pattern description from aerial photographs[J]. Photogrammetria, 1977,32(5):161-182.

[8]
Irvin B J, Ventura S J, Slater B K . Fuzzy and isodata classification of landform elements from digital terrain data in Pleasant Valley, Wisconsin[J]. Geoderma, 1997,77(2-4):137-154.

[9]
Pennock D J, Zebarth B J, Jong E D . Landform classification and soil distribution in hummocky terrain, Saskatchewan, Canada[J]. Geoderma, 1987,40(3-4):297-315.

DOI PMID

[10]
Heuvelink G B M, Burrough P A . Error propagation in cartographic modelling using boolean logic and continuous classification[J]. International Journal of Geographical Information Systems, 1993,7(3):231-246.

[11]
史同广, 闫业超, 王林林 , 等. 基于DEM的大尺度季风风速空间分布模拟研究[J]. 地理与地理信息科学, 2007,23(2):26-29.

[ Shi T G, Yan Y C, Wang L L , et al. Large -scale wind speed simulation based on DEM[J]. Geography and Geo-Information Science, 2007,23(2):26-29. ]

[12]
田瑞云, 王玉宽, 傅斌 , 等. 基于DEM的地形单元多样性指数及其算法[J]. 地理科学进展, 2013,32(1):121-129.

[ Tian R Y, Wang Y K, Fu B , et al. DEM-based topographic unit diversity index and its algorithm[J]. Progress in Geography, 2013,32(1):121-129. ]

[13]
Burrough P A, Gaans P F M V, Hootsmans R. Continuous classification in soil survey: Spatial correlation, confusion and boundaries[J]. Geoderma, 1997,77(2-4):115-135.

[14]
Burrough P A, Gaans P F M V, MacMillan R A. High-resolution landform classification using fuzzy k-means[J]. Fuzzy Sets and Systems, 2000,113(1):37-52.

[15]
MacMillan R A, Pettapiece W W, Nolan S C , et al. A general procedure for automatically segmenting landforms into landform elements using DEMs, heuristic rules and fuzzy logic[J]. Fuzzy Sets and Systems, 2000,113(1):81-109.

[16]
Qin C Z, Zhu A X, Shi X , et al. Quantification of spatial gradation of slope positions[J]. Geomorphology, 2009,110(3-4):152-161.

[17]
MacQueen J B. Some methods for classification and analysis of multivariate observations[C]. Proceedings of 5 th Berkeley Symposium on Mathematical Statistics and Probability , 1967: 281-297.

[18]
陈锐, 陈明剑, 姚翔 , 等. 利用导航大数据挖掘城市热点区域关联性[J]. 地球信息科学学报, 2019,21(6):826-835.

[ Chen R, Chen M J, Yao X , et al. Detecting urban hotspot region association by navigation big data mining[J]. Journal of Geo-information Science, 2019,21(6):826-835. ]

[19]
Rodriguez F, Maire E, Courjault‐Radé P, et al. The black top hat function applied to a DEM: A tool to estimate recent incision in a mountainous watershed (Estibère Watershed, Central Pyrenees)[J]. Geophysical Research Letters, 2002,29(6):9-1-9-4.

[20]
施慧慧, 王妮, 滕文秀 , 等. 结合Gabor小波和形态学的高分辨率图像树冠提取方法[J]. 地球信息科学学报, 2019,21(2):249-258.

[ Shi H H, Wang N, Teng W X , et al. Tree canopy extraction method of high resolution based on Gabor filter and morphology[J]. Journal of Geo-information Science, 2019,21(2):249-258. ]

[21]
毛韶阳, 李肯立 . 优化K-means初始聚类中心研究[J]. 计算机工程与应用, 2007,43(22):179-181.

[ Mao S H, Li K L . Research of optimal k-means initial clustering center[J]. Computer Engineering and Applications, 2007,43(22):179-181. ]

[22]
吴夙慧, 成颖, 郑彦宁 , 等. K-means方法研究综述[J]. 现代图书情报技术, 2011,27(5):28-35.

[ Wu S H, Chen Y, Zheng Y N , et al. Survey on k-means algorithm[J]. New Technology of Library and Information Service, 2011,27(5):28-35. ]

[23]
Arthur D, Vassilvitskii S. K-means++: The advantages of careful seeding[C]. Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 2007: 1027-1035.

Options
文章导航

/

〈 〉