EN中文

地球信息科学学报 >

2020 , Vol. 22 >Issue 5: 1120 - 1132

DOI: https://doi.org/10.12082/dqxxkx.2020.190443

“空间综合人文学与社会科学”专辑

基于交通网络的乡村中小学优化布局

  • 陈玉龙 1, 2 ,
  • 赖志柱 3 ,
  • 王铮 , 2, 3, *
展开
  • 1.河南大学 黄河文明与可持续发展研究中心暨黄河文明传承与现代文明建设河南省协同创新中心,开封 475001
  • 2.河南大学环境与规划学院,开封 475004
  • 3.华东师范大学地理信息科学教育部重点实验室,上海 200241
* 王 铮（1954— ）,男,云南陆良人,博士生导师,教授,主要从事政策模拟、地理计算、区域科学与管理研究。E-mail:

陈玉龙（1989— ）,男,河南栾川人,博士,讲师,主要从事地理计算研究。E-mail:chenyulong0203@163.com

收稿日期: 2019-08-13

  要求修回日期: 2019-12-07

  网络出版日期: 2020-07-25

基金资助

国家自然科学基金项目(41671396)

版权

版权所有，未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
收起

Optimization of Rural Primary and Secondary School Location based on Traffic Network

  • CHEN Yulong 1, 2 ,
  • LAI Zhizhu 3 ,
  • WANG Zheng , 2, 3, *
Expand
  • 1. Key Research Institute of Yellow River Civilization and Sustainable Development & Collaborative Innovation Center on Yellow River Civilization of Henan Province, Henan University, Kaifeng 475001, China
  • 2. College of Environment and Planning, Henan University, Kaifeng 475004, China
  • 3. Key Laboratory of Geographical Information Science, Ministry of Education of China, East China Normal University, Shanghai 200241, China
* WANG Zheng, E-mail:

Received date: 2019-08-13

  Request revised date: 2019-12-07

  Online published: 2020-07-25

Supported by

National Natural Science Foundation of China(41671396)

Copyright

Copyright reserved © 2020
Fold

摘要

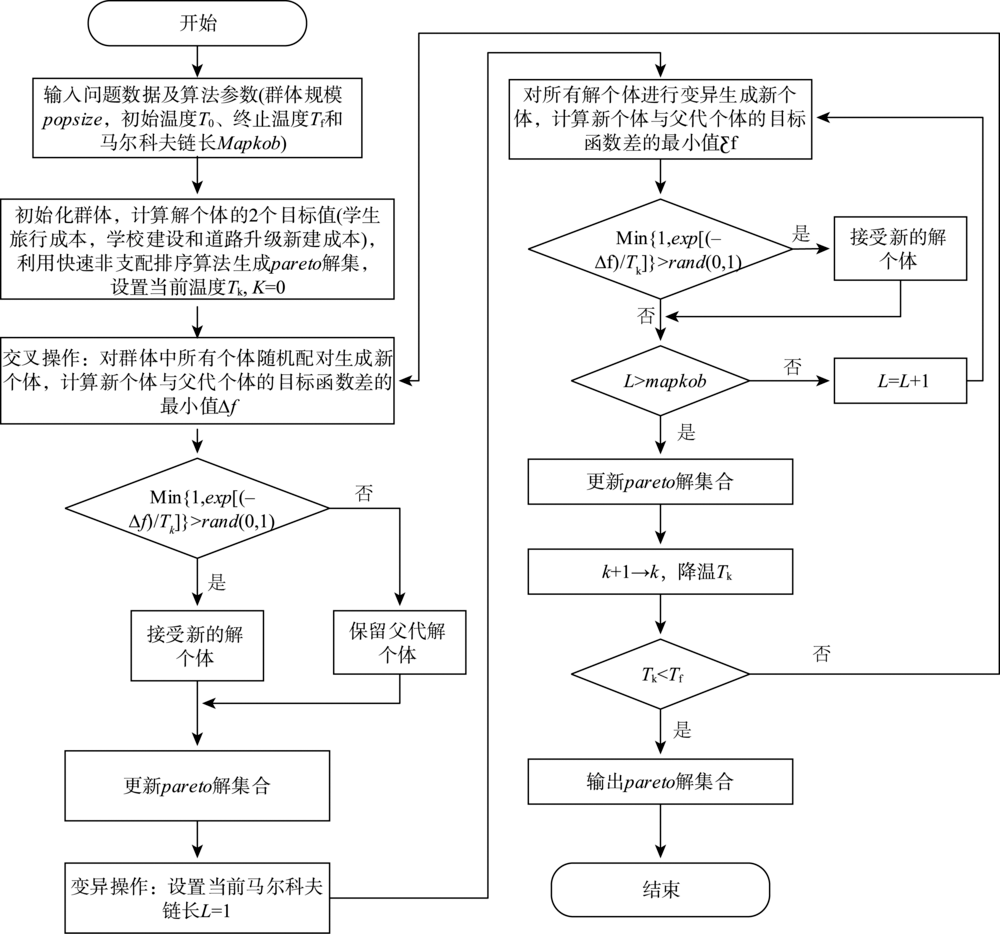
合理规划中小学布局是优化教育资源配置、提高办学效益以及实现教育均衡发展的重要途径。本研究针对中国乡村建设的需要和中国多山的地理环境,考虑山地环境对乡村中小学选址的影响,构建多山环境下乡村中小学的区位模型,运用地理信息科学方法,以Visual Studio. Net 2010为开发平台,使用C#语言和ArcGIS Engine 10.0组件库,同时结合MATLAB编程,开发出基于交通网络的乡村中小学区位优化系统。最后将系统应用于贵州省某镇的小学布局优化中,分别在只考虑已有道路、假设道路可升级、假设道路可新建或升级3种情景下,通过改进的模拟退火算法,确定新建学校的最佳位置,以及新道路的修建和原有道路的升级情况,从而得到不同情景下各居民点学生的上学耗时。结果表明,交通网络对乡村中小学布局优化具有重要影响,改善交通网络条件能够有效提高学生的就学效率上学速度。

关键词： 乡村中小学; 交通网络; 学校布局; 区位优化; 山区; 多目标设施区位-网络设计模型; 模拟退火算法; 贵州省

本文引用格式

陈玉龙 , 赖志柱 , 王铮 . 基于交通网络的乡村中小学优化布局[J]. 地球信息科学学报, 2020 , 22(5) : 1120 -1132 . DOI: 10.12082/dqxxkx.2020.190443

Abstract

The rational planning of school location is an important way to optimize the allocation of educational resources, improve the efficiency of school running and realize the balanced development of education. The accessibility must be considered in optimizing the location of rural schools, which is an important difference from the location of urban schools. Many scholars have studied the location problem of rural schools, but most of them have neglected the impact of transportation network conditions on the location of schools. On the basis of previous studies, this study will consider the impact of traffic network on the optimization location of primary schools in mountainous environment. The object of this study is to minimize the total transportation costs for students, construction costs for new schools, construction and upgrade costs for roads on a traffic network. We regard a set of villages as demand nodes exists in a geographical region, a set of roads as transfer links. The road links in the network contain existing and new potential road links. A set of schools exists in the region and it is clearly desired to locate a set of new schools, to construct new road links, to improve the existing road links such that the total investment costs (including the travel costs for students, construction costs for school facilities, construction and upgrading costs for roads) are minimized. Thus, a multi-objective optimization model for this problem is proposed. The multi-objective facility location-network design model constructed in this paper is an extension of FLNDP problem, and also belongs to NP-hard problem. In order to facilitate the model application, this study use geographic information science method, take Visual Studio. Net 2010 as the development platform, use C# language, MATLAB language and ArcGIS Engine 10 component library to develop a location optimization system of rural primary and secondary school based on transportation network. Finally, the system is applied to the optimization of the primary school location of a town in Guizhou province. Aiming at the location optimization problem of rural primary, this paper considers three scenarios (only consider the existing road, assume that the road can be upgraded and the road can be built or upgraded) which are different from the problem of urban primary school location. In geographic calculation, this paper explores an improved multi-objective simulated annealing algorithm to determine the best location of new schools, as well as the construction of new roads and the upgrading of existing roads.

Key words： rural primary and high school; traffic network; school location; location optimization; mountain area; multi-objective facility location network design model; simulated annealing algorithm; Guizhou

1 引言

中共“十九大”报告提出实施乡村振兴战略,乡村振兴的一个重要方面是发展乡村教育。中国从1990年代中期就开始实施“撤点并校”政策,对教育资源进行优化整合,所以如何合理布局乡村中小学解决偏远地区学生上学难的问题成为中国地理规划迫切需要研究的课题。
通常在地理计算中,学者们通过空间运筹评价学校的区位问题,如Dost [1],Pizzolato等[2]的研究。对于学校布局问题,在城市环境中,一般需要最小化学生到达学校的路径距离,因为城市内的道路通常被认为能够处处可达,该计算往往是一个平面上的需求点到设施点的线距离和最小问题。但是乡村学校布局因为道路有限,在布局时可能需要同时构建道路。已有部分学者针对乡村学校的优化选址进行了研究,较早的有Tewari等[3],研究了印度农村中学的选址问题,他们使用最大覆盖模型分析具有固定数量的学校如何最大限度地覆盖居民点。国内,彭永明等[4]则在P-重心模型的基础上吸收了P-中心思想提出了新的区位模型,该模型既保证了学生上学距离加权之和最小,又能让偏远地区学生上学相对方便。之后,戴军等 [5]以场势理论为指导,通过建立分量指标评价体系,探讨了乡村基础教育设施布局的优化模式。也有部分学者对城市地区教育设施的优化布局进行了研究。其中,戴特奇等[6]在彭永明等[4]的研究基础上增加考虑了学校规模约束,改进了P-重心模型,并将改进后的模型应用于北京市延安区的小学优化布局研究中。张煊宜 [7]针对教育均衡问题,探索了如何使用GIS技术对教育资源和适龄人口实现动态更新,并建立均衡性评价指标体系对上海市浦东新区的教育资源进行优化配置。刘科伟 [8]通过构建城市边缘区基础教育设施布局规划模型,研究了西安市长安区的小学布局问题。除了学校的布局问题之外,部分学者也研究了其他公共服务设施的优化布局问题,如丁愫等[9]从可达性和公平性角度评估了城市地区医疗设施的空间布局合理性;詹庆明等[10]对乡村应急公共设施的选址布局问题进行了研究。
遗憾的是,目前这些工作并没有考虑道路的通行条件,仍然不能满足地处山地环境设施布局的特殊需要,这是因为山地地区道路通达性不好,山地乡村中小学的布局区位必须考虑道路的可通行性;山地乡村道路崎岖度高,各地道路因为崎岖度不同建设成本也不一样,学校优化布局必须考虑道路的崎岖度。更进一步,处于山地乡村地区政府的财政支出水平往往是有限的,而山地环境的道路建设成本高,因此在乡村地区学校的布局应尽量减少新建或升级设施和道路的数量以节约成本,需要在布局学校过程中把道路成本计入,这就使得计算变得更为复杂。总之,乡村学校布局优化为一个必须考虑道路崎岖度权重的设施区位-网络设计问题。国外部分学者[11,12,13,14,15,16,17]已对设施区位设计-网络设计问题进行了研究,但并没有将设施区位-网络设计方法应用于学校的优化布局中。
在此背景下,本项研究将从我国知名的山地省份贵州省取实验区,将其应用于贵州省某镇的小学布局优化中,从而获取实证经验。

2 模型构建和算法

2.1 模型构建

为了对比分析在不同交通网络条件下学校设施的优化布局情况,以便更好的分析交通网络条件对乡村中小学布局的影响,依据Melkote[12]的研究,以最小化学生旅行成本和道路修建升级成本为目标,构建包含3种道路情景的多目标设施区位-网络设计模型：① 情景1考虑中小学布局只利用已有道路网络,这种情况出现在乡村道路建设比较发达的地区;② 情景2假设已有道路网络可升级,这种情况出现在大多数乡村建设中,尤其在山地环境中;③ 情景3假设道路网络可升级且需修建（不仅考虑对已存道路进行升级,还要考虑新道路的修建）,这种情况多发生在我国西部地区。
需要注意的是,在传统的设施区位模型中,需求点的需求直接到设施节点寻求服务,而在设施区位-网络设计问题中,需求点需求可能需要中转到其他需求点才能到达设施点,我们称这类能起到中转作用的需求点为中转节点。所以模型中包含两大种类型的节点,分别是设施节点和需求节点。对于设施节点来说,由于设施没有容量限制,故所有流入设施节点的需求流量都被该设施节点所服务,都不会再流出,而需求节点其节点本身处没有设施。区别于传统的设施区位问题,需求节点又分纯粹需求点和中转节点,其中中转节点是指节点本身必须是需求点,且流入该节点的流量要到其他地方寻找服务,而纯粹需求节点只有流出量没有流入量。
这里假设：① 乡村体系构成网络体系,每一个网络节点代表一个自然村或者居民点;② 每个居民点都可建设小学且有需要上学的学生;③ 学校必须建设在居民点上;④ 每个居民点上最多只能建设一所学校;⑤ 所有的道路网络连接都是定向的即居民点居民不会在节点之间做重复往返运动;⑥ 由于当前乡村人口流失严重,乡村学生人数有限,故假设学校无容量限制即每个居民点的学生都作为整体寻求服务,不能被拆分。
为此本文对模型所用到的符号约定如下： N 表示道路网络中的节点集合,且网络节点集合 i , j , k ∈ { 1,2 … | N | } ; F 表示设施节点集合（包含新建学校和已有学校）; L 表示已有道路和潜在道路网络链接集合,且 ( i , j ) ∈ L ; L ' 表示已有道路网络链接集合,且 L ' ∈ L ; D k 表示居民点 k 的需求（每个居民点的需求等于小学生人数）; f i 表示在节点 i 处建设学校的花费成本; c ij 表示修建或升级道路链接 ( i , j ) 的成本花费; t r ij 表示在道路链接 ( i , j ) 上每个学生的旅行成本; t r ij k 表示 k 居民点需求在链接 ( i , j ) 间的旅行成本,且 t r ij k = t r ij D k ; p 表示新建学校个数; R 表示道路崎岖度系数。决策变量包括 Z i 、 X ij 、 E ij 、 Y ij k 和 W i i ,其中 Z i = 1 表示在 i 节点布置了设施（学校）, Z i =0表示 i 节点无设施（学校）; X ij = 1 表示道路链接 ( i , j ) 被修建或升级, X ij = 0 表示道路链接 ( i , j ) 没有被修建或升级; E ij = 1 表示道路链接 ( i , j ) 存在（包含修建升级道路和已有道路）, E ij = 0 表示道路链接 ( i , j ) 不存在; Y ij k = 1 表示居民点 k 的学生需要经过道路链接 ( i , j ) , Y ij k = 0 表示居民点 k 的学生不需要经过道路链接 ( i , j ) ,且有 Y ij i = E ij 即 i 居民点学生经过 ( i , j ) 链接到其他地方寻求服务,表示 ( i , j ) 链接存在; W i k = 1 表示居民点 k 的学生到学校点 i 接受服务, W i k = 0 表示居民点 k 的学生不到学校点 i 接受服务,且有 W i i = Z i 即 i 节点到 i 节点寻求服务,表示在 i 节点存在学校设施。
因此,由上述约定,可以将3种情景的模型构建结果归纳如下：
（1）情景1（已有可利用道路）
目标函数：
Min ∑ ∑ R t r ij k Y ij k
Min ∑ f i Z i
约束条件：
Z i + ∑ Y ij i = 1 , ∀ i ∈ N
∑ ∑ Y ji k D k + D i = ∑ ∑ Y ij k D k , ∀ i ∈ N , i ∉ F
Z k + ∑ W i k = 1 ,    ∀ k ∈ N
W i k ≤ Z i , ∀ i , k ∈ N : i ≠ k
Y ij k ≤ E ij ,     ∀ i , j , k ∈ N , ( i , j ) ∈ L '
Y ij i + Y ji j ≤ 1 , ∀ i , j ∈ N , ( i , j ) ∈ L '
∑ Z i = p
Z i ∈ { 0,1 } ,   ∀ i ∈ N
Y ij k ≥ 0 ,   ∀ ( i , j ) ∈ L ' , k ∈ N
W i k ≥ 0 ,   ∀ i , k ∈ N : k ≠ i
目标函数中包含式（1）、（2）2个目标函数,分别表示使所有学生上学的旅行成本和学校建设成本之和最小,式（3）—（12）为约束条件。其中式（3）表示 i 居民点学生要么被 i 节点服务,要么从其他地方获取服务。当 Z i = 1 时,表明 i 居民点存在学校, i 居民点学生不需要到其他居民点寻求服务即 ∑ Y ij i = 0 ,反之, i 居民点不存在学校即 Z i = 0 , i 居民点的学生就必须到其他居民点寻找学校即 ∑ Y ij i = 1 。式（4）保证流量守恒即 i 节点的流入量等于 i 节点的流出量,其中 i 节点为中转节点。其中等式的左侧有2项,第一项 ∑ ∑ Y ji k D k 表示 k 居民点学生经过中转居民点 j 或直接（当 j = k 时为直接流入）流入到 i 居民点的总流入量,第二项 D i 表示 i 居民点本身的学生数量（需求量）,二者相加表示 i 节点的总流入量。等式右边 ∑ ∑ Y ij k D k 表示 k 居民点以及 i 居民点学生从 i 居民点流出到其他居民点寻求服务（即上学）。式（5）保证所有学生都有学校上学;式（6）保证只有在有学校的居民点处,才能获取服务;式（7）表示只有在已创建的道路链接上才有流量;式（8）保证为单向链接,这是因为学生如果从 i 居民点到 j 居民点,就不会再从 j 居民点到 i 居民点即不会做重复往返移动;式（9）表示新建学校个数为 p ;式（10）中 Z i 为（0,1）决策变量,表示在 i 居民点处是否需要学校,如果需要学校则为1,否则为0。
（2）情景2（需要道路升级）
目标函数：
Min ∑ ∑ Rt r ij k Y ij k
Min ∑ R c ij X ij + ∑ f i Z i
约束条件：
式（3）—（12）中：
X ij ∈ { 0,1 } , ∀ ( i , j ) ∈ L '
和情景1相比,情景2的目标函数式（14）增加考虑了道路网络的升级情况,在约束条件中增加式（15）即为0,1决策变量,表示道路连接是否被升级,如果被升级则为1,否则为0。
（3）情景3（需要道路修建并升级）
在情景2的基础上,情景3的目标函数增加考虑了道路网络的新建情况。另外,更改情景2模型中的 L ' 为 L 表示已有道路和潜在道路网络链接集合,使用 X ij 表示道路连接 ( i , j ) 是否被修建或升级。

2.2 算法

本文所构建的模型是一个NP难问题,更是计算地理学的空间运筹的难题[20]。故将使用多目标优化（Multi-objective Optimization）方法来解决多目标设施区位—网络设计问题,区别于单目标优化问题,多目标优化的解不是唯一的,而是存在一个最优解集合,集合中的元素称为Pareto最优解或非劣解[21]。针对多目标问题比较常见的智能求解方法是NSGA（Non-dominated Sorting Genetic Algorithm）以及在其基础上发展而来的非支配排序遗传算法NSGA-II（A Fast and Elitist Multi-Objective Genetic Algorithm） [21,22,23],但二者都是以遗传算法为基础的,从遗传算法的交叉和变异算子产生的后代个体通常未必会比父代个体更好,这在一定程度将影响到解的精度。然而遗传算法具有同时处理群体中多个个体即同时对搜索空间中的多个解进行评估,使其具有较好的全局搜索性能,并易于并行化,搜索效率高。进一步地,本文在多目标模拟退火算法（Multi-Objective Simulated Annealing Algorithm,MOSA）[24,25]的基础上吸收了遗传算法的群体搜索、变异和交叉思想,并结合快速非支配排序（Fast Non-dominated Sorting）提出改进的多目标模拟退火算法（Improved Multi-Objective Simulated Annealing Algorithm,IMOSA）。改进后的算法采用Metropolis准则接受后代,所产生的后代大部分比父代个体更好,这样解的精度将得到保障,故使用改进的多目标模拟退火算法对模型进行求解。
本文的主要求解思路是随机初始化群体,群体中每个个体代表一种解决方案（新建学校位置、道路升级和新建方案）,然后计算每个个体的学校建设成本、道路升级新建成本以及学生旅行成本;利用快速非支配排序算法生成Pareto解集（学生旅行成本和建设成本）;在逐渐降温的过程中对当前群体所有个体随机配对进行交叉（单点交叉）和变异,依据Metropolis准则确定新个体,并更新Pareto解集;重复上述过程直到当前温度抵达最低温度算法结束,输出最终的Pareto解集。改进多目标模拟退火算法的主要流程如图1所示。
图1 改进的多目标模拟退火算法流程

Fig. 1 Flow chart of improved multi-objective simulated annealing algorithm

2.3 计算实验

2.3.1 多目标优化算法评价指标
为了检验所提出改进多目标模拟退火算法（IMOSA）的可行性和有效性,通过计算实验将该算法和经典多目标模拟退火算法（MOSA）进行对比。由于多目标优化问题中的Pareto解集均为未知,考虑用非劣解数目（Non-dominance Number, NN）、修正距离（Modified Generation Distance, MGD）以及分散性（Spacing, SP）3个应用性评价指标对算法优化结果进行评价[26,27]:
（1）非劣解数目：当非劣解数量足够多的时候,才能更真实地反映Pareto前沿曲线,相反过少的非劣解很难反应实际的前沿曲线,特别是在Pareto前沿不均匀或不平衡的条件下。
（2）修正距离：该指标的计算结果可表明所得解与近似Pareto解集的逼近程度,其值可通过以下公式计算获得：
MGD = 1 n ∑ i = 1 n d i 2
式中： n 表示算法运行所得解的个数; d i 表示第 i 个解到近似Pareto解集最短距离,当 MGD = 0 时表明所得解均隶属于近似Pareto解集。
（3）分散性：通过计算该指标值可反映Pareto前沿分布的均匀程度,该值可通过以下公式计算获得：
SP = 1 n - 1 ∑ i = 1 n ( d ̅ - d i ) 2
式中： n 表示算法运行所得解的个数; d i 表示第 i 个解所对应目标向量与其最近目标向量之间的距离; d ̅ 为 d i 的平均距离。当 SP = 0 时,说明算法运行所得解均匀分布在Pareto前沿。
2.3.2 算例分析
这里使用Melkote[12]研究中的21节点网络作为算例（图2）,图2中显示了各节点的设施建设成本、需求量以及各节点间网络链接（已有链接和潜在链接）距离。假设新建2个设施,在上文模型构建的基础上,分别利用改进多目标模拟退火和经典多目标模拟退火以及NSGA-II 3种算法进行计算,并对比分析3种算法的性能指标。
图2 21节点网络算例[12]

注：$后的数字表示设施成本;（）里的数字表示需求;线段上的数字表示距离。

Fig. 2 The 21-node network

为了消除实验随机性对算法性能指标评价的影响,分别用这3种算法重复计算10次,分别得到算例最终的Pareto最优前沿解集。然后使用非劣解数目（NN）、修正距离（MGD）、分散性（SP）和计算时间t共4个指标进行算法性能对比分析,并分别运行30次得到各指标的平均值和标准方差,最终计算结果如表1所示。
表1 3种算法性能指标值对比

Tab. 1 Comparisons of performance indicators of three algorithms

算法 NN MGD SP 平均时间/s
平均值/个 总和/个 平均值 标准方差 平均值 标准方差
MOSA 7 216 537.41 246.30 924.29 639.11 84.77
NSGA-II 15 456 276.30 106.20 726.30 315.65 68.62
IMOSA 22 647 130.60 40.12 525.14 170.04 59.53
从表1中可看出,相比MOSA和NSGA-II算法,IMOSA算法计算时间大幅度缩短,得到的Pareto解数目更多,运算效率明显提升。对比3种算法分别运行30次后所得到的各项指标均表明IMOSA算法优于MOSA和NSGA-II算法,IMOSA算法的计算结果能够更好地逼近真实情况,具有更好的收敛性和分布性,且在目标空间分布更加均匀。

3 乡村中小学布局优化系统开发

由于空间运筹算法的复杂性,本文采用开发专门的空间分析平台来处理设施优化布局的技术路线。研究以Visual Studio. Net 2010为开发平台,使用C#语言和ArcGIS Engine 10.0组件库并结合MATLAB编程,开发出基于交通网络的乡村中小学布局优化系统。系统的数据服务层主要包含空间数据和属性数据,其中点线面等矢量数据由SHP文件保存,而居民点人口、学生人数以及道路等级等属性数据存储在DBF文件中。系统使用MATLAB软件编写模拟退火算法计算学校的选址和道路修建升级情况,然后在ArcGIS Engine开发过程中,通过COM组件接口调用MATLAB编写的数学模型函数,最终结合ArcGIS Engine组件库完成数据加载和计算结果显示。
在系统中,我们设计用户首先要获取各居民点学生人数作为需求点需求量,并根据需要输入系统计算所用到的数据（道路图层和需求点图层等）,输入的图层数据将自动保存到数据库中。然后,用户可以根据自己的意图设置设施区位-网络设计模型参数和改进的多目标模拟退火算法参数。接着,用户可通过模拟退火算法并配合从数据库读入的空间数据和属性数据进行计算分析,得到设施新建位置及道路修建升级方案,并通过Arc Engine地图控件将所得结果反馈给用户。图3是设施区位—网络设计系统计算流程图。图4是本文研发的系统运行界面图,系统运行界面中的菜单栏主要包括文件、参数设置、优化结果、属性查询和地图显示等,通过菜单栏的“参数设置”菜单项可进行模型参数以及改进的多目标模拟退火算法参数设置,系统的最终运行结果可通过地图显示模块和结果输出窗口反馈给用户。
图3 设施区位-网络设计系统计算流程

Fig. 3 Flow chart of facility location-network design system calculation process

图4 乡村中小学优化布局系统运行另外界面

Fig. 4 Operation interface of rural schools optimized layout system

4 实例应用

4.1 数据来源和参数设定

为了检验本文提出模型和算法可行性和研发的空间运筹系统的有效性,我们选择贵州省某镇进行实例研究,本研究的基础数据主要包括道路网络图层（高级、中级和低级道路）、居民点图层、已有学校布局图层和行政区划背景图层（从当地相关部门收集图件数据,并使用ArcGIS矢量化获得）,具体如图5所示。通过实地调查,在该实例中,该镇有26个自然村,面积 161.3 km2,人口 24 392人,已有2所小学。各个居民点人口数量的估算参考了彭永明等[4]的方法,具体为使用Google earth获得每个村庄的居民区面积,计算总的居民区面积,然后统计出各村居民区面积和总居民区面积的比例关系,根据此比例关系利用该镇总人口数计算各村人口数量。
图5 包含潜在道路的道路网络

Fig. 5 Road network map containing potential roads

利用ArcGIS软件整理道路数据（已有道路和潜在道路）成道路图层,每条路段的属性包括道路长度和所需时间,依据道路等级（高级、中级和低级）,赋予道路不同的速度,获取路段通行时间,在此基础上构建道路网络拓扑关系,然后创建网络数据集,计算出各个居民点间的最短网络距离（考虑到研究区域较小,距离单位为米）和最短通行时间,使用通行时间作为小学生旅行成本。需要注意的是潜在道路（待修建道路）一定是高级道路,本研究依据Google earth中研究区的实际地形地貌加入6条潜在道路,包含潜在道路的道路网络图如图5所示。假设小学生步行速度为1 m/s,低级道路速度为小学生步行速度,中等级道路为步行速度3倍,高级道路为步行速度4倍。同样假设道路修建升级成本和道路距离成正比例关系,那么新建一条道路、低级道路升高级以及中级道路升高级的成本分别设定为130乘以道路距离、65（130×0.5）乘以道路距离和39（130×0.3）乘以道路距离;依据各个居民点的人口数量确定各个居民点的学校建设成本（分5个等级,等级差为5万）在40万~60万的范围内。参照蒋轩[28]对全国各县地表崎岖度的计算结果,针对该研究区设置模型中的崎岖度系数为1.169。另外,根据模型的计算规模并参考既有研究,初始温度 T 0 取经验值500;终止温度 T f 设置为0.1;降温系数 α 取值为0.95;当前温度下马尔科夫链长 L 设置为30。

4.2 计算与比较分析

4.2.1 情景1优化结果
当新建设施个数为1、2、3时求解得到情景一双目标模型的Pareto最优解集,表2中的每一个解都表示一种最优的选址方案。在求得Pareto最优解集之后,决策者可根据自己的偏好在这些方案中挑选最终的决策方案。由于篇幅所限,仅讨论新建2所学校的情况。如表1所示,新建2所学校所对应的决策方案编号为3—6,旅行成本随着设施建设成本的增大而减小,表明旅行成本的减少是以增加设施建设成本为代价的,2个目标不能同时达到最优,要有所取舍,这也符合双目标优化的特征。其中方案3尽管能保证设施建设成本相对较低,但学生旅行成本较高;方案6尽管能确保学生旅行成本最小,但设施建设成本较高。结合当地的实际情况,在保证学生上学旅行成本尽可能小的情况下,也要兼顾考虑当地政府部门的财政支出状况,所以可从方案4或5中选择,这里选择方案5作为最终决策方案。在方案5中,新建学校位置是15和21。小学生旅行成本总值（第一目标值）为1 315 524,学校设施新建成本为90万（寨云村和风花村）,新建学校位置如图6所示。根据旅行成本值计算可得平均每个学生的上学时间大概为13.2 min。在这26个居民点中,到九龙小学就学的学生数为633,来自 11个居民点;到寨云小学就学的学生数为382,来自6个居民点;到长兴堡小学就学的学生数为516,来自6个居民点;剩下3个居民点的130名学生到风花小学就读。如前所述,按照原教育部规定学生上学时间一般不超过45 min的标准,居民点1、19和25的学生（占总学生数5.4%）上学时间都超过了45 min,而居民点2、10、3和8的学生（占总学生数7.5%）上学时间在40~45 min之间,其他居民点学生的上学时间都小于40 min。
表2 情景1 Pareto最优解对应的方案及目标值

Tab. 2 Scheme and objective function value of Pareto optimal solution in scenario 1

方案编号 新建设施个数(p) 设施选址位置 旅行成本（第一目标值） 设施建设成本（第二目标值）
1 1 1 1 642 335 400 000
2 1 15 1 488 424 450 000
3 2 1,22 1 495 064 800 000
4 2 1,15 1 331 460 850 000
5 2 15,21 1 315 524 900 000
6 2 15,17 1 303 802 1 000 000
7 3 15,17,21 1 130 902 1 450 000
8 3 1,15,21 1 158 560 1 300 000
9 3 1,11,22 1 379 636 1 200 000
10 3 1,11,15 1 216 032 1 250 000
11 3 9,15,17 1 121 438 1 550 000
12 3 1,15,17 1 146 838 1 400 000
图6 情景1下方案5的学校布局结果

Fig. 6 School locations results for scenario 1

4.2.2 情景2优化结果
当新建设施个数为1、2、3时,计算得到情景2双目标模型的Pareto最优解集,如表3所示。和情景1相同,仅讨论新建2所学校的情况,即从编号为7—15的方案中选择。其中方案7尽管能保证设施建设成本相对较低,但学生旅行成本较高;方案15尽管能确保学生旅行成本最小,但设施建设成本较高。在确保学生上学旅行成本尽可能小的同时,也要考虑乡村地区的财政支出,故从方案10—12中选择,这里选择方案12作为最终决策方案。在方案12中,新建学校位置是15和17（寨云村和岩科村）。小学生旅行成本总值（第一目标值）为 622 996,学校设施新建成本为100万,新建学校位置如图7所示。有11条道路由低级升为高级,升级成本为981 305。同样根据旅行成本值可计算得到平均每个学生的上学时间为6.3 min,和情景1相比每个学生上学时间大约减少了7 min,明显提高了学生的就学效率。情景2的学校新建位置和道路升级方案如图7所示。道路升级之后,各居民点学生上学时间均低于45 min,其中居民点1和19的上学时间分别由情景1的54 min和46 min减小到升级后的26.5 min和15 min。另外,居民点8和9的学生上学时间由原来的40 min和36 min减少到升级后的15 min 和9 min。
表3 情景2 Pareto最优解对应的方案及目标值

Tab. 3 Scheme and objective function value of Pareto optimal solution in scenario 2

方案编号 新建设施个数(p) 设施选址位置 旅行成本（第一目标值） 建设成本（第二目标值）
1 1 15 1 295 687 559 000
2 1 15 1 132 810 787 155
3 1 15 1 068 135 890 765
4 1 15 1 002 049 991 840
5 1 15 864 630 1 271 470
6 1 15 807 618 1 431 305
7 2 15,17 1 000 392 1 267 605
8 2 15,17 855 648 1 466 570
9 2 15,17 742 158 1 687 960
10 2 15,17 713 800 1 736 255
11 2 15,17 655 768 1 865 215
12 2 15,17 622 996 1 981 305
13 2 15,17 610 746 2 078 610
14 2 15,17 593 241 2 195 025
15 2 15,17 553 786 2 313 000
16 3 1,15,17 857 898 1 712 325
17 3 1,15,17 750 337 1 874 305
18 3 1,15,17 692 305 2 003 265
19 3 1,15,17 580 291 2 118 835
20 3 1,15,17 548 536 2 199 760
21 3 1,15,17 536 285 2 297 065
22 3 1,15,17 508 400 2 458 200
图7 情景2下方案12的学校布局和道路升级结果

Fig. 7 School locations and road upgrade results for scenario 2

4.2.3 情景3优化结果
当新建设施个数为1、2、3时,计算得到情景3双目标模型的Pareto最优解集,如表4所示。和情景1,2相同,仅讨论新建2所学校的情况,即从编号为8—16的方案中选择。其中方案8尽管能保证设施建设成本相对较低,但学生旅行成本较高;方案16尽管能确保学生旅行成本最小,但设施建设成本较高。为了综合考虑旅行成本和建设成本两个因素,从方案11—12中选择,这里选择方案12作为最终决策方案。在方案12中,新建学校位置是15和17（寨云村和岩科村）,其中小学生旅行成本总值为567 661,学校新建成本为100万。有10条道路由低级升成高级,同时修建了2条新道路,升级和新建道路的成本花费为932 035。情景3的道路升级和新建情况以及新建学校位置如图8所示。升级并新建道路后,除了居民点10,其他居民点学生的上学时间都在20 min以内,相比情景2各个居民点学生上学时间进一步减少。
表4 情景3 Pareto最优解对应的方案及目标值

Tab. 4 Scheme and objective function value of Pareto optimal solution in scenario 3

方案编号 新建设施个数(p) 设施选址位置 旅行成本（第一目标值） 建设成本（第二目标值）
1 1 15 969 011 1 049 911
2 1 15 909 984 1 176 466
3 1 15 797 970 1 292 036
4 1 15 764 372 1 420 996
5 1 15 752 155 1 479 340
6 1 15 720 408 1 560 265
7 1 15 689 716 1 781 031
8 2 15,17 861 953 1 458 445
9 2 15,17 805 014 1 580 320
10 2 15,17 717 808 1 753 675
11 2 15,17 650 227 1 782 035
12 2 15,17 567 661 1 932 035
13 2 15,17 549 277 2 012 960
14 2 15,17 521 388 2 174 095
15 2 15,17 506 368 2 292 070
16 3 15,17,21 897 560 1 859 931
17 3 15,17,21 736 467 2 098 156
18 3 15,17,21 646 687 2 308 041
19 3 15,17,21 522 456 2 481 955
20 3 15,17,21 515 037 2 549 215
21 3 15,17,21 400 220 2 724 416
22 3 15,17,21 372 331 2 885 551
图8 情景3下方案12的学校布局和道路升级及修建结果

Fig. 8 School locations, road upgrades and construction results for scenario 3

4.2.4 各情景下上学时间空间分布
将3个情景下居民点学生上学时间花费分为4个等级（0~15 min, 16~30 min, 31~45 min和46~60 min）,并对各情景下居民点学生上学时间花费的空间分布变化进行分析,具体如图9所示。图9(a)中可看出有13个居民点的学生上学时间小于15 min,学生人数为1073,占总学生数的64.6%,主要分布在高级道路沿线附近。上学时间处于16~30 min之间的居民点有5个,学生数为310,占总人数的8.7%。上学时间大于30 min的居民点有8个,学生数为278人,占总学生数的26.7%,主要分布在道路等级低、人口少的研究区外围地区,其中居民点1的学生上学时间超过了45 min。在情景2中上学时间小于15 min的居民点有20个,学生数为1459人,占学生总数的87.8%,相比情景1多了居民点2、9、13、16和23,说明受道路升级的影响,这5个居民点的学生上学效率有了明显提高（图9（b））。同时在图 9（b）中上学时间大于30 min的居民点由情景1的8个减少到情景2的1个,学生数为155,占总学生数的0.9%。且情景2中没有红色点分布,表明所有居民点的学生上学时间都小于45 min。在情景3中,有23个居民点的上学时间小于15 min,相比情景2又多了3个,学生数为1573人,占总学生数的94.7%（图9（c））。
图9 各情景下各居民点学生上学时间花费空间分布

Fig. 9 The spatial distribution of students' time to school at each village for different scenarios

5 结论与讨论

本文对基于交通网络的乡村中小学优化布局使用的设施区位设计问题的模型与算法进行了探讨,以最小化学生旅行成本、学校建设、道路修建和道路升级成本为目标构建多目标模型,分别在只考虑已有道路、假设道路可升级、假设道路可新建或升级3种情景下进行模型构建和求解分析。研究结果表明：使用改进的多目标模拟退火算法,是可以解决处于山地环境的农村中小学布局的设施区位设计问题,且改进的多目标模拟退火算法吸收了遗传算法的群体搜索、变异和交叉思想,克服了传统多目标模拟退火算法单个个体进化,搜索效率低、精确度有限的问题。另外,本文利用GIS二次开发技术结合MATLAB编程所开发的乡村中小学优化布局系统实现了分析、计算、显示等功能,能够有效解决乡村中小学的优化布局问题,具有很好的可使用性和通用性。经过运行测试,利用改进的多目标模拟退火算法大大提高了系统的运行效率,且具有很好的稳定性。作为应用成果,使用该系统计算了山地省贵州某镇的乡村中小学布局问题,发现相比情景1,情景2学生上学耗时有所减少,情景3学生上学耗时下降明显,学生的就学效率得到了大幅度提升。通过分析可知,交通网络条件对乡村中小学布局优化具有重要影响,合理改善交通条件能够有效提高乡村学生的就学效率,也有利于合理配置和利用教学资源。
目前国内外针对学校优化布局的研究已经有很多,现有研究大多忽略了道路崎岖度以及交通条件对学校选址的影响,不能满足地处山地环境学校布局的特殊需要。基于此,本研究着重考虑了山区交通通行条件对学校选址的影响,并使用设施区位—网络设计方法确定新建学校的最佳位置,优化山区的交通道路网络,从而为乡村地区中小学的优化布局提供决策帮助。本研究也存在一定的局限性,在模型构建过程中没有考虑学校设施的规模限制,本文研究的只是静态的设施区位-网络设计问题,没有考虑各居民点学生数以及设施道路升级创建成本等参数会随时间的推移而变化,同时也没有考虑参数的不确定性,这是今后需进一步解决的问题。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Dost J. Reassessment of the school location problem: A multifunctional role for the school in the urban environment[J]. The Annals of Regional Science, 1968,2(1):136-141.

[2]
Pizzolato N D, Barcelos F B, Lorena N, et al. School location methodology in urban areas of developing countries[J]. International Transactions in Operational Research, 2004,11(6):667-681.

[3]
Tewari V K, JENA S. High school location decision making in rural India and location-allocation. In: GHOSH A, RUSHTON G, editors. Spatial Analysis and Location-Allocation Models[M]. New York: Van Nostrand Reinhold, 1987: 137-162.

[4]
彭永明, 王铮. 农村中小学选址的空间运筹[J]. 地理学报, 2013,68(10):1411-1417.

[ Peng Y M, Wang Z. Space operation of rural primary and secondary school location[J]. Journal of Geography, 2013,68(10):1411-1417. ]

[5]
戴军, 苑惠丽, 马颖忆. 西部乡村基础教育设施“场势效应”评价与空间优化——以海东市蒲台乡为例[J]. 农业现代化研究, 2019,40(4):692-701.

[ Dai J, Yuan H L, Ma Y Y. Spatial optimization of field intensity effect of rural basic education infrastructure in rural Western China: A case study of Putai Township, Haidong, Qinghai[J]. Research of Agricultural Modernization, 2019,40(4):692-701. ]

[6]
戴特奇, 王梁, 张宇超, 等. 农村学校撤并后规模月数对学校优化布局的影响——以北京延庆区为例[J]. 地理科学进展, 2016,35(11):1352-1358.

[ Dai T Q, Wang L, Zhang Y C, et al. Optimizing school distribution with constraints of school size after school consolidation in rural China: A case study of Yanqing District, Beijing City[J]. Progress in Geography, 2016,35(11):1352-1358. ]

[7]
张煊宜. 基于GIS的教育资源均衡性及其空间布局调整分析——以上海市浦东新区为例[D]. 上海:华东师范大学, 2019.

[ Zhang X Y. Research on balanced development and optimization of educational facilities based on GIS: A case study of Pudong New District, Shanghai[D]. Shanghai: East China Normal University, 2019. ]

[8]
刘科伟, 史茹, 唐智渊. 基于供需关系的城市边缘区基础教育设施布局研究——以西安市长安区韦曲街道为例[J]. 地域研究与开发, 2018,37(5):83-88.

[ Liu K W, Shi R, Kang Z Y. Research on the layout planning method of fundamental education facility in Urban fringe based on supply and demand[J]. Areal Research and Development, 2018,37(5):83-88. ]

[9]
丁愫, 陈报章. 城市医疗设施空间分布合理性评估[J]. 地球信息科学学报, 2017,19(2):185-196.

[ Ding S, Chen B Z. Rationality assessment of the spatial distributions of urban medical facility[J]. Journal of Geo-information Science, 2017,19(2):83-88. ]

[10]
詹庆明, 杨爽. 村镇应急公共设施选址布局优化研究[J]. 地球信息科学学报, 2019,21(5):641-653.

[ Zhang Q M, Yang S. Optimization of emergency facilities layout in villages[J]. Journal of Geo-information Science, 2019,21(5):641-653. ]

[11]
Daskin M S, Hurter A P, Vanbuer M G. Toward an integrated model of facility location and transportation network design, Working Paper, Transportation Center[M]. Northwestern University, 1993.

[12]
Melkote S. Integrated models of facility location and network design[D]. Industrial Engineering and Management Science, Northwestern University, Doctor of Philosophy, Evaston, Illinois, 1996.

[13]
Drezner Z, Wesolwsky G O. Network design: Selection and design of links and facility location[J]. Transportation Research Part A, 2003,37(3):241-256.

[14]
Murawski L, Church R L. Improving accessibility to rural health services: The maximal covering network improvement problem[J]. Socio-Economic Planning Sciences, 2009,43:92-110.

[15]
Bigotte J F, Krass D, et al. Integrated modeling of urban hierarchy and transportation network planning[J]. Transportation Research Part A, 2010,44:506-522.

[16]
Contreras I, Fernandez E, Reinelt G. Minimizing the maximum travel time in a combined model of facility location and network design[J]. Omega, 2012,40(6):847-860.

[17]
Rahmamiani R, Ghaderi A. A combined facility location and network design problem with multi-type of capacitated links[J]. Applied Mathematical Modelling, 2013,37:6400-6414.

[18]
Ghaderi, A., Jabalameli, M.S. Modeling the budget-constrained dynamic un-capacitated facility location-network design problem and solving it via two efficient heuristics: A case study of health care[J]. Mathematical and Computer Modelling. 2013,57:382-400.

[19]
Rahmaniani, R., Ghaderi, A. An algorithm with exploration mechanisms: Experimental results to capacitated facility location/network design problem[J]. Expert Systems with Applications, 2015,42:3790-3800.

[20]
王铮, 吴静. 计算地理学[M]. 北京: 科学出版社, 2016.

[ Wang Z, Wu J. Computation Geography[M]. Beijing: Science Press, 2016. ]

[21]
Chankong V, Haimes Y Y. Multi-objective decision making theory and methodology[M]. New York: North-Holland, 1983.

[22]
Deb K, Agrawal S, PRATAP A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II//International Conference on Parallel Problem Solving from Nature[C]. Berlin: Springer-Verlag, 2000: 849-858.

[23]
Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE Trans on Evolutionary Computation, 2002,6(2):182-197.

[24]
Metropolis N A, Rosebnluth A, Tellernad A, et al. Equation of state calculations by fast computing machines[J]. Journal of Chemical physical, 1953,21:1087-1092.

[25]
Kirkpatrick S, Gelat C D, Vecchi M P, Optimization by simulated annealing[J]. Science, 1983,220:671-680.

[26]
张明明, 赵曙光, 王旭. 一种自适应多目标离散差分进化算法[J]. 计算机工程与应用, 2009,45(26):16-20.

[ Zhang M M, Zhao S G, Wang X. Adaptive multi-objective discrete differential evolution[J]. Computer Engineering and Applications, 2009,45(26):16-20. ]

[27]
刘思远, 柳景青. 一种新的多目标改进和声搜索优化算法[J]. 计算机工程与应用, 2010,46(34):27-30.

[ Liu S Y, Liu J Q. Novel improved multi-objective harmony search optimization algorithm[J]. Computer Engineering and Applications, 2010,46(34):27-30. ]

[28]
蒋轩. 基于新经济地理学连片特困地区致贫因子分析[D]. 上海:华东师范大学, 2017: 10-24.

[ Jiang X. Analysis of poverty factors in contiguous destitute areas: An analysis based on new geographic economics three nature theories[D]. Shanghai: East China Normal University, 2017: 10-24. ]

Options
文章导航

/

〈 〉