

基于刷卡数据的公共汽车客流网络复杂性日内变化研究
|
赵韶雅(1994— ),女,山西长治人,硕士生,主要研究方向为大数据与城市交通。E-mail: zhaoshaoya0820@mail.bnu.edu.cn |
收稿日期: 2019-10-05
要求修回日期: 2019-11-28
网络出版日期: 2020-08-25
基金资助
国家自然科学基金面上项目(41871128)
版权
Within-Day Variation of the Complexity of Bus Passenger Flow Network based on Smart Card Data
Received date: 2019-10-05
Request revised date: 2019-11-28
Online published: 2020-08-25
Supported by
National Natural Science Foundation of China(41871128)
Copyright
大城市公共交通是一个典型的复杂巨系统,采用复杂网络方法分析大城市公共交通网络系统对于城市交通发展具有重要意义。已有大量的研究采用复杂网络理论进行了公共交通线路网络分析,也有研究基于刷卡数据分析了公共交通客流网络的复杂特征,但少有研究探讨客流网络复杂性日内变化特征。鉴于此,本文基于北京市公共汽车刷卡数据识别的不同时间段客流双向邻接矩阵,通过复杂网络指标对比分析公共汽车客流网络的日内变化特征。结果表明:① 各个时间段公共汽车客流分布遵循距离衰减规律,5 km以下的短距离出行约占总出行量的一半左右;② 度中心性和加权度中心性的空间格局在不同时间段整体呈现出明显的核心-边缘特征,但随时间有一定程度的变化,加权度中心性排名前10的节点存在较大变化;③ 累积度分布和累积加权度分布服从指数分布,属于小世界网络。本文还进一步讨论了基于大数据的动态复杂网络研究对城市交通规划建设的启示意义。
赵韶雅 , 杨星斗 , 戴特奇 , 张超 . 基于刷卡数据的公共汽车客流网络复杂性日内变化研究[J]. 地球信息科学学报, 2020 , 22(6) : 1254 -1267 . DOI: 10.12082/dqxxkx.2020.190576
Public transportation in large cities is a typical complex giant system. The use of complex network methods to analyze large city public transport network systems is of great significance for urban transport development. Most of current studies take public transport stations as nodes and routes as connecting edges to construct an abstract network adjacency matrix, so to analyze the complexity characteristics of public transport networks according to indicators such as average (shortest) path length, clustering coefficient, degree distribution, node proximity or median centrality. However, the complexity of urban public transport network is not a static topology network composed of bus stops, routes, and their interconnections, but also the dynamic traffic information, which is seldom considered in existing studies. Distinguishing the characteristics of the passenger flow network in different time periods is of great value for formulating time-sharing public transport management policies. Meanwhile, the widely used big data recently provide high-precision traffic information for the study of dynamic traffic network structures. In this paper, we constructed the bidirectional adjacency matrix of passenger flows in different time periods based on swipe card data of Beijing buses, then compared and analyzed the within-day variation of the bus passenger flow network through complex network indexes. In terms of the structural characteristics, the bus passenger flow network in each time period had a small average shortest path and a large clustering coefficient, meaning a small-world network; the distribution of accumulation degree was fitted as an exponential distribution, which indicates that the bus passenger flow network did not have scale-free characteristics. The bus passenger flow distribution in each time period had an obvious distance attenuation rule, and it was mainly for short-distance travels below 10km, which suggests the bus line and operation management should focus on the distance range below 10 km. Degrees centricity and weighted degree centrality of the spatial pattern in different times presented an obvious core-edge character but changing over time; the weighted degree centrality in the top 10 nodes changed a lot, according to which dynamic public transport hubs should be considered in a precious and accurate traffic planning and management. Our findings provide a reference for public transport planning and management policies. In the future, more comprehensive passenger flow data should be used to explore the structural characteristics from a multi-scale perspective.

表1 北京市公共汽车刷卡数据示例Tab. 1 Examples of data records of smart cards in the Beijing bus system |
| 卡号信息 | 卡号类型 | 刷卡次序 | 交易时间 | 线路号 | 车牌号 | 上车站点 | 下车站点 |
|---|---|---|---|---|---|---|---|
| 75487061 | 1 | 622 | 20150814073030 | 62026 | 87501 | 6 | 14 |
| 71755266 | 18 | 598 | 20150814080505 | 331 | 420099 | 18 | 22 |
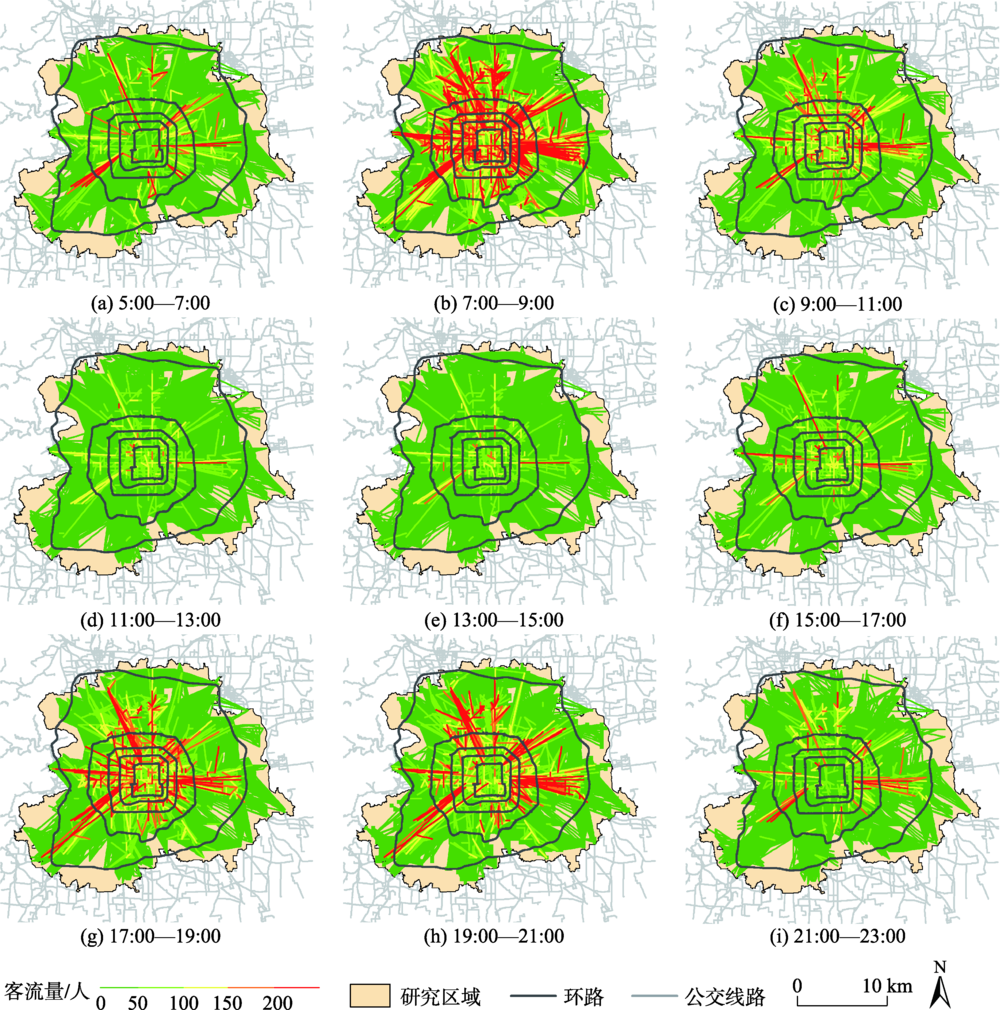
图1 北京市2015年8月13日各个时间段的客流网络联系Fig. 1 Passenger flow network for each time period on August 13, 2015, Beijing |
表2 北京市2015年8月13日各个时间段的栅格间流量基本属性Tab. 2 Statistics of the passenger flow between grids for each time period on August 13, 2015, Beijing |
| 时段 | 总量/万人 | 最大值/人 | 最小值/人 | 均值/人 | 方差 |
|---|---|---|---|---|---|
| 5:00—7:00 | 29.02 | 497 | 1 | 6.71 | 14.35 |
| 7:00—9:00 | 137.15 | 2223 | 1 | 18.99 | 46.01 |
| 9:00—11:00 | 74.46 | 1272 | 1 | 11.45 | 24.12 |
| 11:00—13:00 | 47.33 | 870 | 1 | 8.02 | 15.56 |
| 13:00—15:00 | 41.83 | 612 | 1 | 7.47 | 14.36 |
| 15:00—17:00 | 51.16 | 773 | 1 | 8.58 | 17.40 |
| 17:00—19:00 | 100.35 | 1849 | 1 | 14.74 | 34.00 |
| 19:00—21:00 | 75.09 | 1460 | 1 | 11.70 | 27.70 |
| 21:00—23:00 | 32.03 | 547 | 1 | 7.25 | 15.02 |
表3 北京市2015年8月13日各个时间段距离衰减模式主要参数的拟合结果Tab. 3 Main coefficients of distance decay models of the traffic flow for each period on August 13, 2015, Beijing |
| 客流时段 | a | b | R2 | F | F(α=0.01)≈13.75 |
|---|---|---|---|---|---|
| 5:00—7:00 | 2.33 | 0.21 | 0.98 | 376.07 | 通过检验 |
| 7:00—9:00 | 2.27 | 0.21 | 0.99 | 826.48 | 通过检验 |
| 9:00—11:00 | 2.07 | 0.21 | 1.00 | 1717.13 | 通过检验 |
| 11:00—13:00 | 1.85 | 0.20 | 1.00 | 4813.44 | 通过检验 |
| 13:00—15:00 | 1.87 | 0.20 | 1.00 | 2630.49 | 通过检验 |
| 15:00—17:00 | 1.97 | 0.210 | 1.00 | 1535.94 | 通过检验 |
| 17:00—19:00 | 1.84 | 0.201 | 1.00 | 4893.22 | 通过检验 |
| 19:00—21:00 | 1.74 | -0.19 | 1.00 | 1501.15 | 通过检验 |
| 21:00—23:00 | 2.91 | -0.23 | 1.00 | 498.83 | 通过检验 |
图5 北京市2015年8月13日各个时间段加权入度中心性空间格局Fig. 5 Spatial pattern of the weighted in degree centrality for each time period on August 13, 2015, Beijing |
表4 北京市2015年8月13日各个时间段加权度中心性排名前10的节点Tab. 4 Weighted centrality of the top 10 nodes for each time period on August 13, 2015, Beijing |
| 时段 | 加权度中心性 | 排名前10的节点 |
|---|---|---|
| 5:00—7:00 | 入 | 国贸、六里桥东、四惠、东直门、国贸东、天通苑北、六里桥北、燕莎桥南、北京西站、北京儿童医院 |
| 出 | 六里桥北、六里桥东、东直门、国贸东、北皋、国贸、四惠、东坝中路南口、东坝、大屯 | |
| 7:00—9:00 | 入 | 国贸、四惠、国贸东、东直门、大屯、北京儿童医院、六里桥东、西直门、中关村、天通苑北 |
| 出 | 国贸、四惠、东直门、六里桥北、六里桥东、大屯、北京儿童医院、航天桥、马甸桥、西直门 | |
| 9:00—11:00 | 入 | 国贸、中关村、东直门、四惠、国贸东、大屯、白石桥东、北京儿童医院、西直门、红庙路口 |
| 出 | 国贸、四惠、东直门、大屯、六里桥北、北京西站、红庙路口、六里桥东、西直门、国贸东 | |
| 11:00—13:00 | 入 | 国贸、东直门、大屯、四惠、前门、北京西站、六里桥东、国贸东、北京儿童医院、六里桥北 |
| 出 | 国贸、东直门、四惠、北京西站、大屯、北京儿童医院、六里桥北、六里桥东、西直门、国贸东 | |
| 13:00—15:00 | 入 | 国贸、东直门、大屯、四惠、北京西站、北京儿童医院、六里桥东、前门、六里桥北、国贸东 |
| 出 | 国贸、四惠、东直门、北京西站、大屯、六里桥东、北京儿童医院、木樨园桥、六里桥北、国贸东 | |
| 15:00—17:00 | 入 | 国贸、东直门、四惠、北京西站、大屯、六里桥北、六里桥东、前门、牡丹园、西直门 |
| 出 | 国贸、东直门、四惠、北京西站、大屯、北京儿童医院、动物园、西直门、六里桥东、木樨园桥 | |
| 17:00—19:00 | 入 | 六里桥北、四惠、国贸、大屯、东直门、六里桥东、牡丹园、通惠、西直门、八宝山 |
| 出 | 国贸、四惠、大屯、北京儿童医院、六里桥东、国贸东、东直门、北京西站、六里桥北、木樨园桥 | |
| 19:00—21:00 | 入 | 四惠、国贸、六里桥北、大屯、通惠、东直门、六里桥东、北京西站、沙河、红庙路口 |
| 出 | 国贸、四惠、国贸东、东直门、中关村、天通苑北、六里桥东、大屯、北京西站、六里桥北 | |
| 21:00—23:00 | 入 | 六里桥北、大屯、四惠、国贸、北京西站、北京西站、六里桥东、牡丹园、东直门、立水桥 |
| 出 | 国贸、中关村、四惠、国贸东、天通苑北、大屯、东直门、立水桥、北京西站、六里桥东 |
表5 北京市2015年8月13日各个时间段客流网络和随机网络的网络特性对比Tab. 5 Comparison of network characteristics between the passenger flow network and random network for each time period on August 13, 2015, Beijing |
| 时段 | L | Lr | C | Cr |
|---|---|---|---|---|
| 5:00—7:00 | 3.32 | 2.54 | 0.41 | 0.02 |
| 7:00—9:00 | 2.84 | 2.20 | 0.52 | 0.03 |
| 9:00—11:00 | 2.89 | 2.26 | 0.50 | 0.03 |
| 11:00—13:00 | 2.90 | 2.31 | 0.48 | 0.03 |
| 13:00—15:00 | 2.93 | 2.33 | 0.47 | 0.02 |
| 15:00—17:00 | 2.94 | 2.30 | 0.48 | 0.03 |
| 17:00—19:00 | 2.88 | 2.24 | 0.51 | 0.03 |
| 19:00—21:00 | 2.87 | 2.27 | 0.49 | 0.03 |
| 21:00—23:00 | 3.06 | 2.43 | 0.41 | 0.02 |
| [1] |
|
| [2] |
吴康, 方创琳, 赵渺希. 中国城市网络的空间组织及其复杂性结构特征[J]. 地理研究, 2015,34(4):711-728.
[
|
| [3] |
陈光, 温广辉, 虞文武. 基于复杂网络的城市公交网络研究综述[J]. 南京信息工程大学学报(自然科学版), 2018,10(4):401-408.
[
|
| [4] |
王姣娥, 莫辉辉, 金凤君. 中国航空网络空间结构的复杂性[J]. 地理学报, 2009,64(8):899-910.
[
|
| [5] |
段德忠, 刘承良, 杜德斌, 等. 基于二分网络的北京公交线路布局的空间依赖性[J]. 地理学报, 2016,71(12):2185-2198.
[
|
| [6] |
唐秋生, 冯海峰, 李维. 基于复杂网络理论的长沙市公交网络拓扑性质研究[J]. 交通信息与安全, 2013,31(4):49-52.
[
|
| [7] |
许晴, 祖正虎, 徐致靖, 等. 330个中国城市P空间下公交复杂网络实证研究[J]. 交通运输系统工程与信息, 2013,13(1):193-198.
[
|
| [8] |
钟少颖, 王宁宁, 陈锐. 北京市公交网络枢纽性和抗毁性——基于复杂网络分析方法的研究[J]. 城市发展研究, 2016,23(6):123-132.
[
|
| [9] |
王姣娥, 焦敬娟, 黄洁, 等. 交通发展区位测度的理论与方法[J]. 地理学报, 2018,73(4):666-676.
[
|
| [10] |
|
| [11] |
王凯, 甘畅, 杨亚萍, 等. 长江中游城市群市域旅游经济网络结构演变及其驱动因素[J]. 地理与地理信息科学, 2019,35(5):118-125.
[
|
| [12] |
孟德友, 冯兴华, 文玉钊. 铁路客运视角下东北地区城市网络结构演变及组织模式探讨[J]. 地理研究, 2017,36(7):1339-1352.
[
|
| [13] |
余红楚, 方志祥, 陆锋, 等. 重要经济发展区域间海运网络时空演变特性分析[J]. 地球信息科学学报, 2018,20(5):582-592.
[
|
| [14] |
刘帅宾, 杨山, 王钊. 基于人口流的中国省域城镇化空间关联特征及形成机制[J]. 地理学报, 2019,74(4):648-663.
[
|
| [15] |
陈少沛. 城市地铁网络拓扑时空演变特征模型研究[J]. 地理空间信息, 2019,17(9):5-9.
[
|
| [16] |
龙瀛, 张宇, 崔承印. 利用公交刷卡数据分析北京职住关系和通勤出行[J]. 地理学报, 2012,67(10):1339-1352.
[
|
| [17] |
孟斌, 黄松, 尹芹. 北京市居民地铁出行出发时间弹性时空分布特征研究[J]. 地球信息科学学报, 2019,21(1):107-117.
[
|
| [18] |
刘瑜, 詹朝晖, 朱递, 等. 集成多源地理大数据感知城市空间分异格局[J]. 武汉大学学报·信息科学版, 2018,43(3):327-335.
[
|
| [19] |
徐晓宇, 李梅. 基于开源大数据的北京地区餐饮业空间分布格局[J]. 地球信息科学学报, 2019,21(2):215-225.
[
|
| [20] |
尹芹, 孟斌, 张丽英. 基于客流特征的北京地铁站点类型识别[J]. 地理科学进展, 2016,35(1):126-134.
[
|
| [21] |
赵梓渝, 魏冶, 杨冉, 等. 中国人口省际流动重力模型的参数标定与误差估算[J]. 地理学报, 2019,74(2):203-221.
[
|
| [22] |
徐敏, 黄震方, 曹芳东, 等. 基于大数据分析的城市旅游地网络结构特征及其演化模式——以新浪微博签到数据为例[J]. 地理研究, 2019,38(4):937-949.
[
|
| [23] |
刘大均. 长江中游城市群旅游流空间格局及发展模式[J]. 经济地理, 2018,38(5):217-223.
[
|
| [24] |
黄爱玲, 关伟, 毛保华, 等. 北京公交线路客流加权复杂网络特性分析[J]. 交通运输系统工程与信息, 2013,13(6):198-204.
[
|
| [25] |
陈培文, 陈峰, 胡映月, 等. 基于复杂网络的城市轨道交通网络中心性研究[J]. 复杂系统与复杂性科学, 2017,14(2):97-102,109.
[
|
| [26] |
冯佳, 许奇, 李夏苗, 等. 城市轨道交通系统网络复杂性研究[J]. 交通运输系统工程与信息, 2017,17(6):242-247.
[
|
| [27] |
黄洁, 王姣娥, 靳海涛, 等. 北京市地铁客流的时空分布格局及特征——基于智能交通卡数据[J]. 地理科学进展, 2018,37(3):397-406.
[
|
| [28] |
|
| [29] |
莫辉辉, 王姣娥. 复杂交通网络: 结构、过程与机理.北京:经济管理出版社, 2012.
[
|
| [30] |
吴建军, 高自友, 孙会君, 等. 城市交通系统复杂性——复杂网络方法及其应用[M]. 北京: 科学出版社, 2010.
[
|
| [31] |
王静, 刘剑锋, 马毅林, 等. 北京市轨道交通车站客流时空分布特征[J]. 城市交通, 2013,11(6):18-27.
[
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
王成金. 中国交通流的衰减函数模拟及特征[J]. 地理科学进展, 2009,28(5):690-696.
[
|
| [36] |
陈卓, 金凤君, 杨宇, 等. 高速公路流的距离衰减模式与空间分异特征——基于福建省高速公路收费站数据的实证研究[J]. 地理科学进展, 2018,37(8):1086-1095.
[
|
/
| 〈 |
|
〉 |