一种逐级合并OD流向时空联合聚类算法

项秋亮; 邬群勇; 张良盼

doi:10.12082/dqxxkx.2020.190276

地球信息科学学报 >

2020 , Vol. 22 >Issue 6: 1394 - 1405

DOI: https://doi.org/10.12082/dqxxkx.2020.190276

数据共享与数据挖掘

一种逐级合并OD流向时空联合聚类算法

项秋亮 ¹^,²^,³ ,
邬群勇 ^,¹^,²^,³^,^* ,
张良盼 ¹^,²^,³

展开

1. 数字中国研究院（福建）,福州 350003
2. 福州大学卫星空间信息技术国家地方联合工程研究中心,福州 350108
3. 空间数据挖掘与信息共享教育部实验室,福州 350108

* 邬群勇（1973— ）,男,山东诸城人,博士,研究员,研究方向为时空大数据分析、地理信息服务。 E-mail: qywu@fzu.edu.com

项秋亮（1995— ）,男,安徽黄山人,硕士生,研究方向为空间数据挖掘。E-mail: qiuliangxiang@outlook.com

收稿日期: 2019-06-03

要求修回日期: 2020-02-13

网络出版日期: 2020-08-25

基金资助

国家自然科学基金项目(41471333)

中央引导地方科技发展专项项目(2017L3012)

版权

收起

An OD Flow Spatio-temporal Joint Clustering Algorithm based on Step-by-step Merge Strategy

XIANG Qiuliang ¹^,²^,³ ,
WU Qunyong ^,¹^,²^,³^,^* ,
ZHANG Liangpan ¹^,²^,³

Expand

1. The Academy of Digital China (Fujian), Fuzhou 350003, China
2. National & Local Joint Engineering Research Center of satellite-spatial Information Technology, Fuzhou University, Fuzhou 350108, China
3. Key Laboratory of Spatial Data Mining & Information Sharing of MOE, Fuzhou 350108, China

* WU Qunyong, E-mail: qywu@fzu.edu.com

Received date: 2019-06-03

Request revised date: 2020-02-13

Online published: 2020-08-25

Supported by

National Natural Science Foundation of China(41471333)

The Central Guided Local Development of Science and Technology Project(2017L3012)

Copyright

Fold

摘要

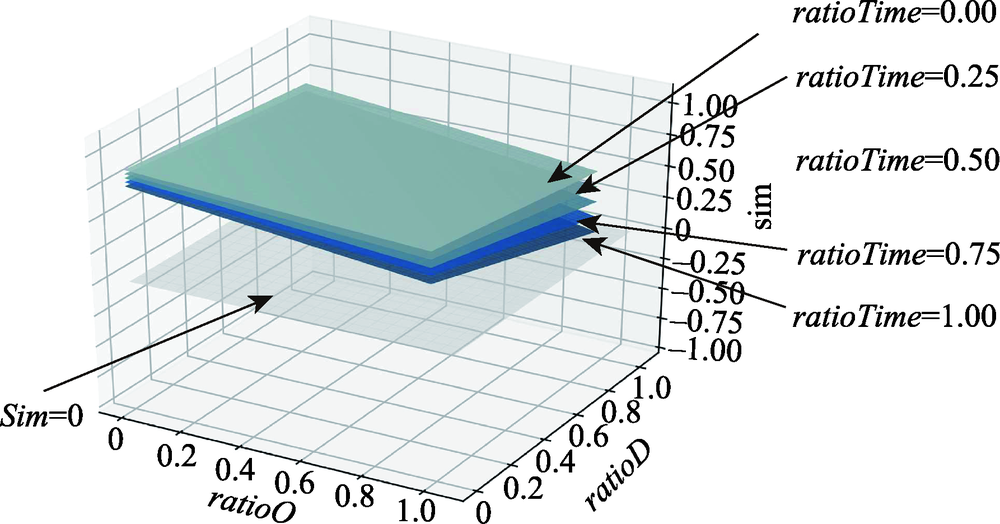
现有OD流向聚类多将O点和D点相分离或者将OD流向看作4维空间的数据点进行聚类处理,忽视了流向长度、方向、时间对流向聚类的影响。本文以流向作为研究对象,提出一种基于流向间相似性度的逐级合并OD流向时空联合聚类算法。首先在充分研究OD流向的空间信息和时间信息的基础上,构建合理的OD流向间时空相似性度量方法,对OD流向间的时空相似性进行量化;然后提出逐级合并OD流向聚类策略,优化类簇合并的顺序,以减少层次聚类的时间开销,实现OD流向的时空联合聚类。以成都市的滴滴出行OD数据和纽约市出租车数据为例对本文方法进行了验证,结果表明：① 本算法聚类获得的流向类簇不仅带有空间特征还具备时间特征;② 在不同参数下本方法可以得到不同时空尺度的聚类结果;③ 与现有较高水平的流向聚类算法相对比,本文方法的聚类效果更好。这体现在流向类簇内部的流向之间有着充分的相似性,以及本文方法不仅可以提取出显著的流向类簇,还可以提取出非热点区域之间的流向类簇。本算法顾及空间因素和时间因素,可以通过调整时空相似性度量方法中的时间参数和空间参数以实现不同时空尺度的流向聚类,这使得从不同时空角度研究城市居民出行模式成为可能。本文提出的OD流向时空联合聚类算法从联合时间信息和空间信息的角度获得对运动数据的新见解,有助于合理全面地研究居民的移动模式、区域之间的空间联系、已知出行结构的确定以及出行目的的探索,是后续一系列分析工作的基础。

关键词： OD流向; 时空联合聚类; 时空相似性度量; 逐级合并策略; 层次聚类; 时空尺度; 移动模式; 空间联系

本文引用格式

项秋亮 , 邬群勇 , 张良盼 . 一种逐级合并OD流向时空联合聚类算法[J]. 地球信息科学学报, 2020 , 22(6) : 1394 -1405 . DOI: 10.12082/dqxxkx.2020.190276

Abstract

Most of the existing OD flow clustering methods adopt the strategy of dividing the OD flow into O point and D point or considering flow as the four-dimensional point to implement flow clustering, which ignores the effects caused by the length, direction and time information on the clustering process. In this paper, we proposedabrand-new spatio-temporal flow clustering method based on the similarity between flows with a strategy of merging flow clusters under different grading. Firstly, a reasonablespatio-temporal similarity measurement formula of OD flow was constructed to quantify the spatio-temporal similarity between OD flows on the basis of full stydy of OD flow's spatial information and temporal information. Then, with the purpose of optimizing the order of merging flow clusters, reducing the time consumption of clustering process, a strategy of merging flow clusters under different grading was used to complete flow clustering. In this method, both of time information and spatial information weretaken into consideration. By modifying the parameters of the spatio-temporal similarity measurement formula, our method can obtain clustering results for different time scales and spatial scales, which makes it possible to analyze the movement patterns from a multi-scale perspective. To verify the effective of our method, a series of experiments on real dataset was executed. The clustering results demonstrate that: ①flow clusters discovered by our method not only hadspatial characteristic but also hadtemporal characteristic; ② our method can discover different spatio-temporal OD flow cluster under different spatio-temporal parameters; ③ by comparingthe clustering results of our method with previous work of advanced technology level, it turnedout that our method hada better clustering performance, which was reflected in the fact that flows within the same flow cluster satisfied the similarity relationship and our method can not only find the obvious movements patterns but also capture inconspicuous movements patterns between non-hot zones. Thespatio-temporal joint OD flow clustering method proposed in this paper obtains new insights into motion from the perspective of joint temporal and spatial information, which is conducive to a reasonable and comprehensive study of residents' movement patterns, spatial linkage between regions, the determination of the known travel structure, and the exploration of the purpose of travel. The process of OD flow clutsering is the beginning of a series of subsequent analysis.

Key words： OD flow; spatio-temporal joint clustering; spatio-temporal similarity measure; step-by-step merge strategy; hierarchical clustering; spatio-temporal scales; movement patterns; spatial linkage

1 引言

随着移动定位技术的快速发展与普及,移动轨迹数据,如人类日常活动轨迹数据、群体迁徙轨迹数据以及车辆轨迹数据等越来越容易被获取^[1]。移动轨迹数据及其空间交互关系的研究对理解复杂的地理现象以及其时空动态变化具有重要意义^[1,2,3,4]。OD流向数据是一种比较特殊的移动轨迹数据,它只保留了Origin（起始点）与Destination（终止点）的位置信息但忽略了实际的轨迹信息^[5]。OD流向可以视为2个地理位置之间的空间关联,对OD流向数据进行分析研究可以发掘出不同地点之间是否存在关联关系以及存在着怎样的关联关系,广泛应用在疾病^[6-7,16]、经济^[8,16]、交通^[9-12,16]、移民^{[13,14,15,16]}等领域。

流向聚类是对OD流向进行分析的一个重要研究手段^[17,18]。流向数据可视在地图上可以直观反映不同位置之间关联关系及群体或货物的流动模式,随着OD流向数量的增加,流向间的相互遮挡现象会十分严重,导致可视分析效果越来越差,通过对多条在地理上相邻近的OD流向聚合到一组流向类簇中,将有效地减轻流向间的遮挡现象。此外,通过对流向进行聚类,不同地理位置之间的关联关系将显示得更为明显,群体或货物流动的空间结构将更容易确定。Gao等^[1]将OD流向看做四维空间中的数据点,在空间扫描统计方法的基础上拓展出一种多维空间扫描统计方法的基础上结合假设检验对OD流向类簇识别,识别得到的类簇的O点范围和D点范围均为圆形。Song等^[16]提出了一种基于蚁群优化算法的空间扫描统计方法用于识别OD流向类簇,识别得到的类簇的O点范围和D点范围是任意形状的。虽然经过拓展和优化的空间扫描统计方法可以有效地识别OD流向类簇,但是忽视了OD流向聚类的整体流程。基于层次聚类算法的OD流向聚类算法通过计算流向之间在O点和D点处的距离结合预定义的研究单元划分^[17,19]或KNN算法^[3]等进行聚类,得到的聚类结果与所选取的参数有关,通常选取不同的参数可以得到不同的聚类效果。基于层次聚类的OD流向聚类方法通常会遇到最优化参数选取的问题。Zhou等^[18]将OD流向的O点和D点分离,利用改进的DBSCAN算法计算每个点周边O点和D点 2种类簇点的密度,进而提取点的类簇。Pei等^[15]利用基于密度的传统聚类方法设计聚类方法,得到的聚类结果具有任意形状且该聚类算法过滤噪声的效果较好。但是以上聚类算法多数将OD流向的O点和D点相分离或者将OD流向看作4维空间的数据点^[1]进行聚类处理,忽视了流向长度、方向、时间对流向聚类的影响,如Gao等^[1]中得到的结果对较短的OD流向进行类簇识别的效果较差。He等^[5]剖析了OD流向长度对流向相似性的影响,在此基础上结合熵理论知识和概率分布模型提取OD流向类簇,保证了聚类结果具有统计学意义,但是该方法忽略了OD流向在时间上的相关性。Yao等^[20]从OD流向的方向、角度和长度研究OD流向之间的空间相似性,提出了一种分步策略的流向聚类方法,先对流向数据进行空间聚类,再对空间聚类的结果进行时间聚类,得到的OD流向类簇同时具有时空属性,但该方法对流向之间的时间相似性判断上要求两条流向的时间存在重合,同时割裂了时间因素和空间因素对流向聚类的共同影响。

本文针对OD流向长度、方向、时间对流向聚类的影响,提出一种OD流向时空联合聚类方法。首先,分析OD流向长度和方向对聚类的影响,研究OD流向间的空间相似性度量方法,针对时间聚类的影响,研究OD流向间的时间相似性度量方法,整合空间和时间相似性度量方法,计算OD流向间的时空相似度;然后,基于OD流向的时空相似性度量方法构建类簇合并的合并限制规则,提出一种逐级合并策略的OD流向层次聚类方法,控制OD流向类簇的合并顺序并减少迭代次数,加快运行效率。

2 OD流向时空相似性度量

2.1 OD流向空间相似性计算

2条OD流向相似,不仅要求其O点和D点在地理上相邻近,还要求这2条流向的方向应该保持相似。研究2条流向（f_i,f_j）之间的相似性关系,如图1（a）所示。

显示原图|下载原图ZIP|生成PPT

图1 OD流向空间相似度关系比对示意

Fig. 1 Comparison diagram of OD flow spatial similarity relationship

图1中,O_i,D_i,O_j,D_j分别为流向f_i,f_j的O点和D点,半径disLimit是判断f_i与f_j空间相似的距离阈值,分别以O_i,D_i为圆心,以disLimit为半径画一个圆,如果O_j,D_j分别在对应的圆中,则说明f_j是f_i的相似流向,即满足下述条件：

（1）

dist O i, O j ≤ disLimt ⋂ dist D i, D j ≤ disLimit

式中：

dist O i, O j

为2条流向f_i,f_j在O点处的距离;

dist D i, D j

为f_i,f_j在D点处的距离。

由式(1)可知,disLimit的取值大小是判断2条流向之间的相似性的关键。如果disLimit是固定值,流向判别将会出现以下错误：图1（a）较之于图1（b）f_j和f_i的相似性程度更高,但在固定值的disLimit下,图1（a）和图1（b）的

dist O i, O j disLimit

和

dist D i, D j disLimit

相近,将会导致在判断相似性程度时出现定量上的错误。图1（c）中流向f_i和f_j在目视判别下显然不相似,但利用式（1）则判断f_j是f_i的相似流向,这是固定值的disLimit在定性上的错误。

He等^[5]在定义流向之间的空间相似性过程中,提出了流向长度不小于搜索半径的2/sin 45°（≈2.83）倍,这保证了2条位置相邻的OD流向之间的夹角小于45°。故本文设定disLimit是一个与中心流向f_i长度相关的数值,二者关系如式（2）所示。

（2）

disLimit = lengt h (f i) k

其中,k≥2.83。在实验过程中用户可以通过调整参数k的数值,得到不同空间精度的实验结果。综合式（1）和式（2）对OD流向的空间相似性进行计算。需要注意的是,当OD流向长度过长时会导致disLimit过长,这将导致对应的流向类簇的O/D区域跨越较大的空间范围,模糊了聚类的空间特征,为防止该情况,需要对人为地对disLimit的设置做出限制,即流向长度大于一定长度时,disLimit被设置为固定值。这种限制的设定依赖于经验与研究需求,用户可以根据自己的研究数据和研究需求来判断是否需要添加该限制,如果研究的目为精细地研究出行模式,用户可在流向长度较短时添加限制,如果研究旨在宏观把握出行特点,可以在流向长度较长时添加限制或者不添加限制。

2.2 OD流向的时间相似性计算

每一条流向中都带上车点时间oTime和下车点时间dTime,可以通过判断两条流向的上车点时间或者下车点时间是否相近判断两条流向在时间上是否相似,如图2所示。图2中

span (tim e i, tim e j)

为流向f_i与f_j之间的时间间隔,timeLimit是人为设置的一个判断流向间相似性的时间参数,如果

span (ti m e i, tim e j) ≤ timeLimit

,则说明f_j在时间上与f_i相似,反之亦反。

显示原图|下载原图ZIP|生成PPT

图2 OD流向间时间相似关系判断

Fig. 2 OD flow time similarity relationship judgment

结合OD流向间的空间相似性和时间相似性,构建了OD流向间的相似性度量方法。

（3）

sim f i, f j = 1 - func ratioO × func ratioD × func (ratioTime) / 23

其中,

（4）

ratioO = dist (O i, O j) disLimit

（5）

ratioD = dist (D i, D j) disLimit

（6）

ratioTime = span (tim e i, tim e j) timeLimit

（7）

func ratio = ratioratio ≤ 1 ∞ rati o > 1

由式（3）可知,当满足条件ratioO≤1∩ratioD≤1∩ratioTime≤1,则2条流向相似。ratio值(ratioO、ratioD、ratioTime)越小,2条流向在空间/时间上越相似。

为避免在流向相似性计算过程中,某一个ratio接近0抵消了另外ratio值大于1的影响导致本不相似的流向纳入相似流向的范畴,定义了分段函数func( ),在ratio≤1时,在ratio数值的基础上加1防止func(ratio)接近0时产生的错误影响。当ratio>1时,func(ratio)的值为无穷大,有效防止了上述因局部ratio值较小导致的错误影响。当两条流向根据式（3）和（7）计算得到的相似性值在区间[0, 7/8],则可以说明该2条流向相似。图3展示了3个ratio变量与相似度数值的关系,可看出当变量ratioO和ratioD固定的时候,相似度数值随着ratioTime值的增大而减小;同理,当ratioO和ratioTime固定的时候,相似度数值随着ratioD值的增大而减小,当ratioD和ratioTime固定的时候,相似度数值随着ratioO值的增大而减小。图3表明了OD流向相似性度量公式能有效判断OD流向之间的时空相似性。

显示原图|下载原图ZIP|生成PPT

图3 ratio变量与sim值关系

Fig. 3 Relationship between ratio and sim

3 逐级合并OD流向层次聚类算法及效率分析

3.1 算法设计

本文利用自底向上的层次聚类方法对OD流向类簇进行识别,不尝试去计算OD流向的聚类中心获取流向类簇,而是以合理的顺序逐步对流向类簇进行合并以得到最终的聚类结果。在对OD流向聚类的初始阶段,将每一条流向看作一个初始的OD流向类簇。考虑到层次聚类

O (n 3)

的算法时间复杂度以及OD流向数据的大数据量规模,本文对层次聚类的合并过程进行改进,以减少流向聚类的运算时间。经典的自底向上的层次聚类算法在对点进行聚类的过程中,对所有数据点中距离最近的2个数据点进行组合并反复迭代这一过程,每次迭代都需要计算所有点之间的距离且只合并2个数据点,运行效率较低,在数据量规模较大的情况下算法运行时间较长。为了使OD流向类簇的合并能够以正确的顺序进行并且同时克服经典的自底向上的层次聚类算法的高时间复杂度在大数据量的流向聚类过程中带来运行时间过长的影响,本文提出一种逐级合并策略的OD流向层次聚类算法。为此定义一个在流向类簇合并时需要考虑的流向类簇间高相似度的概念。

定义1：类簇间高相似度：即2个流向类簇之间两两呈现高度相似的流向组合个数占所有组合的比值。计算公式如下：

（8）

h ig h Sim (C m, C n) = ∑ i = 1 m ∑ j = 1 n max sim f i, f j, sim f j, f i ≥ t h res h old ? 1 : 0 m × n

式中：m、n分别为流向类簇C_m,C_n中流向的个数; f_i∈C_m,f_j∈C_n;threshold为高相似度参数,其选取区间为[0,7/8],将设置多个等级。考虑到流向间的相似性度量公式的非对称性即sim(f_i, f_j)≠sim(f_j, f_i),流向间的相似性数值取2种计算方式下的较大值。

基于层次聚类算法的逐级合并策略关键在于将流向类簇合并的顺序分成多个等级,流向类簇从高等级到低等级逐步完成合并。合并的等级划分又涉及到高相似度参数的等级划分和类簇间高相似度的等级划分。在合并类簇的过程中,将高相似度参数设置成a个等级t₁, t₂, …, t_i, …, t_a（其中0.875≥t₁>t₂>…>t_i>…>t_a>0）,类簇间高相似度设置成b个等级h₁, h₂, …, h_j, …, h_b（其中1≥h₁>h₂>…>h_j>…>h_b≥0）。

图4中当高相似度参数等级为t_i,类簇间高相似度等级为h_j时,有关类簇合并的合并条件为：

（1）

h ig h Sim C m, C n ≥ h j

（threshold=t_i）;

（2）当t_i不是高相似度参数的最低等级时,

h ig h Sim C m, C n = 1

（threshold=t_i₊₁）;当t_i为高相似度参数的最低等级时,类簇C_m与类簇C_n间的流向满足两两相似。

显示原图|下载原图ZIP|生成PPT

图4 逐级合并策略流程

Fig. 4 Flow chart of step-by-step merge strategy

条件（2）为条件（1）的进一步限制条件,其作用为：① 图5（a）中有2个OD流向类簇Cluster1、Cluster2,其中2个类簇之间flow2和flow3相似,flow1与 flow4不相似,如果没有条件（2）的限制,Cluster1与Cluster2将进行合并,合并生成的新类簇将产生类簇内部流向存在不相似的情况;② 图5（b）中有 3个流向类簇Cluster1、Cluster2、Cluster3,其中flow2与flow3相似性程度最高,Cluster2与Cluster3各流向类簇之间相似性均大于flow1和flow4之间的相似度,且均小于flow2和flow3之间的相似度,如果没有条件（2）的限制,Cluster1将与Cluster2进行合并,这导致2个总体相似程度较差的类簇Cluster1与Cluster2优先于总体相似程度较好的类簇Cluster2与Cluster3合并,造成了合并顺序的混乱。

显示原图|下载原图ZIP|生成PPT

图5 类簇合并的合并条件比对

Fig. 5 Comparison diagram of clusters' consolidation condition

为了更好地理解和分析该逐级合并策略,利用模拟数据作为示例进行介绍。模拟数据中有6条OD流向,该6个OD流向之间的相似性数值如表1所示,在OD流合并过程开始前,将每条流向看作一个初始类簇。图6（a）是待合并的模拟流向数据;图6（b）是在不设置合并等级时可能会出现的合并顺序和合并结果,因为合并的顺序是随机产生,导致最后的聚类结果可能比较差;图6（c）是以经典的自底向上的层次聚类方法进行类簇合并的顺序和合并结果,合并依据最优的合并顺序进行,每次迭代只合并一个类簇组合;图6（d）是将高相似度参数设为0.7和0.5共2个等级,利用逐级合并的层次聚类进行类簇合并的顺序和合并结果,每次迭代合并处于同一合并等级内的多个合并组合。将图6（c）和图6（d）相比较,发现得到聚类的结果虽然一致,但经典的自底向上的层次聚类方法的合并顺序更准确,同时迭代的次数也更多,考虑到每次迭代需要计算所有类簇两两之间的高相似度,当OD流向数据量较大的情形下聚类时间也更长。

表1 模拟数据的OD流向之间的相似性数值

Tab. 1 The similarity value between the OD flows of the synthesized sample data

$flowi$	$flowj$	$max (si m ij, si m ji)$	$flowi$	$flowj$	$max (si m ij, si m ji)$
flow1	flow2	0.85	flow2	flow6	<0
flow1	flow3	0.55	flow3	flow4	0.30
flow1	flow4	0.10	flow3	flow5	0.10
flow1	flow5	<0	flow3	flow6	0.05
flow1	flow6	<0	flow4	flow5	0.55
flow2	flow3	0.60	flow4	flow6	0.50
flow2	flow4	0.15	flow5	flow6	0.80
flow2	flow5	<0

显示原图|下载原图ZIP|生成PPT

图6 不同聚类方法下的类簇合并顺序和合并结果

Fig. 6 Clusters' merging order and results under different clustering methods

结合以上对基于层次聚类的逐级合并策略的介绍和示例可以看出,逐级合并策略通过对合并等级的设置,使OD流向类簇的合并以一个合理的顺序进行,保证了聚类结果的合理性;同时相较于经典的层次聚类算法,逐级合并策略使OD流向类簇每次迭代有多个类簇合并组合,极大减少了迭代次数,提高了聚类的运行效率;作为逐级合并策略中的关键—高相似参数和类簇间高相似度等级的设置可以在其值域范围内等间隔设置,当逐级合并策略的合并等级设置得越精细时合并所需时间越长,但合并的顺序越合理。

3.2 算法效率分析

本文的算法的伪代码描述如下：

算法：逐级合并策略的OD流向聚类

输入：OD流向数据

F ← f i

,时间参数

timeLimit

,距离参数

k

,多等级高相似参数

T ← t i

,多等级类簇间高相似度

H ← h i

输出：OD流向类簇

C ← c i

function FLOW_CLUSTER(

F, timeLimit, k

)
step 1: //将每条OD流向组织成一个流向类簇

c i ← f i

C ← c i

step 2: for

t i

T

do
for

h i

H

do
step 2.1: //计算高相似参数

t i

下所有类簇组合的类簇间高相似度
Calculate

highSim 1 (c i, c j)

step 2.1: //计算高相似参数

t i - 1

下所有类簇组合的类簇间高相似度
Calculate

highSim 2 (c i, c j)

step 2.1: //寻找满足所有合并条件的类簇组合并合并
if

highSim 1 (c i, c j) > h i

and

highSim 2 (c i, c j) = = 1

merge {c i, c j}

update C
end if
end for
end for
end function

给定n条OD流向,最后生成k个OD流向类簇,在此基础上进行时间复杂度的分析。其中step 1的时间复杂度为O(n),step 2主要拆分成以下3个步骤分析其复杂度：

（1） step 2.1的计算次数最多的情况为每条流向单独为一个类簇时,此时有n×(n-1)/2个类簇组合,每个类簇组合计算一次流向间的相似度,故计算次数为n×(n-1)/2,对应的时间复杂度为O(n²);step 2.1的计算次数最少的情况是分为k个类簇,每个类簇内n/k条流向(这是一种理想化的情况),这种情况下有k×(k-1)/2个类簇组合,每个类簇组合计算n²/k²次流向间的相似度,故计算次数为

n 2 × (k - 1) 2 × k

,对应的时间复杂度为O(n²)。结合2种情况可知step 2.1的算法复杂度为O(n²)。

（2） step 2.2的时间复杂度与step 2.1相同,均为O(n²)。

（3） step 2.3的时间复杂度与类簇组合的个数有关,类簇组合个数最多时为n×(n-1)/2个,个数最少时为k×(k-1)/2,故step 2.3最坏情况下的时间复杂度为O(n²),最好情况下的时间复杂度为O(1)。

结合以上3个步骤的时间复杂度看,step 2中合并一次的时间复杂度为O(n²)+O(n²)+O(n²)=O(n²)。经典的层次聚类需要迭代n-k次,故其算法复杂度为(n-k)×O(n²)+O(n)≈O(n³),而逐级合并策略只需迭代|T|×|H|次,故其算法复杂度为|T|×|H|×O(n²)+O(n)≈O(n²)。对比2种方式的时间复杂度可以得出,逐级合并策略相较于经典的层次聚类在计算效率上有很大的提升。

4 实验数据及结果分析

4.1 实验数据

本文使用2个数据集对本文提出的聚类算法进行分析。① 数据集1以成都市为研究区域,其数据来源是北京小桔科技有限公司开放的成都市2016年11月1日的滴滴出行数据^[21],其中,滴滴出行数据包括车辆标识、上车时间（unix时间戳格式,下同）、下车时间、上车点经度（GCJ-02坐标系坐标,下同）、上车点纬度、下车点经度、下车点纬度。2016年11月1日全天有181 172条数据,数据的经度范围为103.8275~104.2719（WGS-84坐标,下同）,纬度范围为30.4878~30.8809。本文利用数据集1对算法中的实验参数和成都市出行模式进行分析。② 数据集2取自Gao等^[1]中的实验数据,研究区域为纽约市,数据为2015年1月11日纽约市211 867条出租车数据,数据包括上车点与下车点坐标(WGS-84)以及时间信息。本文利用数据集2将本文的算法与当前先进的流向聚类算法进行对比分析。

4.2 结果与分析

4.2.1 不同空间参数实验示例

为比较不同空间参数k时OD流向聚类结果在空间范围上的差异性,本节展示了参数timeLimit=60 min,空间参数分别取值为3、4、5时OD流向的聚类结果。图7（a）展示了2组流向类簇在不同空间参数下的展示图,图7（a）上图展示了时间段大致为9:40—10:30花满庭小区至升仙湖站的OD流向类簇;图7（a）下图展示了成都市区至双流飞机场的OD流向类簇,从这2组OD流向类簇可以直观地看出随着空间参数数值的增大,得到的OD流向类簇的空间尺度越小;图7（a）中用流向类簇O点处和D点处的平均坐标点绘制流向代表OD流向类簇中心,图7（b）则展示了类簇中心流向的长度与该类簇内的O/D点间的最远距离的关系曲线,随着类簇中心流向越长,类簇内O/D点间的最远距离越长,反映disLimit的值与流向长度成正比,同时空间参数的值越大,类簇内OD点间的最远距离越小,即类簇的空间尺度越小。

显示原图|下载原图ZIP|生成PPT

图7 不同k值流向类簇的空间范围对比

Fig. 7 Comparison of spatial ranges of flow clusters under different values of parameter k

4.2.2 不同时间参数实验示例

为比较不同时间参数timeLimit时OD流向聚类结果在时间范围上的差异性,展示了空间参数取值为4,时间参数分别取值为30、60、90 min时OD流向的聚类结果。图8展示了不同时间参数时上午 7:00—9:00花满庭小区至升仙湖站的OD的流向类簇及各类簇对应的时间跨度和类簇中流向数量,可发现在相同时间段同一流向方向,时间参数取值越大,聚类得到的类簇数量越少,得到的类簇中流向越大且类簇的时间跨度越大。通过控制时间参数的取值,可得到不同时间尺度的OD流向类簇。

4.2.3 早晚高峰时刻OD流向聚类结果及分析

设置OD流向聚类参数k=4,timeLimit=3h的对该天数据进行粗时间尺度聚类,分别选取时间上与早高峰时期（7:00—10:00）和晚高峰时期（17:00—20:00）大致相同的流向数量较大的几组OD流向类簇进行可视化展示,结果如图8所示,需要注意的是,在图7（b）中可以发现类簇内O/D点处的最远距离与OD流向长度成正比关系,为了防止当流向长度过长导致聚类结果的空间范围过大的情况,本节的聚类实验中还添加了一个限制条件,即当流向长度大于5000 m（该值选取由经验得到,用户可以根据自己数据情况手动调节）时,disLimit为固定值5000/k（单位：m）,这使得聚类类簇内O/D点间的最远距离不超过1250 m。图9中值得关注的是：升仙湖是一个与其他地区关联较多且关联强度较大的地方,且与其关联的地区多为位于其西北方向的居住小区,在观察了成都市的地铁线路之后,发现升仙湖处的地铁站为成都市地铁1号线的第二站,地铁1号线的的第一站位于升仙湖的东北方向且升仙湖站附近的交通比较发达,故位于升仙湖西北方向的居住小区与升仙湖在早晚高峰时刻有着较强的关联。

显示原图|下载原图ZIP|生成PPT

图8 不同时间参数下OD流向类簇对比。。。

Fig. 8 Comparison of flow clusters under different values of time parameter。。。

注：图8中黑色粗线表示流向类簇中心;彩色细线表示各类簇内部的流向,不同颜色的流向线归属于不同类簇。

显示原图|下载原图ZIP|生成PPT

图9 成都市早高峰与晚高峰）时流向数量较大的流向类簇

Fig. 9 Chengdu's OD flow clusters of a large number at early rush hour and late rush hour

4.2.4 算法对比分析

采用数据集2将本文中的算法与Gao等^[1]中的算法进行实验比较,本文算法的聚类结果如图10和图11所示。图10展示了流向数量前5的流向类簇及其类簇中心,图11则分等级地展示了不同数量级的流向类簇中心,Gao等^[1]中最大聚类半径为2.5 km时前5大类簇展示如图12。比较图10与图12可以直观发现聚类的结果并不一致,图12中的5个类簇中,第1、2、3、5个类簇的O点区域和D点区域存在重合,这意味着同一类簇中的流向可能朝相反方向移动,仔细观察图12中第5个流向类簇,可以发现该类簇的O点区域和D点区域足够近,可以将该类簇的D区域分成2部分。Gao等^[1]中方法只关注最大的聚类半径对实验的影响,没有把握流向相似度与流向长度之间的关系,必然导致聚类结果不足够精确,这将对研究居民出行模式产生影响。

显示原图|下载原图ZIP|生成PPT

图10 本文算法获得的纽约市出租车数据前五大流向类簇

Fig. 10 Top five flow clustersof New YorkCitytaxi data discovered by our method

显示原图|下载原图ZIP|生成PPT

图11 本文算法获得的纽约市出租车数据不同量级的类簇中心。。。

Fig. 11 Centers of flow clusters of New York City taxi data with different volumes。。。

注：子图名中的Size表示簇内流向数量/条。

显示原图|下载原图ZIP|生成PPT

图12 Gao等^[1]识别的纽约市出租车数据前五大流向类簇

Fig. 12 Top five flow clustersof New York City taxi data discovered by Gao's method

Gao等^[1]中方法的目的在于发掘出全局范围数量级大的类簇,但是忽略了一些对研究局部地区仍有重大意义的次数量级类簇,不同于此,本文方法可以获取不同量级的流向类簇,如图11所示,这有助于全面地探索热点区域、非热点区域的居民出行特征。

5 结论

本文构建了一个度量OD流向间时空相似性的方法,并提出了基于层次聚类的逐级合并策略,在保证聚类结果合理性的前提下提高了聚类效率,结合二者可以实现OD流向的时空联合聚类,解决了现有的OD流向聚类算法中无法有效地顾及时间因素进行聚类的问题。本文以成都市滴滴出行数据为例实施聚类实验,对聚类结果进行可视化展示和分析表明,该OD流向聚类算法具有如下特点：

（1）有效地流向数据进行时空聚类,得到的聚类类簇不仅包含空间属性还包含时间属性;

（2）通过调节时空相似性度量方法中的参数k值,可以得到不同空间尺度（精细程度）的聚类类簇;

（3）通过调节时空相似性度量方法中的参数timeLimit值,可以得到不同时间尺度的聚类类簇;

（4）与具有先进水平的OD流向聚类算法对比,因本文算法在聚类过程中涉及到了流向间的相似性度量,使获得的聚类结果更合理。

本聚类算法在调节参数得到不同时空尺度的聚类结果的基础上可以挖掘出研究地点的群体出入的流动特征、地点与地点之间的空间联系强度及该空间联系强度随时间变化的趋势。本文方法的优势在于聚类得到的流向类簇带有时间属性,对于精确把握群体或货物流动的时空特征和地点间的时空关联关系具有重大意义,同时本算法可以通过设置不同数值的空间/时间参数得到不同时空尺度的OD流向类簇。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

[1]	Gao Y Z, Li T, Wang S W, et al. A multidimensional spatial scan statistics approach to movement pattern comparsion[J]. International Journal of Geographical Information Science, 2018,32(7):1304-1325.

[2]	Gonzalez M C, Hidalgo C A, Barabasi A L. Understanding individual human mobility patterns[J]. Nature, 2008,458(7235):779-782.

[3]	Guo D, Zhu X. Origin-destination flow data smoothing and mapping[J]. IEEE Transactions on Visualization and Computer Graphics, 2014,20(12):2043-2052. PMID

[4]	王祖超, 袁晓如. 轨迹数据可视分析研究[J]. 计算机辅助设计与图形学学报, 2015,27(1):9-25. [ Wang Z C, Yuan X R. Visual analysis of trajectory data[J]. Journal of Computer-Aided Design & Computer Graphics, 2015,27(1):9-25. ]

[5]	He B, Zhang Y, Chen Y, et al. A simple line clustering method for spatial analysis with origin-destination data and Its application to bike-sharing movement data[J]. ISPRS International Journal of Geo-information, 2018,7(6):203-219.

[6]	Wesolowski A, Eagle N, Tatem A J, et al. Quantifying the impact of human mobility on malaria[J]. Science, 2012,338(6104):267-270. DOI PMID

[7]	Koylu C, Delil S, Guo D, et al. Analysis of big patient mobility data for identifying medical regions, spatio-temporal characteristris and care demands of patients on the move[J]. International Journal of Health Geographics, 2018,17(1):32-49. DOI PMID

[8]	Zanin M, Papo D, Romance M, et al. The topology of card transaction money flows[J]. Physica A-Statistical Mechanics and Its Application, 2018,462:134-140.

[9]	Guimera R, Mossa S, Turtschi A, et al. The worldwide air transportation network: Anomalous centrality, community structure, and cities' global roles[J]. Proceedings of the National Academy of Science of the United States of America, 2005,102(22):7794-7799.

[10]	邬群勇, 张良盼, 吴祖飞. 顾及空间异质性的出租载客与公交客流回归分析[J]. 地球信息科学学报, 2019,21(3):337-345. [ Wu Q Y, Zhang L P, Wu Z F. Regression analysis of taxi pick-up and bus passenger flow considering the spatial heterogeneity[J]. Journal of Geo-information Science, 2019,21(3):337-345. ]

[11]	邬群勇, 苏克云, 邹智杰. 基于MapReduce的海量公交乘客OD并行推算方法[J]. 地球信息科学学报, 2018,20(5):647-655. [ Wu Q Y, Su K Y, Zou Z J. Spatial and temporal analysis of bus passenger flow based on massive smart card data[J]. Journal of Geo-information Science, 2018,20(5):647-655. ]

[12]	信睿, 艾廷华, 杨伟, 等. 顾及出租车OD点分布密度的空间Voronoi剖分算法及OD流可视化分析[J]. 地球信息科学学报, 2015,17(10):1187-1195. [ Xin R, Ai T H, Yang W, et al. A new network voronoi diagram considering the OD point density of taxi and visual analysis of OD flow[J]. Journal of Geo-information Science, 2015,17(10):1187-1195. ]

[13]	Guo D. Flow mapping and multivariate visualization of large spatial interaction data[J]. IEEE Transactions on Visualization and Computer Graphics, 2009,15(6):1041-1048. DOI PMID

[14]	Rea A. From spatial interaction data to spatial interaction information?Geovisualisation and spatial structures of migration from the 2001 UK census[J]. Computers Environment and Systems, 2009,33(3):161-178.

[15]	Pei T, Wang W Y, Zhang H C, et al. Density-based clustering for data containing two types of points[J]. International Journal of Geographical Information Science, 2015,29(2):175-193. DOI

[16]	Song C, Pei T, Ma T, et al. Detecting arbitrarily shaped clusters in origin-destination flows using ant colony optimization[J]. International Journal of Geographical Information Science, 2019,33(1):134-154. DOI

[17]	Andrienko N, Andrienko G. Spatial generalization and aggregation of massive movement data[J]. IEEE Transactions on Visualization and Computer Graphics, 2011,17(2):205-219. DOI PMID

[18]	Zhou Z, Meng L, Tang C, et al. Visual abstraction of large scale geospatial origin-destination movement data[J]. IEEE transactions on visualization and computer graphics, 2018,25(1):43-53. DOI

[19]	Guo D, Zhu X, Jin H, et al. Discovering spatial patterns in origin-destination mobility data[J]. Transactions in GIS, 2012,16(3):411-429. DOI

[20]	Yao X, Zhu D, Gao Y, et al. A stepwise spatio-Temporal flow clustering method for discovering mobility trends[J]. IEEE ACCESS, 2018,6:44666-44675. DOI

[21]	盖亚开发数据计划:https://outreach.didichuxing.com/research/opendata/DB/OL]. [ GAIA Open Dataset:https://outreach.didichuxing.com/research/opendata/[DB/OL]. ]

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 引言

2 OD流向时空相似性度量

2.1 OD流向空间相似性计算

图1 OD流向空间相似度关系比对示意

2.2 OD流向的时间相似性计算

图2 OD流向间时间相似关系判断

图3 ratio变量与sim值关系

3 逐级合并OD流向层次聚类算法及效率分析

3.1 算法设计

图4 逐级合并策略流程

图5 类簇合并的合并条件比对

表1 模拟数据的OD流向之间的相似性数值

图6 不同聚类方法下的类簇合并顺序和合并结果

3.2 算法效率分析

4 实验数据及结果分析

4.1 实验数据

4.2 结果与分析

图7 不同k值流向类簇的空间范围对比

图8 不同时间参数下OD流向类簇对比。。。

图9 成都市早高峰与晚高峰）时流向数量较大的流向类簇

图10 本文算法获得的纽约市出租车数据前五大流向类簇

图11 本文算法获得的纽约市出租车数据不同量级的类簇中心。。。

图12 Gao等[1]识别的纽约市出租车数据前五大流向类簇

5 结论

参考文献

图12 Gao等^[1]识别的纽约市出租车数据前五大流向类簇