EN中文

地球信息科学学报 >

2020 , Vol. 22 >Issue 8: 1617 - 1629

DOI: https://doi.org/10.12082/dqxxkx.2020.190378

地球信息科学理论与方法

基于LSTM神经网络的青藏高原月降水量预测

  • 刘新 ,
  • 赵宁 ,
  • 郭金运 , * ,
  • 郭斌
展开
  • 山东科技大学测绘科学与工程学院,青岛 266590
*郭金运（1969— ）,男,山东菏泽人,博士,教授,博导,主要从事空间大地测量,物理大地测量等研究。 E-mail:

刘 新（1969— ）,女,山东肥城人,博士,副教授,主要从事空间数据挖掘和机器学习等研究。E-mail:

收稿日期: 2019-07-16

  要求修回日期: 2019-10-01

  网络出版日期: 2020-10-25

基金资助

国家自然科学基金项目(41774001)

国家科技基础性工作专项(2015FY310200)

版权

版权所有，未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
收起

Prediction of Monthly Precipitation over the Tibetan Plateau based on LSTM Neural Network

  • LIU Xin ,
  • ZHAO Ning ,
  • GUO Jinyun , * ,
  • GUO Bin
Expand
  • College of Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
*GUO Jinyun, E-mail:

Received date: 2019-07-16

  Request revised date: 2019-10-01

  Online published: 2020-10-25

Supported by

National Natural Science Foundation of China(41774001)

The Basic Science and Technology Project of China(2015FY310200)

Copyright

Copyright reserved © 2020
Fold

摘要

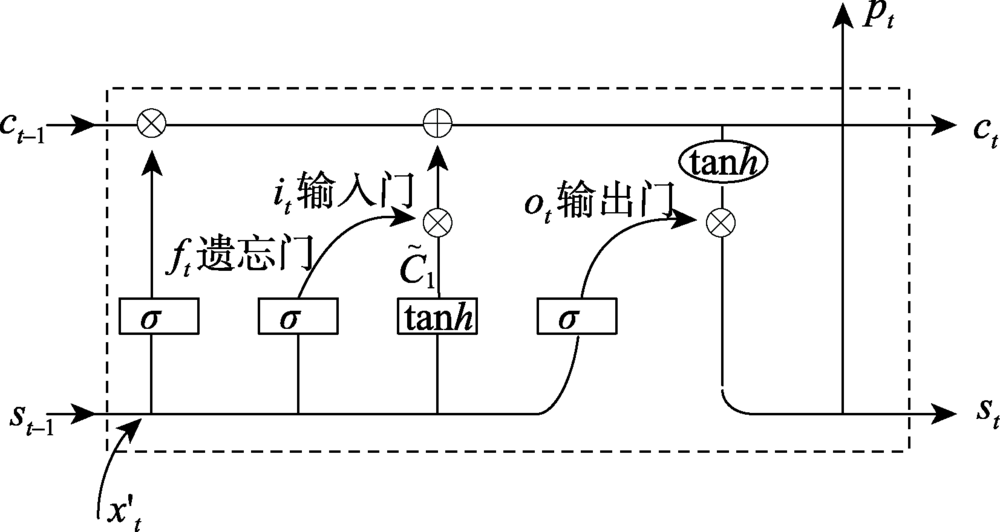
青藏高原的降水量预测不仅为该地区水资源合理规划利用提供依据,同时对中国及周边国家气候变化研究有着重要的意义。论文利用1990—2016年青藏高原降水量数据,采用长短期记忆神经网络（LSTM）对青藏高原月降水量进行预测,主要包括：① 使用青藏高原86个测站1990—2013年的月降水资料,预测各个测站2014—2016年的月降水量,并与传统的RNN、NAR、SSA和ARIMA预测模型相比,平均决定系数R2分别提高了0.07、0.15、0.13和0.36,均方根误差（RMSE）和平均绝对误差（MAE）表现更低;② 分析了降水量预测精度的空间分布特征,将各模型的R2在青藏高原地区内插值,分析R2的空间分布特征,发现所有模型降雨稀少的干旱地区和降雨多的湿润地区R2较低,在气候稳定、降水规律性明显的地区R2较高,且LSTM模型R2≥0.6的空间范围远大于传统模型;③ 分析了不同预测长度对各模型预测精度的影响,发现所有模型会随着预测长度增加而预测精度降低,但在不同的预测长度下LSTM预测的RMSE值都低于其他模型。

关键词： 长短期记忆网络; 降水量; 预测; 循环神经网络; 青藏高原; 时间序列; 机器学习

本文引用格式

刘新 , 赵宁 , 郭金运 , 郭斌 . 基于LSTM神经网络的青藏高原月降水量预测[J]. 地球信息科学学报, 2020 , 22(8) : 1617 -1629 . DOI: 10.12082/dqxxkx.2020.190378

Abstract

Precipitation prediction on the Qinghai-Tibet Plateau not only provides a basis for rational planning and utilization of water resources, but also has significance for climate change research in China and neighboring countries. In this paper, the Long Short Term Memory neural network （LSTM） was used to predict the monthly precipitation over the Qinghai-Tibet Plateau using data from 1990 to 2016. Firstly, the monthly precipitation data of 86 stations in the Qinghai-Tibet Plateau from 1990 to 2013 were used to predict the monthly precipitation of each station from 2014 to 2016. Comparing with the traditional RNN, NAR, SSA, and ARIMA prediction models, LSTM increased the average coefficient of determination （R2） by 0.07, 0.15, 0.13, and 0.36, respectively. Simultaneously, LSTM had lower Root Mean Squared Error （RMSE） and Mean Absolute Error （MAE）. Among them, the observation of station 56106 showed that the LSTM model predicted the period more accurately with less displacement deviation, and that the prediction of the valley between July and September was more accurate with R2 reaching 0.87. Secondly, the spatial distribution characteristics of precipitation prediction accuracy were analyzed. The R2of each model was interpolated in the Qinghai-Tibet Plateau, and the spatial distribution characteristics of R2were analyzed. All the drought areas with rare rainfall and the wet areas with heavy rainfall were of lower R2, while the areas with stable climate and obvious precipitation were of higher R2. Areas of R2 over 0.6 were much larger when using the LSTM model than the traditional model. Finally, influence of different prediction lengths on the prediction accuracy was analyzed for each model. All models showed decreased prediction accuracy as the prediction length increased, yet the RMSE values predicted by LSTM were lower than by other models with the varying prediction lengths.

Key words： LSTM neural network; precipitation; prediction; RNN neural network; Qinghai-Tibet Plateau; time series; machine learning

1 引言

青藏高原平均海拔4000 m以上,被称为亚洲水塔,它是长江、黄河、雅鲁藏布江、恒河和印度河等大河的发源地,为20亿人口提供了重要的水源[1,2]。由于它的热力和动力作用,不仅影响中国的气候,且对东亚乃至全球大气环流都有一定影响。降水作为气候因素之一,该地区的降水量的变化是具有超前性的,以往研究表明：青藏高原不仅是中国气候变化的启动区[3],也是全球气候变化的驱动机和放大器[4]。例如,冬季青藏高原多雨年,夏季西太平洋副热带高压北移往往明显偏迟,致使中国主要雨带持续偏南,造成长江流域降水异常偏多[5]。另外,冰川和积雪的形成依靠降水作为原料,青藏高原上的冰川活动与高原东南地区和西北地区的降水变化有关[6]。因此该地区降水量的预测成为了一个有重要意义的研究。
由于气候系统受多因素的影响,降水虽然有一定的规律性,但仍然有较强的复杂性和不确定性,因此预测降水量是一件困难的事。目前,关于降水量预测的传统方法有很多,可分为单个模型预测和组合模型预测。单个模型预测,如Nayagam等[7]建立线性回归模型实现对喀拉拉邦夏季风季节的降水预测;赵莹[8]使用灰色模型预测葠窝水库的年降水量;潘刚等[9]使用马尔科夫链模型实现了漳河水库主汛期降水量的预测;Feng[10]使用奇异谱分析（Singular Spectrum Analysis, SSA）预测石家庄市夏季降水量。Burlando等[11]使用滑动平均自回归模型（Auto-regressive Moving Average, ARMA）对美国科罗多拉州小时降水量实现预测。组合模型预测,如Liu等[12]采用灰色模型与马尔科夫链组合模型实现了对中国夏季日降水量的预测;宋帆等[13]将聚类方法与模糊马尔科夫链结合实现对江苏省年降水量实现预测。
近几年机器学习技术的进步也使其在预测领域中发挥了重要的作用,尤其是人工神经网络 （Artificial Neural Network, ANN）,由于其具有很强的非线性拟合能力,因此在时间序列预测问题上有良好的表现。关于降水量预测的神经网络方法也逐渐发展,也同样包括单个模型预测和组合模型预测。单个预测模型方面,Luk等[14]使用多层前馈神经网络（Multi-layer Feedforward Neural Network, MLFN）,偏循环神经网络和时间延迟神经网络3种人工神经网络方法,对帕拉马塔河流域上游地区的10次暴雨事件的降水量进行预测,结果表明3种 类型的网络在最佳的参数时有相同的预测能力;Nanda等[15]使用基于小波的非线性自回归神经网络（Nonlinear Autoregressive Neural Network, NAR）对默哈讷迪河上游地区进行实时洪水预测;Chattopadhyay等[16]使用共轭梯度下降和 Levenberg-Marquardt梯度优化算法的MLFN对印度夏季平均降水量进行降水量预测,表明该方法具有良好的预测效果。组合预测模型方面,如Nasseri等[17]将遗传算法与ANN相结合,对帕拉马塔河流域上游地区降水进行短期预测,结果表明参数选优算法的使用可以提高预测精度;Baratta等[18]将MLFN与SSA结合对台伯河流域预测日降水量,有效解决了非连续序列的预测问题;Wu等[19]将ANN与移动平均（Moving Average,MA）和SSA结合分别对日降水量和月降水量进行预测,结果表明在与MA模型结合时,预测效果更好;Yaseen等[20]将自适应模糊神经系统（Adaptive Neuro Fuzzy Inference System, ANFIS）与萤火虫优化算法（Firefly Optimization Algorithm, FFA）结合方法对马来西亚彭亨河进行月降水量预测,取得了较好的预测结果;Chau等[21]将极限学习机（Extreme Learning Machine, ELM）与马尔科夫蒙特卡洛方法、Copula和Bat算法结合实现了巴基斯坦3个农业带的月降水量的预测,在降水量预测算法上实现了新的突破。
然而,无论是传统预测模型还是人工神经网络模型,先前的研究已经证实传统的ANN无法捕获输入序列的长期记忆,由于梯度消失和梯度爆炸问题,当time-lag为5—10时训练是很困难的[22]。长短期记忆网络（Long Short Term Memory Networks, LSTM）是众多循环神经网络（Recurrent Neural Networks, RNN）当中的一个变体。它弥补了RNN的梯度消失和梯度爆炸、长期记忆能力不足等问题,使得循环神经网络能够真正有效地利用长时间的时序信息[23]。与传统的RNN不同,LSTM有着更复杂的记忆单元,能够对长时间跨度的时间序列保持良好的记忆,因此该模型在时间序列的预测问题上有着突出的表现,是近年来机器学习领域的研究热点。
本文首次将LSTM神经网络应用到地学领域中的降水量时间序列预测,预测青藏高原地区的月降水量,并与现有的降水量预测模型：自回归差分滑动平均模型（Autoregressive Integrated Moving Average Model, ARIMA）、NAR模型、SSA模型和RNN模型进行试验对比。

2 研究区概况及数据源

2.1 研究区概况

青藏高原位于中国西南部,总面积约为250 km2,经度范围为73°18′52″ E—104°46′59″ E,纬度范围为26°00′12″ N—39°46′50″ N。高原气候类型多样,气候分布受地形影响明显。青藏高原的水汽主要来自于印度洋的孟加拉湾和阿拉伯海。孟加拉湾的暖湿气流沿布拉马普特拉河、雅鲁藏布江、横断山三江流域向高原输送水汽。青藏高原东南地区地势低平,水汽在进入雅鲁藏布江大拐弯后深入高原腹地,从而为高原带来降水。青藏高原整体降水特征表现为：① 平均年降水量自藏东南4000 mm以上向柴达木盆地逐渐减少;② 5-9月为高原雨季,降水主要集中在此时段;③ 降水多发生在夜间。④ 东南部夏半年由于受索马里急流和东南季风的影响,降水比较稳定。在近年全球变暖的趋势下,青藏高原的气温与降水加速增长,积雪显著减少。

2.2 数据源

本文数据来源于中国国家气象中心网站提供的中国地面气候资料日值数据集（V3.0）（http://data.cma.cn）。数据的范围为1990—2016年青藏高原地区86个气象观测站实测降水量观测数据,测站的分布如图1所示,主要分布在青藏高原的东部及南部地区。累加测站的日降水量得到测站的月降水量,保留精度为1 mm,其中少量的缺失值做相邻月份降水量的平均值填充处理。
图1 青藏高原气象测站分布

Fig. 1 Distribution of weather stations over the Qinghai-Tibet Plateau

3 研究方法

3.1 LSTM模型

LSTM神经网络由Sepp Hochreiter和Jurgen Schmidhuber于1997年首次提出[22]。不同于传统神经网络,其隐含层的基本单元被称为存储块（Memory Block）,存储块的结构如图2所示。存储块包含3个门（输入门（ i ）、输出门（ o ）和遗忘门（ f ））和记忆单元（ c ）,符号 ⊕ 代表两个向量的加法运算,符号 ⊗ 代表两个向量的点乘运算, σ 代表sigmoid激活函数, tanh 为双曲正切激活函数,计算公式分别如下：
σ ( x ) = 1 1 + e - x
tanh ( x ) = e x - e - x e x + e - x
图2 LSTM存储块结构

Fig. 2 LSTM memory block structure

网络从输入到输出的具体计算过程如下：
f t = σ ( W f ∘ [ s t - 1 , x t ] + b f )
i t = σ ( W i ∘ [ s t - 1 , x t ] + b i )
o t = σ ( W o ∘ [ s t - 1 , x t ] + b o )
c ˜ t = tanh ( W c ∘ [ s t - 1 , x t ] + b c )
c t = f t ∘ c t - 1 + i t ∘ c ˜ t
s t = o t ∘ tanh ( c t )
式中：符号“ ∘ ”表示2个向量的点乘; W f 、 W i 、 W o 、 W c 分别代表遗忘门、输入门、输出门和记忆单元的权值向量; b f 、 b i 、 b o 、 b c 分别代表遗忘门、输入门、输出门和记忆单元的偏置向量; x t 表示t时刻网络的输入。
输入门决定了输入层信息如何传递到记忆单元;遗忘门决定了如何保留历史信息;输出门决定了记忆模块的信息如何传递给下一时刻的存储块。3个门控制器的结构相同,t（ t = 1,2 , 3 , … , n ）时刻每个门的输入数据都是上一时刻的输出 s t - 1 与当前时刻输入 x t 构成的向量 [ s t - 1 , x t ] 与其权重的点乘。门控制器描述了信息能够通过的比例, σ 函数取值范围是[0, 1], σ 函数取值为0表示没有信息能够通过,取值为1表示所有信息都能通过。 f t 、 i t 和 o t 是t时刻 σ 函数的输出, c ˜ t 为t时刻tanh函数的输出,取值范围是[-1, 1]。t时刻长期记忆 c t 和短期记忆 s t 传入到下一个存储块中,同时 s t 也是t（ t = 1,2 , 3 , … , n ）时刻的预测结果 p t 。
LSTM模型训练过程中权值向量、偏置向量等参数的更新采用误差反向传播算法,参数更新方主要有：随机梯度下降[24]、AdaGrad、RMSProp[25]和适应性动量估计（Adaptive Moment Estimation,Adam）等算法。其中,Adam优化算法是一种有效的基于梯度的随机优化方法,算法融合了AdaGrad和RMSProp算法的优势,对不同参数计算适应性学习率并且占用较少的存储资源。相比于其他随机优化方法,Adam算法在实际应用中整体表现更优[26],因此本文采用Adam算法。
设降水量时间序列为 x = { x t } , t = 1,2 , 3 , … , n ,其中, x t 为t时刻的降水量。给定神经网络的窗口长度（Window Size）L,该参数表示使用时间长度为L的历史降水量 x t , x t + 1 , … , x t + L - 1 序列来预测下一时刻的降水量 p t + L 。根据L确定LSTM神经网络的拓扑结构（图3）,其中LSTMt为t时刻的存储块。
图3 LSTM神经网络拓扑结构

Fig. 3 LSTM neural network topology structure

利用该LSTM神经网络结构,对降水数据进行训练和预测,首先训练过程如下：
（1）网络初始化。初始化权值W和偏置向量b,设定存储块的总个数N,窗口长度L,学习率 η=0.001,迭代的阈值ε=0.00001,最大迭代次数 T=3000,初始记忆c0=0,初始输出s0=0。
（2）数据标准化。对数据集 x 进行min-max标准化,得到标准化的数据集 x ' = { x 1 ' , x 2 ' , … , x n ' } ,其中：
x t ' = ( x t - x min ) / ( x max - x ) 1 ≤ t ≤ n , t ∈ N min
（3）数据划分。划分 x ' 为训练集 x tr ' = { x 1 ' , x 2 ' , … x d ' } 和测试集 x te ' = { x d + 1 ' , x d + 2 ' , … , x n ' } 。
根据L对训练集进行划分子集,结果为 { x tr 1 ' , x tr 2 ' , ... x tr t ' , … , x trd - L + 1 ' } ,其中 x trt ' = { x t ' , x t + 1 ' , … , x t + L - 1 ' } ,每个 x trt ' 即为LSTM网络的一次输入,其对应的输出结果为 { x t + L ' , x t + L + 1 ' , … , x t + 2 L - 1 ' } 。
（4）建立LSTM网络,模型训练算法如下：
for k=1, 2, …, T do
for t=1, 2, …, d -L+1 do
计算 f t , i t , o t , c ˜ t , c t
得到输出 p t + L = s t + L
end for
误差计算：计算输出层输出与理论输出之间的误差项 E = 1 2 ( p t + L - x t + L ) 2
权值、阈值更新：基于误差项E使用Adam梯度优化算法更新W和b。
当更新后的值与更新前的值差的绝对值小于ε时结束 循环
end for
使用上述训练好的LSTM网络参数进行迭代预测,过程如下：
（1）首先使用训练子集的最后一组数据 x trd - L + 1 ' 得到预测值 p d + 1 ,将该值与 x trd - L + 1 ' 的后 L - 1 个值合并成新子集 { x d - L + 2 ' , x d - L + 2 ' , ... , x d ' , p d + 1 } ,将该子集输入到网络中得到预测值 p d + 2 ,以此类推,即可得到最终的预测结果 { p d + 1 , p d + 2 , ... , p n }
（2)将 { p d + 1 , p d + 2 , ... , p n } 反标准化得到最终预测结果 { y d + 1 , y d + 2 , ... , y n } ,反标准化公式为：
y t = p t ( x max - x min ) + x min ( 1 ≤ t ≤ n , t ∈ N )
式中： y t 为反标准化后的结果,即最终的降水量预测结果。

3.2 对比模型

3.2.1 RNN模型
RNN是一种节点定向连接成环的人工神经网络,这种网络的内部状态可以展示动态时序行为,LSTM网络正是基于此网络发展而来。其循环体的结构如图4所示。
图4 RNN循环体的结构

Fig. 4 Structure of the RNN loop body

循环体包括输入层、隐含层和输出层。 x t 为t时刻输入层的输入值, s t 为t时刻隐含层神经元的输出值, o t 为t时刻输出层的输出值, U 为输入层与隐含层间的连接矩阵, V 是隐含层与输出层之间的连接矩阵, W 为隐含层之间的连接矩阵。网络输出计算过程为：隐含层神经元的输入值: a t = U x t + W s t - 1 ;隐含层神经元的输出值： s t = tanh ( a t + b s ) ;输出层的输入值： V s t ,输出层的输出值： o t = V s t + b o ,其中 b s 和 b o 分别为隐含层和输出层的偏置向量。
可以看出,当前时刻t的输出值 o t 不仅与当前时刻的输入层的输入 x t 有关,还依赖于前一时刻隐含层的输出值 s t - 1 ,不同神经元共享参数（U, V, W）极大的降低计算量。使用RNN模型的训练和预测方法与LSTM相同,此处不再详述。
3.2.2 NARNAR神经网络模型
NAR神经网络模型通常用作为时间序列的预测的工具。一个NAR网络通常由输入层、隐含层和输出层及延迟函数构成,其基本结构如图5所示。
图5 NAR神经网络结构示意

Fig. 5 NAR neural network structure diagram

图5中,y（t）是神经网络的输出,即t时刻的降水量,1:12中的12表示延迟阶数,W表示权值,b为阈值,NAR网络可表示为：
y ( t ) = f ( y ( t - 1 ) , y ( t - 2 ) , … , y ( t - d ) )
式中：t表示时刻;d表示延迟阶数,图5中d=12。式（11）表明NAR网络为带有延迟函数的BP神经网络,即使用过去d个值 y ( t - 1 ) , y ( t - 2 ) , … , y ( t - d ) 来预测下一个值y（t）,延迟阶数d决定了神经网络的输入个数。预测时,延迟函数将输出值返回到输入层中,从而实现降水量的动态预测。通过对延迟阶数、神经元数目的调节就可筛选出比较好的模型。
3.2.3 SSA模型
SSA模型是一种经典的时间序列预测模型。SSA是对一维的时间序列进行主成分分析的方法,它将时间序列分解为不同的信号,如趋势信号、周期信号和噪声信号。根据Vautard等[27]的方法,使用SSA建模,共分为4步：第①步为嵌入,根据窗口长度L构建降水时间序列的轨迹矩阵X;第②步为奇异值分解（Singular Value Decomposition, SVD）,获得X的奇异向量和奇异值;第③、④步为分组和重构,生成与原始序列相同长度的重建成分。最后使用迭代的方式实现预测。在实际使用中,要确定的2个参数为嵌入子过程的窗口长度L和分组过程的分组类别G。本文根据文献[28]提出的方法确定这2个参数的取值范围并取其最大值。
3.2.4 ARIMA模型
ARIMA模型是时间序列分析的经典理论和方法,其基本参数p、d、q分别为自回归项数、差分次数、移动平均项数[29]。本文的降水时间序列为非平稳序列,通过一阶差分可转为平稳序列,然后再运用ARMA模型进行预测。参数p、q需要通过计算自相关系数（ACF）和偏自相关系数（PACF）的拖尾和截尾特征来确定,使其能达到AIC（Akaike Information Criterion）的值最小。本文按照表1的方式来确定p和q。
表1 ARMA模型类型及阶数确定

Tab. 1 ARMA model type and order determination

自相关系数 偏相关系数 模型定阶
拖尾 p阶截尾 AR（p）模型
q阶截尾 拖尾 MA（q）模型
拖尾 拖尾 ARMA（p, q）模型

3.3 精度评价方法

本文使用均方根误差RMSE（Root Mean Square Error）、平均绝对误差MAE（Mean Absolute Deviation）和决定系数R2（Coefficient of Determination）作为评价降水预测模型精度的指标：
RMSE = ∑ t = 1 T ( y t - y ˆ t ) 2 T
MAE = 1 T ∑ t = 1 T y - t y ˆ t
R 2 = 1 - ∑ t = 1 T ( y t - y ˆ t ) 2 ∑ t = 1 T ( y t - y ̅ ) 2
y ̅ = 1 T ∑ t = 1 T y t
式中： y t 和 y ˆ t 分别为t时刻降水的观测值和预测值;T为测试数据集中数据的个数。

4 结果及分析

4.1 单个测站预测结果与分析

利用LSTM模型建立青藏高原的降水预测模型。1990—2013年共计288个月的数据为训练数据集,预测2014—2016年共36个月的降水量。采用Python 3.6语言与TensorFlow 1.9函数库实现建模。实验中发现,在LSTM神经网络中,过拟合或欠拟合现象主要是受存储块的个数N的影响,当N较低时,可能会出现欠拟合,当N过高时,可能会出现过拟合现象。对本文的降水数据进行反复实验发现,当N值取100时,预测结果的过拟合与欠拟合现象并不明显,因此取N为100。另外在初始化的参数时,对预测结果影响最大的参数为窗口长度L,因此本文以56106号测站为例试验不同的L对预测结果的影响。由于月降水量有显著的年周期性,因此我们选取了1~12及一些12的倍数作不同的窗口长度来对比误差大小,结果如图6所示。根据图6,随着L的增大,RMSE会降低,当L≥36时,预测结果的RMSE才能达到一个比较低的值,此时误差基本保持平稳。本文选取L的规则是选取降雨量预测精度RMSE最低值时的L。56106号测站降雨量预测精度RMSE最低时L为60,不同的测站建立的LSTM网络的L并不相同。
图6 不同窗口长度的RMSE变化

Fig. 6 RMSE changes for different window sizes

以56106号测站为例,预测36个月的拟合及预测结果如图7所示。可以看出LSTM模型对月降水量的周期变化预测比较准确,12个月为周期的变化与实际相符,没有出现位移偏差。预测值与观测值的误差比较小,RMSE和MAE分别为19.69和14.06,且对波峰和波谷的预测比较准确,没有出现波峰过高和波谷过低。通过观察历史降水量数据,发现56106号测站的降水量在7—9月偶尔会出现一个较低值（相比相邻的2个月）,本文采用的LSTM方法拟合并预测出了7—9月降水量出现一个较低的情况,体现了LSTM模型长期记忆能力的优势。
图7 56106号测站LSTM模型降水量预测结果

Fig. 7 Precipitation prediction results of the LSTM model at station 56106

图8为传统时间序列预测RNN、NAR、SSA和ARIMA模型的预测效果。可以看出,ARIMA模型对7—9月降水量较低值是可预测的,但其出现了一些一个月的向后位移偏差,并且预测结果出现了较多的负值。而RNN、NAR和SSA的预测结果比较接近,虽然能准确把控周期性,但7—9月降水量的较低值并不能预测。
图8 56106号测站RNN、NAR、SSA和ARIMA模型降水量预测结果

Fig. 8 Precipitation prediction results of the RNN, NAR, SSA, and ARIMA models at station 56106

图9显示了不同模型的预测结果散点图。对比5种模型的预测结果散点分布状况可看出,LSTM模型的预测值与真实值更接近,表明预测精度更高,R2达到了0.87。RNN、NAR和SSA模型的降水量预测值大多低于实测的降水量值,R2值分别为0.70、0.65、0.61,而ARIMA模型的预测值低于实测值的数量与其高于实测值的数量大致相等,R2为0.28。
图9 56106号测站不同模型降水量预测结果散点图

Fig. 9 Scatter plots of different model precipitation prediction results at station 56106

5种预测模型的预测精度统计结果如表2所示。根据表2,预测精度由高到低依次为：LSTM、RNN、NAR、SSA和ARIMA,LSTM模型的RMSE和MAE均为最低,RMSE比其他模型平均低了17.86,MAE比其他模型平均低了12.34,R2比其他模型平均高了0.31。由此可以说明,对56106测站来说LSTM模型的预测效果最优。
表2 56106号测站不同模型精度评价指标对比

Tab. 2 Comparison of different model accuracy evaluation indexes at station 56106

评价指标 LSTM RNN NAR SSA ARIMA
RMSE 19.69 29.82 32.15 33.77 54.46
MAE 14.06 18.57 24.17 22.17 40.67
R2 0.87 0.70 0.65 0.61 0.28

4.2 全部测站预测结果与分析

为了进一步验证使用LSTM模型在降水量预测的广泛性,选取了青藏高原86个测站的测站数据,建立了86个测站的LSTM降水模型,并与其他方法建立的降水模型对比,如图10所示。LSTM、RNN、SSA、NAR和ARIMA模型的RMSE、MAE和R2取平均值,如表3所示。根据图10,大部分测站LSTM模型的RMSE和MAE指标小于其余4种模型,R2高于其余4种模型。根据表3,降水量预测精度由高到低依次为LSTM、RNN、SSA、NAR和ARIMA,其中LSTM模型的R2要比后4种模型分别提高了0.07、0.15、0.13和0.36。
图10 青藏高原所有测站不同模型的降水量预测精度对比

Fig. 10 Comparison of precipitation prediction accuracy of the different models at 86 stations on the Qinghai-Tibet Plateau

表3 5种模型在青藏高原降水量预测精度对比

Tab. 3 Comparison of prediction accuracy of the five models at 86 stations

评价指标 LSTM RNN NAR SSA ARIMA
RMSE 26.83 28.87 31.64 30.17 38.01
MAE 17.91 20.65 22.77 21.04 26.47
R2 0.61 0.55 0.46 0.48 0.25
根据图10,个别测站的LSTM模型预测精度略低于RNN模型的预测精度,R2平均低了0.05。这可能是由于在相同的训练次数下,LSTM网络由于结构更复杂,网络收敛速度更慢,训练次数不足导致预测结果低于RNN。尽管如此,LSTM模型在青藏高原月降水量上依然有很大的优势。
另外,ARIMA模型的部分测站R2出现了小于 0的情况（图10（c））。出现这种现象的原因有： ① ARIMA模型的结构较简单,对复杂性较强的降水量时间序列预测效果难以适应;② 这些测点主要分布在降水量稀少的柴达木盆地和降水量充沛的喜马拉雅山南侧地区（图11）,可能是由于该地区气候不稳定导致降水存在更强的随机性和不确定性,因此模型预测效果较差。
图11 不同模型的降水量预测精度R2在青藏高原内的空间插值分布

Fig. 11 Distribution of R2 of different precipitation prediction models over the Tibetan Plateau after spatial interpolation

为分析5种模型预测精度的空间分布情况,以便观察模型在不同区域的适用性。在青藏高原区域内对所有测站的R2进行插值,结果如图11所示。根据图11,不同模型的精度在空间分布上具有一定的差异性和相似性。
模型精度空间分布的差异性。LSTM模型在柴达木盆地和的喜马拉雅山南侧地区的精度R2≤0.2,其余大部分区域的预测精度在R2≥0.6,整体而言该方法的降水量预测效果是好的;与LSTM模型相比,RNN模型在东部和南部区域扩大了R2≤0.6的空间范围;NAR模型的预测精度主要集中在R2≤0.6,并且青藏高原北部和南部地区预测精度更低;SSA模型较NAR模型有略微的提高,但仍低于RNN模型和LSTM模型;而ARIMA模型只在少部分区域预测精度R2≥0.6,其余大部分区域预测精度R2≤0.6,部分地区出现负值以R2为精度评价标准,精度由高到低排序为：LSTM,RNN,SSA,NAR和ARIMA,造成该现象的原因可能与模型的结构有关,LSTM模型的存储了长期记忆,因此可以对变化复杂的降水序列取得较好的预测效果。相反,其他模型没有长期记忆的存储结构,因此预测精度较低。
模型精度空间分布相似性。5种降水模型预测精度R2较低的区域位置大致相同,主要集中在青藏高原北部的柴达木盆地和西南部的喜马拉雅山南侧地区。根据柴达木盆地地区测站降水量记录,近27年年平均降水量只有47.29 mm,该地区的降水量极少,属极度干旱。喜马拉雅山南侧地区处于迎风坡,受地形和大气环流因素影响,该地区降水量充沛。这表明,在降水量极度稀少和降水量非常充沛的地区,降水量的预测精度R2低。另外,在LSTM模型预测较好的地区（如Chang Tang高原、KunLun山脉等地区）,其他模型的预测效果也相对较好于其他地区,这可能是因为该地区的气候非常稳定,降水的规律性非常明显等原因。

4.3 不同预测长度对预测精度的影响与分析

结合上文5种模型预测36个月降水量的结果,不改变模型中的神经元个数、学习率等超参数,只将预测长度设置为24、12和6个月（图12）。取所有测站点RMSE平均值,结果如表4所示。根据表4,除了ARIMA模型在预测长度为12时的RMSE略高于预测长度为24时的RMSE,其余情况下,随着预测长度的增加,5种预测模型的RMSE都有所提高,即预测精度都有所下降。本次试验中LSTM模型在不同预测长度下,其RMSE都要低于其他4种模型,并且从低到高依次为LSTM、RNN、SSA、NAR和ARIMA,因此可得出在降水时间序列预测中,LSTM模型预测精度更高。
图12 不同模型在预测长度分别为6、12、24和36个月时RMSE的变化

Fig. 12 RMSE changes of the different models at predicted lengths of 6, 12, 24, and 36 months respectively

表4 不同模型在不同预测长度下的平均RMSE

Tab. 4 Average RMSEs of the different models at different predicted lengths

预测长度/个月 LSTM RNN NAR SSA ARIMA
36 26.83 28.87 31.64 30.17 38.01
24 26.23 28.16 30.45 29.37 35.82
12 25.21 27.52 29.95 28.78 36.24
6 19.89 23.85 26.58 25.10 27.30

5 结论

在过往国内外研究中,已有不少降水量预测方法如SSA、ARIMA等,本文将LSTM神经网络应用在降水量预测方面并探讨其可行性,本文使用1990年1月—2013年12月之间的月降水量时间序列数据训练LSTM网络,动态预测了2014年1月—2016年12月的降水量,实验结果如下：
（1）单个测站LSTM模型的预测精度优于传统模型的预测精度。分析56106号测站的预测结果,发现LSTM模型对周期的预测更准确,较少出现位移偏差;对7-9月之间的低谷值预测更准确;对比RNN、NAR、SSA和ARIMA模型预测结果的RMSE和MAE,发现LSTM模型的RMSE和MAE均更低,R2更高,达到了0.87。
（2）全部测站LSTM模型的预测精度整体优于传统模型的预测精度。对全部测站进行预测,再对精度进行插值。发现LSTM模型在除北部和西南部少部分区域预测效果较差以外,其他大部分区域预测精度是较高的;对比RNN模型、NAR模型、SSA模型和ARIMA模型的R2值发现,LSTM模型的R2平均值比RNN、NAR、SSA和LSTM模型的R2平均值分别提高了0.07、0.15、0.13和0.36。
（3）不同预测长度时,LSTM模型的预测精度优于传统模型的预测精度。探讨在预测长度分别为6、12、24和36个月时模型预测精度变化情况,结果显示5种模型均随着预测长度增加RMSE会上升,但在这几种预测长度中,LSTM模型均为最优,且精度由高到底的顺序为：LSTM,RNN,SSA,NAR和ARIMA。LSTM模型的优势在于：LSTM独特的网络结构能对序列进行选择性记忆,对降水的规律有更深一步的挖掘。因此该模型具有良好的预测效果。
论文研究了LSTM方法在降水预测领域中的适用性,发现使用LSTM网络预测青藏高原的月降水量在预测精度上较传统方法有了一定的提高,将LSTM方法应用范围拓展到构建降水量模型,为气象预测提供了新的思路。指出在降水预测中使用人工智能算法,将是一条有效的途径。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Immerzeel W W, Beek L P H V, Bierkens M F P. Climate change will affect the asian water towers[J]. Science, 2010,328(5984):1382-1385.

DOI PMID

[2]
Song C, Sheng Y. Contrasting evolution patterns between glacier-fed and non-glacier-fed lakes in the Tanggula Mountains and climate cause analysis[J]. Climatic Change, 2016,135(3-4):1-15.

[3]
冯松, 汤懋苍, 王冬梅. 青藏高原是我国气候变化启动区的新证据[J]. 科学通报, 1998,43(6):633-636.

[ Feng S, Tang M C, Wang D M. The Qinghai-Tibet Plateau is a new evidence for the climate change start-up zone in China[J]. Chinese Science Bulletin, 1998,43(6):633-636. ]

[4]
潘保田, 李吉均. 青藏高原:全球气候变化的驱动机与放大器-Ⅲ.青藏高原隆起对气候变化的影响[J]. 兰州大学学报, 1996,32(1):108-115.

[ Pan B J, Li J J. Qinghai-Tibetan Plateau: A driver and amplifier of the global climatic change[J]. Journal of LanZhou University, 1996,32(1):108-115. ]

[5]
Yao T, Thompson L, Yang W, et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings[J]. Nature Climate Change, 2012,2(9):663-667.

[6]
Ke L, Ding X, Li W, et al. Remote sensing of glacier change in the central Qinghai-Tibet Plateau and the relationship with changing climate[J]. Remote Sensing, 2017,9(2):114-130.

[7]
Nayagam L R, Janardanan R, Mohan H S R. An empirical model for the seasonal prediction of southwest monsoon rainfall over Kerala, a meteorological subdivision of India[J]. International Journal of Climatology, 2010,28(6):823-831.

[8]
赵莹. 葠窝水库降雨量灰色预测模型应用分析[J]. 中国水能及电气化, 2016,141(12):68-70.

[ Zhao Y. Analysis on application of rainfall grey prediction model for Shenwo reservoir[J]. China Water Power & Electrification, 2016,141(12):68-70. ]

[9]
潘刚, 芦冰, 邹兵, 等. 马尔可夫链在水库主汛期降雨状态预测中的应用[J]. 水利科技与经济, 2011,17(6):33-36.

[ Pan G, Lu B, Zou B, et al. Markov chain state in the reservoir the main flood season rainfall forecast[J]. Water Conservancy Science & Technology & Economy, 2011,17(6):33-36. ]

[10]
Feng C Y. Application of singular spectrum analysis to summer precipitation prediction[J]. Meteorological Monthly, 2002,28(11):22-25.

[11]
Burlando P, Rosso R, Cadavid L G, et al. Forecasting of short-term rainfall using ARMA models[J]. Journal of Hydrology, 1993,144(1-4):193-211.

[12]
Liu C, Tian Y, Wang X H. Study of rainfall prediction model based on GM (1, 1) - Markov chain[C]. Xi'an: 2011 International Symposium on Water Resource and Environmental Protection, 2011,18(1):744-747.

[13]
宋帆, 杨晓华, 武翡翡, 等. 基于聚类分析的模糊马尔科夫链在降雨量预测中的应用[J]. 节水灌溉, 2018,278(10):38-41,46.

[ Song F, Yang X H, Wu F F, et al. Rainfall prediction using clustering-fuzzy-markov chain model[J]. Water Saving Irrigation, 2018,278(10):38-41,46. ]

[14]
Luk K C, Ball J E, Sharma A. An application of artificial neural networks for rainfall forecasting[J]. Mathematical & Computer Modelling, 2001,33(6):683-693.

[15]
Nanda T, Sahoo B, Beria H, et al. A wavelet-based non-linear autoregressive with exogenous inputs (WNARX) dynamic neural network model for real-time flood forecasting using satellite-based rainfall products[J]. Journal of Hydrology, 2016,539(87):57-73.

[16]
Chattopadhyay S, Chattopadhyay G. Comparative study among different neural net learning algorithms applied to rainfall time series[J]. Meteorological Applications, 2010,15(2):273-280.

[17]
Nasseri M, Asghari K, Abedini M J. Optimized scenario for rainfall forecasting using genetic algorithm coupled with artificial neural network[J]. Expert Systems with Applications, 2008,35(3):1415-1421.

[18]
Baratta D, Masulli F, Cicioni G, et al. Application of an ensemble technique based on singular spectrum analysis to daily rainfall forecasting[J]. Neural Networks, 2003,16(3):375-387.

[19]
Wu C L, Chau K W. Prediction of rainfall time series using modular soft computingmethods[J]. Engineering Applications of Artificial Intelligence, 2013,26(3):997-1007.

[20]
Yaseen Z M, Ghareb M I, Ebtehaj I, et al. Rainfall pattern forecasting using novel hybrid intelligent model based ANFIS-FFA[J]. Water Resources Management, 2017,8(32):105-122.

[21]
Chau K W, Wu C L. A hybrid model coupled with singular spectrum analysis for daily rainfall prediction[J]. Journal of Hydroinformatics, 2010,12(4):458-473.

[22]
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997,9(8):1735-1780.

DOI PMID

[23]
Graves A . Supervised sequence labelling with recurrent neural networks[J]. Studies in Computational Intelligence, 2012,2(385):42-45.

[24]
Graves A, Schmidhuber J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures[J]. Neural Networks, 2005,18(5-6):602-610.

DOI PMID

[25]
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. Journal of Machine Learning Research, 2011,12(7):257-269.

[26]
Kingma D P, Ba J. Adam: A method for stochastic optimization[C]. 3rd International Conference for Learning Representations, 2015,78(1):116-130.

[27]
Vautard R. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals[J]. Physica D: Nonlinear Phenom. 1992,9(58):95-126.

[28]
Golyandina N, Korobeynikov A. Basic singular spectrum analysis and forecasting with R[J]. Computational Statistics & Data Analysis, 2014,71(12):934-954.

[29]
Box G E, Jenkins G M. Time series analysis: Forecasting and control rev.ed.[J]. Journal of Time, 1976,31(4):238-242.

Options
文章导航

/

〈 〉