EN中文

地球信息科学学报 >

2020 , Vol. 22 >Issue 9: 1868 - 1877

DOI: https://doi.org/10.12082/dqxxkx.2020.190514

遥感科学与应用技术

交叉点结构特征约束的机载LiDAR点云与多视角航空影像配准

  • 王广帅 ,
  • 万一 ,
  • 张永军 , *
展开
  • 武汉大学遥感信息工程学院,武汉 430079
*张永军（1975— ）,男,内蒙古鄂尔多斯人,博士,教授,博导,主要从事数字摄影测量与遥感、计算机视觉、多源数据融合等的研究。E-mail：

王广帅（1994— ）,男,山东菏泽人,硕士生,主要从事激光点云与影像配准研究。E-mail：

收稿日期: 2019-09-10

  要求修回日期: 2019-11-12

  网络出版日期: 2020-11-25

基金资助

国家自然科学基金项目(41871368)

版权

版权所有，未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
收起

Registration of Airborne LiDAR Data and Multi-View Aerial Images Constrained by Junction Structure Features

  • WANG Guangshuai ,
  • WAN Yi ,
  • ZHANG Yongjun , *
Expand
  • School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
*ZHANG Yongjun, E-mail:

Received date: 2019-09-10

  Request revised date: 2019-11-12

  Online published: 2020-11-25

Supported by

National Natural Science Foundation of China(41871368)

Copyright

Copyright reserved © 2020
Fold

摘要

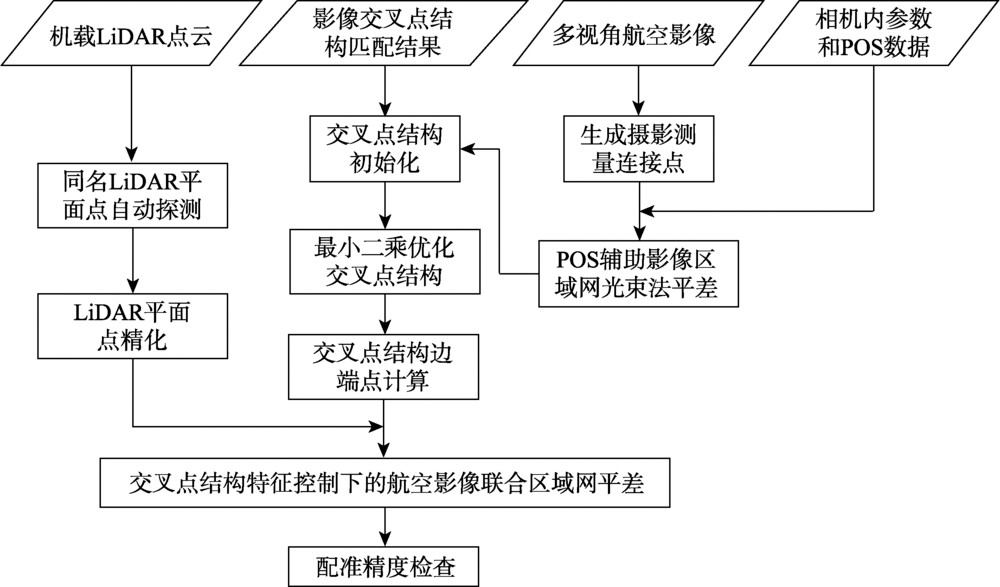
针对机载点云与航空影像配准精度受点云密度影响较大的问题,本文提出一种交叉点结构特征约束下的机载点云影像配准方法。该方法充分利用激光测距精度较高这一优势,采用点云中的平面结构对影像区域网进行绝对定向约束。首先,利用POS辅助平差后的影像内外方位元素和影像交叉点结构匹配结果,以反投影距离为测度,按照最小二乘准则交会得到交叉点物方结构;然后,在LiDAR点云中自动探测交叉点结构的同名LiDAR平面点;最后,进行交叉点结构特征约束下的航空影像联合区域网平差,得到精确的相机内参数和影像外方位元素。实验结果表明,本文方法在平面和高程方向上均可达到1~2个像素的配准精度。与基于建筑物角特征的配准方法相比,有效克服了点云密度对配准精度的影响,当点云密度较低时,本文方法依然可以取得较高的配准精度。

关键词： 机载LiDAR; 航空影像; 配准; 交叉点结构; 平面特征; 区域网平差

本文引用格式

王广帅 , 万一 , 张永军 . 交叉点结构特征约束的机载LiDAR点云与多视角航空影像配准[J]. 地球信息科学学报, 2020 , 22(9) : 1868 -1877 . DOI: 10.12082/dqxxkx.2020.190514

Abstract

：The integration of Airborne LiDAR data and aerial imagery is useful in data interpretation, land monitoring, and 3D reconstruction. As the first step of these tasks, the geometric registration of the two types of data should be conducted to ensure their alignment. The alignment is sometimes difficult because of differences in their data acquisition mechanisms. The LiDAR data is more reliable and more accurate on smooth surfaces like grounds, walls, and roofs which are difficult to extract from aerial imagery. LiDAR points are mostly sparser than the pixels on aerial images. Considering that the a priori ranging error (1~5 cm) of airborne LiDAR data is usually much smaller than the average point distance (10~50 cm), this paper introduced a plane-constrained block adjustment model to align the two types of data, where the planes were obtained by the intersection of corresponding junction structures. The planar constraints were implemented by forcing surrounding LiDAR points to be on the planes. The proposed block adjustment model is a mixture of the conventional POS-aided and self-calibrated bundle adjustment model and two more types of observing equations. One is the distance between image junction structure observations, and reprojection of the spatial junction structure should be zeros. The other is the normal distance between LiDAR points, and the spatial planes obtained by junction structure should be zeros. In this paper, firstly junction structures in object space were solved based on least squares theory. Then, conjugate planes of junction structures in LiDAR points were detected automatically. Finally, the aerial images block adjustment under constraints of junction structure was performed to obtain the precise interior and exterior orientation parameters. The experimental results showed that both the horizontal and the vertical accuracy of the proposed method could reach 1~2 pixels of the aerial images, which was obviously better than the building-corner-based method. In order to probe into the influence of point cloud density, the LiDAR points were thinned randomly before the geometric registration. The results showed that the accuracy of the proposed method was not influenced but the accuracy of building-corner-based method decreased when the point cloud density decreased, especially the horizontal accuracy. In conclusion, the proposed method takes the advantage of the high-ranging accuracy of LiDAR data to reach high registration accuracy and avoids the influence of the point cloud density. When the density of the LiDAR point cloud is low, a high registration accuracy can be reached using the proposed method.

Key words： Airborne LiDAR; aerial imagery; registration; junction structure; plane feature; block adjustment

1 引言

随着硬件和数据处理算法的迅速发展,机载激光雷达（Airborne Light Detection and Ranging, LiDAR）已成为一种重要的地表信息获取手段[1,2]。与传统的航空摄影测量技术相比,LiDAR具有效率高、穿透力强以及受天气条件影响小的特点,可直接获取地面物体的空间位置信息。将传统航空摄影测量与LiDAR相结合,可直接获取空间和语义信息,在地物自动提取与分类[3,4],变化检测[5,6],真正射影像生成[7]和城市建筑物建模[8,9]等领域具有广泛的应用前景。
联合使用LiDAR和航空影像数据的前提是建立LiDAR三维数据与航空影像间的映射关系,即将两者精确配准。然而,由于点云和影像在数据组织形式上的巨大差异,二者间的高精度配准还存着较大的难度[10,11]。目前LiDAR点云和影像的配准方法可以归纳为以下3类[12]：① 根据强度或高度信息将LiDAR点云内插为二维图像,然后采用图像配准方法进行处理。如基于SIFT的配准方法[13]、基于频率域的配准方法[10]以及基于互信息的配准方法[14,15,16]。此类方法借鉴了当前成熟的图像配准思路,自动化程度较高,缺点是点云内插成图像时会引入误差,降低配准精度;② 基于多视图几何的配准方法。首先根据图像匹配结果和多视图几何原理生成摄影测量点云,然后采用点云配准方法估计变换模型参数[17,18,19]。此类方法对参数初始值较为敏感,当初始值精度较低时,易陷入局部最优解;③ 基于特征的方法,包括点、线和面特征等,这类方法直接建立点云与影像特征间的对应关系,并据此计算二者间的几何变换参数[20,21,22]。此类方法避免了点云和影像间转换所引入的误差,但由于LiDAR点云的离散采样特性,如何从点云中获取高精度控制信息仍是一个难点。
综上可知,配准的核心步骤是2类数据间同名控制信息的获取,而控制信息的精度更是直接决定了最终配准精度。本文设计了一种平面结构特征,其精度由激光测距精度决定,不受点云密度的影响。以其为控制基元,进行影像区域网平差,有效克服了点云密度对配准精度的影响,实现了点云影像高精度配准。

2 技术路线及计算方法

2.1 技术路线

LiDAR点云与影像的配准精度由LiDAR点云密度、影像分辨率以及场景复杂性等因素决定[23]。针对现有方法配准精度受点云密度影响较大问题,本文充分利用激光测距精度较高这一优势,提出了一种交叉点结构特征约束下的机载点云影像配准方法。① 利用POS辅助平差后的影像内外方位元素和影像交叉点结构匹配结果重建物方交叉点结构;② 在LiDAR点云中自动探测交叉点结构的同名LiDAR平面点;③ 进行交叉点结构特征约束下的航空影像区域网平差,得到精确的相机内参数和影像外方位元素。本文的技术流程如图1所示。
图1 本文配准算法流程

Fig. 1 Flowchart of the proposed registration method

2.2 交叉点结构的物方表达

交叉点结构即为相交于某一点的两条空间直线所形成的平面结构,其广泛分布于城区场景下,建筑物墙面铅锤的棱线与屋顶边缘直线即可形成一个交叉点结构。如图2所示,空间交叉点结构由交叉点中心点和过该点的两条边构成。本文采用中心点坐标 S X , Y , Z 和两边的方向 Sp θ 1 , φ 1 、 Sq θ 2 , φ 2 进行描述,共7个参数。其中 θ ∈ [ - π 2 , π 2 ] , φ ∈ 0 , 2 π 。利用交叉点结构角参数,可以计算交叉点结构边的方向向量。若交叉点结构某条边的单位方向向量 L → = l , m , n ,其中 l 、 m 和 n 分别为 X 、 Y 和 Z 方向的坐标分量,则：
图2 交叉点结构描述示意

Fig. 2 Schematic illustration of the junction structure

l = cos θ cos φ m = cos θ sin φ n = sin θ
利用影像内外方位元素和影像交叉点结构匹配结果,可以交会得到交叉点物方结构。对于交叉点结构的两边,分别计算两两空间投影平面（摄影中心与影像交叉点结构边形成的平面）之间的夹角,以两边的夹角平均值作为两影像交叉点结构的交会角。取交会角最大的两张影像,通过平面相交计算得到交叉点结构参数作为初始值。
最小二乘优化交叉点结构参数。以交叉点结构在影像上的反投影结构与相应影像观测结构间的距离作为代价,列出代价方程。整体代价函数形式如下：
C = ∑ k D P f J Pt , T k , m k + D J f J Line , T k , l k
式中： C 表示交叉点结构求解整体代价; D P ( * ) 为交叉点中心反投影点到对应像点的距离函数; D J ( * ) 为影像直线段到交叉点结构边反投影直线段的距离函数; f ( * ) 表示反投影函数; T k 为能观测到该交叉点结构的第k张影像的内外方位元素; J Pt 表示交叉点中心; J Line 表示交叉点结构边; m k 表示影像上对应的交叉点中心像点; l k 表示影像上对应的交叉点结构边。
根据式（2）,按照最小二乘平差准则,可精确求解物方交叉点结构参数。将影像交叉点结构边端点投影中心连线记为“端点光线”,计算物方交叉点结构边上距离“端点光线”最近的点,即为该影像交叉点结构边端点在物方交叉点结构边上的投影点。将所有影像交叉点结构边端点投到物方交叉点结构边上,取其中距离最远的两个点作为物方交叉点结构边端点。如图3所示,绿线和红线分别表示左、右像交叉点结构在物方的投影,则该交叉点结构两边的端点别为 S j 和 T i 。
图3 交叉点结构两视图投影几何

Fig. 3 Projection geometry of the junction structure in two-views

相较于文献[21]提出的用2条空间直线段构成的角特征,本文采用的交叉点结构特征本质上为带有结构信息的平面特征,其与实际场景中的建筑物面状结构更为一致。此描述方式不含冗余信息,平差解算更为严密。

2.3 同名LiDAR平面点自动探测

为了获得影像交叉点结构在LiDAR点云中的同名平面点,本文设计了同名LiDAR平面点自动探测方法,具体步骤如下：
（1） 交叉点结构前方交会。根据式（2）所示交叉点结构交会模型,利用影像交叉点匹配结果和内外方位元素,得到交叉点物方结构;
（2）生成长方体探测空间。如图4所示,以交叉点结构平面为中心面,沿其法方向分别向两侧膨胀,单侧膨胀宽度为 δ 。统计落入该探测长方体内的LiDAR点数目;
图4 同名LiDAR平面点自动探测示意

Fig. 4 Automatic detection of conjugate LiDAR plane points

（3）将探测长方体沿交叉点结构平面法方向向两侧移动 δ ,统计落入探测空间内的LiDAR点数目;
（4）迭代步骤（3） N 次, N = INT ( σ C / δ ) ,其中 σ C 为点云影像坐标系统初始概略偏差。则上述过程共得到 ( 2 N + 1 ) 组LiDAR点,取其中点数最多的LiDAR点探测结果作为候选结果;
（5）LiDAR平面点精化。对步骤（4）得到的候选LiDAR点进行RANSAC最小二乘平面拟合,得到拟合内点率 R P 和内点数 N P 。若 R P ≥ R MIN 且 N P ≥ N MIN ,则探测成功,将RANSAC拟合内点作为最终结果,否则探测失败。本文 R MIN = 0.5 , N MIN = 20 ,RANSAC最小二乘拟合距离阈值为0.03 m。

2.4 交叉点结构约束下的航空影像联合区域网平差 模型

本文以交叉点结构作为绝对定向控制基元,采用摄影测量连接点保持区域网内部一致性,设计了交叉点结构约束下的航空影像联合区域网平差模型。如图5所示,空间交叉点结构在影像上的观测结构为 SAB ,其在影像上的反投影结构为 sab 。则 SAB 与 sab 间的距离 d 反映了影像位置姿态与物方空间交叉点结构的一致性,可表示为：
图5 交叉点结构特征约束下的点云影像配准模型

Fig. 5 Registration model under constraints of junction structure features

d = d 1 + d 2 + d 3
式中： d 为交叉点结构反投影距离; d 1 为交叉点中心反投影像点到相应观测像点的距离, d 2 和 d 3 分别为影像交叉点结构边端点到反投影交叉点结构边的距离。对于影像区域网,利用初始相机内参数和影像外方位元素,交叉点结构整体反投影代价函数可表示如下：
C ImgJunction = ∑ ∑ d f J i , T k , j ik
式中： C ImgJunction 表示交叉点结构反投影代价; f ( * ) 表示交叉点结构投影函数; J i 表示第 i 个交叉点结构; T k 表示能观测到该交叉点结构的第 k 张影像的待优化参数,包括外方位元素和相应相机内参数; j ik 表示第 i 个交叉点结构在第 k 张影像上的观测值; d ( * ) 表示交叉点反投影结构与观测值间的距离函数。
当LiDAR点云与影像配准时,物方空间某一平面上LiDAR点应位于摄影测量交叉点结构所形成的平面内,即LiDAR点到交叉点结构平面的法向距离为0,此时该组LiDAR点即为交叉点结构的同名对应。LiDAR点到交叉点平面的距离代价表达式如下：
C NorDis = ∑ ∑ d n ( J i , P ik )
式中： C NorDis 表示LiDAR点到交叉点平面的距离代价; J i 表示第 i 个交叉点结构参数; P ik 为第 i 个交叉点结构对应的第 k 个LiDAR点; d n ( * ) 表示点到平面的距离,计算方法如下：
D = ( X P - X O ) ∙ n x + ( Y P - Y O ) ∙ n y + ( Z P - Z O ) ∙ n z n x 2 + n y 2 + n z 2
n x = cos θ 1 sin φ 1 sin θ 2 - sin θ 1 cos ( θ 2 ) sin ( φ 2 ) n y = sin ( θ 1 ) cos θ 2 cos ( φ 2 ) - cos θ 1 sin φ 1 sin θ 2 n z = cos θ 1 cos ( φ 1 ) cos θ 2 sin φ 2 - cos θ 1 sin φ 1 cos θ 2 cos ( φ 2 )
式中： D 表示LiDAR点到交叉点平面的距离; n x , n y , n z 为交叉点平面的单位法向量; ( X P Y P Z P ) 为LiDAR点的坐标;( X O Y O Z O θ 1 φ 1 θ 2 φ 2 )为交叉点结构参数。
此外,对于摄影测量连接点像点观测值,根据摄影测量共线条件方程列出代价方程,形式如下：
C Poin t = ∑ i ∑ k D P f P i , T k , m ik
式中： C Point 表示摄影测量连接点反投影代价; D P * 为反投影点到对应像点的距离函数; P i 表示第 i 个物方点坐标; T k 为第k张影像的内外方位元素; m ik 表示第 i 个连接点在第 k 张影像上对应的像点观测值。
综上,交叉点结构控制下的航空影像联合区域网平差模型的误差方程如下：
V 1 = A M ∆ t + B M ∆ c + C M ∆ k + D M ∆ p - b TiePt , W 1 V 2 = A J ∆ t + B J ∆ c + C J ∆ k + D J ∆ q - b Junction , W 2 V 3 = D S ∆ q - b LdrPt , W 3
式中： V 1 、 V 2 和 V 3 分别为摄影测量连接点反投影距离残差、交叉点结构反投影距离残差和LiDAR点到交叉点结构平面的距离残差; ∆ t 、 ∆ c 、 ∆ k 、 ∆ p 和 ∆ q 分别为影像外方位元素、内方位元素、镜头畸变系数、摄影测量连接点物方坐标以及交叉点结构参数改正数向量; A M 、 B M 、 C M 、 D M 、 A J 、 B J 、 C J 、 D J 和 D S 分别为一阶偏导矩阵; b TiePt 、 b Junction 和 b LdrPt 为常数向量; W 1 、 W 2 和 W 3 为权重, W 1 = σ 0 2 / σ P 2 , W 2 = σ 0 2 / σ J 2 , W 3 = σ 0 2 / σ D 2 ,其中, σ 0 为单位权中误差, σ P 和 σ J 分别为连接点和交叉点结构在影像上的提取中误差, σ D 为LiDAR点到LiDAR点拟合平面的距离。

3 配准实验与分析

3.1 实验数据

为了验证算法的实际效果,本文选用宁波和广州2组机载点云影像数据进行实验,详细信息如表1所示。图6展示了广州测区影像和LiDAR点云概况,图7展示了宁波测区检查点概况,其中绿色点表示人工利用RTK量测的检查点。
表1 实验数据详细信息

Tab. 1 Details of the experimental data

数据集 Ⅰ Ⅱ
航空
影像		 测区位置 广州 宁波
航高/m 500 900
地面分辨率/m 0.032 0.048
像幅大小/pixels 10 336×7788 11 608×8708
相机数 5 5
影像总数 2415 1451
LiDAR 点云密度/(pts/m2) 16 10
点云间距/m 0.25 0.30
总点数 43 971 092 45 154 384
图6 广州测区影像与LiDAR点云概况

Fig. 6 Overview of the image data and LiDAR point cloud for the Guangzhou data set

图7 宁波测区检查点概况

Fig. 7 Overview of check points for the Ningbo data set

3.2 实验结果与分析

在2组数据集中,人工从测区内均匀选取30个交叉点结构作为控制信息,利用本文方法进行配准,图8展示了部分影像交叉点结构量测结果,红色和紫色线段为交叉点结构两边,绿色十字丝中心表示交叉点中心点。为了直观展示配准效果,利用影像色彩对点云进行渲染。图9展示了广州测区某建筑配准前后的点云赋色效果,配准后的点云色彩与实际场景高度一致。为了检查局部区域的配准效果,选取若干典型建筑物屋顶点云,分别利用配准前后的参数将其反投影到相应影像上。广州测区和宁波测区的投影效果对比分别如图10、图11所示,其中图10(a)和图11(a)为配准前的屋顶点云投影效果,图10(b)和图11(b)为相应区域配准后的投影效果,红点为屋顶LiDAR点的反投影像点。由于初始相机参数和影像外方位元素不准确,配准前LiDAR点投到影像上的误差较大,点云和影像间存在明显错位。经过本文方法配准后,错位情况得到较好纠正,点云与影像实现了准确对齐。
图8 广州测区部分影像交叉点结构量测结果

Fig. 8 Measurements of image junction structures for the Guangzhou data set

图9 广州某区域点云赋色结果

Fig. 9 LiDAR point cloud colored by aerial images for the Guangzhou data set

图10 广州测区点云影像配准前后投影效果对比

Fig. 10 Comparison of the fitness of LiDAR points to images before and after registration for the Guangzhou data

图11 宁波测区点云影像配准前后投影效果对比

Fig. 11 Comparison of the fitness of LiDAR points to images before and after registration for the Ningbo data

为了定量评定配准精度,对于广州数据,人工量测12个交叉点结构及同名LiDAR平面点用作检查,其中平面和高程方向各6个。对于宁波数据,本文采用人工量测的22个检查点评定配准精度,检查点坐标为外业通过RTK技术采集得到,其分布如图7(a)中绿色点所示,这种评定方式更加符合摄影测量通行标准。此外,本文将文献[21]提出的建筑物角特征配准方法与交叉点配准方法进行精度对比。表2展示了用2种方法对广州数据配准后,检查LiDAR平面点到相应交叉点结构平面的距离。交叉点配准方法的平面和高程配准中误差分别为0.042 m和0.058 m,优于角特征方法的0.052 m和0.101 m。表3给出了宁波数据配准后,检查点的坐标残差统计。交叉点配准方法的平面精度为0.057 m,约为1.18个像素,优于角特征方法的0.109 m（约2.27个像素）;高程方向上交叉点配准方法亦明显优于角特征方法。
表2 广州测区配准精度对比

Tab. 2 Comparison of registration accuracy for the Guangzhou data set

类别 角特征配准方法/m 交叉点配准方法/m
dXY dZ dXY dZ
残差中误差 0.052 0.101 0.042 0.058
残差平均值 0.035 0.069 0.038 0.054
残差最大值 0.126 0.249 0.116 0.097
表3 宁波测区检查点残差对比

Tab. 3 Comparison of check points residuals for the Ningbo data set

类别 角特征配准方法/m 交叉点配准方法/m
dX dY dXY dZ dX dY dXY dZ
残差中误差 0.076 0.063 0.109 0.100 0.051 0.025 0.057 0.063
残差平均值 -0.031 0.002 0.089 0.062 0.045 0.003 0.051 -0.044
残差最大值 -0.176 -0.141 0.183 0.296 0.096 -0.054 0.099 -0.112
为了验证点云密度对配准精度的影响,文中对点云数据随机抽稀,从而降低点云密度,然后利用本文方法和角特征方法进行配准。图12和图13分别展示了2种方法对广州和宁波数据的配准精度,其中红色折线为交叉点配准方法配准精度随点云密度降低而变化的趋势,深蓝色折线表达了角特征方法的配准精度变化趋势。由图可知,在各个点云密度层级上,交叉点配准方法的平面和高程配准精度均优于角特征配准方法。随着点云密度降低,交叉点配准方法在平面和高程方向上的精度基本不受影响。当点云密度降低为原始密度0.1倍时,本文方法的平面和高程的配准精度依然可以达到0.05~0.08 m,约为1~2个像素。而角特征方法的平面配准精度随点云密度的降低明显降低,高程方向上精度略有降低。这是由于角特征方法利用建筑物边缘的LiDAR点拟合线特征,并将线特征的交点作为控制基元。随着点云密度降低,拟合直线段的误差增加,其平面控制精度下降,这也是许多基于点、线特征配准方法的缺陷。角特征方法在高程方向上的精度主要由建筑物屋顶点云高程方向精度决定,受点云密度影响较小。相比之下,交叉点配准方法利用LiDAR点云中的面特征对各个方向进行约束,其精度由激光测距精度所决定,基本不受点云密度影响。故而本文方法有效克服了点云密度对配准精度的影响,在点云密度较低的情况下,也能取得较高的配准精度。
图12 广州测区点云抽稀后配准精度对比

Fig. 12 Comparison of registration accuracy using thinning point clouds for the Guangzhou data set

图13 宁波测区点云抽稀后配准精度对比

Fig. 13 Comparison of registration accuracy using thinning point clouds for the Ningbo data set

4 结论与讨论

针对机载点云影像配准精度受点云密度影响较大的问题,本文充分利用激光测距精度较高这一优势,将平面结构作为控制信息引入影像区域网平差中,提出了一种交叉点结构特征约束下的机载点云与多视角航空影像配准方法。本文采用广州和宁波2组数据进行了验证实验,并对LiDAR点云进行抽稀,探究交叉点配准方法在点云密度较低时的配准效果。主要研究结论如下：
（1）以反投影距离为测度解算交叉点物方结构,利用长方体探测法可以获取其对应的同名LiDAR平面点。基于LiDAR点与交叉点结构的共面关系,能够有效实现影像区域网在各个方向上的绝对定向。
（2）实验结果表明,基于交叉点结构的配准方法在平面和高程方向上均可以达到1~2个像素的配准精度,明显优于基于建筑物角特征的配准方法。
（3）基于交叉点结构的配准方法有效克服了点云密度对配准精度的影响,当点云密度降低时,该方法亦可以取得较高的配准精度。
本文提出了一种利用平面结构特征实现点云影像配准的新思路,但本文方法需要以影像交叉点匹配结果作为输入信息,这在一定程度上限制了本方法的自动化程度。今后将对交叉点结构的自动化匹配进行深入研究,进一步完善本方法。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Ackermann F. Airborne laser scanning: Present status and future expectations[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999,54(1):64-67.

[2]
Zhang J, Lin X. Advances in fusion of optical imagery and LiDAR point cloud applied to photogrammetry and remote sensing[J]. International Journal of Image and Data Fusion, 2016,8(1):1-31.

[3]
袁鹏飞, 黄荣刚, 胡平波, 等. 基于多光谱LiDAR数据的道路中心线提取[J]. 地球信息科学学报, 2018,20(4):452-461.

[ Yuan P F, Huang R G, Hu P B, et al. Road extraction method based on multi-spectral LiDAR data[J]. Journal of Geo-information Science, 2018,20(4):452-461. ]

[4]
Huang J, Zhang X, Xin Q, et al. Automatic building extraction from high-resolution aerial images and LiDAR data using gated residual refinement network[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019,151(1):91-105.

[5]
Peng D F, Zhang Y J. Building change detection by combining LiDAR data and ortho image[J]. ISPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, XLI-B3(1):669-676.

[6]
Ali-Sisto D, Packalen P. Forest change detection by using point clouds from dense image matching together with a LiDAR-derived terrain model[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017,10(3):1197-1206.

[7]
Gharibi H, Habib A. True orthophoto generation from aerial frame images and LiDAR data: An update[J]. Remote Sensing, 2018,10(4):581-509.

[8]
程亮, 龚健雅, 李满春, 等. 集成多视航空影像与LiDAR数据重建3维建筑物模型[J]. 测绘学报, 2009,38(6):494-501.

[ Cheng L, Gong J Y, Li M C, et al. 3D building model reconstruction from multi-view aerial images and LiDAR data[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(6):494-501. ]

[9]
Jung J, Sohn G. A line-based progressive refinement of 3d rooftop models using airborne LiDAR data with single view imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019,149(1):157-175.

[10]
Wong A, Orchard J. Efficient FFT-accelerated approach to invariant optical-LiDAR registration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008,46(11):3917-3925.

[11]
张靖, 江万寿. 激光点云与光学影像配准:现状与趋势[J]. 地球信息科学学报, 2017,19(4):528-539.

[ Zhang J, Jiang W S. Registration between laser scanning point cloud and optical images: Status and trends[J]. Journal of Geo-Information Science, 2017,19(4):528-539. ]

[12]
Peng S, Zhang L. Automatic registration of optical images with airborne LiDAR point cloud in urban scenes based on line-point similarity invariant and extended collinearity equations[J]. Sensors (Basel), 2019,19(5):1086-1103.

[13]
Abedini A, Hahn M, Samadzadegan F. An investigation into the registration of LIDAR intensity data and aerial images using the SIFT approach[C]// The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, 2008: 169-176.

[14]
Parmehr E G, Fraser C S, Zhang C, et al. Automatic registration of optical imagery with 3d lidar data using local combined mutual information[J]. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013, II-5/W2(1):229-234.

[15]
Parmehr E G, Fraser C S, Zhang C, et al. Automatic registration of optical imagery with 3d LiDAR data using statistical similarity[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014,88(1):28-40.

[16]
Parmehr E G, Fraser C S, Zhang C. Automatic parameter selection for intensity-based registration of imagery to LiDAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016,54(12):7032-7043.

[17]
Zhao W, Nister D, Hsu S. Alignment of continuous video onto 3d point clouds[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005,27(8):1305-1318.

DOI PMID

[18]
Teo T A, Huang S H. Automatic co-registration of optical satellite images and airborne LiDAR data using relative and absolute orientations[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013,6(5):2229-2237.

[19]
Huang R Y, Zheng S Y, Hu K. Registration of aerial optical images with LiDAR data using the closest point principle and collinearity equations[J]. Sensors, 2018,18(6):1770-1791.

[20]
Mitishita E, Habib A, Centeno J, et al. Photogrammetric and LiDAR data integration using the centroid of a rectangular roof as a control point[J]. The Photogrammetric Record, 2010,23(121):19-35.

[21]
张永军, 熊小东, 沈翔. 城区机载LiDAR数据与航空影像的自动配准[J]. 遥感学报, 2012,16(3):579-595.

[ Zhang Y J, Xiong X D, Shen X. Automatic registration of urban aerial imagery with airborne LiDAR data[J]. Journal of Remote Sensing, 2012,16(3):579-595. ]

[22]
张良, 马洪超, 高广, 等. 点、线相似不变性的城区航空影像与机载激光雷达点云自动配准[J]. 测绘学报, 2014,43(4):372-379.

[ Zhang L, Ma H C, Gao G, et al. Automatic registration of urban aerial images with airborne LiDAR data[J]. Acta Geodaetica et Cartographica Sinica, 2014,43(4):372-379. ]

[23]
Mishra R, Zhang Y. A review of optical imagery and airborne LiDAR data registration methods[J]. The Open Remote Sensing Journal, 2012,5(1):54-63.

DOI

Options
文章导航

/

〈 〉