EN中文

地球信息科学学报 >

2020 , Vol. 22 >Issue 10: 2023 - 2037

DOI: https://doi.org/10.12082/dqxxkx.2020.200078

专栏：城乡生态环境综合监测

融合土地覆盖和土壤水分产品的近地表空气温度空间化方法

  • 高亮 , 1, 2 ,
  • 杜鑫 1 ,
  • 李强子 , 1, * ,
  • 王红岩 1 ,
  • 张源 1 ,
  • 王思远 1, 2
展开
  • 1.中国科学院空天信息创新研究院,北京 100101
  • 2.中国科学院大学,北京 100049
*李强子（1970—）,男,河南洛阳人,博士,研究员,主要从事农业遥感和生态遥感方面的研究。 E-mail:

高亮（1994— ）,男,甘肃定西人,硕士生,主要从事农业遥感和农业气象灾害方面的研究。E-mail:

收稿日期: 2020-02-17

  要求修回日期: 2020-05-12

  网络出版日期: 2020-12-25

基金资助

国家重点研发计划资助项目(2017YFD0300404-1)

国家重点研发计划资助项目(2017YFD0300402)

版权

版权所有，未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
收起

A Near-surface Air Temperature Spatialization Method Integrating Landuse and Soil Moisture Products

  • GAO Liang , 1, 2 ,
  • DU Xin 1 ,
  • LI Qiangzi , 1, * ,
  • WANG Hongyan 1 ,
  • ZHANG Yuan 1 ,
  • WANG Siyuan 1, 2
Expand
  • 1. Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100101, China
  • 2. University of Chinese Academy of Sciences, Beijing 100049, China
*LI Qiangzi, E-mail:

Received date: 2020-02-17

  Request revised date: 2020-05-12

  Online published: 2020-12-25

Supported by

National Key Research and Development Program of China(2017YFD0300404-1)

National Key Research and Development Program of China(2017YFD0300402)

Copyright

Copyright reserved © 2020
Fold

摘要

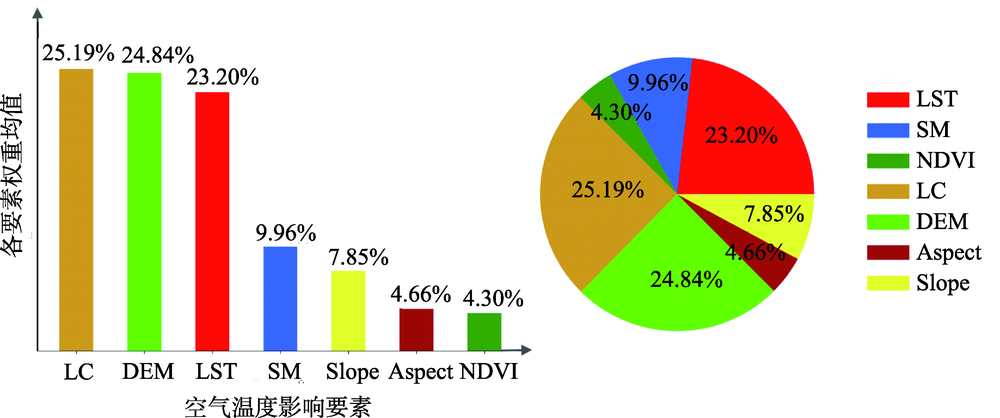
空气温度是评价人居环境的重要指标,与人类的生产生活息息相关;其观测对于水文、环境、生态和气候变化等方面的研究具有重要意义。传统的大范围空气温度观测数据一般通过气象站点获取,但由于气象观测站点空间分布离散稀疏的特点,所获取的数据不能精确描述空间连续的空气温度变化情况。因此,实现基于遥感数据的近地表空气温度精准估算具有重要的现实意义。本研究基于精细的地表覆盖类型、空间连续的土壤水分、地表温度（LST）数据,并结合其他辅助数据,构建了近地表空气温度空间化模型,并对近地表空气温度影响因子进行评估,发现地表覆盖类型对近地表空气温度的影响最大,土壤水分为最活跃的影响因素,经验证,模型精度较高,R2接近0.85,RMSE为0.5℃。本研究获取的精确空间连续的近地表空气温度信息,能够充分表达其空间异质性,为农业气象灾害灾变过程监测、农作物生长过程模拟、区域气候变化分析等研究提供良好的近地表空气温度数据支撑。

关键词： 近地表空气温度; 地表温度; 空气温度影响要素; 机器学习; 土地覆盖; 土壤水分; 空间化; 变量重要性分析

本文引用格式

高亮 , 杜鑫 , 李强子 , 王红岩 , 张源 , 王思远 . 融合土地覆盖和土壤水分产品的近地表空气温度空间化方法[J]. 地球信息科学学报, 2020 , 22(10) : 2023 -2037 . DOI: 10.12082/dqxxkx.2020.200078

Abstract

Air temperature is an important attribute for evaluating the living environment, and its studies and observations are closely related to human production and life. Air temperature observation data is of great significance for the study of hydrology, environment, ecology, and climate change. Traditional description of large-scale air temperature is generally obtained through meteorological stations. As affected by land surface condition and atmospheric state, the air temperature is spatially heterogeneous. However, due to the sparse spatial distribution of meteorological station sites, the data obtained from these meteorological stations cannot accurately describe the continuous spatial variation of air temperature across large areas. Hence, accurate inversion of near-surface air temperature based on remote sensing data is regarded as an effective and reasonably practicable solution. There are already some studies about obtaining spatially continuous near-surface air temperature using land surface temperature and other remote sensing data. In this study, we have used the remote sensing data, specifically the precise surface coverage type and spatially continuous soil moisture data, as the new input to improve the accuracy of temperature inversion. On this basis, we built a near-surface air temperature spatialization model using Land Surface Temperature (LST), land cover, soil moisture, land surface temperature, NDVI, DEM, aspect, and slope as the influencing factors. In order to fit the complex relationship between air temperature and its influencing factors, we chose four widely used machine learning algorithms and compared their accuracy to select the most reasonable model. At the same time, we also validated the results and evaluated the contribution of the influencing factors. Based on the results of the designed experiments, we found that precise surface cover type and spatially continuous soil moisture data played the most important role in near-surface air temperature spatialization model. The surface cover type has the greatest influence on the near-surface air temperature, and soil moisture is the most active influencing factor. The model validation results showed that the spatialization model has a relatively high accuracy, with an R2value close to 0.85, and a RMSE of 0.5℃. Comparing with traditional methods, the results of near-surface air temperature spatialization model in our study could express more refined spatial distribution pattern. The high precision near-surface air temperature inversion model proposed by our research is expected to provide effective data support to the study on the dynamic monitoring of agricultural meteorological disasters, simulation of crop growth processes, and analysis of regional climate change.

Key words： Near-surface air temperature; Land surface temperature; Factors affecting air temperature; Machine learning; Land cover; soil moisture; spatialization; importance analysis

1 引言

近地表空气温度是指距离地表两米大气薄层的温度[1]。近地表是人类从事生活和生产活动的主要场所,近地表空气温度为评价近地表生态系统状态的重要指标,所以其监测对农业生产、气象灾害监测、气候变化等研究具有重要的意义[2]。
气象站点观测是获取近地表气温的传统方式,其优点是可以获得局部地区近地表空气温度的连续变化信息,但其观测值往往只能代表周围一定范围内的气温状况,然而气象站点的离散分布阻碍了空间连续的气温获取。地理空间插值是将站点观测气温加工为空间连续气温产品的常用方法,该方法利用空间统计分析理论将站点观测数据进行空间外推,得到整个区域范围内的近地表气温。常用的空气温度空间插值方法包括反距离加权、克里金、地理加权回归等[3,4,5]。这类方法的估算精度高度依赖于站点分布和站点密度,难以保证插值产品的精度[6,7],因此,实现大范围近地表气温空间分布高精度监测难度较大。
遥感技术为及时、准确、大范围地观测地表属性提供了新的手段。遥感反演的地表温度数据,能够在获取地表温度空间连续分布状态的同时,更加详细地描述其空间异质性特征[8,9,10,11,12,13]。
受下垫面类型和地表热辐射交换等多种因素影响,遥感获取的地表温度和近地表气温存在物理含义和数值差异[1]。但是由于空间位置相近,近地表大气和地表地物之间频繁的物质和能量交换,使遥感反演地表温度和近地表气温之间存在强相关关系[14],奠定了基于地表温度估算气温的理论基础[15]。基于遥感地表温度的近地表空气温度监测方法可以简单地概括为2类：① 统计方法,该类方法通过统计近地表空气温度和遥感数据之间的关系,建立两者之间的线性或非线性关系模型[16,17]; ② 物理方法,该类方法主要通过地气能量交换的模拟来描述地表温度对于近地表气温的影响过程,如能量平衡法[14]。相比于统计方法,其具有更加坚实的物理基础,适用范围更加广泛[14]。但是,能量平衡法在计算能量平衡方程各项参数时所需输入数据繁多、参数变量繁多且难以便捷获取,实际应用效果并没显示出明显的优势[18]。
徐伟燕等[18]证实了多因子统计方法相较物理方法的优势,选择空气温度影响要素是统计方法的重要环节。遥感反演的地表温度与近地表气温之间受到近地表热辐射平衡和各种影响辐射机理的因素影响,具有很强的相关性,在物理模型和各种统计方法中常被用做协同变量或条件变量。植被指数、地形、饱和水汽压等影响近地表热辐射交换的因素经常被考虑使用[3,15,18-20]。这些因素既有相关性,又有不可替代的独特性。其中地形信息主要包括高程、坡度和坡向信息,除了高程抬升造成的气温下降因素,坡度和坡向还影响着空气流动和热量交换过 程[21]。饱和水汽压影响空气的比热容和加热速率,植被指数主要反映地表生态系统的蒸散发能力。这些因素中,空气中的水分信息是最变化活跃和难以度量的信息,它既影响着空气的比热容,决定了空气升温和降温的速率,同时决定了地-气界面水热交换模式。目前利用遥感数据估计近地表空气温度均要考虑水分信息或影响水分交换模式的因素,如植被指数、不透水面、饱和水汽压等。研究表明饱和水汽压与近地表空气温度高度相关,超过了地形、地表反照率和植被指数等的影响[18],但是由于其同样是采用站点观测模式,无法反映近地表空气温度的高度异质性特征。而且饱和水汽压并不是空气湿度的真实反映,而是最大可能湿度的反映。因此,利用遥感反演地表温度进行近地表空气温度的空间化,还需要更多地引入能够表征空气湿度空间分布的信息。考虑到空气湿度主要受到下垫面性质（如植被、裸土、不透水层等）的影响,采用最直接的土地覆盖产品,并结合决定空气中水分来源的土壤湿度产品,可以较饱和水气压具有更加直接的优势。
综上所述,本文综合考虑土地覆盖和土壤水分产品,并结合地表温度、地形、植被指数等产品,以机器学习算法为基础进行精细尺度的近地表气温空间化方法探索,以获得更具可靠性的近地表空气温度空间化方法。

2 实验区概况与数据来源

2.1 实验区概况

本研究选择黄淮海平原（40°N—60°N,110°E—120°E）作为实验区,具体为MODIS观测条带（h27v05）与该区域的重叠部分。该区域具有我国东部地区典型的地形地貌特征,区域内大部分地区地势平坦,边缘为山地和丘陵地貌。试验区处于为东亚季风气候区,夏季高温多雨,冬季寒冷干燥,四季分明,全年温差较大。黄淮海平原且同时具有农田、森林、水体、城市等各种典型的地表覆盖类型。研究区丰富的地表覆盖和地貌类型,以及实验区内春秋季频繁的温度变化等使本研究中所关注的各种空气温度影响因素均有良好的代表性。
同时,黄淮海地区也是我国的重要粮食产区,冬小麦种植面积超过全国总面积3/4,玉米种植面积超过全国1/3。每年温度类灾害,包括倒春寒、干热风、高温干旱均有发生。例如,清明节前后的低温,可能导致小麦出现半截穗、哑巴穗等病态,导致产量下降超过1/3以上。因此,对于黄淮海地区的温度空间化提出了更高的需求,以支持灾害的预测预警和损失评估。

2.2 数据来源

大量研究表明地表温度、土壤水分、地表覆盖类型和地形等多种要素对近地表空气温度有重要的影响[22,23,24,25,26],本研究搜集整理了遥感反演地表温度LST、土壤水分含量、植被指数、地表覆盖类型和地形等数据支持近地表空气温度的空间化方法建模。
2.2.1 空气温度数据
本研究收集了实验区内均匀分布的394个气象站点2018年4—12月的近地表空气温度实测数据（图1）,该数据集来源于中国气象数据网（http://data.cma.cn/）,包含逐小时的近地表气温观测数据。根据气象观测标准,本研究用到的近地表气温一般指距离地表2 m的空气温度。实验过程中,本研究选用与遥感卫星过境时刻相近的近地表气温观测数据,以尽可能地消除因为观测时间不同步带来的误差。
图1 实验区地表覆盖类型和气象站点分布示意

Fig. 1 The distribution of meteorological stations and Land cover in study area

2.2.2 MODIS LST产品
遥感反演地表温度（Land Surface Temperature,LST)产品表征的是特定时刻地球表面温度的空间分布状态。MODIS LST数据是常用的地表温度产品之一,本研究中所使用的MODIS LST数据为MODIS L3级地表温度产品,该数据集来源于NASA的EARTHDATA网站（https://search.earthdata.nasa.gov/）。L3级的MODIS LST数据产品是利用通用分裂窗算法反演得到的,空间分辨率为1 km[27]。
2.2.3 土壤水分数据
土壤水分是地表向空气中水分蒸散的来源,因此本研究将它列为重点参考信息之一,以反映不同区域的空气湿度水平。本研究所使用的土壤水分数据为AMSER-E土壤水分产品,来源于美国国家冰雪数据中心(http://nsidc.org/data/amsre/index.html)。搭载在Aqua卫星的AMSER-E（Advanced Microwave Scanning Radiometer-Earth）是继SMMR、SMM/I、AMSER后的主要微波传感器,共有12个通道分别接收6个不同频率的水平和垂直极化地面亮温数据。AMSER-E的数据产品包括L1A、L1B、L2A、L2B、L3共5个等级,每个等级的数据集包含不同的数据单元,本文使用了L3数据的土壤水分产品。AMSER土壤水分数据为基于Qp模型的双通道算法反演结果[28],其数值为单位体积土壤的含水量/（ m 3 / m 3 ）,每天获取升轨和降轨2次观测数据,空间分辨率为25 km。
2.2.4 地表覆盖类型数据
地表覆盖数据反映了地球表面不同的生态系统类型,决定着地气界面水热交换的模式和途径,不同地表覆盖类型和近地表大气有不同的热交换模 式[20,22-23,29-30],因此,本研究重点考虑土地覆盖产品对近地表空气温度空间化的影响。本研究用到的地表分类数据来源于“一带一路”沿线生态环境监测数据集（http://www.chinageoss.org/geoarc/2015/B/sjxz.html）,为全球首套30 m分辨率土地覆盖制图（FROM-GLC）,包括农田、森林、草地、灌丛、湿地、水体、苔原、不透水层和裸地9个地物类别[31]。本实验区内的地表地物以农田、森林、水体和不透水层为主（图1）。
2.2.5 MODIS NDVI产品
植被指数产品在一定程度上反映了植被生态系统的生长活力,能够间接区分农田、森林和草地等植被生态系统的水热交换能力。植被作为所有地物中相对复杂的地表类型之一,其生长状况和空间分布对近地表空气温度的影响也同样复杂,而植被指数通过表征地表植被的生长状态,可以在一定程度上表现植被状态对其附近空气影响的差异[32]。
本研究使用MODIS的16 d合成NDVI产品,空间分辨率为1 km,来源于美国航空航天局网站(https://search.earthdata.nasa.gov/)。Terra、Aqua两颗卫星的NDVI产品交替使用可以使数据的实际时间分辨率达到8 d[33]。
2.2.6 地形数据
本研究选用了全球多分辨率地形高程数据集（GMTED2010）,该数据集是美国地质调查局（USGS）和国家地理空间情报局（NGA）合作开发的一种全球高程模型。本文所使用的GMTED2010数据来源于USGS网站（https://earthexplorer.usgs.gov/）。GMTED2010数据集发表以来,逐渐取代了GTOP30成为全球大范围DEM应用的新选择,有研究证明,相比于其他全球地形数据GMTED2020有更高的精度[34]。数据集有多个分辨率产品,本研究选择了其中的1 km分辨率DEM数据,坡度和坡向数据在该DEM的基础上利用ArcGIS空间分析工具计算得到。

3 研究方法

本研究重点考虑地表温度、地表覆盖类型、植被指数和土壤水分等反映地-气热交换的敏感因素,同时结合地形因素,作为影响近地表空气温度空间化的重要变量。在此基础上采用随机森林、支持向量机、AdaBoost和岭回归4种机器学习模型拟合站点观测近地表空气温度和影响要素的关系,通过与传统空间插值方法的对比分析,优选对近地表空气温度空间化最具稳定性和精确性的算法,并对不同影响因素在近地表空气温度空间化过程中的重要性及变化特性进行了评价。最终利用最优的机器学习算法和空气温度影响要素,空间化得到实验区精确的近地表温度场信息（图2）。
图2 近地表空气温度空间化流程

Fig. 2 The flowchart of near-surface air temperature Spatialization

3.1 近地表空气温度影响要素预处理

为了提高数据的质量,以建立更加精确的模型,本研究对模拟近地表空气温度影响要素的数据做了以下预处理：
（1）土地覆盖
土地覆盖类型信息是地表状态的最直接反应,为了对地表状况做精确的表达,本研究使用了高分辨率的地表覆盖类型数据。为了使地表覆盖类型和其他数据的分辨率保持一致,本研究通过描述空间化格网内不同地物类型的比例结构信息来定量化表达地表覆盖类型状态,即,每个LST像元内各地表覆盖类型的面积占比向量 Type _ Vecto r j ,其计算方法如式（1）和式（2）所示。
Fractio n i , j = are a i , j Are a j
Type _ Vecto r j = Fractio n 1 , j , … , Fractio n n , j
式中： Fractio n i , j 表示MODIS LST像元j中第i类地物所占的面积比例。 Are a j 表示MODIS LST像元j的面积, are a i , j 表示MODIS LST像元j中第i类地物的面积。MODIS LST像元j中的每类地物的面积比例 Fractio n i , j 按照固定顺序排列得到 Type _ Vecto r j 。
（2）土壤湿度
土壤湿度是影响地表温度变化和近地表空气温度空间分布状态的重要要素[35,36],空间连续的土壤水分数据能够表明其在空间上的变化,本研究使用了AMSER-E的土壤水分产品参与建模。为了与MODIS数据NDVI和LST的空间分辨率保持一致,本研究利用双线性插值把土壤水分数据重采样到1 km。
（3）地表温度
遥感反演的LST数据可以反映出近地表空气温度的空间分布差异[26]。本研究对LST数据产品进行了数据筛选,基于数据集的质量控制层QC文件选取第2和3位数据质量标记为00的质量较好的数据,去除了质量控制中不确定性较大的LST像元,仅采用质量好的LST像元参与近地表气温空间化建模,从而保证了输入数据的可靠性和模型的有效性。
（4）植被指数
植被类型和生长状态能够影响近地表水热交换[23]。本研究中使用NDVI来区分不同植被状态对于近地表空气温度的影响。通常在短时间内地表的植被长势和类型等都不会有很大的变化。因此,本研究用有效时间分辨率为8 d的NDVI产品表示该时间段的植被状况。数据处理过程中,通过质量控制信息对NDVI数据进行筛选,优选反演精度较高的晴空像元数据参与近地表气温空间化建模。
（5）地形要素
地形要素是影响空气温度空间分布的要素之 一[37],本研究所使用的地形要素有高程（DEM）、坡度（Slope）和坡向（Aspect）。坡度和坡向通过ArcGIS空间分析工具在DEM数据的基础上计算得到,其计算原理如式（3）和式（4）所示[7],其中 dz dx 和 dz dy 表示高程在x和y方向的变化率。
Slope = atan dz dx 2 + dz dy 2 × 57.29578
A spect = atan 2 dz dy , - dz dx × 57.29578
基于上述数据处理,本研究以地表温度、地表覆盖类型、土壤含水量、植被指数、高程、坡度和坡向等多种环境要素为基础,对地气能量交换过程中多要素的耦合及相互影响进行简化模拟,尝试构建基于上述多种环境要素的近地表气温空间化方法。

3.2 机器学习算法

近地表空气温度与其影响要素之间存在复杂的相关关系,地表温度、地表覆盖类型、土壤水分、植被指数和地形要素等共同作用,使该过程很难利用简单的线性模型准确地模拟。因此,本研究拟采用对复杂的非线性关系拟合能力很强的机器学习方法来构建近地表气温空间化模型[38,39]。
利用机器学习算法进行近地表空气温度的空间化,应当综合考虑多种机器学习算法,以比较不同机器学习模型的性能,最终选择对本研究中近地表空气温度影响要素拟合效果最好的模型。大量研究表明随机森林（RF）、支持向量机（SVM）、AdaBoost、岭回归（Ridge）等常用的机器学习算法在多元非线性拟合中有良好表现[40,41],因此本研究选取上述4种机器学习算法进行近地表气温空间化建模对比。
（1）随机森林模型
随机森林模型是以决策树为基础的一种集成学习方法,对于回归和分类问题均具有较好的效果,由于其具有较强的抗噪效果且不容易过拟合,已经被广泛用于多元非线性回归和高维特征空间的分类问题[42]。已有研究利用随机森林模型对近地表空气温度进行了空间化,取得了较好的效果[15]。
（2）支持向量机
支持向量机为最常用的回归方法之一,其基本原理为VC统计理论和风险最小理论[43]。支持向量机可以对输出变量进行量化分析得到相关变量之间的回归关系,该模型利用核函数实现数据和分类超平面在高低维特征空间映射,得到最优的拟合关系[44]。大量研究证明,支持向量机对于多元非线性回归问题有很好的效果。
（3）AdaBoost
AdaBoost方法采用迭代的思想构建模型,该算法首先训练多个弱学习器,并将这些弱学习器进行组合得到一个强学习器[45]。从弱学习器到强学习器的逐步递进过程中,模型每次都聚焦于上次分类错误的样本,对错分样本的权重加强,最后得到对整个训练样本数据拟合效果最好的回归关系模型。
（4）岭回归
岭回归本质是对最小二乘估计的改进,该方法可以消除自变量间的线性关系对于回归模型的影响,所得模型具有很大的稳定性,在多元非线性回归中具有广泛的应用[46]。

3.3 实验设计

3.3.1 实验数据集选择
为了评价空间化模型的性能与实验效果,本研究选择了多期数据作为实验数据集进行模型测试。由于云雨天气造成遥感数据缺失,研究区内部分气象站点难以在所有日期获取其对应的遥感反演LST和NDVI数据。本研究将在特定日期具有对应遥感数据的气象站点定义为有效气象站点。研究证明,训练模型需要一定数量的样本支持[47],为保障高质量模型训练和验证所需的样本数量,本研究将阈值设定为200,特定日期有效气象站点数量高于该阈值才会被选择用来建模。本研究在以上规则的指导下选取了2018年97个日期的数据构建了实验数据集,详见图3绿色标记。实验数据集包含春（3—5月）、夏（6—8月）、秋（9—11月）、冬（12—2月）各个季节的数据,基于此建模可以分析在不同季节模型变量对近地表空气温度状态的影响模式。
图3 实验数据集数据时间分布

Fig. 3 Time distribution of data

3.3.2 模型训练与空间化过程
本研究随机选取80%的站点数据作为训练样本,其余20%的站点数据作为验证样本。机器学习模型训练阶段,以气象站点的空气温度观测数据和其对应的地表覆盖类型比例向量、植被指数、LST、土壤水分、高程、坡度和坡向分别为因变量和自变量训练模型。为了评价模型的质量,对比验证样本的模型计算结果和观测值,实现模型的精度评价。最后把所得模型作用于空间数据进行外推,得到整个研究区的近地表空气温度空间化结果。
经过大量实验,本研究选择了各机器学习模型对近地表空气温度空间化效果最好的参数设置。具体各种模型的参数设置如下：AdaBoost回归模型中设置学习速率为1,最大学习器数目为50,在迭代学习过程中选择线性损失函数;支持向量机模型训练过程中选择了高斯核函数（rbf）;岭回归中设置正则化强度为1;随机森林模型中设置树的数目为10,树的最大深度为2,选择衡量分裂质量的标准为MSE。
为了测试所得的近地表空气温度空间化模型的适用性,本研究在对卫星过顶时间的空气温度空间化的同时也进行了每日的最高、最低、平均气温的空间化分析,以考察本研究中的模型对于每日近地表空气温度极值和平均值的空间化能力。
3.3.3 对照实验
为了对本研究提出的近地表空气温度空间化模型进行评价,本研究还设置了对比实验,通过和传统空气温度插值方法进行对比,对本模型的精度水平进行评价。反距离加权（IDW）、样条函数（Spline）、克里金（Kriging）等空间插值方法被广泛应用于空气温度的空间化,并取得了较好的效果[48,49]。IDW基于地理统计中的相近相似原理,即距离越小属性值相似度越高。该模型以空气温度估算点和样本点之间的距离平方的倒数为权重,最终通过加权得到估算点的温度值[50]。样条函数插值方法是在薄板样条函数基础上订正之后的一种空间插值方法,它广泛应用于空间面数据的精确插值[3]。克里金法以变异函数为基础,根据插值对象的空间连续性和无值点与样本点的空间位置关系,对其无值点进行无偏最优估计,克里金以插值样本没有潜在的全局趋势为假设,用局部的样本点就能对所估计区域的值进行估算[49]。在本研究中,插值方法都通过ArcGIS的空间分析工具实现,Spline插值方法选择的模型为规则样条。Kriging插值方法选择的模型为普通克里金。最终插值结果的空间分辨率为1 km。
3.3.4 模型变量贡献权重计算
本研究中,模型变量贡献权重通过节点不纯度减少值（IncNodePurity）和均方误差减少值（IncMSE）来评价[51]。其中节点不纯度通过基尼指数计算[52],以变量a为例,基尼指数的计算原理如式（5）。p(k|t)表示在节点t使用变量a作为划分属性时,样本属于第k类的概率估计值,其中,k=1,2,…,n,n为样本种类数。
G t = 1 - ∑ k = 1 n p 2 k t
变量a在节点t的贡献权重,即节点t分枝前后的基尼指数变化量为：
Δ G t = G t - G t l - G t r
G t l 和 G t r 分别表示节点t分裂形成的2个新节点的基尼指数, Δ G t 则为节点不纯度减少值,变量a的权重贡献通过其在模型内所有树中的节点不纯度减少值的均值表示。
均方误差减少值同样为评价模型中变量权重的一个指标[53]。在随机森林模型中通过验证样本计算出MSE0,对验证样本集数据的变量a的值进行随机混排,计算得到MSE1,则均方误差减少值（ IncMSE ）为均方误差减小的百分比,如式（7）所示。
IncMSE = MSE 1 - MSE 0 MSE 0 × 100 %
3.3.5 模型评价
本研究主要通过决定系数（R2）和均方根误差（RMSE）来对近地表空气温度的空间化结果进行评估,其计算过程如式（8）—式（10）所示。
R 2 = 1 - ∑ i = 1 n ( Tem p i - Tem p i ˆ ) 2 ∑ i = 1 n ( Tem p i - Tem p i ¯ ) 2
e i = Tem p i - Tem p i ˆ
RMSE = 1 n ∑ i = 1 n e i 2
$\overline{Temp_{i}}=\frac{1}{n}\lgroup\sum^{n}_{i=1}Temp_{i}\rgroup$
式中： Tem p i 为近地表气温的观测值,本研究中为气象站点观测数据; Tem p i ˆ 为近地表气温的模型计算值; e i 为误差,即气象观测近地表气温和模型计算值之差。$\overline{Temp_{i}}$为近地表气温观测值的均值,其计算如式（11）所示。

4 结果分析

4.1 不同模型的近地表空气温度空间化结果对比 分析

本文采用4种机器学习方法和3种空间插值方法对实验数据集中全年97个日期的近地表空气温度进行了空间化,并进行了平均精度对比分析（图4）。
图4 近地表空气温度空间化模型平均精度参数统计箱形图

Fig. 4 Boxplot of average accuracy parameters of near-surface air temperature spatialization model

综合分析图4中7种近地表空气温度空间化模型的平均R2和RMSE箱形图,可以得出如下结论：
（1） 4种机器学习模型对近地表气温的空间化普遍具有较高的决定系数（R2均大于0.6）,和较低的均方根误差（RMSE均值在1.3 ℃以内）,表明这4种机器学习模型能够较好地拟合近地表空气温度和其影响要素之间的关系。
（2）机器学习算法中RF的表现最为突出（R2为0.85,RMSE为0.5 ℃）。SVM和AdaBoost模型的R2和RMSE都有较大范围的波动,其稳定性比RF较差。Ridge方法表现最差,决定系数在0.6左右。
（3） 3种插值方法的R2约为0.7,RMSE均值基本稳定在1 ℃左右。其中,Kriging方法具有最大的决定系数（接近0.8）和最小的RMSE（接近1 ℃）。Spline具有最低的决定系数和最大的RMSE,但RMSE的波动范围最小。由于插值方法对复杂条件下的近地表空气温度空间分布拟合能力较弱,具有较大的误差波动范围。
综合来看,机器学习方法的计算结果普遍比空间插值方法的结果精度更高、模型拟合效果更好。其中,RF模型在所有的机器学习模型中对近地表空气温度的空间化效果最好,其表现也远远好于插值模型,所以本研究选择以RF模型为基础构建近地表空气温度空间化模型。

4.2 近地表空气温度空间化模型精度分析

通过对所有日期的空间化结果进行精度评估分析（图5）可看出：
图5 近地表空气温度空间化模型精度时间序列变化曲线

Fig. 5 Near-surface air temperature spatialization model error time series change curve

（1）本研究的近地表空气温度空间化模型的决定系数整体比较高（大于0.8）。表明所选择的RF模型对近地表空气温度和其影响要素有较好的拟合效果,模型中的近地表空气温度影响要素能够很好地解释近地表空气温度空间化问题。
（2）模型空间化结果的RMSE整体低于1.0 ℃,平均值为0.5 ℃,最大值为0.8 ℃,最小为0.2 ℃。表明模型对不同地表状态引起的近地表空气温度空间分布差异表现较好,所有的温度状态都能被模型所模拟。
（3）从RMSE变化曲线的总体变化趋势来看,RMSE在夏季较小且比较平稳,春秋季节有较大的变化,表明模型受一定的季节性的影响。
同时,为确定模型性能的空间差异,本研究深入分析了近地表空气温度空间化模型计算结果的误差（计算如式（9））和空间要素（高程、坡度和坡向）之间的关系。由图6可看出,近地表空气温度误差并没有表现随高程、坡度和坡向而呈现明显变化趋势,在不同地形条件下,近地表空气温度空间化模型所得结果的精度都相对比较稳定,90%以上的估算值与观测值之间误差处于-1.0~1.0 ℃之间,表明模型对不同空间条件差异的近地表空气温度拟合效果都相对较好。
图6 近地表空气温度空间化模型误差在不同空间条件分布散点图

Fig. 6 Distribution of near-surface air temperature spatialization model error in spatial feature

4.3 近地表空气温度空间化的效果分析

为了评价本研究的近地表空气温度空间化效果,本文选取了2018年春夏秋冬4个日期RF模型模拟结果与空间插值效果最好的克里金方法插值结果进行对比（图7）。为了能够显示空气温度空间细节,图7对实验区的一块区域（34.5°N—37.5°N;114°E—118°E）进行了放大展示,图中的日期用儒略日表示。
图7 近地表空气温度空间化效果对比

Fig. 7 Near-surface air temperature distribution compare

从图7可以看出,本研究所得结果和克里金插值结果所表现的空气温度空间分布格局一致,如2018年163日数据,二者都表现出中部地区温度较低,南部和西南部温度较高的空间分布状态;2018年247日数据都表现出中部温度较低,周边温度较高的趋势;2018年272日数据的空间化结果都表现出北部温度较低,中西部和东北部温度较高的空间分布格局;2018年346日数据都表现出中部温度较低,西北部、东部和南部温度较高。但是,本研究的方法所得到的空气温度结果具有更高的空间异质性。与插值方法相比,本研究得到的近地表空气温度具有更加丰富的空间细节信息,如在本研究所得结果RF2019-247和RF-272中,由于河流引起的从西南到中部地区的空气温度低值条带在图中清晰可见,其对应的克里金空间插值结果中却得不到此细节信息。此现象表明,本研究的结果中地表覆盖类型和土壤水分信息对近地表空气温度的影响具有明显的表现。
受地表状态的影响,近地表空气温度在具有空间连续性的同时又有一定的空间异质性,本研究引入的精细地表类型、土壤水分条件、植被状态和地形众多要素造成的空气温度空间分布变化细节信息在结果中可以直观表现出来,所得结果更符合近地表空气温度的实际状态。

4.4 近地表空气温度空间化各要素权重贡献分析

为了对近地表空气温度影响要素有更加深入的认识,本研究利用式（6）和式（7）对近地表空气温度空间化过程中的各要素权重贡献进行了评估。分析发现：
（1）土地覆盖类型、高程和地表温度最具有重要性,从模型各变量的平均权重贡献图（图8）可以看出,它们对近地表空气温度空间化模型贡献了74%以上的信息。其中,地表覆盖类型对模型的权重贡献最大,达到了25.19%,本研究使用地表覆盖类型比例向量作为模型参量,更加精确地表现了地表细节信息,其对模型的贡献主要表现为不同地表引起的近地表气温空间异质性。其他变量的贡献权重依次为高程24.84%,地表温度23.2%,土壤水分9.96%,坡度7.85%,坡向4.66%,植被指数最小为4.3%。
图8 近地表空气温度空间化影响要素平均权重贡献

Fig. 8 Influencing factors average weights of near-surface air temperature

（2）从各要素贡献权重的变化（图9）来看,地表温度、地表覆盖类型和高程对模型的权重贡献一直处于较高水平,但土壤水分最具变化特性,对近地表空气温度空间化的影响最为直接。其中,土壤水分含量变化较大的时间阶段,其对模型的权重贡献较大,此现象为降雨等天气使得土壤水分的空间分布不均匀造成的近地表空气温度差异在模型中的体现。这表明土壤水分对空气中水分含量和比热容的影响比较直接。NDVI对模型的贡献权重最小,且大小稳定无较大波动。植被状态的变化相对缓慢,其渐变不会引起空气温度空间分布格局的剧烈变化。地形要素为定值,其对空气温度空间化模型的贡献权重变化为其他影响要素权重变化带来的结果。
图9 近地表空气温度空间化影响要素贡献权重时序变化

Fig. 9 Influencing factors weights change of Near-surface air temperature

（3）季节性分析（图10）发现：① 不同季节各项空间化要素的地位不同。冬季起决定作用的要素是地表温度;夏季则是地表土地覆盖类型,高程、地表温度和土壤水分的影响依次下降;春秋季高程信息最为重要,土地覆盖类型次之。② 空气温度影响要素在不同季节对模型的权重贡献有一定的差异。土壤水分在夏季对模型的贡献权重明显高于其他季节,实验区夏季雨水丰富,区域降雨不均匀造成空间上土壤水分含量差异较大,由此会造成近地表空气温度的空间分布变化,该信息在模型中有一定的表现。NDVI在春季对模型的贡献权重最大,夏季和秋季相对春季较小,冬季最小。植被在春季处于全年生长最快的阶段,覆盖度差异较大,NDVI能区分出地表植被覆盖度的差异以及植被非植被地表,此时段NDVI对近地表空气温度空间分布有较大的影响。土地覆盖类型在冬季对模型的影响和其他季节对比具有明显的差异。
图10 不同季节近地表空气温度空间化影响要素权重贡献均值直方图

Fig. 10 Seasonal variations of Near-surface temperature influencing factors average weights

4.5 日最高、最低和平均空气温度空间化预测能力 分析

温度极值和温度均值对于气象灾害监测和气候变化评价有重要的意义,因此,本研究在对卫星过顶时间的空气温度空间化的同时也进行了每日的最高、最低、平均气温的空间化分析,以考察本研究中的模型对于每日近地表空气温度极值的空间化能力。在日最大、最小和平均温的空间化过程中,将原来模型中卫星过境附近时刻的近地表空气温度替换成了上述温度。本研究对模型的精度做了统计如图11所示。
图11 近地表空气温度日极值和均值空间化精度参数统计箱形图

Fig. 11 Boxplot of daily extreme and mean Near-surface temperature statistical parameters

通过分析图11中日最高温、最低温和平均温空间化模型的R2和RMSE,可以得到如下结论：
（1）本研究所构建的近地表空气温度空间化模型具有较高的可靠性。每日最高温、最低温和平均温模型的R2均超过了0.8,其中最高温模型的R2达到0.85左右,最低温和平均温也达到0.8以上。表明利用本研究所构建的空间化模型和所选的温度影响要素能够较好地解决近地表空气温度的空间化问题。
（2）本研究的近地表空气温度空间化模型所得结果的精度较高。最高温和平均温具有较小的RMSE,平均不超过0.6 ℃,最高不超过0.7 ℃。最低温的RMSE接近0.8 ℃,但最高不超过1 ℃。表明本研究所构建的模型与目前大多数研究的结果相比,处于较高水平。

5 结论与讨论

本研究在精细的地表覆盖类型数据、空间连续土壤水分数据和其他多种数据的基础上,利用多种环境变量的协同参与,构建了近地表空气温度的高精度空间化方法。结论如下：
（1）在本研究选取的机器学习模型中,RF模型对空气温度影响要素的拟合效果最好,空间化结果精度较高,平均R2达到了0.85,RMSE均值达到了0.5 ℃。
（2）本研究所选择的空气温度影响要素对近地表气温的影响均在模型中得到了相对合理的表达。经过对全年多期数据建模分析发现,地表覆盖类型对近地表气温的影响最大,其次分别是高程、地表温度、土壤水分、坡度、坡向和植被指数,他们对模型的贡献权重分别为25.19%、24.84%、23.2%、9.96%、7.85%、4.66%和4.3%,且土壤水分和NDVI对模型的贡献权重随季节变化明显。
（3）精细地表覆盖类型和空间连续土壤水分数据的使用对近地表空气温度空间化模型构建有重要的意义。其中,地表类型对模型的贡献权重最大,土壤水分在不同时间对模型的贡献变化较大,是最活跃的空气温度影响要素。
（4）本研究基于多种要素建立的RF近地表空气温度空间化模型具有广泛的适用性。在对卫星过顶时段的近地表空气温度进行研究的基础上,本研究对日最高温、最低温和平均温在实验区的空间分布状态进行了空间化模拟,也取得了较好的结果。
本研究在机器学习方法基础上建立了近地表空气温度空间化模型,通过和已有方法对比发现,本研究的主要优势在于：
（1）本研究以不同地表覆盖类型的比例向量参与近地表空气温度的空间化,可以更加充分地表征不同下垫面的空间分布对于地气界面水热交换特性的影响,能够表达出更多的近地表空气温度空间分布的细节信息。
（2）土壤水分信息决定地表空气湿度,对近地表水热交换模式有很大的影响。本研究所使用的土壤水分数据具有空间连续的特点,可以减少饱和水汽压等点状要素空间插值带来的误差。
（3）多种机器学习算法的比较表明,随机森林算法具有更强的拟合能力和大区域适应性优势。
同时,本研究中未能处理的问题还包括：① 没有考虑由于风等天气现象造成的空气平流和空间相邻位置空气温度的邻域效应等影响。② 土壤水分产品空间尺度较粗,可能在一定程度上影响了空间化表达,使得空间分布中表现出一定的颗粒现象,今后可以选择使用更具有细节表达能力的降尺度产品。③ LST、NDVI等遥感产品的缺失问题尚未考虑,在后续的研究中应该就此方面深入研究。④ 本研究只获取了近地表气温的水平空间分布,而空气温度廓线监测对近地表温度场的状态及其变化研究同样具有重要的意义,今后研究工作将再深入这一方向。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Prihodko L, Goward S N. Estimation of air temperature from remotely sensed surface observations[J]. Remote Sensing of Environment, 1997,60(3):335-346.

[2]
Vancutsem C, Ceccato P, Dinku T, et al. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa[J]. Remote Sensing of Environment, 2010,114(2):449-465.

[3]
崔晓临, 程贇, 张露, 等. 基于DEM修正的MODIS地表温度产品空间插值[J]. 地球信息科学学报, 2018,20(12):1768-1776.

[ Cui X L, Cheng Y, Zhang L, et al. Spatial interpolation of MODIS land surface temperature products based on DEM correction[J]. Jounal of Geo-information Science, 2018,20(12):1768-1776. ]

[4]
Lu N, Liang S, Huang G, et al. Hierarchical Bayesian space-time estimation of monthly maximum and minimum surface air temperature[J]. Remote Sensing of Environment, 2018,211:48-58.

[5]
Szymanowski M, Kryza M, Spallek W. Regression-based air temperature spatial prediction models: An example from Poland[J]. Meteorologische Zeitschrift, 2013,22(5):577-585.

[6]
Zhao D, Zhang W, Shi J X. A neural network algorithm to retrieve nearsurface air temperature from landsat ETM+ imagery over the Hanjiang River Basin, China; proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, F, 2007 [C]. IEEE.

[7]
Burrough P A, Mcdonnell R, Mcdonnell R A, et al. Principles of geographical information systems[M]. Oxford: Oxford University Press, 2015.

[8]
Li Z L, Tang B H, Wu H, et al. Satellite-derived land surface temperature: Current status and perspectives[J]. Remote Sensing of Environment, 2013,131:14-37.

[9]
郑文武, 曾永年. 地表温度的多源遥感数据反演算法对比分析[J]. 地球信息科学学报, 2011,13(6):840-847.

[ Zheng W W, Zeng Y N. Comparative analysis of two land surface temperature retrieval algorithms based on multi-source remote sensing data[J]. Journal of Geo-information Science, 2011,13(6):840-847. ]

[10]
陈冰倩, 张友水, 程璟媛, 等. 福州市地表温度热点及时空变化分析[J]. 地球信息科学学报, 2019,21(5):710-719.

[ Chen B Q, Zhang Y S, Cheng J Y, Zhao X. The hot spot and spatiotemporal changes of the land surface temperature in Fuzhou[J]. Journal of Geo-information Science, 2019,21(5):710-719. ]

[11]
李娅丽, 汪小钦, 陈芸芝, 等. 福建省地表温度与植被覆盖度的相关性分析[J]. 地球信息科学学报, 2019,21(3):445-454.

[ Li Y L, Wang X Q, Chen Y Z, Wang M M. The correlation analysis of land surface temperature and fractional vegetation coverage in Fujian province[J]. Journal of Geo-information Science, 2019,21(3):445-454. ]

[12]
李召良, 段四波, 唐伯惠, 等. 热红外地表温度遥感反演方法研究进展[J]. 遥感学报, 2016,20(5):899-920.

[ Li Z L, Duan S B, Tang B H, et al. Review of methods for land surface temperature derived from thermal infrared remotely sensed data[J]. Journal of Remote Sensing, 2016,20(5):899-920. ]

[13]
李召良, 唐伯惠, 唐荣林, 等. 地表温度热红外遥感反演理论与方法[J]. 科学观察, 2017,12(6):57-59.

[ Li Z L, Tang B H, Tang R L, et al. Theory and method of surface infrared thermal remote sensing inversion[J]. Science Focus, 2017,12(6):57-59. ]

[14]
Sun Y J, Wang J F, Zhang R H, et al. Air temperature retrieval from remote sensing data based on thermodynamics[J]. Theoretical and Applied Climatology, 2004,80(1):37-48.

[15]
白琳, 徐永明, 何苗, 等. 基于随机森林算法的近地表气温遥感反演研究[J]. 地球信息科学学报, 2017,19(3):390-397.

[ Bai L, Xu YM, He M, et al. Remote Sensing Inversion of near surface air temperature based on random forest[J]. Journal of Geo-information Science, 2017,19(3):390-397. ]

[16]
Cresswell M P, Morse A P, Thomson M C, et al. Estimating surface air temperatures, from Meteosat land surface temperatures, using an empirical solar zenith angle model[J]. International Journal of Remote Sensing, 1999,20(6):1125-1132.

[17]
Florio E N, Lele S R, Chi C Y, et al. Integrating AVHRR satellite data and NOAA ground observations to predict surface air temperature: A statistical approach[J]. International Journal of Remote Sensing, 2010,25(15):2979-2994.

[18]
徐伟燕, 孙睿, 金志凤, 等. 基于MODIS数据的近地表气温估算[J]. 气象与环境科学, 2015,38(1):1-6.

[ Xu W Y, Sun R, Jin Z F, et al. Estimation of Near Surface Air Temperature Based on MODIS data[J]. Meteorological and Environmental Sciences, 2015,38(1):1-6. ]

[19]
曲培青, 施润和, 刘朝顺, 等. 基于MODIS地表参数产品和地理数据的近地层气温估算方法评价——以安徽省为例[J]. 国土资源遥感, 2011,91(4):78-82.

[ Qu P Q, Shi R H, Liu C S, et al. The Evaluation of MODIS data and geographic data for estimating near surface air temperature[J]. Remote Sending For Land & Resources 2011,91(4):78-82. ]

[20]
帅晨, 沙晋明, 林金煌, 等. 不同下垫面遥感指数与地温关系的空间差异性研究[J]. 地球信息科学学报, 2018,20(11):1657-1666.

[ Shuai C, Sha J M, Lin J H, et al. Spatial difference of the relationship between remote sensing index and land surface temperature under different underlying surfaces[J]. Journal of Geo-information Science, 2018,20(11):1657-1666. ]

[21]
李羽滢. 基于夏季微气候优化的成都市绿道景观设计研究[D]. 成都:西南交通大学, 2019.

[ Li Y Y. Chengdu greenway landscape design based on summer microclimate optimization in hot and humid areas[D]. Chengdu: SouthWest Jiaotong University, 2019. ]

[22]
Cheng K S, Su Y F, Kuo F T, et al. Assessing the effect of landcover changes on air temperatu×re using remote sensing images: A pilot study in northern Taiwan[J]. Landscape and Urban Planning, 2008,85(2):85-96.

[23]
Flerchinger G N, Reba M L, Link T E, et al. Modeling temperature and humidity profiles within forest canopies[J]. Agricultural and Forest Meteorology, 2015,213:251-262.

[24]
Pape R, LöFFLER J. Modelling spatio-temporal near-surface temperature variation in high mountain landscapes[J]. Ecological Modelling, 2004,178(3-4):483-501.

[25]
Stisen S, Sandholt I, NøRGAARD A, et al. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa[J]. Remote Sensing of Environment, 2007,110(2):262-274.

[26]
Shamir E, Georgakakos K P. MODIS Land Surface Temperature as an index of surface air temperature for operational snowpack estimation[J]. Remote Sensing of Environment, 2014,152:83-98.

[27]
Wan Z, Hook S, Hulley G. MOD11A1 MODIS/terra land surface temperature/emissivity daily L3 global 1 km SIN grid V006[M]. Washington DC: NASA EOSDIS LP DAAC, 2015: 10-50.

[28]
Koike T, Nakamura Y, Kaihotsu I, et al. Development of an advanced microwave scanning radiometer (AMSR-E) algorithm for soil moisture and vegetation water content[J]. Proceedings of Hydraulic Engineering, 2004(2), 48:217-222.

[29]
胡媛媛, 仲雷, 马耀明, 等. 青藏高原典型下垫面地表能量通量的模型估算与验证[J]. 高原气象, 2018,37(6):1499-1510.

[ Hu Y Y, Zhong L, Ma Y M, et al. Model esimation and validation of the surface energy fluxes at typical underlying surfaces over the Qinghai-Tibetan Plateau[J]. Plateau Meteorology, 2018,37(6):1499-1510. ]

[30]
张舒婷, 段四波, 幸泽峰, 等. 地表组分温度遥感反演算法研究进展[J]. 中国农业信息, 2019,31(1):11-23.

[ Zhang S T, Duan S B, Xin Z F, et al. Progress in land surface component temperature retrieval algorithms from remote sensing data[J]. China Agricultural Informatics, 2019,31(1):11-23. ]

[31]
Gong P, Wang J, Yu L, et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data[J]. International Journal of Remote Sensing, 2013,34(7):2607-2654.

[32]
Van D E, Griend A A, OWE M. On the relationship between thermal emissivity and the normalized difference vegetation index for natural surfaces[J]. International Journal of Remote Sensing, 2007,14(6):1119-1131.

[33]
Didan K. MOD13A2 MODIS/terra vegetation indices 16-Day L3 global 1km SIN grid V006[M]. Washington DC : NASA EOSDIS LP DAAC. 2015: 10-45.

[34]
Danielson J J, Gesch D B. Global multi-resolution terrain elevation data 2010 (GMTED2010)[M]. US Department of the Interior, US Geological Survey, 2011.

[35]
Corbari C, Sobrino J A, Mancini M, et al. Land surface temperature representativeness in a heterogeneous area through a distributed energy-water balance model and remote sensing data[J]. Hydrology and Earth System Sciences, 2010,14(10):2141-2151.

[36]
王倩倩, 覃志豪, 王斐. 基于多源遥感数据反演地表温度的单窗算法[J]. 地理与地理信息科学, 2012,8(3):24-26, 62, 113.

[ Wang Q Q, Qin Z H, Wang F. Improved case-based reasoning based cellular automaton for simulating land cover change[J]. Geography and Geo-information Science, 2012,8(3):24-26, 62, 113. ]

[37]
Chuan Y Z, Zhong R N, Guo D C. Methods for modelling of temporal and spatial distribution of air temperature at landscape scale in the southern Qilian mountains, China[J]. Ecological Modelling, 2005,189(1-2):209-220.

DOI

[38]
王奕森, 夏树涛. 集成学习之随机森林算法综述[J]. 信息通信技术, 2018,12(1):49-55.

[ Wang Y S, Xia S T. A survey of Random Forests Algorithms[J]. Information and Communications Technologies, 2018,12(1):49-55. ]

[39]
杨浩浩. 几种机器学习算法及其集成模型在回归问题中的应用与比较[D]. 兰州:兰州大学, 2018.

[ Yang H H. The application and comparison of several machine learning algorithms and their integrated models in regression problems[D]. Lanzhou: Lan Zhou University, 2018. ]

[40]
Elith J, Leathwich J R, Hastle T. A working guide to boosted regression trees[J]. J Anim Ecol, 2008,77(4):802-813.

PMID

[41]
Cao L J. Support vector machines experts for time series forecasting[J]. Neurocomputing, 2003,51:321-339.

[42]
郭云开, 刘雨玲, 张晓炯, 等. 利用辐射传输模型和随机森林回归反演LAI[J]. 测绘工程, 2019,28(6):17-21,29.

[ Guo Y K, Liu Y L, Zhang X T, et al. LAI inversion using radiation transfer model and random forest regression[J]. Engineering of Surveying and Mapping, 2019,28(6):17-21,29. ]

[43]
Awad M, Khannna R. Efficient learning machines[M]. Berlin: Springer, 2015: 67-80.

[44]
Yeh C Y, Huang C W, Lee S J. A multiple-kernel support vector regression approach for stock market price forecasting[J]. Expert Systems with Applications, 2011,38(3):2177-2186.

[45]
陈天昕. 基于AdaBoost与SVM集成算法的高炉炉温状态解析[D]. 南昌:江西财经大学, 2019.

[ Chen T X. Analysis of blast furnace temperature state based on AdaBoost and SVM integrated algorithms[D]. Nanchang: Jiangxi University of Finance and Economics, 2019. ]

[46]
张曼, 刘旭华, 何雄奎, 等. 岭回归在近红外光谱定量分析及最优波长选择中的应用研究[J]. 光谱学与光谱分析, 2010,30(5):1214-1217.

[ Zhang M, Liu X H, He X K, et al. Study on the application of ridge regression to near-infrared Sspectroscopy quantitative analysis and optimum wavelength selection[J]. Spectroscopy and Spectral Analysis, 2010,30(5):1214-1217. ]

[47]
Van Niel T G, Mcvicar T R, Datt B. On the relationship between training sample size and data dimensionality: Monte Carlo analysis of broadband multi-temporal classification[J]. Remote Sensing of Environment, 2005,98(4):468-480.

[48]
李军龙, 张剑, 张丛, 等. 气象要素空间插值方法的比较分析[J]. 草业科学, 2006,23(8):6-11.

[ Li J L, Zhang J, Zhang C, et al. Comparative analysis of spatial interpolation methods of meteorological elements[J]. Pratacultural Science, 2006,23(8):6-11. ]

[49]
马秀霞, 黄领梅, 沈冰. 陕西省月平均气温空间插值方法研究[J]. 水资源与水工程学报, 2017,28(5):100-105.

[ Ma X X, Huang L M, Shen B. Study on spatial interpolation method of monthly mean temperature in Shaanxi Province[J]. Journal of Water Resources and Water Engineering, 2017,28(5):100-105. ]

[50]
杨永川, 杨轲, 王志浩, 等. 空间插值法在热环境流动观测中的应用[J]. 中南大学学报(自然科学版), 2012,43(9):3741-3748.

[ Yang Y C, Yang K, Wang Z H, et al. Application of spatial interpolation in moving observations of thermal environment[J]. Journal of Central South University (Science and Technology), 2012,43(9):3741-3748. ]

[51]
Louppe G. Understanding random forests: From theory to practice[J]. Eprint Arxiv, 2014.10.13140/2.1.1570.5928

[52]
Jiang R, Tang W, Wu X, et al. A random forest approach to the detection of epistatic interactions in case-control studies[J]. BMC Bioinformatics, 2009,10(1):S65.

[53]
GRöMPING U. Variable importance assessment in regression: linear regression versus random forest[J]. The American Statistician, 2009,63(4):308-319.

Options
文章导航

/

〈 〉