EN中文

地球信息科学学报 >

2021 , Vol. 23 >Issue 3: 492 - 504

DOI: https://doi.org/10.12082/dqxxkx.2021.200536

遥感科学与应用技术

多核学习算法及其在高光谱图像分类中的应用研究进展

  • 李广洋 , 1 ,
  • 寇卫利 , 1, * ,
  • 陈帮乾 2 ,
  • 代飞 1 ,
  • 强振平 1 ,
  • 吴超 1
展开
  • 1.西南林业大学,大数据与智能工程学院,昆明 650224
  • 2.中国热带农业科学院橡胶研究所/农业农村部儋州热带作物科学观测实验站,海口 571101
*寇卫利（1979-）,男,陕西西安人,博士,教授,主要从事林业信息化、遥感大数据、图像智能分析等研究。E-mail:

李广洋（1994- ）,男,河北唐山人,硕士生,主要从事林业遥感与信息技术研究。E-mail:

收稿日期: 2020-09-17

  要求修回日期: 2020-12-30

  网络出版日期: 2021-05-25

基金资助

国家自然科学基金项目(31760181)

国家自然科学基金项目(31400493)

国家自然科学基金项目(31860181)

国家自然科学基金项目(1860320)

云南省农业基础研究联合专项项目(2017FG001-034)

云南省农业基础研究联合专项项目(2018FG001-059)

生物资源数字化开发应用(202002AA10007)

云南省“万人计划”青年拔尖人才项目

西南林业大学科研启动基金项目(111821)

版权

版权所有，未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
收起

Multiple Kernel Learning Algorithm and its Application Research Progress in Hyperspectral Image Classification

  • LI Guangyang , 1 ,
  • KOU Weili , 1, * ,
  • CHEN Bangqian 2 ,
  • DAI Fei 1 ,
  • QIANG Zhenping 1 ,
  • WU Chao 1
Expand
  • 1. Southwest Forestry University, College of Big Data and Intelligence Engineering, Kunming 650224, China
  • 2. Rubber Institute, Chinese Academy of Tropical Agricultural Sciences/ Danzhou Tropical Crop Scientific Observation and Experiment Station of Ministry of Agriculture and Rural Affairs, Haikou 571101, China
*KOU Weili , E-mail:

Received date: 2020-09-17

  Request revised date: 2020-12-30

  Online published: 2021-05-25

Supported by

National Natural Science Foundation of China(31760181)

National Natural Science Foundation of China(31400493)

National Natural Science Foundation of China(31860181)

National Natural Science Foundation of China(1860320)

The Joint Special Project of Basic Agricultural Research in Yunnan Province(2017FG001-034)

The Joint Special Project of Basic Agricultural Research in Yunnan Province(2018FG001-059)

Digital Development and Application of Biological Resources(202002AA10007)

Yunnan "Ten Thousand People Plan" Youth Top-notch Talent Project

Southwest Forestry University Scientific Research Start-up Fund project(111821)

Copyright

Copyright reserved © 2021
Fold

摘要

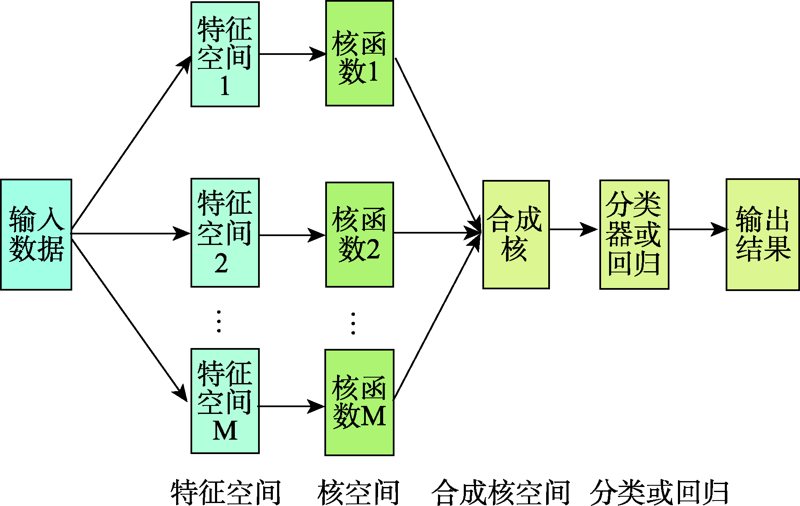
多核学习算法在高光谱图像分类领域占据着十分重要的地位。与灰度图像、全色图像和多光谱图像等相比,高光谱图像因具有很强的分类识别能力等多方面优势而被广泛应用。为进一步提高高光谱图像的分类精度,促进多核学习算法在高光谱图像分类中的应用,本文对多核学习算法及其在高光谱图像分类中的应用进行了总结。首先在回顾核方法的基础上阐述了多核学习框架,其次对多核学习核函数组合方法进行综述,随后根据求解多核学习组合系数方法的不同将多核学习分为两类：固定规则的多核学习算法和基于优化的多核学习算法,并对两类多核学习算法在高光谱图像分类中的应用进行综述,总结各类算法在高光谱图像分类的应用进展。同时,为了便于研究者对多核学习算法及其在高光谱图像分类问题中的应用研究,本文对常用核函数和高光谱图像数据集进行了整理归纳。最后,讨论了多核学习算法在高光谱图像分类研究方面的不足,并对未来研究方向进行了展望,以期为该领域的研究和应用提供参考。

关键词： 支持向量机; 多核学习算法; 遥感; 高光谱; 图像分类; 核函数; 多视图; 特征融合

本文引用格式

李广洋 , 寇卫利 , 陈帮乾 , 代飞 , 强振平 , 吴超 . 多核学习算法及其在高光谱图像分类中的应用研究进展[J]. 地球信息科学学报, 2021 , 23(3) : 492 -504 . DOI: 10.12082/dqxxkx.2021.200536

Abstract

Hyperspectral images have been widely used in target detection, spectral decomposition, classification, and many other fields. They have higher recognition ability than grayscale images, panchromatic images, and multispectral images. However, how to effectively use hyperspectral images with large number of bands, huge data volume, and increased information redundancy is an important topic. Multiple kernel learning is a typical multi-view learning method that can make different kernel functions according to different feature spaces and group multiple kernel functions into an optimal kernel function for hyperspectral image classification. Compared to single kernel method, multiple kernel learning has unique advantages in solving problems such as the uneven spatial distribution of high-dimensional features, using information more efficiently, and improving classification accuracy greatly. At present, the research difficulty of multiple kernel learning algorithm are the combination of kernel functions and the selection of optimal weight coefficients. In order to improve the classification accuracy and promote the application of multiple kernel learning algorithm in hyperspectral image classification, we review the development history and current research progress of multiple kernel learning algorithms. First, the kernel learning method and the framework of multiple kernel learning algorithm are introduced. The specific methods of kernel function combination used in multiple kernel learning algorithm are summarized. According to many researches, it can be concluded that the linear method has been widely used because of its simplicity and efficiency. Moreover, according to the methods of determining weight coefficients in multiple kernel learning algorithm combination, multiple kernel learning algorithms can be generally divided into two categories: fixed-rule multiple kernel learning algorithm and optimization-based multiple kernel learning algorithm. Then, the applications of different multiple kernel learning algorithms from each category in hyperspectral image classification are reviewed. In order to facilitate researchers to discuss the problems of multiple kernel learning algorithm and hyperspectral image classification, the commonly used kernel functions and the widely used data sets in hyperspectral image classification are also reviewed. Finally, we discuss the deficiencies of multiple kernel learning algorithms in the field of hyperspectral image classification and point out the future research direction to help solve practical application problems.

Key words： Support Vector Machine; multiple kernel learning; remote sensing; hyperspectral; image classification; kernel function; multiple views; characteristics of the fusion

1 引言

自20世纪80年代以来,高光谱遥感已经逐渐成为遥感领域的前沿技术,与传统遥感相比具有不同特点,如波段众多、光谱范围窄、波段连续、数据量大以及信息冗余增加。高光谱遥感能更加有力地利用光谱特征分析研究地物,对地物进行更加精细的分类与识别,并且随着高光谱传感器技术的发展,高光谱图像的空间分辨率也得到了很大的提高[1]。目前,高光谱图像被应用到目标检测、光谱分解、分类等多种应用中[2]。
高光谱图像分类是遥感图像数据信息提取的常用技术。通过分类实现对影像中的信息提取,进而达到目标识别、地物反演等实际应用需求,提取信息包括土地覆盖、树种、植被、农作物、水体、房屋、遗迹、灾害等多种类型。由于高光谱遥感图像数据的维数较高而标记训练样本相对较少,因而容易产生休斯现象（Hughes Phenomenon）和“维数诅咒”[3]。为了解决该类问题,支持向量机（Support Vector Machine,SVM）等多种基于核的分类方法相继被提出用于高光谱遥感图像分类并表现出良好的性能[4,5]。基于核方法的分类器性能取决于核函数及其参数的选择。一般通过交叉验证等[6]算法从多个候选核中选出一个能够准确描述所考虑数据的核函数,但是核函数选择不当可能导致更差的分类性能。为解决这一问题,多核学习算法（Multiple Kernel Learning, MKL）[7]引起了高光谱遥感研究者的广泛关注。
MKL作为一种典型的多视图学习（Multi-View Learning, MVL）方法[8],其能够通过核方法有效地利用各视图特征间的结构关联,使得数据得到更完善的表达,从而显著的提高学习性能,因而多种基于MKL的算法在高光谱图像分类中被提出并广泛应用。本文首先对高光谱图像分类与核方法进行简单概述,然后由SVM算法引入MKL算法,后续对MKL算法在高光谱图像分类领域现有的算法及研究成果进行综述,并整理归纳了常用高光谱图像分类数据集。最后,论述了MKL算法在高光谱图像分类领域所面临的问题,并对未来研究方向进行了展望。

2 核方法

核方法的目的是找出并学习一组数据中的相互关系,是一类以核函数为基础的模式识别算法,比神经网络（Neural Networks,NNs）和主成分分析（Principal Component Analysis, PCA）等方法可更高效地解决非线性问题。众多核方法中最著名且应用最为广泛的是SVM,其能通过核函数将向量映射到高维空间,将线性不可分的问题在高维空间线性可分。早期的SVM均是单核SVM,对于异构特征效果并不是很理想,单个核函数并不能满足实际应用的需求,因此多核学习算法被提出。因其能够将多个核函数进行组合,使得到的多核函数能够包含各个核函数的特性而成为了更好的选择。

2.1 核函数

核函数是用来计算映射到高维空间后的内积的一种方法,其定义为[9]：
对于某空间的所有点 x , y ∈ R n ,有一个函数 K ( x , y ) 满足式（1）：
K x , y = ∅ x ∙ ∅ y
且满足Mercer条件,则 K ( x , y ) 就称为核函数。
Mercer条件[10]：对于任意的对称函数 K x , x ' 为某个特征空间中的内积运算的充分必要条件是：对于任意 φ x ≠ 0 并且 ∫ φ 2 x d x < ∞ 满足式（2）：
∬ K x , x ' φ x φ x ' d x d x ' > 0
根据Hilbert-Schmid定理,用于构建核函数只要给定的变换 ∅ 满足Mercer条件就可以。
在实际应用中常用的核函数[11,12,13]如表1所示。
表1 常用的核函数公式和特点比较

Tab. 1 Commonly used kernel functions

名称 公式 编号 参数介绍 特点
线性核函数 kxi,xj=xi,xj（3） xi,xj表示xi和xj的内积 线性核函数参数少,速度快,对于线性可分的数据具有优良的性能,但不能对线性不可分的数据进行分类
多项式核函数 kxi,xj=xi,xj+bd,d∈N（4） 参数d为阶数,对核函数的特征空间维数起决定性作用。参数b用于空值不同阶数的单项式权重,一般令b=1 多项式核依靠升维使线性不可分的数据变得可分,但其参数较多,计算复杂程度也相对较高,因此应用相对较少
径向基核函数
（高斯核）		 kxi,xj=exp-xi-xj22σ2,σ∈R（5） 参数σ为尺度参数,用来控制核函数对样本的相似性度量能力 该核函数以欧氏距离来度量样本之间的相似性,因其计算相对简单且具有平移不变性等优点而成为应用最广泛的核函数,但也存在一定缺陷,如可解释性差、容易过拟合等
sigmoid核函数 kxi,xj=tanhaxi,xj-bd,a,b∈R（6） 参数a是控制输入数据的幅度调节参数,b是控制映射阈值的位移参数 Sigmoid核来自神经网络的阈值函数,具有很强的分类能力,但由于其包含两个参数,增加了应用难度,且其只有在特定条件下才是半正矩阵,因此该核不是Mercer核,受到一定的应用限制
小波核函数 kxi,xj=∏i=1Nψxi-xjs（7） s为尺度参数 小波核函数在多尺度分析方面具有优势,其可以逼近任意非线性函数,提升分类精度

2.2 常用核方法

目前常用的核方法包括支持向量机（SVM）、核主成分分析（Kernel Principal Component Analysis, KPAC）[14]、线性核判别分析（Kernel Linear Discriminant Analysis, KLDA）[15]、核最小平方误差（Kernel Minimal Square Error, KMSE）[16]等。其中最著名且应用最为广泛的是SVM,其能通过核函数将向量映射到高维空间,将线性不可分的问题在高维空间线性可分。
2.2.1 支持向量机
起初核方法作为一种线性到非线性的桥梁并未受到重视,直到Vapnik等[6]提出了SVM,利用核方法将SVM扩展到非线性分类中,核方法才被业界广泛关注。在众多单核方法中,SVM是最经典的一种算法,属于监督学习方式[17]。Guo等[18]通过实验将SVM算法与其他算法相比较,结果表明SVM容错率最低,且应用面更广。SVM算法特点是能够同时最小化经验误差和最大化分类间隔,即通过寻找一个超平面使两类数据之间间隔最大化的同时又能保证分类精度（图1）。
图1 SVM最优分类超平面[19]

Fig. 1 SVM optimal classification hyperplane

设一组训练样本集 x i , y i , x i ∈ R n , y i ∈ + 1 , - 1 , i = 1,2 , ⋯ , l 。
对于线性可分的问题,可得到决策函数为式（8）[20]：
f x = sgn ∑ i = 1 l a i y i x i ∙ x + b
式中： y i 为训练样本 x i 得到的类值; x = x 1 , x 2 , ⋯ , x m 为输入向量 x i 的支持向量; ∙ 为内积; a i 为决定超平面的参数; b 为超平面的偏置量。
对于非线性问题,其决策函数为式（9）：
f x = sgn ∑ i = 1 l a i y i k x i , x + b
式中：k为核函数;其他参数含义与式（3）一致。
SVM促进了核方法的发展,核方法也为SVM带来了更广阔的应用空间。相比于其他分类器,SVM可以有效地规避过度拟合问题。肖博林[19]基于SVM算法提出了一种高光谱影像分类机制,并在帕维亚大学和印度松树数据集上进行了实验验证,总体分类精度分别达到了90.38%和76.51%,Kappa系数分别为87.19%和72.79%。张玲等[21]设计了一种SVM的多目标分类方法,将分类精度提高到了85%以上。
2.2.2 其他常用核方法
（1）PKAC方法是一种非线性形式的主成分分析方法,其利用积分算子核函数,能够有效地计算高维特征空间中的主成分。PKCA方法提供了比对应数量的线性主成分更好的识别率,相比线性情况其拥有更高的性能。并且PKAC方法的计算复杂度不会随着特征维数的增长而增加[14]。
（2）KLDA方法是一种基于Fisher判别的非线性分类技术,其能够在特征空间中有效的计算Fisher判别式。KLDA方法的复杂性随着训练模式的数量而变化,在解决方案中该方法使用所有样本,相比于SVM的使用支持向量,KLDA方法往往能够有更优的表现[15]。
（3）KMSE方法通过使用核思想和添加不同的正则项来产生的新的非线性学习机,可以使该方法在数值计算中更加稳定,并能控制其泛化能力,通常用来处理线性、非线性的分类和回归问题。该方法与KLDA方法相同,并且等价于SVM的最小二乘版本[16]。

3 多核学习算法及其在高光谱图像分类中的应用

SVM等传统的单核方法均基于单个特征空间,其需要按照经验选择不同的核函数,并指定不同的参数,虽然能在一定程度上解决高光谱图像分类中的高维特征问题,但高光谱影像的数据特点使单核方法在分类方面也具有一定的局限性[22]。简单地说,在分类的问题中往往存在异构特征,如颜色特征、纹理特征等,不同的特征所对应的核函数也不尽相同,那么共用相同的核函数则会导致得不到最优映射。为了解决此类问题,MKL算法应运而生。该算法能将不同的核函数或同核不同参的核函数对应不同的特征空间,将众多核函数组合成最优核函数来进行分类,在组合的过程中寻找最优的权重系数以达到提高分类效果的目的。因此,多个核函数的组合方法以及参数寻优问题则成为了MKL算法的关键问题。一个合适的核函数组合方法及参数寻优算法不仅能有效提高分类精度,更能降低多核学习算法的训练时间。本节将对在高光谱图像分类问题中多核学习算法原理、核函数组合方法以及参数算法进行论述,并对常用的高光谱数据集进行了归纳整理。

3.1 多核学习算法原理及其在高光谱图像分类中的 应用

单核函数的缺点是处理多维多类数据时泛化能力较弱,于是Lanckriet等[23]提出了一种同时考虑多个核函数的MKL算法,其较单核方法的优势是MKL算法提供了更加灵活的框架,能够将众多核函数探测到的结果在核层面融合,更加有效地挖掘信息。该算法介于特征层融合与决策层融合之间的核层融合,是一种新型信息融合形式。MKL算法结构框架如图2所示。
图2 多核学习算法结构框架[11]

Fig. 2 Multiple kernel learning algorithm structure framework

不同的核函数对应不同视图,MKL算法为MVL提供了一种融合不同视图数据的有效方式。该算法是单核SVM的拓展,具体来说,它的形式是将适合于不同类型特征的核函数进行最优组合,以达到多源信息融合的目的。其表达形式为式（10）[24]：
k η x , z = f η k m x m , z m m = 1 P | η
式中： f η : R P → R 是线性或非线性的函数,参数 η 用来确定组合系数。样本数据 x = x m m = 1 P 包含P个特征,且 x m ∈ R D m , D m 为特征维数。P个特征分别用P个核函数来表示 k m : R D m × R D m → R m = 1 P 。P个核函数则成为基核函数。
MKL将多个基本核进行组合替代了单核,有效的改进了核方法并被广泛应用。因单核SVM分类精度较低,所以余旭初等[25]将高斯核和多项式核进行组合,联合纹理和光谱特征,采用多核学习算法的MKSVM分类器对上海技术物理研究所研制的PHI成像光谱仪获取的江苏常州地区乡村影像的房屋、水体、土壤、树木、农作物以及道路6种地物类型进行分类试验。该方法不仅消除了单核SVM利用交叉验证选择核函数系数的缺点,同时有效地解决了“麻点”现象,将总体分类精度提高到了98.21%。高巍等[12]提出了马氏距离多核算法（Mahal-MKL）,并与传统的基于高斯核函数的单核算法、代表性多核算法以及基于核非负矩阵分解的算法进行对比。在Indian Pine数据集上（去除4类样本数较少的类别后包含农业用地和森林用地共12类地物类别）的实验结果表明,训练样本少于20的极端条件下,传统的多核学习算法分类结果不如单核算法,而Mahal-MKL方法可以将总体精度和Kappa系数提高4%,并且随着样本增加分类效果一直稳定处于最佳表现。在University of Pavia数据集上（包含道路、草地、树木、房屋等共计9类地物类别）的实验表明Mahal-MKL方法总体精度和Kappa系数比单核算法提高了近5%,比传统多核学习算法提高了2%。在2个数据集上的实验结果表明与单核和传统多核学习算法相比较,Mahal-MKL方法能够更好地区分较强相似性的地物类别,有效地提高分类精度和Kappa系数,尤其更适用于训练样本较少的极端条件。Deng等[26]提出了一种基于域自适应的主动框架MKL算法,不仅节省了昂贵的计算成本和人工标注工作,并通过在Pavia中心数据集与大数据集上进行实验证明该方法可以使分类精度最高达到97%,与SVM、RS、DTMKL和SKV等传统算法相比能够显著提高分类精度。Cui等[27]提出了一种基于自学习和互学习的高光谱图像分类框架,该方法使用许多未标记的样本来提高分类性能,与主动学习方法相比,该方法在添加伪标签的过程中不需要人工干预,训练过程实现了自动化。在Indian Pines数据集、University of Pavia数据集以及Salinas数据集上的实验结果表明,与SV-CV、SimpleMKL、RMKL等方法相比,该方法在分类精度方面表现优异。为了获得多个特征视图空间的补充信息和样本的先验信息,Wang等[28]提出了将经验核学习与多经验核学习相结合的多重经验核学习（Multiple Universum Empirical Kernel Learning, MUEKL）方法,并通过在UCI和KEEL数据集上与6个具有代表性算法（USVM、MultiK-MHKS、SimpleMKL、NLMKSVM、SVM和EasyMKL）的对比,实验表明MUEKL算法不仅解决了平衡问题,平均精度也达到了88.27%,性能优于其他算法。Liu等[29]针对基于互联网的高光谱数据检索提出了基于准共形映射核机器学习的只能高光谱数据分类算法,该方法提出基于拟共形映射的多核学习网络框架,将马氏距离核函数作为网络节点,比基于欧氏距离的核函数拥有更高的判别能力。在Indian Pine数据集和University of Pavia数据集上的实验结果表明所提方法对高光谱图像分类是有效的,在利用互联网上的图像、视频等数据信息构建大规模训练样本方面具有优势。

3.2 多核学习核函数组合方法及其在高光谱图像分类中的应用

图谱合一作为高光谱图像典型的特征,指将高光谱图像所包含的空-谱信息完整的进行结合。MKL算法在处理异构特征融合的问题方面具有独特的优势,其作用就是将特征提取结果在核层面进行融合,通过将多个对不同特征拥有不同解译能力的核函数进行集成,得到更适合具体情况的核函数,是目前的解决空-谱分类问题行之有效的方法。那么核函数之间的组合方法成为了关键问题,空谱混合核是最早将多核学习算法与高光谱图像分类问题相结合的范例[15]。Camps-Valls G等[9]提出的分类方法利用复合核方法来组合高光谱的光谱和空间信息;Li等[30]通过复合核方法将空谱相结合,实现了扩展支持向量机算法。单核学习算法是在众多基核中挑选一个最合适的核,与单核学习方法不同的是组合核是对这些基核进行选择并组合,原理类似于分类器组合。目前多核学习核函数组合方式可以分为线性组合、非线性组合以及数据相关组合方式[4]。
（1）大多数研究都集中在线性组合方法上,如直接求和核、加权求和核和加权多项式扩展核等[31],如表2所示。
表2 多核学习线性组合方法公式和特点比较

Tab. 2 Multiple kernel learning linear combination method

名称 公式 编号 参数介绍 特点
直接求和核 kx,z=∑m=1Mkmx,z （11） M为核的个数 构造简单,学习性能较为突出
加权求和核 kx,z=∑m=1Mβmkmx,z,βm&gt;0,∑m=1Mβm=1 （12） β表示核权重,即组合系数,M为常数 通过调整权重,可以更加灵活的调节混合核的学习能力,提升分类性能。相比于其他组合方式,更加适用于高光谱影像分类
加权多项式
扩展核		 kx,z=αk1px,z+1-αk2px,z,0&lt;α&lt;1（13） kpx,z是核函数kx,z的扩展 当选取合适的权重系数时,能有效地保证模型的局部学习特性和全局扩展能力,使测试误差和训练误差均保留在一个较小的范围
加权求和核应用较为广泛,但当采用固定权值或训练较优的权值时与直接求和核的方法差异性较小时则采用直接求和核。
（2）非线性组合方式为使用核的非线性函数,如乘积、幂和指数[32]。
（3）Diego等[32]提出一种数据相关组合方式,假设 K m x i , x j ∈ 0,1 ∀ i , j , m ,其遵循的方法为式（14）：
K * x i , x j = ∑ m = 1 M w m x i , x j K m x i , x j
式中：M是常数; η m x i , x j 是加权函数。
该组合方式为每个数据实例指定特定的内核权重,他们可以识别数据中的局部分布,并为每个区域学习适当的核组合规则。
在基核的组合方式上,线性方法因简单高效而被广泛应用。谭熊等[22]提出了一种多核SVM高光谱影像分类方法,对提取出的光谱特征通过加权求和的多核组合方法和SMKL的理论方法进行图像分类,并通过在AVIRIS成像光谱仪获取的Indian Pines数据集和由推扫式成像光谱仪PHI-1307于2009年5月获取的山东省某码头的航空高光谱影像上（包含房屋、树木、水体、植被等8类地物类别）通过实验验证了分类精度,结果表明在2类数据集上该组合方式分类正确率分别为91.22%和94.70%,分类精度均优于使用基于高斯核和基于多项式核的单核SVM。但该方法只利用了高光谱图像的光谱信息,未考虑其空间信息,对分类精度的提升存在明显的瓶颈;李湘眷等[33]采用加权求和核的方法对空-谱特征进行结合,该方法根据训练样本的特性来优化权重可以使分类器具有更强的学习能力,突出样本的主要特性。实验部分采用的是源于英国布里斯托大学的高光谱数据库,将召回率作为训练样本数的函数对文中所提方法和单独光谱特征、波段选择空间特征级联的3种单核SVM分类器、随机三波段空间特征级联以及随机三波段空间特征级联与光谱特征相结合共5种方法进行比较,结果表明所提方法能够获得较优的召回率（>99.5%）以及较低的虚警率（<0.2%）,具有最好的类别区分性;Li等[2]利用加权求和核的方法将基核组合成复合核,将空-谱信息结合起来,在Indian Pines、University of Pavia和Salinas image 3个著名的真实高光谱数据集上进行了分类实验,并将结果与SVM、SRC、JSRC、SAJSRC、KSRC-SF、AKSR-SF和AKSR-MF多种先进分类器进行对比,表明所提方法AKSR-MFL拥有更好的分类性能,最高准确率达到了99.19%。除此之外也有一些研究尝试使用非线性方法[34],但分类结果都不太理想。

3.3 多核学习组合系数求解算法及其在高光谱图像分类中的应用

在多核学习等训练类算法中,“学习率”作为组合函数的系数,其影响着算法性能。学习率太大则会导致算法不能收敛到一个较为准确的值,反之又会导致收敛速度过慢,导致效率不高[35]。因此,在高光谱图像分类中,一个合适的针对权重系数优化的算法是影响多核学习算法分类精度的关键所在。目前的线性多核学习算法根据计算权重系数策略的不同,一般分为2大类：固定规则的MKL算法和基于优化的MKL算法（图3）。
图3 基于求解组合系数的多核学习算法分类[36]

Fig. 3 Classification of multiple kernel learning algorithm based on solving combination coefficients

3.3.1 固定规则的MKL算法
固定规则MKL不考虑任何优化策略,一种固定规则算法是将所有基核进行求和构成复合核,另一种是将M个基核的平均值构成复合核[3],由于其计算复杂度低而被广泛应用于高光谱图像分类中[9]。基于固定规则的MKL方法不需要对权重系数进行训练,但并未考虑不同数据间的特点[37]。
3.3.2 依赖于分类器的MKL算法
依赖于分类器的算法目的是通过最小化SVM分类误差来联合学习分类器参数和核权重,一般把该类方法分为2个子类,即直接MKL算法与包装器MKL算法。
（1）直接MKL算法
在直接MKL算法中,通过优化MKL的对偶问题来直接估计核权重和支持向量机参数。Lanckriet等[23]介绍了用半正定规划（Semidefinite Programming, SDP）优化MKL算法,但该算法优化过程复杂,适合小规模MKL算法;半无限性规划（Semi-infinite Linear Program, SILP）[38]也被用来优化MKL算法对偶问题,该算法充分利用现有分类器训练方法,适用于大规模多核学习算法问题。Bach等[5]利用序列极小化（Sequential Minimal Optimization, SMO）来对优化问题进行求解。
（2）包装器MKL算法
包装器算法是使用两步优化过程来获得核权重和支持向量机参数。在给核权赋初值后,第1步构造复合核并求解支持向量机参数。第2步,将支持向量机的参数固定在第一步得到的值上,然后根据核权重对支持向量机的目标函数进行优化。SimpleMKL[39]是最著名的包装器MKL算法之一,该算法采用投影梯度子代作为优化算法,其需要考虑梯度迭代的步长值,因此导致计算复杂度过高。 Gu等[40,41]将该方法用于高光谱图像分类中,并针对计算效率进行了改进;谭雄等[42]在SVM基础上以线性加权的方式对核函数进行组合,并利用SimpleMKL方法求解组合系数来实现分类;郭志民等[43]利用该算法将空-谱信息进行最优组合,得到了良好的分类效果。广义MKL（Generalized MKL, GMKL）[44]是另一种包装器算法,为了推导核权重, Xu等[45]提出一种基于GMKL的（Group Lasso MKL, GLMKL）算法,并被Liu等[46]引用到高光谱图像分类中。GLMKL不需要在每次迭代时计算对偶问题的梯度,因此它比SimpleMKL和GMKL更快且更适合大规模多核学习问题。
3.3.3 独立于分类器的MKL算法
独立于分类器的MKL算法与依赖分类器的MKL算法相比,其拥有更简单的优化算法,可以更加容易的处理多个核,并且降低了计算效率。该类算法可以分为4个不同的子类：基于相似性的算法、基于泛化误差的算法、基于子空间的算法以及启发式MKL算法。
（1）基于相似性的MKL算法
基于相似性的MKL算法的目标函数为复合核和目标核之间的相似性度量,常用的为核对齐（Kernel Alignment, KA）[47]。定义 k 1 和 k 2 2个核函数对于给定样本集 S = x 1 , x 2 , ⋯ , x N 的核矩阵为 K 1 和 K 2 , k 1 和 k 2 的核对齐值可以按照式（15）进行计算：
A S , k 1 , k 2 = K 1 , K 2 F K 1 , K 1 F K 2 , K 2 F
式中： K 1 , K 2 F = ∑ i , j = 1 N K 1 x i , x j K 2 x i , x j 为2个核矩阵的内积。
王庆超等[48]针对空间信息利用不足的问题提出了多核融合多尺度特征的核稀疏表示算法,充分利用空谱信息,并使用核对齐方法求解了核权重系数,最终在Indian Pines和Pavia University 2个数据集上设计实验并与SVM、PAC+SVM、MKSVM、SRC、JSRC、MKSRC多种方法进行精度对比,实验在2类数据集上的分类结果分别为99.51%和97.96%,分类效果均优于其他方法,表明文中所提方法具有更好的通用性和鲁棒性。
（2）基于泛化误差的MKL算法
MKL框架的最新进展之一是通过最小化误差的上限来确定组合系数。其中最简单的一种方法是梯度下降法[49]。晁拴社等[50]将采样技术与多核学习算法相结合,并运用梯度下降法选择了最优的核参数,比传统的SVM分类方法总体分类精度提高了4.07%,并解决了高光谱图像分类中数据规模大、地物种类复杂以及因样本分布不规则引起的鲁棒性差和分类精度不高等问题;楚恒等[51]提出一种基于MK-LSSVM的不平衡分类方法,采用梯度下降求解组合系数,并通过在Indian Pines数据集上设计实验证明该方法比传统的LSSVM和MK-LSSVM方法训练时间更短,分别减少了171.2 s和291.68 s,Kappa系数分别提高了0.149和0.078,少数地类分类精度也有所提高。但以上方法均只利用了光谱信息而忽略了丰富的空间信息。
（3）基于子空间的MKL算法
基于子空间的MKL算法首先将基核整形为向量并叠加成矩阵,然后利用子空间学习方法从矩阵中学习一维子空间。将矩阵到提取子空间的投影向量作为核权向量。代表性多核学习（RMKL）是第一种基于子空间的算法,该算法利用奇异值分解来学习子空间[40],根据统计显著性来确定要保留的核及其权重,该文最终通过在Kennedy Space Center、Indian Pines和Pavia University 3组数据集上实验,并将结果与SKSVM、SWKSVM和SimpleMKL 3种算法相比较,结果表明所提方法不仅具有低计算成本和方便可行性的优点,更具有良好的小样本分类能力和不平衡分类能力。此外,基于非负矩阵分解（Non-negative Matrix Factorization, NMF）[52]的MKL算法也属于该类算法,Gu等[52]利用该方法学习最优组合核,并引入核NMF（Kernel NMF, KNMF）来代替NMF,通过在Salinas、Indian Pines和Pavia University 3组数据集上实验证明该方法能在较少标记样本的情况下比SK-KA、SK-CV、SimpleMKL、RMKL和MeanMKL 5种典型的算法拥有突出的分类性能,解决了高维空间中使用很少标记样本这一高光谱图像分类的难题。
（4）启发式MKL算法
启发式MKL算法通过使用一些启发式规则来估计核权重,一种简单的启发式方法利用交叉验证,在该过程中,权重是从预定义的候选值中选择的。Wang等[53]提出了一种基于交叉验证的多重映射核框架（Multiple-Mapping Kernel Framework, MMKF）,并通过在two moons人工数据集和Indian Pines高光谱数据集上进行实验证明所提方法在高光谱图像分类中的有效性,结果表明MMKF算法比单高斯核总体精度提高1.13%,平均精度提高0.78%,Kappa系数提高0.0136,但随着计算参数的增多,MMKF算法耗时也相对较长。陈允杰 等[54]通过五折交叉验证选出SVM的训练参数,并提出了2种边缘修正的超像素空间光谱核分类法,通过在Indian Pines和Pavia University 2组数据集上设计对比实验,与基于超像素的空间特征提取方法（SPCK）、自适应空间TV正则项的多项式逻辑回归方法(SMLR-SpTV)、支持向量机组合核分类方法（SVMCK）以及基于超像素的多核学习方法（SCMK）4种前沿分类方法相比较,实验结果为文中所提方法分类精度在Indian Pines数据集上高于97%,在Pavia University数据集上高于89%,分类效果都要优于其它4种算法。Wang等[55]将Boosting框架和MKL相结合,提出了一种MKBoost算法,并在Kennedy Space Center、Indian Pines和Pavia University 3组实际高光谱数据集上进行实验,结果表明该方法能够比RMKL方法在处理高光谱图像数据方面的分类精度提高1%~4%。Li[56]等同样结合MKL与Boosting算法,并在浮游生物反射光谱数据、Salina数据集和Pavia University数据集上设计实验证明所提方法比SVM、KNN、BAYES、SR-OMP等方法具有更好的性能,能够显著特高分类精度。

3.4 高光谱图像分类的常用数据集

为了便于研究者对高光谱图像分类问题进行研讨,本文查找了高光谱图像分类中的一些常用数据集,并进行了整理归纳和对比（表3）。
表3 高光谱图像分类常用数据集信息比较

Tab. 3 Commonly used data sets for hyperspectral image classification

编号 数据集
名称		 采集
年份		 传感器 数据
地点		 像素 空间
分辨率/m		 所包含地物类型数量 参考
文献
1 Indian Pines数据集 1992 机载可视/红外成像光谱仪(AVIRIS) 美国印第安纳州一块印度松树 145×145 20 16类 [12][29]
2 Pavia University数据集 2003 机载反射光学光谱成像仪(ROSIS-03) 意大利的帕维亚城所成的像的部分高光谱数据 610×340 1.3 9类 [26][27]
3 Salinas数据集 机载可视/红外成像光谱仪(AVIRIS) 美国加利福尼亚州的Salinas山谷 512×217 3.7 16类 [56]
4 Cuprite数据集 1997 机载可视/红外成像光谱仪(AVIRIS) 美国内华达州的Cuprite地区 20 [57]
5 Kennedy Space Center数据集 1996 机载可视/红外成像光谱仪(AVIRIS) 佛罗里达州肯尼迪航天中心(KSC) 18 13类 [58]
6 Botswana数据集 2001 NASA EO-1卫星 博茨瓦纳的奥卡万戈三角洲 30 14类 [59]
7 Washington DC数据 Hydice传感器 华盛顿购物中心 1208×307 7类 [60]
8 Houston数据 2013 ITRES CASI-1500传感器 休斯顿大学校园和邻近的城市地区 349×1905 2.5 15类 [61]
9 Houston数据 2012 Compact Spectrographic Image(CASI) 休斯敦大学校园及其附近地区 1905×349 2.5 20类 [62]
10 航空高光谱影像 Chikusei 2014 Headwall Hyperspec-VNIR-C传感器 日本筑西市（Chikusei） 2517×2335 2.5 19类 [63]

4 讨论

高光谱图像是遥感领域的一项进展,如何充分利用影像数据,从庞大的数据中选取有效的信息,是目前学者们所需研究的重要课题。综上所述,多核学习算法已经成为高光谱图像分类问题中的重要手段,较传统分类方法能极大地提高分类精度。但还存在一些问题与挑战需要进一步研讨,主要体现在以下几个方面：
（1）多核学习算法在解决高光谱图像分类问题时效率较低[20]。高光谱图像高维数据带来庞大的计算量,在分类精度上MKL算法虽高于单核学习算法,但在计算繁琐程度、占用的存储资源以及时间消耗上前者也远大于后者,所以寻找一种高效稳定的方法来解决传统MKL算法中的优化问题仍是具有挑战性的难题。
（2）高光谱图像分类中空间特征利用不充分[48]。单纯的使用光谱信息导致分类效果并不理想,只应用空间信息虽然能取得不错的分类精度,但却浪费了高光谱影像拥有巨大光谱信息量的优势。空谱特征联合是目前能取得高分类精度的有效方法,但目前大多数空谱联合方法对空间信息的利用并不足够充分,最终也会影响分类精度。所以如何充分利用高光谱图像所包含的信息尚需投入大量研究。
（3）随着监测目标的多样化以及对提高监测精度与日俱增的需求,高光谱图像的应用也越来越普及,且不同算法适用范围也不尽相同,后续需在更多的数据集上实验,对现有算法进行验证和优化以提升算法的泛化能力[20]。
（4）如何利用其他机器学习、模式识别等方法与MKL相结合来改进其在遥感影像中的分类效果,提高分类精度,也需深入研讨。
（5）在高光谱图像分类问题中,不同数据间的特征融合问题目前的研究还相对较少,多核学习算法中各个核函数及不同的数据源均可对应不同的视图,从更多的视图角度来分析高光谱图像的分类问题,如多源MKL算法等,有助于进一步提高分类精度。
（6）目前大多研究处于理论阶段,在实际应用中并不能完全发挥作用。
（7）寻找更加适合高光谱图像数据特点的新核函数并探索更多的核函数组合方式将是下一步研究的方向。

5 结论

多核学习算法在遥感图像分类中受到越来越广泛的关注,较传统的分类方法其能够有效地提高分类精度。本文回顾了多核学习算法的发展历程,对多核学习核函数组合方法以及求解组合系数算法进行综述,总结其在高光谱图像分类问题中的研究进展。此外,还整理归纳了多核学习算法常用的核函数及高光谱图像分类的数据集。最后本文对多核学习算法在高光谱图像分类中存在的问题与挑战进行了讨论,对进一步促进多核学习算法在高光谱遥感图像的应用提供参考。多核学习算法在高光谱图像分类领域目前存在众多问题需要去进一步研讨,如耗时高、计算量大、空谱信息利用不充分、在实际应用不能完全发挥作用、可用核函数较少等问题对于目前的研究进展仍然充满了挑战,但前景也相应的充满了机遇,其未来必将在更多的领域广泛应用。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Chen G, Zhang Y, Wang S. Hyperspectral remote sensing IQA via learning multiple kernels from mid-level features[J]. Signal processing: Image communication, 2020,83:115804.

DOI

[2]
Li D, Wang Q, Kong F. Adaptive kernel sparse representation based on multiple feature learning for hyperspectral image classification[J]. Neurocomputing, 2020,400:97-112.

DOI

[3]
Zhou Y C, Peng J, Chen C L P. Extreme learning machine with composite kernels for hyperspectral image classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015,8(6):2351-2360.

DOI

[4]
Liu X, Wang L, Zhu X, et al. Absent multiple kernel learning algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020,42(6):1303-1316.

DOI PMID

[5]
Bach F R, Lanckriet G R G, Jordan M I. Multiple kernel learning, conic duality, and the SMO algorithm[C]. Proceedings of the twenty-first international conference on Machine learning, 2004: 6.

[6]
Vapnik V N, Chervonenkis A. A note on one class of perceptrons[J]. Automation and Remote Control, 1964: 25(1):103-109.

[7]
Lanckriet G R G, Cristianini N, Bartlett P, et al. Learning the kernel matrix with semidefinite programming[J]. Journal of Machine Learning Research, 2004,5:27-72.

[8]
Yarowsky D. Unsupervised word sense disambiguation rivaling supervised methods[C]. 33rd annual meeting of the association for computational linguistics, 1995: 189-196.

[9]
Camps-Valls G, Gomez-Chova L, Muñoz-Marí J, et al. Composite kernels for hyperspectral image classification[J]. IEEE Geoscience and Remote Sensing Letters, 2006,3(1):93-97.

DOI

[10]
宋恺涛, 彭甫镕, 陆建峰. 基于多核学习的协同滤波算法[J]. 数据采集与处理, 2018,33(3):496-503.

[ Song K T, Peng F R, Lu J F. Collaborative filtering algorithm based on multiple kernel learning[J]. Journal of Data Acquisition & Processing, 2018,33(3):496-503. ]

[11]
高巍. 基于多核学习的高光谱图像分类方法研究[D]. 哈尔滨:哈尔滨工业大学, 2019.

[ Gao W. Study on hyperspectral image classification based on multiple kernel learning[D]. Harbin: Harbin Institute of Technology, 2019. ]

[12]
高巍, 彭宇. 基于马氏距离多核学习的高光谱图像分类[J]. 仪器仪表学报, 2018,39(3):250-257.

[ Gao W, Peng Y. Hyperspectral image classification based on Markov Distance multiple kernel learning[J]. Acta Instrumentation, 2008,39(3):250-257. ]

[13]
邓利芳, 党建武, 王阳萍. 等. 结合混合核特征映射的空域图像隐写分析[J/OL]. 计算机工程与应用,2020:1-10, http://kns.cnki.net/kcms/detail/11.2127.TP.20200805.1833.034.html.

[ Deng L F, Dang J W, Wang Y P. et al. Spatial image steganography analysis combined with hybrid nuclear feature mapping [J/OL]. Computer engineering and application, 2020:1-10, http://kns.cnki.net/kcms/detail/11.2127.TP.20200805.1833.034.html]

[14]
Schölkopf B, Smola A, Müller K R. Kernel principal component analysis[C]. International conference on artificial neural networks. Berlin: Springer, 1997: 583-588.

[15]
Mika S, Ratsch G, Weston J, et al. Fisher discriminant analysis with kernels[C]. Neural Networks for Signal Processing IX: Proceedings of the 1999 IEEE Signal Processing Society Workshop. IEEE, 1999: 41-48.

[16]
Xu J, Zhang X, Li Y. Kernel MSE algorithm: A unified framework for KFD, LS-SVM and KRR[C]. IJCNN'01. International Joint Conference on Neural Networks. Proceedings (Cat. No. 01CH37222). IEEE, 2001,2:1486-1491.

[17]
王福斌, 潘兴辰, 王宜文. 基于SVM的多核学习飞秒激光烧蚀光斑图像分类[J]. 激光杂志, 2020,41(4):86-91.

[ Wang F B Pan X C Wang Y W. Classification of ablation spot by femtosecond laser based on multi-kernel learning SVM[J]. Laser Journal, 2020,41(4):86-91. ]

[18]
Guo G, Li S Z, Chan K L. Support vector machines for face recognition[J]. Image and Vision Computing, 2001,19(9):631-638.

DOI

[19]
肖博林. 基于支持向量机的高光谱遥感影像分类[J]. 科技创新与应用, 2020(4):22-24.

[ Xiao B L. Hyperspectral remote sensing image classification based on Support vector Machine[J]. Science and Technology Innovation and Application, 2020(4):22-24. ]

[20]
汪廷华, 陈峻婷. 核函数的选择研究综述[J]. 计算机工程与设计, 2012,33(3):1181-1186.

[ Wang T H, Chen J T. Survey of research on kernel selection[J]. Computer Engineering and Design, 2012,33(3):1181-1186. ]

[21]
张玲, 陈路路, 梁进科, 等. 一种基于支持向量机的雷达多目标分类方法[J]. 无线电工程, 2020,50(1):53-56.

[ Zhang L, Chen L L, Liang J K. et al. A radar multi-target classification method based on support vector machine[J]. Radio Engineering, 2020,50(1):53-56. ]

[22]
谭熊, 余旭初, 秦进春, 等. 高光谱影像的多核SVM分类[J]. 仪器仪表学报, 2014,35(2):405-411.

[ Tan X, Yu X C, Qin J C, et al. Multiple kernel SVM classification for hyperspectral images[J]. Chinese Journal of Scientific Instrument, 2014,35(2):405-411. ]

[23]
Lanckriet G R G, Cristianini N, Bartlett P, et al. Learning the kernel matrix with semidefinite programming[J]. Journal of Machine Learning Research, 2004,5(Jan):27-72.

[24]
Liu X, Wang L, Zhu X, et al. Absent multiple kernel learning algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020,42(6):1303-1316.

DOI PMID

[25]
余旭初, 谭熊, 付琼莹, 等. 联合纹理和光谱特征的高光谱影像多核分类方法[J]. 测绘通报, 2014(9):38-42.

DOI

[ Yu X C, Tan X, Fu Q Y, et al. Combined texture-spectral feature for multiple kernel classification of hyperspectral images[J]. Bulletin of Surveying and Mapping, 2014(9):38-42. ]

[26]
Deng C, Liu X, Li C, et al. Active multi-kernel domain adaptation for hyperspectral image classification. Pattern Recognition, 2018,77:306-315.

DOI

[27]
Cui B, Zhong L, Yin B, et al. Hyperspectral image classification based on multiple kernel mutual learning[J]. Infrared Physics & Technology, 2019,99:113-122.

[28]
Wang Z, Hong S S, Yao L J, et al. Multiple universum empirical kernel learning[J]. Engineering Applications of Artificial Intelligence, 2020,89:103461.

DOI

[29]
Liu J, Qiao Y. Quasiconformal mapping kernel machine learning-based intelligent hyperspectral data classification for internet information retrieval. Wireless Communications and Mobile Computing, 2020: 1-14.

[30]
Li J, Marpu P R, Plaza A, et al. Generalized composite kernel framework for hyperspectral image classification[J]. IEEE Transactions on Geoence & Remote Sensing, 2013,51(9):4816-4829.

[31]
李旭, 王士同. 原信息与映射信息组合的多核学习降维方法[J]. 计算机科学与探索, 2019,13(2):310-321.

[ Li X, Wang S T. Multiple kernel learning dimension reduction method for combination of original information and mapping information[J]. Computer Science and Exploration, 2019,13(2):310-321. ]

[32]
Diego I M, Muñoz A, Moguerza J M. Methods for the combination of kernel matrices within a support vector framework[J]. Machine Learning, 2009,78(1/2):137-174.

DOI

[33]
李湘眷, 张峰, 李宇, 等. 基于波段选择和空-谱组合核函数的高光谱图像目标检测[J]. 国外电子测量技术, 2019,38(5):101-108.

[ Li X J, Zhang F, Li Y, et al. Hyperspectral image object detection based on band selection and spatial-spectral composite kernel[J]. Foreign Electronic Measurement Technology, 2019,38(5):101-108. ]

[34]
Sonnenburg S, Rätsch G, Schäfer C, et al. Large scale multiple kernel learning[J]. Journal of Machine Learning Research, 2006,7:1531-1565.

[35]
郭跃东, 宋旭东. 梯度下降法的分析和改进[J]. 科技展望, 2016,26(15):115-117.

[ Guo Y D, Song X D. Analysis and improvement of gradient descent method[J]. Science and Technology Outlook, 2016,26(15):115-117. ]

[36]
Niazmardi S, Demir B, Bruzzone L, et al. Multiple Kernel Learning for Remote Sensing Image Classification[J]. IEEE Transactions on Geoence and Remote Sensing, 2017,56(3):1425-1443.

[37]
Liu K H, Lin Y, Chen C S. Linear spectral mixture analysis via multiple-kernel learning for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015,53(4):2254-2269.

DOI

[38]
Sonnenburg S, Rätsch G, Schäfer C, et al. Large scale multiple kernel learning[J]. Journal of Machine Learning Research, 2006,7:1531-1565.

[39]
Rakotomamonjy A, Bach F, Canu Stéphane, et al. SimpleMKL[J]. Journal of Machine Learning Research, 2008,9(3):2491-2521.

[40]
Gu Y F, Wang C, You D, et al. Representative multiple kernel learning for classification in hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012,50(7):2852-2865.

DOI

[41]
Gu Y, Gao G, Zuo D, et al. Model selection and classification with multiple kernel learning for hyperspectral images via sparsity[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014,7(6):2119-2130.

DOI

[42]
谭熊, 余旭初, 张鹏强, 等. 基于多核支持向量机的高光谱影像非线性混合像元分解[J]. 光学精密工程, 2014,22(7):1912-1920.

[ Tan X, Yu X C, Zhang P Q, et al. Nonlinear mixed pixel decomposition of hyperspectral imagery based on multiple kernel SVM[J]. Optics and Precision Engineering, 2014,22(7):1912-1920. ]

[43]
郭志民, 孙玉宝, 耿俊成, 等. 谱-空图嵌入的高光谱图像多核分类算法[J]. 小型微型计算机系统, 2018,39(11):2545-2550.

[ Guo Z M, Sun Y B, Geng J C, et al. Multiple Kernel Classification algorithm for Hyperspectral Images embedded in Spectrum-null graphs[J]. Minicomputer System, 2008,39(11):2545-2550. ]

[44]
Varma M, Babu B R. More generality in efficient multiple kernel learning[C]. Proceedings of the 26th Annual International Conference on Machine Learning , 2009: 1065-1072.

[45]
Xu Z, Jin R, Yang H, et al. Simple and efficient multiple kernel learning by group lasso[C]. ICML. 2010: 1175-1182.

[46]
Liu T, Gu Y, Jia X, et al. Class-specific sparse multiple kernel learning for spectral-spatial hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016,54(12):7351-7365.

DOI

[47]
Cristianini N, Shawe-Taylor J, Elisseeff A, et al. On kernel-target alignment[C]. Advances in neural information processing systems, 2002: 367-373.

[48]
王庆超, 付光远, 汪洪桥, 等. 多核融合多尺度特征的高光谱影像地物分类[J]. 光学精密工程, 2018,26(4):980-988.

[ Wang Q C, Fu G Y, Wang H Q, et al. Classification of Hyperspectral Features with multiple learning Fusion and Multi-scale Characteristics[J]. Optical Precision Engineering, 2016,26(4):980-988. ]

[49]
Liu Y, Liao S, Hou Y. Learning kernels with upper bounds of leave-one-out error[C]. Proceedings of the 20th ACM international conference on Information and knowledge management, 2011: 2205-2208.

[50]
晁拴社, 楚恒, 王兴. 高光谱图像数据的多尺度多核SVM分类[J]. 计算机与现代化, 2016(2):11-14,20.

[ Chao S S, Chu H, Wang X. Multi-scale multiple kernel SVM classification for hyperspectral imagery data[J]. Computer and Modernization, 2016(2):11-14,20. ]

[51]
晁拴社, 楚恒. 基于稀疏MK-LSSVM的高光谱图像不平衡分类[J]. 城市勘测, 2016(2):69-73.

[ Chao S S, Chu H. The imbalanced hyperspectral image classification based on sparse MK-LSSVM[J]. Urban Geotechnical Investigation & Surveying, 2016(2):69-73. ]

[52]
Gu Y, Wang Q, Wang H, et al. Multiple kernel learning via low-rank nonnegative matrix factorization for classification of hyperspectral imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015,8(6):2739-2751.

DOI

[53]
Wang L, Hao S, Wang Q, et al. A multiple-mapping kernel for hyperspectral image classification[J]. Geoence and Remote Sensing Letters, IEEE, 2015,12(5):978-982.

[54]
陈允杰, 马辰阳, 孙乐, 等. 基于边缘修正的高光谱图像超像素空谱核分类方法[J]. 电子学报, 2019,47(1):73-81.

[ Chen Y J, Ma C Y, Sun L, et al. A new method based on edge correction for hyperspectral images is proposed[J]. Electronic Journals, 2019,47(1):73-81. ]

[55]
Wang Y, Gu Y, Gao G, et al. Hyperspectral image classification with multiple kernel Boosting algorithm[C]. 2014 IEEE International Conference on Image Processing (ICIP), IEEE, 2014: 5047-5051.

[56]
Li F, Lu H, Zhang P. An innovative multi-kernel learning algorithm for hyperspectral classification[J]. Computers & Electrical Engineering, 2019,79:106456.

[57]
钮宇斌, 王斌. 一种新的用于高光谱图像小目标探测的目标光谱学习算法[J]. 红外与毫米波学报, 2017,36(4):471-480.

[ Niu Y B, Wang B. A novel target spectrum learning algorithm for small target detection in hyperspectral imagery[J]. Journal of Infrared and Millimeter Waves, 2017,36(4):471-480. ]

[58]
任守纲, 万升, 顾兴健, 等. 基于多尺度空谱鉴别特征的高光谱图像分类[J]. 计算机科学, 2018,45(12):243-250.

[ Ren S G, Wan S, Gu X J, et al. Hyperspectral image classification based on multi-scale discriminative spatial-spectral features[J]. Computer Science, 2018,45(12):243-250. ]

[59]
张婧, 袁细国. 基于小样本学习的高光谱遥感图像分类算法[J]. 聊城大学学报(自然科学版), 2020,33(6):1-11.

[ Zhang J, Yuan X G. HSI classification algorithm based on few-shot learning[J]. Journal of Liaocheng University (Natural Science Edition), 2020,33(6):1-11. ]

[60]
Li L, Sun C, Lin L, et al. A dual-kernel spectral-spatial classification approach for hyperspectral images based on Mahalanobis distance metric learning[J]. Information Sciences, 2018,429:260-283.

DOI

[61]
万震. 基于深度学习的多源遥感数据融合分类方法研究[D]. 重庆:重庆大学, 2019.

[ Wan Z. Study on multi-source remote sensing Data Fusion Classification Method based on Deep learning[D]. Chongqing: Chongqing University, 2019. ]

[63]
职露, 余旭初, 邹滨, 等. 多层级二值模式的高光谱影像空-谱分类[J]. 武汉大学学报·信息科学版, 2019,44(11):1659-1666.

[ Zhi L, Yu X C, Zou B, et al. A multi-layer binary pattern based method for hyperspectral imagery classification using combined spatial-spectral characteristics[J]. Geomatics and Information Science of Wuhan University, 2019,44(11):1659-1666. ]

Options
文章导航

/

〈 〉