EN中文

地球信息科学学报 >

2021 , Vol. 23 >Issue 3: 505 - 513

DOI: https://doi.org/10.12082/dqxxkx.2021.200292

遥感科学与应用技术

基于线段检测算法的倾斜摄影直角像控点目标检测方法

  • 许承权 , 1, * ,
  • 柳庆威 2
展开
  • 1.闽江学院海洋学院,福州 350108
  • 2.中国地质大学（武汉）地理与信息工程学院,武汉 430074

许承权（1980- ）,男,福建莆田人,博士,副教授,主要从GNSS精密定位研究。E-mail:

收稿日期: 2020-06-08

  要求修回日期: 2020-09-26

  网络出版日期: 2021-05-25

基金资助

国家自然科学基金项目(41404008)

福建省自然科学基金项目(2020J01834)

版权

版权所有，未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
收起

Detection of Tilted Aerial Photography Right-Angled Image Control Points Target based on LSD Algorithm

  • XU Chengquan , 1, * ,
  • LIU Qingwei 2
Expand
  • 1. Ocean College of Minjiang University, Fuzhou 350108, China
  • 2. College of Information Engineering, China University of Geosciences, Wuhan 430074, China
*XU Chengquan, E-mail:

Received date: 2020-06-08

  Request revised date: 2020-09-26

  Online published: 2021-05-25

Supported by

Natural Science Foundation of China(41404008)

Natural Science Foundation of Fujian Province(2020J01834)

Copyright

Copyright reserved © 2021
Fold

摘要

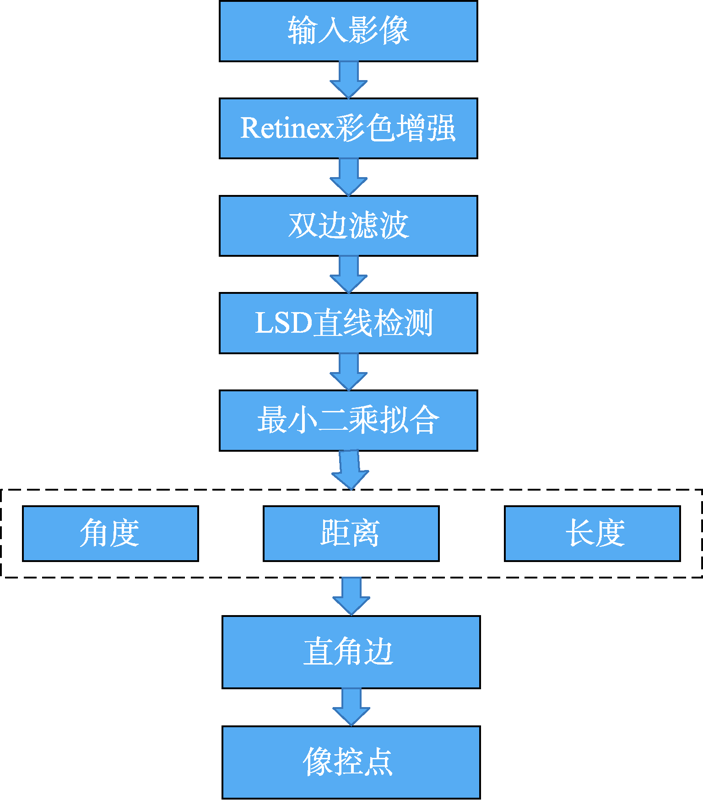
针对航空摄影测量中空三加密时数据内业精校正的人工刺点效率低下,误差较大等问题,本文提出了一种基于线段检测（Line Segment Detector,LSD）算法的直角像控点目标检测方法。该方法首先通过Retinex算法增强影像彩色信息;再对影像进行双边滤波,在去除噪声的同时能很好的保留边缘信息;然后使用LSD算法提取线段,并结合最小二乘拟合将线段进行合并;经角度、距离和长度信息筛选出最外沿直角边,最后相交得到直角像控点。采用大疆无人机拍摄的“L”形像控点80景影像,“X”形像控点69景影像进行实验,结果表明,本文算法在复杂背景下的直角像控点检测中具有较高的准确率和精度,整体像控点提取准确率达到93.75%,像控点定位精度可以到2.37个像素,在复杂背景和目标失真的情况下依然能保持很高的准确率,定位精度明显优于人工刺点,相对于Radon和PPHT算法,本文算法的像控点组检测准确率明显提高,表明其检测精度受拍摄角度的影响较小。

关键词： 倾斜摄影; LSD直线检测; Retinex彩色增强; 直角像控点检测; 像控点; 空中三角测量; 目标检测; 双边滤波

本文引用格式

许承权 , 柳庆威 . 基于线段检测算法的倾斜摄影直角像控点目标检测方法[J]. 地球信息科学学报, 2021 , 23(3) : 505 -513 . DOI: 10.12082/dqxxkx.2021.200292

Abstract

Aiming at the problems of low accuracy and large error in artificial prick points during the internal work's precise correction of the aerial triangulation data during aerial photogrammetry, we propose a method in this paper for detecting the right-angled edge control points based on the LSD algorithm. First, the image is bilateral filtered to remove noise while preserving edge information and image color information enhanced by Retinex algorithm. Then, the right-angled edges of the image control point are extracted by LSD line detection, and the outermost right-angled edge is filtered by the angle, distance, and length information. Finally, the right-angled image control points are obtained through the intersection. We tested our method using 80 images of "L" image control points and 69 images of "X" image control points taken by Dajiang UAV. Results show that this method can get accurate pixel coordinates of image control points, and maintain a high accuracy in cases with complex background and target distortion. The overall image control point extraction accuracy rate was 93.75%, and the image control point positioning accuracy reached 2.3 pixels, which significantly overcame the artificial puncture points. Compared with Radon and PPHT algorithms, the accuracy of the image control point group detection is significantly improved in our results, which indicates a higher detection accuracy with less influence from the shooting angle.

Key words： aerial photography; LSD line detection; Retinex color enhancement; right-angled image control points detection; image control point; aerial triangulation; target detection; Bilateral filtering

1 引言

近年来,随着无人机技术的快速发展,倾斜摄影测量技术得到了广泛的应用[1]。倾斜摄影测量通过多台传感器从多角度进行数据采集,颠覆了传统航空摄影只从正摄角度采集影像的方式,其所获得的三维数据可以真实反映地物的外观和坐标等属性[2]。目前,无人机倾斜摄影三维建模技术已经大量应用于生产实践,在数字城市一体化建设中发挥着越来越重要的作用[3]。
倾斜摄影在进行航拍工作时,常需要布置地面像控点来对后期数据进行精校正,像控点的精度和数量直接影响了空三加密处理精度,从而影响三维模型的建模精度。外业通过GNSS采集已获得像控点地面精确坐标;然而内业仍然使用传统人工刺点的方式,易引入人为误差且效率低下,若刺点精度不合格会造成返工,从而导致工期延长,工程成本增加,难以满足高精度三维快速建模的需求。因此,研究像控点自动检测算法具有重要的实践意义。
为了在影像中方便识别地面像控点,一般由地面人员在空旷平坦地区绘制成“L”形或“X”形,在直角点处放置GNSS测量仪获取实际坐标,然后在影像中获取对应直角点的像素坐标。因此,在角点检测中直角点检测是一个重要且基础的研究问题[4]。当前对于角点的检测研究已开展了不少工作,主要可以分为三大类：
（1）基于模板特征的检测方法。主要有Harris角点[5],SUSAN角点[6]和基于尺度不变特征变换的SIFT角点[7]等。对于直角检测,基于USAN区域,构造一种arc圆弧模板,综合Susan角检测和Harris角检测的嵌套方法以实现直角点检测,但是该算法并不适用于实际自然影像[8]。
（2）基于边缘特征的检测方法。这类算法最早由Freeman[9]提出,即先对边缘轮廓进行Freeman链码,再根据链码的改变规则来判定角点[10]。紧接着,Mokhtarian和Suomela提出了曲率尺度空间角点检测算法CSS(Curvature Scale Space),即在多尺度下对边缘影像跟踪定位以确定角点位置[11]。有学者还对CSS算法进行了改进[12,13]。对于此类方法,二值边缘提取的结果在很大程度上会影响角点检测。
（3）基于直线特征的检测方法。在直线提取算法中,比较经典的有Hough变换(HT)[14]、Radon变换(RH)[15]和自动化程度较高的Line Segment Detector(LSD)变换[16],以及改进的fast Hough transform(FHT)[17],Progressive Probabilistic Hough Transform(PPHT)[18]。但Hough和Radon变换对边缘检测结果依赖性强,容易受噪声点的干扰,需要手动设置阈值,且整体运行效率不高。
综上所述,因线段检测（Line Segment Detector,LSD）变换无需参数调整且不受边缘提取结果的影响而具有广泛适用性,因此,本文结合直角的特点,提出了基于LSD的倾斜摄影直角相控点自动检测算法,以提高内业刺点效率。

2 研究方法

2.1 技术路线

针对直角相控点的特点,本文方法主要包括3个部分：影像预处理、LSD线段检测以及基于阈值的直角边筛选与相交,主要技术路线如图1所示。
图1 LSD算法流程

Fig. 1 LSD algorithm flowchart

在影像预处理阶段,因本文实验中的像控点是红色油漆绘制的地面标志点,且部分实验样本处于建筑物阴影下,为了增强目标与背景的对比度,因此,采用Retinex彩色增强[19],突出目标信息与恢复颜色信息。此外,由于常用滤波方法易造成像控点边缘信息丢失,因此,本文在前一步基础上采用双边滤波算法,该算法可在去除噪声的同时,能有效的保留边缘信息,便于后续直线检测。紧接着,基于LSD算法对线段进行检测,能获得包含直角边在内的多数线段,由于LSD算法区域生长的不稳定性,使得一条直线容易被检测成多条线段,需采用最小二乘拟合合并,最后通过长度阈值、角度阈值和距离阈值约束筛选出两条直角边,将直角边相交即可得像控点的精确坐标。本文采用的相关研究算法如下。

2.2 Retinex彩色增强

Retinex是Ediwn Land于1963年提出的关于人体视觉感知的生物学理论[19],其名称是由视网膜(Retina)和皮层(Cortex)结合构成。Retinex理论认为颜色恒常性只由物体对红、绿和蓝光线的反射能力决定,与入射强度无关,其原理如图2所示。
图2 Retinex原理[19]

Fig. 2 Retinexschematic[19]

该理论的基本假设为一幅图像是由亮度图像和反射图像构成,Retinex算法不同于传统图像增强算法只能增强某一类特征,它可以在动态范围压缩、边缘增强和颜色恒常之间达到平衡,可对各类图像进行自适应增强。主要模型有以下3种。
（1）Single-ScaleRetinex(SSR)
根据Retinex理论可建立如下模型：
I x , y = L x , y ∙ R x , y
I x , y 表示观察到的反射图像信息, L x , y 是入射光信息, R x , y 是物质的反射特性,转换到对数域中可得：
r x , y = log R x , y = log I x , y L x , y = log I x , y - log L x , y = log I x , y - log I x , y * F x , y
式中： r x , y 是输出图像信息; * 为卷积运算; F x , y 是中心环绕函数,常用一个高斯卷积函 数表示：
F x , y = λ e - x 2 + y 2 c 2
式中： c 是高斯环绕尺度; λ 是常量矩阵,它使得：
∬ F x , y dxdy = 1
（2）Multi-Scale Retinex(MSR)
多尺度Retinex算法(MSR)是对单尺度算法的加权平均,如下式所示：
r x , y = ∑ k K w k log I x , y - log I x , y × F k x , y
式中： K 为尺度个数; w k 是各尺度所占权重;一般 K 取值为3;则 w k = 1 / 3 ,同时兼有高、中、低3个尺度,能保证在完成动态范围压缩的同时,保持图像色感。
（3）Multi-Scale Retinex with Color Restoration(MSRCR)
MSRCR是在MSR算法的基础上加上了彩色恢复因子 C ,降低了色彩失真的影响,如式（6）所示。
R MSRC R i x , y = C i x , y R MS R i x , y
其中：
C i x , y = f I i ' x , y = f I i x , y ∑ i = 1 S I i x , y = β log α I i ' x , y = β log α I i ' x , y - log ∑ i = 1 S I i x , y
式中： C i x , y 为色彩空间的第 i 个波段的彩色恢复因子; f 是颜色空间的映射函数; S 是波段总数; β 为增益常数; α 控制非线性强度。MSRCR通过控制彩色恢复因子来调节原始影像各波段的权值,使得图像色彩增强效果更符合人眼视网膜观测下的真实场景。

2.3 双边滤波

双边滤波是一种为解决边缘模糊而产生的非线性滤波器。它是在高斯滤波的基础上,根据辐射差异给予不同的权重,在像素值变化较大的区域,辐射差异权重差异变大,使得在去除噪声的同时,能较好地保留边缘信息。双边滤波公式如下：
B F p = 1 W p ∑ G σ s | p - q | G σ r I p - I q I q
W p = ∑ G σ s | p - q | G σ r I p - I q
G σ s | p - q | = e - x - u 2 + y - v 2 2 σ s 2
G σ r I p - I q = e - I p - I q 2 2 σ r 2
式中：图像I中坐标点p=(x, y)的灰度值是 I p ; I q 是点q=(u, v)点的灰度值;q属于中心像素p的邻域集合S; B F p 是滤波后输出p点灰度; W p 是归一化系数; G σ s 是空域权重; G σ r 是辐射差异权重; σ s 和 σ r 分别是2个高斯函数的标准差; σ s 确定了双边滤波函数作用的空间范围; σ r 的设置影响滤波函数处理的细节。

2.4 基于LSD的直线检测

Hough变换是直线提取的经典算法,但是该算法基于概率密度模型,容易受到噪声点干扰,且没有结合方向信息,导致适用性有限,因此本文采用Rafael Grompone于2010年提出的一种线段检测器算法[16],Grompone在文献[20]算法上进行改进,并融合了Helmholtz原理[21],实验表明该算法能够在线性时间内得到亚像素级精度的检测结果,该算法主要分为以下3步。
2.4.1 生成线支撑区域
在该算法中,首先要了解2个基本概念：图像梯度和基准线（图3）。LSD算法首先计算图像中每个像素的基准线角度,生成一个基准线场。为减少计算量对梯度值进行伪排序,从梯度最大值作为种子点,根据八方向区域生长算法将所有基准线方向相同的相邻像素合并成为线支撑区域,如图4所示。
图3 图像梯度和基准线

Fig. 3 Image gradient and gradient angle

图4 线段支持域

Fig. 4 Image gradient and gradient angle

2.4.2 区域矩形近似
将2.4.1节中生成的每一个线支撑区域用矩形来拟合,可以把线性支撑区域看作刚体,线段支持域质心用来表示矩形的中心,第一惯性轴用来表示矩形的主方向,像素点梯度大小用作该点的质量,矩形的长度和宽度为包含整个区域的最小外接矩形（图5）,该矩形作为2.4.3节线段验证的基础。
图5 线段支撑区域矩形近似

Fig. 5 Rectangular approximation of the line segment support region

2.4.3 线段验证
LSD算法基于Helmholtz原则[21],即在完美噪声图像中不应该检测到目标,假设在一个基准线方向随机且独立服从平均分布在 0,2 π 相位空间的相对图像模型,通过比较观察图中对齐点所占比例与相对模型中对齐点比例大小的概率,来判断矩形是否为真实直线并定义错误警报数Number of False Alarms (NFA)如下：
NFA r , i = NM 5 / 2 γ ∙ B n r , k r , i , p
式中：N和M分别是图像长宽;n为矩形的像素的总数;k为p-aligned点数;P是相对模型中矩形内像素对齐的概率;r是某个矩形;i是某个图像。当NFA小于阈值e时,矩形被判断为线段。
具体实现步骤如下：
（1）通过高斯降采样进行尺度缩放,减弱消除图像锯齿效应;
（2）计算梯度和梯度角;
（3）将梯度值均分成1024个等级进行伪排序,减少时间复杂度;
（4）梯度小于阈值像素不参与线性支撑区域和矩形的构建;
（5）使用最大梯度值等级中的像素作为种子点,八方向邻域生长,当未使用像素的梯度角和区域角的夹角小于角度容忍度时添加到线支撑区域,并更新区域角;
（6）每一个线段支撑区域对应一个近似矩形;
（7）计算每个矩形的NFA值,当NFA小于阈值e时,判断为候选直线段;
（8）计算矩形内梯度角与区域角相等的点密度,密度小于阈值则分割成2个更小的矩形;
（9）修改矩形参数改善NFA值。

2.5 直线合并与筛选

在LSD算法检测中,只有线支撑区域的分割,而缺少线支撑区域的合并。这样的结果导致在很多实际应用中,人眼能识别的完整直线边界容易被分割成多条直线段,需要将检测到的直线段进行合并。因此,本文根据直线段检测结果,设置距离阈值和斜率阈值 th r d 和 th r θ ,只有满足阈值的两条线段才能被合并成一条直线段,如图6所示。
图6 直线合并示意

Fig. 6 Straight line merging

取 d min = d AC , d BC , d AD , d BD ,2条直线的夹角为 α ,当满足 d min < th r d 且 α < th r θ 时,则将2条直线段进行最小二乘拟合。
设拟合直线方程为：
y = ax + b
根据最小二乘原理求解即可得拟合直线方程的系数a和b。
在进行LSD线段提取后可得到大量包含目标像控点直角边在内的线段,但部分直角边因遮挡或边界模糊导致提取不完整,为了只保留所需两条直角边,根据像控点特征先验信息和实验统计,保留长度在实际平均直角边长度的[1/3, 4/3]之内的线段,本文实验像控点平均直角边在30个像素左右。因为人工绘制像控点误差,保留夹角大致在 90 ± 5 ° 范围内的线段组,此角度范围满足大多数像控点直角边的相交夹角。对于“L”形像控点,可再根据邻接关系,两直角边的交点与两直角边中心距离应在实际平均直角边长度的[1/3, 1]之内,“X”形像控点则保证两直角边的交点与两直角边中心距离在实际平均直角边长度的1/3以内,如图7所示。
图7 长度、距离和角度阈值示意

注：红色代表像控点,蓝色线段表示提取到的线段。

Fig. 7 Sketch of length, distance and angle threshold

图7中,长度阈值是对线段长度的约束;距离阈值是对一组相交线段的中心点到交点的距离约束;角度阈值是相交线段夹角的约束,通过这3条约束可以去除大部分线段,得到最终的2条直角边线段。

2.6 精度评价

为了评价本文算法的精度,设计了3个指标如下：
像控点检测准确率：
P all = [ Na _ successNa ]
式中： N a _ success 为检测成功像控点数; N a 表示检测像控点总数。
定位精度 :
P acc = ∑ i = 1 n p x i , y i ' - p x i , y i 2 n
式中： n 是检测像控点总数; p x i , y i ' 为算法定位的像控点像素坐标; p x i , y i 为实际像控点精确像素坐标。
像控点组检测准确率：
P group = N g _ success N g
式中： N g _ success 为检测成功像控点组数; N a 表示检测像控点组总数,若所有不同角度拍摄的同一个像控点全部检测成功,则表示该组像控点检测成功。

3 结果与分析

为了验证本文直角边像控点检测算法的性能,采用大疆无人机拍摄的莆田市某地区的多组无人机像控点影像进行实验,其中“L”形像控点共有80景影像,包含了22组像控点,“X”形像控点共有69景影像,包含了19组像控点,平均每个像控点又有从不同角度拍摄的3~4景影像。先人工裁剪出包含复杂背景的像控点图像,在此基础上再进行精确的像控点像素坐标定位。实验的系统配置为：Intel(R) Core(TM) i5-4210H CPU@3.00GHz,8 GB内存,所有实验都是在Win10系统下,以Visual Studio 2013为开发环境。
分别采用3种算法进行彩色增强对比结果（图8）,可以看出各算法均恢复了阴影图像对比度,亮度和彩色信息得到了改善,但是使用SSR和MSR算法,会发现细节保持不理想,图像清晰度不高,边缘信息缺失严重。而MSRCR算法的结果色调恢复自然,清晰度高细节明显,虽然引入了部分白噪声,但是并不影响线段的提取,且双边滤波可平滑掉部分白噪声,因此本文采用MSRCR算法进行图像增强。
图8 像控点增强算法对比

Fig. 8 Comparison of image control point zenhancement algorithms

通过前面的2.3节分析可知, σ s 和 σ r 的取值将会影响双边滤波的效果,本文参考文献[22]-[24]的设置,取 σ s = max Wid th , Height / 16 , σ r 设置为图像动态范围的10%。当窗口内的灰度变化低于 σ r 时,辐射差异权重接近1,双边滤波器对窗口进行平滑模糊;当窗口内的灰度变化高于 σ r 时,辐射差异权重变化较大,双边滤波器保留细节。图9是双边滤波与高斯滤波的对比结果,可以看出双边滤波能在平滑图像的同时保持边缘锐化信息。
图9 双边滤波与高斯滤波对比结果

Fig. 9 Comparison results of bilateral filtering and Gaussian filtering

在前面增强与锐化的基础上,采用本文的LSD检测算法与形态学处理后的传统Radon变换和累计概率霍夫变换PPHT的结果进行对比,效果如图10所示,检测精度如表1所示。
图10 像控点提取结果对比

Fig. 10 Comparison of image control point extraction results

表1 像控点检测精度对比

Tab. 1 comparison of detection accuracy of image control points (%)

Pall Pacc Pgroup
形态学+Radon 44.30 10.33 17.07
形态学+PPHT 61.07 3.17 46.34
本文方法 93.96 2.25 82.93
图10中,蓝色直线表示提取的直角边,没有绘制则表示未提取到直角边,当且仅当提取到像控点的2条直角边时,则表明提取成功。从图10中可以看出,当背景单一、图像前景和背景差异明显时,Radon和PPHT算法都能够较好的提取到像控点坐标;但Radon变换易受噪声或者其他边缘提取的影响,整体定位性能最弱,且定位精度容易偏移,如图10编号4图像a中Radon变换即使定位到了“X”形像控点中心,但却出现了偏移误差;而对于光照不均的情况,本文算法可以保持较好性能,如图10编号5、6和8图像中彩色增强可以去除光照不均的影响,背景单一时PPHT也可以定位到像控点,但 Radon变换仍会受其他边缘的影响;而对于边缘模糊的情况,甚至像控点部分被遮挡或者损坏,部分边缘信息丢失,本文方法通过最小二乘拟合,结合已有的直线段方向,可以恢复像控点直角边信息,准确的提取出像控点,如图10编号9-11图像;在图10编号12-16图像中,背景包含了较多复杂地物时,a和b准确率会下降非常明显,而本文算法都能保持良好的精度,这是因为Radon和PPHT算法都比较依赖于二值边缘提取的结果,二值影像中会混入很多背景轮廓干扰目标提取。LSD算法基于局部区域生长原理,避免了全局噪声的影响,在提取像控点后再进行线段合并,无需参数调整,能去除绝大部分背景的干扰,但背景中出现规整纹理时,如图10编号16图像容易误提取到背景像素。
在生产实践中,人工刺点较为粗糙,效率低下且容易引入人为误差。在测试实验中,随机抽样选择50份生产工程中的人工刺点结果,刺点平均定位精度达10.8个像素。精度 P acc 中实际像控点的精确坐标通过ENVI软件,多名领域专业人员同时对地面像控点进行刺点,为避免随机误差,剔除异常坐标值后取平均值。表1显示了本文算法在复杂背景下的直角像控点检测中具有较高的准确率和精度,整体像控点提取准确率达到93.75%,像控点定位精度可以到2.37个像素,定位精度明显优于人工刺点,相对于其他2种算法,本文算法的像控点组检测准确率明显提高,表明其检测精度受拍摄角度的影响较小。

4 结论

像控点内业刺点精度直接影响了倾斜摄影测量空三加密处理精度,从而影响三维模型的建模精度。针对倾斜摄影像控点人工刺点精度较低且效率较低等问题,并考虑到实际工作中大部分采用直角边像控点,本文提出了基于LSD的倾斜摄影直角边像控点的检测算法,算法主要包括影像预处理、LSD线段检测以及基于阈值的直角边筛选与相交 3个部分内容。为保证算法的普适性,同步考虑到了“X”形像控点的检测问题,采用大疆无人机拍摄的22组“L”形、19组“X”形像控点影像进行实验。结果表明,本文建议的算法同时适用于常见的“L”形、X”形像控点影像,在像控点边缘模糊、损毁严重、光照不均和背景复杂的情况下,定位精度明显优于人工刺点,且检测准确率优于Radon和PPHT算法,算法鲁棒性较强。不足之处在于算法在线段拟合和筛选时基于全局遍历,时间复杂度高,下一步将对其进行优化和改进,或增加部分人工交互功能,以提高算法的效率与实用性。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
张祖勋, 张剑清. 数字摄影测量学[M]. 武汉: 武汉大学出版社, 2012.

[ Zhang Z X, Zhang J Q. Digital photogrammetry[M]. Wuhan: Wuhan University Press, 2012. ]

[2]
杨国东, 王民水. 倾斜摄影测量技术应用及展望[J]. 测绘与空间地理信息, 2016,39(1):13-15,18.

[ Yang G D, Wang M S. The tilt photographic measuration technique and expectation[J]. Geomatics & Spatial Information Technology, 2016,39(1):13-15,18. ]

[3]
张祖勋, 张剑清. 城市建模的途径与关键技术[J]. 世界科技研究与发展, 2003,25(3):23-29.

[ Zhang Z X, Zhang J Q. Solutions and core techniques of city modeling[J]. World Sci-Tech R & D, 2003,25(3):23-29. ]

[4]
郭斯羽, 卢建刚, 孔亚广. 一种基于Hough变换的直角角点检测算法[J]. 电子测量与仪器学报, 2008,22(1):43-47.

[ Guo S Y, Lu J G, Kong Y G. Right angled corner detection method based on hough transform[J]. Journal of Electronic Measurement & Instrument, 2008,22(1):43-47. ]

[5]
张见双, 张红民, 罗永涛, 等. 一种改进的Harris角点检测的图像配准方法[J]. 激光与红外, 2017,47(2):230-233.

[ Zhang J S, Zhang H M, Luo Y T, et al. Image registration method based on improved Harris corner detection algorithm[J]. Laser and Infrared, 2017,47(2):230-233. ]

[6]
吴一全, 王凯. 基于SUSAN算子和角点判别因子的目标边缘检测[J]. 中国科学院大学学报, 2016,33(1):128-134.

[ Wu Y Q, Wang K. Target edge detection based on SUSAN operator and corner discriminant factor[J]. Journal of The University of Chinese Academy of Sciences, 2016,33(1):128-134. ]

[7]
洪磊, 嵇保健, 洪峰. 一种基于亚像素角点的SIFT立体匹配算法研究[J]. 计算机技术与发展, 2016,26(1):48-52.

[ Hong L, Ji B J, Hong F. Research on a SIFT stereo matching algorithm based on Sub-pixel corners[J]. Computer Technology and Development, 2016,26(1):48-52. ]

[8]
Li J, et al. A method based on arc template to detect right-angle corner[C]. 2018 International Conference on Artificial Intelligence and Big Data. 2018: 179-184.

[9]
Freeman H, Davis L S. A corner-finding algorithm for Chain-Coded curves[C]. Computers, IEEE Transactions on 1977,C-26:297-303.

[10]
刘相湖, 王涛, 张小哲. 对Freeman链码分析的角点检测算法[J]. 计算机系统应用, 2018,27(4):202-208.

[ Liu X H, Wang T, Zhang X Z. Corner detection algorithm based on freeman code analysis[J]. Computer Systems & Applications, 2018,27(4):202-208. ]

[11]
Mokhtarian F, Suomela R. Robust image corner detection through curvature scale space[J]. Ieee Transactions on Pattern Analysis and Machine Intelligence, 1998,20(12):1376-1381.

[12]
He X C, Yung N H C. Curvature scale space corner detector with adaptive threshold and dynamic region of support[C]. International Conference on Pattern Recognition, 2004, 791-794.

[13]
张小洪, 雷明, 杨丹. 基于多尺度曲率乘积的鲁棒图像角点检测[J]. 中国图象图形学报, 2007,12(7):1270-1275.

[ Zhang X H, Lei M, Yang D. Robust image corner detection based on Multi-scale curvature product[J]. Journal of Image & Graphics, 2007,12(7):1270-1275. ]

[14]
Ballard D H. Generalizing the Hough transform to detect arbitrary shapes[J]. Pattern Recognition, 1981,13(2):111-122.

[15]
Cormack A.M. Representation of a function by its line integrals, with some radiological applications[J]. Journal of Applied Physics, 1964,35(9):2722-2727.

[16]
von Gioi R G, et al. LSD: A fast line segment detector with a false detection control[J]. Ieee Transactions on Pattern Analysis and Machine Intelligence, 2010,32(4):722-732.

PMID

[17]
Li H W, Lavin M A, Lemaster R J. Fast hough transform: A hierarchical approach[J]. Computer Vision Graphics and Image Processing, 1986,36(2-3):139-161.

[18]
Matas J, Galambos C, Kittle. Robust detection of lines using the progressive probabilistic Hough transform[J]. Computer Vision and Image Understanding, 2000,78(1):119-137.

[19]
Land E.H. Recent advances in retinex theory and some implications for cortical computations: Color vision and the natural image[J]. Proceedings of the National Academy of Sciences of the United States of America-Physical Sciences, 1983,80(16):5163-5169.

[20]
Burns J B, Hanson A R, Riseman E M. Extracting straight lines[M]. Ieee Transactions on Pattern Analysis and Machine Intelligence, 1986,8(4):425-455.

[21]
Desolneux A L, Morel J M. Meaningful Alignments[J]. International Journal of Computer Vision, 2000,40(1):7-23.

[22]
Reza A M. Realization of the Contrast Limited Adaptive Histogram Equalization (CLAHE) for Real-Time Image Enhancement[J]. Journal of Vlsi Signal Processing, 2004,38(1):35-44.

[23]
Durand F, Dorsey J. Fast bilateral filtering for the display of High-Dynamic-Range Images[J]. ACM Transactions on Graphics, 2002,21(3):257-266.

[24]
Paris S, Frédo Durand. A fast approximation of the bilateral filter using a signal processing approach[J]. International Journal of Computer Vision, 2009,81(1):24-52.

Options
文章导航

/

〈 〉