EN中文

地球信息科学学报 >

2021 , Vol. 23 >Issue 8: 1382 - 1390

DOI: https://doi.org/10.12082/dqxxkx.2021.200672

地球信息科学理论与方法

全球离散格网系统结构要素一体化编码与生成方法

  • 陈艺航 , 1 ,
  • 王金鑫 , 2, * ,
  • 曹泽宁 1 ,
  • 秦子龙 1 ,
  • 石焱 1
展开
  • 1.郑州大学水利科学与工程学院,郑州 450001
  • 2.郑州大学地球科学与技术学院,郑州 450001
* 王金鑫（1968— ）,男,河南泌阳人,博士,副教授,主要从事空间信息网格和农业遥感应用研究。E-mail:

陈艺航（1996— ）,男,河南郑州人,硕士生,主要从事全球离散格网和空间数据模型研究。E-mail:

收稿日期: 2021-11-09

  要求修回日期: 2021-01-18

  网络出版日期: 2021-10-25

基金资助

河南省科技攻关项目(212102210377)

河南省地质矿产勘查开发局2018年财政规划项目(HNGM2018103)

版权

版权所有,未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
收起

The Uniform Encoding and Generation Method of Structure Elements of Discrete Global Grid Systems

  • CHEN Yihang , 1 ,
  • WANG Jinxin , 2, * ,
  • CAO Zening 1 ,
  • QIN Zilong 1 ,
  • SHI Yan 1
Expand
  • 1. School of Water Conservancy Engineering, Zhengzhou University, Zhengzhou 450001, China
  • 2. School of Earth Science and Techology, Zhengzhou University, Zhengzhou 450001, China
* WANG Jinxin, E-mail:

Received date: 2021-11-09

  Request revised date: 2021-01-18

  Online published: 2021-10-25

Supported by

Science and Technology Project of Henan Province(212102210377)

The 2018 Financial Planning Project of Henan Provincial Bureau of Geology and Mineral Exploration and Development(HNGM2018103)

Copyright

Copyright reserved © 2021
Fold

摘要

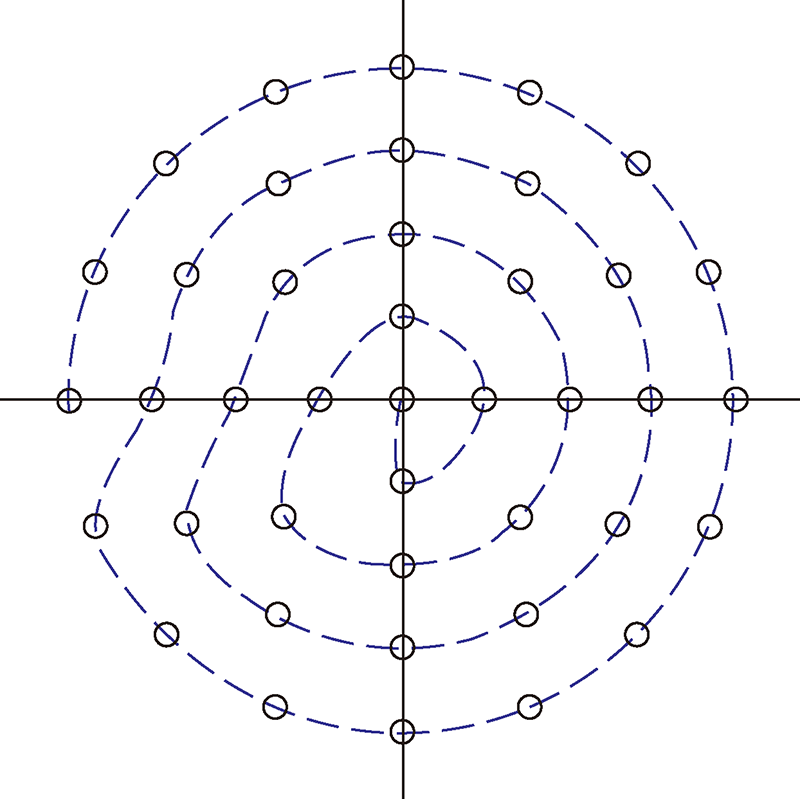
全球离散格网系统是用于构建数字地球的一种有效空间数据组织框架,其中,三角形、四边形和六边形等多种单元形状的格网已在各领域广泛应用。各具特色的格网满足了各专业领域的应用需求,但也因其格网类型的差异而阻碍了跨领域的数据共享,同时单一格网在面向多领域科学问题上存在一定的局限性,因此实现多类型离散格网系统之间的互操作功能具有重要的研究意义。不同类型格网结构要素相互转换机制的建立,是实现异构格网数据集互操作的关键。本文针对这一问题,首先,研究了三类全球离散格网系统结构要素的统一特征及格点和格元的相互关系,进一步揭示了其等差圈层的分布模式;其次,以球面四元三角网为例,建立了格点的等差圈层编码,随后,根据格点与格元的关系提出了基于格点索引的全球离散格网一体化编码与生成方法;最后,利用该方法生成了河南省地表高程的格点模型、三角形格网模型、菱形格网模型和六边形格网模型,并验证了其正确性和可行性,为全球离散格网的互操作机制提供一种新思路。

关键词： 全球离散格网; 格点; 三角形格网; 菱形格网; 六边形格网; 一体化编码; 互操作

本文引用格式

陈艺航 , 王金鑫 , 曹泽宁 , 秦子龙 , 石焱 . 全球离散格网系统结构要素一体化编码与生成方法[J]. 地球信息科学学报, 2021 , 23(8) : 1382 -1390 . DOI: 10.12082/dqxxkx.2021.200672

Abstract

As the supporting technology of the digital Earth platform, the Discrete Global Grid System is a frontier and hotspot in the field of Earth information science and has been the subject of abundant researches. It can subdivide an ellipsoid without changing its grid shape. Each subdivision level has a regular structure, so there are strict transformation relations between grids at different subdivision levels, which provides a unified expression model for the fusion of geographic data with arbitrary distribution and different scales. In Discrete Global Grid System, triangular, diamond, and hexagon grid cells are widely used. Although each grid system has its own characteristics and can meet the application needs in various professional fields, but the differences among different grid systems inevitably hinder cross-field data sharing. Different grid systems have their own advantages and disadvantages in solving different scientific problems, and their corresponding spatial operation and computational analysis also vary in complexity. Furthermore, because the data representation of a single type of grid division is limited in multi-domain scientific problems, the development of an interoperation function of a multi-type Discrete Global Grid System is of great significance. The key to realize the interoperation of heterogeneous grid data sets is to establish a mechanism for the interconversion of different types of grid structure elements. Aiming at this problem, this paper studied the unified characteristics of structural elements in three Discrete Global Grid Systems, the relationships between vertices and grids, as well as the distribution patterns of the arithmetic layer. Secondly, taking the Quaternary Triangular Mesh as an example, the arithmetic layer encoding and generation method of the vertices were established while the uniformity of the vertices was analyzed. Then, according to the relationships between the vertices and grids, this paper proposed a uniform encoding and generation method for Discrete Global Grid System based on the vertices index. Finally, using this method, we generated the vertex model, triangle grid model, diamond grid model, and hexagonal grid model of surface elevation of Henan Province. We further verified the correctness and feasibility of the methods. This study provides a theoretical basis for exchanging, unifying, and standardizing the data in different types of Discrete Global Grid Systems and a new idea for the interoperability mechanism of different Discrete Global Grid Systems.

Key words： Discrete Global Grid System; vertex; triangular grid; diamond grid; hexagon grid; uniform encoding; interoperability

1 引言

全球离散格网（Discrete Global Grid System,DGGS）是一种适合表达大区域或全球尺度地理空间的格网系统,它可以在不改变格网形状的情况下无限地细分（椭）球面,且每个细分层次都有规则的结构,保证了不同细分层次的格网之间存在严格的转换关系,为任意分布、不同尺度的地理数据融合提供了统一的表达模型[1,2,3,4]。而现代矩阵论和场论则为DGGS统一描述和表达复杂、多样的地理现象提供了可靠的理论基础[3]。此外,DGGS具有离散性、层次性和全球连续性特征,它不受地图投影类型的限制,也满足了符合计算机对离散化数据处理的要求,有望从根本上解决传统投影模型在全球时空数据管理与尺度操作上的数据裂缝、几何变形和拓扑不一致等问题[5,6]。
全球离散格网的格网单元形状主要有三角形、菱形和六边形,不同的格网单元形状给予了DGGS不同的特性,增加了其发展的多样性和可行性。同时正因为模型构建过程中的这些差异,导致了不同格网之间的互联互通存在很多困难。并且在实际运用中,单一格网单元的数据表达在面向多领域科学问题上存在局限性,因此实现多类型离散格网系统之间的互操作功能具有重要的研究意义[7]。
为了交换、统一或标准化不同框架中DGGS表示的数据,Arimi[8]首先对DGGS的索引进行了分类,然后提出了DGGS编码的通用转换映射方法。杜灵瑀[9]发现了六边形格网与三角形格网、菱形格网之间的“弱对偶”关系,从确保格心最大限度重合的角度分别实现了基于“弱对偶”的矢量线三角形、菱形格网表达算法,建立了异构格网及相应矢量线格网表达模型之间的统一转化关系。除此之外,大多数研究都以菱形的兼容性为基础,建立了菱形逻辑结构组织各种格网,Arimi[10]借助这种想法实现了适用于多种六边形格网的高效可视化算法,贲进[11]将正八面体的相邻三角形面组合为“四边形逻辑结构”建立了不同六边形格网的生成算法。赵志鹏[12]、刘坤[13]以菱形格网为基础,并将三角形和六边形格网融入,构建了面向空间数据表达和模式计算的DGGS。DGGS作为空间参考系统,格网单元需要明确标识其地理空间位置,便于空间查询,因此格网单元必须规定唯一索引,在描述格网单元的4种结构要素（格元、格点、格边和格心）中,格心和格点能够为所有格网单元提供系统和统一的空间参考点,也是对象、数据与格元建立联系的常用关联点[14,15,16]。尽管目前对于全球离散格网互操作的研究在数据转换、生成方式等方面取得了长足进展,但从诸多研究成果所提出的方案来看,多数是以不同格网单元形状的拓扑关系入手,缺乏对全球离散格网系统结构要素的一体化编码方案以及统一特征的研究。
在全球离散格网的构建过程中,格点位置及拓扑关系属于基础问题,格元形态的不同取决于格点的连接方式,因此本文尝试以格点为核心,研究格点的分布模式及格点与格元的相互关系,并提出基于格点索引的全球离散格网结构要素一体化编码及通用构建方法,以期为全球离散格网的互操作机制研究提供一种新思路。

2 等差圈层特征

正多面体离散格网表面的规则剖分,从根本上确立了格网的底层数学规律,并决定了格点的数量和分布,进而影响格点的连接方式以及格元形状与位置。以球面四元三角网（Quaternary Triangular Mesh,QTM）[17]为例,其格点、格心及格元的数量与分布模式按照拓扑关系从极点到赤道呈“等差圈层”特征,即第m行点的数量与第m+1行差值为4（极点作为特殊情况,其与相邻层之间点的数量差为3,如图1所示）,对于一个卦限差值为1。
图1 格点分布示意

Fig. 1 Schematic diagram of grid point distribution

假设内接多面体为正八面体,剖分层次为N,圈层总数为S,三角形、四边形、I类六边形格网的分布模式如表1所示。
表1 不同格网的分布模式（北半球）

Tab. 1 Distribution pattern of different grids in the Northern Hemisphere

格网单元 类型 总圈层数（L） 第m圈层上点的数量 相邻圈层点的数量的等差公式
三角形 格心 2N 8m-4 Sm-Sm-1=8
格点 2N+1 4 m Sm-Sm-1=4
菱形 格心 2N 4 m Sm-Sm-1=4
格点 2N+1 4 m Sm-Sm-1=4
六边形 格心 2N+1 4 m Sm-Sm-1=4
格点 2N 8m-4 Sm-Sm-1=8

3 全球离散格网的一体化编码构建方法

3.1 全球离散格网的格点生成方法

从形状特征来看,三角形、四边形和六边形具有固定的对应关系[18],例如：三角形与六边形互为对偶图形,2个三角形上下合并即可组成菱形。因此在点、线、面层次上,不同类型格网之间存在着有机的拓扑关系。按照格点的连接方式,不同格网的关系如表2（孔径为4）及图2[11]。经分析可知,每种格网N层和N+1层的格点和格心都可以表达另外 2种格网的格点。
表2 不同格网的格心与格点的对应关系

Tab. 2 Distribution pattern of different grids in the Northern Hemisphere

单元形状 类型 点的对应关系
三角形 菱形 六边形
三角形 格心 格点
格点 格点/格心 格心
菱形 格心 格点 格心
格点 格点 格心
六边形 格心 格点 格点
格点 格心
图2 第二层中不同类型的格点和格心之间的对应关系

Fig. 2 Diagram of corresponding relationships between vertices and centroids of different types in the second level

在全球离散格网的构建中,四面体、立方体、正八面体、正十二面体和正二十面体5种柏拉图立体格网均可模拟地球,其中正八面体的形状规则,顶点与球面经纬度坐标之间的转换比较容易。三角形由于结构简单,与菱形和六角形格网转换方便,适用性较广。综上,本文以QTM的格点作为研究基础。其生成方法主要可分为投影经线平分法和纬度平分法,投影经线平分法以0°E/W、90°E、180°E/W、90°W经线投影线（y=0,0≤x≤R;x=0,0≤y≤R;y=0,0≤x≤-R;y=0,0≤x≤-R）为基准,在平面上按 层次进行递归中点划分,最后逆投影到球面上（图3）。纬度平分法不经过投影,直接在球面等纬度小圆弧上生成规则的格点（图4）。2种方法均可以保证投影后的点全部位于球面的特征线之上（纬度）,且构建方法简单。
图3 南半球球面投影

Fig. 3 Diagram of pole projection

图4 纬度平分法

Fig. 4 Diagram of parallel splitting the lines of latitude

3.2 格点编码

格网单元的编码运算是DGGS的核心,支撑着整个系统空间数据的快速索引及应用分析的高效计算[19,20],剖分规则决定着格点的数量与分布,进而影响格点的连接方式以及格元形状与位置,是建立格点编码的理论依据。根据格点的等差圈层特征,其分布如图3、图4所示,引入圈层码作为格点编码的核心,具体表现形式为L_A_N,L指圈层,极点为0,赤道圈为2N,A指格点在第S圈层上的位置,从起点到终点依次为-2S+1——2S,N指剖分层次,并以正负号区分南北半球。如第2层剖分的北半球第2圈层编码分别为,2_-1_2;2_0_2;2_1_2;2_2_2。此种编码将层次编码与整数坐标有机融合,既保证了点的层次性,又便于编码运算,并且具有一维螺旋曲线的特征（图5）。根据编码的圈层特征,对于投影经线平分法,其与平面坐标的转换采用复数极坐标形式,方法如式（1）所示,求得平面坐标P后利用球极逆投影公式便可得到球面坐标。对于纬度平分法,其与空间坐标的转换方法为,首先根据圈层码按照式（2）计算点的Z值（北半球为ZN,南半球为ZS）,之后根据位置码计算点的X、Y值,如式（3）、式（4）所示。
P = R × L × cos π A 2 L 2 N + i × R × L × sin π A 2 L 2 N
Z N = R × sin π 2 N - L 2 N + 1 Z S = - R × sin π 2 N - L 2 N + 1
X = R × cos π 2 N - L 2 N + 1 × cos π A 2 L
Y = R × cos π 2 N - L 2 N + 1 × sin π A 2 L
式中：R为地球半径6 371 393 m;L指圈层码;A指位置码;N指剖分层级。
图5 编码的螺旋曲线

Fig. 5 Coding continuity

3.3 编码与地理坐标的转换方法

全球离散格网系统本质上属于栅格模型。与矢量模型以坐标串表示实体位置不同,栅格模型采用编码表示实体的位置。编码到传统坐标系的相互转换（即解码）是DGGS应用必须解决的核心关键问题[4]。本文所述编码可以实现与地理坐标的直接转换。纬度主要由圈层码决定,经度主要由位置码决定,根据点的生成方式不同,其计算公式有一定区别,投影经线平分法和纬度平分法分别可根据式（5）、式（6）完成编码与地理坐标的转换。
Lon = 90 | A | L Lat = 90 - 360 × arctan L 2 N π
Lon = 90 | A | L Lat = 90 × 2 N - L 2 N
式中：Lon为经度;Lat为纬度;L为圈层码;A为位置码;其中当A=0,Lon=0°E/W,0<A<L时,Lon为东经,A=L时,Lon=180°E/W,A<0时,Lon为西经;南北纬由编码的第三部分决定。

3.4 邻近搜索

格点的邻近搜索是支撑全球离散格网系统数据管理的基础[21],是实现空间聚类、索引[19]、动态扩张[22]和范围查询[23]等空间操作的核心机制。本文提出的编码,具有整数坐标编码的特征,因此邻近搜索较为简单,根据格点所处位置不同,大体可分为位于0°E/W、90°E、180°E/W、90°W上卦限边界上的点（图6（b））,以及其他位置的点（图6（a））。下面给出北半球格点的邻近搜索规则,如表3（南半球与此类似,不再赘述）。
图6 格点的6个邻近点

注：相同颜色的点表示它们位于一个圈层上。

Fig. 6 Six neighbors of the vertex

表3 邻近搜索规则

Tab. 3 Neighbor finding rules for points in the northern hemisphere

位置 Adjacent_1 Adjacent_2 Adjacent_3 Adjacent_4 Adjacent_5 Adjacent_6
非边界 (L-1,a-1,N) (L-1,a,N) (L,a+1,N) (L+1,a+1,N) (L+1,a,N) (L,a-1,N)
边界 (L-1,a,N) (L,a+1,N) (L+1,a+1,N) (L+1,a,N) (L-1,a-1,N) (L,a-1,N)

3.5 均匀性分析

全球离散格网的几何特征分析是进行地学统计等相关空间分析操作以及自适应生成多重格网的基础,且点的均匀性是衡量该模型质量优劣的重要指标[24,25]。为此本文对格点的均匀性进行了相关实验分析,选取1/8球面（北半球,东经0—90°）进行层次划分,用点与其6个邻近点（其中极点的邻近点为4个）的距离均值分布度量格点的均匀性,并根据最大距离与最小距离的比值δ表示随层级变化的距离变形情况,如式（7）、式（8）及图7、图8所示。
L ̅ = ∑ i = 1 6 R × arccos 2 cos α - α i cos β cos β i + sin β sin β i 6
δ = L ̅ min L ̅ max
式中： L ̅ 指任意一点P与其邻近6个点的距离均值;R指地球半径;α指点P的纬度角;β指点P的经度角;αi指点P第i邻近的纬度角;βi指点P第i邻近的经度角。
图7 最大距离与最小距离之比

Fig. 7 Ratio of maximum to minimum distance

图8 相邻点的距离均值分布

Fig. 8 Average distance distribution of adjacent points

通过分析可得出如下结论：① 2种方法所有格点与邻近点的最大/最小距离都随着剖分层次递增,但总体呈收敛趋势,其中纬度均分法与投影经线平分法的δ值相比较小,且趋势平稳。这说明层次越高,单元形状的变化越小。②图8分别展示了2种方法在第10及12层级的格点邻近距离均值分布情况,大致呈现出高、中、低纬度3个层次,并逐步收敛于极点,其中纬度均分法的均匀性与投影经线平分法相比较优,且纬度均分法收敛速度更快。

3.6 一体化编码

在点、线、面层次上,全球离散格网存在着有机的联系。面向不同的科学问题,不同形态的格网具有自身的优势和不足,相应的空间操作、计算分析的复杂程度也不同。因此为了满足日益复杂化、多源化的时空大数据的分析计算,集成不同格网单元的优势,本文基于格点索引提出了全球离散格网结构要素的一体化编码及生成方法。
3种格网单元的统一特征可以为一体化编码提供参考,同时也是3种格网单元交换数据的重要基础。因此根据格元的等差圈层分布模式,三角形、菱形及六边形格网的编码如图9所示,此处格元编码的结构等同于格点编码“L_A_N”。格元的邻近搜索与3.4节中所述方法一致。菱形和六边形格元编码与其格点编码的对应关系可根据邻近搜索推求,三角形格元编码与其格点编码的对应关系按照三角形的朝向分为上、下2种情况,如表4所示（表中三角形格元编码为“LT_AT_N”,格点编码为“LP_AP_N”）。在由格点编码推求其隶属格网编码时,为了避免一个格点对应多个格元导致重复性计算,因此需要根据格点与格元的数量关系,判定格点与格元的隶属问题,三角形按照一个格点控制上下2个三角形,其中极点处为特殊情况,1个点对应4个三角形;对于菱形而言,除却卦限边界以及极点处为特殊情况,其他均为一个格点控制一个菱形;三角形和六边形互为对偶图形,一个格点对应一个六边形。
图9 格网的一体化编码

Fig. 9 The integrated indexing method of grids

表4 三角形格元编码与其格点编码的对应关系

Tab. 4 The correspondence between triangular code and its grid vertices code

格点 上三角形LT_AT_N 下三角形LT_AT_N
顶点 L_2A_N L-1_(A+1)/2_N
左格点 L+1_A/2_N L_(A-1)/2_N
右格点 L+1_A/2+1_N L_(A+1)/2_N

4 全球离散格网的通用生成方法

图10分别展示了采用格点、三角形格网、菱形格网、六边形格网生成的中国河南省地表高程模型,所采用的数据为ASTER GDEM 30M[27],其中高程较低的地方为蓝色,较高的地方为绿色。其具体生成方法为：首先利用格点生成高程模型,其次根据格网与格点之间的隶属关系,得到该区域的所有格网编码,最后依次生成3种格网高程模型。在实际运用过程中可以根据需求不同生成所需要的格网模型,同时由于格网编码设计均基于格点编码,因此可以轻易的完成数据共享。
图10 河南省地表高程模型

Fig. 10 Surface elevation model of Henan Province

目前对于DGGS的编码研究已有多种方案,例如QTM的固定方向编码[21]、Quaternary编码[19],菱形格网的四分码[26],六边形格网的“四元平衡结构”编码[28]、代数编码[15]等,这对于DGGS的发展起到了关键性作用,但同时也造成了不同编码下的DGGS数据交换困难的问题。对于同一网格的编码表达虽然各异,但在相同投影下其所包含的位置信息是相同的,而本文所述的等差圈层编码方式是由格元及格点的分布模式推求得出的,因此可以借助此种编码作为其他编码之间交换的“桥梁”,具体思路为首先计算得到编码A所对应的等差圈层编码,随后将等差圈层编码转换为编码B,若编码A与B所对应的格网单元形状不同,则可借助格点编码完成转换,此种方法避免了2个DGGS之间数据迁移时重采样带来的浮点数运算,详细方法将在下一阶段的研究中进行论述。

5 结论

本文研究以QTM格点为例,建立了全球离散格网结构要素的一体化编码及生成方法,主要研究成果如下：
（1）研究了三类全球离散格网（三角形、菱形和六边形）系统结构要素的统一特征,及格点和格元的相互关系,揭示了其等差圈层的分布模式。
（2）建立了全球离散格网格点的生成方法及基于等差圈层特征的格点等差圈层编码,并对格点的均匀性进行了分析。
（3）根据格点与格网单元图形的相互关系提出了基于格点索引的全球离散格网结构要素一体化编码及生成方法,并利用该方法生成了河南省地表高程的格点模型、三角形格网模型、菱形格网模型和六边形格网模型,验证了其正确性和可行性。
综上,本文提出的全球离散格网结构要素一体化编码及生成方法,为交换、统一或标准化不同类型中DGGS表示的数据提供了理论基础,初步实现了异构格网数据集之间的互操作功能。同时由于各种剖分都具备类似的分布特征,因此可以通过等差圈层编码完成相同投影下不同编码形式或不同类型格网单元图形的DGGS的数据迁移,这对于全球离散格网系统互操作的发展和全球地理信息管理和表达具有重要意义。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Purss M B J, Peterson P R, Strobl P, et al. Datacubes: A discrete global grid systems perspective[J]. Cartographica[1] Purss M B J, Peterson P R, Strobl P, et al. Datacubes: A tdhe International Journal for Geographic Information and Geovisualization, 2019, 54(1):63-71.

[2]
Kolar J. Representation of the geographic terrain surface using global indexing[C]. Proceeding of 12th International Conference on Geoinformatics. Sweden , 2004:321-328.

[3]
赵学胜, 贲进, 孙文彬, 等. 地球剖分格网研究进展综述[J]. 测绘学报, 2016, 45(S1):1-14.

[Zhao X S, Ben J, Sun W B, et al. Overview of the research progress in the earth tessellation grid[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1):1-14. ]

[4]
Dutton Geoffrey H. A hierarchical coordinate system for geoprocessing and cartography[M]. Berlin Heidelberg: Spring-Verlag, 1999: 230.

[5]
Goodchild M F. Reimagining the history of GIS[J]. Annals of GIS, 2018, 24(1):1-8.

DOI

[6]
Bowater D, Stefanakis E. The rHEALPix discrete global grid system: Considerations for Canada[J]. Geomatica, 2018, 72(1):27-37.

DOI

[7]
Amiri A, Samavati F, Peterson P. Categorization and conversions for indexing methods of discrete global grid systems[J]. ISPRS International Journal of Geo-information, 2015, 4(1):320-336.

DOI

[8]
杜灵瑀, 贲进, 马秋禾, 等. 基于弱对偶的平面三角形格网离散线转化生成算法[J]. 武汉大学学报·信息科学版, 2020, 45(1):105-110.

[Du L Y, Ben J, MA Q H, et al. An algorithm for generating discrete line transformation of planar triangular grid based on weak duality[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1):105-110. ]

[9]
杜灵瑀, 贲进, 马秋禾, 等. 基于弱对偶的平面三角形格网离散线转化生成算法[J]. 武汉大学学报·信息科学版, 2020, 45(1):105-110.

[Du L Y, Ben J, Ma Q H, et al. An algorithm for generating discrete line transformation of planar triangular grid based on weak duality[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1):105-110. ]

[10]
Mahdavi-Amiri A, Harrison E, Samavati F. Hexagonal connectivity maps for Digital Earth[J]. International Journal of Digital Earth, 2015, 8(9):750-769.

DOI

[11]
贲进, 童晓冲, 周成虎, 等. 正八面体的六边形离散格网系统生成算法[J]. 地球信息科学学报, 2015, 17(7):789-797.

DOI

[Ben J, Tong X C, Zhou C H, et al. Construction algorithm of octahedron based hexagon grid systems[J]. Journal of Geo-information Science, 2015, 17(7):789-797. ]

[12]
赵志鹏. 面向模式计算的球面复合菱形离散格网硏究[D]. 南京:南京师范大学, 2015:11-93.

[Zhao Z P. Research on model-oriented spherical rhombus discrete grids[D]. Nanjing: Nanjing Normal University, 2015:11-93. ]

[13]
刘坤. 基于Fiber Bundle的全球离散格网通用数据模型[D]. 南京:南京师范大学, 2019:11-22.

[Liu K. A universal data model of discrete global grid system based on fiber bundle theory[D]. Nanjing: Nanjing Normal University, 2019:11-22. ]

[14]
周成虎, 欧阳, 马廷. 地理格网模型研究进展[J]. 地理科学进展, 2009, 28(5):657-662.

[Zhou C H, Ou Y, Ma T. Progresses of geographical grid systems researches[J]. Progress in Geography, 2009, 28(5):657-662. ]

[15]
Ben J, Li Y L, Zhou C H, et al. Algebraic encoding scheme for aperture 3 hexagonal discrete global grid system[J]. Science China Earth Sciences, 2018, 61(2):215-227.

DOI

[16]
Wang R, Ben J, Zhou J B, et al. Indexing mixed aperture icosahedral hexagonal discrete global grid systems[J]. ISPRS International Journal of Geo-information, 2020, 9(3):171.

DOI

[17]
Dutton G. Geodesic modelling of planetary relief[J]. Cartographica, 1984, 21(2):188-207.

DOI

[18]
白建军. 基于正八面体的四孔六边形球面格网编码及索引[J]. 遥感学报, 2011, 15(6):1125-1137.

[Bai J J. Location coding and indexing aperture 4 hexagonal discrete global grid based on octahedron[J]. Journal of Remote Sensing, 2011, 15(6):1125-1137. ]

[19]
Bartholdi J J, Goldsman P. Continuous indexing of hierarchical subdivisions of the globe[J]. International Journal of Geographical Information Science, 2001, 15(6):489-522.

DOI

[20]
Sahr K, White D, Kimerling A J. Geodesic discrete global grid systems[J]. Cartography and Geographic Information Science, 2003, 30(2):121-134.

DOI

[21]
Gold C, Mostafavi M A. Towards the global GIS[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2000, 55(3):150-163.

DOI

[22]
Lee M, Samet H. Navigating through triangle meshes implemented as linear quadtrees[J]. ACM Transactions on Graphics, 2000, 19(2):79-121.

DOI

[23]
王金鑫, 陈艺航, 曹泽宁, 等. 球面四元三角网修正方向编码的邻近搜索算法[J]. 测绘科学, 2021, 46(5):196-202.

[Wang J X, Chen Y H, Cao Z N, et al. Algorithm of neighbor finding on quaternary triangular mesh with modified direction coding[J]. Science of Surveying and Mapping, 2021, 46(5):196-202. ]

[24]
Gregory M J, Kimerling A J, White D, et al. A comparison of intercell metrics on discrete global grid systems[J]. Computers Environment and Urban Systems, 2008, 32(3):188-203.

DOI

[25]
贲进, 童晓冲, 张永生, 等. 球面等积六边形离散格网的生成算法及变形分析[J]. 地理与地理信息科学, 2006, 22(1):7-11.

[Ben J, Tong X C, Zhang Y S, et al. A generation algorithm of spherical equal -area hexagonal discrete gird and analysis of its deformation[J]. Geography and Geo-information Science, 2006, 22(1):7-11. ]

[26]
白建军, 赵学胜, 陈军. 基于线性四叉树的全球离散格网索引[J]. 武汉大学学报·信息科学版, 2005, 30(9):805-808.

[Bai J J, Zhao X S, Chen J. Indexing of discrete global grids using linear quadtree[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9):805-808. ]

[27]
地理空间数据云. (http://www.gscloud.cn/sources/accessdata/310 ).

[Geospatial Data Cloud. (http://www.gscloud.cn/sources/accessdata/310 ).]

[28]
Tong X C, Ben J, Wang Y, et al. Efficient encoding and spatial operation scheme for aperture 4 hexagonal discrete global grid system[J]. International Journal of Geographical Information Science, 2013, 27(5):898-921.

DOI

Options
文章导航

/

〈 〉