EN中文

地球信息科学学报 >

2021 , Vol. 23 >Issue 9: 1608 - 1616

DOI: https://doi.org/10.12082/dqxxkx.2021.200728

地球信息科学理论与方法

义务教育就近入学优化建模研究

  • 王玉璟 , 1, 2 ,
  • 孔云峰 , 1, *
展开
  • 1. 河南大学黄河中下游数字地理技术教育部重点实验室,开封 475000
  • 2. 河南大学计算机与信息工程学院,开封 475000
*孔云峰（1967— ）,男,河南洛阳人,教授,主要从事空间分析、空间优化等研究。E-mail:

王玉璟（1980— ）,女,河南新乡人,博士生,从事空间优化研究。E-mail:

收稿日期: 2020-12-02

  网络出版日期: 2021-11-25

基金资助

国家自然科学基金项目(41871307)

版权

版权所有,未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
收起

Optimization Modeling for Nearby School Enrollment of Compulsory Education

  • WANG Yujing , 1, 2 ,
  • KONG Yunfeng , 1, *
Expand
  • 1. Key Laboratory of Geospatial Technology for the Middle and Lower Yellow River Regions, Ministry of Education, Henan University, Kaifeng 475000, China
  • 2. College of Computer and Information Engineering, Henan University, Kaifeng 475000, China
*KONG Yunfeng, E-mail:

Received date: 2020-12-02

  Online published: 2021-11-25

Supported by

National Natural Science Foundation of China(41871307)

Copyright

Copyright reserved © 2021.
Fold

摘要

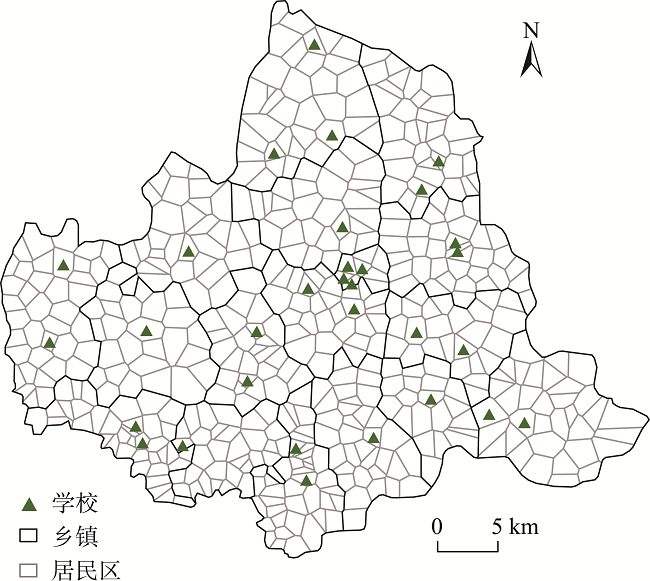
就近入学是国内外义务教育的基本共识,也是我国义务教育制度的重要组成部分。为满足就近入学需求,引入优化建模方法进行义务教育空间布局规划。首先,定义了4种就近入学场景：严格就近入学、学额限制的相对就近入学、学区连续的就近入学,以及学校布局调整下的就近入学,并构造了相关的优化模型,讨论了每个模型的优势与局限。其次,以河南省某县516个居民区和31所初级中学为例,尝试进行多个实验情景下的最优就近入学安排,并进行比较分析。案例研究发现：① 基于现有学校的布局,严格就近入学缺乏可行性;② 打破乡镇行政边界招生,能够显著地降低学生入学距离;③ 考虑学校学额限制后,学生入学距离比严格就近入学增加40.75%;④ 空间连续的学区划分方便义务教育管理,对学生入学距离影响不明显;⑤ 通过模拟少数学校扩建、新建或撤销,学校布局明显改善,学生入学距离比学区连续入学将下降31.32%。整体上,本文将空间指派、服务区划分、设施选址等优化模型用于义务教育就近入学分析,能够为基层义务教育管理提供规划决策建议,也能为其他公共服务设施规划提供参考。

关键词： 义务教育; 就近入学; 优化; 指派问题; 设施服务区问题; 区位问题; 整型线性规划; 案例研究

本文引用格式

王玉璟 , 孔云峰 . 义务教育就近入学优化建模研究[J]. 地球信息科学学报, 2021 , 23(9) : 1608 -1616 . DOI: 10.12082/dqxxkx.2021.200728

Abstract

Nearby school enrollment is one of the fundamental principles of the compulsory education in China. In this paper, the spatial optimization methods have been applied to local education planning in order to comply with the educational policy on nearby school enrollment. Four planning scenarios are defined: the nearest school enrollment, the optimal nearby school enrollment constrained by the school quotas, the optimal nearby school enrollment constrained by the school quotas and contiguous service areas, and the optimal nearby school enrollment by adjusting school locations. The Mixed Integer Linear Programming (MILP) models for the four scenarios were formulated. The optimization models were tested on a real instance in a county of Henan Province, China. There are 516 residential areas and 31 junior middle schools in the study region. All the instance models were successfully solved by the IBM ILOG CPLEX Optimizer. The case study shows that: (1) It is not feasible to assign all the students to their nearest schools because some schools will be severely overloaded. (2) The total travel distance of students can be significantly reduced by assigning some students to the schools outside their township boundary. (3) Compared with the nearest school enrollment, the total travel distance of students will increase by 40.75% when the school quotas are considered. (4) The design of contiguous service areas of schools is convenient for managing school enrollment, which has no obvious influence on the total travel distance of students. (5) The school service will be significantly improved by adjusting locations of three schools and expanding quotas of two schools in the study area, which will reduce the total travel distance of students by 31.32%. The case study indicates that the nearby school enrollment of compulsory education could be spatially designed by solving the mathematical models such as the generalized assignment problem, the facility service area problem, and the capacitated facility location problem. Both the generalized assignment problem and the facility service area problem aim to minimize the travel distance of students to existing schools, while the capacitated facility location problem is capable of searching better school locations and thus reducing the travel distance of students.

Key words： compulsory education; nearby school enrollment; optimization; assignment problem; facility service area problem; location problem; mixed integer linear programming; case study

1 引言

就近入学是国内外义务教育的基本共识,也是我国义务教育制度的重要组成部分。我国义务教育法中明确规定地方人民政府应当合理配置教育资源,促进义务教育均衡发展,保障适龄儿童、少年在户籍所在地学校就近入学。随义务教育法的贯彻实施和不断完善,我国义务教育取得了显著的成效。近几年,随我国社会经济发展和城镇化加快,城乡义务教育出现了一些新趋势：学生数量增加、学校数量减少,学生向城镇集中的现象[1]。在城镇学生学校数量增长的同时,农村学生和学校数量在减少。一方面,城镇学校学位紧张,择校现象突出;另一方面,农村学校的规模缩小、数量减少,出现了师资流失、学生入学距离增加等问题。统筹中小学校布局,落实学生就近入学,对于城市发展和乡村振兴具有重要意义。
就近入学与学校布局密切相关,属于设施区位（Location-Allocation, LA）问题,是空间优化问题的典型应用[2]。20世纪60年代,国外学者就开始了学校区位问题的相关研究[3,4,5]。由于各国家、各地区的义务教育政策存在差异和变化,国内外学者的研究内容和需要考虑的具体要求有所不同。国内学者的研究主要集中在中小学教育设施布局调整[6,7,8,9,10,11,12,13]、学校空间可达性[14,15,16]、学生入学公平性[17,18]、学区划分[19,20,21]等方面。这些研究多以运筹学理论为基础,使用LA经典模型、改进模型和GIS技术等方法,以学生入学距离、时间或费用等为主要优化目标。结合我国城乡具体情况,考虑不同需求,构建相应的LA模型进行求解,对学校的布局、可达性、公平性和学区进行分析评价,并提出规划建议。目前,相关研究有从不同角度对学校进行最优选址实现就近入学[6,7,8,9,10,11,12,13,14,15,16];也有在学校位置不变的情况下,探讨学校分配方式[17,18,19];以及满足学区管理的空间连续要求,以就近入学为原则求解学校分区[20,21]。
本文针对义务教育就近入学原则,综合考虑学生区位、学校区位、学额约束及可能的学校布局调整,定义了4种就近入学场景,以学生入学总距离最小为目标,构造相关数学模型。以河南某县为实验区,设计7种实验情景,应用相应空间模型,对义务教育就近入学的实现进行探讨。

2 义务教育就近入学优化模型

在一个教育行政管理区内,以学生所在的村或社区等居民区为基本地理单元,用点状或面状数据来表达。令集合U表示一个教育行政管理区,其中包含m个居民区,则记为U={1, 2, …, m}。每个居民区i都有一个属性Ai,表示居民区i内需要入学学生数。学校集合S={1, 2, …, K}表示该地区有K所学校。每个学校k都有一个属性Bk,表示该学校的学额。变量Dik表示居民区i与学校k之间的距离,可以采用欧氏距离、曼哈顿距离或交通网络距离。如果居民区是面状数据,可以用居民区的重心点坐标(xi, yi)计算距离。要求一个居民区只能指派给一个学校,保持居民区完整而不分割,可构建以下就近入学模型。

2.1 严格就近入学

所谓严格就近入学,其实就是不考虑学校学额,将每个地理单元按照到各学校的最短距离直接指派给相应学校。此时,所有居民区的学生入学总距离f最小,模型1如式（1）所示。
模型1： f = ∑ i∈U min ( A i D ik , ∀ k ∈ S )

2.2 学额限制的相对就近入学

现实中,学校的招生能力是有限的。需要在学额限制下,尽量满足就近入学。这是一个典型的带有容量限制的广义指派问题(Generalized Assignment Problem, GAP)。构建学额限制的相对就近入学模型,模型2如式（2）—式（5）所示。
模型2： Min f = ∑ i∈U ∑ k∈S A i D ik x ik
s.t. ∑ k∈S x ik = 1 , ∀ i ∈ U
∑ i∈U A i x ik ≤ B k , ∀ k ∈ S
x ik = 0,1 , ∀ i ∈ U , k ∈ S
函数（2）为优化目标,求最小的学生入学总距离。决策变量xik表示居民区i是否指派给学校k。约束条件（3）要求每个居民区i必须且唯一指派到某一学校。约束条件（4）就是学校学额限制,要求每一所学校入学学生总数不能超过学校招生数,否则即为超额。约束条件（5）指明xik的取值只能是0或1。

2.3 连续学区划分

学额的分配决定了学校的招生范围,也就是学区。教育政策制定和行政管理往往需要空间连续的学区。空间连续性是地理区划问题的典型特征[22],使得问题的建模和解决更加困难[23]。学区连续的就近入学受学额和空间连续性双约束。
学区内居民区空间邻接,是检验学区是否空间连续的一个依据。如果是点状居民区数据,可以转换为泰森多边形,从而获取各居民区的邻接关系。变量Cij代表居民区i与j是否邻接。居民区i的邻接单元集合表示为Ni={ j | Cij =1}。
参考文献[24],使用网络流模型来进行表示学区的空间连续性约束。构建模型3（式（6）—式（14））,在学额限制和学区连续约束下,求最小的学生入学总距离。
模型3： Min f = ∑ i∈U ∑ k∈S A i D ik x ik
s.t. ∑ k∈S x ik = 1 , ∀ i ∈ U
∑ i∈U A i x ik ≤ B k , ∀ k ∈ S
f ijk ≤ x ik m - K , ∀ i ∈ U , j ∈ N i , ∀ k ∈ S
f ijk ≤ x jk m - K , ∀ i ∈ U , j ∈ N i , ∀ k ∈ S
∑ j ∈ N i f i j k - ∑ j ∈ N i f j i k ≥ x i k , ∀ i ∈ U \ S , ∀ k ∈ S
∑ j ∈ N i f i j k - ∑ j ∈ N i f j i k ≥ K - m , ∀ i ∈ S , ∀ k ∈ S
f ijk ≥ 0 , ∀ i ∈ U , j ∀ N i , k ∈ S
x ik = 0,1 , ∀ i ∈ U , k ∈ S
约束条件（9）—（12）是基于网络流概念构造的,保证学区k的空间连续性。决策变量fijk表示学区k内居民区i到j的流量。约束条件（9）—（10）保证属于同一个学区k的2个相邻居民区i和j才可能产生流。学区k中,如果居民区i内没有学校,约束条件（11）确保其产生1个单位流量;如果居民区i中有学校,约束条件（12）保证其最多汇入m-K个单位流量。约束条件（13）指明决策变量fijk是非负整数。

2.4 学校布局调整

决定就近入学的关键因素是学校位置和学额大小。调整学校布局,例如扩大学额、迁移学校,甚至新建学校,都会影响就近入学。在现有学校和拟建学校的基础上,可以先进行学校选址,再划分学区,实现学校布局调整下的就近入学。
参考文献[8]的学校选址P-Median问题模型,构建模型4（式（15）—式（20））。该问题属于设施区位问题,用于调整学校布局。假设学校集合S有n所备选学校,包含现有学校和拟建学校,从中选择K所学校。然后,求解模型3,划分K个学区,实现相对就近入学。
模型4： M i n f = ∑ i ∈ U ∑ k ∈ S A i D i k x i k
s . t . ∑ k ∈ S x i k = 1 , ∀ i ∈ U
∑ i ∈ U A i x i k ≤ B k y k , ∀ k ∈ S
∑ k ∈ S y k = K
x ik = 0,1 , ∀ i ∈ U , k ∈ S
y k = 0,1 , ∀ k ∈ S
决策变量yk表示备选学校是否被选中。约束条件（17）保证每一所学校不超额。约束条件（18）保证从n所备选学校中选择K所学校。约束条件（20）要求yk的取值只能是0或1。需要说明的是,为了降低模型复杂度,这里没有考虑新建/扩建学校成本。

3 实证分析

3.1 实验区概况及数据来源

选择河南省某县为实验区,对县域内实行义务教育的初级中学尝试进行最优就近入学安排。该地区面积约1307 km2,人口97.6万人,17个乡镇、街道办事处,共516个行政村和社区,31所初级中学,如图1所示。学校总学额12 539人,入学总人数 10 697人。从高德地图获取居民区和学校的经纬度坐标。借助GIS工具对居民区的点状数据构造泰森多边形转换为面状数据。实验区基本数据来源于政府网站[25],学校数据通过县教育局调研获取。
图1 实验区的居民区和学校分布示意

Fig. 1 Distribution of units and schools in the study area

3.2 实验情景设置和求解方法

目前,我国县级义务教育初级中学的招生计划、建设投入、均衡发展等相关工作由县教育体育局指导规划和统筹管理,由各乡镇具体实施。本文按照乡镇、县市两种管理区域,结合4种优化模型,设置7个不同的就近入学实验情景,分别进行就近入学问题求解,如表1所示。
表1 实验情景主要特征

Tab. 1 Characteristics of the experimental scenarios

实验情景 应用区域 优化模型 主要特征
1A 乡镇域 模型1 严格就近入学
1B 县域
2A 乡镇域 模型2 学额限制+就近入学
2B 县域
3A 乡镇域 模型3 学区连续+学额限制+就近入学
3B 县域
4B 县域 模型4 调整布局+学区连续+学额限制+就近入学
前6种实验情景分别在乡镇域、县域采用模型1—3基于现有学校进行就近入学规划,其差异主要在于是否考虑学校规模、是否考虑学校服务区空间连续。
第7种实验情景在县域内使用模型4尝试进行学校空间布局调整,通过优化学校区位和规模,降低学生入学距离。通过调研考察,确定需要扩建、迁移和新建的学校,给出拟建学校位置和扩招学额,暂不考虑建校成本。将拟建学校和现有学校一起作为备选学校,先采用模型4选择学校,再调用模型3划分学区,实现就近入学。
本文使用Python语言建立实验区案例模型,调用IBM ILOG CPLEX优化器(https://www.ibm.com/analytics/cplex-optimizer)进行求解。其中,CPLEX的参数MIPGap、Timelimit和Parallel分别设置为 10-10、7200和-1,其他参数为缺省值。

3.3 计算结果

实验情景1A、1B基于就近原则,严格按照距离居民区最近的学校进行指派。不考虑其他约束,求解容易。实验情景2A、2B采用学额限制的相对就近入学模型2。实验情景2A的实验范围限制在乡镇内。而某些乡镇统计的入学学生数已经超过了学校学额。这会导致模型2无解,此时换用模型1。实验情景3A、3B使用有学额限制和学区连续约束的模型3。实现时,为了能够较快发现可行解,在模型中增加了超额惩罚函数。这6种实验情景是基于现有学校布局尝试的,学校位置和学额都保持不变。模型计算结果统计如表2所示,求解后的学区划分如图2所示。
表2 6种实验情景模型计算结果统计

Tab. 2 Modelling results for 6 experimental scenarios

应用区域 实验情景 优化模型 学生入学总距离/km 超额/人 学区连续 计算时间/s
乡镇域 1A 模型1 34 726.86 2339 否 0.07
2A 模型2 34 730.91 2334 否 1.71
3A 模型3 35 055.92 2044 是 1.92
县域 1B 模型1 31 561.06 2524 否 0.02
2B 模型2 44 421.41 0 否 24.10
3B 模型3 44 475.81 0 是 7201.89
图2 6种实验情景学区示意

Fig. 2 School districts for 6 experimental scenarios

从学生入学总距离、超额、学区连续3个方面对基于现有学校布局的6种就近入学安排进行对比分析。实验情景1A、2A、3A限制在乡镇内,按照学校位置安排就近入学,学生入学总距离差别不大（图3）。乡镇地理范围有限,学校数量少,就近入学安排容易,学区管理方便。现实中多采用这种管理方式。由于某些乡镇地形特殊,实验情景1A、2A求解后均出现明显学区不连续。这不符合政策和管理要求。双约束下的实验情景3A保证了学区连续。但是,各乡镇人口分布不均匀,乡镇学校教育资源也不均衡,实验结果显示乡村学校多数超额,县城学额明显冗余。
图3 6种实验情景学生入学总距离

Fig. 3 Total traveling distances for 6 scenarios

县域内,实验情景1B、2B、3B不受乡镇边界限制,进行就近入学安排。实验情景1B是比较理想的就近入学方式。此时,学生入学总距离最小（图3）,学区形状也最为紧凑。但是,现实是超额最多（图4）,缺乏可行性。实验情景2B增加学额限制后,解决了超额问题,但是学生入学总距离增加40.75%。学区形状也不再紧凑,甚至出现明显不连续。再增加空间连续约束,实验情景3B的学生入学总距离略微增长,学区形状较为松散,但是各个学区都保持了空间连续。
图4 6种实验情景学校超额学生数量

Fig. 4 Overload number of students for 6 scenarios

对比各模型求解结果,严格就近入学模型求解速度最快。得到了最小优化目标值,学区形状紧凑,但是学校超额严重,且不保证学区连续。学额限制的就近入学模型,在县域内起到明显作用,消除了超额。可是,学生入学总距离增加,学区形状改变较大,仍不保证学区连续。学区连续的就近入学模型,既有学额限制,又有空间连续性约束。县域范围获得的各学区明显空间连续且不超额,但各学区形状发生了很大变化,学生入学总距离最大。还需要指出,空间连续性约束使得空间模型计算更加复杂。对比上述各模型计算时间即可发现,实验情景3B的求解时间远高于其他实验情景。在2 h(7200 s)内,没有获得最优解。但发现了质量较高的可行解,与下界的差异百分比仅有0.16%。同时指出,学生入学总距离、学额、学区连续三者相互制约。学生入学总距离最少的入学安排,可能超额,可能学区不连续;满足学额且学区连续的入学方式,又可能导致优化目标值大幅增加,学区形状松散。
整体看来,实验区义务教育初级中学分布不够均匀,学校教育资源分配也不足够均衡。县城学校相对集中,学额较多,登记适龄学生少于招生数,学额冗余较多;乡村学校分布较散,学校资源和规模有限,登记适龄学生数多,学额相对不足。若严格就近入学,则整体超额现象严重。县域下实行学额限制,可以很好的解决超额问题。增加连续性约束检测,可以保证各学区的空间连续,更方便职能部门管理。实验数据和结果显示,不考虑乡镇行政管理边界,城乡统筹安排,更能满足义务教育就近入学的需求。归根结底,就近入学安排是否合理取决于学校的位置和学额,也就是学校布局。
简单来说,为了获得更好的解决方案,需要调整学校布局。新建学校、扩建学校、增加师资、扩大招生等措施,常被用来解决义务教育就近入学问题。在不考虑建校成本和师资投入的前提下,根据前期调研和实验结果,在县域内增加7所拟建学校。其中,新建4所,原校址扩建3所。现有31所学校和7所拟建学校都作为备选学校。38所备选学校位置如图5所示。
图5 实验区38所备选学校

Fig. 5 Candidate locations for school planning

县域内,实验情景4B采用模型4调整学校布局,从38所备选学校中,选择31所学校;再调用模型3实现学区连续的就近入学。实验结果统计如表3所示。
表3 学校布局调整计算结果统计

Tab. 3 Modeling results for school location planning

应用区域 实验情景 数学模型 学生入学总距离/km 超额/人 学区连续 计算时间/s
县域 4B 模型4 30 547.80 0 是 306.03
结果显示,现有学校直接保留26所,需要扩建2所、新建3所学校。与之前3种县域内的就近入学实验相比,实验情景4B调整学校布局后,保持总入学学生数不变,总学额却减少了。学生入学总距离比实验情景3B下降31.32%,甚至小于实验情景1B。各学区形状紧凑且空间连续,如图6所示。实验情景4B虽然分二步执行,但求解质量和计算时间都优于实验情景3B。由此可以看出,合理的学校布局可以降低复杂问题的求解难度。
图6 实验区学校调整布局后的学区

Fig. 6 The selected schools and their service areas

4 结论与讨论

本文探讨了义务教育就近入学优化建模方法。定义了4种就近入学场景：严格就近入学、学额限制的相对就近入学、学区连续的就近入学,以及学校布局调整下的就近入学,并构造了相关的数学模型。理论上,学额限制的就近入学使用了广义指派问题模型,学区连续的就近入学是在广义指派问题模型中加入了服务区空间连续约束,而学校布局调整使用带容量约束的设施区位问题模型。尽管这3个模型的计算复杂度很高,但得益于MIP优化器技术的快速发展,较大规模的案例能够高效求解,获得最优解或近似最优解。
以河南省某县初级中学为例,设计7种就近入学情景,模型计算结果表明：
（1）基于现有的学校布局,严格就近入学缺乏可行性,原因在于学校布局规划不够合理,严格遵循就近入学原则,部分学校的入学学生大幅度地超过其服务能力;受地理环境、人口分布、教育设施布局历史演变等因素的影响,优化调整学校布局可以改善就近入学,仍难以满足严格的就近入学。
（2）考虑学校学额限制进行最优学额分派,学生入学距离比严格就近入学增加了40.75%。入学距离大幅增加的原因在于学校布局及规模不尽合理,例如,学生密集地区附近无学校或者附近学校规模偏小,学校空间分布不均衡。出现这一情况,有必要对学校进行布局优化。
（3）学区划分方便义务教育管理,在学生指派模型中加入学区连续约束,模型计算难度大幅增加,学生入学距离略有增加,但增加幅度不明显。基于现有学校布局,考虑学额限制,无论是否要求学区连续,最优的学校服务区均出现了形状松散怪异的现象,原因在于学校布局不够合理。
（4）通过模拟少数学校扩建、新建或撤销,学校布局明显改善。案例中,扩建2所学校、调整3所学校位置,学生入学距离能够下降31.32%。这一情况说明,农村义务教育就近入学仍有潜力可挖,设施区位问题为解决这一问题提供了技术方案。另外,打破乡镇行政边界招生,能够显著地降低学生入学距离。在很多农村地区,学校招生计划按乡镇统筹。考虑到义务教育资源是在县级政府统筹,可以打破乡镇边界招生,有利于学生就近入学。在学校布局较为合理的县域,使用学额限制的指派模型,能够较好地完成就近入学政策要求;而在学校空间布局失衡的区域,通过学校布局优化调整才有可能达到就近入学政策目标。
应当注意,本文仍有一定的局限性,需要进一步深入研究。① 学生数据根据户籍人口推算,可能不够准确,也不能准确反映居住地。基于此数据的计算结果可能与实际情况有一定的偏差。本文提供了就近入学建模方法,但在实际应用中,应该进行充分的调研,获取翔实可靠的学生居住地与入学需求信息,保证模型计算结果具有实用价值。② 学校是典型的公共服务设施,与基层卫生服务、垃圾处理、社区养老等公共服务的布局规划有类似的准则,有必要开展更多的案例研究,验证本文方法的可用性及普适性。③ 可以在理论上将设施区位问题和设施服务区划分问题作为一个问题进行问题建模和求解算法设计。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
《中国农村教育发展报告2019》发布[N]. 中国民族报, 2019-02-19(003).

[ China rural education development report 2019 was released[N]. China Nationalities Daily, 2019-02-19(003). ]

[2]
Tong D Q, Murray A T. Spatial optimization in geography[J]. Annals of the Association of American Geographers, 2012, 102(6):1290-1309.

DOI

[3]
Koenigsberg E. Mathematical analysis applied to school attendance areas[J]. Socio-Economic Planning Sciences, 1968, 1(4):465-475.

DOI

[4]
Franklin A D, Koenigsberg E. Computed school assignments in a large district[J]. Operations Research, 1973, 21(2):413-426.

DOI

[5]
McKeown P, Workman B. A study in using linear programming to assign students to schools[J]. Interfaces, 1976, 6(4):96-101.

[6]
孔云峰, 王震. 县市级义务教育学校区位配置优化设计与实验[J]. 地球信息科学学报, 2012, 14(3):299-304.

DOI

[ Kong Y F, Wang Z. Optimal location-allocation for County-level compulsory school site selection using GIS and integer linear programming[J]. Journal of Geo-information Science, 2012, 14(3):299-304. ]

DOI

[7]
彭永明, 王铮. 农村中小学选址的空间运筹[J]. 地理学报, 2013, 68(10):1411-1417.

DOI

[ Peng Y M, Wang Z. Space operation of rural primary and secondary school location[J]. Acta Geographica Sinica, 2013, 68(10):1411-1417. ]

[8]
孔云峰, 王新刚, 王震. 使用MIP优化器求解p-median问题——以学校选址为例[J]. 河南大学学报(自然科学版), 2014, 44(6):725-730.

[ Kong Y F, Wang X G, Wang Z. Solving p-Median problem with MIP optimizers: A case study of school site selection[J]. Journal of Henan University (Natural Science), 2014, 44(6):725-730. ]

[9]
戴特奇, 王梁, 张宇超, 等. 农村学校撤并后规模约束对学校优化布局的影响——以北京延庆区为例[J]. 地理科学进展, 2016, 35(11):1352-1359.

DOI

[ Dai T Q, Wang L A, Zhang Y C, et al. Optimizing school distribution with constraints of school size after school consolidation in rural China: A case study of Yanqing District, Beijing City[J]. Progress in Geography, 2016, 35(11):1352-1359. ]

[10]
刘科伟, 史茹, 康智渊. 基于供需关系的城市边缘区基础教育设施布局研究——以西安市长安区韦曲街道为例[J]. 地域研究与开发, 2018, 37(5):83-88.

[ Liu K W, Shi R, Kang Z Y. Research on the layout planning method of fundamental education facility in urban fringe based on supply and demand[J]. Areal Research and Development, 2018, 37(5):83-88. ]

[11]
赵韶雅, 戴特奇, 张超, 等. 农村地区学校布局优化与土地整理——以新仁苗族乡为例[J]. 小城镇建设, 2019, 37(4):32-38.

[ Zhao S Y, Dai T Q, Zhang C, et al. School optimization and land consolidation in rural China: A case study of xinren Miao township[J]. Development of Small Cities & Towns, 2019, 37(4):32-38. ]

[12]
戴军, 苑惠丽, 马颖忆. 西部乡村基础教育设施“场势效应”评价与空间优化——以海东市蒲台乡为例[J]. 农业现代化研究, 2019, 40(4):692-701.

[ Dai J, Yuan H L, Ma Y Y. Spatial optimization of field intensity effect of rural basic education infrastructure in rural Western China: A case study of Putai Township, Haidong, Qinghai[J]. Research of Agricultural Modernization, 2019, 40(4):692-701. ]

[13]
陈玉龙, 赖志柱, 王铮. 基于交通网络的乡村中小学优化布局[J]. 地球信息科学学报, 2020, 22(5):1120-1132.

DOI

[ Chen Y L, Lai Z Z, Wang Z. Optimization of rural primary and secondary school location based on traffic network[J]. Journal of Geo-information Science, 2020, 22(5):1120-1132. ]

[14]
孔云峰, 李小建, 张雪峰. 农村中小学布局调整之空间可达性分析——以河南省巩义市初级中学为例[J]. 遥感学报, 2008, 12(5):800-809.

[ Kong Y F, Li X J, Zhang X F. Analysis of spatial accessibility for school redistricting in rural China: A case study of the secondary schools in Gongyi city, Henan Province[J]. Journal of Remote Sensing, 2008, 12(5):800-809. ]

[15]
孔云峰, 吕建平. 就近入学空间模型分析——以河南省巩义市初级中学为例[J]. 地理与地理信息科学, 2011, 27(5):87-90,98.

[ Kong Y F, Lv J P. Spatial modeling and analysis of the nearby school enrollment: A case study of the junior middle schools in Gongyi city, Henan Province[J]. Geography and Geo-information Science, 2011, 27(5):87-90,98. ]

[16]
张腾, 常军, 孙艺璇. 济南市中小学教育资源空间布局与可达性分析[J]. 测绘科学技术学报, 2019, 36(4):418-423.

[ Zhang T, Chang J, Sun Y X. Analysis of spatial distribution and accessibility of educational resources in primary and secondary schools of Jinan[J]. Journal of Geomatics Science and Technology, 2019, 36(4):418-423. ]

[17]
戴特奇, 廖聪, 胡科, 等. 公平导向的学校分配空间优化——以北京石景山区为例[J]. 地理学报, 2017, 72(8):1476-1485.

DOI

[ Dai T Q, Liao C, Hu K, et al. Secondary school allocation optimization towards equal access: A case study on Shijingshan District, Beijing[J]. Acta Geographica Sinica, 2017, 72(8):1476-1485. ]

[18]
戴特奇, 赵韶雅, 廖聪. 概率分布相似最大化的“就近—随机”入学机会公平优化——以北京市西城区为例[J]. 经济地理, 2019, 39(11):18-24.

[ Dai T Q, Zhao S Y, Liao C. Maximum spatial equality of educational opportunity based on the proximity-random system: A case study of Xicheng district, Beijing[J]. Economic Geography, 2019, 39(11):18-24. ]

[19]
孔云峰. 利用GIS与线性规划学校最优学区划分[J]. 武汉大学学报·信息科学版, 2012, 37(5):513-515.

[ Kong Y F. Optimal school allocation using GIS and linear programming[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5):513-515. ]

[20]
孔云峰, 朱艳芳, 王玉璟. 学校分区问题混合元启发算法研究[J]. 地理学报, 2017, 72(2):256-268.

DOI

[ Kong Y F, Zhu Y F, Wang Y J. A hybrid metaheuristic algorithm for the school districting problem[J]. Acta Geographica Sinica, 2017, 72(2):256-268. ]

[21]
孔云峰, 朱艳芳, 王玉璟. 整型规划求解空间连续约束学校分区问题[J]. 河南大学学报(自然科学版), 2017, 47(5):514-521.

[ Kong Y F, Zhu Y F, Wang Y J. Integer programming for the spatially-contiguity constrained school districting problem[J]. Journal of Henan University (Natural Science), 2017, 47(5):514-521. ]

[22]
Kalcsics J. Districting problems[M]//Location Science. Cham: Springer International Publishing, 2015:595-622.

[23]
Keane M. The size of the region-building problem[J]. Environment and Planning A: Economy and Space, 1975, 7(5):575-577.

DOI

[24]
Duque J C, Church R L, Middleton R S. The p-regions problem[J]. Geographical Analysis, 2011, 43(1):104-126.

DOI

[25]
开封市统计局. 开封统计年鉴-2019[EB/OL]. http://tjj.kaifeng.gov.cn/ym/xxyd/lhfw/2020/0214/1566.html 2020-02-14.

[Kaifeng Bureau of Statistics. Kaifeng statistical yearbook-2019[EB/OL]. http://tjj.kaifeng.gov.cn/ym/xxyd/lhfw/2020/0214/1566.html 2020-02-14.]

Options
文章导航

/

〈 〉