EN中文

地球信息科学学报 >

2021 , Vol. 23 >Issue 10: 1743 - 1755

DOI: https://doi.org/10.12082/dqxxkx.2021.210094

地球信息科学理论与方法

海陆岸线多尺度矢量数据获取方法及其尺度效应评估

  • 张应华 , *
展开
  • 中国科学院地理科学与资源研究所 陆地水循环及地表过程重点实验室,北京 100101

张应华（1977— ）,男,河南上蔡人,博士,主要从事自然地理学研究。E-mail:

收稿日期: 2021-02-24

  要求修回日期: 2021-04-30

  网络出版日期: 2021-12-25

基金资助

国家自然科学基金重点项目(41730749)

国家重点研发计划项目(2017YFA0604701)

版权

版权所有,未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
收起

Methods to Generate Different Scale Data of Coastline and Its Scale Effect Evaluation

  • ZHANG Yinghua , *
Expand
  • Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
* ZHANG Yinghua, E-mail:

Received date: 2021-02-24

  Request revised date: 2021-04-30

  Online published: 2021-12-25

Supported by

National Natural Science Foundation of China(41730749)

National Basic Research Program of China(2017YFA0604701)

Copyright

Copyright reserved © 2021
Fold

摘要

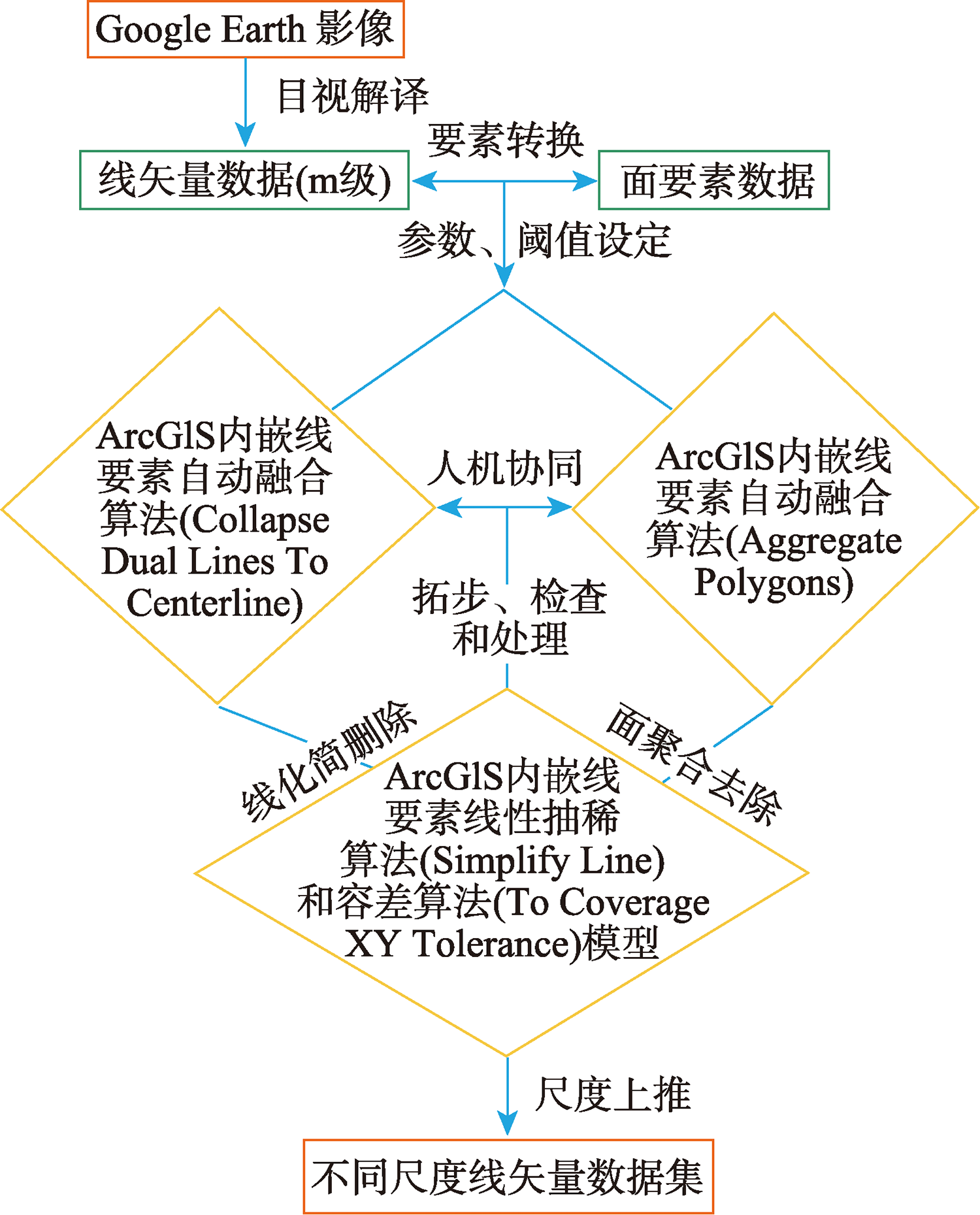
地理空间数据的多尺度表征是制图学的基石,是支撑地理数据多尺度建模分析的前提。通过对从遥感影像获取的一定尺度的地理要素矢量数据进行选择、化简、聚合或其他处理,以获取多尺度矢量数据,但多种综合处理模型和方法会导致多尺度矢量数据存在着不同程度的信息损失。本文基于地理信息系统（ArcGIS 10.6）的矢量数据制图综合功能模块,通过整合多种内嵌的自动算法和模型,结合人机协同的辅助处理方法,构建了一套系统的海陆岸线空间尺度上推方法体系,并将其应用于南美洲大陆海陆岸线矢量数据从m级空间尺度上推到30 m、250 m和1 km。基于分形理论,首次提出线矢量数据复杂度指数概念,用以表征海陆岸线地理要素特征和对比其信息精细化程度。在此基础上,对获取的30 m、250 m和1 km海陆岸线矢量数据进行信息损失评估,结果显示制图综合引起陆地和水域空间属性的改变,不同尺度表征的地理要素信息精细度存在显著差异：相比m级基础数据,30 m、250 m和1 km海陆岸线矢量数据陆地图斑数量损失分别为32.07%、90.46%和98.61%,岛屿线矢量长度信息损失分别为6.32%、49.26%和75.47%;南美洲大陆海岸线矢量数据信息精细度分别降低1.97%、25.33%和45.39%。本文构建的计算机自动综合模型和人工处理相结合的海陆岸线矢量数据空间尺度上推方法,可以实现海陆岸线矢量数据空间尺度上推获取不同尺度的线矢量数据,并描述了不同空间尺度矢量数据的信息损失状况。

关键词： 南美洲; 海岸线; 尺度; 地理信息系统; 数据融合; 算法模型; 人机协同; 矢量数据

本文引用格式

张应华 . 海陆岸线多尺度矢量数据获取方法及其尺度效应评估[J]. 地球信息科学学报, 2021 , 23(10) : 1743 -1755 . DOI: 10.12082/dqxxkx.2021.210094

Abstract

Multi-scale of geospatial data is the cornerstone of cartography, and plays a key role in supporting geographic element analysis and feature recognition. Multi-scale vector data can be generated by selecting, simplifying, aggregating, or other processing of geographic element vector data of a certain scale obtained from remote sensing images. However, a variety of comprehensive processing models and methods will also lead to various levels of information loss in multi-scale vector data. The global coastline is a geographic information element with a wide coverage area, complex curves, various island combinations, and complicated structures of land and water regions. The variation of coastline vector data attributes shows different properties at different scales. For the special coastline vector data, there are multiple influencing factors, and the relationships between them are ambiguous. Therefore, it is impossible to judge the attributes of the elements only based on the combinations of a single or a small number of characteristics of the node or line elements. Meanwhile, using a single mathematical model or algorithm for simplification, the drawing effect often has a large deviation from the actual situation, and it cannot meet the drawing needs of different regions and different scales. Thus, we used Geographic Information System (ArcGIS 10.6) technology to support the automatic comprehensive function of geospatial data mapping, integrated different embedded automatic algorithms and models, and combined human-machine collaboration to build a systematic scale-up method system to achieve different scales of coastline data. Based on fractal theory, the concept of line vector data complexity index was first proposed to characterize the coastline geographic elements and to compare the degree of declination of their information. With the m-scale coastline data interpreted by manual visual interpretation, the scale-up is used to generate coastline data on the scales of 30 m, 250 m, and 1 km, respectively. The information loss assessment was performed on the obtained 30 m, 250 m and 1 km coastline vector data, and the results showed that the mapping integration caused changes in the spatial attributes of land and water. There are significant differences in the fineness of geographic element information represented by different scales. Compared with the m-scale coastline data, the loss of the number of islands on the scales of 30 m, 250 m, and 1 km is 32.07%, 90.46%, and 98.61%, respectively, the information loss of the coastline length is 6.32%, 49.26%, and 75.47%, respectively, and the information granularity of the vector data of the coastline of South America is reduced by 1.97%, 25.33%, and 45.39%, respectively. With the processes of the up-scale of the coastline, it has an increasing trend of the median, mean of the islands area and their complexity index from the m-level to 30 m, 250 m, and 1 km scales. The scale-up method constructed in this paper to combine the computer automatic synthesis model with the artificial processing of the coastline vector data has the potential to efficiently realize the scale-up of the coastline vector data, and describe the information loss of vector data at different spatial scales.

Key words： South America; coastline; different scales; geographic information system; data fusion; algorithm model; human-machine collaboration; vector data

1 引言

随着人类活动和全球变化的加剧,受海岸带的加速开发利用和全球海平面上升等作用影响,海陆岸线变迁速率加快、复杂性加剧和生态环境恶化。不同尺度的海陆岸线数据作为一项基础性的数据支撑工作,对有关海岸带科学研究、监测管理方面具有重大的意义。国内外研究学者通过阈值法、边缘检测法、面向对象法等计算机自动解译和人工目视解译对遥感影像进行海陆岸线的提取[1]。计算机自动解译提取的海陆岸线不仅分辨率和精度受到遥感影像分辨率和计算算法局限性限制,也与人工目视解译提取的一样,存在单一尺度的缺陷。在海岸线基础数据获取方面,国内外学者针对不同数据源和利用不同方法开展了海岸线提取和空间尺度转换的研究[2,3,4],特别是近些年,人类活动和全球变化影响越来越深,海岸线全球尺度和区域尺度的研究越来越受到重视。由于海岸线数据的空间尺度效应,为了使不同尺度海岸线数据具有可比性,应用于跨尺度的海陆岸线变化检测,以及满足不同尺度（局部地区、区域和全球尺度）的科学研究和实际应用需求,海岸线数据必须经过空间数据的多尺度表示,实现不同尺度数据的聚合或有机整合。
自然科学与社会科学诸多研究中,依赖尺度的空间数据源与实际的研究问题存在观测尺度、分析尺度、应用尺度等尺度不一致性的问题,对此地学和相关学科领域众多学者针对尺度依赖的理论、方法和应用科学问题开展了广泛研究[5,6,7,8]。只有正确选择应用尺度,才能避免科学研究中错用空间尺度分析,导致研究变量之间因果关系出现偏差的错误。通过不同数据源、数据融合等获取相关的地理数据,因在一个尺度上获得的信息通常不能直接用在另一个尺度上,获取多尺度矢量空间数据就成为制约地理信息系统广泛应用的瓶颈[9]。使用不同分辨率的遥感图像通过尺度转换检测不同尺度空间数据的变化的研究,受到数据源质量问题的约束,并且生成的不同尺度的数据一致性问题很难准确的进行评估。为了弥补上述不足,如果能获得超高空间分辨率数据,则可以通过各种规模地理信息表示的地图泛化[10],进行由大比例尺向小比例尺的空间矢量数据的制图综合,得到不同分辨率的空间数据。
在地学研究中,尺度变化的空间属性意味着地理变量的属性差异,使得不同尺度空间分布函数表征或可视化表达不同,而这与所有的环境过程密切相关[11]。基于非线性科学的分形理论,因分形对空间分布特征变化、复杂程度和趋势的重要反映,分形方法用来定量表达多尺度空间数据的信息量及其复杂性,具体表现在空间尺度效应上[12,13,14]。
伴随着地理信息系统的兴盛,通过各种模型、算法,采用人机交互的方式,对地理要素进行图形交互编辑和计算机自动制图综合已成为GIS 研究的重要内容。制图综合的应用实践不乏地理要素特征选择,化简,聚合,放大或以其他方式修改要素以较小比例显示的模型、算法,包括选择和细化地理要素特征的信息熵模型[15]、层次分析法[16]、模糊识别和遗传算法[17,18],线要素化简的支持向量机[19]、卷积神经网络[20]、遗传算法[21]和许多以节点为化简单元的算法[22,23],面状要素的消除、扩大和聚集的算 法[24,25,26,27]。模型算法有力地推动了制图智能化的进程,同时大多数算法的制图效果依赖于算法的选择、参数的设置和阈值的确定,需要高度依赖人工反复修正。尽管有研究者使用国家测绘机构创建的地图或数据库作为评估标准,对不同模型和算法的制图功效进行比较,但对制图综合技术在不同实践案例中的评估仍然具有挑战性,且难以复制[10]。
全球海岸线是一个覆盖区域广阔、曲折复杂多样、海岛形状各异、水陆区域类型和结构复杂的地理信息要素,海陆属性随尺度相关的变异在不同尺度上表现出不同的性质[28]。对于特殊的线状地物海陆岸线的扩陆缩海不同尺度的化简需求,非单一的影响因素之间的模糊关系,无法依据节点或线要素弯曲的单个或少量的特征指标的组合进行取舍判断,采用统一的数学模型或算法进行描述[7,29-31],制图效果与实际情况往往存在较大偏差,无法满足不同区域、不同尺度下的制图需求。因此,本文在实际的制图综合环境中,基于最高空间分辨率数据m级海陆岸线数据,借助GIS集成各种算法的自动综合能力,通过人机协同决策机制,获取同一制图综合环境下不同尺度的海陆岸线数据的应用案例,为其他制图综合研究提供参考,避免不断试错的繁琐过程,降低集成算法工具的使用难度,同时对比分析了尺度上推过程中地理要素之间的差异及其成因,为其他科学研究制图综合技术不同应用案例的对比评估提供参考。

2 研究方法

2.1 多尺度数据获取方法

通过Google Earth最高分辨率影像目视解译获得的线矢量数据,进行面状要素转换,根据不同尺度可识别的最小图斑所设定的阈值,进行不同尺度面状要素的去除,即对岛屿图斑进行融合删除,舍去小于规定尺寸的岛屿,保持海陆岸线图形的基本特征。
依据制图综合中的的面状要素聚合方法,根据不同尺度需求,设定要素之间合并时的阈值,目的是去掉岛屿之间小于一定距离的水域,进行制图对象岛屿不同尺度级别的合并,通过ArcGIS 10.6的内嵌的制图工具（Cartography Tools） 所提供的多边形自动融合算法（Aggregate Polygons）模型,完成面状要素的自动聚合。
针对不同尺度级别,设定融合去除阈值,舍去小于规定尺寸的弯曲,保持岛屿图形的基本特征,进行海陆岸线矢量数据线段的融合删除,利用 ArcGIS 10.6内嵌的制图工具（Cartography Tools）提供的线段自动融合算法（Collapse Dual Lines to Centerline）模型,完成小于规定尺寸宽度的线矢量数据,即岛屿岸线（狭长陆地或水域）的去除。
在面状要素和线矢量数据自动算法模型应用过程中,对存在的镂空多边形和线断点进行拓步检查,结合人机协同模式,对线矢量数据自动处理过程中产生的断点进行处理。
维持海陆几何特性、几何位置和地理特征准确度基础上,针对不同尺度海岸线级别,设定对应的阈值,利用ArcGIS 10.6版内嵌的制图工具（Cartography Tools）提供的线性抽稀算法（Simplify Line）模型和转换工具（Conversion Tools ）提供的抽稀容差算法（To Coverage XY Tolerance）模型,完成海陆岸线的尺度上推。不同尺度线矢量数据获取方法如图1所示。
图1 线矢量数据尺度上推流程示意

Fig. 1 Schematic diagram of systematic scale-up method system on line vector data

2.2 不同尺度空间数据复杂性评估

基于遥感影像最高分辨率目视解译的m级线矢量数据,从统计意义上对尺度上推获得的不同线型矢量数据进行比较,通过几何要素特征和变化幅度进行不同尺度空间数据复杂性评价。考虑到线矢量数据的空间结构特征,引入分形理论中最核心的概念与内容,即Mandelbrot用分形维数（D）表征表面曲线复杂性[32]时,提出的闭合曲线的周长-面积关系的分维关系为面积（P）与周长（L）二次方成L∝P1/2的简单正比关系、面积与周长的分形维数关系为L~P1-D;基于上述分形理论,以圆形为参考标准（自然界最佳形状趋圆性,复杂度指数为1）,提出用于评估不同尺度线矢量数据空间结构特征信息变化的复杂度指数（Complexity Index,CI）,如式（1）所示。
CI = L 2 π P
该指数简洁明了且可实现ArcGIS系统自动计算,也可用以表征线要素形状的复杂性表达。

3 数据来源及处理

3.1 数据来源

海岸线提取的数据源主要有国际上的Landsat、SPOT、SAR影像和国内的高分系列卫星、IKONOS、WorldView影像等,各种数据源在分辨率、时长序列、图幅幅度、价格等方面具有不同的优点和缺陷。本研究使用了中国科学院地理科学与资源研究所全球变化科学研究数据出版系统提供的m级空间分辨率的全球海陆岸线数据集[33]。该数据集以Google Earth在2015年或前后1—2年的遥感影像为信息源,该影像具有免费、区域广、高分辨率等优点,通过计算机辅助人工目视解译生成。数据中,最小图斑（岛屿）面积分别为6 m²,数据集采用地理坐标系统,数据为线状数据.shp格式。

3.2 多尺度数据获取

为了输出空间数据结果能与其他来源数据在空间参考体系、空间尺度以及数据精度上互相匹配,避免科学研究中出现错误的空间尺度观察问题和因果关系的曲解,因此,考虑到不同学科的研究领域和研究目的,相关数据源的精度与比例尺,全球海陆岸线数据输出结果与当前国内外流行的数据集,如Landsat的30 m分辨率卫星遥感影像数据、MODIS数据集（250 m或1 km）、全球土地覆盖或地表覆盖数据集GLC2000、GLCC和UMD （1 km）等相匹配,本研究基于以下原则,如延伸入水域分别小于相应尺度（30 m、250 m和1 km）宽度的狭长陆地融合去除变为水域、延伸入陆地分别小于相应尺度（30 m、250 m和1 km）宽度的狭长水域融合去除变为陆地和分别小于相应尺度（30 m、250 m和 1 km）距离的岛屿融合合并等,数据融合过程主要包括小面积岛屿的去除、临近岛屿的合并、狭长陆地或水域的融合和尺度上推,输出结果包括30 m、250 m和1 km的3种空间尺度识别海岸线能力的海陆岸线数据集。
南美洲大陆海岸线相对于亚欧大陆和北美洲较为平直,而岛屿和海湾相对于非洲和大洋洲数量较多,综合考虑大陆海岸线、岛屿和海湾的地理要素属性,选择南美洲海陆岸线矢量数据作为应用案例。针对不同尺度海陆岸线制图综合过程中有关地理信息的要素计算,需要将数据源进行不同空间参考坐标进行预处理。针对南美洲海陆岸线需要计算长度、距离时,对数据源进行兰勃特等角圆锥投影（Lambert_Conformal_Conic）,计算面积时,对数据源进行阿尔伯斯等积圆锥投影（Albers）。同时,为了提高尺度上推计算机自动处理的准确度和效率,对线性节点非常密集（亚米级）、文件太大的南美洲海陆岸线数据集,预先进行线性节点Simplify Line抽稀（容差设置为1 m）。
通过数据预处理,在ArcGIS 10.6版本中实现海陆岸线的不同尺度制图综合,步骤如下：
（1）不同尺度小图斑岛屿的去除：进行南美洲大陆周围的岛屿岸线的线型矢量→面要素转换,计算岛屿面积,并根据岛屿图斑30 m、250 m和1 km尺度可识别距离的圆面积最大原则,分别去除面积小于706.8、49 087.4和785 398.2 m2的岛屿。
（2）小于设定距离的邻近岛屿合并。通过内嵌的自动制图工具Aggregate Polygons功能,对相互距离小于30 m、250 m和1 km的岛屿进行合并。
（3）小于设定距离岛屿边界狭长线段数据融合。进行线面要素转换,将将面状岛屿转为线矢量,对岛屿岸线沿线狭长的陆地或水域进行融合去除。通过内嵌的线段融合算法模型（Collapse Dual Lines To Centerline）功能,将狭长的线段合并成一条线然后删除,并新建GeoDatabase数据库,保存融合去除的线矢量数据,对该数据进行断点拓扑查错和修正,去除数据融合导致的悬挂线（点）,再利用Snap和Extend功能分别进行30 m、250 m和1 km距离的修正连接,尽可能的将未封闭的线要素闭合成为岛屿岸线。
（4）数据融合未能成功的岛屿筛选。有些岛屿因面积过大、形状复杂、弯曲尺寸小且密和岛屿岸线曲折系数（线路总长度/线路两端直线距离）变异大的因素,导致步骤（3）中拓扑查错和修改后仍无法形成封闭的岛屿岸线。将步骤（3）中处理后的线矢量转换为面,重复步骤（2）中进行编辑修改。按照要素选择规则,即具有相同重心（Have Their Centroid in the Source Layer Feature）、被包含（Ae within the Source Layer Feature）和相同（Are Identical to the Source Layer Feature）的原则,删除与步骤（3）中有重叠或交叉的封闭岛屿。
（5）数据融合产生小图斑的消除与合并：步 骤（3）中的线段近距离合并去除会在岛屿内部产生许多重叠的图斑和内部镂空的图斑,需要对这些图斑进行消除与合并。进行步骤（3）中的封闭岛屿线矢量→面转换,按照要素选择规则被包含（Are within the Source Layer Feature）的方法,消除被步 骤（4）所筛选出的岛屿包含的图斑;然后再对面进行拓扑查错和修改（规则为Must Not Overlap）,将岛屿内部重叠的图斑消除,最后通将面转化为线矢量进行相同的规则拓扑查错和修改,将内部镂空的图斑消除,即是将岛屿合并中产生的内嵌镂空多边形填补。对步骤（4）的岛屿按照要素选择规则共边（Share a Line Segment with the Source Layer Feature）的方法筛选,剪切复制小图斑并粘贴保存,再通过内嵌的融合算法（Merge）与步骤（3）中的小图斑进行融合合并。
（6）大陆岸线与邻近岛屿的融合。基于南美洲大陆岸线线矢量数据,按照要素选择规则测距（Are within a Distance of the Source Layer Feature）的方法,分别对距离南美洲大陆岸线小于30 m、250 m和1 km步骤（5）中的岛屿进行最初筛选;再按照要素选择规则与步骤（4）中岛屿包含（Contain the Source Layer Feature）关系方法,对岛屿进行再次筛选;然后重复步骤（3）的数据融合、悬挂线手工封闭和步 骤（5）的小图斑消除的处理;重复步骤（2）中相同的岛屿合并功能,将处理后的岛屿、最初筛选的其他岛屿和南美洲大陆合并,实现大陆与邻近岛屿融合;进行面要素→线矢量转换,并新建GeoDatabase数据库,建立数据集,保存线矢量数据。,依据拓扑规则Must Not Overlap对该数据进行拓扑查错和修正,将岛屿合并中产生的内嵌镂空多边形填补。
（7）海陆岸线数据融合。对以上步骤处理后的海陆线矢量数据,利用内嵌的融合算法（Coverage和Merge功能）,设置容差（XY Tolerance）15 m、 125 m和500 m分别进行30 m、250 m和1 km尺度上推的转换,转换后的线矢量融合形成抽稀后的线矢量数据。
（8）拓扑校验与手工处理。将线矢量→面要素→线矢量转换,进行拓扑（Must Not Overlap）查错和修改,线矢量数据分为海陆岸线和数据融合过程产生的多边形小图斑（水域或陆地）;分别将海陆线矢量和小图斑线矢量转化为面,通过共边的方法筛选出与海陆共边的小图斑,未筛选出的小图斑直接删除,然后基于制图综合的基本方法,人工判识筛选出的小图斑水域或陆地性质,分别进行消除或合并的操作;小图斑融合和消除完成后,通过相交（Intersect the Source Layer Feature）的方法,对在步骤（7）中造成的与大陆面要素共点的岛屿实行人工分离隔开;最后对线矢量,依据4项拓扑原则（Must Not Have Dangles、Must Not Self-Overlap、Must Not Self-Intersect和Must Not Intersect Or Touch Interior） 进行拓扑查错和修改,对应不同尺度去除面积小于706.8、49 087.4和785 398.2 m2的岛屿,获得最终的不同尺度海陆岸线数据集。

4 结果与分析

4.1 海陆岸线矢量数据空间尺度上推

（1）面状要素的消除、扩大和聚集
岛屿的消除与合并操作过程中,根据一般性制图规则,岛屿的最大宽度或长度均小于特定尺寸,即本研究中的30 m、250 m或1 km的应给予消除,其对应的岛屿形状最大极限面积是以这些尺寸为直径的圆,因此首先对原始数据（图2(a)）在阿尔伯斯等积圆锥投影,去除面积分别小于对应尺寸圆面积的岛屿（图2(b)）。图2(b)中本应该消除的小岛屿,如果没有去除,在进行数据融合和尺度上推过程中会产生非常多的悬挂线或共点多边形,不仅会影响到计算机自动处理速度,也会造成处理结果的严重偏差。岛屿合并过程中,会出现岛屿及其之间的水域完全合并成岛屿、合并的岛屿中间形成镂 空的水域和岛屿之间以宽度小于该尺度下（30 m、250 m或1 km）的狭长陆地相连3种情况（图2(c)中①、②和③）,后面2种情况分别需要进一步拓扑检查修正、数据融合或尺度上推的处理,分别完成内部镂空水域多边形的填补和岛屿的分离。
图2 岛屿的消除与合并结果

注：图（b)、(c)中的紫色线为红色线与蓝色线重合后的线。

Fig. 2 The results of removal and merging of coastline vector data

岛屿合并之后,内部延伸的狭长水域和外部边界延伸出的狭长陆地,其最大宽度分别小于特定尺度尺寸（30 m、250 m或1 km）的给予消除。对原始数据（图3(a)）在兰勃特等角圆锥投影下,将距离小于上述相应尺寸的2条线段融合成中心线并删除。融合消除过程中,会出现狭长陆地合并（图3(c)中①）、狭长水域合并（图3(c)中②）、中间形成镂空的水域（图3(c)中③）和岸线形成悬挂线（图3(b)中④）4种情况。前面2种情况根据融合后的线矢量数据属性值（LnType值为1）,直接批量删除处理,但同时会产生个别的悬挂线（图3(b)中④ -Ⅰ）。后面2种情况需要进一步拓扑检查修正,通过计算机自动处理完成内部镂空水域多边形的填补和悬挂点距离近的多边形连接闭合（图3(b)中④ -Ⅰ）,但悬挂点距离大于特定尺度尺寸的多边形需要通过人工处理来完成闭合（图3(b)中④ -Ⅱ）。悬挂线之间悬挂点的距离过大需要人工处理进行封闭的情况,多出现在悬挂线本身曲折系数较大和悬挂线所处岛屿复杂度较高的矢量线中。
图3 数据融合不同处理结果

Fig. 3 The different processing results of coastline vector data fusion

（2）线要素化简
数据融合利用合并双线到中心线的功能,因线矢量数据的复杂形状和特征,有时无法达到预期满意的效果[7]。本研究中海陆岸线非常复杂,重复多次合并双线功能仍无法将全部小于给定距离的双线合并成中心线,尤其是包围面积较大的大陆岸线,需要进一步将岸线线矢量数据从中间分成2部分,再重复进行数据融合,尽可能的完成双线合并中心线。
数据融合过程中如果能彻底完成狭长陆地或水域的融合消除,则可用简单的抽稀算法模型（Simplify Line）完成尺度上推的计算机自动处理操作。但是,过多次的重复合并双线到中心线功能和悬挂线的人工处理是个非常耗时、耗量的工作,特别是非常复杂的大陆岸线,其悬挂线数量多、密度大、悬挂点之间距离远,人工处理更麻烦。利用要素类转Coverage功能,实现尺度上推能避免上述数据融合的不足,可是由于该功能是以500个折点为线段进行容差计算,相比数据融合,尺度上推过程可能会造成要素类共点的缺陷。线要素经过化简处理,会出现如下7种情况（图4）：
图4 尺度上推不同处理结果

Fig. 4 The different processing results of the scale-up coastline

（1）狭长的水域转换为线（图4(b)中①）,再通过线面要素转换融合去除;
（2）水域转换为内嵌多边形（图4(b)中②）,再通过拓扑核查与修正,融合填补成陆地;
（3）狭长陆地转化为线,邻近水域转换为内嵌多边形（图4(b)中③和④）,再通过拓扑查错和修改,人工处理融合去除或修正为水域;
（4）狭长陆地经过要素转换自动融合消除（图4(b)中⑤）;
（5）距离小于融合尺度的狭长陆地转化为外延共边多边形（图4(b)中⑥）,再通过拓扑查错和修改,人工处理融合去除或修正为水域;
（6）陆地转换为2个共点多边形岛屿,通过拓扑查错和修改,进行人工处理分离（图4(c)中⑦）;
（7）狭长陆地要素转换自动融合消除,与其相连的远端陆地转换为岛（图4(d)中⑧）。

4.2 空间尺度效应对比

如图5所示,对比分析初始岛屿（封闭曲线）、数据融合后线矢量（悬挂线）和数据融合过程去除的线矢量片段（消除线）之间的复杂度和曲折系数。结果表明,面积大于100 km2的岛屿占比13%,其数据融合产生悬挂线的岛屿占比18%;复杂度指数大于5的岛屿占比5%,其数据融合产生悬挂线的岛屿占比高达42%;产生悬挂线的岛屿中,悬挂点之间的曲折线曲折系数大于10,且折线（长于融合尺度）数目多于1的线段均被消除,而悬挂点之间仅存在唯一的曲折线其曲折系数为5左右的线段也均被消除。
图5 岛屿线矢量数据特征对比

Fig. 5 Comparison of vector data features of coastlines

海陆岸线数据经过不同尺度上推,线矢量数据之间存在明显差异,尤其是在狭长陆地或水域区间,差异性更加显著。造成这种差异的主要原因是邻近岛屿的合并（图6(b)）和不同尺度下狭长水域或陆地属性的改变（图6(c)）。从尺度上来看（图6）,m 级、30 m级差别相对较小,而250 m级、1 km级差异显著。如图6(c)中所示,m级和30 m级均没有改变该区域水域的属性,仍旧是海域;250 m级由于陆地之间狭长水域的融合去除,水域变成内泻湖,大陆岸线将包含此区域;1 km级由于水域之间狭长陆地融合消除,狭长陆地属性被改变,变成水域属性;陆地、水域属性随尺度而发生转变造成海陆岸线矢量数据的差异。
图6 不同尺度海陆岸线对比

Fig. 6 Comparison of coastlines at different scales

通常情况下,遥感影像的空间分辨率与提取的相应海岸线长度密切相关,采用的空间分辨率越高,抽取的海岸线长度越长。作为自然界中不规则几何形体的海陆,不仅受固有的空间尺度效应影响,也受制图综合过程中信息损失的影响,导致不同尺度几何要素存在显著差异（表1、图7）。南美洲大陆岸线和岛屿岸线总长度随尺度的增加而减小,南美洲大陆的面积随尺度的增加而增大,而岛屿截然相反,岛屿总面积随尺度的增加而减小。造成南美洲大陆和岛屿的面积与尺度相关关系不同的原因,主要是邻近岛屿的合并和小图斑岛屿的去除。南美洲岛屿中最大岛屿的周长与面积与空间尺度的相关关系,与南美洲大陆的则完全一致,即随尺度上推,周长减小、面积增大,表明面积较大的岛屿周围的岛屿聚集度更高,导致的岛屿合并较多,虽然因尺度影响长度减小,但面积却增大。从不同尺度岛屿的数量来看,岛屿的合并和去除,造成m级和30 m尺度岛屿数量差距不大,但是与250 m和 1 km尺度上的岛屿数量相差非常悬殊。这是由于在尺度分辨率和粒度角度上,群岛主岛的周围分布的岛屿距离主岛多小于250 m的分辨率,以及整体上小于30 m分辨率的岛屿数量众多。
表1 不同尺度海陆几何要素对比

Tab. 1 Comparison of coastline geometric elements at different scales

尺度 南美洲大陆 南美洲岛屿
长度 /103 km 面积 /106 km2 CI 总数 /个 总长度 /103 km 总面积 /103 km2 最大周长 /km 最大面积 /103 km2
m级 90.17 17.493 6.08 44 484 159.69 247.15 5731.48 47.54
30 m 88.41 17.495 5.96 30 218 149.59 245.16 5693.01 47.54
250 m 67.43 17.574 4.54 4242 81.02 176.81 5036.91 47.58
1 km 49.38 17.602 3.32 620 39.16 161.81 4311.98 49.55
图7 不同尺度陆地面积分布箱型图

Fig. 7 Boxplot of island area at different scales

由表1可以看出,通过尺度上推获得的30 m、250 m和1 km尺度的线矢量数据,南美洲大陆岸线的线要素长度分别为原m 级尺度的98.05%、74.78%和54.76%,长度要素信息损失在1 km尺度上高达45.24%;面要素图斑的面积变化最大幅度仅为原m 级尺度的0.6%,表明面要素几乎没有改变,故线要素数据空间结构特征信息的复杂度指数CI变化幅度与长度要素信息变化相一致,30 m、250 m和1 km尺度的线矢量数据信息精细度相比m级分别降低1.97%、25.33%和45.39%。南美洲岛屿图斑要素的数量分别为m 级尺度的67.93%、9.54%和1.39%,图斑的陆海属性要素信息损失个数在1 km尺度上高达98.61%;相对于原m 级尺度,30 m、250 m和1 km尺度上岛屿线矢量长度要素信息损失分别为6.32%、49.26%和75.47%;面要素图斑的陆海属性要素信息损失分别为0.81%、28.46%和34.53%（表1）。随着尺度的上推,图斑面积要素均值和中值在m 级,30 m、250 m和1 km尺度上均呈现递增的趋势（图7）,表明随尺度上推面状要素趋于聚合的尺度效应。
制图泛化过程中的线性抽稀算法,使得海陆岸线的复杂度指数随着尺度的上推而下降,说明线性抽稀算法将会降低图块表征的精细度（表1,图8）。通过计算岸线复杂度指数（CI）与陆地面积在不同尺度m级、30 m、250 m和1 km的相关性程度（Pearson系数分别为0.06、0.06、0.08和0.11;Spearman系数分别为0.40、0.27、0.32和0.32）,说明尺度上推过程中尺度融合算法的侧面缩放造成的图块叠加并不影响图块的表征。由图8可以看出,制图综合过程中的尺度上推造成海陆岸线的复杂度指数的均值呈现递增,但中位数在1 km尺度上却相比于250 m尺度减少,表明尽管尺度线性抽稀造成的单个图块复杂度指数下降,但是尺度融合过程对图块的合并去除偏向于复杂度指数较小的陆地,致使复杂度指数均值增加,并且250 m和 1 km尺度上悬殊的岛屿数量差异及其与主岛的距离（多数小于250 m）,使得海陆岸线复杂度指数中位数1 km尺度小于250 m尺度。尽管线要素化简降低了线矢量数据的精细度,但面要素的聚合和删除却增加了整体空间结构特征的复杂性,使得随尺度上推,线矢量数据的复杂度指数呈现升高的尺度效应。
图8 不同尺度海陆岸线复杂度指数（CI）分布箱型图

Fig. 8 Boxplot of complexity index of coastline at different scales

5 结论

利用南美洲海陆岸线数据,采用ArcGIS 10.6版内置的多种算法和模型,提出了抽稀、数据融合、尺度上推等计算机自动转换与人工处理相结合的制图综合方法体系,进行m 级、30 m、250 m和1 km不同尺度上的制图应用,对比分析尺度上推过程中出现的不同情境和结果,可以明显看出：
（1）针对复杂多样、形状各异、结构多变的海陆地理信息要素数据,单一的计算机算法或模型无法完成地理数据不同尺度的表示。提出的综合多种计算机算法模型和人工处理相结合的尺度上推方法体系,即通过ArcGIS提供的线矢量数据自动融合算法（Collapse Dual Lines to Centerline）模型、抽稀容差算法（To Coverage XY Tolerance）模型和多边形自动融合算法（Aggregate Polygons）模型,进行不同尺度地理要素的自动制图,并对自动处理过程中产生的断点结合人工处理方式,完成不同尺度线矢量数据的拓步检查。该体系可以应用到海陆岸线数据的不同尺度数据获取中,通过实例验证了方法的有效性和实用性。
（2）海陆线矢量数据具有明显的尺度效应,在不同的空间尺度上,陆地或水域的属性存在差异。制图综合引起岛屿几何形状、数量等空间属性的相应改变,特别是狭长的陆地或水域的合并与去除,这种空间属性的转变,造成不同尺度的海陆岸线几何要素之间的显著差异。尺度上推获得的30 m、250 m和1 km尺度的线矢量数据,相对于m级尺度,在1 km尺度上,长度信息损失南美洲大陆岸线高达45.24%、岛屿岸线高达75.47%;岛屿图斑的数量损失数高达98.61%。随着尺度的上推,在m级,30 m、250 m和1 km尺度上图斑面积中值、均值和海陆岸线复杂度指数均呈现递增的趋势。
本研究中提出的适合海陆岸线的尺度上推方法,仅从数据处理、制图学以及海陆自然地理属性角度展开,由于受单一属性线矢量数据的局限,当应用于属性复杂的线矢量数据尺度上推时,需要开展线矢量数据属性选取、不同属性线矢量数据尺度效应评估的深入研究。另外,基于不同尺度海陆岸线数据进行科学研究,需结合具体研究目的,定量评价地图泛化方法的精度,通过对比和综合分析获得不同尺度下准确无误的科学结论。然而,不同的应用领域和目标、不同的化简方法或模型获得的结果存在一定的差异,探讨本文中的尺度上推方法体系在其他领域的应用是下一步的研究重点。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
梁立, 刘庆生, 刘高焕, 等. 基于遥感影像的海岸线提取方法综述[J]. 地球信息科学学报, 2018, 20(12):1745-1755.

DOI

[ Liang L, Liu Q S, Liu G H, et al. Review of coastline extraction methods based on remote sensing images[J]. Journal of Geo-information Science, 2018, 20(12):1745-1755. ]

[2]
张华国, 黄韦艮. 基于分形的海岸线遥感信息空间尺度研究[J]. 遥感学报, 2006, 10(4):463-468.

[ Zhang H G, Huang W G. Study on spatial scale of shoreline remote sensing information based on fractal theory[J]. Journal of Remote Sensing, 2006, 10(4):463-468. ]

[3]
闸旋, 滕惠忠, 王俊超, 等. 基于天绘一号卫星多光谱影像的海岸线自动提取方法[J]. 海洋测绘, 2018, 38(4):58-62.

[ Zha X A, Teng H Z, Wang J C, et al. A method of automatic coastline extraction based on multi-spectral image of TH-1[J]. Hydrographic Surveying and Charting, 2018, 38(4):58-62. ]

[4]
原晓慧, 王萍, 张英, 等. 基于边缘检测的海岸线自动提取研究[J]. 北京测绘, 2019, 33(2):148-152.

[ Yuan X H, Wang P, Zhang Y, et al. Research on edge detection and object-oriented for automatic extraction of coastline[J]. Beijing Surveying and Mapping, 2019, 33(2):148-152. ]

[5]
Ge Y, Jin Y, Stein A, et al. Principles and methods of scaling geospatial Earth science data[J]. Earth-Science Reviews, 2019, 197:102897.

DOI

[6]
Zhou S, Jones C B. Shape-aware line generalisation with weighted effective area[J]. Developments in Spatial Data Handling, 2005:369-380.

[7]
ERsi. "Automation of Map Generalization: The Cutting-Edge Technology"[Z]. Technical Paper. Download address: http://downloads.esri.com/support/whitepapers/ao_/mapgen.pdf 1996.

[8]
胡云锋, 徐芝英, 刘越, 等. 空间尺度上推方法的精度评价——以内蒙古锡林郭勒盟土地利用数据为例[J]. 地理研究, 2012, 31(11):1961-1972.

[ Hu Y F, Xu Z Y, Liu Y E, et al. Accuracy analysis of up-scaling data: A case study with land use data in Xilin Gol of Inner Mongolia, China[J]. Geographical Research, 2012, 31(11):1961-1972. ]

[9]
孟斌, 王劲峰. 地理数据尺度转换方法研究进展[J]. 地理学报, 2005, 60(2):277-288.

[ Meng B, Wang J F. A review on the methodology of scaling with geo-data[J]. Acta Geographica Sinica, 2005, 60(2):277-288. ]

[10]
Kronenfeld B J, Buttenfield B P, Stanislawski L V. Map generalization for the future: Editorial comments on the special issue[J]. ISPRS International Journal of Geo-Information, 2020, 9(8):468-471.

DOI

[11]
Atkinson P M, Tate N J. Spatial scale problems and geostatistical solutions: A review[J]. The Professional Geographer, 2000, 52(4):607-623.

DOI

[12]
栾海军, 田庆久, 余涛, 等. 根据分形理论与五指标评价体系构建NDVI连续空间尺度转换模型[J]. 遥感学报, 2015, 19(1):116-125.

[ Luan H J, Tian Q J, Yu T, et al. Establishing continuous spatial scaling model of NDVI on fractal theory and five-index estimation system[J]. Journal of Remote Sensing, 2015, 19(1):116-125. ]

[13]
Duffaut Espinosa L A, Posadas A N, Carbajal M, et al. Multifractal downscaling of rainfall using normalized difference vegetation index (NDVI) in the Andes plateau[J]. PLoS One, 2017, 12(1):e0168982.

DOI

[14]
Jiang J L, Liu X N, Liu C H, et al. Analyzing the spatial scaling bias of rice leaf area index from hyperspectral data using wavelet-fractal technique[J]. Ieee Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6):3068-3080.

DOI

[15]
Liu Y, Li W J. A new algorithms of stroke generation considering geometric and structural properties of road network[J]. ISPRS International Journal of Geo-information, 2019, 8(7):304.

DOI

[16]
Han Y, Wang Z H, Lu X M, et al. Application of AHP to Road Selection[J]. ISPRS International Journal of Geo-information, 2020, 9(2):86.

DOI

[17]
Fiedukowicz A. The role of spatial context information in the generalization of geographic information: using reducts to indicate relevant attributes[J]. ISPRS International Journal of Geo-information, 2020, 9(1):37.

DOI

[18]
Karsznia I, Sielicka K. When traditional selection fails: how to improve settlement selection for small-scale maps using machine learning[J]. ISPRS International Journal of Geo-Information, 2020, 9(4):230.

DOI

[19]
段佩祥, 钱海忠, 何海威, 等. 基于支持向量机的线化简方法[J]. 武汉大学学报·信息科学版, 2020, 45(5):744-752,783.

[ Duan P X, Qian H Z, He H W, et al. A line simplification method based on support vector machine[J]. Geomatics and Information Science of Wuhan University, 2020, 45(5):744-752,783. ]

[20]
Courtial A, El Ayedi A, Touya G, et al. Exploring the potential of deep learning segmentation for mountain roads generalisation[J]. ISPRS International Journal of Geo-information, 2020, 9(5):338.

DOI

[21]
武芳, 邓红艳. 基于遗传算法的线要素自动化简模型[J]. 测绘学报, 2003, 32(4):349-355.

[ Wu F, Deng H Y. Using genetic algorithms for solving problems in automated line simplification[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4):349-355. ]

[22]
钱海忠, 何海威, 王骁, 等. 采用三元弯曲组划分的线要素化简方法[J]. 武汉大学学报·信息科学版, 2017, 42(8):1096-1103.

[ Qian H Z, He H W, Wang X, et al. Line feature simplification method based on bend group division[J]. Geomatics and information science of wuhan university, 2017, 42(8):1096-1103. ]

[23]
应申, 李霖. 基于约束点的曲线一致性化简[J]. 武汉大学学报·信息科学版, 2003, 28(4):488-491.

[ Ying S, Li L. Consistent line simplification based on constraint points[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4):488-491. ]

[24]
Sayidov A, Aliakbarian M, Weibel R. Geological map generalization driven by size constraints[J]. ISPRS International Journal of Geo-information, 2020, 9(4):284.

DOI

[25]
Li C, Wu P, Yin Y, et al. An improved partitioning method for dissolving long and narrow patches[J]. Computers and Geosciences, 2020, 138:104358.

DOI

[26]
Kronenfeld B J, Stanislawski L V, Buttenfield B P, et al. Simplification of polylines by segment collapse: Minimizing areal displacement while preserving area[J]. International Journal of Cartography, 2020, 6(1):22-46.

DOI

[27]
Shen Y, Ai T. A raster-based methodology to detect cross-scale changes in water body representations caused by map generalization[J]. Sensors, 2020, 20(14):3823.

DOI

[28]
Lloyd C D. Scale in spatial data analysis: Key concepts[M]. John Wiley & Sons, Ltd, 2014.

[29]
Douglas D H, Peucker T K. Algorithms for the reduction of the number of points required to represent a line or its caricature[M]. John Wiley & Sons, Ltd, 1973.

[30]
Falconer K J. The hausdorff dimension of self-affine fractals[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1988, 103:339-350.

DOI

[31]
Wang Z S, Müller J C. Line generalization based on analysis of shape characteristics[J]. Cartography and Geographic Information Systems, 1998, 25(1):3-15.

DOI

[32]
Mandelbrot B B. How long is the coastline of Britain[J]. Science, 1967, 156:636-638.

PMID

[33]
刘闯, 石瑞香, 张应华, 等. 基于Google Earth遥感影像全球多尺度海陆(岛)岸线数据集(2015)[J/DB/OL]. 全球变化数据仓储电子杂志(中英文), 2019.

[ Liu C, Shi R X, Zhang Y H, et al. Global Multiple Scale Shorelines Dataset Based on Google Earth Images (2015)[J/DB/OL]. Digital Journal of Global Change Data Repository, 2019. ]

Options
文章导航

/

〈 〉