EN中文

地球信息科学学报 >

2021 , Vol. 23 >Issue 10: 1767 - 1777

DOI: https://doi.org/10.12082/dqxxkx.2021.210016

地球信息科学理论与方法

Douglas-Peucker算法全自动化的多尺度空间相似关系方法

  • 王荣 , 1, 2, 3 ,
  • 闫浩文 , 1, 3, * ,
  • 禄小敏 1, 3
展开
  • 1.兰州交通大学测绘与地理信息学院,兰州 730070
  • 2.天水师范学院资源与环境工程学院,天水 741001
  • 3.地理国情监测技术应用国家地方联合工程研究中心,兰州 730070
* 闫浩文（1969—）,甘肃民勤人,博士,“长江学者”特聘教授,主要从事地图综合及多尺度空间理论研究。E-mail:

王 荣（1986— ）,女,甘肃天水人,博士生,主要从事多尺度空间相似关系研究。E-mail:

收稿日期: 2021-01-12

  要求修回日期: 2021-03-12

  网络出版日期: 2021-12-25

基金资助

国家自然科学基金项目(41930101)

国家自然科学基金青年基金项目(41801395)

甘肃省教育厅创新基金项目(2021A-110)

版权

版权所有,未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
收起

Automation of the Douglas-Peucker Algorithm based on Spatial Similarity Relations

  • WANG Rong , 1, 2, 3 ,
  • YAN Haowen , 1, 3, * ,
  • LU Xiaomin 1, 3
Expand
  • 1. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China
  • 2. College of Resources and Environmental Engineering, Tianshui Normal University, Tianshui 741001, China
  • 3. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, Lanzhou 730070, China
* YAN Haowen, E-mail:

Received date: 2021-01-12

  Request revised date: 2021-03-12

  Online published: 2021-12-25

Supported by

Youth Foundation of National Natural Science Foundation of China(41930101)

Youth Foundation of National Natural Science Foundation of China(41801395)

Innovation Foundation of Education Department of Gansu(2021A-110)

Copyright

Copyright reserved © 2021
Fold

摘要

地图综合本质上是空间相似变换,研究Douglas-Peucker算法及其参数的设置,实质是研究算法的最佳距离阈值与尺度变化间的定量关系,但目前二者关系未知,导致参数设置及化简结果的选择主观性强。为此,提出以多尺度线要素空间相似关系为契合点,利用阈值参数寻优原理确定二者间定量关系,以实现基于DP算法线要素的全自动化简。结果表明：① 二次函数是描述最佳距离阈值与尺度变化间定量关系的最优函数;② 针对来源于相同地理特征区,如长江下游平原,的线要素可行,利用同一最佳距离阈值可实现基于DP算法线要素的全自动化简,且化简结果与已有成果数据吻合度较高;而来源于不同地理特征区域,如长江下游平原和江淮平原,的线要素,用同一最佳距离阈值化简是不合理。因此,应选择不同的最佳距离阈值,以实现不同地理特征区域线要素的DP算法全自动化简。

关键词： 地图综合; 空间相似关系; 尺度变化; 参数寻优; 几何精度; Douglas-Peucker算法; 地理特征; 最佳距离阈值

本文引用格式

王荣 , 闫浩文 , 禄小敏 . Douglas-Peucker算法全自动化的多尺度空间相似关系方法[J]. 地球信息科学学报, 2021 , 23(10) : 1767 -1777 . DOI: 10.12082/dqxxkx.2021.210016

Abstract

Map generalization is in essence a spatial similarity transformation of maps. Studying the Douglas-Peucker algorithm and its parameter setting is in essence studying the relationship between the optimal distance threshold of the algorithm and map scale change. However, the quantitative relationship between them is still unknown, which leads to strong subjectivity in parameter setting and selection of simplification results. Therefore, in order to realize the automated simplification of polyline based on DP algorithm, this paper proposes to take the spatial similarity evaluation model of multi-scale polylines as the coincidence point, and determine the quantitative relationship between them using the principle of threshold parameter optimization. The results indicate that quadratic function is the optimal function to describe the quantitative relationship between the optimal distance threshold and map scale change. It is feasible to use the same optimal distance to automatically simplify the polylines from the same geographical feature area based on the Douglas-Peucker algorithm, such as the polylines from the Lower Yangtze River plain. The simplification results match well with the existing target scale data. However, it is unreasonable to use the same optimal distance threshold to simplify the polylines from different geographical feature areas, such as polylines from the Lower Yangtze River plain and the Jianghuai plain. Therefore, different optimal distance thresholds should be selected to realize full automated simplification of DP algorithm for polylines from different geographical feature areas.

Key words： map generalization; spatial similarity relations; map scale change; parameter optimization; geometric accuracy; Douglas-Peucker algorithm; geographic feature; optimal distance threshold

1 引言

在线要素化简过程中,化简算法参数设置及化简结果的选择对制图者主观依赖性强,导致化简效率低,化简结果不确定 [1]。针对线要素化简,不同学者提出了不同算法[2,3,4,5],如Douglas-Peucker algorithm(DP)[6],Li-Openshaw[7],弯曲组算法[8]等,各算法化简效果不尽相同,如Li-Openshaw算法综合结果点为圆与目标线的交点,原始点位未得到保留等。DP算法作为最经典线要素化简算法[1,9],在地图综合中得到广泛应用,但其执行过程中仍需制图者不断输入距离阈值,化简中间结果需制图人员不断比较,以半自动化为主,化简结果不确定。研究化简算法及其参数设置,实质是研究算法的综合程度与尺度变化之间的关系。
地图综合本质上是一种多尺度地图间的空间相似变换。因此,多尺度空间相似关系及其在地图综合算法的自动化、综合过程控制及综合结果评价等方面的研究受到国内外制图学者的广泛关注[10,11],但目前国内外多尺度空间相似关系理论的研究仍处于萌芽期,研究主要集中在利用多尺度空间相似关系评价不同算法的化简结果,且研究成果甚少,在综合算法的自动化及综合过程控制方面的应用几乎空白。究其原因：① 综合算法化简过程转折条件的判断依据模糊,如DP算法化简过程中,无法确定中间结果地图与目标比例尺地图间的对应关系,导致算法半自动化,化简结果不确定;② 多尺度线要素S与C及DP算法T与C之间定量关系不明确。如Chehreghan[12]认为S与C之间不存在线性或非线性关系,Yan[10]的观点相反;③ 区域地理特征作为地图综合的客观依据,其对S与C或T与C之间定量关系的影响不明确,如Li[13]认为地图综合的根本原因是比例尺发生了变化,而综合前后制图区域地理特征保持不变,如地形破碎度;王家耀[14]认为应予以考虑。以上问题的解决对实现基于多尺度线要素空间相似关系DP算法的全自动化至关重要。
因此,本文以地图综合的本质-多尺度空间相似关系为契合点,通过构建多尺度线要素间相似度评价模型,以相似度作为DP算法化简过程转折条件的判断依据,利用尺度变化自动确定DP算法中距离阈值参数,以实现DP算法的全自动化,减少人为干预,提高综合算法化简结果精度,为实现地图综合算法的全自动化、空间数据匹配及国家基础矢量数据库的构建等提供方法体系及支撑。

2 空间相似度评价模型及DP算法 参数寻优原理

单从建模角度来看,DP算法的最佳距离阈值与尺度变化间具有依赖关系,随距离阈值的增大,DP算法化简的中间结果地图与目标比例尺地图之间的相似性逐渐增大,超过一定阈值后相似度随过渡化简而逐渐减小;即当两者间相似度达到最大时,化简结果最优,对应的阈值即为原比例尺地图综合为目标比例尺地图的最佳距离阈值。因此,本文通过设置对照实验,首先构建多尺度线要素空间相似度评价模型,其次利用该评价模型计算每次循环中DP算法化简的中间结果地图(Li)与已有目标比例尺成果地图(LM2)之间的相似度(Si),从而自动确定目标比例尺对应的DP算法最优阈值参数,建立最优阈值参数(T)与尺度变化(C)间的定量关系,最后以同一地理特征区的不同类型线状地物数据为对象,1:25万、1:100万成果数据为参照,从几何特征保持和位置精度两方面对化简结果进行评价,研究方法流程图(图1)。
图1 基于多尺度线要素空间相似关系DP算法全自动化方法流程

Fig. 1 Fully automated flow of DP algorithm based on the spatial similarity relations of multi-scale polylines

2.1 多尺度线要素空间相似度评价模型的构建

多尺度线要素空间相似度评价模型的构建是确定DP算法T与C之间的定量函数关系的前提。众多学者[15,16]针对多尺度线要素空间相似性度量指标进行研究,多尺度线要素相似性度量指标主要包括：① 基于距离的改进Hausdorff方法[15];② 基于弯曲程度的曲率[17,18]描述法;③ 基于形态描述函数的转角函数法;④ 顾及整体形态的缓冲区限差法[19,20],权重分别设置为0.31、0.23、0.11及0.35。
通过4种评价指标的原理及已有研究文献可知：尽管Hausdorff距离是GIS中衡量目标间距离最常用的指标,但其对目标形状,尤其是复杂异常目标形状非常敏感,甚至不满足多尺度相似性变化规律,即随尺度变化增大,距离逐渐减小[12],而改进的Hausdroff距离Mean-Hausdroff表现更稳定。形状相似性是通过多尺度线要素间的重合度来度量的。不同学者[19,21-22]通过实验对比分析节点保留率、双边弯曲森林及转角函数等形状描述指标,结果表明,累计转角函数（式（1））能排除细节差异的干扰,更适合同一目标多尺度线要素间的比较[23]（图2）。
Sim ˆ L 1 , L 2 Shp = ∫ f θ L 1 - θ L 2 d s 1 2 = ∫ 0 1 T A L 1 d s - ∫ 0 1 T A L 2 ds 1 2
图2 多尺度线要素L1与L2间累计转角函数

Fig. 2 Cumulative angle function of the multi-scale polylines L1 and L2

式中： f θ L 1 - θ L 2 = θ L 1 - θ L 2 θ L 1 - θ L 2 ≤ 180 ° 360 ° - θ L 1 - θ L 2 θ L 1 - θ L 2 > 180 °, Sim ˆ L 1 , L 2 Shp值越大,L1与L2间的形状相似度越小。若转角为顺时针,αi为正;若转角为逆时针, α i '为负,且 α i = 360 ° - α i '。
根据视觉对图上位置偏离的感知程度,缓冲区限差中缓冲区半径的大小一般设置为目标比例尺图上2个点要素间最小距离值（0.2 mm）的1~2倍[16]。
评价指标中有些为正向指标,如距离、形状、曲率等,即尺度变化越大,距离相似度值越大;有些为负向指标,如缓冲区限差,即尺度变化越大,缓冲区限差相似度值越小;且各评价指标相似度的单位和量纲不同,其数值的变异很大。因此,在建立空 间相似度评价模型前,需采用“极差标准化”差 （式（2））将各指标空间相似度值归一化到[0, 1]。
Si m L i , L j P k = Sim ˆ L i , L j P k - MIN 1 ≤ i ≤ N Sim ˆ L i , L j P k MAX 1 ≤ i ≤ N Sim ˆ L i , L j P k - MIN 1 ≤ i ≤ N Sim ˆ L i , L j P k ( 当 Sim ˆ L i , L j P k 为正向因子 ) MAX 1 ≤ i ≤ N Sim ˆ L i , L j P k - Sim ˆ L i , L j P k MAX 1 ≤ i ≤ N Sim ˆ L i , L j P k - MIN 1 ≤ i ≤ N Sim ˆ L i , L j P k ( 当 Sim ˆ L i , L j P k 为负向因子 )
空间相似度计算模型[1]：
Sim L i , L j = ∑ k=1 n W p k Si m L i , L j p k
式中： Sim L 1 , L 2 ∈ ( 0,1 ]; W p k ∈ 0,1;n为评价指标总数,n=4。

2.2 DP算法参数寻优原理

DP算法作为最经典的线要素化简算法[6],已被广泛用于地图综合中[1,24],其阈值参数寻优原理如 图3所示。
图3 Douglas-Peucker算法化简原理

Fig. 3 Simplification fundamentals of the Douglas-Peucker algorithm

由图3可知：DP算法线要素化简程度取决于最佳距离阈值T,包括初始阈值λ0及其步长△λ。因此,确定T与C之间的定量函数关系是实现DP算法全自动化的关键。而线要素化简过程中点被删除的顺序与点被保留的次序相反,即通过对点的保留顺序取反,可知点的删除顺序。因此,依据算法阈值寻优原理可确定λ0及T。如图3中,点保留顺序为A和H, D, F, C, G, B, E,则E为第1个被删除的点,可确定λ0（λ0=dPE,dPE为点E到AH的垂直距离）。若点E被删除,对应中间化简结果为L1{ABCDFGH},基于多尺度线要素空间相似度评价模型计算L1与LM2间相似度S1;设第i步DP算法阈值为λi=λi-1+△λ,对应中间化简结果Li与LM2间相似度Si;依次循环,直到第K次循环结束,且 S k - 1 < S k > S k + 1,则对应的距离阈值λk即为线要素从原比例尺M1化简为目标比例尺M2对应的最佳距离阈值T;依次循环并记录每轮循环对应点对（C, T）,利用（非）线性模型及最小二乘法原理可确定T与C之间的定量关系。算法及距离阈值寻优流程如图4所示。
图4 线要素全自动化简算法与距离阈值寻优计算流程

注：△λ为动态变化步长,LM1与Li间相似度Si越大,△λ取值越小,如设线要素从1:5万综合到1:2.5万,若 S i ∈ 0,0.6,则△λ=0.02 km;若 S i ∈ 0.6,0.8,则△λ=0.01 km;若 S i ∈ 0.8,1,则△λ=0.005 km。

Fig. 4 Full simplification algorithm of polylines and the optimization calculation process of distance threshold

2.3 非线性定量模型的确定

重构复杂地理系统时,地理要素间既有线性,也有幂函数关系、指数及对数函数等非线性关系。DP算法中T随C增大逐渐增大,且3次及以上一元多次函数具有多个单调递增区间,符合该变化趋势的候选函数有一元线性及一元二次( a < 0)、对数函数等非线性关系。而空间相似度S与尺度变化C负相关,因此,拟合S与C之间定量关系的候选函数包括：
y = a 2 x 2 + a 1 x + a 0 a 2 > 0 , x ∈ 1 , - a 1 2 a 2 y = aIn x + a 0 ( a < 0 , x ≥ 1 ) y = a x b ( a > 0 , - 1 < b < 0 , x ≥ 1 ) y = a e bx ( a > 0 , b < 0 , x ≥ 1 ) y = ax + b ( a < 0 , x ≥ 1 )
非线性复杂系统的解决需线性化处理,即利用最小二乘法及线性分析思想建立新模型,并进行显著性检验,将模型还原为非线性关系;模型建立后,需对模型的可信度进行R2检验,以确定模型质量[1]。

2.4 线要素图形简化几何精度评估

在线要素制图综合中,算法化简对线要素几何精度的影响主要体现在曲线化简前后几何特征和位置精度的改变[23,25]。线的长度和曲折度的评估反映了曲线几何特征的改变;当比例尺变化时,需对化简结果曲线的位置精度评估,其主要体现在综合前后线要素的局部及整体位移,可采用位移标准差(SMD)、位置误差(PE)、矢量位移,面积位移及缓冲区限差等指标进行评价。SMD主要反映曲线局部位移的最大值,最适合比较不同算法化简同一线要素时的位移值[26],但该指标对曲线整体位移情况的描述不够精准,为此进一步提出用PE评价曲线的整体位移精度[17,27]。因此,本文主要采用长度比(LR)[15]、曲折度(SD)[18]及SMD[25]、PE[17,27]评估化简曲线几何特征及位置精度。
长度比用来评估算法对曲线上的点的压缩程度,比值越小,压缩量越大[28]。线的曲折度由曲线上相邻的直线段组成的夹角累加得到[23];线的长度变化越大,曲折度变化越小,算法对曲线几何特征保持越好;SMD越小,曲线的局部位移越小,化简后线要素相交的可能性越小;PE值越小,算法对曲线上点位的整体位置精度保持的越好。

3 实验结果分析与比较

对照组与实验组数据来源于GF-2全色与多光谱Pansharpening融合后,空间分辨率为1 m的影像数据,在ArcGIS 10.6对应不同比例尺随机采样提取的多尺度矢量数据集,包括1:1万、1:2.5万、1:5万、1:10万、1:25万及1:50万6种尺度平原地区（图5）河流及道路数据,其中位于华北平原南侧的淮北平原河流样本12组;长江下游平原样本19组,其中河流12组,道路7组,且部分来源于江淮平原,部分来源于长江三角洲平原;1:5万、1:10万、1:25万、1:50万及1:100万5种尺度山西山地道路、河流数据,多尺度边界线数据来源于已有成果数据。对照组由地理特征不同的区域的多尺度线要素数据集组成,实验组由地理特征相同的区域的多尺度线要素数据集组成;空间相似度评价模型精度验证的5组多尺度数据来源于矢量化采集已有研究Yan[10]论文中的 图2—图4及Chehreghan[12]论文中的图11、图13的数据,以确定S与C、T与C之间的定量关系并初步探究制图区域地理特征对定量关系的影响。
图5 平原地区实验数据采集区及多尺度河流、道路样例数据

Fig. 5 Sampling area of experimental data and sampling data of multi-scale river and road in the plain area

3.1 多尺度线要素空间相似关系实验

因各组多尺度数据集的变化趋势一致,研究以淮北平原地区12组多尺度数据集为例,符合多尺度线要素S与C之间变化规律的5个候选函数拟合结果如图6所示。
图6 淮北平原多尺度线要素S与C间候选函数拟合结果及其R2

Fig. 6 Fitting results of five functions and its R2 of multi-scale polylines from the Huaibei plain

图6表明：幂函数R2最接近1（R2=0.8152）,即幂函数（式（5））是表达多尺度线要素空间相似度与尺度变化间定量关系的最佳函数,该结论与Yan[1]研究结论一致。
Sim L i , L j = 1 若 L 1 , L 2 为直线 Sim L i , L j = a C ( L i , L j ) b 若 L 1 , L 2 为曲线
式中： a > 0 , - 1 < b < 0 ; Sim L i , L j ∈ ( 0,1 ] ; C L i , L j ∈ 1 , + ∞。
为了验证该评价模型的可靠性,研究选取5组已有研究[10,12]中的多尺度验证数据集,与已有评价模型[10]对比分析。结果表明：本文提出的评价模型拟合精度提高了4.22%~11.52%（图7）;通过图8(a)、图8(b)与图8(c)对比分析可知：31组多尺度数据集均为平原地区线状目标,地理特征相同的区域相同\不同要素的多尺度线要素S与C之间定量关系,均可用一条幂函数曲线拟合,如图8(c)中长江下游平原地区的河流与道路的S与C之间定量函数关系为S=0.9269C-0.122,R2=0.7966;而地理特征不同的区域的多尺度线要素,无论是相同要素还是不同要素,尽管变化趋势相同,但无法用同一条幂函数曲线拟合,如图8(a)与图8(b)中,淮北平原河流与长江下游河流,拟合精度仅为0.5005;淮北平原河流与长江下游道路,拟合精度为0.4155。
图7 验证数据S与C之间定量关系拟合结果

注：图中A、C、E分别对应Yan[10]论文中的图2、图3、图4;B、D分别对应Chehreghan[12]论文中的图11、图13。

Fig. 7 Quantitative relationships fitting results of validation data between S and C

图8 地理特征相同/不同的区域多尺度线要素S与C拟合结果

Fig. 8 Fitting results between S and C of the multi-scale polylines from the same or different geographical feature area(s)

3.2 距离阈值的确定

DP算法化简的实质是最远的中间点到首末两点连线的垂直距离与T相比较,T决定了线要素被化简的程度,因此,T的定量选择是实现DP算法自动化的核心与关键。依据多尺度线要素空间相似度幂函数模型及2.2节中参数寻优原理,确定T与C之间的定量关系。
因各组多尺度线要素数据集的变化趋势相同,随机选取一组数据集对应(C, T)坐标点对, T = f ( C )候选函数寻优结果如图9。
图9 T与C之间候选函数寻优结果

Fig. 9 Optimization result of candidate functions between T and C

图9表明：一元二次线性函数的拟合精度最趋近1(R2=0.9585),即一元二次函数（式（6)）是描述DP算法T与C之间定量关系的最佳函数。
T = 0 ( C = 1 ) T = a C 2 + bC + d ( a < 0 , C ∈ ( 1 , max { C i } ] )
图10(a)、图10(b)分别为对照组与实验组多尺度线要素数据集T与C间定量函数关系拟合结果。
图10 多尺度线要素T与C之间定量关系拟合结果

Fig. 10 Quantitative relationship fitting results between T and C

DP算法T与C之间拟合结果R2≥0.8521,拟合精度较满意。从图10（a）可知：无论是相同或不同要素,如B与C均为道路,而D为边界线,E为海岸线,二者为不同地物,地理特征不同的区域的多尺度线要素的T与C之间的变化趋势相同(R2≥0.9585),但无法用同一条二次函数曲线拟合,R2仅为0.4636。换而言之,基于DP算法利用相同T自动化简地理特征不同的区域的线要素是不合理的。与对照组（图10（a））相反,无论是相同或不同地物目标,如F与I均为道路,G与H为不同地物,地理特征相同的区域多尺度线要素的T与C之间的定量关系均可用同一条二次函数曲线拟合（图10（b））,如山西山地道路、河流及边界线的拟合精度为0.9012,长江下游平原地区的拟合精度为0.8521;即基于多尺度线要素空间相似关系评价模型可实现地理特征相同的区域线要素DP算法的全自动化简,以上结论与3.1节中多尺度线要素空间相似关系理论研究结论相印证。因此,后续研究对象为地理特征相同的区域的线要素。

3.3 基于参数寻优结果线要素自动化简

分别以山西山地、长江下游平原地区为例,依据T与C之间定量关系计算不同尺度变化对应的DP算法理论最佳距离阈值,以地理特征相同的区域多尺度线要素的全自动化简,T寻优结果（表1）。
表1 多尺度线要素T寻优结果

Tab. 1 Parameter T optimally results of multi-scale polylines

山西山地 T= -0.0001C2+0.0098C-0.037 (C ∈(1,50]) 长江
下游
平原		 T= -0.00003C2+0.0026C-0.0008 (C ∈(1,50])
C 5 10 25 50 C 2.5 5 10 25 50
T/km 0.0095 0.0510 0.1455 0.2030 T/km 0.0056 0.0114 0.0222 0.0455 0.0542
依据T与C之间的定量函数关系,若原比例尺M1和目标比例尺M2已知,则可确定理论最佳距离阈值T,如山西山地原比例尺为1:5万,目标比例尺为1:25万,则C=5,根据表1可知,λ=0.0095 km。为了验证研究方法的可靠性,研究以山西山地为例,基于尺度变化对应的理论最佳距离阈值,利用DP算法自动化简地理特征相同的区域的边界线、道路、河流3类不同地物,最佳距离阈值化简结果与 1:25万、1:100万成果数据（红色）叠加显示如图11。
图11 本文的化简结果与成果数据叠加

注：图中红线为化简结果。

Fig. 11 Overlay of simplification results and reference result data

3.4 精度评价

为了检验本文化简结果,分别以1:25万、1:100万成果数据为参照,研究选取长度比、弯曲度、PE及SMD等评估指标[23],从几何特征、位置精度保持 2个方面对化简结果几何精度进行评估。
从图12可以看出：整体来看,化简结果几何特征指标与作为参照的1:25万、1:100万成果数据吻合程度非常高,反映了算法参数设计的合理性。化简结果的长度与成果参照数据吻合度非常高,即化简结果压缩比与成果参照数据基本一致(表2)。各线要素目标的长度比及弯曲度变化率等几何评估指标误差率△LR、△SR均非常小(图11）,其中河流的误差值最大,△LR、△SR分别为0.0265、0.0111,边界△LR误差最小,仅为0.0004,道路△SR误差最小,仅为0.0011(表3),即与LM2相比,化简结果几何特征误差基本趋于0,化简结果的几何特征保持的较好。
图12 化简结果几何特征及位置精度指标误差率

Fig. 12 Error rate comparison of geometric and position accuracy of simplification results

表2 化简结果几何精度评估

Tab. 2 Geometric accuracy comparison of the simplification results

几何指标 原比例尺数据（LM1） 成果参照数据（LM2） 本文的化简结果（L）
边界线 道路 河流 边界线 道路 河流 边界线 道路 河流
长度/km 198.9993 27.0565 153.7918 165.6861 26.1494 152.7020 165.6059 26.2379 148.6358
弯曲度 1.4493 1.5547 25.5883 1.1969 1.5103 25.0681 1.2067 1.5121 25.5663
表3 几何精度对比

Tab. 3 Comparison of geometric and position accuracy

线要素 成果参照数据 本文算法化简结果
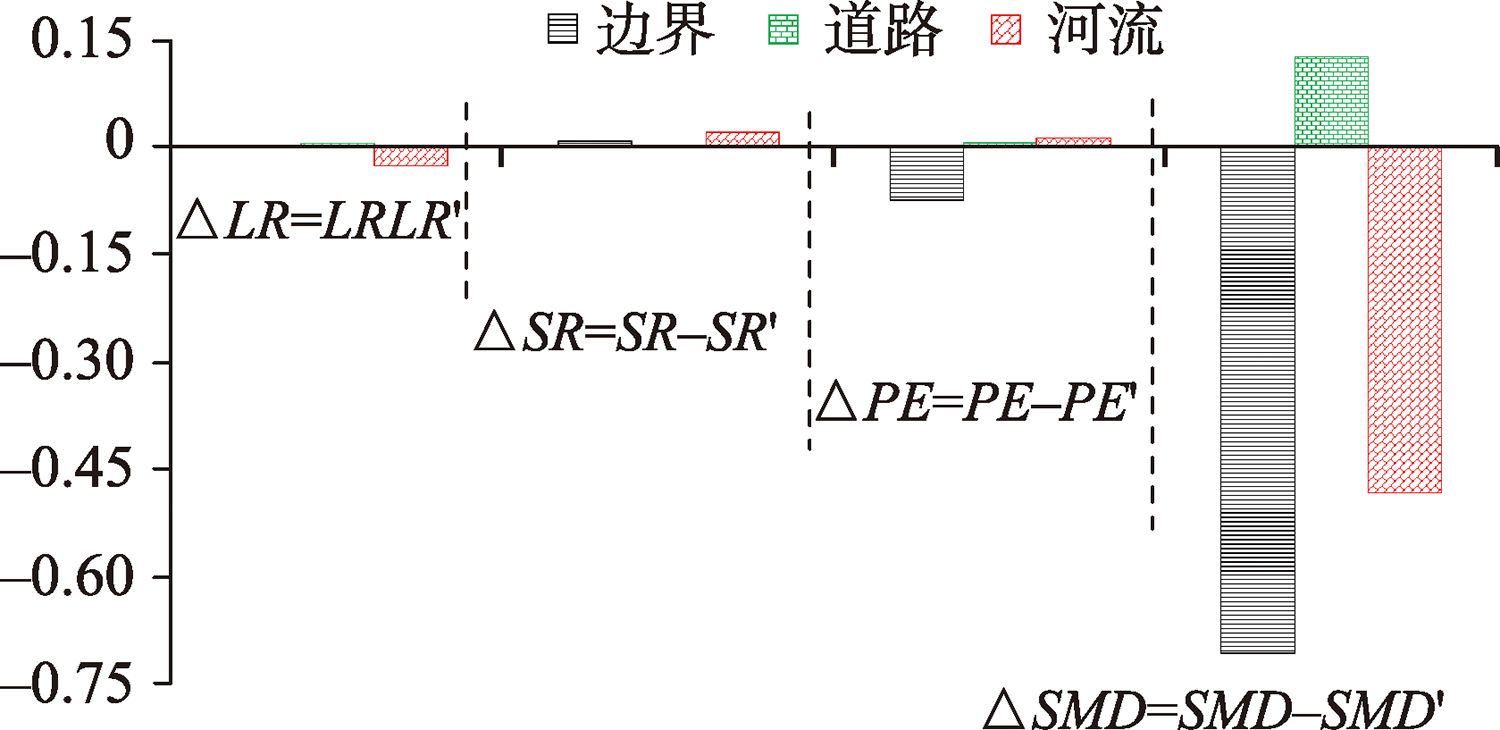
LR SR PE/km SMD LR′ SR′ PE′/km SMD′
边界 0.8326 0.8258 0.2063 0.8070 0.8322 0.8324 0.1306 0.0998
道路 0.9665 0.9714 0.0054 0.3323 0.9697 0.9725 0.0114 0.4565
河流 0.9929 0.9796 0.0058 0.6046 0.9664 0.9991 0.0169 0.1203
从位置精度来看,与作为参照的1:25万、1:100万成果数据相比,除道路化简结果SMD略大于1:25万成果参照数据,SMD误差为0.1203,其他要素化简结果的SMD均小于成果数据,即本文曲线化简结果的局部位移更小。道路与河流化简结果的整体位置精度误差与成果参照数据非常接近,△PE分别为-0.006,-0.0111(表3),边界化简结果的整体位置精度小于成果参照数据,即边界线、道路与河流的化简结果对曲线点位的整体位置精度保持较好。该实验结果与武芳等[23]通过比较不同线要素化简算法得出的结论一致。综上可知,与1:25万、1:100万成果参照数据相比,本文化简结果能较好保持曲线的几何特征及其局部与整体位置精度。
由实验结果可以得出：
（1）幂函数(a>0,-1<b<0)、一元二次函数( a < 0 , C ∈ ( 1 , max { C i } ])分别为定量描述S与C、T与C之间定量关系的最佳函数。若尺度变化C已知,则可确定其对应的空间相似度S及DP算法的最佳距离阈值T,反之亦然。与已有模型[1]相比,本文提出的相似度评价模型精度提高了4.22%~11.52%。
（2）与多尺度线要素空间相似度和尺度变化之间变化规律相印证,DP算法最佳距离阈值T与尺度变化C之间也存在共同规律：地理特征相同的区域的多尺度线要素可用同一条二次函数曲线拟合;地理特征不同的区域的线要素,变化趋势相同,但无法用同一条二次函数曲线表达。换而言之,针对地理特征相同的区域的线要素,基于多尺度线要素空间相似关系理论可实现DP算法的全自动化;而利用同一最佳距离阈值T自动化简地理特征不同的区域的线要素是不合理的,应结合制图区域地理特征采用不同的最佳距离阈值进行化简。比例尺、制图区域的地理特征作为影响地图综合的两方面主要客观因素,该结论表明不同制图区域线要素化简,受制图区域地理特征与比例尺共同影响;而同一制图地理特征区域,比例尺发生了变化是线要素化简的根本原因,化简前后制图区域地理特征保持不变,后者与Li等[13]观点一致。
（3）基于多尺度线要素空间相似关系理论的DP算法自动化简结果与已有成果数据吻合度较高,整体来看,几何特征保持较好,整体位置精度较高,但道路的局部位移略差。综合来看,本文线要素化简结果的几何特征保持较好,曲线上点位的局部与整体位置精度较高。

4 结语

大多数情况下,线要素化简过程中不可避免地需要用户在算法执行过程中不断输入参数,不同制图人员得到的化简结果不同。研究化简算法及其参数的自动设置,实质是研究算法的综合程度与比例尺之间的关系[16],而该问题的解决依赖于空间相似度与地图尺度变化之间的关系[11]。基于该思想,本文提出以地理特征相同/不同的区域的多尺度线要素为对象,通过设置对照实验,基于多尺度线要素空间相似关系理论实现了DP算法阈值参数自动寻优及同一地理特征区线要素的全自动化简;以 1:25万、1:100万已有成果数据为参照,从几何和位置精度对化简结果精度进行评价。
与传统制图人员不断输入参数、主观确定化简结果的方法相比,本文方法的优势在于：
（1）与仅考虑长度与距离的传统模型相比,本文提出的考虑曲率、缓冲区限差的综合指标多尺度线要素相似性评价模型精度提高了4.22%~11.52%;一元二次函数是描述最佳距离阈值与尺度变化间定量关系的最佳函数。
（2）减少反复试错调参过程,通过计算化简中间结果与目标尺度成果数据之间的相似度,实现了DP算法阈值参数的自动寻优及地理特征相同的区域线要素的自动化简,减少了制图人员对化简结果判断的主观性,提高了参数设置、算法效率及化简结果精度。
（3）考虑了不同制图区域地理特征对多尺度线要素空间相似关系的影响,即制图区域地理特征与比例尺共同影响多尺度线要素空间相似关系;利用DP算法自动化简不同的区域的线要素时,应结合制图区域地理特征,采用不同的最佳距离阈值,该结论为后续多尺度空间相似关系研究提供了新的研究思路。
值得说明的是,本文是针对算法阈值设定的优化,得到的算法化简结果与人工化简结果之间不可避免地存在一定的差异,化简效果的完善依赖于算法本身的改进。本文以多尺度单个线状目标为例,对线状地物的化简进行了研究,但线群(组)目标地物的综合并非仅依赖于地物本身特征,而与周围地物密切相关;因DP化简算法自身缺陷导致化简结果可能存在自相交或与其他相邻线要素相交的情况,如,DP算法化简的相邻等高线可能出现相交的情况。因此,进一步研究可考虑： ① 参考以往学者对DP算法的改进,设置对照实验,将本文方法应用于线群(组)目标带参数的化简算法的自动化及不同算法综合结果的评价中; ② 利用二分查找法提高算法效率的研究;③ 结合机器学习进一步探究规律、推广实验,以便为地图全自动综合、空间数据匹配及国家基础地理矢量数据库的建立等提供支撑。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Yan H W, Li J. Concepts of spatial similarity relations in multiscale map spaces[M]//Spatial Similarity Relations in Multi-scale Map Spaces. Cham: Springer International Publishing, 2014:45-80.

[2]
McMaster R B. Automated line generalization[J]. Cartographica: the International Journal for Geographic Information and Geovisualization, 1987, 24(2):74-111.

DOI

[3]
Ai T H, Ke S, Yang M, et al. Envelope generation and simplification of polylines using Delaunay triangulation[J]. International Journal of Geographical Information Science, 2017, 31(2):297-319.

DOI

[4]
Shen Y L, Ai T H, Wang L, et al. A new approach to simplifying polygonal and linear features using superpixel segmentation[J]. International Journal of Geographical Information Science, 2018, 32(10):2023-2054.

DOI

[5]
Kronenfeld B J, Stanislawski L V, Buttenfield B P, et al. Simplification of polylines by segment collapse: Minimizing areal displacement while preserving area[J]. International Journal of Cartography, 2020, 6(1):22-46.

DOI

[6]
Douglas D H, Peucker T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[M]//Classics in Cartography. Chichester, UK: John Wiley & Sons, Ltd, 2011:15-28.

[7]
Li Z L, Openshaw S. Algorithms for automated line generalization1 based on a natural principle of objective generalization[J]. International Journal of Geographical Information Systems, 1992, 6(5):373-389.

DOI

[8]
钱海忠, 何海威, 王骁, 等. 采用三元弯曲组划分的线要素化简方法[J]. 武汉大学学报·信息科学版, 2017, 42(8):1096-1103.

[ Qian H Z, He H W, Wang X A, et al. Line feature simplification method based on bend group division[J]. Geomatics and Information Science of Wuhan University, 2017, 42(8):1096-1103. ]

[9]
Ramer U. An iterative procedure for the polygonal approximation of plane curves[J]. Computer Graphics and Image Processing, 1972, 1(3):244-256.

DOI

[10]
Yan H W. Quantitative relations between spatial similarity degree and map scale change of individual linear objects in multi-scale map spaces[J]. Geocarto International, 2015, 30(4):472-482.

DOI

[11]
Yan H W, Shen Y Z, Li J. Approach to calculating spatial similarity degrees of the same river basin networks on multi-scale maps[J]. Geocarto International, 2016, 31(7):765-782.

DOI

[12]
Chehreghan A, Ali Abbaspour R. An assessment of spatial similarity degree between polylines on multi-scale, multi-source maps[J]. Geocarto International, 2017, 32(5):471-487.

DOI

[13]
Li Z L, Sui H G. An integrated technique for automated generalization of contour maps[J]. The Cartographic Journal, 2000, 37(1):29-37.

DOI

[14]
王家耀, 何宗宜, 蒲英霞. 地图学[M]. 北京: 测绘出版社, 2016.

[ Wang J Y, He Z Y, Pu Y X. Cartography[M]. Beijing: Sino Maps Press, 2016. ]

[15]
Chehreghan A, Ali Abbaspour R. An assessment of the efficiency of spatial distances in linear object matching on multi-scale, multi-source maps[J]. International Journal of Image and Data Fusion, 2018, 9(2):95-114.

DOI

[16]
何海威, 钱海忠, 段佩祥, 等. 线要素化简及参数自动设置的案例推理方法[J]. 武汉大学学报·信息科学版, 2020, 45(3):344-352.

[ He H W, Qian H Z, Duan P X, et al. Automatic line simplification algorithm selecting and parameter setting based on case-based reasoning[J]. Geomatics and Information Science of Wuhan University, 2020, 45(3):344-352. ]

[17]
McMaster R B. A statistical analysis of mathematical measures for linear simplification[J]. The American Cartographer, 1986, 13(2):103-116.

DOI

[18]
Anderson D L, Ames D P, Yang P. Quantitative methods for comparing different polyline stream network models[J]. Journal of Geographic Information System, 2014, 6(2):88-98.

DOI

[19]
Fan H C, Zipf A, Fu Q, et al. Quality assessment for building footprints data on OpenStreetMap[J]. International Journal of Geographical Information Science, 2014, 28(4):700-719.

DOI

[20]
Fan H C, Yang B S, Zipf A, et al. A polygon-based approach for matching OpenStreetMap road networks with regional transit authority data[J]. International Journal of Geographical Information Science, 2016, 30(4):748-764.

DOI

[21]
Li B N, Fonseca F. TDD: A comprehensive model for qualitative spatial similarity assessment[J]. Spatial Cognition & Computation, 2006, 6(1):31-62.

[22]
Zhang M. Methods and implementations of road-network matching[EB/OL]. 2009.

[23]
武芳, 朱鲲鹏. 线要素化简算法几何精度评估[J]. 武汉大学学报·信息科学版, 2008, 33(6):600-603.

[ Wu F, Zhu K P. Geometric accuracy assessment of linear features' simplification algorithms[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6):600-603. ]

[24]
顾腾, 陈晓勇, 刘成强. 一种Douglas-Peucker与Li-Openshaw结合改进的曲线化简方法[J]. 东华理工大学学报(自然科学版), 2016, 39(4):396-400.

[ Gu T, Chen X Y, Liu C Q. A modified line simplification method combined Douglas-peucker with Li-openshaw[J]. Journal of East China University of Technology (Natural Science), 2016, 39(4):396-400. ]

[25]
陈竞男, 钱海忠, 王骁, 等. 提高线要素匹配率的动态化简方法[J]. 测绘学报, 2016, 45(4):486-493.

[ Chen J N, Qian H Z, Wang X A, et al. Improving the matching rate of line feature by using dynamic simplification[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4):486-493. ]

[26]
郭仁忠. 空间分析(2版)[M]. 北京: 高等教育出版社, 2001.

[ Guo R Z. Spacial analysis[M]. Beijing: Higher Education Press, 2001. ]

[27]
White E R. Assessment of line-generalization algorithms using characteristic points[J]. The American Cartographer, 1985, 12(1):17-28.

DOI

[28]
李成名, 郭沛沛, 殷勇, 等. 一种顾及空间关系约束的线化简算法[J]. 测绘学报, 2017, 46(4):498-506.

[ Li C M, Guo P P, Yin Y, et al. A line simplification algorithm considering spatial relations between two lines[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4):498-506. ]

[29]
Joao E M. Causes and consequences of map generalization[M]. London: Taylor and Francis, 1998.

Options
文章导航

/

〈 〉