EN中文

地球信息科学学报 >

2021 , Vol. 23 >Issue 12: 2244 - 2260

DOI: https://doi.org/10.12082/dqxxkx.2021.210057

遥感科学与应用技术

基于深度学习的滑坡灾害易发性分析

  • 王毅 , 1, * ,
  • 方志策 1 ,
  • 牛瑞卿 1 ,
  • 彭令 2
展开
  • 1.中国地质大学（武汉）地球物理与空间信息学院,武汉 430074
  • 2.中国地质环境监测院,北京 100081

王 毅（1979— ）,男,湖北武汉人,博士,教授、博士生导师,主要从事遥感技术与应用、地学信息数据挖掘和环境影响评价等研究。E-mail: cug.yi.

收稿日期: 2021-02-01

  要求修回日期: 2021-04-14

  网络出版日期: 2022-02-25

基金资助

国家自然科学基金项目(61271408)

国家自然科学基金项目(41602362)

智能机器人湖北省重点实验室(武汉工程大学)开放基金项目(HBIR202002)

版权

版权所有,未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
收起

Landslide Susceptibility Analysis based on Deep Learning

  • WANG Yi , 1, * ,
  • FANG Zhice 1 ,
  • NIU Ruiqing 1 ,
  • PENG Ling 2
Expand
  • 1. Institute of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China
  • 2. China Institute of Geo-Environment Monitoring, Beijing 100081, China
*WANG Yi, E-mail:

Received date: 2021-02-01

  Request revised date: 2021-04-14

  Online published: 2022-02-25

Supported by

National Natural Science Foundation of China(61271408)

National Natural Science Foundation of China(41602362)

Open Fund of Hubei Key Laboratory of Intelligent Robot (Wuhan Institute of Technology)(HBIR202002)

Copyright

Copyright reserved © 2021
Fold

摘要

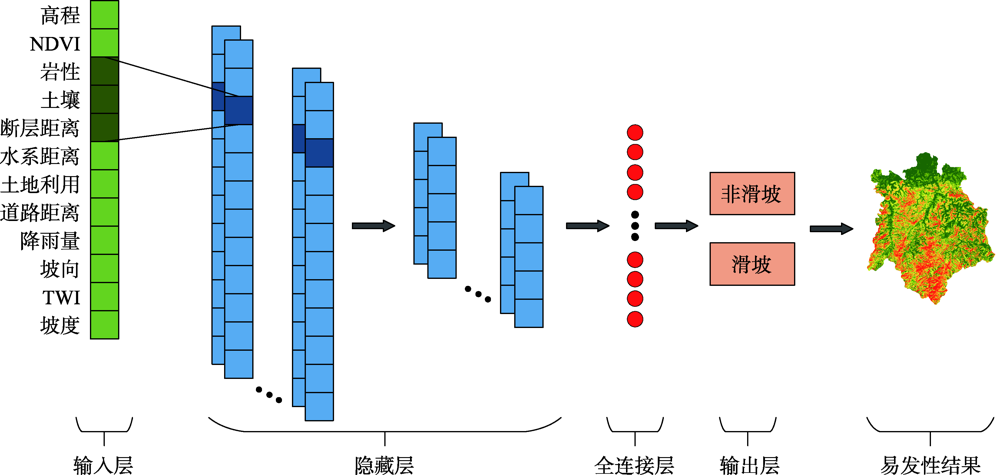
滑坡灾害成因机理复杂、影响因素众多,深度学习作为当前人工智能领域的热点,能够更好地模拟滑坡灾害的形成并准确预测潜在的斜坡。为了挖掘深度学习在滑坡易发性的应用潜能,本文构建了一维、二维和三维的滑坡数据表达形式,并提出3种基于卷积神经网络模型（Convolutional Neural Networks, CNN）的滑坡易发性分析处理框架：基于CNN分类器、基于CNN与逻辑回归的融合和基于CNN集成,最后以江西省铅山县为研究对象进行验证,结果表明：所有基于CNN的易发性模型都能够获得准确且可靠的滑坡易发性分析结果。其中,基于二维数据的CNN模型在所有单分类器中预测精度最高,为78.95%。此外,二维CNN特征提取能够显著提升逻辑回归的预测精度,其准确率提升7.9%。最后,异质集成策略能够大幅度提升基于CNN分类器的滑坡预测精度,其准确率提升4.35%~8.78%。

关键词： 滑坡; 易发性分析; 数据表达; 卷积神经网络; 特征提取; 逻辑回归; 异质集成; 铅山县

本文引用格式

王毅 , 方志策 , 牛瑞卿 , 彭令 . 基于深度学习的滑坡灾害易发性分析[J]. 地球信息科学学报, 2021 , 23(12) : 2244 -2260 . DOI: 10.12082/dqxxkx.2021.210057

Abstract

The formation mechanism of landslide disasters is complicated and there are many influencing factors. It is imperative to explore a low-cost and highly applicable method to manage and prevent landslide disasters. As a hot spot in the current artificial intelligence field, deep learning can better simulate the formation of landslide disasters and accurately predict potential slopes. Thus, to explore the application potential of deep learning, this paper constructs one-dimensional, two-dimensional, and three-dimensional forms of landslide data, and then introduces three Convolutional Neural Networks (CNN)-based landslide susceptibility analysis frameworks, including CNN-based classifiers, integrated models, and ensemble models. The proposed deep learning methods were applied to Yanshan County, Jiangxi Province for experiments. 16 landslide influencing factors were first selected for modelling based on the geomorphological, hydrological, and geological environment conditions of the study area. These factors include altitude, aspect, distance to faults, land use, lithology, normalized difference vegetation index, plan curvature, profile curvature, rainfall, distance to rivers, distance to roads, slope, soil, stream power index, sediment transport index, and topographic wetness index. Then, the multi-collinearity analysis and relief-F algorithm were used to analyze and screen the influencing factors. All CNN-based methods were constructed and validated based on several statistical measures of accuracy, root mean square error, mean absolute error, sensitivity, specificity, and the receiver operation characteristic curve. Finally, the susceptibility value of each pixel in the study area was predicted based on the CNN-based methods, and the entire study areas were reclassified into five susceptibility categories: very low, low, moderate, high, and very high. The factor analysis results show that the plan curvature, profile curvature, stream power index, and sediment transport index are redundant factors and should be removed from further modelling process. The model evaluation results demonstrate that all CNN-based models can obtain accurate and reliable landslide susceptibility mapping results. The two-dimensional CNN model achieved the highest prediction accuracy of 78.95% among single CNN models. Moreover, the performance of logistic regression was effectively improved by combining the two-dimensional CNN for feature extraction, with an accuracy improvement of 7.9%. Besides, the heterogeneous ensemble strategy can greatly improve landslide prediction accuracy when using CNN classifiers, with an accuracy improvement between 4.35% and 8.78%. Generally, the CNN has been proven to have huge application potential in landslide susceptibility analysis and can be implemented in other landslide-prone areas with similar geo-environmental conditions.

Key words： landslide; landslide susceptibility analysis; data representation; convolutional neural networks; feature extraction; logistic regression; heterogeneous ensemble; Yanshan County

1 引言

滑坡地质灾害由于其本身具有空间分布范围广、时间发生频率高以及破坏性强等特点,因此对人类生命安全构成严重威胁,同时也给社会经济带来巨大损失[1]。滑坡灾害易发性评价是通过分析历史和现存滑坡灾害的空间分布,考虑研究区地形地貌、水文气象、基础地质等各类斜坡不稳定因素,对滑坡空间分布及其发生概率进行预测的方法。作为滑坡灾害风险评估的关键步骤,滑坡易发性分析能够为滑坡管理、滑坡风险评估和土地资源管理等工作提供可靠的科学依据。
自20世纪70年代中期开始,许多学者开展了区域滑坡灾害易发性分析的研究。根据理论基础和预测手段的不同,滑坡灾害易发性分析方法可分为5大类,分别为基于地貌学方法、基于滑坡编录分析方法、基于物理力学方法、启发式方法和统计学方法。基于地貌的滑坡易发性制图强烈依赖于研究人员评估现存和潜在边坡失稳状况的能力[2],而最终易发性分区图的质量一方面取决于实验人员的滑坡知识储备能力,另一方面则与研究区地形地貌复杂程度有关。基于滑坡编录分析方法是最原始、最直接的一种区域滑坡灾害易发性预测方法。例如,DeGraff和Canuti[3]利用滑坡历史灾害图构建滑坡空间等值线图,再进一步对区域局部地质条件进行定性评估,从而将研究区划分为6个滑坡危险等级。上述基于地貌学方法和基于滑坡编录分析方法可以看作定性易发性评价手段,该类方法强烈依赖研究人员对实际和潜在斜坡体的评估及分析能力,这会导致不同调查人员得到的易发性结果各不相同,因此该类方法具有较高的不确定性。
基于物理力学方法也称之为确定性方法,该方法通常利用简单的斜坡极限平衡模型来评估斜坡稳定性,从而达到区域滑坡易发性预测的目的[4]。例如,邱骋等[5]以斜坡单元为评价单元,利用三维力学模型对日本49号公路边坡进行滑坡易发性研究,最后通过实地调查发现预测的高危斜坡单元确实发生滑坡灾害。兰恒星等[6]在SINMAP模型计算过程中增加动水压力项,再用其预测云南小江流域滑坡易发性。基于物理力学方法能较好的挖掘滑坡灾害与致灾因子之间的关系,然而该方法也面临诸多问题,例如数据收集困难、致灾因子具有空间变化性,此外,复杂的坡体岩石单元的也会使模型的可靠性大大降低。启发式方法根据主观经验对影响斜坡不稳定因素进行排序和加权从而判断区域滑坡发生的概率大小。具有代表性的启发式方法包括层次分析法[7,8]、模糊逻辑法[9]和线性权重组 合[10]等。该方法能够稳定发挥性能取决于研究人员是否了解该区域滑坡发生的真正原因,以及能够合理的评估不稳定因素的权重。
随着科学技术的发展,空间数据获取的便捷性与可靠性不断提升,统计学方法近年来被广泛的应用于滑坡易发性分析,包括：证据权法[11]、逻辑回 归[12]（Logistic Regression, LR）和支持向量机[13,14]等。相比于传统统计学方法,支持向量机不需要数据符合某种特定分布,能够利用内积核函数代替向高维空间的非线性映射,从而取得较好的预测效果。近些年来,地质灾害数据的质量和数量大幅度提升,这些数据具有多源性、时空性和非线性等特点,如何对海量灾害数据进行准确且可靠的分析十分重要。深度学习作为当前人工智能领域的研究热点,在各个领域引起的广泛的关注。其中,作为深度学习中最具代表性的方法之一,卷积神经网络（Convolutional Neural Networks, CNN）具有强大的表征学习能力,能够按其阶层结构对输入信息进行平移不变分类,也被成功的应用于图像处理[15,16,17]、语音识别[18,19]、场景理解[20,21]、自动驾驶[22,23]等领域中。对于滑坡灾害来说,其成因机理复杂、影响因素众多,深度学习模型在理论上能够更好地模拟滑坡灾害的形成并准确预测潜在的滑坡。因此,基于CNN的滑坡易发性分析方法具有广阔的应用前景。
鉴于此,本文构建了一维、二维和三维的滑坡数据表达形式,并提出3种基于CNN的滑坡易发性分析处理框架：基于CNN分类器、基于CNN与逻辑回归的融合和基于CNN集成,一方面为滑坡风险评估提供依据,另一方面探索CNN在滑坡易发性分析中的适用性。然后以江西省上饶市铅山县为实验区进行验证和讨论。

2 滑坡易发性分析模型

本文总体技术路线如图1所示,首先收集与整理滑坡易发性分析需要的多源数据,并从中提取相应的滑坡评价因子数据和滑坡空间分布信息,再利用多重共线性分析与Relief-F算法筛选出评价因子用于后续建模。然后,通过不同的数据表达方式将滑坡原始数据转换为一维数据、二维数据和三维数据,并根据不同维度数据构建相应的CNN网络结构。最后,将3种基于深度学习的滑坡易发性分析处理框架进行应用。
图1 基于卷积神经网络的易发性分析技术路线

Fig. 1 Flowchart of landslide susceptibility analysis based on convolutional neural networks

2.1 CNN理论基础

CNN最初是由LeCun等[24]针对手写数字识别而提出的一种特殊的神经网络模型,可用于处理具有已知网格拓扑结构的数据。它除了拥有与普通神经网络共有的输入层和输出层之外,其结构还包含卷积层、池化层和全连接层。卷积层中的卷积核可用于提取数据的初级特征,其具体计算公式如下：
C j = ∑ i N f w j × x i + b j , j = 1,2 , · · · , k
式中：k为卷积核的个数; C j表示第j个卷积核的输出;f表示非线性激活函数;i为卷积操作的空间位置; x i表示卷积窗口对应的输入数据; w j和 b j分别表示权重和偏置。
池化操作可以降低卷积层输出特征图的维度,因此层间参数也会相应的减少,从而达到降低模型复杂度,提高计算效率的目的。以二维最大池化为例,其具体计算公式如下：
o i = max i ∈ N a i n × n
式中：i为池化的位置; a i n × n为该次池化操作在位置i上对应的输入数据; o i为池化操作的输出。

2.2 基于CNN的滑坡数据表达方法

由于CNN能通过不同的卷积、池化操作对不同维度的输入数据进行处理,因此它能在许多领域的应用中展现优异性能。将CNN引入滑坡易发性分析的首要问题是如何为CNN模型构建合适的滑坡数据表达方式。本文针对滑坡易发性分析的应用场景将分别构建一维、二维和三维3种滑坡数据表达形式。
（1）如图2左半部分所示,堆叠所有的滑坡评价因子图层组成一幅多通道图像,该图像上各像素均可看作是一个一维特征向量,这些向量构成了一维滑坡数据表达方式。
图2 一维和二维滑坡数据表达形式

Fig. 2 One-dimensional and two-dimensional data forms

（2）为了构建二维滑坡数据,本文在一维滑坡数据表达的基础上,利用改进的独热编码预处理将一维特征向量转换为n×n的二维数据（n表示评价因子个数与因子类别数目之间的较大值）。本文最初选取16个滑坡评价因子,随后通过特征选择移除4个不重要的因子。因此,此处以12个滑坡评价因子为例对滑坡数据表达方法进行描述。如图2所示,一维特征向量的第一个元素为4,则首先构建一个长度为24且元素都为0的向量,再将该向量的第4个元素的值替换为1。通过此处理,12个元素可以编码成一个12×24的矩阵。为了保证输入二维CNN结构的数据长宽一致,可用补零的方式将矩阵填充为24×24的矩阵,这就构成了二维滑坡数据表达。
（3）根据地理学第一定律,地物距离越近,其间相关性越大。因此,滑坡的发生与周围地理区域密切相关。本文通过构建局部窗口来挖掘滑坡空间信息,构建三维滑坡数据表达形式。如图3所示,通过构建了一个5×5的局部窗口,逐个像素提取滑坡数据,其中每个三维数据的数值都与中心像素的数值相一致。
图3 三维滑坡数据表达形式

Fig. 3 Three-dimensional data form

2.3 基于CNN分类器的易发性模型

在本节中,CNN模型将直接作为分类器进行滑坡易发性预测。首先,将滑坡原始数据转换成2.2节所述的3个维度的数据。然后,面对不同维度的数据构建出相应的CNN网络结构。最后,基于不同维度的数据以及对应的CNN结构进行易发性分析。为简便起见,以一维CNN结构为例来详述易发性分析处理过程,如图4所示。首先,一维CNN结构接受的输入数据为一系列12×1的因子向量,经过隐藏层中的卷积与池化操作后,再将提取出来的高维滑坡信息经过全连接层映射到低维特征空间中。最后,通过非线性激活函数将其映射到样本标记空间,输出滑坡与非滑坡的标签与其概率值（滑坡易发性指数）大小。通过一维CNN模型预测每一个栅格单元的易发性指数,得到最终的滑坡易发性结果。
图4 一维CNN结构

Fig. 4 1D-CNN architecture

2.4 基于CNN与逻辑回归的易发性模型

特征工程是机器学习框架中极其重要的一步,它可以把原始数据转换为高质量的特征,从而达到提升预测模型性能的目的[25]。在滑坡易发性分析流程中,研究人员基于多源数据提取出各种滑坡评价因子的过程可看作为初始特征提取。从滑坡灾害防治管理人员或研究人员的角度来看,提取出的滑坡评价因子对分析滑坡成灾机理具有切实的指导意义。对于滑坡智能模型来说,其根本目的在于学习已知样本范式从而预测未知样本。这些评价因子虽易于人们理解,但在模型层面没有足够的区分度;同时,CNN模型在模式识别、场景理解等领域取得良好效果的关键原因就是其强大的特征提取能力[26,27,28]。因此,本节基于CNN对滑坡数据进行特征提取,再将提取出来的高质量特征输入到经典统计学模型中进行易发性预测。从2.2节可知,本文构建了3个CNN网络结构对不同维度的滑坡数据形式进行处理,本节基于这3个CNN结构对不同维度的滑坡数据进行特征提取,再将提取出的特征输入到逻辑回归模型中进行易发性预测。为简便起见,以一维CNN结构为例来详述基于CNN和逻辑回归的易发性模型框架,如图5所示。其中,输入数据为一系列12×1的因子向量,随着隐藏层中卷积、池化等操作,高级特征被映射到低维空间并储存到全连接层中的神经单元中。最后,与2.3节不同的是,CNN模型并不直接输出易发性结果,而是将高级特征输入到逻辑回归模型中进行易发性预测。
图5 基于CNN和逻辑回归的易发性模型结构

Fig. 5 Structure of the hybrid modelling process of CNN and LR

2.5 基于CNN集成的易发性模型

集成学习的基本思想是通过特定的策略整合多个预测模型,和单一的模型相比,集成学习有着更强大泛化能力[29]。本节基于3种不同思想的异质集成策略,对2.2节提出的3种CNN模型进行融合,实现滑坡灾害易发性分析。
（1） Stacking集成
Stacking集成策略利用元学习器将不同的初级分类器融合到一起[30]。该集成算法首先通过交叉验证的方式,使用训练初级学习器未使用的样本来产生元学习器的训练样本。以k折交叉验证为例,初始训练集被划分为k个大小相同的集合D1,D2,…,Dk。令其中一个集合为初级测试集,剩余的k-1个集合为初级训练集训练初级分类器,再利用该初级分类器对初级测试集进行预测,预测值作为元学习器训练集的一部分,重复k次得到元学习器的训练集。最后,利用该训练集训练元学习器并进行预测。
（2） Blending集成
与Stacking类似,Blending利用元学习器将不同的初级分类器融合到一起[31],它们的区别在于Blending未使用交叉验证产生元学习器的训练样本,而是使用留一法产生新的训练集。相对于Stacking集成策略,Blending结构更为简单且能够避免信息泄露问题,但因其没有使用全部的训练集训练初级分类器,可能会产生过拟合问题。
（3）加权平均集成
加权平均法的使用最早可以追溯到1952年[32],其在集成学习领域具有极其重要的地位,后续的各种集成策略都可以看作他的变体。本文作者利用加权平均融合3个CNN模型用于易发性分析,该集成策略中的权重由个体分类器的受试者工作特征（Receiver Operating Characteristic, ROC）曲线下方面积大小值（Area Under Curve, AUC）确定。加权平均的计算公式如下：
p WA = AU C i ∑ i N AU C i p i
式中：N为基分类器的个数;AUCi和pi分别表示第i个基分类器的AUC值和预测概率值。

2.6 模型评价指标

本文选用准确率（Accuracy, ACC）、均方根误差（Root Mean Square Error, RMSE）、平均绝对误差（Mean Absolute Error, MAE）、敏感度（Sensitivity, SEN）和特异度（Specificity, SPE）共5个统计学指标评价模型,相应的描述和公式如表1所示。其中,ACC、敏感度和特异度取值范围在0到1之间,其中值越接近于1表示对应的模型性能越好,而RMSE和MAE的值越接近于0则表示模型性能越好。另外一个本文使用的评价指标为ROC曲线,其AUC值用来衡量模型的优劣。AUC值越接近于1,表明该模型性能更优异。
表1 模型评价指标

Tab. 1 Model evaluation measures

评价指标 变量含义 公式编号
ACC = TP + TN TP + TN + FP + FN 真阳性（True Positive, TP）表示正确分类的滑坡样本个数,假阳性（False Positive, FP）表示错误分类的非滑坡样本个数,真阴性（True Negative, TN）表示正确分类的非滑坡样本个数,假阴性（False Negative, FN）表示错误分类的滑坡样本个数 （4）
SEN = TP TP + FN （5）
SPE = TN TN + FP （6）
RMSE = 1 n ∑ i = 1 n ( o i - p i ) 2 n为样本个数, o i和 p i分别代表第i个样本的观测值和预测值 （7）
MAE = 1 n ∑ i = 1 n o i - p i （8）

3 研究区概况与数据分析

3.1 研究区概况

铅山县位于江西省东北部,属上饶市辖县, 如图6所示。该县占地面积约2178.17 km2,占全省面积的1.3%。铅山县在地理位置上距海洋较近,容易受到亚洲大陆和太平洋季风交错影响。铅山县属亚热带温湿型气候,该区域气候温和,雨量充沛,年均温度约17.9 ℃。1959—2016年年均降雨量在1700~2100 mm之间,辖区内4—7月的降雨量占全年降雨量的58%。铅山县内发育的各时代地层均有出露,仅缺少奥陶系、志留系与泥盆系地层。境内岩浆岩分布广泛,占全县面积的34.43%。从岩性类别上看,基性、酸性、中性岩均有分布。从形成时间上来看,加里东期、燕山期均有岩浆活动。县褶皱构造主要分布在研究区中部,由上石炭统至下侏罗地层单位构成。受自然与人为因素影响,研究区内地质灾害类型众多,各类地质灾害发生频繁且分布范围较广,给人民的生命财产造成了重大的影响。滑坡是研究区境内发生数量最多,危害最为严重的地质灾害类型,占灾害点总数的50%[33]。由于特殊的地质环境,区内滑坡灾害虽然规模不大,但是具有隐蔽性与突发性的特点,给社会带来的极大的危害。距相关资料,全县因滑坡灾害而毁坏的房屋达到数百间,直接或间接的毁坏公路、水渠、农田等,直接经济损失高达数百万元[33]。
图6 铅山县2010年前滑坡灾害分布

Fig. 6 Distribution map of landslide locations in Yanshan County before 2010

3.2 滑坡数据

本文通过实地调查、Google Earth解译以及历史编录数据统计得到研究区滑坡编录数据,如图6所示。研究区共有380处滑坡,其中滑坡最大总面积为15 722 m2,最小为172 m2。境内滑坡以小型滑坡为主,占比高达99%,其中又以土质滑坡居多。区内滑坡均为牵引式滑坡,大多数呈舌形和半圆形。滑坡厚度一般在0.5~10 m之间,均为浅层滑坡。

3.3 滑坡评价因子确定及数据来源

评价因子的选取对于滑坡易发性分析至关重要。本文通过野外调查研究及相关文献分析[10,14,34-36],综合考虑研究区的地形地貌、基础地质、水文条件等因素,最终选取16种滑坡评价因子,如图7所示。其中,DEM数据提取于1：50 000地形图;坡向、坡度、平面曲率和剖面曲率因子基于ArcGIS软件从DEM数据中提取;径流强度指数（Stream Power Index, SPI）、输沙指数（Sediment Transport Index, STI）、和地形湿度指数（Topographic Wetness Index, TWI）因子基于SAGA软件从DEM数据中提取;岩性和断层距离因子提取于中国地质调查局2002年完成的1: 200 000地质图;降雨量数据由江西省气象局提供,并对其进行克里金插值处理;水系网和道路网提取于1：50 000地形图,再利用欧氏距离工具得到水系距离和道路距离因子;利用支持向量机对2010年获取的Landsat-7卫星影像进行分类得到土地利用因子,该影像数据下载于地理空间数据云（http://www.gscloud.cn/）;植被归一化指数（Normalized Difference Vegetation Index, NDVI）因子基于ENVI软件利用波段计算工具对卫星影像进行处理得到;土壤因子基于中国地质调查局1995年编制的1: 1 000 000土壤类型图矢量化所得。在滑坡易发性分析中,滑坡灾害编录中记录的滑坡通常发生在不同时间段,且由于滑坡评价因子的来源不同,无法保证所有的因子处于同一时间节点。其中,岩性和土壤类型在短时间内不会发生太大的变化,但土地利用和NDVI可能在数年间发生较大改变。因此,为了降低数据源获取时间不同所带来的影响,本文在收集数据的过程中尽量避免时间差异过大。
图7 滑坡评价因子专题图

Fig. 7 Thematic maps of landslide influencing factors

为了保证空间一致性,本文将这些因子图层重采样至具有相同空间分辨率25 m,与DEM数据分辨率保持一致。在此基础上,根据历史文献及专家经验对连续型图层进行重分类,再对所有图层子类别进行赋值处理。
（1）高程。不同高程区域有着不同的植被覆盖率和土壤湿度等特征。同时,相对海拔低的地区,人类工程活动较多,而在高海拔地区,人口聚集相对稀疏。本研究区高程数据分为6个等级：< 200 m、200~400 m、400~600 m、600~1000 m、1000~1400 m和> 1400 m。
（2）坡向。不同斜坡坡向具有不同强度的太阳辐射,导致植被覆盖和地表含水率不同,进而影响斜坡的稳定程度。坡向通常分为平地、北、东北、东、东南、南、西南、西、西北。
（3）坡度。坡度对于滑坡的孕育与演化具有极其重要的作用,通常只有斜坡才有可能孕育出滑坡灾害。本研究区坡度分为7个等级：0~10°、10~20°、20~30°、30~40°、40~50°、50~60°和60~70°。
（4）曲率。斜坡坡面的扭曲变形程度影响了斜坡内部应力分布,从而对滑坡灾害的发育具有不同程度的影响。本文平面曲率和剖面曲率的计算方法采用四阶曲面模型[37],且均分为3个等级：< 0.4、-0.4~0.5、>0.5和<-1、-1~0.2、>0.2。
（5）岩性。岩体的物理力学特性以及层间机构决定了岩土体应力分布,进而影响到斜坡的稳定性。同时不同岩性的风化程度决定了斜坡滑动的难易程度。据野外地质调查,本研究区共有24种岩性类型。
（6）断层距离。构造断层对其一定范围内的岩体产生破坏作用,从而影响斜坡的完整性。另一方面,断层的产生也会为地下水流动提供通道,从而加速斜坡的变形与滑动。本研究区断层距离分为5个等级：< 2000 m、2000~5000 m、5000~8000 m、8000~11 000 m和> 11 000 m。
（7）降雨量。少量的降雨会使雨水渗入地表成为地下水的一部分,一旦地下水含量增多,斜坡的应力状态相应受到改变,进而影响到斜坡的稳定。大量的降雨会对坡体起到强烈的冲刷作用,从而直接引起滑坡的产生。本文采用年均降雨量,分为5个等级：< 1000 mm,1000~1200 mm,1200~1300 mm,1300~1400 mm和> 1400 mm。
（8）水系距离。河流的浸泡使斜坡的软化夹层泥化,从而降低了斜坡的抗剪程度。同时,在靠近水系区域,水流的冲刷使斜坡坡脚土体大量流失,增大临空面,从而影响斜坡稳定。本研究区水系距离分为4个等级：< 200m、200~400 m、400~700 m和> 700 m。
（9）土地利用。本研究区山地分布广泛,居民房屋的修筑往往紧挨斜坡;同时伴随修筑时的切坡填土工作,影响了斜坡的稳定状态。本文利用支持向量机分类器将研究区Landsat 7卫星影像分成6种地物：草地,水体,林地,耕地,建筑用地和裸土地。
（10）道路距离。不合理的削山填谷、水土流失和植被减少常常会使斜坡处于失稳状态。本研究区道路距离分为4个等级：< 600 m、400~1300 m、1300~2300 m和> 2300 m。
（11） NDVI。密集的植被覆盖一方面可以遮挡雨水,降低雨水对斜坡的负面影响;另一方面,植被生长时的根劈作用对岩石裂隙壁产生挤压,引起岩石的破坏,进而加大了水流的渗入,影响斜坡稳定状态。本研究区NDVI分为5个等级：< 0.1、0.1~0.2、0.2~0.3、0.3~0.4和> 0.4。
（12）土壤。在欠饱和条件下,质地较细的土壤比粗糙的土壤有更强的储水能力。一旦发生强降雨,强储水能力的土壤会加大斜坡体的重量,从而引起坡体的滑动。本研究区共有6个土壤类型：人为堆积土（Cumulic Anthrosols, ATc）、简育低活性强酸土（Haplic Acrisols, ACh）、腐殖质低活性强酸土（Humic Acrisols, ACu）、简育高活性淋溶土（Haplic Luvisols, LVh）、简育高活性强酸土（Haplic Alisols, ALh）和腐殖质雏形土（Humic Cambisols, CMu）。
（13） SPI。SPI可用于描述地形表面给定地点水流的潜在侵蚀能力。随着流域面积和坡度的增加,来自于上坡面积的水量及流速也会相应增加,从而增大了侵蚀风险。本文将研究区SPI信息分成5个等级：< 10、10~20、20~35、35~50和> 50。
（14） STI。STI源于流域演变侵蚀理论,用于表示地形表面水流的泥沙输送量,也相应的反映了地形表面的侵蚀与沉积过程。本文将研究区STI信息分为5个等级：< 4、4~8、8~14、14~20和> 20。
（15） TWI。TWI是描绘地面土壤湿度的指标,它能够定量评估径流趋势以及径流汇聚的位置。本文将研究区TWI信息分为5个等级：<5、5~7、7~9、9~11和>11。

4 结果与分析

4.1 滑坡评价因子多重共线性与重要性分析

根据历史研究及专家经验,初步选取的滑坡评价因子之间可能存在统计学上的共线性关系,这会导致易发性模型无法准确的分析评价因子与滑坡之间的真实关系。此外,影响滑坡因素众多,评价因子中存在的冗余信息可能会影响易发性结果的精度。因此,本文从共线性分析及重要性分析2个角度对滑坡评价因子进行定量评价与筛选。本研究区评价因子多重共线性分析结果如表2所示,其中STI的VIF（方差膨胀系数）和TOL（容忍度）值分别为10.466和0.096,表明STI与其他评价因子之间存在共线性,应该在后续建模中剔除。
表2 滑坡评价因子多重共线性分析结果

Tab. 2 Multicollinearity analysis results of landslide influencing factors

滑坡评价因子 统计值
TOL VIF
坡度 0.249 4.020
坡向 0.935 1.069
断层距离 0.865 1.156
土地利用 0.695 1.438
岩性 0.776 1.289
NDVI 0.700 1.428
平面曲率 0.569 1.756
剖面曲率 0.726 1.378
降雨量 0.590 1.695
水系距离 0.828 1.207
道路距离 0.852 1.174
坡度 0.310 3.221
土壤 0.351 2.846
SPI 0.102 9.802
STI 0.096 10.466
TWI 0.443 2.258
此外,本文选用Relief-F方法来定量分析滑坡评价因子的重要性。该算法根据评价因子对近距离样本的区分能力来确定因子的贡献大小,其核心思想是重要的特征应该使同类别样本的距离靠近,而使不同类样本之间更加分散[38]。滑坡评价因子的重要性排序如图8所示,其中高程相对其他因子而言对滑坡贡献最大,而平面曲率、剖面曲率和SPI因子重要性统计值为负,可视为冗余因子而剔除。因此,剩余的12个评价因子用于后续的模型构建。
图8 滑坡评价因子重要性

Fig. 8 Importance of landslide influencing factors

4.2 CNN模型构建

在进行滑坡易发性预测之前,需要选取训练样本和测试样本用于构建滑坡易发性模型,且训练集与测试集均由滑坡样本和非滑坡样本共同组成。由2.2节可知,研究区共有380个滑坡样本,本文从非滑坡区域随机选取380个样本点作为非滑坡样本。从滑坡样本和非滑坡样本中随机选取70%的数据进行模型训练,而剩余的30%样本用于模型测试。
本文以Python作为编程语言,利用深度学习库Keras进行CNN模型的构建。首先,在CNN训练过程中确定一个初步的CNN网络结构及其超参数,再利用试错法对超参数进行微调,将相对最优的超参数用于滑坡灾害易发性分析。最后,基于调整好的网络进行最终的滑坡易发性分析。为了简便起见,将基于一维、二维和三维滑坡数据构建的CNN模型分别命名为1D-CNN、2D-CNN和3D-CNN。这3种CNN网络相同,在输入层后跟随一个卷积层、一个最大池化层和一个全连接层。其中,1D-CNN、2D-CNN和3D-CNN卷积核个数分别为15、15和40;1D-CNN、2D-CNN和3D-CNN全连接层神经元个数为20、15和40。CNN模型其他重要超参数如表3所示。
表3 本文CNN模型超参数设置

Tab. 3 Hyperparameter settings of the proposed CNN models

超参数 1D-CNN 2D-CNN 3D-CNN
卷积核大小 3×1 3×3 3×3
池化核大小 2×1 2×2 2×2
激活函数 Tanh ReLU ReLU
优化器 Adagrad
损失函数 交叉熵损失函数
学习率 0.01 0.005 0.005
Dropout rate 0.2 0.3 0
Epoch 120 80 110

4.3 基于CNN分类器的易发性分析结果

3种CNN模型的精度如表4所示。其中,2D-CNN的总体精度、敏感度和特异度值最高,RMSE和MAE值最小。因此,其性能最优。此外,1D-CNN和3D-CNN有着相似的ACC、RMSE和MAE值,而1D-CNN具有高敏感度和低特异度,表明1D-CNN将部分非滑坡预测为滑坡,可能导致不必要的人力、物力和财力的耗费,但也能减少潜在的滑坡危害。3种模型的ROC曲线如图9所示,可以看出2D-CNN具有最高的AUC值,这也再次印证了2D-CNN的优异性能。
表4 基于CNN分类器的精度评价

Tab. 4 Performance of different CNN classifiers

模型 ACC/% RMSE MAE 敏感度 特异度
1D-CNN 76.31 0.4867 0.2368 0.7105 0.8158
2D-CNN 78.95 0.4588 0.2105 0.7193 0.8596
3D-CNN 76.32 0.4866 0.2368 0.6754 0.8509
图9 3种CNN分类器的ROC曲线

Fig. 9 ROC curves for three CNN classifiers

3种CNN模型的滑坡易发性分区图如图10所示。可以看出,3个分区图在空间分布上具有相似性。例如,极低易发区和极高易发区主要分布在研究区北部和南部。此外,3个分区图也存在少许差异。例如,2D-CNN的中易发区（黄色区域）分布最少,其次为3D-CNN,而1D-CNN具有较多的中易发区。
图10 CNN分类器易发性评价

Fig. 10 Landslide susceptibility maps of different CNN classifiers

4.4 基于CNN与逻辑回归的易发性分析结果

本文利用CNN对滑坡原始数据进行特征提取,再通过LR模型预测研究区易发性。论文将3种CNN与LR进行融合,分别命名为1D-CNN-LR、2D-CNN-LR和3D-CNN-LR。这3种融合模型的精度以及ROC曲线分别如表5和图11所示。可以看出,3种模型的精度明显比LR模型高,这说明经过CNN提取后的特征能显著提升原始LR模型的性能,其准确率提升2.64%至7.9%。此外,二维CNN特征提取操作对提升LR精度效果最为明显,ACC、敏感度、特异度和AUC分别提升了7.9%、0.0263、0.1316和0.05,RMSE和MAE降低了0.0785和0.0790。
表5 融合模型和LR模型的精度评价

Tab. 5 Performance of the proposed integrated models and LR

模型 ACC/% RMSE MAE 敏感度 特异度
1D-CNN-LR 75.00 0.5000 0.2500 0.7281 0.7719
2D-CNN-LR 78.51 0.4636 0.2149 0.7193 0.8509
3D-CNN-LR 73.25 0.5172 0.2675 0.7105 0.7544
LR 70.61 0.5421 0.2939 0.6930 0.7193
图11 融合模型和LR模型的ROC曲线

Fig. 11 ROC curves for proposed integrated models and LR

基于3种融合模型和LR的滑坡易发性分区结果如图12所示,可以看出4种模型得到的易发性图具有类似的空间分布：极低易发区和极高易发区位主要位于研究区北部和南部。此外,LR模型易发性图中极低易发区较少,且北部区域包含少许中易发区和高易发区。
图12 融合模型和LR模型易发性评价

Fig. 12 Landslide susceptibility maps of the proposed integrated models and LR

综合4.3节和4.4节的易发性结果来看,2D-CNN模型无论是直接用于易发性预测还是用于特征提取都能发挥其优异性能。由于CNN结构的特殊性,模型性能的优劣离不开数据的表达方式。在本文中,一维滑坡数据只包含滑坡评价因子序列信息,而二维数据是对一维数据的一种二维扩张,这种转变使得滑坡评价因子信息以图像形式表现出来,同时该数据形式也赋予了评价因子空间相对位置关系,因此CNN模型能够更加便捷全面的分析因子与因子之间关系,以及挖掘评价因子与滑坡发生之间的函数关系。由于滑坡的发生不仅与自身位置属性信息有关,也离不开附近环境信息,因此三维滑坡数据表达方式不仅包含了评价因子信息,还引入了局部空间信息。易发性结果表明基于 3D-CNN的易发性预测和特征提取结果比1D-CNN更为优异,这也证明了该数据表达方式的效性。然而,3D-CNN的精度相对2D-CNN较低,这可能是因为三维数据虽然能提供重要的空间信息,但也会带来冗余信息从而对易发性建模产生负面影响。

4.5 基于CNN集成的易发性分析结果

为了获得性能更优的滑坡灾害易发性模型,本研究将1D-CNN、2D-CNN和3D-CNN模型通过3种异质集成进行融合,这3种集成策略分别为Stacking、Blending和WA。在建模过程中,基分类器超参数见表3所示。WA集成方法无额外超参数,Stacking和Blending需优化的超参数分别为交叉验证折数和留一法验证集比例。实验表明,Stacking使用七折交叉验证时可达最优;Blending则在留一法验证集比例为0.5时达到最优。
为了展现集成模型的性能优势,作者将4.3节中CNN分类器和集成模型进行比较,其预测精度如表6所示。相对于基分类器,集成模型的性能具有较为明显的优势。在3种集成策略中,Stacking的ACC高达85.09%,比基分类器高出6.14%~8.78%。WA虽然在集成模型中精度最低,但其ACC仅比Stacking低1.79%。集成模型的ROC曲线如图13所示,可以看出集成模型AUC值比基分类器高0.061~0.085,其中Blending具有最高的AUC值。
表6 集成模型和CNN分类器的精度评价

Tab. 6 Performance of the proposed ensemble models and CNN classifiers

模型 ACC/% RMSE MAE 敏感度 特异度
集成模型 Stacking 85.09 0.3862 0.1491 0.8684 0.8333
Blending 83.88 0.4082 0.1667 0.8070 0.8596
WA 83.30 0.4082 0.1667 0.7632 0.9035
基分类器 1D-CNN 76.31 0.4867 0.2368 0.7105 0.8158
2D-CNN 78.95 0.4588 0.2105 0.7193 0.8596
3D-CNN 76.32 0.4866 0.2368 0.6754 0.8509
图13 集成模型和CNN分类器的ROC曲线

Fig. 13 ROC curves for ensemble methods and CNN classifiers

集成模型的易发性分区结果如图14所示,可以看出各个易发性分区空间分布与前面所述模型相似。3种集成模型易发性图中部地区都能发现与2D-CNN易发性图相似的一个类似椭圆的结构,这说明集成策略在结合综合各基分类器优点的同时,也能够继承基分类器的特征。
图14 异质集成模型易发性评价

Fig. 14 Landslide susceptibility maps of the proposed heterogeneous ensemble models

5 结论

CNN有着强大的表征提取能力,能够从高维数据中挖掘出隐藏的函数关系。在滑坡易发性建模中,CNN拥有挖掘滑坡高级特征并准确预测易发性的潜力。本文以江西省上饶市铅山县为研究区,选取高程、坡度、坡向、平面曲率、剖面曲率、岩性等16个滑坡评价因子,通过不同的数据表达方式将滑坡原始数据转换为一维数据、二维数据和三维数据,并根据不同维度数据构建相应的CNN网络结构,最后以3种不同的应用模式将CNN用于滑坡灾害易发性分析。最终得到如下结论：
（1）一维、二维和三维数据表达方法能将滑坡数据与CNN模型有机联系起来,基于不同数据表达方法建立的CNN结构在3种滑坡易发性处理框架中都能取得可靠的预测结果。当CNN作为分类器直接用于易发性预测时,2D-CNN的预测性能最佳,其AUC和ACC分别为0.833和78.95%。
（2）CNN特征提取能够得到更优质的滑坡特征集,并显著提升逻辑回归模型的预测精度,其准确率提升2.64%~7.9%。其中,2D-CNN特征提取带来的精度提升最高,AUC提升了0.05,ACC提升了7.9%,说明二维数据结构能较好的呈现滑坡与环境影响因素之间的联系。
（3）本文通过Stacking,Blending和WA这3种异质集成策略将1D-CNN,2D-CNN和3D-CNN融合起来能够得到精度更高、鲁棒性更强的模型,其AUC较基分类器提升0.061~0.085,ACC提升4.35%~8.78%。其中,WA集成模型精度提升虽然不是最高,但有着结构简单,无额外超参数和易于复现等优点,具有更为广阔的应用前景。
综上所述,本文不仅证明了CNN模型在滑坡易发性分析有着巨大的应用潜力,同时提供了CNN模型的不同的应用模式,这为其他深度学习模型的应用打下了基础。此外,CNN模型在滑坡易发性分析中的应用也存在训练样本不足、超参数寻优较复杂的问题,解决这些问题并探索更有效的深度学习模型将是未来的研究目标。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
晏同珍, 杨顺安, 方云. 滑坡学[M]. 武汉: 中国地质大学出版社, 2000.

[ Yan T Z, Yang S A, Fang Y. Landslidologies[M]. Wuhan: China University of Geosciences Press, 2000. ]

[2]
Seeley M W, West D O. Approach to geologic hazard zoning for regional planning, Inyo National Forest, California and Nevada[J]. Bulletin of the Association of Engineering Geologists, 1990, 27(1):23-35.

[3]
Degraff J V, Canuti P. Using isopleth maps of landslide deposits as a tool in timber sale planning[J]. Bulletin of the Association of Engineering Geologists, 1985, 22(4):445-453.

[4]
Montgomery D R, Dietrich W E. A physically based model for the topographic control on shallow landsliding[J]. Water Resources Research, 1994, 30(4):1153-1171.

DOI

[5]
邱骋, 王纯祥, 江崎哲郎等.基于边坡单元的公路沿线滑坡危险度概率分析[J]. 岩土力学, 2005, 26(11):40-45.

[ Qiu C, Wang C X, Jiang Q Z L, et al. Slope unit based probabilistic analysis of slope stability along highway routes in Japan[J]. Rock and Soil Mechanics, 2005, 26(11):40-45. ]

[6]
兰恒星, 周成虎, 伍法权, 等. GIS支持下的降雨型滑坡危险性空间分析预测[J]. 科学通报, 2003, 48(5):507-512.

[ Lan H Q, Zhou C H, Wu F Q, et al. Spatial analysis of rainfall-induced landslide hazard based on GIS[J]. Chinese Science Bulletin, 2003, 48(5):507-512. ]

[7]
许嘉慧, 孙德亮, 王月, 等. 基于GIS与改进层次分析法的奉节县滑坡易发性区划[J]. 重庆师范大学学报(自然科学版), 2020, 37(2):36-44,封2.

[ Xu J H, Sun D L, Wang Y E, et al. Landslide susceptibility mapping of Fengjie County based on GIS and improved analytic hierarchy process[J]. Journal of Chongqing Normal University (Natural Science Edition), 2020, 37(2):36-44,封2. ]

[8]
楚敬龙, 杜加强, 滕彦国, 等. 基于GIS的重庆市万州区滑坡灾害危险性评价[J]. 地质通报, 2008, 27(11):1875-1881.

[ Chu J L, Du J Q, Teng Y G, et al. Landslide hazard evaluation of Wanzhou District, Chongqing City, China based on GIS[J]. Geological Bulletin of China, 2008, 27(11):1875-1881. ]

[9]
沈玲玲, 刘连友, 许冲, 等. 基于多模型的滑坡易发性评价——以甘肃岷县地震滑坡为例[J]. 工程地质学报, 2016, 24(1):19-28.

[ Shen L L, Liu L Y, Xu C, et al. Multi-models based landslide susceptibility evaluation—illustrated with landslides triggered by Minxian earthquake[J]. Journal of Engineering Geology, 2016, 24(1):19-28. ]

[10]
王进, 郭靖, 王卫东, 等. 权重线性组合与逻辑回归模型在滑坡易发性区划中的应用与比较[J]. 中南大学学报(自然科学版), 2012, 43(5):1932-1939.

[ Wang J, Guo J, Wang W D, et al. Application and comparison of weighted linear combination model and logistic regression model in landslide susceptibility mapping[J]. Journal of Central South University, 2012, 43(5):1932-1939. ]

[11]
胡燕, 李德营, 孟颂颂, 等. 基于证据权法的巴东县城滑坡灾害易发性评价[J]. 地质科技通报, 2020, 39(3):187-194.

[ Hu Y, Li D Y, Meng S S, et al. Landslide susceptibility evaluation in Badong County based on weights of evidence method[J]. Bulletin of Geological Science and Technology, 2020, 39(3):187-194. ]

[12]
Zhao Y, Wang R, Jiang Y J, et al. GIS-based logistic regression for rainfall-induced landslide susceptibility mapping under different grid sizes in Yueqing, Southeastern China[J]. Engineering Geology, 2019, 259:105147.

DOI

[13]
Pandey V K, Pourghasemi H R, Sharma M C. Landslide susceptibility mapping using maximum entropy and support vector machine models along the highway corridor, Garhwal Himalaya[J]. Geocarto International, 2020, 35(2):168-187.

DOI

[14]
武雪玲, 任福, 牛瑞卿, 等. 斜坡单元支持下的滑坡易发性评价支持向量机模型[J]. 武汉大学学报·信息科学版, 2013, 38(12):1499-1503.

[ Wu X L, Ren F, Niu R Q, et al. Landslide susceptibility prediction based on slope units and support vector machines[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12):1499-1503. ]

[15]
Pelt D M, Sethian J A. A mixed-scale dense convolutional neural network for image analysis[J]. Proceedings of the National Academy of Sciences of the United States of America, 2018, 115(2):254-259.

[16]
Zhang K, Zuo W, Chen Y, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7):3142-3155.

DOI PMID

[17]
Kim J, Nguyen A D, Lee S. Deep CNN-based blind image quality predictor[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(1):11-24.

DOI

[18]
Hinton G, Deng L, Yu D, et al. Deep neural networks for acoustic modeling in speech recognition[J]. Ieee Signal Processing Magazine, 2012, 11:82-97.

[19]
黄玉蕾, 罗晓霞, 刘笃仁. MFSC系数特征局部有限权重共享CNN语音识别[J]. 控制工程, 2017, 24(7):1507-1513.

[ Huang Y L, Luo X X, Liu D R. Local finite weight sharing of MFSC coefficients based CNN speech recognition[J]. Control Engineering of China, 2017, 24(7):1507-1513. ]

[20]
Pinheiro P H, Collobert R. Recurrent convolutional neural networks for scene labeling[C]. 31st International Conference on Machine Learning(ICML), 2014.

[21]
Pan X G, Shi J P, Luo P, et al. Spatial as deep: Spatial cnn for traffic scene understanding[C]. Thirty-Second AAAI Conference on Artificial Intelligence, 2018.

[22]
Oh M, Cha B, Bae I, et al. An urban autodriving algorithm based on a sensor-weighted integration field with deep learning[J]. Electronics, 2020, 9(1):158.

DOI

[23]
Chen Y-H, Krishna T, Emer J S, et al. Eyeriss: An energy-efficient reconfigurable accelerator for deep convolutional neural networks[J]. IEEE Journal of Solid-state Circuits, 2016, 52(1):127-138.

DOI

[24]
Lecun Y, Boser B, Denker J S, et al. Backpropagation applied to handwritten zip code recognition[J]. Neural Computation, 1989, 1(4):541-551.

DOI

[25]
孙鑫. 机器学习中特征选问题研究[D]. 长春:吉林大学, 2013.

[ Su X. Research on Feature Selection for Machine Learning[D]. Changchun: Jilin University, 2013. ]

[26]
Lee C, Landgrebe D A. Feature extraction based on decision boundaries[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(4):388-400.

DOI

[27]
Weimer D, Scholz-Reiter B, Shpitalni M. Design of deep convolutional neural network architectures for automated feature extraction in industrial inspection[J]. CIRP Annals - Manufacturing Technology, 2016, 65(1):417-420.

DOI

[28]
Guanbin Li, Yizhou Yu. Visual saliency detection based on multiscale deep CNN features[J]. IEEE Transactions on Image Processing, 2016, 25(11):5012-5024.

DOI PMID

[29]
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.

[ Zhou Z H. Machine learning[M]. Beijing: Tsinghua University Press, 2016. ]

[30]
Wolpert D H. Stacked generalization[J]. Neural Networks, 1992, 5(2):241-259.

DOI

[31]
Fang Z C, Wang Y, Peng L, et al. A comparative study of heterogeneous ensemble-learning techniques for landslide susceptibility mapping[J]. International Journal of Geographical Information Science, 2021, 35(2):321-347.

DOI

[32]
Hm M. Portfolio selection[J]. Journal of Finance, 1952, 7(1):77-91.

[33]
文琼. 浅谈铅山县滑坡发育特征及形成条件[J]. 中国金属通报, 2018, 11:142-143.

[ Wen Q. Research on the development characteristics and forming conditions of landslides in Yanshan County[J]. China Metal Bulletin, 2018, 11:142-143. ]

[34]
Reichenbach P, Rossi M, Malamud B, et al. A review of statistically-based landslide susceptibility models[J]. Earth-science Reviews, 2018, 180:60-91.

DOI

[35]
许冲, 戴福初, 姚鑫, 等. GIS支持下基于层次分析法的汶川地震区滑坡易发性评价[J]. 岩石力学与工程学报, 2009, 28(S2):3978-3985.

[ Xu C, Dai F C, Yao X, et al. GIS-based landslide susceptibility assessment using analytical hierarchy process in Wenchuan earthquake region[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S2):3978-3985. ]

[36]
王佳佳, 殷坤龙, 肖莉丽. 基于GIS和信息量的滑坡灾害易发性评价——以三峡库区万州区为例[J]. 岩石力学与工程学报, 2014, 33(4):797-808.

[ Wang J J, Yin K L, Xiao L L. Landslide susceptibility assessment based on gis and weighted information value: A case study of Wanzhou district, Three Gorges reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(4):797-808. ]

[37]
Zevenbergen L W, Thorne C R. Quantitative analysis of land surface topography[J]. Earth Surface Processes and Landforms, 1987, 12(1):47-56.

DOI

[38]
Guyon I, Elisseeff A. An introduction to variable and feature selection[J]. Journal of Machine Learning Research, 2003, 3:1157-1182.

Options
文章导航

/

〈 〉