EN中文

地球信息科学学报 >

2022 , Vol. 24 >Issue 5: 837 - 850

DOI: https://doi.org/10.12082/dqxxkx.2022.210535

地球信息科学理论与方法

基于LDA和优化蚁群的OD流向时空语义聚类算法

  • 张晗 , 1, 2, 3 ,
  • 邬群勇 , 1, 2, 3, *
展开
  • 1.福州大学空间数据挖掘与信息共享教育部重点实验室,福州 350108
  • 2.卫星空间信息技术综合应用国家地方联合工程研究中心,福州 350108
  • 3.福州大学数字中国研究院（福建）,福州 350003
* 邬群勇（1973— ）,男,山东诸城人,博士,研究员,主要从事时空数据挖掘和地理信息服务研究。 E-mail:

张 晗（1994— ）,男,福建永安人,硕士生,主要从事时空数据挖掘研究。E-mail:

收稿日期: 2021-09-06

  要求修回日期: 2021-11-10

  网络出版日期: 2022-07-25

基金资助

国家自然科学基金项目(41471333)

中央引导地方科技发展专项(2021H0036)

版权

版权所有,未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
收起

A Spatio-temporal Semantic Clustering Algorithm for OD Flow Direction based on LDA and Ant Colony Optimization

  • ZHANG Han , 1, 2, 3 ,
  • WU Qunyong , 1, 2, 3, *
Expand
  • 1. Key Lab of Spatial Data Mining and Information Sharing of Ministry of Education, Fuzhou University, Fuzhou 350108, China
  • 2. National & Local Joint Engineering Research Center of Satellite Geospatial Information Technology, Fuzhou 350108, China
  • 3. The Academy of Digital China (Fujian), Fuzhou 350003, China
* WU Qunyong, E-mail:

Received date: 2021-09-06

  Request revised date: 2021-11-10

  Online published: 2022-07-25

Supported by

National Natural Science Foundation of China(41471333)

Central Guided Local Development of Science and Technology Project(2021H0036)

Copyright

Copyright reserved © 2022.
Fold

摘要

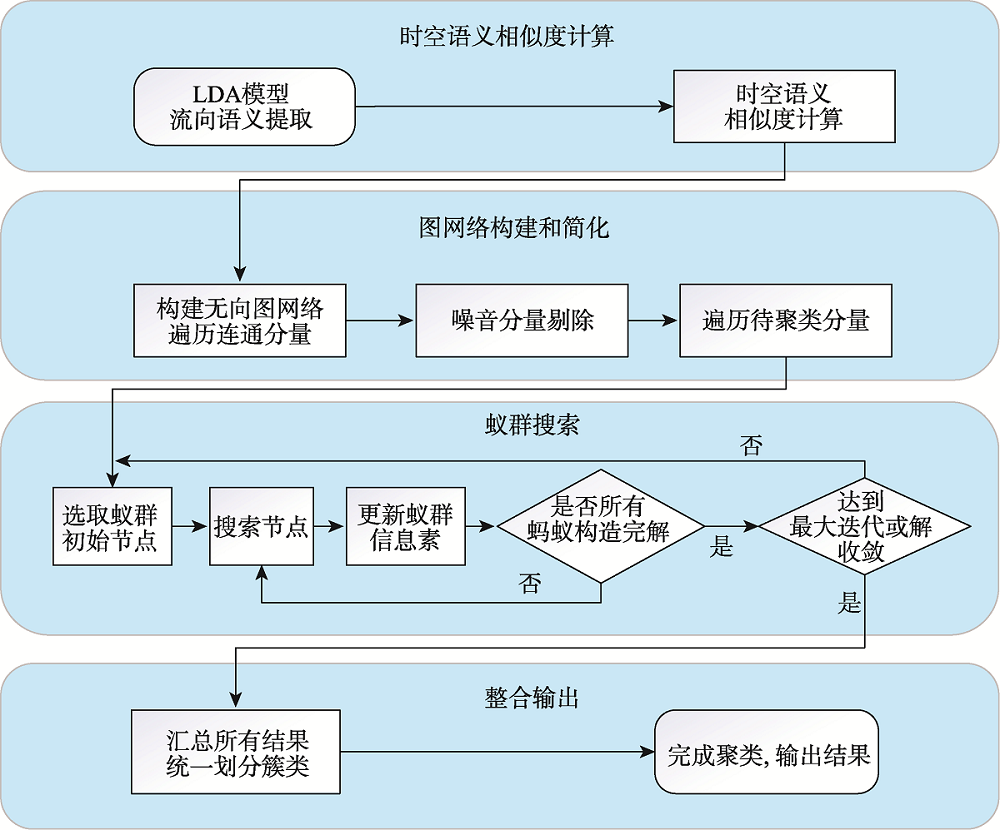
针对OD流向聚类中语义信息考虑不足和流向语义提取困难的问题,本文提出了一种基于隐含狄利克雷分布模型（Latent Dirichlet Allocation,LDA）和优化蚁群的OD流向语义聚类算法。算法首先以流向终点的POI类别为词汇构建流向文档,采用LDA主题模型提取流向语义,量化OD流向间的语义相似度,融合时间、空间和语义相似度构建流向时空语义相似度;接着以流向为节点,以流向时空语义相似度为边构建流向图,利用高斯函数映射以及图连通分量,剔除不相似的流向,实现数据精简;之后借鉴了密度峰值聚类算法思想,利用节点的介数中心性优化蚁群初始位置选取;最后基于多路切图准则（Multiway Normalized Cut, MNCUT）强化蚁群搜索的目的性,优化蚁群搜索的聚类效果,实现OD流向的时空语义聚类。以厦门市出租车公开数据集与厦门市高德地图POI数据为例进行分析与验证,结果表明本文基于LDA模型的语义提取方法可以有效提取流向的语义信息,构建有效的流向相似度度量;基于高斯函数和图连通分量特性的映射策略可以有效剔除了流向数据中的噪音,有效节省无向图构建的计算开支,大约节省了88.5%~88.8%的运行时间;基于介数中心性和多路切图准则优化的蚁群搜索聚类算法,可以有效进行流向语义聚类。相比已有方法本文方法能够更好地衡量流向间的语义相似程度,可实现按主题进行聚类划分,划分更加精细,更方便有效地进行流向语义的相关分析。

关键词： OD流向; 地理信息; 数据挖掘; 时空语义聚类; LDA; 流向语义相似度; 蚁群算法; 移动模式

本文引用格式

张晗 , 邬群勇 . 基于LDA和优化蚁群的OD流向时空语义聚类算法[J]. 地球信息科学学报, 2022 , 24(5) : 837 -850 . DOI: 10.12082/dqxxkx.2022.210535

Abstract

In order to solve the problem that semantic information is not fully considered in existing OD flow clustering algorithms and it is difficult to mine OD flow semantic information, this paper proposes an OD flow clustering algorithm based on the Latent Dirichlet Allocation (LDA) model and ant colony optimization algorithm. Firstly, the LDA Topic model is used to extract OD flows' semantics, and the JS divergence (Jensen-Shannon divergence) is used to quantify the semantic similarity between OD flows. We also propose a spatiotemporal semantic similarity calculation method that is constructed by integrating temporal, spatial, and semantic similarity, which provides data basis for flow clustering. Then, the graph network data structure is constructed according to the spatiotemporal semantic similarity, and the Gaussian function mapping and the connected component of the graph are used to simplify the data and eliminate the noise data. Based on the idea of CFDP algorithm (Clustering by fast search and find of density peaks algorithm), the intermediate centrality of nodes is used to optimize the selection strategy of the initial position of ant colony. Finally, the Multi-path Normalized Cut (MNCUT) graph criterion is used to strengthen the purpose of ant colony search, optimize the clustering effect of ant colony search, and realize the spatiotemporal semantic clustering for OD flow direction. Taking Xiamen taxi open data set and Xiamen map POI data as examples, the proposed method is verified. The experimental results show that: (1) The proposed method can effectively extract the semantic information of flow direction and measure the similarity degree between flow directions more comprehensively compared with the existing methods; (2) The Gaussian function mapping strategy and graph connected component feature are adopted to effectively eliminate the noise in the flow direction data, which saves the computational cost of undirected graph construction effectively by 88.5%~88.8% of the running time; (3) Compared with the existing algorithms, the clustering division of the proposed algorithm is more precise, and the correlation analysis of flow semantics can be carried out conveniently and effectively.

Key words： OD flow; geographic information; data mining; spatiotemporal semantic clustering; LDA; Flow semantic similarity; ant colony algorithm; mobile model

1 引言

现代城市系统中人流、交通流是不可缺少的重要组成部分[1],而其中OD流数据是人流、交通流的重要数据载体,其可以反映城市的区域关联特征[2,3]、出行特征[4]等信息,对于挖掘区域关联特征、居民出行模式等具有重要意义。
目前,聚类分析是挖掘OD流向数据较为主流的方法。根据聚类对象的不同,主要分为针对OD点和流向整体的聚类。在针对流向OD点的聚类算法中,目前成熟应用的有K-Means[5]、DBSCAN[6]等。近年来也有许多改进算法,郭殿升等[7]提出了一种基于共享邻居数的空间点聚类算法,算法通过定义一种基于共享邻居数目的量度相似性量度建立Delaunay三角网,在三角网上进行邻居点搜索以加速聚类过程。然而针对点的流向聚类,将流向整体割裂成了起点和终点,造成关联信息缺失,加剧了数据的有偏性。因此近年来的研究倾向于将OD流作为整体进行聚类分析。Gao等[8]采用向量积联系O点与D点,构造四元组OD流模型并映射到四维空间,再将空间扫描统计拓展到高维并与假设检验相结合以识别类簇。Song等[9]将空间扫描统计模型与蚁群算法相结合,采用LLR作为相似度量,通过蚁群算法最大化LLR,从而搜索出OD流数据中具有全局最优似然数的簇类。项秋亮等以时空相似性度量为基础,提出了自下而上逐级合并的时空联合聚类[10]和自顶向下基于最小生成树和最优分割的流聚类[11],细致考虑了OD流向数据的时空属性。项秋亮等在时空联合聚类中给出了OD流向时空相似度计算方法,并优化了层次聚类合并策略,减少了时间开销;在最小生成树和最优分割流聚类中依据离散数学的图谱理论,更好地利用数据不同维度的特点进行层次聚类划分。
上述流向聚类算法中,广泛被作为聚类维度的是空间和时间维度。而目前在流向的语义维度[12]上文献资料较少,为此,本文的重点之一是提取流向的语义信息并将其融合进聚类算法。传统的语义提取方法采用向量空间模型[14],该模型仅注重词频,缺少同义词、近义词考量。而在近年的研究中,主流的提取方法是采用LDA主题模型[13]进行主题聚类。LDA主题模型则通过文档-词汇-主题的二重概率分布,一方面解决了传统向量空间模型的弊端,另一方面更适合大规模数据挖掘文本隐含主题。在交通数据挖掘研究中使用LDA主题模型时,通常将研究对象抽象为文档进行语义挖掘。陈世莉[15]等将城市功能区映射为文档,将区域功能看作主题,区域内车辆轨迹活动作为文档词汇,利用LDA模型挖掘功能区语义,巧妙地将语义挖掘与功能区划分相结合,用LDA模型的语义主题视角完成功能区划分。Chu等[12]利用LDA主题模型提出了一种基于轨迹语义的聚类方式,将出租车运动轨迹抽象为文档,轨迹所经过的街道名称抽象为文档词汇,使聚类过程转化为LDA主题模型的语义分析过程。冷彪等[16]将地铁抽象为文档,将基于OD数据提取地铁乘客的出行模式和地铁站客流模式作为词汇,通过LDA主题模型将规律相似的地铁站聚为一类,进而进行区域功能和客流分析。Chu等[12]和冷彪等[16]都利用主题模型特点,将LDA模型迁移应用于聚类问题,通过语义主题划分完成聚类,但此类应用仅从语义角度聚类,忽略了研究对象时间与空间上的数量关系,不能具体量化相似度,存在准确性不足的短板。总的来说上述研究都采用LDA模型提取了不同研究对象语义信息,为提取OD流向的语义信息提供了可靠思路。
本文的关键问题之一是获得流向的语义信息后,如何在语义信息的基础上进行流向聚类是,而OD流向聚类问题本质上是一类NP-hard问题,加入语义维度后在严格约束下更加难以找到最优解,因此如何在有限时间内得到相对较优解是目前算法研究的主要方向。而启发式算法是主流的解决方法之一,其中的蚁群算法[9,17]属于群体智能启发式算法。算法通过多个蚂蚁独立搜索通过信息素的积累实现相互协作从而表现出群体智能,具有启发式搜索、分布计算、信息正反馈等特点,对于复杂问题的全局优化有较好效果。但一般蚁群算法节点选择方式并不适用于聚类问题,因此考虑采用切图准则[18]优化选择过程。切图准则源于谱聚类算法无向图切图,通过将数据组成的无向图切分为若干子图实现聚类。目前主流方法分为二分切图和多路切图,二分切图将无向图迭代二分,而多路切图准则（MNCUT）从全局出发通过评价准则切分出所有子图,因此多路切图准则的多路特点十分适合与蚁群算法相结合。
本文侧重考虑流向的语义信息,将语义与时间、空间等因素综合起来,研究流向的时空语义聚类方法。论文首先提出了OD流向时空语义相似度计算方法,采用LDA模型提取OD流向的语义信息并将其加入相似度计算。之后根据时空语义相似度构建图网络数据结构,并基于高斯函数和图连通分量特性进行映射,完成数据精简和噪音剔除。最后基于介数中心性和多路切图准则优化蚁群搜索加快运行效率,在图网络上完成聚类。

2 基于LDA和优化蚁群的OD流向时空语义聚类方法

本节主要介绍OD流向时空语义聚类方法,主要由OD流向时空语义相似度计算、流向图网络构建和简化、蚁群搜索3个主要部分组成。首先以LDA主题模型提取流向语义改进流向相似度计算方法,之后在相似度基础上利用图论思想组织数据结构并简化,最终将流向聚类过程转化为优化蚁群实现的图网络切图过程。
在语义相似度计算部分,采用LDA主题模型提取流向语义。因其可以较好地解决传统向量空间模型忽略近、同义词的弊端,并在高效挖掘大数据集[13,15]的同时可以有效地迁移应用于不同研究对象相结合。通过以流向为“文本”,以POI为“词汇”进行迁移应用以提取流向语义信息。之后将提取的语义信息与文献[11]提出的流向时间和空间相似性结合,获得更细致的时空语义相似度。在流向图网络构建和简化部分,本文将时空语义相似度作为图网络中边的权值,流向数据作为节点,组织为图网络结构。将无向图划分为数个连通分量后,根据分量节点个数进行分类并剔除噪音数据,简化无向图。在最后的蚁群搜索部分,以简化后的连通分量为基础,进行蚁群搜索聚类,对每个待聚类的连通分量,采用多进程的蚁群算法并行聚类。算法中蚁群由一群行为简单的低智能的蚂蚁个体组成,个体利用网络节点的介数中心性选取初始位置,并依据改进的启发式函数计算选择概率,进行解的搜索,而在蚁群个体之间则通过信息素的正反馈作用进行通信实现智能搜索,算法流程如图1。
图1 OD流向时空语义聚类算法流程

Fig. 1 Flow chart of OD flow direction spatio-temporal semantic clustering algorithm

2.1 OD流向时空语义相似度计算

相似度是评价流向样本间相似程度的度量,是流向聚类算法的基础,通常采用欧氏距离、余弦相似度等指标计算相似度。但同时OD流向数据具有时间、空间、语义等多维度特性,传统方法无法较好地衡量其样本间的相似程度。因此本文在OD流向语义的基础上,提出了时空语义相似度。
2.1.1 基于LDA模型的流向语义提取
LDA模型（隐含狄利克雷分布模型）[13]是一种非监督学习的主题模型,该模型通过词袋模型,挖掘文本中隐含的主题,通过统计学方法计算文档的主题概率分布以及每个主题词语概率分布。“POI词汇-流向”分布将由 “POI词汇-主题”ϕ分布、“主题-流向”θ分布共同决定,其计算方法如式(1)所示。
P POI 词汇 | 流向 = ∑ P POI 词汇 | 主题 × P 主题 | 流向
式中： P POI 词汇 | 流向为某一流向下POI词汇出现的频率,即流向的POI频率; P POI 词汇 | 主题表示每个主题中POI词汇的出现概率,即主题对应的各类POI概率; P 主题 | 流向为每条流向对应各主题的概率,即流向的主题概率
通常情况下流向的终点反映出行的目的,因此本文通过对D点建立缓冲区,依据缓冲区内的POI构建流向语料库。而出行泊车的相关研究表明[19]大中型城市中95%的乘客下车后到最终目的地可接受的最大步行距离为350 m,并且大多数人认为下车后步行距离在220~250 m为正常步行距离,因此本文将缓冲区范围取为250 m,以搜索相匹配的POI点。具体训练过程如下：
（1）构建缓冲区,为流向匹配POI,根据POI点类别进行加权,以POI类别为词汇构建流向文档;
（2）选择合适的主题数K,对流向主题进行随机初始化,为每个流向文档随机赋值一个主题Z;
（3）再次遍历语料库,采用吉布斯采样公式更新每个词汇所属的流向主题;
（4）根据吉布斯采样,不断迭代更新词汇的流向主题,直到吉布斯采样收敛;
（5）统计每个主题下词汇的分布得到,”词汇-主题”ϕ分布;统计每个流向的主题,得到”主题-流向”θ分布;
（6）基于模型预测流向主题概率。
通过训练,本文取得了10个流向主题及其对应的“词汇-主题”分布情况。依据各主题的词汇概率进行主观目译,得出各个主题的语义解释,流向主题及其所属词汇的主要概率分布情况如表1所示。
表1 LDA模型“主题-词汇”概率分布表及其语义解释

Tab. 1 The topic-word probability distribution table of LDA model and semantic interpretation

主题编号 主题词汇分布 语义解释
Topic0 0.549×"汽车服务" + 0.103×"公司企业" + 0.087×"购物" + 0.062×"美食" + 0.054×"生活服务" 租车购车
Topic1 0.390×"旅游景点" + 0.084×"美食" + 0.065×"购物" + 0.059×"生活服务" + 0.058×"公司企业" 游玩出行
Topic2 0.331×"教育培训" + 0.302×"生活服务" + 0.087×"美食" + 0.081×"交通设施" + 0.076×"购物" 教育培训
Topic3 0.550×"交通设施" + 0.333×"教育培训" + 0.098×"美食" + 0.017×"购物" + 0.002×"生活服务" 交通出行
Topic4 0.568×"公司企业" + 0.074×"购物" + 0.067×"金融" + 0.063×"美食" + 0.050×"生活服务" 工作通勤
Topic5 0.715×"房地产" + 0.091×"交通设施" + 0.075×"美食" + 0.045×"生活服务" + 0.044×"购物" 探亲访友
Topic6 0.430×"购物" + 0.255×"美食" + 0.072×"生活服务" + 0.055×"公司企业" + 0.041×"休闲娱乐" 购物出行
Topic7 0.336×"休闲娱乐" + 0.168×"美食" + 0.164×"酒店" + 0.068×"交通设施" + 0.057×"公司企业" 休闲娱乐
Topic8 0.356×"金融" + 0.123×"美食" + 0.098×"购物" + 0.089×"公司企业" + 0.087×"生活服务" 金融理财
Topic9 0.319×"医疗" + 0.127×"购物" + 0.119×"美食" + 0.077×"金融" + 0.061×"生活服务" 就医出行
根据训练好的LDA模型解得所有流向的主题概率分布,即“主题—流向”分布。该分布描述了流向属于各个主题的概率,反映了流向的语义信息。
2.1.2 OD流向时空语义相似度
本文基于LDA模型获取得各流向的主题分布（即语义信息）后,采用JS散度计算两个主题概率分布的距离以衡量流向两两之间的语义相似程度。JS 散度的本质是2个概率分布间的距离,通过在KL散度基础上改进为具有对称性的、无向的度量,其分布完全相同时值为0,完全不同时值为1。语义相似性参数计算方法如式(2)、式(3)所示。
si m s = JS ( P 1 | | P 2 ) = 1 2 KL ( P 1 | | P 1 + P 2 2 ) + 1 2 KL ( P 2 | | P 1 + P 2 2 )
KL p ∥ q = ∑ p ( x ) log p x q x
式中： si m s为语义相似距离; P 1、 P 2为流向的主题概率分布;p(x)、q(x)为在概率分布p和q下流向属于主题x的概率。将以上所得的流向语义相似度和项秋亮等提出的流向时间和空间相似性参数 si m dis、 si m t相结合计算流向时空语义相似度。其计算方法如式(2)、式(4)、式(5)所示。
si m od = exp - x - μ 2 2 σ 2
x = si m dis + si m t + si m s 3
式中： si m od为时空流向语义相似度; si m dis、 si m t、 si m s分别为项秋亮等提出的空间、时间相似性参数和前文计算的语义相似性参数;x为三项距离的平均数; μ为位置参数,决定函数的对称轴的位置; σ为尺度参数,决定函数图像的形状。
其中,式（4）借鉴了谱聚类[20]算法中常用的无向权重图的构建策略,采用高斯核函数进行映射。由于时间、空间相似性参数和JS散度都与流向的相似程度呈反比,采用高斯函数映射主要有2个方面作用。一方面将距离转换成相似度（距离与相似程度成反比关系,转换为相似度的正比关系）,另一面通过调整高斯函数参数控制有效数值的分布,使2条不相似流向间的时空语义相似度近似为零,识别出和所有其他点都不相似的噪音数据。该方法与回归分析法、阈值筛选等传统噪音剔除方法相比,具有简单高效的优点。一方面节省了回归法中拟合函数花费的大量计算成本,另一方面避免了阈值设定,可以通过调参直接控制噪音剔除的精度。当尺度参数 σ 2越小,高斯函数在峰值附近的图像越陡峭趋,越快趋近于零。基于此特点,进行精度限制后即可控制有效数值范围,剔除部分噪音。

2.2 OD流向图网络构建与噪音剔除

在本阶段中,算法以流向为网络节点,以两两流向之间的时空语义相似度为边的权重,构建无向图复杂网络G(V,E)。由于高斯函数控制了有效数据范围,剔除了部分噪音,因此无向图G将是一个非连通图,一方面避免了全连接网络的大量数据冗余,另一方面为进一步识别噪音数据提供了条件。
在连通分量划分阶段,首先将无向图G划分为连通分量,再根据连通分量的节点数进行分类,节点数量为1的连通分量划分为噪音分量,节点数量大于1且图内最小相似度大于0.8的直接划分为一类簇类,其余则划分为待聚类的连通分量进行并行蚁群聚类。以图2为例,图G为13个节点的示例无向图,将图G分解得到 G 1 、 G 2 、 G 3 、 G 44个连通分量,假设 G 2中最小相似度数值为0.85,则其中 G 3 、 G 4分类为噪音, G 2划分为一类簇类, G 1分类为待聚类的连通分量进行蚁群搜索。
图2 连通分量划分示意

注： G i为无向图连通分量; V i为流向数据节点; E i - j为节点间的边,权值为时空语义相似度。

Fig. 2 Schematic diagram of connected component partition

2.3 基于介数中心性和多路切图准则的蚁群优化

在本阶段中,本文在文献[18]蚁群搜索的基础上做出了两方面改进,一方面基于介数中心性优化了蚁群搜索的初始位置,另一方面基于多路切图准则增强蚁群搜索的目的性。
2.3.1 基于介数中心性优化蚁群初始位置
在初始位置选择阶段,本文借鉴密了度峰值聚类算法[21]策略,并主要从以下2个方面进行考虑, ① 初始节点应具有较强的与其余节点沟通的能力,② 各个初始节点之间的相对距离较远且互不相邻。为了使初始位置能够更好连接其余相似的节点,应尽量选择介数中心性高的节点作为初始节点。由于本文边权值为流向间的相似度与距离的定义正好相反,因此在计算距离时采用相似度倒数进行计算（图3）。介数中心性计算方法如式(6)所示。
B C i = ∑ n st i g st
式中： n st i表示从节点s到节点t并且经过节点i且为最短路径的路径数量（其中节点s、t、i不相同）; g st表示连接s和t的最短路径的数量。
图3 初始节点选择策略流程

Fig. 3 Flow chart of initial node selection strategy

类比密度峰值聚类算法[21],本文期望选取的初始节点之间相对距离较远,故以网络上的最短路径距离替代密度峰值聚类算法的欧氏距离,截断距离 δ i计算方法如式(7)所示。
δ i = min d ij B C j > B C i max d ij B C j ≤ B C i
式中： δ i为节点i的截断距离; d ij为节点i和节点j在网络上的最短路径距离; B C i为节点i的介数中心性数值; B C j为节点j的介数中心性数值。
基于上述介数中心性和截断距离,借鉴密度峰值聚类算法思想提出初始点选择度量 γ i,计算方法如式(8)所示。
γ i = δ i × B C i
式中： γ i为初始点选择度量; δ i为节点i的截断距离 ; B C i为节点i的介数中心性数值
在选择度量基础上,选取数值最高且互不相邻的前2%[21]的的节点为初始位置（图3）。
2.3.2 基于切图准则的蚁群搜索优化
在聚类算法中,期望蚁群搜索过程中每只蚂蚁能够选择与该蚂蚁途经节点最为相似,且与其他蚂蚁最不相似的节点（即类内节点相似度尽可能高,类间相似度尽可能低）。故利用多路切图准则构造切图影响因子 ∆ MNCut,使蚁群倾向于选择选择切图影响因子变化较小的节点,切图影响因子计算方法如式(9)所示。
∆ MNCu t k , ij t = ∑ j ∈ allow Cu t t A k j , V - A k j asso c t A k j + Cu t t - 1 A k - 1 , V - A k - 1 asso c t - 1 A k - 1 + … + Cu t t - 1 A 1 , V - A 1 asso c t - 1 A 1
式中： MNCu t ( k , ij ) t为t时刻在i节点的蚂蚁k选择j节点的切图影响因子;Cut( A k, V - A k)为 A k类节点与其他类的节点间边权值之和; assoc A k为 A k类各节点间边权值之和。
此时若选择的节点与类内的节点越相似则 ∆ MNCut数值越小,与类间节点越相似则 ∆ MNCut数值越大。基于切图影响因子以上特点,故以相似度与切图影响因子的除数替代传统启发式因子,使得概率计算时相似度较大、切图影响因子较小的节点能够获得较高的概率。改进后选择概率计算方法如式(10)、式(11)所示。
P ij k t = phe r ij t α × η ij t β ∑ g ∈ allow phe r ig t α × η ig t β
η ij t = si m od i , j ∆ MNCu t k , ij t
式中： P ij k t为t时刻在节点i的蚂蚁k选取节点j为下一节点的选取概率; η ij t为t时刻在节点i选取节点j的启发式函数; phe r ij t为t时刻在节点i选取节点j的信息素因子; α 、 β分别为信息素重要性参数、启发函数重要性参数,此处均取1; si m od ( i , j )为节点i与节点j之间的时空语义相似度。
经以上改进,蚁群在搜索时倾向于选择使得类内相似度大而类间相似度小的节点。之后利用蚁群信息素更新,使选择倾向在信息素的信息增益下随迭代次数增加越来越明显。

2.4 算法实现和效率分析

本文算法的伪代码描述如下：

算法1 基于LDA和优化蚁群的OD流向时空语义聚类算法
输入：OD流向数据F←{ f i},连通分量划分阈值r,信息素重 要性参数 α,启发函数重要性参数 β
输出：OD流向类簇C={ c i},噪音集合N={ n i}
function LDA_MNCUT_ANT_CLUSTER(G,r,α,β)
Step1: //无向图构图阶段,无向图G(V,E),其中V是点集合V ←{ v i},E是边集合E ←{ e ij}
for i in F do
for j in F do
creat v i , v j , e ij add v i , v j , e ij to G
Step2://连通分量划分阶段,划分连通分量Graphs{ g i},并简化噪音获得待聚类集合C_Graphs{ g i}
Graphs=divide(G,r)
for g i in Graphs do
C_Graphs=classify( g i)
Step3: //对待聚类连通分量进行聚类,计算出初始位置inital,K只蚂蚁搜索求解,最后整合聚类结果
for g i in C_Graphs do
while Not_End_Condition do //迭代搜索,直到满足停止条件
K,inital=Initialize( g i)
for k in K do
res=Search(k,inital,α,β)
Res=Merge(res,C)
假定数据共有n条流向,g个连通分量,最多迭代搜索m次,进行时间复杂度分析。在Step1数据组织阶段,时空语义相似度需计算为 n 2 - n次,对应时间复杂度为 O ( n 2 )。在Step2噪音识别阶段,划分连通分量的算法时间复杂度为 O n,连通分量分类简化过程的计算次数取决于连通分量个数g,故时间复杂度为 O n + O g = O ( n )。在Step3蚁群搜索阶段,假设第i个连通分量有 n i个节点,进行了 m i次迭代搜索。蚁群确定 k i个初始节点的时间复杂度为 O ( n i 2 )。在搜索过程中,算法仅计算图网络结构上的相邻节点,假设有 d i个邻接节点（ d i小于 n i）,故 k i只蚂蚁仅对 d i个邻接节点进行概率搜索,此时每只蚂蚁最多进行 n i次搜索,每次计算 d i个邻接节点的概率,故时间复杂度为 O ( k i × n i × d i )。最后整合过程的时间复杂度为 O ( k i )。综上g个连通分量执行Step3的总时间复杂度如式(12)所示。
O ∑ i = 1 g m i × n i 2 + k i × n i × d i + k i ≈ O ∑ i = 1 g m i × n i 2
综合以上3步,算法整体时间复杂度为 O n 2 + n + ∑ i = 1 g m i n i 2,因分量个数g、迭代次数m为常数值,因此算法整体时间复杂度在 O n 2,但算法的时间花费同时与图网络结构和收敛次数有着密切关系。

3 实验与分析

本文采用2020年6月26日厦门市出租车数据和2020年厦门市高德地图POI数据进行流向语义分析与算法对比分析。厦门市出租车数据来源于厦门市大数据安全开放创新应用大赛,数据包括车辆标识、上车时间、下车时间、上车坐标（WGS_84坐标,下同）、下车坐标。2020年6月26日全天共有185 006条数据,数据的经度范围为118.33°E—117.91 °E,纬度范围为24.88 °N—24.43 °N。POI数据爬取自高德地图API,数据包括了医疗、教育等15个大类。本文具体实验环境如下Intel i7-9700 处理器计算机、Windows10操作系统、Pycharm编译器、MongoDB数据库。

3.1 LDA主题个数分析

对于主题个数K的选择,本文根据模型困惑度（perplexity）[22,23]和一致性（Topic Coherence Measure）[24]进行评估并结合结果的可解释性进行选择。困惑度量化的是模型主题的不确定性,一般情况下困惑度越低模型效果越好,但是困惑度数值会随主题个数增加逐步减小,所以仅依靠困惑度难以确定主题个数。而一致性量化的是主题下词语的语义关联程度即模型中主题的质量,一致性越高效果越好。
基于以上论述,本文针对主题个数的选取计算了模型在不同主题个数下模型的一致性和困惑度,结果如图4所示,当主题个数取为10时,模型一致性取得较大极值,此时困惑度较小且逐渐趋缓,故本文最终确定主题个数为10。
图4 不同主题数一致性及困惑度

Fig. 4 Coherence and Perplexity among different number of topics

3.2 各模块效果分析

为了验证基于LDA模型改进的时空语义相似度、介数中心性初始位置优化、MNCUT优化搜索的有效性及其对于聚类效果的影响,实验以时空相似度、随机初始位置、传统蚁群搜索作为基准模型进行消融实验。以邓恩指数（Dunn Validity Index,DVI）[25]、Calinski-Harabaz指数（Calinski-Harabaz Index,CHI）、戴维森堡丁指数（Davies-Bouldin Index,DBI）为评价指标。DVI指数以任意类之间最小距离除以类内最大距离,其数值与类间距离呈正比,类内距离呈反比。CHI指数以类间协方差除以类内协方差,其数值与类内紧密度、类间分离度呈正比。DBI指数以类内平均距离之和除以聚类中心最大距离,其数值越小类内平均距离越小,类间中心距离越大。
实验结果如表2当算法采用LDA+介数中心性+MNCUT三项优化时,DVI指数、DBI指数都处于最好水平,而CHI指数、运行时间均处于次优水平。运行时间相较于基准模型缩短了约12%,DVI指数提升了约20%,CHI指数提升了约34%,DBI指数下降了约31%。① 当消融LDA模型优化模块时,整体上CHI指数达到最优,DVI指数、DBI指数仍在较优水平,说明经过LDA模型优化相似度计算之后,流向被赋予了语义信息,类内相似程度得到优化,但原本同一类的流向可能被分为两类,导致类间的协方差有所减小,CHI指数有所减小。② 当消融介数中心性优化模块时,算法运算时间相比2、3号实验迅速增加,且各项指数均有不同程度下降,说明经过介数中心性初始位置优化,有效提高了算法效率,一定程度上改善了聚类效果。③ 当消融MNCUT优化模块时,算法运算时间大量减少,各项指数相比2、3号实验均有所下降,说明MNCUT优化可以一定程度改善聚类效果,但该优化模块花费了大量运算成本,使得一定程度上降低了程序运行速度。
表2 LDA、中心性、MNCUT模块实验评估结果

Tab. 2 Experimental evaluation results of LDA, centrality and MNCUT modules

序号 基准 LDA 中心性 MNCUT DVI CHI DBI 时间/s
1 √ 0.9186E-22 0.13486 2.6478 1747
2 √ √ √ √ 1.1598E-22 0.18349 1.7699 1535
3 √ √ √ 1.1468E-22 0.18615 1.7817 1517
4 √ √ √ 0.9345E-22 0.15876 1.9683 1964
5 √ √ √ 1.1198E-22 0.17145 2.1784 1418

3.3 高斯函数尺度参数分析

本文算法中,高斯函数的参数取值决定了图网络结构,直接影响噪音识别和聚类效果。为比较不同高斯函数参数值对于噪音识别效果的影响,本小节截取当日部分数据对比不同情况下的实验结果。图5展示了不同参数的高斯函数映射下算法各项指标对比。结果说明采用高斯函数映射能够控制有效数据范围,精简数据有效节省了运行时间和计算开支,在剔除噪音后节省了约88.5%~88.8%的运行时间,同时有效降低了类内平均距离,在DVI指数、CHI指数、DBI指数3项聚类结果指标上均有一定程度改善。
图5 不同情况下算法指标对比

注：时间为左坐标轴,类内平均距离、DVI指数、CHI指数、DBI指数为右坐标轴。

Fig. 5 Comparison of noise elimination and clustering results of different scale parameter

图6统计了不同参数的噪声数量与3项指数,可以看出尺度参数在1.1~1.5范围内时,噪音数量与DVI、CHI指数都处在相对较低水平而DBI相对较高,此时高斯函数无法很好分离相似/不相似数据,聚类效果较差。而当参数在0.2~1范围内时,噪声数量随着参数减小而增加,而DVI、CHI指数处于较高水平且趋于平稳,DBI指数降至较低水平,此时高斯函数能较好区分相似/不相似数据,且聚类结果具有较高的类内相似度,类之间的分离程度较好。当尺度参数为0.1时,剔除噪音的数量逐渐稳定,而DVI、CHI指数均出现下降,DBI指数有所上升,出现一定的过拟合现象,聚类效果下降。图7展示了尺度参数为1、0.5、0.1时算法的噪音识别与聚类结果,随着尺度参数减小,聚类效果不断改善,而噪音流向则不断增加。当尺度参数为1时,噪音识别略有不足,而聚类效果与尺度参数为0.5时仅有细微差别。当尺度参数减小到0.1,出现簇类内流向过少,部分误识别为噪音的过拟合现象。
图6 各项指数变化折线图

Fig. 6 Line chart of exponential changes

图7 不同尺度参数噪音剔除和聚类结果对比

Fig. 7 Comparison of noise elimination and clustering results of different scale parameters

3.4 OD流向语义聚类与分析

本节选择交通出行、就医出行、工作通勤、探亲访友4类较为有代表性的流向主题进行了OD流向语义聚类分析和实验,图8中标出了流向簇类附近的主要地理实体,以验证语义识别结果,在四类出行主题中交通、就医出行的聚类结果较为集中,簇类体量较大,3项指数表现较好,结果与地理实体的分布情况吻合度较高,而工作通勤、住宅拜访出行的聚类结果较为分散,簇类较细碎,相对于前者吻合度较低,3项指数的表现也相对较低,并且存在一些簇类终点不存在标志地理实体,或主要地理实体类型与得到的语义不同。考虑出现这种情况的原因可能一方面是因为交通、医疗类型的POI数据具有较为明确的等级,加权后能够为聚类提供的更为明确的语义,而公司、住宅等无明确等级的POI类型,语义信息相对缺乏,容易被其他类型POI稀释,另一方面因为城市规划等原因,交通、医疗类POI数据分布较为集中,而企业、住宅类型POI分布较为分散。这造成了交通、医疗主题语义准确度相对较高,聚类出的簇类体量较大,而后者存在部分的错误识别,且聚类结果更偏向体量较小较为分散的簇类。
图8 四类主题聚类效果及地理实体验证对比

Fig. 8 Comparison diagram of clustering effect and geographical entity verification of four types of topics

综上,本文算法在语义聚类方面对于不同出行类型效果聚类有所差别。若对应的POI类型具有明确等级且分布集中,则算法聚类效果较好且识别出的簇类体量大易获得热点区域流向,而等级信息不明确、分布分散的POI类型,则识别出体量极小不具备代表性,获得的是非热点区域的流向簇类。

3.5 算法对比分析

将本文算法与文献[11]提出的流向时空联合聚类、GC-ACO聚类[17]、FHC-LDP聚类[26]、DBSCAN聚类、AP聚类进行实验比较,统计其耗时、DVI、CHI、DBI以比较聚类效果。如图9本文算法在DVI指数具有相对较高的水平,而运行时间、DBI指数与CHI指数都处于中游水平。DVI指数对于离散点聚类的测评效果较好,较高的DVI指数说明本文算法能够针对离散分布的流向数据做出较合理聚类。平均水平的DBI指数与CHI指数说明本文算法的类内分布相对均匀,类间界限较为明显。
图9 不同算法各项指标对比

Fig. 9 Comparison chart of various indicators of different algorithms

图10中比较了本文算法和时空联合聚类、FHC-LDP聚类、GC-ACO聚类算法在不同量级簇类上的聚类结果。本文将簇类分为大中小3类,簇内流向数大于80条为大体量簇类,大于30条并且小于等于80条为中体量簇类,小于30条的为小体量簇类。经实验,本文聚类算法与流向时空联合聚类算法得到了较详细的簇类,而FHC-LDP、GC-ACO算法由于未对流向聚类做特殊处理,识别效果不如前两种算法。其中本文算法识别出大体量簇类32簇、中体量簇类314簇、小体量簇类601簇,在中、小体量上结果与时空联合聚类算法大致相同,而对于较大体量簇类,本文算法识别出的簇类数多于其它算法,集中于厦门第一码头、火车站以及吕厝附近,而其他3种聚类方法主要集中在东渡码头、火车站、吕厝。此外本文算法还聚出一些分散的大体量簇类,这揭示了相对更多的信息,因此一定程度上具有更强挖掘能力,但这些簇类分布较为分散,对于热点区域的把握有所不足。
图10 不同量级簇类核心流向对比

Fig. 10 Comparison of core flow direction of cluster classes of different magnitude

4 结论与讨论

本文改进了流向相似度计算方法,将流向的语义与时间、空间信息相结合提出了时空语义相似度,为流向聚类提供了有效的语义信息。在蚁群算法基础上,利用图论优化噪音剔除、初始位置选择,并通过多路切图准则增强搜索的目的性,提出一种基于多路切图准则优化蚁群算法的OD流向聚类算法。以厦门市出租车公开数据和2020年厦门市高德地图POI数据为例进行了聚类实验和可视化对比分析,主要结论如下：
（1）实验比较了不同主题数量下LDA模型的困惑度与一致性,最终生成了10个语义主题。基于流向的主题概率分布设计了流向语义相似程度计算方法。在项秋亮等的时间空间相似度基础上加入了语义维度,更为全面地衡量流向间的相似程度。
（2）经过高斯函数映射策略通过限制精度控制有效数据范围,可以有效剔除流向数据中的噪音数据,剔除噪音后节省了约88.5%~88.8%的运行时间,剔除噪音数据有效降低了类内平均距离,在各项聚类指标上均有一定程度改善。
（3）本文算法通过语义主题的划分、初始节点优化、搜索过程优化,运行时间相较于基准模型缩短了约12%,DVI指数提升了约20%,CHI指数提升了约34%,DBI指数下降了约31%,同时使得划分得到的簇类具有主题信息,使聚类划分更加精细,可以更方便有效地进行流向语义的相关分析。而在与时空联合聚类、GC-ACO等算法的对比实验中,本文算法在DVI指数上表现优于其他算法,CHI指数仅次于AP算法,而DBI指数、运行时间则处于中游水平。
（4）算法对不同出行类型效果聚类有所差别,对于POI类型有明确等级且分布集中的类型,聚类效果较好,可以有效挖掘该类主题的主要流向,而对于POI类型等级不明确且分布分散的类型,易聚类出体量小且分布细碎的簇类。综上所述,本文从为OD流向聚类方法增加了时空语义角度,并以图论和切图准则优化了聚类过程,为城市流向语义分析提供了技术基础,为城市关联特征挖掘、居民出行模式发现等研究提供了一种新途径。
然而目前算法存在着主题语义准确性不足、时间复杂度较高等问题。造成主题语义准确性不足问题主要原因可能是语义来源过于单一,后续研究将尝试在模型训练中加入微博签到等多源数据或加入融合了出行时间的语料以提升流向语义的准确性。而对于时间复杂度高的弊端则需尝试改进聚类策略,学习更先进的聚类算法思想进行更加有针对性的改进。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
杨延杰, 尹丹, 刘紫玟, 等. 基于大数据的流空间研究进展[J]. 地理科学进展, 2020, 39(8):1397-1411.

[ Yang Y, Yin D, Liu Z W, et al. Research progress on the space of flow using big data[J]. Progress in Geography, 2020, 39(8):1397-1411. ] DOI: 10.18306/dlkxjz.2020.08.013

DOI

[2]
李涛王, 姣娥, 黄洁. 基于腾讯迁徙数据的中国城市群国庆长假城际出行模式与网络特征[J]. 地球信息科学学报, 2020, 22(6):1240-1253.

DOI

[ Li T, Wang J E, Huang J. Research on Travel pattern and network characteristics of inter-city travel in China's urban agglomeration during National Day week based on Tencent Migration data[J]. Journal of Geo-information Science, 2020, 22(6):1240-1253. ] DOI: 10.12082/dqxxkx.2020.190686

DOI

[3]
张政, 陈艳艳, 梁天闻. 基于网约车数据的城市区域出行时空特征识别与预测研究[J]. 交通运输系统工程与信息, 2020, 20(3):89-94.

[ Zhang Z, Chen Y Y, Liang T W. Regional Travel Demand Mining and Forecasting Using Car-hailing Order Records[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(3):89-94. ] DOI: 10.16097/j.cnki.1009-6744.2020.03.014

DOI

[4]
杨格格, 宋辞, 裴韬, 等. 北京对外交通枢纽乘客OD时空分布特征[J]. 地球信息科学学报, 2016, 18(10):1374-1383.

DOI

[ Yang G G, Song C, Pei T, et al. 2016. Passengers' OD temporal-spatial distribution characteristics of the external traffic hubs in Beijing[J]. Journal of Geoinformation Science, 2016, 18(10):1374-1383. ] DOI: 10.3724/SP.J.1047.2016.01374

DOI

[5]
Guo X G, Xu Z J, Zhang J Q, et al. An OD flow clustering method based on vector constraints: A case study for Beijing taxi origin-destination data[J]. ISPRS International Journal of Geo-information, 2020, 9(2):128. DOI: 10.3390/ijgi9020128

DOI

[6]
Duan L, Xu L D, Guo F, et al. A local-density based spatial clustering algorithm with noise[J]. Information systems (Oxford), 2007, 32(7):978-986. DOI: 10.1016/j.is.2006.10.006

DOI

[7]
Guo D S, Zhu X, Jin H, et al. Discovering spatial patterns in origin-destination mobility data[J]. Transactions in GIS, 2012, 16(3):411-429. DOI: 10.1111/j.1467-9671.2012.01344.x

DOI

[8]
Gao Y Z, Li T, Wang S W, et al. A multidimensional spatial scan statistics approach to movement pattern comparison[J]. International journal of geographical information science : IJGIS, 2018, 32(7):1304-1325. DOI: 10.1080/13658816.2018.1426859

DOI

[9]
Song C, Pei T, Ma T, et al. Detecting arbitrarily shaped clusters in origin-destination flows using ant colony optimization[J]. International Journal of Geographical Information Science : IJGIS, 2019, 33(1):134-154. DOI: 10.1080/13658816.2018.1516287

DOI

[10]
项秋亮, 邬群勇, 张良盼. 一种逐级合并OD流向时空联合聚类算法[J]. 地球信息科学学报, 2020, 22(6):1394-1405.

DOI

[ Xiang Q L, Wu Q Y, Zhang L P. An OD flow spatio-temporal joint clustering algorithm based on step-by-step merge strategy[J]. Journal of Geo-information Science, 2020, 22(6):1394-1405. ]

[11]
Xiang Q L, Wu Q Y. Tree-Based and optimum cut-based origin-destination flow clustering[J]. ISPRS international journal of geo-information, 2019, 8(11):477. DOI: 10.3390/ijgi8110477

DOI

[12]
Chu D, Sheets D A, Zhao Y, et al. Visualizing hidden themes of taxi movement with semantic transformation[A]. 2014 IEEE Pacific Visualization Symposium, 2014.DOI: 10.1109/PacificVis.2014.50

DOI

[13]
Blei D M, Ng Andrew, Jordan M I. Latent dirichlet allocation[J]. The Journal of Machine Learning Research, 2003, 3(4-5):993-1022.

[14]
Salton G, Wong A, Yang C. Salton G. A vector space model for automatic indexing[J]. Communications of the ACM, 1975, 18(11):613-620. DOI: 10.1145/361219.361220

DOI

[15]
陈世莉, 陶海燕, 李旭亮, 等. 基于潜在语义信息的城市功能区识别——广州市浮动车GPS时空数据挖掘[J]. 地理学报, 2016, 71(3):471-483.

DOI

[ Chen S L, Tao H Y, Li X L, et al. Discovering urban functional regions using latent semantic information: Spatiotemporal data mining of floating cars GPS data of Guangzhou[J]. Acta Geographica Sinica, 2016, 71(3):471-483. ] DOI: 10.11821/dlxb201603010

DOI

[16]
冷彪, 赵文远. 基于客流数据的区域出行特征聚类[J]. 计算机研究与发展, 2014, 51(12):2653-2662.

[ Leng B, Zhao W Y. Region ridership characteristic clustering using passenger flow data[J]. Journal of Computer Research and Development, 2014, 51(12):2653-2662. ] DOI: 10.7544/issn1000-1239.2014.20131124

DOI

[17]
叶小莺, 万梅, 唐蓉, 等. 基于图聚类与蚁群算法的社交网络聚类算法[J]. 计算机应用研究, 2020, 37(6):1670-1674,1687.

[ Ye X Y, Wan M, Tang R, et al. Clustering algorithm of social network based on graph clustering and ant colony optimization algorithm[J]. Application Research of Computers, 2020, 37(6):1670-1674,1687. ] DOI: 10.19734/j.issn.1001-3695.2018.12.0881

DOI

[18]
白璐, 赵鑫, 孔钰婷, 等. 谱聚类算法研究综述[J]. 计算机工程与应用, 2021, 57(14):15-26.

[ Bai L, Zhao X, Kong Y T, et al. Survey of spectral clustering algorithms[J]. Computer Engineering and Applications, 2021, 57(14):15-26. ] DOI: 10.3778/j.issn.1002-8331.2103-0547

DOI

[19]
张文会, 苏永民, 戴静, 等. 居住区共享停车泊位分配模型[J]. 交通运输系统工程与信息, 2019, 19(1):89-96.

[ Zhang W H, Su Y M, Dai J, et al. Distributing model For shared parking in the residential zones[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(1):89-96. ] DOI: 10.16097/j.cnki.1009-6744.2019.01.014

DOI

[20]
Von L U. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4):395-416. DOI: 10.1007/s11222-007-9033-z

DOI

[21]
Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191):1492-1496.DOI: 10.1126/science.1242072

DOI PMID

[22]
Hoffman M-D, Blei D-M, Bach F-R. Online learning for latent dirichlet allocation[A]. International Conference on Neural Information Processing Systems Curran Associates Inc, 2010.

[23]
王婷婷, 韩满, 王宇. LDA模型的优化及其主题数量选择研究——以科技文献为例[J]. 数据分析与知识发现, 2018, 2(1):29-40.

[ Wang T T, Han M, Wang Y. Optimizing LDA model with various topic numbers: Case study of scientific literature[J]. Data Analysis and Knowledge Discovery, 2018, 2(1):29-40. ] DOI: 10.11925/infotech.2096-3467.2017.0715

DOI

[24]
Mimno D M, Wallach H M, Talley E M, et al. Optimizing semantic coherence in topic models[A]. Proceedings of the 2011 Conference on Empirical Methods in Natural Language Processing, EMNLP 2011, 27-31 July 2011, John McIntyre Conference Centre, Edinburgh, UK, A meeting of SIGDAT, a Special Interest Group of the ACL. Association for Computational Linguistics, 2011.

[25]
Rathore P, Ghafoori Z, Bezdek J C, et al. Approximating dunn's cluster validity indices for partitions of big data[J]. IEEE transactions on cybernetics, 2019, 49(5):1629-1641.DOI: 10.1109/TCYB.2018.2806886

DOI PMID

[26]
Guan J Y, Li S, He X X, et al. Fast hierarchical clustering of local density peaks via an association degree transfer method[J]. Neurocomputing (Amsterdam), 2021, 455(3):401-418. DOI: 10.1016/j.neucom.2021.05.071

DOI

Options
文章导航

/

〈 〉