EN中文

地球信息科学学报 >

2022 , Vol. 24 >Issue 6: 1047 - 1060

DOI: https://doi.org/10.12082/dqxxkx.2022.210691

基于多尺度时空聚类的共享单车潮汐特征挖掘与需求预测研究

  • 姜晓 ,
  • 白璐斌 ,
  • 楼夏寅 ,
  • 李梅 , * ,
  • 刘晖
展开
  • 北京大学地球与空间科学学院 遥感与地理信息系统研究所,北京 100871
*李 梅(1978— ),女,陕西西安人,博士,副教授,主要从事地学信息可视化,实时GIS与应急研究。 E-mail:

姜 晓(1992— ),男,江苏徐州人,硕士生,主要从事地学信息可视化与数据挖掘研究。E-mail:

收稿日期: 2021-10-30

  修回日期: 2021-12-25

  网络出版日期: 2022-08-25

基金资助

中国博士后科学基金项目(2021M690201)

收起

Usage Patterns Identification and Flow Prediction of Bike-sharing System based on Multiscale Spatiotemporal Clustering

  • JIANG Xiao ,
  • BAI Lubin ,
  • LOU Xiayin ,
  • LI Mei , * ,
  • LIU Hui
Expand
  • Institute of Remote Sensing and Geographic Information System, School of Earth and Space Sciences, Peking University, Beijing 100871, China
*LI Mei, E-mail:

Received date: 2021-10-30

  Revised date: 2021-12-25

  Online published: 2022-08-25

Supported by

China Postdoctoral Science Foundation(2021M690201)

Fold

摘要

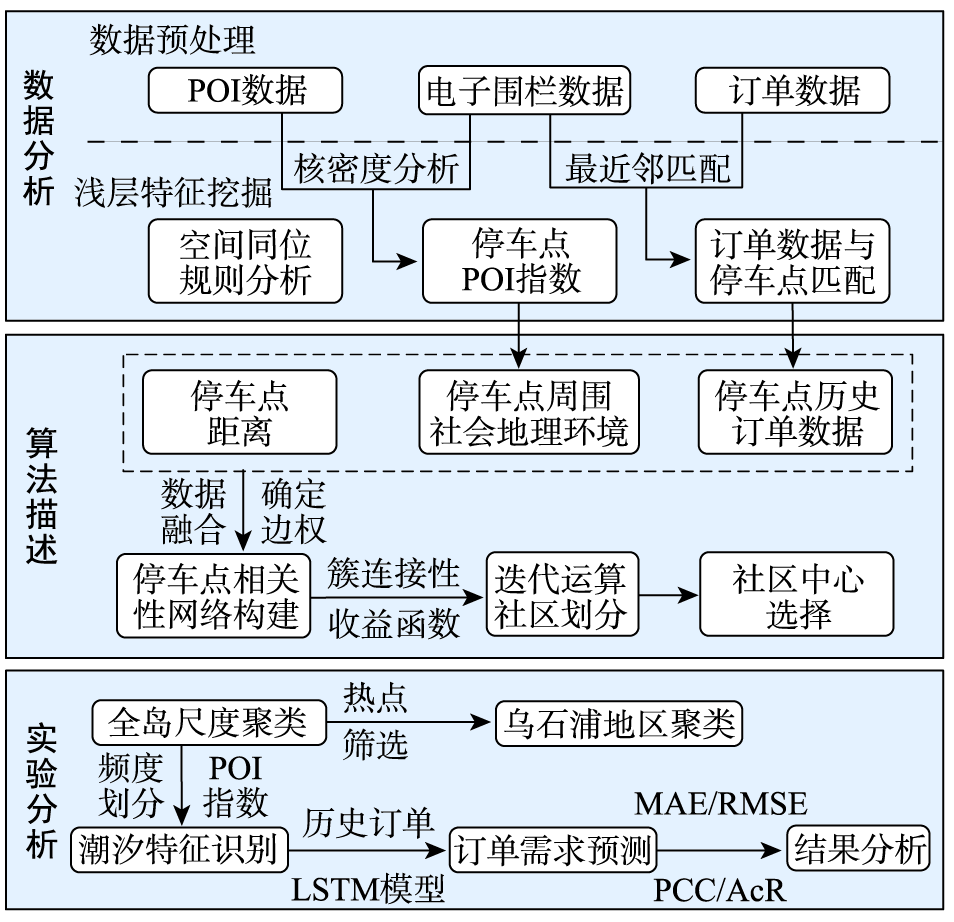
当前,我国政府和单车企业多以划定电子围栏停车点的方式进行共享单车的规范化管理,由于单个电子围栏内部单车流入流出的随机性和不确定性较大,以单个围栏为单位进行单车管理的工作量大且不具现实意义。因此,有必要对电子围栏停车点进行聚类划分,实行区域化的管理与调度。基于此,本文提出一种基于时空约束的网络图聚类算法,该算法综合考虑空间因素（地理位置、地理环境特征）和时间因素（历史订单）,只需通过距离阈值设定即可实现电子围栏的多尺度聚类划分,实验分别在3000 m和700 m距离阈值条件下对厦门岛和乌石浦地区电子围栏进行聚类,结果显示该算法不仅能够将具有相似时空特征的电子围栏聚到同一社区簇内,而且能够使得单车流动主要集中在划分后的社区内部;随后,在社区划分基础上进行单车潮汐特征挖掘,能够有效识别和定位单车使用的热点地区;最后,利用长短时记忆神经网络（Long-Short Time Memory network, LSTM）进行单车订单需求预测,结果显示有84%以上社区的预测准确率在85%以上,平均预测准确率为91.301%,预测效果较好,可有效满足单车调度需求。本文研究成果可服务于电子围栏停车点规划与共享单车的区域化管理与调度工作。

关键词： 共享单车; 电子围栏; 数据挖掘; 时空约束; 多尺度聚类; 使用模式; 需求预测; 厦门岛

本文引用格式

姜晓 , 白璐斌 , 楼夏寅 , 李梅 , 刘晖 . 基于多尺度时空聚类的共享单车潮汐特征挖掘与需求预测研究[J]. 地球信息科学学报, 2022 , 24(6) : 1047 -1060 . DOI: 10.12082/dqxxkx.2022.210691

Abstract

At present, China government and bike-sharing companies mostly use electronic fence parking stations to manage the shared bicycles normatively. Electric fence parking stations for free-floating bike-sharing are predetermined 'virtual fences' to guide users to park bikes in designated zones and regulate inappropriate parking behaviors. However, due to the randomness and uncertainty of the inflow and outflow of bicycles at a single parking station, the scheduling of bicycles based on an independent parking station is hard to realize. Therefore, it is necessary to group fence stations into clusters and implement regional management. In this paper, we proposed a network clustering algorithm based on spatiotemporal constraints, which comprehensively considered spatial factors (location and geographical environment of the parking stations) and temporal factors (historical bike-sharing system orders) as the clustering partition basis, and this algorithm can realize the multi-scale groups division of parking stations only by setting a distance threshold. We chose Xiamen Island as the research region. Using the distance thresholds of 3000 m and 700 m respectively, we carried out clustering experiments on the electronic fence parking stations in the whole Xiamen Island and its Wushipu block. The results showed that this algorithm can not only gather the parking stations with similar temporal and spatial characteristics into the same group, but also make the shared bike flow mainly concentrated in the streets within each group, which is convenient for regional management. Then, we mined the characteristics of shared bikes among the partitioned groups, which can effectively identify and locate hot areas for shared bikes. The results showed that subway stations, office buildings, parks, hospitals, shopping malls, and residential areas had a greater impact on the usage pattern of shared bikes. In particular, it is necessary to focus on the accumulation of shared bikes near office buildings, shopping malls, hospitals, and subway stations, and the shortage of bicycles near the residential areas, parks, and factories during the morning rush hours. Finally, we used the Long Short Time Memory network (LSTM) to predict the orders of shared bikes. The results showed that 84% of the groups had a prediction accuracy of more than 85%, and the average of the overall prediction accuracy was 91.301%, which can meet the needs of bike-sharing system scheduling. Our research provides scientific suggestions for relevant departments to arrange electronic fence parking stations, and the LSTM model has high accuracy in predicting bicycle flow, which is effective in reducing the scheduling cost of bike-sharing system and improve the management efficiency.

Key words： bike-sharing system; electronic fence; data mining; spatiotemporal constraints; multiscale clustering; usage pattern; demand forecast; Xiamen island

1 引言

共享单车的迅速普及,方便了市民短途出行,既改善了交通,也为城市环境保护做出贡献。然而,随着单车快速发展,逐渐暴露出诸多问题,其中较为严重的就是乱停乱放问题,影响市容的同时,也影响公共交通安全[1]。
当前,通过设置电子围栏停车点来规范用户的停车行为是一种主流的共享单车管理方式,电子围栏停车点是预先划定的虚拟停车框,用于引导用户根据单车app的指引将单车停放在指定区域内[2]。实际使用中,由于用户骑行出发点和目的地的不同,单车使用具有较大的随机性和不确定性,容易导致一些地区单车过剩,一些地区无车可用的供需不平衡问题[3]。若以单个停车点为单位进行管理和调度,工作量大且繁琐,不易实现,因此有必要对单车停车点进行合理的区域划分,实行区域化的管理与调度。
聚类分析在共享单车研究中应用广泛,能够有效解决单车的区域划分问题。聚类是指将研究对象的集合划分为不同的簇,使得同一簇中的对象特征最大程度地相似,不同簇间的对象特征最大程度的不同[4]。传统聚类方法包括划分聚类和层次聚类[5],不同学者采用不同的方法进行共享单车聚类问题的研究。划分聚类方面,高楹等[6]、靳爽等[7]利用基于距离的K-means方法对城市轨道交通接驳共享单车停靠点进行聚类分析,揭示不同区域的共享单车运行规律,但该方法在聚类前需要提前确定聚类类别个数,且只考虑距离因素对聚类的影响;Zhang等[2]、 Yu等[8]、Hua等[9]利用基于密度的 DBSCAN方法进行聚类,通过设置停车点邻域半径和密度阈值,确定共享单车的聚集热点,该方法受点密度影响较大,单车停车点受城市功能区和人流量的影响,其分布密度并不一定均匀,因此该方法聚类结果的精细度不高,随机性较强。层次聚类方面,Jia等[10]提出一种两级高斯混合模型聚类算法,在考虑站点间自行车迁移趋势和地理位置信息的情况下,将自行车站点进行分组;Du等[11]使用层次聚类的方法,研究不同站点在邻近区域的时间使用模式,将具有相似使用频率时间序列的站点分组到相同的集群中。另有文献采用基于网格的方法进行共享单车聚类分析,如刘畅 等[12]采用网格划分方法,描述共享单车空间分布情况,但该方法同样依赖于密度阈值,且在网格边缘处易将聚集的停车点割裂开[13]。
上述方法所考虑的聚类依据各不相同,以空间要素为主,较少的考虑时间要素,类别较为单一。空间要素如停车点地理位置、不同停车点间的流动性、停车点周围地理环境的相似性对单车使用均有较大影响[10],而时间因素如停车点的历史订单情况也是表征停车点相似性的重要特征[14]。因此,应综合考虑上述时空要素,使聚类所依据的特征信息更加丰富,更贴近实际情况。同时,共享单车停车点聚类的最终目的在于方便管理和优化调度,当前研究较少地将聚类、特征发掘与需求预测问题结合起来,而这一过程是相辅相成的,通过聚类分析优化共享单车的区域划分,进而发掘各区域内部单车使用特征,进行单车需求预测,能够更好地指导共享单车管理与调度工作。基于此,本文提出基于时空约束的网络图聚类算法GC2（Geographically-Constrained Graph Clustering）算法,对共享单车电子围栏停车点网络进行聚类划分,基于划分结果,从不同角度分析共享单车的潮汐特征,并进行订单需求的预测,以期帮助政府和相关企业合理规划共享单车电子围栏,提高单车管理与调度效率。

2 研究方法

2.1 技术路线

如图1所示,本研究方法包括数据分析、算法描述和实验分析3个部分。其中数据分析部分包括数据预处理和浅层特征发掘,算法描述部分详细介绍基于时空约束的网络图聚类算法,最后在厦门全岛和乌石浦地区2个尺度下进行聚类划分实验,并在全岛聚类划分的基础上对单车潮汐特征挖掘和订单需求预测进行研究。
图1 技术路线

Fig. 1 The specific technical route

2.2 数据源及数据预处理

本研究的实验数据清单如表1所示,其主要来源包括2部分：
表1 实验数据清单

Tab. 1 Experimental data list

数据名称 数据时间 数据规模 数据描述
字段名称 字段含义
厦门岛共享单车订单数据 2020年12月21—25日6：00 am—10：00 am 58万条左右 BICYCLE_ID 加密后的单车ID号
LATITDUE 纬度/°
LONGITUDE 经度/°
LOCK_STATUS 锁状态
UPDATE_TIME 锁状态更新的时间
厦门岛共享单车电子围栏数据 2020年12月 1.4万个左右 FENCE_ID 电子围栏唯一编号
FENCE_LOC 电子围栏位置坐标串
厦门岛POI数据 2021年1月 8000条左右 POI_TYPE POI地物类别
LATITDUE 纬度/°
LONGITUDE 经度/°
厦门岛路网数据 2021年1月 8000条道路 Length 道路长度/m
name 道路名称
（1）2021年数字中国大赛公开数据[15]：包括2020年12月21日至2020年12月25日厦门岛早高峰期间共享单车订单脱敏数据和电子围栏脱敏数据。
（2）网络爬虫数据[16]：使用爬虫技术从高德地图API中爬取的厦门岛内各类地物兴趣点（POI, Point of Interest）数据和路网数据。
主要数据预处理过程如下：
（1）订单数据预处理：对于连续状态相同的开关锁状态、相邻两条数据时间过短或距离过近的订单数据进行清洗,方法如图2所示。
图2 订单数据的处理流程

Fig. 2 Processing steps of order data

（2）电子围栏数据预处理：计算电子围栏中心坐标作为其位置参考,计算其外包矩形和面积估算每个站点可以停放的单车数量,方法如图3所示。
图3 电子围栏数据处理流程

Fig. 3 Processing steps of electronic fence data

（3）POI数据预处理：由于爬取到的POI坐标点是火星坐标,为了与订单数据保持一致,将其转换为WGS84坐标。

2.3 数据浅层特征发掘

预处理后的基础数据所含信息难以直接应用,需要进行浅层特征发掘,以分析影响单车使用的主要因素及其影响程度。

2.3.1 POI指数计算

POI数据与人类生活和社会经济活动密切相关,是指具有地理标识的空间地物,包含各类职能设施的位置信息与关联的属性信息,具有样本量大,信息丰富等特点,能够有效、直观地反映城市的各类活动,体现城市不同区域的社会地理特征[17-18]。
为表征停车点周围社会地理环境,本实验选取常见的9类POI地物（公交站点、写字楼、公园、商场、地铁站、居民点、医院、学校、工厂）进行研究,基本涵盖了市民日常活动场所,也是单车流动的主要地点,其位置和属性对停车点的单车使用有较大影响。
首先利用空间同位规则分析法[19]分析9类POI地物数据与电子围栏停车点分布的相关性,通过条件概率的计算得到其同位关系矩阵图（图4）。
图4 各类POI点与共享单车开关锁位置同位关系矩阵

Fig. 4 Matrix diagram of Co-location relationship between POI features and the orders of shared-bikes

图4中第一列表示该9类POI地物附近100 m范围内存在共享单车的概率,可以发现概率值均在0.6以上,其中商场、办公楼、公交站、地铁站等热点地区高达0.9以上,一定程度上说明厦门岛地区共享单车的普及率较高,且与POI地物具有较强的空间相关性。
为了进一步量化POI数据对各停车点单车使用的影响,使用核密度分析方法[20-21]来计算每个停车点周围各类POI对停车点所在位置的影响程度,量化为停车点POI指数。计算公式如下：
D = 1 r a d i u s 2 ∑ i = 1 l 3 π 1 - d i s t i r a d i u s 2 2 F o r d i s t i < r a d i u s
式中： i = 0,1 , … , l,表示输入的某类POI的所有点; d i s t i是点 i与 ( x , y )之间的距离; r a d i u s是该类搜索半径,由式（2）计算得到。
r a d i u s = 0.9 × m i n S D , 1 l n 2 × D m × l - 0.2
D m = ∑ i = 1 l x i - x m 2 + ( y i - y m ) 2 l
S D = ( ∑ i = 1 l x i - x m 2 l + ∑ i = 1 l y i - y m 2 l )
式中： ( x i , y i )为点 i的地理位置坐标; ( x m , y m )为该类POI的中心点; D m计算的是到中心点的平均距离; S D计算的是到中心点的标准距离。
利用上述方法,计算厦门岛所有停车点受该9类POI的影响程度,称其为停车点的POI指数,结果如式（5）所示,式中 P O I _ i n d e x i即为停车点 s i的POI指数,其中9个变量分别表示9类POI类别指数。
P O I i n d e x i = [ D i b u s - s t a t i o n , D i o f f i c e , D i p a r k , D i m a l l , D i s u b s t a t i o n , D i r e s i d e n t , D i h o s p i t a l , D i s c h o o l , D i f a c t o r y ]
实质上POI指数表征的是各个停车点的社会地理环境,距离相近的停车点其POI指数会比较相近,而距离较远的停车点如果周边社会地理环境相似的话,其POI指数也可能相近。因此,此处使用POI指数衡量电子围栏停车点的相似性比单纯使用距离所蕴含的信息更为丰富。

2.3.2 历史订单数据匹配

原始订单数据中只包含该笔订单的开关锁状态和发生位置,具体属于哪个电子围栏停车点没有说明。因此,若以电子围栏停车点为研究对象,需要将各订单数据匹配到具体的停车点上。
最精确的方法是利用电子围栏坐标串轮廓的计算划定每个订单归属,但受用户停车习惯和定位精度影响,实际情况只有很少一部分单车订单落入电子围栏中,大部分单车在围栏附近。因此,采用此方法匹配效率较低且不太贴近实际情况。
KNN（K Nearest Neighbors）最近邻点算法是常用的分类算法之一,适合样本容量比较大的类域的自动分类[22-23]。本文使用KNN进行订单与停车点的匹配,实验设置k=1,即将每笔订单归属到距离与它最近的停车点上。这样对于单个电子围栏停车点 s i,可以获得其历史订单数据 o r d e r i,如式（6）所示。
o r d e r i = [ U i + t 1 , U i - t 1 , … , U i + t K , U i - t K ]
式中： U i + t k表示 t k时段流入（关锁）停车点 s i的所有订单数量; U i - t k表示 t k时段流出（开锁）停车点 s i的所有订单数量。

2.4 基于时空约束的网络图聚类算法

在以上研究基础上,本研究提出基于时空约束的网络图聚类算法GC2。该算法计算步骤包括3个部分：停车点相关性网络构建、基于时空约束的网络聚类、社区中心选择。

2.4.1 停车点相关性网络构建

首先将停车点之间的关系建模成一个相关性网络 G = ( V , E ),其中 V = ( s 1 , … , s N )表示 N个停车点的集合, E是2个停车点之间连线的集合。具体考虑因素及计算流程如下：
（1）停车点距离因素
根据地理学第一定律,相近的事物关联更为紧密。因此,考虑距离是限制共享单车区域划分的首要因素。根据停车站点间的空间距离来判断其是否邻接,使用表达式（7）表示邻接情况。
w D i , j = 1 d i s t ( s i , s j ) ≤ R t 0 d i s t ( s i , s j ) > R t
式中 ： d i s t ( s i , s j )表示2个站点之间的距离; R t为距离阈值。若两站点间距离中 d i s t ( s i , s j )不大于 R t,则判定其邻接,否则判定其不邻接。通过调节该阈值,控制聚类算法的尺度,从而控制每个聚类区域的大小。
（2）社会地理环境与历史订单因素
使用POI指数 P O I _ i n d e x i和历史订单数据 o r d e r i表征停车点周围社区地理环境和时间因素。计算方法如下：
E p s i , s j = 1 + ρ p s i , s j 2 H o s i , s j = 1 + ρ o s i , s j 2
式中： ρ p s i , s j, ρ o s i , s j分别为两停车站点POI指数和历史订单数据的PEARSON相关性系数,将其正则化到[0,1]之间得到 E p s i , s j和 H o ( s i , s j )。通过 μ ∈ [ 0,1 ]控制各自权重大小,得到社会地理环境和历史订单因素的综合权重如下：
w E H s i , s j = μ E p s i , s j + ( 1 - μ ) H o ( s i , s j )
（3）相关性网络构建
将以上3大影响因素进行综合,得到停车点 s i , s j间的边权矩阵 W s i , s j,如式（10）所示。
W s i , s j = w D i , j × w E H s i , s j
最终计算所有停车点两两之间的边权 W s i , s j得到停车点相关性网络 G,此网络中蕴含了停车点之间位置、社会环境和历史订单之间的相似性。

2.4.2 基于时空约束的网络图聚类

在停车点相关性网络构建基础上,进行停车点网络的聚类划分,将具有相似单车使用特征的电子围栏停车站点聚成同一簇,即网络图结构中经常使用的社区探测问题,所谓社区,即为网络图结构中具有相似属性或者起到相似作用的节点集合[24]。本文中的所提到的社区为在算法聚类划分后,具有相似属性的电子围栏停车点的集合。
如图5所示簇间的交集为空,对于给定结点 v,定义其到簇 C的连接性为 v到簇 C内所有停车点的边权之和,即：
C O N v , C = ∑ v ' ∈ C W v , v '
图5 GC2算法聚类示意图

注：黑色圆点表示待聚类的电子围栏站点 v i;其他颜色圆点表示已聚类的电子围栏站点;valuei表示待聚类站点与簇Ci的收益函数值;P表示电子围栏停车点簇集合。

Fig. 5 Schematic diagram of the GC2 clustering method

聚类的最终目标是使得聚类后的每个停车点簇 C i内部的停车点具有相似的特征,且使得每个停车点 v与所属簇的连接性大于与其他任何簇之间的连接性。即：
C O N v , C k ≥ m a x C O N v , C l , C l ∈ P , ∀ v ∈ C k
同时,考虑到停车点间距离是聚类划分的重要依据,设定簇内任意2个站点的距离不能大于距离阈值 r,即：
∀ v , v ' ∈ C k , d i s t ( v , v ' ) ≤ r
最后,在研究标签算法[25]思想基础上,设计停车点 v与各邻接簇的收益函数 v a l u e,如式（14）所示,该收益函数对停车站点与簇间的连接性进行奖励、与簇间的距离进行惩罚[26]。
v a l u e v , C = C O N v , C l o g r m a x d i s t v , v ' v ' ∈ C
通过迭代运算, G C 2算法贪心地将每个停车点分配到收益 v a l u e最大的邻接簇中,直到所有停车点不在簇间移动,从而完成停车点的聚类。算法1流程如下：
算法1 基于时空约束的网络聚类GC2
Require:
输入:停车点相关性网络矩阵,G;
节点集合,V
一次迭代中节点类别交换的最低次数, C m i n
Ensure:
给每个节点初始化一个独一无二的簇标签
repeat
初始化交换次数 C c=0
for v i in V do
从节点集合V中移除当前节点 v i ,记录 v i此时的标 签 l a b e l b e f o r e计算节点 v i与其邻接簇之间的收益value
将节点 v i分配给value最大的簇,将此簇的标签
l a b e l a f t e r赋予 v i,将 v i添加到集合V中
if l a b e l b e f o r e ≠ l a b e l a f t e r then
C c = C c + 1
end if
end if
until C c ≤ C m i n

2.4.3 社区中心的选择

基于时空约束的网络图聚类划分本质上是一种图的社区划分,并没有进行聚类中心的计算。本研究社区中心的选择主要考虑2个因素：度中心性和接近中心性。
度中心性用于反映节点在整个网络中的重要程度,为节点 v i的度与网络节点个数比值,即：
D C i = ∑ j = 0 N w i j N - 1
式中： w i j为相关性矩阵中的边权; N为网络中所有节点的个数。在网络中,停车点的度越大,说明该停车点与其他停车点关联程度越高。
接近中心性用于表达停车点在其所属社区中的中心化程度,计算如式（16）所示。
C C i = n c - 1 ∑ j n c d i j
式中： n c为当前社区中节点的个数; d i j为节点之间的距离。在社区中,接近中心性越大说明该点与其他点越接近,中心化程度越高。
最后,将上述2个指标归一化到[0,1]后相加,取社区中计算结果最大的节点作为该社区的中心,该中心综合了社区内部的接近性及其与临近社区的关联性,相较其他节点更具代表性,可作为共享单车区域的中心代表。

2.5 共享单车需求预测与结果分析

聚类划分目的在于更好地服务单车的管理与调度,而调度工作需要掌握社区内未来一段时间内单车订单情况,因此需要进行单车需求的预测。

2.5.1 LSTM模型预测单车订单需求

长短时记忆神经网络（Long-Short Time Memory network, LSTM）能学习一个序列在较长时间上的依赖关系,具有遗忘门、信息增强门和输出门3大基本结构[27],其网络结构如图6所示。
图6 LSTM网络结构示意图

注： S t表示网络在 t时刻的记忆; U表示输入层到隐藏层之间的权重; W表示隐藏层内部节点之间的权重; V表示隐藏层与输出层之间的权重; δ表示sigmoid激活函数。

Fig. 6 Schematic diagram of LSTM network structure

每个神经元中3个门、隐藏层输出 h t和状态更新 C t的计算表达如下：
f t = δ w f × x t , h t - 1 + b f
i t = δ w i × x t , h t - 1 + b i
o t = δ w o × x t , h t - 1 + b o
C t = t a n h W c × x t , h t - 1 + b f + f t × C t - 1
h t = o t × t a n h C t
社区共享单车订单数量的变化具有趋势性、周期性和时间上的自相关性特征,在单位时间窗口的用量实际是一个时间序列,因此可使用时间序列模型对其进行回归和预测[28]。文献[28]—文献[30]研究结果表明,采用LSTM 神经网络模型对单车需求的预测结果优于线性回归（Linear Regression,LR）、BP神经网络（Back-Propagation,BP）和循环神经网络（Recurrent Neural Network, RNN）等预测模型,因此本研究选取LSTM模型进行单车需求的预测。
实验模型上,输入层的数据特征维度为27,隐藏层中LSTM单元为3层,每个LSTM单元内神经元的个数为4,输出层为一层全连接层,输出维度为1。
实验数据上,使用厦门岛2020年12月21日到25日每天6—10时的共享单车订单数据,总共有 4×5=20 h,以半个小时为时间窗口对数据进行切片,每次取前2个时间窗口的数据作为输入对第 3个时间窗口进行预测。

2.5.2 预测结果分析

以MAE,RMSE、准确率Accuracy和PEARSON相关系数等评价指标对模型的预测误差和预测效果进行评价。
MAE（Mean Absolute Error）为绝对误差平均值,用于表征预测误差情况,计算方法如式（22）所示。
M A E = 1 n ∑ i = 1 n y i ^ - y i
RMSE（Root Mean Square Error）为均方根误差,用于表征预测模型的精度[31],计算方法如 式（23）所示。
R M S E = 1 n ∑ i = 1 n ( y i ^ - y i ) 2
实验定义准确率AcR（Accuracy Rate）如式（24）所示,用于表征预测结果的准确性[32]。
A c R = 1 - y i ^ - y i y i
式中： y i ^为预测值; y i为实际值;n为样本个数。
2个连续变量x,y的皮尔逊相关系数PEARSON用于度量2个变量之间的线性相关程度[33],本实验用其表征预测结果对真实值的拟合效果,计算方法如式（25）所示。
ρ ( x , y ) = c o v ( x , y ) σ x σ y
式中： c o v ( x , y )为协方差; σ x、 σ y为各自的标准差。

3 实验与结果分析

3.1 共享单车多尺度聚类分析

全岛尺度上,使用GC2算法,将距离阈值设置为3000 m进行聚类,结果如图7所示,全岛停车点被划分成了25个社区。可以发现,如图中蓝色框中部分,社区中心呈现一定聚集性特征,说明该算法对于社区中心的选择既考虑了社区内部的联系,也综合了周边社区的影响。图中红色框所框的范围为狐尾山公园地区,该公园周边的电子围栏被狐尾山公园在距离上分隔开,但由于公园周边具有相似的社会地理环境特征,并且周边单车在使用时间上也具有相似性,所以被划分到了同一社区内,说明相较传统算法,该方法不仅考虑了距离因素,同时也综合了地理环境和历史订单因素。
图7 全岛尺度下的社区划分结果

注：大的红色点表示社区聚类中心,上面的数字代表社区号;其余彩色小点表示聚类后不同社区内部的电子围栏中心点。

Fig. 7 Community division results of the whole island

单车流动情况是单车调度工作需要考虑的重要因素,本研究统计了全部25个区域单车订单的历史数据,对于单个订单,如果其出发点和目的地停车点都在同一社区内,则认为其在区域内部流动,如果出发点和目的地停车点不在同一社区内则认为是发生了社区间的流动,将单车流动的统计结果绘制成弦图,如图8所示。图8中环占比越大的社区的单车流动量越大,结合图7中各社区位置分析,可以发现,除图中第21和第4社区,第20和第12社区,第22和第9社区等位置临近的社区间有部分单车流动外,其余大部分集中在社区内部,社区间流动很少。
图8 全岛尺度下的单车流动情况

注：数字表示GC2聚类后各社区号,区间连线表示单车在社区间流动情况,连线越粗,流动量越大。

Fig. 8 Flow of shared-bikes among communities in Xiamen Island

根据全岛尺度下的社区划分可发现,第3、7、9、10号社区单车流动量较大,且在位置上临近,均为乌石浦地铁站附近区域,是单车使用的热点地区。因此选取该4个社区作为研究对象,研究局部尺度下社区内部的单车使用特征与流动情况。将距离阈值设置为700 m进行 G C 2聚类,结果如图9所示,以上 4 个社区最终划分为61个分区。统计各分区的单车流动情况,绘制成弦图,如图10所示。
图9 乌石浦地区聚类划分结果

注：黄色点表示各分区聚类中心,其余彩色点表示聚类后不同分区内部的电子围栏中心点。

Fig. 9 Community division results of Wushipu area

图10 乌石浦地区单车流动情况

注：数字表示GC2聚类后各社区号,区间连线表示单车在社区间流动情况,连线越粗,流动量越大。

Fig. 10 Flow of shared-bikes in Wushipu area

可以发现,局部尺度下,划分后的分区基本沿街道分布,弦图中各分区间的连线错综复杂,说明局部尺度下社区内部的单车流动主要集中在分区间进行,分区间电子围栏停车点联系紧密,具有相似的使用特征。
综上所述,聚类划分的目标在于使划分后的社区内部电子围栏停车点之间的联系紧密,社区之间的联系较小,上述结果正是表明了该聚类算法的有效性。同时,从单车的流动特点来看,应重点关注聚类后社区内部的单车不平衡问题,减少社区间的大规模调度,从而降低调度成本与提高效率。

3.2 社区单车潮汐特征挖掘

社区单车潮汐特征挖掘的目的在于更细粒度地区分单车使用的热点区域,以及分析影响单车使用的主要因素。在厦门全岛的尺度下,为了表征各区域内部单车使用的频繁程度,用每个社区的历史总订单量除以社区内部停车点个数得到该社区内的平均订单量,并以此为标准,将全区25个区域划分为高频、中频、低频3个类别,如图11所示。
图11 全岛共享单车订单频率分布

注：绿色点表示社区聚类中心,上面的数字代表社区号。

Fig. 11 Frequency distribution of shared-bikes orders in Xiamen Island

为研究各类别区域内不同POI地物对单车使用的影响程度,对3个类别区域内所有停车点的POI指数求平均,结果如表2所示。表中最右侧指数和为左边9项指数的和,可以发现高频和中频区域指数和远高于低频地区,说明高频区域和中频区域的社区地理环境更复杂,内部的城市功能区人流量更大,因此单车订单数更高,这一点也与厦门岛实际情况相符,体现出该方法能够有效识别出单车使用的热点区域。同时,地铁站、办公楼、公园、医院、商场和居民区指数相较其他POI地物更高,说明这些地物对单车使用的影响更大,其附近单车的使用更为频繁,需要重点关注供需平衡问题。
表3 厦门岛基于单车使用频率的社区分类与POI指数统计

Tab. 3 Communities division by the frequency of shared-bikes usage and POI index staticstics in Xiamen Island

类别 数目 工厂 医院 公园 学校 地铁 办公楼 公交 居民区 商场 指数和
高频 8 0.262 0.333 0.480 0.214 0.544 0.656 0.078 0.318 0.323 3.209
中频 9 0.212 0.505 0.544 0.302 0.544 0.497 0.201 0.197 0.280 3.281
低频 8 0.204 0.153 0.247 0.105 0.178 0.300 0.054 0.275 0.098 1.613
为了进一步研究早高峰期间,不同POI地物附近的共享单车流入流出的具体情况,在乌石浦地区聚类分区的基础上,根据各分区单车订单流入量与流出量的差值,差值大于0为流入,小于0为流出,将全部61个分区分为单车流入和流出区,分别计算这两类区域各类POI指数均值,结果如表3所示。由表3可以发现,厦门岛早高峰期间,流入区办公楼、商场、医院和地铁站指数相较流出区更高,单车更多表现为流入趋势,需要重点关注这些地物附近单车堆积问题;而流出区居民区、公园和工厂指数相较流入地区更高,单车更多表现为流出趋势,需要重点关注这些地物附近单车短缺问题。
表4 乌石浦地区基于单车流入流出的社区分类与POI指数统计

Tab. 4 Communities division by the inflow and outflow of shared-bikes and POI index staticstics in Wushipu area

类别 数目 工厂 医院 公园 学校 地铁 办公楼 公交 居民区 商场 指数和
流入 26 0.210 0.526 0.385 0.365 0.654 0.467 0.567 0.208 0.441 3.822
流出 34 0.221 0.382 0.407 0.355 0.548 0.323 0.548 0.222 0.298 3.302

3.3 社区共享单车需求预测

为了更精准解决单车供需平衡的问题,还需要预测一段时间内的单车需求量,即预测单车订单情况。在上文厦门全岛划分的25个社区的基础上,利用前文所述LSTM模型,以社区为单位进行训练和预测,实验中取80%数据为训练集,20%为测试集。
根据预测结果,将25个社区整体预测值和真实值进行比较,绘制折线图（图12）。可以发现预测值与真实值拟合效果较好,整体预测差值线维持在较低水平,预测误差较小。
图12 LSTM模型预测社区单车订单量与实际订单量对比

Fig. 12 Comparison between the predicted results and actual values of shared-bikes orders based on LSTM model

为了更进一步描述LSTM模型预测准确性,分别计算25个社区订单预测值与实际值的MAE、RMSE、PEARSON和准确率AcR,统计各指标数据的分布情况如表4所示。从表4中数据可以发现不同社区的预测效果不同。MAE能够较好地反映出预测误差的实际情况,可以发现绝大多数MAE值在50以下,均值为24.080,说明预测误差较为理想;RMSE指数能够反映预测结果的精确度,正常情况下RMSE值越小,预测的精确度越高,但也易受异常值影响,从表中看出大部分社区RMSE值在50以下,均值为38.548,说明模型预测的精确度能够得到保证;PEARSON系数能够反映预测值与真实值的线性相关性,大部分社区PEARSON系数值为90%以上,均值为91.010%,说明大部分社区的预测结果较好地拟合了实际需求量;对所有社区预测准确率数据进行统计,有84%的社区订单预测准确率在85%以上,均值为91.301%,说明模型预测的准确度较高。综合以上指标,表明基于社区划分的LSTM模型的预测结果较好,能够满足单车调度的需要。
表5 LSTM模型预测社区单车需求结果评价

Tab. 5 Evaluation of LSTM model prediction results

社区 评价指标
MAE RMSE PEARSON/% AcR/%
0 12.394 26.682 84.651 86.888
1 27.065 37.996 97.572 94.228
2 21.540 38.921 96.790 96.674
3 60.711 96.166 92.481 86.226
4 48.237 66.411 98.163 97.235
5 11.158 16.725 98.011 95.098
6 6.461 8.509 97.987 95.845
7 33.671 42.844 99.099 95.559
8 5.448 10.145 75.370 91.557
9 44.250 64.302 97.784 97.264
10 25.329 55.762 98.099 95.295
11 19.842 29.365 99.111 97.393
12 35.355 50.229 99.335 95.543
13 2.250 3.806 54.333 78.498
14 7.0785 9.752 95.637 93.854
15 7.211 10.692 92.511 93.463
16 9.106 17.276 78.129 89.304
17 9.171 19.647 87.105 92.711
18 59.250 108.202 95.537 87.758
19 45.013 70.014 97.275 96.156
20 15.644 29.260 98.862 97.189
21 33.316 47.215 99.282 95.957
22 49.750 79.096 90.956 76.763
23 11.092 22.382 68.255 83.070
24 1.671 2.315 82.898 73.008
均值 24.080 38.548 91.010 91.301
最后,为研究单车流量预测结果和真实值的时序特征,对25个社区早高峰期间单车流入和流出订单的预测值和真实值进行统计,以每半小时为时间段绘制曲线（图13）。
图13 全岛尺度下社区单车流入流出时序特征

Fig. 13 Timing characteristics of inflow and outflow of shared-bikes in Xiamen Island

由图分析,首先,从预测差值线上来看,各时段的预测差值线维持在较低水平,预测误差较小;其次,从真实值和预测值曲线的走势上看,单车的流入和流出具有相似的时序特征,6:00—8:00为单车流量的上升期,在8:00左右达到峰值,随后呈下降趋势,说明厦门岛早8:00左右为共享单车使用的高峰时段,需要重点关注8:00前后时段的单车供需平衡问题;最后,从各时段的预测效果上来看,8:00—9:00时段的曲线拟合效果最好,LSTM模型在该时段的预测效果最佳。

4 讨论

共享单车电子围栏技术的应用一定程度上提高了用户的用车规范,但由于城市POI和人流量的动态变动,容易造成单车供需不平衡的现象,因此,需要加强单车的调度和电子围栏的动态优化。本研究通过对电子围栏进行GC2聚类,能够有效探索出不同区域的单车使用情况与流动规律,发现单车使用热点区域,针对热点区域进行单车潮汐特征挖掘和流量预测,有助于有效提升单车调度管理的效率,优化电子围栏停车点的部署。相较以往研究,本文研究特点体现在：
聚类方法上,GC2算法只需通过不同距离阈值的设定即可实现电子围栏停车点的多尺度聚类划分,整个流程不需要预先设置其它参数,算法自适应计算划分的社区类别数量,且在相同数据和阈值条件下,聚类结果一致,不受停车点密度的影响。因此,该算法的适应性较好,易于推广应用。
聚类依据上,本研究提出的GC2算法,既考虑了地理位置、社区地理环境等空间因素,也考虑了历史订单数据这一时间因素,聚类划分的依据更丰富且充分,聚类结果较好地识别了单车的流动性,可充分展现共享单车的实际聚集特征。
研究内容上,本文对于研究区域内共享单车的特征挖掘和订单预测均是在社区聚类划分的基础上进行的,研究内容的针对性强。社区聚类和潮汐特征挖掘的结果能够有效识别和定位单车使用的热点地区,社区订单预测结果误差较小,预测精度和准确度较高,能够满足单车调度需求,对于单车管理和调度工作具有指导意义。
受限于所获取的单车数据规模,本文只对早高峰期间的共享单车潮汐特征进行了研究,未来若能获取到更完整、更大规模数据,则可针对全天的单车使用情况进行分析。此外,共享单车调度问题是解决单车不平衡问题的关键,下步将综合本文成果,进一步研究共享单车区域化调度问题。

5 结论

为有效解决共享单车的区域划分问题,本文提出了基于时空约束的网络图聚类算法GC2,该算法融合了共享单车时空数据,实现了对单车停车点的多尺度社区划分,在社区划分结果的基础上,进行了共享单车潮汐特征发掘和需求预测。本文以厦门岛地区为研究对象,实验结果表明：
（1） GC2聚类通过不同距离阈值的设定实现了不同尺度的社区划分,同时有效识别出了单车的区域流动性。在厦门全岛3000 m尺度下,GC2聚类结果显示,单车的流动主要集中在社区簇内,社区簇间的流动量较少;而在乌石浦地区700 m尺度下,单车流动主要集中在社区内部的各分区簇间,说明社区内部停车点联系紧密,社区间停车点联系较少,体现出GC2聚类算法的有效性与合理性。
（2）基于社区划分的潮汐特征发掘和需求预测能够有效识别和定位单车使用热点区域和重点时段。通过全岛不同社区单车使用频率划分的结果表明,高频和中频地区相较低频区的POI指数更高,地理环境更复杂。早高峰期间,中高频地区的地铁站、办公楼、公园、医院、商场和居民区是影响单车使用的主要因素,其中办公楼、商场、医院和地铁站附近容易发生单车堆积现象,居民区、公园和工厂容易发生单车短缺现象。同时,早8:00前后为厦门岛内单车用车高峰期,8:00前后时段更容易发生单车供需不平衡问题。
（3）基于社区划分的LSTM模型预测误差较小、精确度和准确度较高。各社区需求预测结果的平均MAE值为24.080,平均RMSE值为38.548,平均准确率AcR值为91.301%,平均PEARSON指数为91.010%,预测效果较为理想,能够满足单车调度需要。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
邵鹏, 王齐, 赵超. 共享单车绿色使用行为与意愿的影响因素研究[J]. 干旱区资源与环境, 2020, 34(3):64-68.

[ Shao P, Wang Q, Zhao C. Research on the factors influencing shared bicycle green use behavior and intention[J]. Journal of Arid Land Resources and Environment, 2020, 34(3):64-68. ] DOI: 10.13448/j.cnki.jalre.2020.67

DOI

[2]
Zhang Y P, Lin D, Mi Z F. Electric fence planning for dockless bike-sharing services[J]. Journal of Cleaner Production, 2019, 206:383-393. DOI: 10.1016/j.jclepro.2018.09.215

DOI

[3]
Singla A, Santoni M, Bartok G, et al. Incentivizing users for balancing bike sharing systems[C]. Proceedings of the Twenty-Ninth Aaai Conference on Artificial Intelligence, 2015.

[4]
Rokach L, Maimon O. Clustering methods[M]. Boston: Springer US. 2005. DOI: 10.1007/0-387-25465-X_15

DOI

[5]
章永来, 周耀鉴. 聚类算法综述[J]. 计算机应用, 2019, 39(7):1869-1882.

[ Zhang Y L, Zhou Y J. Review of clustering algorithms[J]. Journal of Computer Applications, 2019, 39(7):1869-1882. ] DOI: 10.11772/j.issn.1001-9081.2019010174

DOI

[6]
高楹, 宋辞, 郭思慧, 等. 接驳地铁站的共享单车源汇时空特征及其影响因素[J]. 地球信息科学学报, 2021, 23(1):155-170.

DOI

[ Gao Y, Song C, Guo S H, et al. Spatial-temporal characteristics and influencing factors of source and sink of dockless sharing bicycles connected to subway stations[J]. Journal of Geo-information Science, 2021, 23(1):155-170. ] DOI: 10.12082/dqxxkx.2021.200351

DOI

[7]
靳爽, 庞明宝. 基于K-means的城市轨道交通社区接驳共享单车停靠点规划[J]. 科学技术与工程, 2019, 19(30):343-347.

[ Jin S, Pang M B. Planning of shared bicycle stop for urban rail transit community connection based on K-means[J]. Science Technology and Engineering, 2019, 19(30):343-347. ]

[8]
Yu J J, Ji Y J, Yi C Y, et al. Estimating model for urban carrying capacity on bike-sharing[J]. Journal of Central South University, 2021, 28(6):1775-1785. DOI: 10.1007/s11771-021-4661-6

DOI

[9]
Hua M Z, Chen X W, Zheng S J, et al. Estimating the parking demand of free-floating bike sharing: A journey-data-based study of Nanjing, China[J]. Journal of Cleaner Production, 2020, 244:1-11. DOI: 10.1016/j.jclepro.2019.118764

DOI

[10]
Jia W Z, Tan Y Y, Liu L, et al. Hierarchical prediction based on two-level Gaussian mixture model clustering for bike-sharing system[J]. Knowledge-Based Systems, 2019, 178:84-97. DOI: 10.1016/j.knosys.2019.04.020

DOI

[11]
Du Y C, Deng F W, Liao F X. A model framework for discovering the spatio-temporal usage patterns of public free-floating bike-sharing system[J]. Transportation Research Part C-Emerging Technologies, 2019, 103:39-55. DOI: 1 0.1016/j.trc.2019.04.006

DOI

[12]
刘畅. 共享单车需求预测及调度研究[D]. 武汉: 武汉理工大学, 2018.

[ Liu C. Research on the demand forecast and scheduling of bike-sharing[D]. Wuhan: Wuhan University of Technology, 2018. ]

[13]
Jia W Z, Tan Y Y, Li J. Hierarchical prediction based on two-level affinity propagation clustering for bike-sharing system[J]. IEEE Access, 2018, 6:45875-45885. DOI: 10.1 109/ACCESS.2018.2865658

DOI

[14]
Ciancia V, Latella D, Massink M, et al. Exploring spatio-temporal properties of bike-sharing systems[C]. 2015 IEEE International Conference on Self-Adaptive and Self-Organizing Systems Workshops (SASOW). IEEE, 2015. DOI: 10.1109/SASOW.2015.17

[15]
数字中国建设峰会. 2021数字中国创新大赛之大数据赛道-城市管理大数据专题[DB/OL].(2021-1-25)[2021-1-31].https://dcic.datafountain.cn/competitions/10 015

[ Digital China Summit. Digital China innovation contest-the big data of urban management, DCIC 2021. [DB/OL]. (2021-1-28)[2021-1-28].https://dcic.datafountain.cn/competitions/10 015

[16]
高德地图. 厦门岛地区POI数据与城市路网数据[DB/OL].(2021-1-31)[2021-1-31]. https://ditu.amap.com/

[ Amap The POI data and urban road network data of Xiamen island[DB/OL]. (2021-1-31)[2021-1-31]. https://ditu.amap.com/

[17]
张景奇, 史文宝, 修春亮. POI数据在中国城市研究中的应用[J]. 地理科学, 2021, 41(1):140-148.

DOI

[ Zhang J Q, Shi W B, Xiu C L. Urban research using points of interest data in China[J]. Scientia Geographica Sinica, 2021, 41(1):140-148. ] DOI: 10.13249/j.cnki.sgs.2021.01.015

DOI

[18]
Xing Y Y, Wang K, Lu J J. Exploring travel patterns and trip purposes of dockless bike-sharing by analyzing massive bike-sharing data in Shanghai, China[J]. Journal of Transport Geography, 2020, 87:1-15. DOI: 10.1016/j.jtrangeo.2020.102787

DOI

[19]
Wang L Z, Bao X G, Chen H M, et al. Effective lossless condensed representation and discovery of spatial co-location patterns[J]. Information Sciences, 2018, 436:197-213. DOI: 10.1016/j.ins.2018.01.011

DOI

[20]
Alcorn L G, Jiao J. Bike-sharing station usage and the surrounding built environments in major Texas cities[J]. Journal of Planning Education and Research, 2019, 3:1-14. DOI: 10.1177/0739456X19862854

DOI

[21]
禹文豪, 艾廷华. 核密度估计法支持下的网络空间POI点可视化与分析[J]. 测绘学报, 2015, 44(1):82-90.

[ Yu Y H, AI T H, The visualization and analysis of POI features under network space supported by kernel density estimation[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1):82-90 ] DOI: 10.11947/j.AGCS.2015.20130538

DOI

[22]
Zhang S C. Cost-sensitive KNN classification[J]. Neurocomputing, 2020, 391:234-242. DOI: 10.1016/j.neucom.2018.11.101

DOI

[23]
Kapuku C, Kho S Y, Kim D K, et al. Modeling the competitiveness of a bike-sharing system using bicycle GPS and transit smartcard data[J]. Transportation Letters-the International Journal of Transportation Research, 2020,1-5. DOI: 10.1080/19427867.2020.1758389

DOI

[24]
Fortunato S. Community detection in graphs[J]. Physics Reports, 2010, 486(3-5):75-174. DOI: 10.1016/j.physrep.2009.11.002

DOI

[25]
Liu X, Murata T. Advanced modularity-specialized label propagation algorithm for detecting communities in networks[J]. Physica a-Statistical Mechanics and Its Applications, 2010, 389(7):1493-1500. DOI: 10.1016/j.physa.2009.12.019

DOI

[26]
Chen L B, Zhang D Q, Wang L Y, et al. Dynamic cluster-based over-demand prediction in bike sharing systems[C]. Ubicomp'16: Proceedings of the 2016 Acm International Joint Conference on Pervasive and Ubiquitous Computing, 2016. DOI: 10.1145/2971648.2971652

[27]
Sherstinsky A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network[J]. Physica D: Nonlinear Phenomena, 2020, 404(8):132306. DOI: 10.1016/j.physd.2019.132306

DOI

[28]
Zhang C, Zhang L N, Liu Y D, et al. Short-term prediction of bike-sharing usage considering public transport: a LSTM approach[C]. IEEE International Conference on Intelligent Transportation Systems-ITSC, 2018. DOI: 10. 109/ITSC.2018.8569726

DOI

[29]
付俐哲. 基于时空聚类与LSTM神经网络的共享单车需求预测模型[D]. 兰州: 西北师范大学, 2021.

[ Fu L Z, Spatiotemporal clustering and LSTM based prediction model of bicycle sharing[D]. Lanzhou: Northwest Normal University, 2021 ]DOI: 10.27410/d.cnki.gxbfu.2021.001767

DOI

[30]
曹旦旦, 范书瑞, 张艳, 等. 基于长短期记忆神经网络模型的共享单车短时需求量预测[J]. 科学技术与工程, 2020, 20(20):8344-8349.

[ Cao D D, Fan S R, Zhang Y, et al. Short-term demand forecasting of shared bicycles based on long short-term memory neural net-work model[J]. Science Technology and Engineering, 2020, 20(20):8344-8349. ]

[31]
Wang W J, Lu Y M. Analysis of the mean absolute error (MAE) and the root mean square error (RMSE) in assessing rounding model[C]. International Conference on Mechanical Engineering, 2018, 324(1). DOI: 10.1088/1757-899X/324/1/012049

DOI

[32]
万敏. 基于数据的共享单车需求预测和调度研究[D]. 南京: 南京大学, 2020.

[ Wan M, Research on forecasting and scheduling of shared bicycle demand based on data[D]. Nanjing: Nanjing University, 2020. ] DOI: 10.27235/d.cnki.gnjiu.2020.000120

DOI

[33]
Adler J, Parmryd I. Quantifying colocalization by correlation: The pearson correlation coefficient is superior to the mander's overlap coefficient[J]. Cytometry Part A, 2010, 77a(8):733-742. DOI: 10.1002/cyto.a.20896

DOI

Options
文章导航

/

〈 〉