EN中文

地球信息科学学报 >

2022 , Vol. 24 >Issue 10: 1883 - 1897

DOI: https://doi.org/10.12082/dqxxkx.2022.220384

城市活力

顾及POI人口吸引力异质性的城市人口空间化方法

  • 桂志鹏 , 1, 2, 3, 4, * ,
  • 梅宇翱 1 ,
  • 吴华意 2, 3, 4 ,
  • 李锐 2, 3, 4
展开
  • 1.武汉大学遥感信息工程学院,武汉 430079
  • 2.武汉大学测绘遥感信息工程国家重点实验室,武汉 430079
  • 3.湖北珞珈实验室,武汉 430079
  • 4.地球空间信息技术协同创新中心,武汉 430079

桂志鹏（1982— ）,男,宁夏吴忠人,博士,副教授,主要从事高性能地理计算与时空大数据分析相关研究。E-mail:

收稿日期: 2022-07-01

  修回日期: 2022-06-07

  网络出版日期: 2022-12-25

基金资助

国家自然科学基金项目(41971349)

国家自然科学基金项目(42090010)

国家自然科学基金项目(U20A2091)

国家重点研发计划项目(2021YFE0117000)

武汉大学知卓时空智能研究基金项目(ZZJJ202201)

收起

Urban Population Spatialization by Considering the Heterogeneity on Local Resident Attraction Force of POIs

  • GUI Zhipeng , 1, 2, 3, 4, * ,
  • MEI Yuao 1 ,
  • WU Huayi 2, 3, 4 ,
  • LI Rui 2, 3, 4
Expand
  • 1. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
  • 2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
  • 3. Hubei Luojia Laboratory, Wuhan 430079, China
  • 4. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
*GUI Zhipeng, E-mail:

Received date: 2022-07-01

  Revised date: 2022-06-07

  Online published: 2022-12-25

Supported by

National Natural Science Foundation of China(41971349)

National Natural Science Foundation of China(42090010)

National Natural Science Foundation of China(U20A2091)

National Key Research and Development Program of China(2021YFE0117000)

Zhizhuo Research Fund on Spatial-Temporal Artificial Intelligence(ZZJJ202201)

Fold

摘要

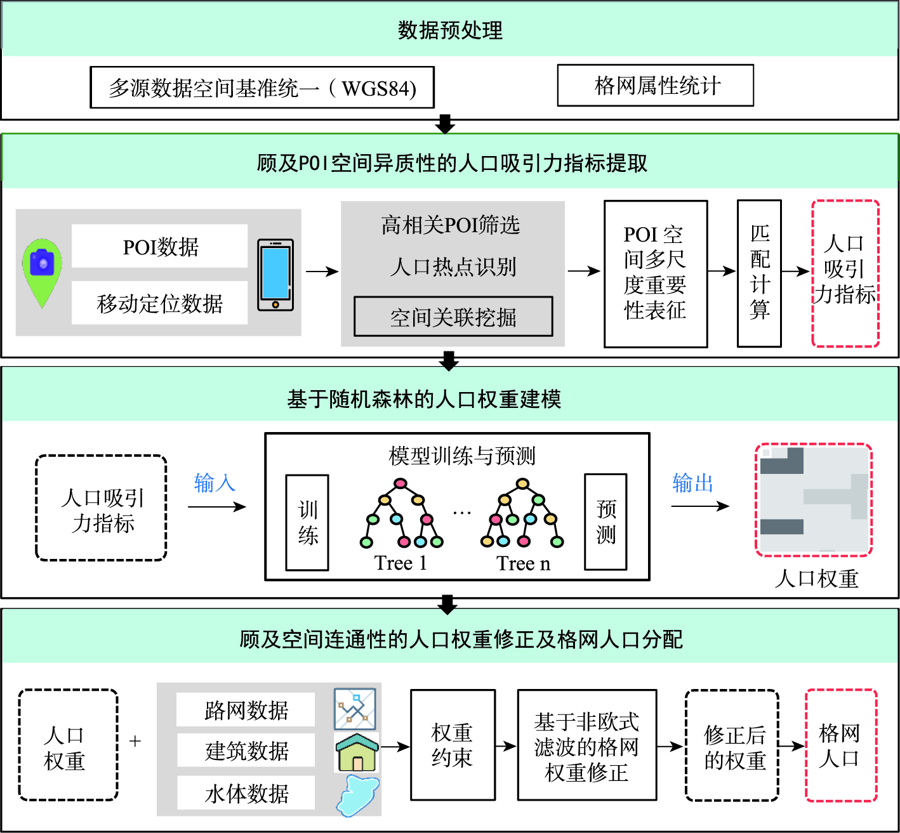
人口空间化是提升人口统计数据空间分辨率的常用手段,现有研究多基于统计建模思想建立多源数据与统计人口的数学模型以预测格网人口。兴趣点（Point of Interest, POI）作为精细人口估算的重要数据源,通常以数量/密度型指标形式参与回归建模,该方式忽略了类型相同但个体规模不同的POI与人口之间数量关系的差异,特征均质化处理造成POI语义细节的损失,导致中心城区人口低估与远城区高估。为此,本文基于随机森林模型,提出一种顾及POI人口吸引力异质性的城市人口空间化方法。该方法在表征POI空间多尺度重要性的基础上,引入移动定位数据构建人口吸引力指标;并基于非欧式滤 波修正格网人口权重,建模人口空间自相关,刻画水体等障碍物对局部空间连通性的影响。本文以武汉市为研究区域开展100 m格网验证,通过与POI密度型回归模型、公开人口数据集的对比和消融实验,展现了人口吸引力指标与权重修正的有效性。结果表明,本文方法平均绝对误差为WorldPop、GPW及对比模型的1/4~2/3,在精细人口空间化场景具有精度优势。此外,本文还讨论了移动定位数据采样率及格网粒度对建模精度的影响。

关键词： 人口格网化; 移动定位数据; 人口吸引力; 多尺度表征; 随机森林; 空间自相关; 非欧式空间滤波

本文引用格式

桂志鹏 , 梅宇翱 , 吴华意 , 李锐 . 顾及POI人口吸引力异质性的城市人口空间化方法[J]. 地球信息科学学报, 2022 , 24(10) : 1883 -1897 . DOI: 10.12082/dqxxkx.2022.220384

Abstract

Population spatialization is a common method to refine the spatial resolution of census data. Existing studies are mostly based on the idea of statistical modeling to establish the association between ancillary data and population at the administrative-unit-level, and then transfer it to predict the gridded population. As an important data input for fine-grained population estimation, Point of Interests (POIs) are usually in the form of quantity or density indexes for regression modeling, which ignores the heterogeneity in the association between population and POIs with same type but different sizes. Such modeling methods cause the loss of semantic details of POIs, in turn leading to the population underestimation in main urban areas and overestimation in suburban areas. To tackle this problem, this paper proposes an urban population spatialization method based on random forest model by considering the heterogeneity of population attraction of POIs. More specifically, on the basis of establishing a multi-scale representation of the spatial importance of POIs, this method constructs population attraction indexes by integrating mobile positioning data. Meanwhile, the spatial autocorrelation of population is modeled based on non-Euclidean spatial filter for weight correction, which considers the influence of obstacles such as water body on local spatial connectivity. We select Wuhan city as the study area to conduct population spatialization experiment at 100 m spatial resolution. Through the comparison with traditional density-based model, popular gridded datasets, and the ablation experiments, the results verify the effectiveness of population attraction indexes and weight correction. The mean absolute error of our method is about 1/4-2/3 of the WorldPop, GPW, and the comparison model (i.e., Ye's model), demonstrating the advantages of our method in fine-grained population spatialization. In addition, the influences of the sampling rate and size of grid of mobile positioning data on the modeling accuracy are also discussed.

Key words： grid transformation of population data; mobile positioning data; population attraction; multi-scale representation; random forest; spatial autocorrelation; non-Euclidean spatial filter

1 引言

精细的人口空间分布数据在商业规划、资源配置、灾害救援及公共卫生等领域具有广泛的应用场景[1]。当前公开渠道可获得的人口普查数据通常是行政单元逐级汇总的统计数据,难以有效反映人口空间分布的差异性[2]。因此,开展人口空间化研究,将统计人口分配到细粒度的空间单元,对城市精细化管理具有重要意义[3-4]。
人口空间分布受到环境、交通、资源等多种因素影响,结合相应的辅助数据,有助于实现精准的格网人口分配[5]。遥感卫星影像因其较高的空间分辨率和较短的采集周期而被广泛用于人口空间化研究。土地利用解译数据描述了人口分布的空间范围,但难以揭示同种土地类型下人口密度的差异[6-7]。夜光遥感数据记录了人类活动产生的光强,一定程度上能够区分人口分布的异质性,反映人口的疏密程度[8-9];但路灯、建筑工地及反射灯光等与人口分布不相干光源引发灯光溢出效应[10],从而导致人口误分配。因此,上述数据难以准确反映城市内部的结构形态并支撑精细人口建模。细粒度的社会感知数据提供了与人口居住环境和分布相关的细节信息。特别是兴趣点包含精确的位置与丰富的空间语义,且具有来源广、易获取等特点,能够反映其周边或内部潜在的人类活动行为,是精细化人口建模的核心数据源[11]。现有研究多基于POI构建密度型指标[12-13]、计算空间分析单元与POI的距离[14-15]或开展城市功能区识别[16-17]实现人口分配。然而,仅考虑POI空间分布数量差异的密度特征提取方法,未顾及不同POI设施人口服务与吸引能力的异质性。例如,711便利店和沃尔玛虽同属于购物类型POI,但在数量/密度型指标中均统计为“1”,造成同类POI与人口的数量关系同质化,从而导致中心城区人口低估与远城区人口高估[18]。
动态定位数据直接记录人类的活动位置,具有丰富的时空语义信息,为解决静态数据无法显式表征人口规模与活动强度提供了潜在解决方 案[19⇓-21]。目前人口空间化建模数据逐渐趋于多源化、精细化、动态化,Patel等[22]在使用土地利用、夜光数据的基础上,融合社交媒体的推文密度作为随机森林的协变量,大幅提高了人口估算的精度。Yao等[23]基于POI与腾讯用户密度等数据生成初始格网人口,并通过可迭代的重力模型将人口分配到建筑物,实现居民分布的精细刻画。Wang等[18,24]将微博签到数据与POI进行匹配构建人口吸引力指数,为解决POI异质性提供了思路。但该类签到数据通常与所匹配的POI不同源（如,新浪微博签到的POI与高德、百度POI不一致）,导致POI与签到数据失配,造成人口吸引力指数存在偏差;同时签到POI多为景点、餐饮、购物等生活娱乐类型,无法准确刻画其他类型POI对人口的吸引力;且该类数据获取较为困难,限制了其广泛应用的可能性。
针对现有人口回归模型中POI同质化建模的问题,本文引入移动定位数据,提出一种顾及POI人口吸引力异质性的城市人口空间化模型。本文选取夜间时段移动定位数据刻画常住人口相对规模的空间分布,并构建POI局部居民吸引力指标替代传统密度型指标,进而基于随机森林建模初始的格网人口权重;同时,考虑到人口分布存在空间自相关[25]且大型障碍物会改变局部空间连通性,设计一种顾及连通性的非欧式滤波对人口权重进行空间自相关修正。本文以武汉市为研究区域开展了100 m分辨率人口空间化实验,并与WorldPop、GPW及同样基于随机森林和POI数据的Ye的模 型[26]进行对比,验证了本文方法的有效性及相对其他数据集与模型的精度优势。此外,本文还讨论了移动定位数据的采样率与格网粒度对人口吸引力指标提取的影响。

2 研究方法

本文方法总体流程如图1所示,共包括数据预处理、人口吸引力指标提取、模型训练与估算、格网权重修正与人口分配4个部分。
图1 本文方法总体流程

Fig. 1 Flowchart of the proposed method

① 数据预处理阶段,将所有数据统一到WGS84坐标系,并进行格网属性统计,包括各类POI数量、夜间时段（23：00—次日3：00）移动定位数据统计量、建筑斑块面积、水体面积、路网密度;② 指标提取阶段,结合夜间时段移动定位数据,通过表征POI空间多尺度重要性构建人口吸引力指标; ③ 人口权重建模阶段,基于随机森林模型,分别在行政单元与格网级别进行训练与估算,将格网级输出结果作为初始人口权重; ④ 权重修正与格网人口分配阶段,首先对人口权重进行约束,将无房屋的格网权重值赋0,进一步采用非欧式滤波对人口权重进行空间自相关修正,最后按修正后的权重将区县人口分配至格网。

2.1 顾及POI异质性的人口吸引力指标提取

人口吸引力指标结合了POI与移动定位数据的数量信息,其在刻画POI空间分布异质性的基础上,借助夜间时段移动定位数据反映不同POI对周边常住居民的吸引和服务能力。相对于密度型指标,该指标可建模POI特征与格网人口间的异质性数量关系,辅助回归模型进行更准确的人口估算。

2.1.1 高人口相关性POI筛选

选取与人口具有高度相关性的POI类型是构建人口吸引力指标的基础。POI筛选流程如图2所示,通过夜间时段移动定位数据提取常住人口热点,并分析其与POI的同位模式频率,可以筛选出高人口相关性POI。
图2 高人口相关性POI筛选流程示意

Fig. 2 Workflow of population-sensitive POIs selection

局部莫兰指数（Anselin Local Moran's I）常用于地理实体的热点、冷点分析[27],本文使用ArcMap的Cluster and Outlier Analysis工具计算格网级移动定位数据夜间时段统计量的Moran's I值,并筛选具有显著高高聚集的格网作为常住人口热点。POI与人口分布及其空间活动存在密切关联[28],通过分析二者的频繁同位模式,可挖掘与人口具有高度相关性的POI类型。考虑到POI与人口热点之间存在一定的辐射影响距离[29],并非POI恰好在人口热点格网时才为同位模式,且各类POI存在数量差异。因此,本文综合考虑多尺度邻域下人口热点与POI的同位模式频率以筛选高相关POI,计算方法如式（1）—式（3）所示。
i t e m i , j = p o i i , j 1 , … , p o i i , j k , … , p o i i , j n
p o i _ f j k = ∑ i = 1 m p o i i , j k m
a v g _ p o i _ f k = ∑ j = 1 J p o i _ f j k J
式中： i t e m i , j表示第 i个人口热点格网在第 j个尺度邻域下与各类POI的同位模式记录; n为POI类型的数量,若人口热点 i的邻域 j内存在第 k类POI,则 p o i i , j k为1,否则为0; p o i _ f j k表示第 k类POI在第 j个邻域下与人口热点的同位频率; m为人口热点的数量; a v g _ p o i _ f k表示第 k类POI在多个尺度邻域下与人口热点的平均同位模式频率; J为所选邻域的数量,最终按照 a v g _ p o i _ f k大小筛选出高人口相关性POI。

2.1.2 人口吸引力指标构建

本文基于筛选的高人口相关性POI,结合夜间时段移动定位数据构建人口吸引力指标。该指标由POI重要程度及附近夜间时段的移动定位数据量共同决定,第 i个格网中第 k类POI的人口吸引力 P O I _ A t t r i k定义如式（4）所示。
P O I _ A t t r i k = P O I _ I m p o r t a n c e i k × M P D i
式中： P O I _ I m p o r t a n c e i k表示第 k类POI的重要程度,作为吸引力系数,用于反映第 k类POI在所有类型POI中的相对重要性; M P D i（Mobile Positioning Data）为第 i个格网的夜间时段移动定位数据统计量,可近似反映不同格网间常住人口的相对规模大小。因此, P O I _ A t t r i k可以刻画格网间第 k类POI集合的人口吸引力异质性。
其中,POI重要程度借鉴词频-逆文档频 率（Term Frequency-Inverse Document Frequency, TF-IDF）[30]的思想定义。空间中POI重要程度可 类比于语料库中词条权重,差别在于,空间实体分布存在尺度效应,即POI在不同空间尺度下分布聚集模式相异,存在不同的重要程度[31]。因此,本文在TF-IDF基础上进一步对POI空间多尺度重要性进行表征,计算方法如式（5）所示。
P O I _ I m p o r t a n c e i k = P O I _ C o u n t i k P O I _ C o u n t i × l o g ( ∏ s = 1 S ( N s N s P O I k + 1 )
式中： P O I _ C o u n t i k为第 i个格网中第 k类POI的数量; P O I _ C o u n t i为第 i个格网中所有POI的数量; s是选取的空间尺度的数量; N s表示第 s个空间尺度范围下格网的总数量; N s P O I k表示第 s个尺度下包含第 k类POI的格网数量。 N s P O I k越小时,表明该类POI空间分布越聚集,即重要程度越高。式（5）通过累乘表征POI在多个空间尺度下的综合重要性,即若该类POI在多个尺度下重要程度均较高,则放大其重要性;若在不同尺度重要性不同,则抵消其重要性。由于用地类型通常以行政单元为单位规划,实验中选取区县、街道、社区3个行政单元尺度进行POI空间多尺度重要性表征。

2.2 人口权重修正与人口分配

2.2.1 顾及空间连通性的人口权重修正

随机森林模型仅建模特征与人口的数量关系,未顾及人口在空间分布上的自相关性。传统空间滤波一定程度上能够刻画这种关系,但滤波基于欧式距离,未考虑障碍物对路径可达性的影响,导致滤波在部分区域失效。因此,本文设计一种顾及空间连通性的非欧式滤波建模人口空间自相关。针对每个中心格网及一定邻域范围内存在的障碍物（如水体）及连通设施（如桥）,滤波权重确定流程如图3所示。
图3 基于非欧式滤波的格网人口权重修正流程

Fig. 3 Workflow of weight correction based on non-euclidean filtering

（1）生成N×N维大小的滤波模板（图3以5×5为例）,将中心格网可达距离 d i s置为0。
（2）从滤波中心出发向四邻开始第r（初始为1）轮搜索,分3种情况：① 若格网无障碍物或障碍物面积占比小于阈值（红色格网）,则将该格网可达距离 d i s赋为r,可参与下轮迭代;② 若障碍物面积占比超过阈值（紫色格网）,则定义为不连通,将该格网标记为白体(方正)1,不参与下轮迭代;③ 若格网障碍物面积占比超过阈值但存在连通性设施（黄色格网）,则定义为有条件的连通,将格网标记为-2,参与下轮迭代。
（3）按照广度优先搜索规则,选取第2步中可参与迭代的格网继续开展第r+1轮的四邻搜索,计算格网的可达距离。
（4）滤波模板中所有格网距离确定后结束迭代,并以可达距离计算滤波权重。具体而言,之前标记为-1和-2的格网滤波权重直接置为0（即障碍物的格网不参与运算）,其余格网根据可达距离将滤波权重置为 γ d i s。其中 γ为衰减系数,取值范围为(0,1)。
（5）基于滤波模板对中心格网进行滤波操作,生成修正后的人口权重。

2.2.2 人口分配

按照修正后的人口权重,将区县的普查人口分配到各个格网,分配方法如式（6）所示。
P O P i j = P O P d i s t r i c t _ j × w p i x e l _ i w d i s t r i c t _ j
式中： P O P i j为第 j个区县中第 i个格网的人口估算值; P O P d i s t r i c t _ j为第 j个区县的人口普查值; w p i x e l _ i为第 i个格网的人口权重; w d i s t r i c t _ j为第 j个区县的人口权重总和。

3 研究区概况与数据来源

3.1 研究区概况

本文的研究区域为湖北省武汉市（图4（a））,武汉下辖13个区县,186个街道,总面积8569.15 km2。2015年武汉市常住人口约1060.7万,占湖北省总人口的18.13%。13个下辖区（图4（b））中,有7个主城区（占总人口的61.67%）,6个远城区（占总人口的38.33%）。186个街道按照人口密度划分为高、中、低3个等级（图4（c））,其中高、中、低人口密度街道数量分别为57、69和60。武汉市江河纵横、水域众多,改变了局部区域之间的空间连通性,为精准建模人口空间自相关带来挑战;同时,武汉市人口分布格局复杂,各区域人口密度差异较大,因此作为研究区域开展人口空间化具有典型性。
图4 武汉市研究区概况

Fig. 4 Overview of the study area of Wuhan city

3.2 数据来源

本文使用的研究数据详情如表1所示。其中,POI与移动定位数据用于构建人口吸引力指标,建筑斑块用于约束权重,水体数据与路网数据用于设计非欧式空间滤波。WorldPop与GPW作为具有代表性的格网人口数据集,广泛应用于各类场景,因此在本文作为对比数据集以验证方法的有效性。
表1 研究数据概况

Tab. 1 Overview of study data

数据 年份 来源 描述
建模数据 POI数据 2017 高德地图
(https://www.amap.com/)		 使用11类POI：休闲娱乐、住宿、停车场、医疗服务、居民小区、政府单位、汽车相关、科研教育、购物、金融服务、餐饮
移动定位数据 2018 维智科技Wayz.AI 数据量为266 460条（每条对应一个定位点记录）,时间段为23：00—次日3：00
建筑斑块数据 2015 武汉市地理国情普查 作为初始人口权重约束的依据;小于200 m2的斑块未被采集
水体数据 2015 清华大学开放数据集
(http://data.ess.tsinghua.edu.cn)		 作为本文实验中的障碍物;30 m分辨率的栅格数据
路网数据 2015 武汉市测绘研究院 利用路网中的桥作为水体的连通设施
武汉市行政区划 2015 武汉市测绘研究院 包括武汉市区县、街道矢量轮廓及常住人口数量信息
对比数据 WorldPop 2015 WorldPop官网
(http://www.worldpop.org.uk/)		 分辨率为100 m
GPW 2015 NASA社会经济数据和应用中心
(http://srtm.csi.cgiar.org)		 分辨率为30弧秒（赤道处约为1 km）

4 实验及结果与分析

4.1 精度评价指标

由于缺失格网真实人口,将格网估算人口在街道进行汇总,并与街道普查人口进行精度对比验证。本文选取的精度评价指标包括平均绝对值误差（Mean Absolute Error, MAE）、平均相对误差（Mean Relative Error, MRE）、均方根误差（Root Mean Square Error, RMSE）和决定系数（Coefficient of Determination, R2）,分别如式（7）—式（10）所示。其中,MAE和MRE刻画估算结果的偏差绝对值与相对值,RMSE反映估算结果稳定程度,R2度量估算结果的拟合优度。为了有效开展精度评价,本文所有实验中的评价指标均为随机森林模型30次估算结果的均值。
M A E = 1 N ∑ i = 1 N P r e d i c t i - R e a l i
M R E = 1 N ∑ i = 1 N P r e d i c t i - R e a l i R e a l i
R M S E = 1 N ∑ i = 1 N P r e d i c t i - R e a l i 2
R 2 = 1 - ∑ i R e a l i - P r e d i c t i 2 ∑ i R e a l i - R e a l ¯ 2
式中： N为街道数; R e a l i为街道 i普查人口; R e a l ¯为所有街道普查人口的平均值; P r e d i c t i为街道 i估算人口。

4.2 人口吸引力指标提取及有效性验证

4.2.1 高人口相关性POI选取

为选取高人口相关性POI类型,本文按照11 类POI与人口热点的同位模式频率降序排列结果（图5（a））,在人口吸引力指标的构建过程中依次去掉排序末位的POI类型,精度结果对比（不含权重修正）如图5（b）所示。实验中选取1×1、3×3、5×5、7×7共4个邻域用于计算常住人口热点与POI的同位模式频率。
图5 高人口相关性POI选取

Fig. 5 The selection of population-sensitive POIs

由图5（b）可知,POI类型从11类减少到7类的过程中,模型的精度与稳定性均有明显提升;若继续减少,则MAE/RMSE/R2基本保持不变,而MRE略有下降。结合图5（a）可知,后4类POI,即政府单位、汽车相关、停车场与住宿,同位频率均小于0.6,与前7类差异较大,与日常认知较为符合。因此,本文选取购物、居民小区、餐饮、医疗服务、科研教育、休闲娱乐及金融设施等同位模式频率排序靠前的 7类POI作为高人口相关性POI,后续实验将基于筛选结果开展。

4.2.2 人口吸引力指标的有效性验证

为验证人口吸引力指标的有效性,将该指标与传统POI密度型指标,以及移动定位数据直接映射的人口（将统计人口按格网间移动定位数据量的比例进行分配）进行精度对比,结果如图6所示。其中,POI密度型指标使用完整的11类POI进行建模,人口吸引力指标分别使用11类POI和7类高相关POI进行建模。
由图6（a）可知,人口吸引力指标精度整体优于POI密度型指标以及移动定位数据直接映射的结果,说明本文指标在一定程度上能够有效融合POI与移动定位数据的语义与数量信息,从而更准确地建模人口空间分布;而基于高人口相关性POI的建模结果进一步提升了估算精度,在各项指标对比中均达到最优,验证了POI筛选方法的有效性。图6（b）—图6（e）展示了街道级别估算人口与真实人口的散点分布,横、纵坐标均采用以10为底的对数坐标来表示。由图6（b）可知,移动定位数据映射结果在高密度街道精度最高（R2=0.864）,中密度街道次之（R2=0.626）,说明移动定位数据能大致反映中心城区人口分布;而低密度街道存在普遍的人口低估现象,这可能是由于移动定位数据有偏,在农村偏远地区存在数据缺失的问题所导致。由图6（c）可知,POI密度型指标在低密度街道的精度相对高、中密度街道较差,整体被严重高估,主要是因为随机森林模型为没有POI的格网统一赋予非0权重,而其中大量格网不存在人口分布。图6（d）、图6（e）表明,相对于POI密度型指标（R2=0.72）,结合移动定位数据的人口吸引力指标在整体精度上有所改善（图6（d）,R2=0.769）,筛 选高人口相关性POI能够进一步提升建模精度 （图6（e）,R2=0.857）,且低密度街道高估现象得到一定程度的缓解。
图6 人口吸引力指标与传统密度型指标、移动定位数据直接映射的精度对比

Fig. 6 Accuracy comparison between regression models that use population attraction indexes, traditional POI density indexes, as well as mapping of mobile positioning data

4.3 权重修正有效性验证

为验证权重修正方法的有效性,将仅利用建筑斑块数据进行权重约束以及进一步利用非欧式空间滤波修正的结果与初始人口权重结果进行对比,并分析非欧式与欧式滤波格网估算人口结果差异,如图7所示。实验中滤波模板大小为7×7,衰减系数 γ为2/3,障碍物面积占比阈值为0.95。
图7 基于初始权重与修正后权重的人口估算精度对比

Fig. 7 Accuracy comparison between the estimated population upon initial weight and that of corrected weight

图7（a）显示,对模型输出的初始人口权重进行修正能够提升人口空间化精度。具体而言,使用建筑斑块数据进行权重约束后,MAE、MRE、RMSE均有下降,R2略有上升,且MRE更加稳定;进一步使用非欧式空间滤波后,MRE基本不变,MAE/RMSE略有下降,R2略有上升,整体精度得到小幅提升。从散点图7（b）可知,由于没有房屋的格网权重被置为0,减少了人口的误分配,低密度街道高估问题有所缓解。图7（c）表明,非欧式滤波修正后,高、中、低密度街道的R2均有小幅度提升（提升0.2%~1.5%）,但由于本文滤波仅在有障碍物处相对欧式滤波模板有权重变化,即局部区域的人口优化分配,故对整体精度提升有限。
图8显示了武汉市中心区域非欧式滤波相对欧式滤波格网估算人口的差值,以及在汉江与长江的交汇口区域的细节对比。可以看出,在水体边缘分布的格网多为绿色,表明在本文滤波方法在水体边缘分配人口少于传统滤波,更加符合真实情况。
图8 水域周边非欧式滤波与欧式滤波的估算人口差异展示

Fig. 8 The difference of estimated population along river side between non-Euclidean spatial filter and Euclidean spatial filter

4.4 人口空间化结果分析

图9展示了基于本文方法的武汉市100 m分辨率人口空间化结果及其部分区域与 WorldPop数据集的对比,其中a、b分别代表本文与WorldPop结果。由图可知,武汉市人口整体呈现“中心聚集,外围多核心”的分布特征结构,中心城区（江岸区、江汉区、硚口区、武昌区）人口密度明显高于武汉周边区域。从图9中a、b对比可看出,WorldPop与本文结果的人口空间分布整体较为相似,对于人口高密度集聚区地理位置的刻画基本相同,但细节方面仍存在差异。本文方法不仅能识别中心城区的人口聚集区,也能够较清晰地提取出武汉外围的人口高密度核心,如前川街道、邾城街道和纸坊街道等。WorldPop数据与土地斑块数据具有的相似空间格局与边界,呈现出覆盖范围广但内部人口分布均质的特点,且难以刻画人口的零星分布。相比之下,本文方法使用POI与移动定位数据建模,结果具有更强的颗粒感与突出的纹理信息,能够揭示集聚区域内人口空间分布的异质性。
图9 本文方法100 m分辨率武汉市人口空间化结果及其部分区域与WorldPop的对比

Fig. 9 Population spatialization results of our method at 100 m resolution in Wuhan city and comparison with WorldPop in selected regions

5 讨论

5.1 与其他人口数据集/模型的精度对比

为验证本文方法的整体有效性,将本文方法与GPW、WorldPop数据集及Ye的模型[26]进行对比。其中,Ye的模型使用POI、道路网、NDVI、海拔、坡度以及夜光亮度等多源数据建模与人口的关系。由表2可知,本文方法整体上具有更高的精度,MAE分别约为GPW、WorldPop和Ye的模型的1/4、1/2和2/3。
表2 本文方法与GPW、WorldPop及Ye的模型精度对比

Tab. 2 Accuracy comparison between our method and GPW, WorldPop and Ye's model

数据集/方法 MAE MRE RMSE R2
GPW 46 919 1.712 81 077 0.49
WorldPop 23 763 3.258 40 500 0.55
Ye的模型 16 922 0.991 25 259 0.74
本文方法 10 887 0.429 16 681 0.91
为进一步分析本文方法与其他数据集和模型的结果差异,将上述4个模型/数据集在街道尺度上进行误差对比,结果如图10所示。图10（a)、图10(d)、图10(g)、图10(j）与图10（b)、图10(e)、图10(h)、图10(k）分别表示街道级别的绝对和相对误差空间分布;图10（c)、图10(f)、图10(i)、图10(l）)为相对误差的直方分布图,灰色折线代表3种等级街道的数量总和,黄色虚线将左右分为低估和高估两部分。
图10 街道级误差的空间分布及直方分布对比

Fig. 10 Spatial and histogram distribution of street-level errors for our method and comparison datasets and model

整体而言,本文方法相对3种对比方法具有精度优势。从绝对误差空间分布看,本文方法在武汉外围误差较大,主要是因为移动定位数据在远城区存在缺失;Ye的模型与WorldPop绝对误差集中分布于中、低密度人口街道;而GPW则在整个武汉均存在误差较大的街道。从相对误差看,本文方法严重低估或高估（-1~ -0.7,1~5,大于5）的街道仅为 5个,而估算较为准确（-0.2~ 0.2）的街道为96个,占所有街道总数的52%;与之相对,Ye的模型、WorldPop与GPW中严重低估或高估的街道分别为26、34和76个,估算较为准确的分别仅占35%、29%与18%。由分析可知,本文方法在低密度街道存在低估问题是由于权重约束导致的修正过度;Ye的模型在低密度街道存在高估,而对高密度街道存在低估,直方分布与本文方法大致相反,是因为该模型使用POI密度作为核心建模指标;WorldPop与Ye的模型类似,但在估算较为准确与严重误估的区域均差于Ye的模型;GPW高估与低估街道数量严重失衡是因为GPW未采用分区密度制图将行政单元人口按照权重分配到格网,而直接根据重叠面积进行格网插值,无法保证人口在行政单元级别的一致性与准确性。

5.2 移动定位数据采样率及统计粒度对精度的影响

移动定位数据与人口吸引力指标的提取直接相关,而可获取的移动定位数据量通常是不确定的,因此可能会对模型的估算精度产生影响。同时,本文使用的移动定位数据是具有经纬度坐标的点数据,可以在任意大小、形状的地理单元内统计。然而,该类定位点数据的获取仍具有一定难度,通常更容易获取的数据类型是较粗粒度的格网统计型数据（如,百度与中国移动的人口网格热力数据）,此时可能存在与人口空间化格网分辨率不一致的问题。为此,本文讨论移动定位数据采样率及统计粒度对精度的影响,以验证人口吸引力指标提取方法的泛化能力。
本文在原始的266 460条移动定位数据基础上,按百分比随机空间抽样,并利用降采样后的数据构建人口吸引力指标,对比分析不同移动定位数据采样率下的人口估算精度,实验结果如图11（a）所示。曲线表明,随着移动定位数据采样率的增加,人口估算精度总体呈上升趋势,并逐渐趋于平稳。具体而言,当采样率处于10%~100%之间时,模型精度较高,MAE与R2在一定的范围区间波动但总体差异不大,最优精度在100%采样率时取得;而当采样率小于10%时,模型精度随着采样率的减小迅速下降,甚至在1%采样率时劣于传统密度模型。由本文的数据介绍可知（表1）,采样率为10%时,移动定位数据量约为2.6万条,占比不到武汉人口总量的0.3%;而3%的采样率（占武汉人口总量0.1%）即可生成优于传统POI密度型指标的估算精度。因此,人口吸引力指标在一定区间内受移动定位数据采样率的影响不大,能够在数据获取受限的情况下提升模型估算精度。
图11 不同移动定位数据采样率及统计粒度下的人口估算精度对比

Fig. 11 Accuracy comparison of population estimation under different sampling rates and different grid size of mobile positioning data

为了验证人口吸引力指标提取方法对移动定位数据的统计粒度具有较好的适应性,本文直接基于粗分辨率格网统计移动定位数据,并根据格网间重叠面积占比将粗分辨率统计值分配到100 m格网中,精度对比结果如图11（b）所示。由图可知,人口估算误差大体呈现随着移动定位数据格网统计粒度变粗而增大的趋势,说明使用粗粒度的移动定位统计数据难以精准建模POI的人口吸引力异质性,从而导致人口空间化精度下降。图中,2500 m格网分辨率时精度最低,此时MAE与R2分别为14 314和0.8,但相比POI密度型指标（MAE为17 616,R2为0.72）仍具有较为显著的优势。由此可知,本文指标对网格统计粒度具有较好适应性,能够通过融合移动定位数据中蕴含的相对人口空间分布信息改善模型精度。

6 结论与展望

本文提出一种顾及POI人口吸引力异质性的城市人口空间化方法。该方法：① 通过表征POI数据的空间多尺度重要性,实现与夜间时段移动定位数据的匹配,进而构建人口吸引力指标,刻画不同类型及个体规模POI与人口分布之间存在的异质性数量关系;② 融合多源数据修正人口权重,采用顾及空间连通性的非欧式滤波建模人口空间自相关,避免人口过度离散分布。本文以武汉市为研究区域开展了100 m格网尺度的人口空间化实验。结果表明,本文方法的平均绝对误差为10 887,仅为其他对比数据集与模型的1/4~2/3,可有效提高城市人口空间化精度。同时,本文人口吸引力指标提取方法对移动定位数据的采样率与统计粒度具有较好的适应性,在10%采样率或2500 m格网下仍能取得比传统POI密度型指标更高的精度,故可为POI特征异质性的精细化建模提供思路。
本文方法仍存在以下不足有待改进。本文在表征POI空间多尺度重要性时选用行政单元作为分析尺度,今后可基于Ripley's K函数[32]研究空间尺度的自适应确定方法。此外,非欧式空间滤波的模板大小、权重衰减系数均基于经验人为设定,未充分顾及其空间异质性,后续研究可尝试引入卷积神经网络、空间表征学习[33]建模多源特征的空间相关性与空间上下文关系。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
董南, 杨小唤, 蔡红艳. 人口数据空间化研究进展[J]. 地球信息科学学报, 2016, 18(10):1295-1304.

DOI

[ Dong N, Yang X H, Cai H Y. Research progress and perspective on the spatialization of population data[J]. Journal of Geo-Information Science, 2016, 18(10):1295-1304. ] DOI: 10.3724/SP.J.1047.2016.01295

DOI

[2]
刘云霞, 田甜, 顾嘉钰, 等. 基于大数据的城市人口社会经济特征精细时空尺度估计——数据,方法与应用[J]. 人口与经济, 2022(1):42-57.

[ Liu Y X, Tian T, Gu J Y, et al. Fine spatial-temporal scale estimation of urban population's socio-economic characteristics based on big data: data, methals and applications[J]. Population & Economics, 2022(1):42-57.] DOI: 10.3969/j.issn.1000-4149.2021. 00.056

DOI

[3]
胡云锋, 王倩倩, 刘越, 等. 国家尺度社会经济数据格网化原理和方法[J]. 地球信息科学学报, 2011, 13(5):573-578.

DOI

[ Hu Y F, Wang Q Q, Liu Y, et al. Index system and transferring methods to build the national society and economy grid database[J]. Journal of Geo-information Science, 2011, 13(5):573-578. ] DOI: 10.3724/SP.J.1047.2011.005 73

DOI

[4]
Hu Q S, Li R, Wu H Y, et al. Construction of a refined population analysis unit based on urban forms and population aggregation patterns[J]. International Journal of Digital Earth, 2022, 15(1):79-107. DOI: 10.1080/17538947.2021.2 013963

DOI

[5]
Stevens F R, Gaughan A E, Linard C, et al. Disaggregating census data for population mapping using random forests with remotely-sensed and ancillary data[J]. PLoS One, 2015, 10(2):e0107042. DOI: 10.1371/journal.pone.01 07042

DOI

[6]
陈晴, 侯西勇. 集成土地利用数据和夜间灯光数据优化人口空间化模型[J]. 地球信息科学学报, 2015, 17(11):1370-1377.

DOI

[ Chen Q, Hou X Y. An improved population spatialization model by combining land use data and DMSP/OLS data[J]. Journal of Geo-information Science, 2015, 17(11):1370-1377. ] DOI: 10.3724/SP.J.1047.2015.01370.[

DOI

[7]
Zeng C Q, Zhou Y, Wang S X, et al. Population spatialization in China based on night-time imagery and land use data[J]. International Journal of Remote Sensing, 2011, 32(24):9599-9620

DOI

[8]
卓莉, 陈晋, 史培军, 等. 基于夜间灯光数据的中国人口密度模拟[J]. 地理学报, 2005, 60(2):266-276.

[ Zhuo L, Chen J, Shi P J, et al. Modeling population density of China in 1998 based on DMSP/OLS nighttime light image[J]. Acta Geographica Sinica, 2005, 60(2):266-276.] DOI: 10.11821/xb200502010

DOI

[9]
柏中强, 王卷乐, 姜浩, 等. 基于多源信息的人口分布格网化方法研究[J]. 地球信息科学学报, 2015, 17(6):653-660.

DOI

[ Bai Z Q, Wang J L, Jiang H, et al. The gridding approach to redistribute population based on multi-source data[J]. Journal of Geo-information Science, 2015, 17(6):653-660. ] DOI: 10.3724/SP.J.1047.2015.00653

DOI

[10]
Zheng H H, Gui Z P, Wu H Y, et al. Developing non-negative spatial autoregressive models for better exploring relation between nighttime light images and land use types[J]. Remote Sensing, 2020, 12(5): 798. DOI:10.3390/rs12 050798

DOI

[11]
Mei Y A, Gui Z P, Wu J H, et al. Population spatialization with pixel-level attribute grading by considering scale mismatch issue in regression modeling[J]. Geo-Spatial Information Science, 2022:1-18. DOI: 10.1080/10095020.2 021.2021785

DOI

[12]
Yang X C, Ye T T, Zhao N Z, et al. Population mapping with multisensor remote sensing images and point-of-interest data[J]. Remote Sensing, 2019, 11(5):574. DOI: 1 0.3390/rs11050574

DOI

[13]
Zhao Li, Zhang, et al. Improving the accuracy of fine-grained population mapping using population-sensitive POIs[J]. Remote Sensing, 2019, 11(21):2502. DOI: 10. 3390/rs11212502

DOI

[14]
Bakillah M, Liang S, Mobasheri A, et al. Fine-resolution population mapping using OpenStreetMap points-of-interest[J]. International Journal of Geographical Information Science, 2014, 28(9):1940-1963. DOI: 10.1080/13658816. 2014.909045

DOI

[15]
淳锦, 张新长, 黄健锋, 等. 基于POI数据的人口分布格网化方法研究[J]. 地理与地理信息科学, 2018, 34(4):83-89,124,2.

[ Chun J, Zhang X C, Huang J F, et al. A gridding method of redistributing population based on POIs[J]. Geography and Geo-Information Science, 2018, 34(4):83-89,124,2. ]

[16]
郑洪晗, 桂志鹏, 栗法, 等. 夜间灯光数据和兴趣点数据结合的建成区提取方法[J]. 地理与地理信息科学, 2019, 35(2):25-32.

[ Zheng H H, Gui Z P, Li F, et al. Urban built-up area extraction method based on nighttime light images and point of interest data[J]. Geography and Geo-Information Science, 2019, 35(2):25-32. ]

[17]
Gao S, Janowicz K, Couclelis H. Extracting urban functional regions from points of interest and human activities on location-based social networks[J]. Transactions in GIS, 2017, 21(3):446-467. DOI: 10.1111/tgis.12289

DOI

[18]
Wang L Y, Fan H, Wang Y K. Improving population mapping using Luojia 1-01 nighttime light image and location-based social media data[J]. Science of the Total Environment, 2020, 730:139148. DOI: 10.1016/j.scitotenv.2020. 139148

DOI

[19]
Zhao S, Liu Y X, Zhang R, et al. China's population spatialization based on three machine learning models[J]. Journal of Cleaner Production, 2020, 256:120644. DOI: 10.1016/j.jclepro.2020.120644

DOI

[20]
Wu H Y, Gui Z P, Yang Z L. Geospatial big data for urban planning and urban management[J]. Geo-Spatial Information Science, 2020, 23(4):273-274. DOI: 10.1080/10095020. 2020.1854981

DOI

[21]
Yu B L, Lian T, Huang Y X, et al. Integration of nighttime light remote sensing images and taxi GPS tracking data for population surface enhancement[J]. International Journal of Geographical Information Science, 2019, 33(4):687-706. DOI: 10.1080/13658816.2018.1555642

DOI

[22]
Patel N N, Stevens F R, Huang Z J, et al. Improving large area population mapping using geotweet densities[J]. Transactions in GIS, 2017, 21(2):317-331. DOI: 10.1111/tgis.12214

DOI PMID

[23]
Yao Y, Liu X P, Li X, et al. Mapping fine-scale population distributions at the building level by integrating multisource geospatial big data[J]. International Journal of Geographical Information Science, 2017, 31(6):1220-1244. DOI: 10.1080/13658816.2017.1290252

DOI

[24]
Wang L Y, Fan H, Wang Y K. Fine-resolution population mapping from international space station nighttime photography and multisource social sensing data based on similarity matching[J]. Remote Sensing, 2019, 11(16):1900. DOI: 10.3390/rs11161900

DOI

[25]
孙小芳. 夜光遥感支持下的城市人口核密度空间化及自相关分析[J]. 地球信息科学学报, 2020, 22(11):2256-2266.

DOI

[ Sun X F. Spatialization and autocorrelation analysis of urban population kernel density supported by nighttime light remote sensing[J]. Journal of Geo-information Science, 2020, 22(11):2256-2266.] DOI: 10.12082/dqxxkx. 2020.200289

DOI

[26]
Ye T, Zhao N, Yang X, et al. Improved population mapping for China using remotely sensed and points-of-interest data within a random forests model[J]. Science of the total environment, 2019, 658:936-946. DOI: 10.1016/j.scitotenv.2018.12.276

DOI

[27]
Zhang C S, Luo L, Xu W L, et al. Use of local Moran's I and GIS to identify pollution hotspots of Pb in urban soils of Galway, Ireland[J]. Science of the Total Environment, 2008, 398(1/2/3):212-221. DOI: 10.1016/j.scitotenv.2008.03. 011

DOI

[28]
许泽宁, 高晓路. 基于电子地图兴趣点的城市建成区边界识别方法[J]. 地理学报, 2016, 71(6):928-939.

DOI

[ Xu Z N, Gao X L. A novel method for identifying the boundary of urban built-up areas with POI data[J]. Acta Geographica Sinica, 2016, 71(6):928-939. ] DOI:10.11821/dlxb20160 6003

DOI

[29]
吴京航, 桂志鹏, 申力, 等. 顾及格网属性分级与空间关联的人口空间化方法[J]. 武汉大学学报·信息科学版, 2021:1-14.

[ Wu J H, Gui Z P, Shen L, et al. Population spatialization by considering pixel-level attribute grading and spatial association[J]. Geomatics and Information Science of Wuhan University, 2021:1-14.] DOI: 10.13203/j.whugis20200379

DOI

[30]
Ramos J. Using TF-IDF to determine word relevance in document queries[J]. Proceedings of the First Instructional Conference on Machine Learning, 2003, 242(1):29-48

[31]
Gui Z P, Peng D H, Wu H Y, et al. MSGC: Multi-scale grid clustering by fusing analytical granularity and visual cognition for detecting hierarchical spatial patterns[J]. Future Generation Computer Systems, 2020, 112:1038-1056. DOI: 10.1016/j.future.2020.06.053

DOI

[32]
Wang Y, Gui Z P, Wu H Y, et al. Optimizing and accelerating space-time Ripley's K function based on Apache Spark for distributed spatiotemporal point pattern analysis[J]. Future Generation Computer Systems, 2020, 105:96-118. DOI: 10.1016/j.future.2019.11.036

DOI

[33]
Liu X, Andris C, Rahimi S. Place niche and its regional variability: Measuring spatial context patterns for points of interest with representation learning[J]. Computers, Environment and Urban Systems, 2019, 75:146-160. DOI: 10.1016/j.compenvurbsys.2019.01.011

DOI

Options
文章导航

/

〈 〉