EN中文

地球信息科学学报 >

2022 , Vol. 24 >Issue 11: 2071 - 2088

DOI: https://doi.org/10.12082/dqxxkx.2022.220077

地球信息科学理论与方法

一种自适应时间步长的场地地表污染扩散元胞自动机仿真模型

  • 王信雷 , 1 ,
  • 芮小平 , 1, * ,
  • 谢宜霖 1 ,
  • 朱益虎 2 ,
  • 杨蕴 1
展开
  • 1.河海大学地球科学与工程学院，南京 211000
  • 2.江苏省地质测绘院，南京 210008
*芮小平（1975-），男，江苏苏州人，博士，教授，主要从事地理信息科学方面的研究。E-mail:

王信雷（1997-），男，江西上饶人，硕士生，研究方向为地理信息系统。E-mail:

收稿日期: 2022-02-22

  修回日期: 2022-04-12

  网络出版日期: 2023-01-25

基金资助

国家重点研发计划项目(2019YFC1804304)

国家自然科学基金项目(41771478)

中央高校基本科研业务费专项资金项目(2019B02514)

收起

A Cellular Automata Simulation Model of Site Surface Pollution Diffusion with Adaptive Time Step

  • WANG Xinlei , 1 ,
  • RUI Xiaoping , 1 ,
  • XIE Yilin 1 ,
  • ZHU Yihu 2 ,
  • YANG Yun 1
Expand
  • 1. School of Earth Sciences and Engineering, Hohai University, Nanjing 211000, China
  • 2. Jiangsu Geologic Surveying and Mapping Institute, Nanjing 210008, China
*RUI Xiaoping, E-mail:

Received date: 2022-02-22

  Revised date: 2022-04-12

  Online published: 2023-01-25

Supported by

National Key Research and Development Program of China(2019YFC1804304)

National Natural Science Foundation of China(41771478)

Fundamental Research Funds for the Central Universities(2019B02514)

Fold

摘要

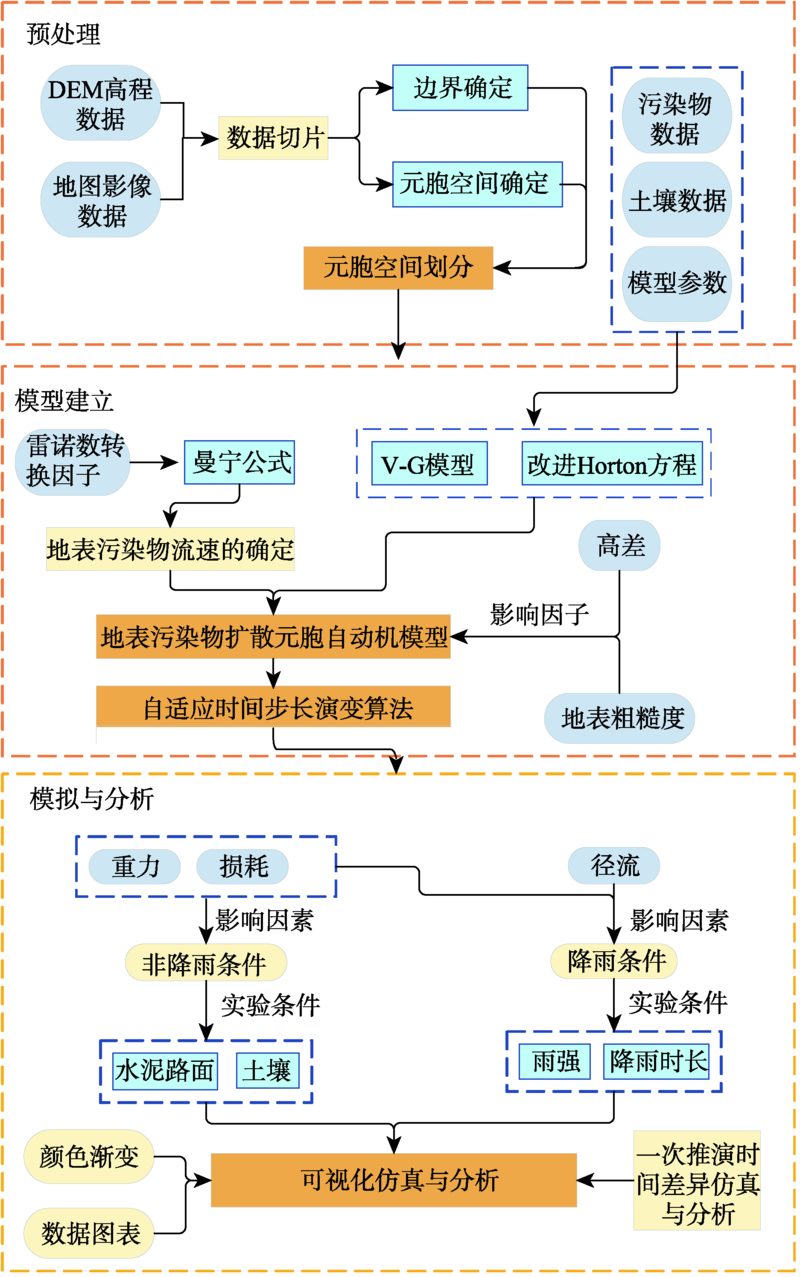
针对传统扩散模型难以动态模拟地表污染物时空不均匀扩散过程的问题，本文提出一种基于元胞自动机模型的污染物地表扩散仿真模型，在综合考虑地表高差及粗糙度对污染物扩散过程影响的基础上，确定了不规则污染场地的元胞边界条件、划分了元胞空间、提出了一种降雨和非降雨条件下污染物扩散流速计算方法，基于分子扩散建立了地表污染扩散模型演变规则。为更好模拟地表污染物扩散情况，本文提出了一种污染物随坡度和质量衰减的元胞自适应时间步长调整算法，该算法能够动态调整元胞自动机的时间步长，防止固定时间步长在污染物快速扩散时错过细节，而缓慢扩散时消耗计算资源。实验设计了降雨和非降雨两种情形对污染物随时间扩散的过程进行仿真与分析。实验结果表明，不同下垫面对污染物扩散速度有很大的影响，污染物在糙率为0.012的水泥地表上的扩散速度约为其在糙率为0.035的一般性土壤地表上的2.7倍；降雨强度和时长能够加快污染物的扩散，且扩散速度随着降雨曲线变化而改变，并在雨强峰值附近达到最大；污染物扩散服从坡度分布特征，且随着时间变化，高污染区域范围和污染物浓度差异渐渐变小，并在一段时间后，浓度变化渐渐趋于平稳；自适应时间步长演变算法能够较好地体现一次演变过程中污染物扩散在不同邻域元胞方向上的细微时间差异，提高污染物时空分布的计算精度。

关键词： 元胞自动机; 自适应步长; 污染物; 降雨; 非降雨; 扩散仿真; 曼宁公式; 流速计算; 模型

本文引用格式

王信雷 , 芮小平 , 谢宜霖 , 朱益虎 , 杨蕴 . 一种自适应时间步长的场地地表污染扩散元胞自动机仿真模型[J]. 地球信息科学学报, 2022 , 24(11) : 2071 -2088 . DOI: 10.12082/dqxxkx.2022.220077

Abstract

Aiming at the problem that it is difficult for traditional pollution simulation models to simulate the uneven diffusion process of surface pollutants dynamically in time and space, this paper proposes a surface pollutants diffusion simulation model based on cellular automata model. In this paper, surface slope and surface roughness are considered as the main factors affecting the diffusion process of pollutants. Based on the irregular contaminated site area, the boundary conditions of the cell were firstly determined to obtain the whole cell space, and then the whole cell space was divided into regular cells. After that, a method for calculating the diffusion velocity of pollutants under rainfall and non-rainfall conditions was proposed. Finally, based on the molecular diffusion rules, The evolution rules of surface pollutant diffusion model under rainfall and non-rainfall conditions were established. For better simulating surface pollutant diffusion, this paper proposes a cellular adaptive time step adjustment algorithm, in which pollutant quality decay with surface slope and pollutant gravity. This algorithm can adjust the cellular automata time step automatically and dynamically, so as to prevent cellular automata model with fixed time steps from missing details when pollution spread quickly and computing resources wasting when they spread slowly. In this paper, two experiments which consider rainfall and non-rainfall conditions respectively are designed to simulate the diffusion process of pollutants over time. The experimental results show that different underlying layers have a great influence on the diffusion rate of pollutants; the diffusion velocity of pollutants on the cement surface with a roughness of 0.012 is about 2.7 times of that on a general soil surface with a roughness of 0.035; under rainfall conditions, the pollution diffusion velocity increases with the increase of rainfall intensity and duration, the diffusion velocity changes with the change of rainfall curve, and reaches the maximum near the peak of rainfall intensity; the pollution diffusion simulation results obey the slope distribution characteristics of the site; with the change of time, the range of high pollution area gradually decreases, and the difference in pollutant concentration between adjacent locations also gradually decreases, and after a period of time, this change gradually becomes stable; in the process of a model evolution, surface pollutants will have subtle differences in diffusion time in different neighborhood cell directions, and the adaptive time step evolution algorithm can better reflect this difference, so it can better improve the calculation accuracy of spatial and temporal distribution of pollutants.

Key words： cellular automata; adaptive step; pollution; rainfall; non-rainfall; diffusion simulation; Manning formula; flow rate calculation; model

1 引言

近几十年来，虽然工业和经济得到快速发展，但是由于工厂自身的管理缺陷和环境保护法律的不完善,各种污染泄露事件时有发生，形成了千奇百怪的污染场地[1]。资料显示，我国污染场地数量日益增多，且一般都位于城市黄金地段，一旦污染事故发生，危险系数极大，不仅会造成严重的环境问题，更会产生严重影响经济和民生的社会问题，甚至可能会成为社会不稳定的诱因[2]。污染事故发生时，污染物首先会到达地表，并从地势高处向地势地处进行流动，同时向下渗入土壤层，污染土壤和地下水，给生态造成持久性危害[3]。一般来说，污染物在地表的扩散范围越大，其在土壤层和地下水中的蔓延范围也越广。因此，准确地模拟污染物在地表的扩散过程，并确定污染物在污染事件发生后在地表的扩散范围是管理决策者首先要解决的问题。
现有对地表污染扩散的研究主要集中在地表流域和地表径流方面。对于污染物在流域中的扩散模拟，多采用SWAT模型、HSPF模型、SPARROW模型，但是这些模型结构复杂，主要面向较大尺度范围的模拟，且受空间不均匀性影响，带有一定的不确定性，并不适用于小范围详细场地模拟。而对于污染物在地表径流中的扩散模拟，多是基于降雨条件，采用城市暴雨模型和地表水污染模型来估算水污染负荷，如Li等[4]采用MIKE模型对西安市城区的水量和水质进行了评价； Prodanovic等[5]提出了一种新的城市雨水模型（FUSS），结合一种城市规划算法，评估城市集水区的污染变化。然而这些模型多用于水污染评价，无法很好地模拟污染物在降雨下的时空动态扩散过程，因此，研究人员采用了流体动力学模型（SPH）模拟地表污染扩散，这种方法能较好地模拟污染物在复杂地表的扩散过程，如Lye等[6]基于SPH模型对降雨、地表径流、污染物进行建模，可以追踪污染物和地表径流在真实地形中的运移情况，但是，描述流体扩散的SPH方程的相关参数难以得到，空间边界难以确定，因此这种方法比较适合理想实验环境，普适性较弱。
元胞自动机模型（Cellular Automata，CA）是一种时间空间都离散的动力学模型，它能很好地简化原有模型，能通过局部推演整体来描述复杂的地理情况，已经有大量的研究证实了元胞自动机在计算机模拟复杂世界方面的优势[7]，如在城市扩展模拟[8]、土地利用变迁[9]、雨洪模拟[10]、森林火灾模拟[11]等领域，元胞自动机模型都显示了强大的功能。元胞自动机模型在地表水污染扩散模拟中也得到了广泛的应用，如Lin等[12]考虑污染物浓度、风速、水流、蒸发等影响，提出了基于二维元胞自动机模型的水污染事故扩散模型，能在短时间内有效地模拟污染物的扩散；Dai等[13]考虑城市屋顶、地表、人工排水网络三层因素，将基于元胞自动机的地表径流路径算法与污染物运移模型结合，对非点源污染进行了模拟；高华等[14]结合河流水流分布特征，建立了基于二维元胞自动机模型的污染物扩散模型，并进行了可视化表达。王璐等[15]以栅格数据为基础，采用二维元胞自动机模型，考虑了流场和风场对污染扩散的影响，对突发性水污染事故进行了动态模拟。
元胞自动机模型的时间步长（即元胞状态根据转化规则更新一次代表的时间）对准确模拟污染扩散过程至关重要。当时间步长设置的过小时，需要多次更新元胞状态才能模拟污染扩散较为缓慢的过程，造成计算资源的浪费；当时间步长设置的过大时，对扩散过程较快的情况，模拟过程会漏掉许多扩散细节，影响管理者进行决策。由于液态污染物的扩散过程受地表重力、地表粗糙度以及外界降雨和水流条件等多重因素的影响，其扩散过程是一个非均匀的过程，而现有的元胞自动机大都以固定的时间步长来模拟，无法准确地模拟出污染物的扩散过程。本文对传统的元胞自动机模型进行改进，根据相邻元胞之间扩散的时间差异、污染物扩散速度随质量衰减的特征，设计了一种自适应调整时间步长的元胞动态时间演变算法，考虑了地表污染物受不同坡度和粗糙度影响下扩散速度不均匀的情况，分别设计无降雨和降雨两种模拟情形，对污染物的时空扩散过程进行仿真。

2 研究方法

本文基于元胞自动机模型建立了降雨与非降雨条件下的污染扩散演变规则，设计了一种更加符合污染扩散规律的自适应步长演变算法，对实验区中的污染扩散过程进行了模拟和分析（图1）。
图1 技术路线

Fig. 1 Technology Roadmap

2.1 元胞自动机模型与元胞空间划分

2.1.1 元胞自动机模型

元胞自动机模型可描述为A = { Ld, S, N, R}，其中A代表整个元胞自动机模型；L代表元胞空间，下标d代表的是元胞的维数；N代表所有邻域元胞的组合；R代表元胞的转化规则[16]。
由于正方形元胞简单直观、便于可视化表达，因此选用正方形元胞作为模型的最小单元；对于污染物在地表的扩散过程，二维元胞自动机模型足以描述其蔓延的过程，因此选用二维元胞自动机模型对污染过程进行三维可视化模拟。元胞的邻域类型决定了污染物一次扩散的影响范围和传递关系，通常有冯诺依曼型、Moore型、扩展Moore型[17]，本文采用二维Moore型元胞，在一次演变过程中，中央元胞受周围8个元胞的影响而改变状态，以当前时刻元胞是否含有污染物作为状态转移因子，通过更新所有的元胞状态来模拟污染物在地表受影响因子的扩散过程。

2.1.2 元胞空间划分

场地边界多是不规则的曲线，为了适应元胞空间边界，本文采用最小包围盒的思想将场地边界进行扩充。包围盒是一个简单的几何空间，空间物体的最小包围盒是包含该物体的最小几何空间，常见的包围盒有轴对齐包围盒AABB（Axis Aligned Bounding Box）、球形包围盒(Sphere)、有向包围盒OBB（Oriental Bounding Box）和离散方向凸包围盒k-Dops（Discrete Orientation Polytope)等[18]。为适应空间坐标轴的方向，本文采用轴对齐包围盒AABB，计算不规则污染场地元胞空间边界。
一个给定对象的AABB包围盒被定义为包含该对象且各边平行于坐标轴的最小六面体，图2展示了一个二维空间上的最小AABB包围盒的构造方式，中间阴影区域为边界不规则的污染场地，水平方向为坐标系的x轴方向，垂直方向为y轴方向，包围盒的长度为场地在x方向的最大距离，高度为在y方向上的最大距离。
图2 AABB包围盒

Fig. 2 AABB bounding box

元胞更小时，空间分辨率会更高，污染扩散模拟精度也会更高，因此，本文根据地形分辨率将元胞设置的尽量小，以获取最高的模拟精度。设元胞大小为m×n m、包围盒大小为x×y m，当对元胞空间进行划分时，由于场地的边界长度并不都是m或n的整数倍，因此本文采取向上取整的方式得到元胞的个数，划分后的元胞个数应为「x/m⌉×「y/n⌉个，其中符号「⌉是指对小数向上取整。如图3所示，根据 x 、 y方向上的长度和元胞大小，对于长度不足的边界，进行多余补充。
图3 元胞空间划分方式

Fig. 3 Cellular space division

2.2 地表污染元胞演变规则的建立

演变规则是根据当前时刻元胞与邻域元胞之间的状态确定下一时刻元胞状态的动力学函数，是元胞自动机模型的关键部分。若污染物在扩散时，没有受到外界环境的影响、是一种无干扰的理想状态，那么其只受到自身浓度的影响，从浓度高的地方向浓度低的地方进行扩散，根据质量守恒定律，可以建立此时的演变公式[19]，即在静水中的推演公式（式（1））。
$\begin{array}{*{35}{l}} M_{i,j}^{t+\Delta t}=M_{i,j}^{t}+ \\ m\left[ \begin{array}{*{35}{l}} \left( M_{i-1,j}^{t}-M_{i,j}^{t} \right)+\left( M_{i,j-1}^{t}-M_{i,j}^{t} \right)+ \\ \left( M_{i,j+1}^{t}-M_{i,j}^{t} \right)+\left( M_{i+1,j}^{t}-M_{i,j}^{t} \right) \\ \end{array} \right]+ \\ md\left[ \begin{array}{*{35}{l}} \left( M_{i-1,j-1}^{t}-M_{i,j}^{t} \right)+\left( M_{i-1,j+1}^{t}-M_{i,j}^{t} \right)+ \\ \left( M_{i+1,j-1}^{t}-M_{i,j}^{t} \right)+\left( M_{i+1,j+1}^{t}-M_{i,j}^{t} \right) \\ \end{array} \right] \\ \end{array}$
式中： M为污染物质量；i、j分别为元胞行列号；m、d分别为垂向和斜向扩散系数，影响污染物在垂向和斜向的扩散速率；t为当前时刻； Δ t为演变时间步长。由于一次演变后元胞中污染物质量变化不能大于原有的污染物质量，所以式中m、d的关系需满足 4   m + 4   m d ≤ 1，由经验得知，当d取0.16，m取0.084时，扩散最接近圆形扩散，模拟效果最佳[20]，故本文垂向、斜向扩散系数分别取0.084、0.16。
污染物在地表的流动和在静水中的流动过程不同，还会受到其他因素的影响。其中最主要的影响因素为重力和坡度，污染物会因重力作用从地势高处向地势低处进行扩散，此外，不同的地表粗糙度也会影响污染物的扩散，地面越光滑，污染物的扩散速度就越快，反之则越慢。本文考虑相邻元胞间的高差与地表粗糙度对污染扩散的影响以及污染物扩散的主要损耗，对上述演变公式进行了改进（式（2））。
$\begin{matrix} & M_{i,j}^{t+\Delta t}=M_{i,j}^{t}+m\left[ \begin{array}{*{35}{l}} {{K}_{i-1,j}}\left( M_{i-1,j}^{t}-M_{i,j}^{t} \right)+ \\ {{K}_{i,j-1}}\left( M_{i,j-1}^{t}-M_{i,j}^{t} \right)+ \\ {{K}_{i,j+1}}\left( M_{i,j+1}^{t}-M_{i,j}^{t} \right)+ \\ {{K}_{i+1,j}}\left( M_{i+1,j}^{t}-M_{i,j}^{t} \right) \\ \end{array} \right]+ \\ & md\left[ \begin{array}{*{35}{l}} {{K}_{i-1,j-1}}\left( M_{i-1,j-1}^{t}-M_{i,j}^{t} \right)+ \\ {{K}_{i-1,j+1}}\left( M_{i-1,j+1}^{t}-M_{i,j}^{t} \right)+ \\ {{K}_{i+1,j-1}}\left( M_{i+1,j-1}^{t}-M_{i,j}^{t} \right)+ \\ {{K}_{i+1,j+1}}\left( M_{i+1,j+1}^{t}-M_{i,j}^{t} \right) \\ \end{array} \right]-us \Delta t \\ \end{matrix}$
式（2）在式（1）的基础上增加了影响系数 K和污染物的损失项 u s Δ t； u s Δ t为当前时间步长内污染物损失的质量，其中 u为污染物损失系数， s为污染扩散方向上通过的横截面积； K通过高差影响系数 K d和粗糙度影响系数 K r计算得到，计算公式为：
$K={{K}_{d}}\times {{K}_{r}}+1$

2.2.1 高差影响系数的计算

元胞自动机模型中的中央元胞与周围8个邻域元胞之间存在高度差，污染物会从高程大的元胞向高程小的元胞进行流动，而中央元胞与多个邻域元胞之间污染物的交换比例是不确定的。本文将中央元胞与邻域元胞之间的高差值转化为高差比例，取值范围为[01]，各元胞邻域的高差比例之和始终为1，比例大的污染物质量交换就大，比例小的污染物质量交换就小。扩散过程只发生在比中央元胞高程值小的邻域元胞上，而在高程值大于中央元胞的邻域元胞方向上则不发生污染扩散。
以第i个元胞的高差影响系数 K d i为例，式（4）为其计算公式。
${{K}_{{{d}_{i}}}}=\frac{{{H}_{i}}-{{H}_{0}}}{\sum ({{H}_{j}}-{{H}_{0}})} \ \ {{H}_{i}}>{{H}_{0}},{{H}_{j}}>{{H}_{0}}$
式中：i、j都分别表示高程大于中央元胞高程的邻域元胞索引； H i、 H j分别为第i、j个元胞的高程； H 0为中央元胞的高程； ∑ ( H j - H 0 )是中央元胞与比其高程小的邻域元胞之间的高差之和。

2.2.2 地表粗糙度影响系数的计算

地表粗糙度有多种计算方式，Slope算法是表达地表粗糙程度和区分地形类型的较佳算法[21]。本文选择Slope算法作为计算粗糙度的算法，通过计算相邻元胞之间的粗糙度比例，来确定各元胞对中央元胞的影响程度。本文取粗糙度的倒数为比例因子，将影响系数转换成与扩散速度呈正相关的形式，当粗糙度越大时，系数越小，粗糙度越小时，系数越大。式（5）为中央元胞在第i个邻域元胞处的地表粗糙度影响系数的计算公式。
${{K}_{{{r}_{i}}}}=\frac{1/{{r}_{i}}}{\sum \left( 1/{{r}_{i}} \right)},{{r}_{j}}>0$
式中：i、j分别表示邻域元胞的索引； r i、 r j表示粗糙度； ∑ 1 / r i表示与中央元胞存在质量输出的元胞的粗糙度倒数之和，其中粗糙度的计算公式为：
${{r}_{i}}=1/\text{tan}\left( slope\times \text{ }\!\!\Pi\!\!\text{ }/180 \right)$
式中：Slope为当前元胞与中央元胞之间的坡度角。

2.3 元胞自适应时间步长演变算法

元胞自动机的演变步长主要与地表环境、坡度、元胞大小和污染物种类有关，不同地表位置的污染物流速不一样，如何根据复杂的地表特征来确定特定位置上污染物流速，从而确定污染物一次演变时间步长，是自适应模拟污染物随时间扩散的关键。

2.3.1 地表污染物平均流速计算

污染物在地表的平均流速可以借助坡面流的思想来计算。坡面流是指降雨或融雪在重力作用下沿坡面向下的水流，根据传统水力学的观点，坡面流流速应为流量和坡度的幂函数，如层流的谢才公式（Chézy formula）和紊流的曼宁公式（Manning formula）[22]，谢才公式是计算明渠和管道均匀流平均流速或沿程水头损失的主要公式，曼宁公式是在此基础上推导的一种速度经验公式，被广泛应用于物理计算、水流建设等领域[23]，如式（7）所示。
$v=\frac{k}{n}R_{h}^{2/3}{{s}^{1/2}}$
式中： k是转换常数，值为1； n是糙率，又称粗糙系数，反映影响流体速度的综合阻力因素，无量纲，糙率越大，流体速度越小； R n是水力半径，是流体截面积与湿周长的比值，根据经验可取流体平均深度来代替[24]； s是坡度，为地表两点之间的高差与距离的比值。
在坡面流的研究中，常采用雷诺数来区分水流流态，雷诺数越小，意味着流体的粘性影响越显著，越大则自身的惯性成为主导，其主要与自身的密度和粘性系数有关[25]。
$Re=\rho vd/\mu $
式中： R e表示雷诺数； ρ为液体的密度； v为液体流速； d为一固定长度，和液体流动环境有关； μ为液体粘性系数。
液态污染物与水流在流动过程中有一定的相似，可以通过雷诺数的大小对两者进行区分。基于此，本文对经典曼宁公式进行进一步处理，在原方程的基础上添加雷诺数转换因子，得到一种更普适的液体均匀流流速计算公式。
$v={{f}_{re}}\frac{k}{n}R_{h}^{2/3}{{s}^{1/2}}$
式中： f r e为转换因子，作用是将一般水流转换为特定的液态污染物，其计算公式为：
${{f}_{re}}=R_{e}^{t}/R_{e}^{o}$
式中： R e t是转换目标流体的雷诺数； R e o是水的雷诺数。转换因子的计算规则是假定外界条件如温度、地表粗糙度等因素都相同的情况下，只受自身密度和粘性系数影响下的比值。
对于污染物扩散而言，某个时刻的扩散状态是未知的，演变公式计算的是污染物在某个时刻的质量或者浓度，而要确定下一时刻污染物的流速，必须要知道污染物扩散方向上的坡度与水力半径，其中坡度可以根据高差和网格长度计算获得，因此水力半径的计算对确定流速至关重要。当存在降雨条件时，污染物将随水流一起扩散，扩散速度将加快，当不存在降雨时，污染物扩散的速度将随扩散的距离变远而渐渐变慢，基于此，本文分别设计了降雨和非降雨条件下的污染物扩散速度计算方法，用以模拟污染物在这两种条件下的扩散过程。

2.3.2 非降雨条件下平均流速的计算

已知水力半径可以用平均水深替代，现假设污染物在每个网格单元的分布是均匀分布，那么可以根据下一时刻污染物的扩散质量以及网格的大小来计算污染物在每个网格内的平均高度，即水力半径，计算公式如下。
${{R}_{h}}=\frac{M}{\rho \times s}$
式中： M是当前网格内的污染物质量； ρ是污染物的密度； s是网格的底面面积。从式中可以看出，当网格内的污染物质量越小时，水力半径也越小，污染扩散的速度也会越慢，符合实际情况中污染扩散速度随距离衰减的情况。
当下垫面为水泥路面时，污染物向下渗入的量几乎可以忽略不计，而对于一般性土壤来说，向下输出的污染物质量不可忽略。在非饱和土壤中，流体在土壤的渗透系数可以表示其向下渗流的强弱，表达式为：
$K=p\rho g/\eta $
式中： K为渗透系数； p为土壤渗透率，和孔隙度有关； ρ为流体密度； η为粘性系数。水的渗透系数一般比较好获取，实验测定了场地非饱和土壤水的渗透系数，通过公式将其转换为污染物在土壤中的渗透系数。由于影响渗透系数的因素主要为流体密度和粘性系数，因此可以采用雷诺数比值 f r e进行转换，转换公式为：
${{K}_{T}}={{f}_{re}}K$
式中： K T为目标流体的渗透系数； K为水的渗透系数。考虑污染物向下渗透的质量流失，根据污染物的渗透系数及一次演变的向下渗入时间 Δ t，计算下渗的污染物质量，对式（11）做出了改进：
${{R}_{h}}=\frac{M}{\rho s}-{{K}_{T}}\text{ }\!\!\Delta\!\!\text{ }t$
为简化模型，在无降雨条件下，根据下垫面的物理化学特性，选取经验值作为地表的粗糙系数。

2.3.3 降雨条件下平均流速的计算

雨水落在地表之后，会形成径流，期间会经过下渗、蒸发、植物截留等作用，扣除降雨过程中损失的降雨量的部分称之为净雨，计算净雨的过程称为产流计算[26]。由于降雨损失以土壤下渗为主、降雨过程中蒸发量和城市地带植物截留量较少，本文考虑降雨作用和下渗作用，计算了不同时刻的净雨量，采用在地表形成的径流深度来代替平均水力半径，从而计算污染物在降雨过程中的流速，式（15）是产流的计算公式。
$R=P-I$
式中：R是产流量；P是降雨量；I是下渗量；单位都为mm。
降雨量可以根据气象站获得，为了简化模型，对下渗量的计算方式采用经验公式。现有计算下渗量的主要方法有Horton方程、Philip方程、Green-Ampt方程，大部分城市雨洪模型多采用Horton方程计算下渗量[27]，它能够反映下渗率随时间的变化关系，如式（16）所示。
$f\left( t \right)={{f}_{c}}+\left( {{f}_{0}}-{{f}_{c}} \right){{e}^{-ut}}$
式中： f t为 t时刻的下渗率； f c为稳定下渗率； f 0为初始下渗率； u为衰减系数。
Horton方程在实际应用中有很多局限性，当其他因素（如灌溉、蒸散）影响土壤水分时，方程不能准确地描述雨水的下渗量，Yang[28]等针对这种现象在Horton方程的基础上提出了一种改进方程，实验表明其能更精确地计算下渗量，因此，本文采用这种改进的Horton方程计算雨水在某个时刻的下渗量，计算公式如下。
$f\left( \theta \right)={{f}_{c}}+\left( {{f}_{0}}-{{f}_{c}} \right){{e}^{-k\left( \frac{\theta -{{\theta }_{0}}}{{{\theta }_{c}}-\theta } \right)}}$
式中： θ 0和 θ c分别是土壤的初始含水率和饱和含水率； θ为t时刻的土壤水分；k为改进系数。
降雨渗入土壤后会继续向下运动，直到渗入潜水面随地下水流流动。对于浅层的非饱和土壤，当降雨强度小于土壤饱和渗透系数时，可以近似认为雨强与渗透系数相同[29]。
土壤水分特征曲线反应了土壤含水量与吸力之间的关系，可估算非饱和带中的渗透系数，Van Genuchten模型是运用最广泛的模型之一。在Van Genuchten模型中，非饱和土壤水渗透系数可以表示成饱和渗透系数和有效饱和度的函数：
$K={{K}_{s}}S_{e}^{l}{{\left[ 1-{{(1-S_{e}^{\left( 1/m \right)})}^{m}} \right]}^{2}}$
式中： K为非饱和土壤水渗透系数； K s为饱和渗透系数； S e为有效饱和度；m为拟合参数，l为模型的经验参数，可取0.5[30]。有效饱和度 S e可表示成土壤体积含水率的函数：
${{S}_{e}}=\frac{\theta -{{\theta }_{r}}}{{{\theta }_{s}}-{{\theta }_{r}}}$
式中： θ为土壤体积含水率/ ( c m 3 / c m 3 )， θ s、 θ r分别为饱和体积含水率和残余体积含水率/ ( c m 3 / c m 3 )。
消去式（18）中的有效饱和度，可建立不同渗透系数和土壤体积含水率的关系，即降雨强度与土壤体积含水率的关系式：
$\theta =f\left( K \right)$
不同时刻降雨强度可以从气象站获得，当降雨强度小于土壤饱和体积含水率时，表层土壤的含水率随雨强的变化而变化，当降雨强度大于土壤饱和体积含水率时，表层土壤的含水率为饱和含水率。
降雨条件下，雨水会冲刷地面，当地面有薄层水流时，会穿过水流击打地面，土壤颗粒物可能会溶出，这对水流流速造成很大影响，此时的坡面流阻力不能只用坡面的粗糙度来替代，还应考虑降雨及降雨时土壤颗粒溶出等因素对流速的影响。如杨坪坪等[31]研究了降雨条件下雨强对坡面流流速的影响，发现流速与降雨强度成正比，表明降雨的增加会显著减少坡面流阻力系数，且随着降雨强度增加而加速减小。
张宽地等[32]推导了一种流速、流量和坡度之间的关系式： u = η Q 1 - m J n，其中m为流态指数，反应流体耗能的主要方式，值越大，表示阻力耗能越大，反之则耗能越小； u为流体流速； η、n为回归系数；J为水力坡度；降雨条件下，流量可以近似用雨强来表示： Q = k R，其中k为转化系数， R为雨强；若只考虑雨强和阻力对流速的影响，原式可以简化为如下的形式。
$u\sim {{R}^{1-m}}$
根据液态指数m的定义，本文将其简化成地表粗糙度系数n，再结合曼宁公式，得出了在雨强 R影响下的地表污染物扩散流速计算公式：
$v={{f}_{re}}{{R}^{1-n}}R_{h}^{2/3}{{s}^{1/2}}$

2.3.4 自适应时间步长演变算法

污染物在地表的流速和地表环境有很大关系，因此不同坡度和粗糙度情况下，污染物的流速不一样，而对于一个元胞网格，不同空间中的网格大小是一样的，因此在一次扩散演变过程中，不同扩散方向上的扩散时间会不一样。
如图4所示，当中央元胞向元胞邻居1、2扩散时，若中央元胞与邻居2的高差是与邻居1的高差的2倍，那么根据曼宁公式，当水力半径相同的情况下，邻居2方向的平均速度为邻居1方向上的2倍，当在元胞长度很小的前提下，两者的运动路程的差异可忽略不计，当坡度差异很大时，不同邻居上污染物的到达时间差异会十分显著。
图4 一次演变示意

Fig. 4 A schematic diagram of evolution

当不同方向上的坡度差异很大时，污染物的流速也会有很大差异，因此污染物到达不同邻域元胞之间的时间会存在一定的差异，此外，污染物质量越小，扩散速度就越小，离污染源越远的位置扩散至下一时刻所需的时间也越长。因此，模拟污染物在一次演变过程中的扩散先后顺序，将更加真实地模拟污染随时间的扩散，同时，准确地确定污染物的演变时间对计算污染物在不同时间的分布范围也十分重要。
本文根据污染物在地表不同位置上的扩散速度设计了一种随污染物质量和坡度衰减的元胞自适应时间步长演变算法，来动态确定一次演变时间的间隔，同时随时间推移来动态表示一次演变中的污染先后过程，从而更真实地模拟污染物在地表随时间的扩散过程，该算法的流程如图5所示。
图5 元胞自适应时间演变算法流程

Fig. 5 Flow chart of cellular adaptive time evolution algorithm

算法的主要思想是引入可变时间步长和参考时间，实现根据不同流速动态确定演变步长和设定时间尺度来加快减慢扩散蔓延速度的功能，并完成浓度梯度的可视化表达。其主要流程是获取当前所有已经被污染的元胞对象，演变一次，剔除已经被污染的元胞，获得下个时刻的所有污染元胞对象，确定该方向上的演变时间t，设定参考时间T，判断污染元胞扩散时间是否已经大于参考时间，若大于，将元胞放入污染池，并更新它的颜色。若参考时间为真实时间，则扩散时间会以真实世界的时间为基准，若缩短为真实世界的一半，则扩散会以2倍的速率进行。
由于一次演变过程中在元胞的不同邻域方向浓度梯度、坡度等的差异，流速会有一些差异，扩散时间也会有些许的不同。那么在不同邻域方向上的时间步长计算公式为：
$\begin{array}{*{35}{l}} \Delta{{t}_{x,y}}=\frac{l}{{{v}_{x,y}}} \\ x\in \left( i-1,i+1 \right),y\in \left( j-1,j+1 \right),\left( x\ne i,y\ne j \right) \\ \end{array}$
式中：x、y分别表示邻域元胞的索引； Δ t x , y为污染物在（x，y）方向上扩散的时间步长；l为元胞边长。那么该时刻的时间步长可以用所有邻域元胞的扩散时间的最大值替代：
$\begin{array}{*{35}{l}}\Delta{{t}_{i,j}}=Max\left( \Delta{{t}_{i-1,j-1}},\Delta{{t}_{i-1,j}},\ldots,\Delta{{t}_{i+1,j+1}} \right) \\ \left(\Delta{{t}_{i,j}}=0 \right) \\ \end{array}$
最后，得到了元胞状态转移方程：
$\begin{array}{*{35}{r}} S_{i,j}^{t+\Delta t}=S_{i,j}^{t}+\frac{\left( v_{i-1,j-1}^{t}\Delta{{t}_{i-1,j-1}}+\ldots +v_{i+1,j+1}^{t}\Delta{{t}_{i+1,j+1}} \right)}{l} \\ \left( \Delta{{t}_{i,j}}=0 \right) \\ \end{array}$
式中： S i , j为元胞状态； v i , j为污染物在i、j方向上的扩散速度； Δ t i , j为时间步长；l为元胞边长。

3 实验区概况与预处理

3.1 实验区

实验区位于南京市六合区葛塘街道浦六北路与葛中路交叉口南侧一处空地，土壤类型为黄褐土，土地利用类型为建设用地（图6）。其北侧为原商翔石油化工有限公司地块，公司由于污染问题进行了搬迁，地块留存了大量的潜在污染源，存在一定的安全隐患，由于该地块存在地表建筑物，地表环境较为复杂，不利于模拟污染受重力和降雨的扩散过程，因此选取地块南侧的一块建设空地作为实验区，选取5个点作为实验区的边界特征点，图6展示了实验区的地理位置和形状。
图6 实验区地理位置

注：底图为OpenStreetMap开源地图。

Fig. 6 Geographical location of the study area

3.2 仿真环境

计算机硬件配置为：CPU Intel Core i5-6300HQ 2.30 GHz，12.0 GB RAM, GPU NVIDIA GeForce GTX 960 M。软件环境为Windows10旗舰版，Visual Studio Code开发工具，主要编程语言为JavaScript和GLSL。采用开源虚拟地球框架Cesium对污染三维场地和漫游过程进行可视化模拟，Cesium是一个基于JavaScript语言编写的开源WebGL虚拟地球引擎，支持多种视图模式和地图浏览，提供了强大的GIS数据渲染和展示功能，同时有很好的兼容性，已被广泛应用于空间数据可视化、数字城市等领域。

3.3 实验区划分

对实验区地块进行包围盒的计算，并利用地块开挖技术，对该包围盒进行三维可视化，并对元胞空间进行划分。以5×5 m的元胞大小为例，将包围盒划分成同等大小的正方形网格，如图7所示，其中影像为Bing地图，地形为Cesium官方提供的最高1 m分辨率的全球地形，来源于开放和商业数据。
图7 元胞空间划分

Fig. 7 Cellular space division

4 仿真结果及分析

4.1 非降雨条件污染物扩散仿真与分析

已知25 °C下的水，密度为997 kg/m3，粘性系数为8.90×10-4 Pa·s，实验采用的苯溶液，密度为 876 kg/m3，粘性系数为6.47×10-4 Pa·s，可以求出转换因子 f r e的值约为0.8274。为了便于观察污染物的扩散过程，实验在场地正中间的一个元胞位置处放置一个瞬时污染源，实验污染物为苯，污染物质量为1000 g，采用颜色映射的方式对污染物浓度进行可视化，污染物浓度越高，对应的颜色就越深。

4.1.1 下垫面为一般性土壤时的污染扩散仿真与分析

由于地表糙率一般需要实地勘测获取，本文基于前人的研究，选择一般性河道的糙率来替代一般性土壤的糙率，此时的曼宁公式的参数n为0.035[33]；经实地勘测，渗透系数取表层杂填土的建议值 1.1×10-5 cm/s。
污染物因自身的重力作用向地表低的位置流动，扩散距离越远，扩散的速度就越慢。由于污染物扩散速度缓慢，为了精细表达污染物的扩散距离，本文选取0.5 m×0.5 m的网格，图8是污染物在地表受自身重力作用下流动1天的污染分布图，其中网格颜色从橘色到蓝色，对应了污染物浓度从高到低。
图8 污染物在土壤地面扩散1 d后的范围

Fig. 8 The range of pollutants diffused on the soil surface for 1 day

污染物的扩散速度十分缓慢，1 d的扩散直线距离约为3.56 m，并且由于离污染源越远的网格内污染质量越小，流速会越慢，几乎可以认为已经不发生新的扩散。
图9展示了污染物扩散不同的距离所花的时间，假设污染物开始扩散时刻为0，从图9中可以看出污染物扩散时间随距离增加，扩散0.70 m，所需时间约为0.10 min；扩散1.41 m，所需时间约为0.80 min；扩散2.12 m，所需时间约为6.30 min；而扩散2.83 m，时间已经超过24 h。实验表明，当污染物每扩散单位元胞长度的距离时，其所花的时间都会成倍的增加，在扩散距离超过2.83 m左右后，扩散时间几乎成90°上升，因此可认为污染物在扩散2.83 m后几乎不发生扩散作用，这也与实际情况中污染物扩散距离随质量衰减的情况相符。
图9 污染物在土壤地面扩散时间随距离的变化

Fig. 9 Variation of pollutant diffusion time on the soil surface with distance

4.1.2 下垫面为水泥路面时的污染扩散仿真与分析

与一般性土壤不同的是，下垫面为水泥路面时，地表的糙率要低很多，污染物向下渗入量可以忽略不计。选取混凝土水泥路面作为研究对象，合理的糙率建议值为0.012，并对污染扩散进行了模拟与分析。
由于只改变了下垫面的糙率，地表的坡度未发生改变，因此图10的扩散范围只在西南方的位置上有所增大，从扩散时间上来看，糙率对扩散速度的影响将更加明显，如图11所示。
图10 污染物在水泥地面扩散1 d后的范围

Fig. 10 The range of pollutants diffused on the cement floor for 1 day

图11 污染物在水泥地面扩散时间随距离的变化

Fig. 11 Variation of pollutant diffusion time on the cement floor with distance

从图11可看出，污染物扩散0.70 m，所需时间约为0.04 min；扩散1.41 m，所需时间约为0.30 min；扩散2.12 m，所需时间约为2.15 min；在扩散距离超过2.12 m左右后，扩散时间几乎成直线上升。
下垫面对污染扩散有很大的影响，从时间尺度上来看，当曼宁系数从0.035降低到0.012时，并略去向下渗入量时，扩散速度将会变为原来的2.7倍左右。

4.2 降雨条件污染物扩散仿真与分析

降雨条件下，污染物的扩散受降雨时长影响，扩散速率会随时间变化，特别是当降雨、降雨入渗强度等也随时间变化时，污染物的扩散速率将是一个复杂的变化曲线，此时的定时间步长的元胞无法很好地描述这种过程，而自适应时间步长可以容纳更多外界可变因素，随着外界条件的改变，调整每次演变的时间，拥有更强的适应性。
实验选取一般性土壤作为下垫面，对比了几组降雨强度和降雨时间的数据，对污染物从开始扩散一段时间内的扩散范围和浓度变化进行了模拟和分析，展示了自适应时间步长算法的优势。
由于不同时刻的土壤含水量需要实际勘测获得，本文根据Yang[28]的实验数据，实验场地为一般性土壤场地，初始土壤含水量为0.27 m3/m3，稳定土壤含水量为0.38 m3/m3，饱和含水量为0.44 m3/m3时，饱和水入渗系数为90~100 mm/h，稳定入渗速率为25~35 mm/h。根据不同降雨强度，确定表层土壤渗透系数，计算对应的土壤含水率，再计算当前雨强的稳定水流入渗量，最后根据式（22）确定污染物在水流中的流速，模拟污染物在降雨影响下的扩散过程。

4.2.1 降雨时长对污染物扩散的影响

图12为恒定35 mm/h的雨强在降雨不同时间后污染物5 min内的扩散范围。当降雨10 min时，污染物的扩散距离约为12.7 m；当降雨20 min时，扩散距离约为19.8 m；当降雨40 min时，扩散距离约为31.1 m；当降雨60 min时，扩散距离约为 43.1 m。从中可以看出，降雨强度是恒定的情况下，随着降雨时长的增加，污染物的扩散距离并不是时间均匀的，定步长模型不能很好地描述这种情况。
图12 降雨不同时间后污染物5 min的扩散范围

Fig. 12 Diffusion range of pollutants in 5 min utes after rainfall at different times

4.2.2 降雨强度随时间变化下污染物的扩散模拟

不同时间下的降雨强度往往是不一样的，为观察随时间变化的降雨强度对污染物扩散的影响，假设雨强是从小到大，又从大到小的过程，可采用二次抛物曲线对其进行模拟。实验最大降雨量为 60 mm/h，最小降雨量为0，降雨时长为30 min，抛物线方程为 r = t ( 30 - t )， t的单位为min， r为降雨量，单位为mm/h。为观察污染物在不同位置上的扩散过程，将污染源放置在实验区西南角一处位置，分别模拟了不同时刻的污染扩散范围。
如图13，当降雨5 min时，扩散距离约为7.1 m；当降雨10 min时，距离约为20.5 m；当降雨15 min时，距离约为38.2 m；当降雨20 min时，距离约为51.6 m；当降雨25 min时，距离约为61.5 m；当降雨30 min时，距离约为70.0 m；污染物浓度随时间的变化可以通过颜色的差异来观察，随着时间的推移，原本是蓝色的位置，会渐渐变为橘黄色，污染物浓度渐渐增大，反映了污染物随时间向地势低处迁移的过程。
图13 降雨强度随时间变化时半小时内污染物的扩散范围

Fig. 13 Diffusion range of pollutants with time-varying rainfall intensity within half an hour

从图14中可以看出，由于降雨是一个二次抛物曲线，随着时间的变化，污染物扩散距离有一个明显的加速过程，一直到15 min左右时，扩散速率最快，之后慢慢变缓。自适应时间步长算法将不同时间下的降雨强度考虑在内，推演出适应的时间步长，用以描述这种外界条件复杂变化的情况。
图14 降雨半小时内污染物扩散随时间变化曲线

Fig. 14 Variation curve of pollutant diffusion with time within half an hour of rainfall

4.2.3 不同地点污染物浓度随时间的变化

为模拟污染物在不同地点上浓度随时间变化的过程，设计了一组在固定降雨降雨强度、入渗速率下污染物扩散随时间变化的模拟实验。为更好地观察污染物的浓度变化，设定了污染物在水中的浓度检出限作为阈值条件，为1.4×10-3 g/l，即污染物的浓度小于检出限时，则认为其为未污染状态；在场地的中心位置放置一个浓度为1000 g/l的污染源；设定了5个不同的浓度区间，作为观察污染物随时间变化差异的指标。
图15（g）为浓度从低到高的五个浓度区间；图15（a）是元胞自动机推演30次的结果示意图，可以看到污染源的附近颜色最深，以污染源为中心向四周的颜色越来越浅；图15（b）是推演50次的结果，发现污染源附近浓度大于24 g/l的元胞越来越少，而处于其他浓度区间的数量越来越多；图15（c）是推演80次的结果，发现浓度大于24 g/l的元胞已经消失；图15（d）是推演100次的结果，发现所有污染区域的浓度都处于18 g/l以下；图15（e）和图15（f）分别是推演100次和300次的结果，发现最后所有污染区域的浓度都小于6 g/l，此时的扩散趋于平稳。
图15 稳定降雨下不同位置污染物浓度随时间变化

Fig. 15 Concentrations of pollutants at different locations with time under stable rainfall

4.2.4 污染扩散结果分析与验证

由于特定降雨曲线下苯污染扩散随时间变化的浓度数据很难获取，而且污染物的扩散范围主要受坡度影响，降雨只是加快了扩散过程，因此本文采用分析实验区的坡度坡向的方式，将实验区坡度与实验得到的扩散范围和不同方向上的扩散速度进行了对比，最终得出了模型的扩散结果与降雨条件下实地的扩散结果基本保持一致的结论。
本文将实验区地表高度划分成5个区间，使用渐变色生成了实验区的坡度图，如图16所示。从图中可看出实验区的坡向整体自西北向东北和正南，而在东南方向也有一个较缓的坡度。
图16 坡度图

Fig. 16 Slope map

为更好地对比，将降雨条件下2个不同时刻污染物的扩散范围与坡度图叠加，如图17所示。从图17中可以看出，污染物主要的扩散方向与坡度的方向基本保持一致，主要向地势更低的东北、西南方扩散，速度较快，而在地势差异较小的东南方向的扩散则较为缓慢。
图17 污染扩散结果与坡度叠加示意

Fig. 17 Schematic diagram of pollution diffusion results and slope overlay

4.3 一次演变中污染物不同方向上的扩散时间差异仿真与分析

由于一次推演时不同方向受到外界的影响因素（如坡度）不同，对于定步长的元胞自动机模型而言，很难表达这种扩散时间差异，而自适应步长算法可以更加细致地描绘这种过程。
本文的元胞自动机模型有8个邻域，对应污染的8个扩散方向，由于不同方向上的坡度差异，一次演变中污染物在不同方向上的扩散时间也会有一定的差异，当邻域方向上的坡度相差较大时，这种差异是非常明显的。为了加快模拟速度，以上述实验中的降雨条件为例，假定已经形成了稳定的坡面水流，水流深度约为0.01 m，那么此时在坡度为0.01 m的方向上，污染扩散速率约为0.4 m/s，本文根据算法设计，设定参考时间为真实时间，进行实时模拟，观察一次演变过程中不同邻域方向上的扩散时间差异，选取了邻域方向之间坡度差异较为明显的第1次、第6次、第10次演变过程，对污染物扩散到不同邻域方向的扩散时刻进行了展示，如图18所示。
图18 第1次演变时不同邻域方向上的扩散时间差异

Fig. 18 Diffusion time difference in different neighborhood directions during the first evolution

图18—图20中的绿色元胞位置都表示某次演变过程中即将发生扩散的位置，但由于一次演变还未完成，需等待其他邻域方向上的到达指定的扩散时间，才会更新这次演变后的所有污染物浓度，并重新计算每个元胞对应的渐变颜色，最后进行绘制。实验模拟了不同时刻污染物在一次演变过程中不同邻域方向上的污染扩散时间差异，这种可变时间步长算法可以更加真实地模拟污染物随时间的变化过程，更加符合真实扩散情况。
图19 第6次演变时不同邻域方向上的扩散时间差异

Fig. 19 Diffusion time difference in different neighborhood directions during the 6th evolution

图20 第10次演变时不同邻域方向上的扩散时间差异

Fig. 20 Diffusion time difference in different neighborhood directions during the 10th evolution

5 结论

本文针对液态污染物在地表的扩散过程，以位于南京市的一处带有潜在污染风险的场地为实验区，基于元胞自动机模型，建立了污染物在降雨和非降雨条件下的推演规则，以苯为例，对其在不同下垫面、降雨时长、降雨曲线条件下的扩散过程进行了模拟，并对模型一次演变中的扩散差异性进行了分析。主要结论如下：
（1）对于不规则场地边界，基于最小包围盒的思想确定了元胞空间，考虑地表高度时影响污染物扩散的主要因素，根据地形最高分辨率设定了元胞大小，并划分了元胞空间，能满足小范围场地的元胞空间划分需求。
（2）地表坡度越大、粗糙度越小时，液态污染物扩散速率越快，基于元胞自动机模型只受分子扩散影响下的推演规则，根据坡度、粗糙度倒数之间的比值，区分了一次推演过程中的污染物扩散通量，建立了污染物受坡度和粗糙度影响的推演规则，实验结果表明苯在坡度较大的方向迁移更为迅速。
（3）本文基于坡面流流速计算方法，提出了一种更普适的液态坡面流流速计算方法，对降雨和非降雨条件的污染扩散进行了模拟。无降雨条件下的污染物扩散速率十分缓慢，在坡度较缓的情况下，苯的最大直线扩散范围保持在2.50 m左右；不同下垫面时苯的扩散速率有较大的差异，下垫面为水泥路面时苯的平均扩散速率约为下垫面为一般性土壤的2.7倍左右。降雨条件下，苯的扩散主要受地表径流影响，降雨对其有促进作用；当降雨强度随时间变化时，苯的扩散速率也是一个不均匀的曲线，最大速率在雨强峰值附近；实验模拟了降雨条件下，同一位置的苯浓度随时间的变化过程，当苯随着水流迁移，高浓度区间范围慢慢变小，低浓度区间范围慢慢变大，浓度差异渐渐 变小。
（4）针对污染物在不同环境下的流速不同，本文提出了一种元胞自适应时间步长动态演变算法，解决了地表污染物扩散元胞自动机模型的扩散时间难以确定的问题。实验对降雨条件下苯的扩散过程进行了分析，由于外界环境的不同，第1次推演所需0.16 min左右，不过在0.04 min和0.06 min时刻污染物扩散状态存在一定的差异，第6次和第10次推演也是如此，在0.1 min的时间内，存在多个时刻扩散特征较为明显的差异。实验符合污染物扩散的实际规律，具有更强的适应性，可更好地模拟时间非均匀情况下污染扩散的时空演变过程。
该模型对地表液态流体的受自身重力或降雨条件的迁移模拟有一定的适用性，同时，模型中基于元胞自动机的自适应时间步长演变算法也更符合真实情况，但由于污染物实时扩散数据很难获取，本文仅是通过分析实验区的坡度图，初步验证了污染物扩散随坡度变化的过程，进一步可通过精确测得获取降雨、污染物浓度、土壤含水率等数据对模型进行调优，以实现更精确的模拟；此外，本文未考虑地表环境中建筑物、地表植物等复杂地物的存在，且进一步需确认边界条件，改进扩散状态转移方程，以适应更加复杂环境下的地表污染物扩散模拟。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
中华人民共和国环境保护部. 场地环境调查技术导则:HJ 25.1—2014[S]. 北京: 中国环境科学出版社, 2014.

[ Ministry of Environmental Protection of the People's Republic of China. Technical guidelines for site environmental site investigation: HJ 25.1—2014[S]. Beijing: China Environmental Science Press, 2014. ]

[2]
苑克帅. 我国污染场地再开发风险管控法律规制研究[D]. 重庆: 西南政法大学, 2016.

[ Yuan K S. Brownfield redevelopment risk control legal regulation research in China[D]. Chongqing: Southwest University of Political Science and Law, 2016. ]

[3]
张亦弛. 工业搬迁遗留场地环境风险管理体系研究[D]. 西安: 长安大学, 2012.

[ Zhang Y C. The system of environmental risk management of former relocation industrial sites[D]. Xi'an: Chang'an University, 2012. ]

[4]
Li J K, Zhang B, Li Y J, et al. Simulation of rain garden effects in urbanized area based on mike flood[J]. Water, 2018, 10(7):860-882. DOI:10.3390/w10070860

DOI

[5]
Prodanovic V, Jamali B, Kuller M, et al. Calibration and sensitivity analysis of a novel water flow and pollution model for future city planning: Future Urban Stormwater Simulation (FUSS)[J]. Water Science and Technology: A Journal of the International Association on Water Pollution Research, 2022, 85(4):961-969. DOI: 10.2166/wst.2022.046

DOI

[6]
Lye X Y, Nakayama A, Nizamani Z. Development of smoothed particle hydrodynamics for simulation of flow and contaminant transport on natural urban terrain and streams[J]. IOP Conference Series: Earth and Environmental Science, 2021, 945(1): 012009. DOI:10.1088/1755-1315/945/1/012009

DOI

[7]
赵莉, 杨俊, 李闯, 等. 地理元胞自动机模型研究进展[J]. 地理科学, 2016, 36(8):1190-1196.

DOI

[ Zhao L, Yang J, Li C, et al. Progress on geographic cellular automata model[J]. Scientia Geographica Sinica, 2016, 36(8):1190-1196. ] DOI:10.13249/j.cnki.sgs.2016.08.009

DOI

[8]
谢志文, 王海军, 张彬, 等. 城市扩展元胞自动机多结构卷积神经网络模型[J]. 测绘学报, 2020, 49(3):375-385.

[ Xie Z W, Wang H J, Zhang B, et al. Urban expansion cellular automata model based on multi-structures convolutional neural networks[J]. Acta Geodaetica et Cartographca Sinica, 2020, 49(3):375-385. ] DOI:10.11947/j.AGCS.2020.20190147

DOI

[9]
Tong X H, Feng Y J. A review of assessment methods for cellular automata models of land-use change and urban growth[J]. International Journal of Geographical Information Science, 2020, 34(5):866-898. DOI:10.1080/13658816.2019.1684499

DOI

[10]
Guidolin M, Chen A S, Ghimire B, et al. A weighted cellular automata 2D inundation model for rapid flood analysis[J]. Environmental Modelling & Software, 2016, 84:378-394. DOI:10.1016/j.envsoft.2016.07.008

DOI

[11]
惠珊, 芮小平, 李尧. 一种耦合元胞自动机的改进林火蔓延仿真算法[J]. 武汉大学学报·信息科学版, 2016, 41(10):1326-1332.

[ Hui S, Rui X P, Li Y. An improved forest fire spread simulation algorithm coupled with cellular automata[J]. Geomatics and Information Science of Wuhan University, 2016, 41(10):1326-1332. ] DOI:10.13203/j.whugis20140811

DOI

[12]
Lin M L, Yao Y P. Simulation of water pollution accident based on cellular automata[C]// CMSS 2018: Proceedings of the 2018 2nd International Conference on Management Engineering, Software Engineering and Service Sciences. 2018:270-274. DOI: 10.1145/3180374.3180380

DOI

[13]
Dai Y, Chen L, Zhang P, et al. Construction of a cellular automata-based model for rainfall-runoff and NPS pollution simulation in an urban catchment[J]. Journal of Hydrology, 2019, 568:929-942. DOI:10.1016/j.jhydrol.2018.11.029

DOI

[14]
高华, 代侦勇. 基于改进元胞自动机的水污染扩散模拟[J]. 测绘地理信息, 2020, 45(6):138-140.

[ Gao H, Dai Z Y. Simulation of water pollution dispersion based on improved cellular automata[J]. Journal of Geomatics, 2020, 45(6):138-140. ] DOI: 10.14188/j.2095-6045.2019431

DOI

[15]
王璐, 谢能刚, 李锐, 等. 基于元胞自动机的水体污染带扩散漂移仿真[J]. 水利学报, 2009(4):481-485.

[ Wang L, Xie N G, Li R, et al. Simulation of drift-diffusion of water pollution zone based on cellular automata[J]. Journal of Hydraulic Engineering, 2009, 40(4):481-485. ] DOI:10.3321/j.issn:0559-9350.2009.04.014

DOI

[16]
周成虎, 欧阳, 马廷, 等. 地理系统模拟的CA模型理论探讨[J]. 地理科学进展, 2009, 28(6):833-838.

[ Zhou C H, Ou Y, Ma T, et al. Theoretical perspectives of CA-based geographical system modeling[J]. Progress in Geography, 2009, 28(6):833-838. ] DOI:10.11820/dlkxjz.2009.06.001

DOI

[17]
Dahal K R, Chow T E. Characterization of neighborhood sensitivity of an irregular cellular automata model of urban growth[J]. International Journal of Geographical Information Science, 2015, 29(3):475-497. DOI:10.1080/13658816.2014.987779

DOI

[18]
于瑞云, 赵金龙, 余龙, 等. 结合轴对齐包围盒和空间划分的碰撞检测算法[J]. 中国图象图形学报, 2018, 23(12):1925-1937.

[ Yu R Y, Zhao J L, Yu L, et al. Collision detection algorithm based on AABB bounding box and space division[J]. Journal of Image and Graphics, 2018, 23(12):1925-1937. ] DOI:10.11834/jig.180050

DOI

[19]
沈敬伟, 彭安琪, 周廷刚, 等. 基于并行元胞自动机的水体污染物扩散模拟[J]. 测绘科学技术学报, 2016, 33(1):105-110.

[ Shen J W, Peng A Q, Zhou T G, et al. Water pollutant spreading simulation based on parallel cellular automata[J]. Journal of Geomatics Science and Technology, 2016, 33(1):105-110. ] DOI:10.3969/j.issn.1673-6338.2016.01.020

DOI

[20]
Karafyllidis I. A model for the prediction of oil slick movement and spreading using cellular automata[J]. Environment International, 1997, 23(6):839-850. DOI:10.1016/S0160-4120(97)00096-2

DOI

[21]
李玉茹, 杨勤科, 王春梅, 等. 面向地形类型区分的地表粗糙度算法比较研究[J]. 西北农林科技大学学报(自然科学版), 2019, 47(8):134-143.

[ Li Y R, Yang Q K, Wang C M, et al. Comparison of surface roughness algorithms for terrain type separation[J]. Journal of Northwest A & F University (Natural Science Edition), 2019, 47(8):134-143. ] DOI: 10.13207/j.cnki.jnwafu.2019.08.017

DOI

[22]
张光辉. 坡面薄层流水动力学特性的实验研究[J]. 水科学进展, 2002. 13(2):159-165.

[ Zhang G H. Study on hydraulic properties of shallow flow[J]. Advances in Water Science, 2002. 13(2):159-165. ] DOI:10.3321/j.issn:1001-6791.2002.02.005

DOI

[23]
赵振国, 黄春花. 明渠均匀流研究[J]. 水利学报, 2013, 44(12):1482-1487.

[ Zhao Z G, Huang C H. Study on the uniform flow in open channel[J]. Journal of Hydraulic Engineering, 2013, 44(12):1482-1487. ] DOI: 10.13243/j.cnki.slxb.2013.12.004

DOI

[24]
张宽地, 王光谦, 王占礼, 等. 人工加糙床面薄层滚波流水力学特性试验[J]. 农业工程学报, 2011, 27(4):28-34.

[ Zhang K D, Wang G Q, Wang Z L, et al. Experiments on hydraulic characteristics of roll wave for sheet flow with artificial rough bed[J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(4):28-34. ] DOI:10.3969/j.issn.1002-6819.2011.04.006

DOI

[25]
吴望一. 流体力学[M]. 北京: 北京大学出版社,1982-1983.

[ Wu W Y. Fluid mechanics[M]. Beijing: Peking University Press, 1982-1983. ]

[26]
刘家琳, 张建林. 基于SWMM模型的山坡型公园子汇水区地表产流特征——以重庆地区为例[J]. 中国园林, 2018, 34(6):81-87.

[ Liu J L, Zhang J L. Analysis on surface runoff characteristics of subcatchment in hillside park based on SWMM—A case study of Chongqing[J]. Chinese Landscape Architecture, 2018, 34(6):81-87. ] DOI:10.3969/j.issn.1000-6664.2018.06.015

DOI

[27]
薛文宇. 城市暴雨积水及街道洪水模拟模型研究[D]. 天津: 天津大学, 2016.

[ Xue W Y. Numerical simulation of stormwater and street flood in city[D]. Tianjin:Tianjin University, 2016. ]

[28]
Yang M Y, Zhang Y Y, Pan X Y. Improving the Horton infiltration equation by considering soil moisture variation[J]. Journal of Hydrology, 2020, 586:124864. DOI:10.1016/j.jhydrol.2020.124864

DOI

[29]
史振宁, 戚双星, 付宏渊, 等. 降雨入渗条件下土质边坡含水率分布与浅层稳定性研究[J]. 岩土力学, 2020, 41(3):980-988.

[ Shi Z N, Qi S X, Fu H Y, et al. A study of water content distribution and shallow stability of earth slopes subject to rainfall infiltration[J]. Rock and Soil Mechanics, 2020, 41(3):980-988.] DOI:10.16285/j.rsm.2019.0474

DOI

[30]
范严伟, 赵文举, 毕贵权. Van Genuchten模型参数变化对土壤入渗特性的影响分析[J]. 中国农村水利水电, 2016(3):52-56.

[ Fan Y W, Zhao W J, Bi G Q. The influence analysis of parameters variations in van genuchten model on the soil infiltration characteristics[J]. China Rural Water and Hydropower, 2016(3):52-56. ] DOI:10.3969/j.issn.1007-2284.2016.03.013

DOI

[31]
杨坪坪, 王云琦, 张会兰, 等. 降雨强度和单宽流量与地表粗糙度交互作用下坡面流阻力特征[J]. 农业工程学报, 2018, 34(6):145-151.

[ Yang P P, Wang Y Q, Zhang H L, et al. Characteristics of overland flow resistance under interaction of rainfall intensity and unit discharge and surface roughness[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(6):145-151. ] DOI:10.11975/j.issn.1002-6819.2018.06.018

DOI

[32]
张宽地, 王光谦, 孙晓敏, 等. 模拟植被覆盖条件下坡面流水动力学特性[J]. 水科学进展, 2014, 25(6):825-834.

[ Zhang K D, Wang G Q, Sun X M, et al. Hydraulic characteristic of overland flow under different vegetation coverage[J]. Advances in Water Science, 2014, 25(6):825-834. ] DOI:10.14042/j.cnki.32.1309.2014.06.009

DOI

[33]
程娅姗, 王中根, 李军, 等. 确定坡面径流过程曼宁糙率系数的实验方法研究[J]. 地理科学进展, 2020, 39(4):651-659.

DOI

[ Cheng Y S, Wang Z G, Li J, et al. Experimental study on determining Manning roughness coefficient during slope runoff process[J]. Progress in Geography, 2020, 39(4):651-659. ] DOI:10.18306/dlkxjz.2020.04.012

DOI

Options
文章导航

/

〈 〉