EN中文

地球信息科学学报 >

2022 , Vol. 24 >Issue 11: 2198 - 2211

DOI: https://doi.org/10.12082/dqxxkx.2022.220050

遥感科学与应用技术

面实体匹配的集成学习CatBoost方法

  • 刘贺 , 1, 2 ,
  • 郭黎 , 2, * ,
  • 李豪 3 ,
  • 张婉晨 2 ,
  • 白翔天 2
展开
  • 1.61363部队，西安 710054
  • 2.信息工程大学， 郑州 450001
  • 3.32021部队， 北京 100094
*郭 黎（1975— ），女，河南滑县人，博士，副教授，主要从事空间数据集成与融合研究。E-mail:

刘 贺（1996— ），男，河南叶县人，硕士生，主要研究方向为空间相似性与空间关联。E-mail:

收稿日期: 2022-01-26

  修回日期: 2022-02-23

  网络出版日期: 2023-01-25

基金资助

科技基础资源调查专项(2019FY202501)

河南省高等教育教学改革研究与实践重点项目(2021SJGLX299)

收起

Matching Areal Entities with CatBoost Ensemble Method

  • LIU He , 1, 2 ,
  • GUO Li , 2 ,
  • LI Hao 3 ,
  • ZHANG Wanchen 2 ,
  • BAI Xiangtian 2
Expand
  • 1. 61363 Troops, Xi'an 710054, China
  • 2. Information Engineering University, Zhengzhou 450001, China
  • 3. 32021 Troops, Beijing 100094, China
*GUO Li, E-mail:

Received date: 2022-01-26

  Revised date: 2022-02-23

  Online published: 2023-01-25

Supported by

Science and Technology Fundamental Resources Investigation Program of China(2019FY202501)

The Teaching Research and Practice Projects of Higher Education in Henan Province(2021SJGLX299)

Fold

摘要

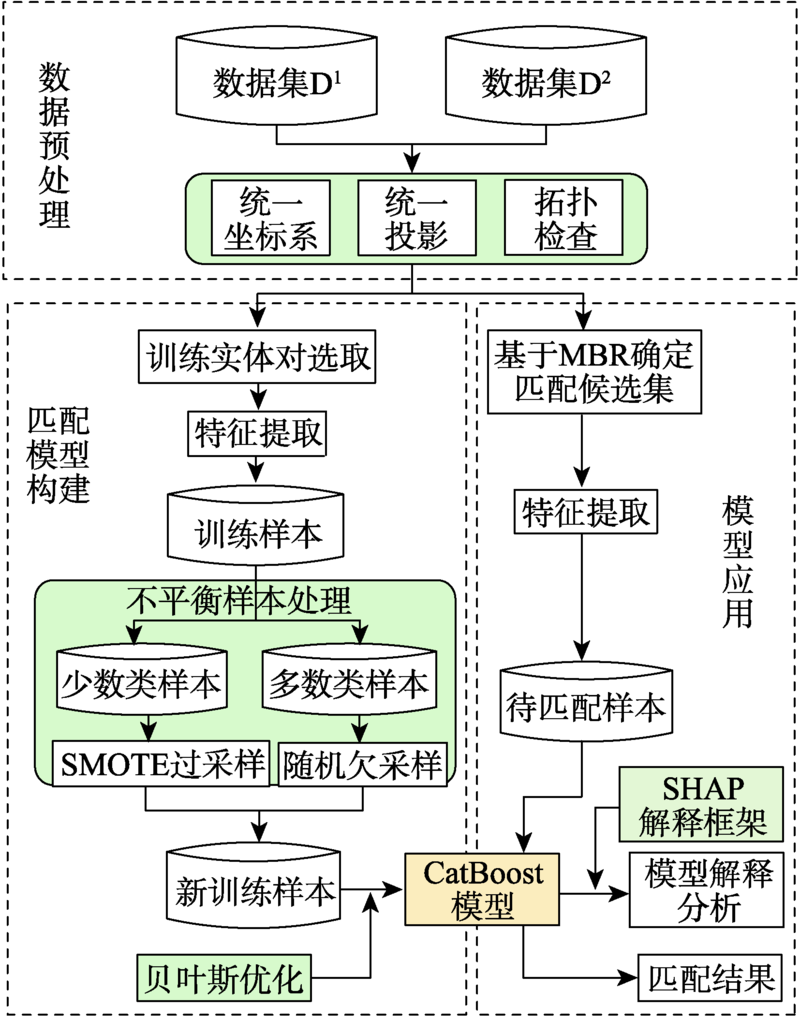
现有的面实体多指标几何匹配方法在计算综合相似度和确定最终匹配实体时面临着指标权重和阈值难以科学量化的难题，集成学习算法通过构建并结合多个机器学习器来完成学习任务，在解决分类问题时体现出了较为明显的性能优势。为此，本文提出了一种基于集成学习算法CatBoost的面实体匹配方法，将匹配问题转化为分类问题。选取形状、面积、方向和位置4个几何特征作为模型分类特征；利用过采样与欠采样相结合的混合重采样技术减轻原始训练样本的类别不平衡度；借助贝叶斯优化算法确定CatBoost模型的最优超参数；引入可解释人工智能领域的SHAP解释框架从全局和局部两个角度解释各输入特征对匹配结果的影响。在青藏高原的面状湖泊数据上对本文提出的方法进行了验证，实验结果表明：对模型预测影响最大的特征是位置，然后依次是面积、形状，影响最小的特征是方向。CatBoost匹配方法在实验数据集上的查准率、查全率和F1-score分别达到0.9937、0.9753和0.9844，相比于直接使用样本不均衡的原始样本进行模型训练，分别提高了约5.8%、0.6%和3.3%。与传统的面实体多指标双向匹配方法和逻辑回归、K近邻、决策树、神经网络等常规机器学习分类算法相比，集成学习算法CatBoost性能表现更加优异，在避免指标权重和阈值设置难题的同时取得了较好的匹配结果。

关键词： 面实体; 相似性; 匹配; 集成学习; CatBoost; 类别不平衡; 贝叶斯优化; SHAP

本文引用格式

刘贺 , 郭黎 , 李豪 , 张婉晨 , 白翔天 . 面实体匹配的集成学习CatBoost方法[J]. 地球信息科学学报, 2022 , 24(11) : 2198 -2211 . DOI: 10.12082/dqxxkx.2022.220050

Abstract

The existing multi-index geometric matching methods for areal entities face the difficulty in scientific quantification of index weights and thresholds when calculating the comprehensive similarity and determining the final matching entity. The ensemble methods in machine learning train multiple base models as ensemble members and combine their predictions into the final output, which have shown excellent performance in solving classification problems. For this purpose, an areal entities matching method based on the CatBoost is proposed in this paper, and this method transforms the matching problem into a classification problem. Firstly, we select four geometric features including shape, area, direction, and position as model classification features. Secondly, to reduce the impact of sample imbalance on model training, we use hybrid resampling combining oversampling and undersampling to alleviate the class imbalance of the original training samples. The Bayesian optimization is used to determine the optimal hyperparameters of the CatBoost model. To improve transparency of ensemble learning models, the SHAP framework in the field of explainable artificial intelligence is introduced to explain the influence of each input feature on the prediction results from both global and local perspectives. Finally, we take the areal lake data of the Qinghai-Tibet Plateau as experimental data to assess the performance of the proposed method. The results demonstrate that the feature with the greatest influence on model prediction is position, followed by area and shape, and the feature with the least influence is direction. The Precision, Recall, and F1-score of this method on the experimental data are 0.9937, 0.9753, and 0.9844, respectively. Hybrid resampling can effectively reduce the impact of unbalanced samples on model training. Compared with the original unbalanced samples for model training, hybrid resampling increases the Precision, Recall, and F1-score by 5.8%, 0.6%, and 3.3%, respectively. Compared with traditional areal entities multi-index bidirectional matching method and conventional machine learning classification algorithms such as logistic regression, K-nearest neighbors, decision trees, and neural networks, the CatBoost performs better and achieves better matching results while avoiding the difficulty of index weights and thresholds setting.

Key words： areal entities; similarity; matching; ensemble methods; CatBoost; class imbalance; Bayesian Optimization; SHAP

1 引言

随着“高分专项”的稳步实施，我国已初步建成了从地面到太空的综合对地观测系统，极大提高了我们快速获取全天候、全天时和全球覆盖地理空间数据的能力[1-2]，为推动生态建设、资源环境保护、防灾减灾等一系列重大社会发展问题的解决，建设现代化经济体系，推进国家治理体系和治理能力现代化提供了有力的数据保障[3]。矢量空间数据作为一种重要的地理空间数据类型，其规模也在不断扩大，但不同生产方式、不同现势性的多源矢量空间数据间存在着诸多的不一致性，给数据的互联互通互操作带来较大困难[4]。对多源异构矢量空间数据进行集成和融合是解决数据不一致性的重要手段。同名实体匹配作为多源异构矢量空间数据集成融合的关键技术，旨在识别出不同数据集中的同一实体，在空间数据库更新、空间查询和变化检测等方面具有重要的应用价值[5]。
面实体在矢量空间数据中占有较大比重，是空间信息表达的重要载体之一。考虑到匹配指标类型的差异，面实体匹配方法主要分为几何匹配、拓扑匹配和语义匹配[6]。拓扑匹配对拓扑关系的差别较为敏感，易导致匹配失败。语义匹配严重依赖于空间数据属性信息完整程度，因而也只能作为辅助匹配方法。几何匹配通过比较实体间几何特征相似度来识别同名实体，是最常用的面实体匹配算法。郭黎等[7]提出了一种基于空间方向相似性的面目标匹配方法，刘凌佳[8]利用面积重叠度作为评估指标实现了多尺度面实体匹配。然而基于单指标的几何匹配结果在可靠性方面往往不能满足实际需求，于是人们更多的考虑综合利用多个相似度指标进行面实体匹配。郝燕玲等[9]提出了一种基于位置、形状和面积指标来计算实体总相似度的算法。汪汇兵等[10]提出了一种多算子加权匹配方法，通过计算质心距离、Hausdorff距离、面积重叠度、对称差、轮廓紧致度和正切空间的加权相似度用于面实体几何匹配。郭敏等[11]在面积、位置和几何形状3个指标的基础上，利用层次分析法完成了面实体匹配。黄宝群等[12]综合利用边界点间的位置、转角和关联边加权相似度，提出了一种基于同名面实体边界点的面实体匹配方法。刘立恒等[13]从构成的面实体的边和角出发，提取出位移、拉伸、旋转和概括程度4个匹配因子，提出了一种多尺度下的面实体匹配方法。姜晶莉等[4]基于2个面实体中心点间的欧式距离和重叠面积2个度量指标实现了同名实体匹配。然而不管是基于单个还是多个几何特征，匹配过程中的阈值或指标权重设置始终是一个难题，目前还没有一个较为成熟的解决方法。作为人工智能的核心，机器学习模型可以通过自主学习样例数据对分类决策过程进行模拟，这也为回避匹配过程中面临的阈值和指标权重设置难题提供了可能。许俊奎等[14]将人工神经网络技术引入居民地匹配实验中，通过人机结合的策略训练神经网络模型完成匹配。Wang等[15]在解决数据集更新问题时提出了一种基于BP神经网络的多特征匹配方法。针对多尺度匹配中同名面实体位置偏移过大引起的无法直接利用重叠面积获得候选匹配的问题，刘凌佳等[16]提出了一种结合MBR组合优化算法与人工神经网络的MBRCO-ANN匹配方法。集成学习是一种基于群体智慧原则的机器学习方法，通过构建及结合多个学习器完成学习任务[17]，常可获取比单一学习器如BP神经网络、决策树等更强的泛化性能，因而被广泛应用于解决分类问题[18⇓-20]。但目前利用集成学习方法进行面实体匹配的研究相对较少。
综上，提出一种基于集成学习算法CatBoost的面实体匹配方法，将面实体匹配问题转化为分类问题，CatBoost分类器根据形状、面积、方向和位置四个几何相似度指标把待匹配实体对分为“匹配”与“不匹配”两类，有效规避了常规匹配方法中阈值和权重设置难题，同时针对集成学习算法存在结构复杂、可解释性差的问题，引入Shapley加法解释（Shapley Additive exPlanation，SHAP）框架[21]量化各个输入特征对模型分类结果的影响，提高CatBoost机器学习黑盒模型的透明度。

2 研究方法

2.1 本文技术路线

基于集成学习算法CatBoost的面实体匹配方法的技术路线如图1所示，主要包括3个部分：① 数据预处理：对待匹配数据集进行地理坐标系、投影坐标系的统一和拓扑检查。② 匹配模型构建：选取训练实体对并计算指标相似度进而生成训练样本,对类别不平衡的训练样本进行混合重采样处理，利用贝叶斯优化方法调整CatBoost模型超参数，在此基础上完成模型训练。③ 模型应用：基于最小外接矩形MBR构建候选匹配集，使用训练好的CatBoost模型完成面实体匹配，利用SHAP解释框架对CatBoost模型进行解释分析。
图1 本文技术路线

Fig. 1 Technology roadmap of our method

2.2 匹配模型构建

2.2.1 集成学习CatBoost算法原理

CatBoost是一种基于梯度提升决策树( Gradient Boosting Decision Tree, GBDT)的改进算法，GBDT将CART回归决策树作为基学习器，通过Boosting方法串行地训练一系列学习器，把所有学习器的输出进行累加作为最终的结果[22-23]。对于给定的具有n个样本的训练集 D = ( x k , y k ) k = 1,2 , … , n，其中 x k = ( x k 1 , x k 2 , . . . , x k m )是一个m维输入特征， y k是对应的一个数值型标签。若经过上一步训练生成的强学习器为 F t - 1，则本轮的训练目标就是从CART树集合H中得到一颗树 h t，使得损失函数 L ∙的期望 E ∙最小化，即
${{h}_{t}}=a\text{rgminE}L\left( y,{{F}_{t-1}}\left( x \right)+{{h}_{t}}\left( x \right) \right)$
式中： ( x , y )是独立于训练集外的一个测试样本；GBDT使用损失函数的负梯度拟合出本轮训练的CART决策树 h t，经过T轮迭代得到如式（2）所示的最终模型 F。
$F={{F}_{0}}+\underset{t=1}{\overset{T}{\mathop \sum }}\,{{a}_{t}}{{h}_{t}}$
式中： F 0表示初始弱学习器； a t表示第t轮训练步长。
CatBoost在传统的GBDT基础上作出了改进。① CatBoost引入了有序提升（Ordered boosting）技术[24]来解决GBDT存在的预测偏移现象（prediction shift）[25]。② CatBoost借鉴在线学习思想引入有序目标统计量（Ordered Target Statistics，Ordered TS）方法[23]直接将类别型特征转换为数值型统计量，增加了对类别型特征的直接支持。③ CatBoost选用对称二叉树作为基学习器，在每一层上执行相同的分裂标准，因而不容易发生过拟合，模型的稳定性和预测速度也有明显的提高。

2.2.2 特征提取

参考文献[26]和文献[27]，本文从形状、面积、延展方向和空间位置4个方面出发，提取匹配模型所需的相似度指标。
（1）形状相似度
Xu等[28]提出了一种叶片识别方法，本文以此为基础提出了一种形状多尺度角度描述方法用于面实体形状相似度计算，其主要思想如图2所示：首先对面实体的外部轮廓进行等距离采样得到N个采样点并满足 N = 2 T（T为正整数，一般取8），图2（a）表示的是一个经重采样后的面实体轮廓，共包含256个采样点。以任一采样点 P i（蓝色五角星表示）的一侧为例，以 P i为起点将整个轮廓三等分，得到第一个等分点 S 6；然后将子轮廓段 P i S 6 ̑进行二等分得到第二个等分点 S 5；将 P i S 5 ̑二等分得到第三个等分点 S 4，以此类推，经1次三等分和5次二等分，可得到 S 6至 S 1共计6个等分点，分别使用红色的圆形、星形、菱形、十字形、三角形和正方形做突出显示，这里将 P i与各个等分点的距离称为尺度。等分点由远及近分布在 P i两侧，与 P i一起实现了对轮廓的多尺度划分。如图2（b）所示，取 P i在不同尺度下对应的角度值 θ作为几何特征。
图2 形状多尺度角度描述构建原理

Fig. 2 Construction principle of shape multiscale angle description

通过为每个轮廓点计算6个尺度下的几何特征，得到形状描述矩阵 Θ N × 6，其中每列对应一个尺度。为消除起始点 P i位置对矩阵 Θ的影响，对每个尺度进行离散傅里叶变换，保留前M项傅里叶低频系数并使用首项低频系数的模进行归一化，得到满足旋转、平移、缩放不变性的形状描述矩阵 Z M × 6。面实体A和B的形状差异度 d i s s h a p e A , B可以通过式（3）改进曼哈顿距离计算，其中 z i j A和 z i j B分别代表两个面实体的归一化形状描述矩阵 Z A和 Z B中的元素。
$di{{s}_{\text{shape}}}\left( A,B \right)=\underset{i=1}{\overset{M}{\mathop \sum }}\,\underset{j=1}{\overset{6}{\mathop \sum }}\,\left| z_{ij}^{A}-z_{ij}^{B} \right|/\left( \left( M-1 \right)\times 6 \right)$
形状相似度通过式（4）计算得到，即
$si{{m}_{\text{shape}}}=1-di{{s}_{\text{shape}}}\left( A,B \right)$
实际应用中轮廓重采样数量N一般取256，傅里叶低频系数项数量M取7即可满足需求，后文3.6节会对如何确定M的取值进行分析。
（2）面积相似度
面积作为判断2个面实体相似程度的指标之一，实体间差异度越小，其面积越接近。设面实体A与B的面积分别表示用 S A与 S B表示，则2个面实体的面积相似度计算方法为：
$si{{m}_{\text{area}}}=m\text{in}\left( {{S}_{A}},{{S}_{B}} \right)/\text{ma}x\left( {{S}_{A}},{{S}_{B}} \right)$
（3）方向相似度
方向相似度用两个面实体主轴轴向的相似程度来表示。首先计算实体的主轴方向角，本文将面实体最小面积外接矩形的长轴设为主轴，主轴与水平方向的夹角即主轴方向角。设 θ A与 θ B分别表示面实体A与B的主轴方向角，且有 θ A ∈ 0 , π， θ B ∈ 0 , π，则方向相似度 s i m d i r e c的计算方法为：
$si{{m}_{\text{direc}}}=1-\frac{\left| {{\theta }_{A}}-{{\theta }_{B}} \right|}{\pi}$
（4）位置相似度
位置的相似程度通过两个面实体质心的欧式距离来计算，用 c e n t r o i d ( A , B )表示面实体A与B的质心距离， d i s t m a x A , B表示面实体A与B任意边界点间距离的最大值。则位置相似度计算方法为：
$si{{m}_{\text{posi}}}=1-\frac{centroid\left( A,B \right)}{dis{{t}_{\text{max}}}\left( A,B \right)}$

2.2.3 不平衡样本处理

设2个数据集 D 1、 D 2分别包含m和n个面实体。若不考虑生成候选匹配集， D 1中一个面实体要与 D 2中每个实体进行遍历匹配，理想情况下 D 2中有一个实体与之相匹配，因此不匹配与匹配2种结果的类别不平衡度为n-1:1。根据概率近似正确学习理论（Probably Approximately Correct, PAC）[29]可知，机器学习模型训练需要较多的样本，才能保证其具有较好的泛化能力。实际情况中受待匹配数据集规模限制，在保证训练样本总量的前提下，会导致选取的训练样本中不匹配样本与匹配样本的数量相差较大出现类别不平衡现象。不平衡的训练样本往往会导致分类模型过分关注多数类别而忽视少数类别，进而影响模型的泛化能力[30]。
SMOTE过采样（Synthetic Minority Over-sampling Technique）[31]通过在2个少数类样本之间进行随机线性内插来产生新的样本。如图3所示，首先为少数类样本 x i产生k个最邻近少数类样本，从中挑选出任一样本 x j，新的样本 x n e w通过式（8）产生，其中 σ是(0,1)之间的随机数。
图3 SMOTE原理示意

Fig. 3 Schematic diagram of SMOTE

${{x}_{\text{new}}}={{x}_{i}}+\sigma \cdot \left( {{x}_{i}}-{{x}_{j}} \right)$
随机欠采样[32]通过随机删除多数类样本来平衡类别分布，直至达到多数类样本和少数类样本之间所需的类别比。
本文采用欠采样和过采样相结合的混合重采样方法[31]对存在类别不平衡的训练样本进行处理。对少数类（匹配）样本进行SMOTE过采样，之后再对多数类（不匹配）样本进行随机欠采样处理，减小原始训练样本的类别不平衡度，以期在待匹配数据集规模较小的情况下保证模型性能。

2.2.4 贝叶斯优化

超参数优化是机器学习任务的一个重要步骤，CatBoost模型结构复杂，超参数搜索空间规模较大，采用手动调参方法、网格搜索方法和随机搜索方法效率较低。本文选择贝叶斯优化方法用于CatBoost超参数优化。贝叶斯优化方法以贝叶斯定理为基础，利用上一步搜索结果的先验信息确定下一步搜索点[33]，因而优化效率更高。贝叶斯优化首先使用高斯过程（Gaussian Processes, GP）作为代理模型用来近似逼近结构未知的模型评估函数，然后通过采样函数从搜索空间中确定下一个最有可能取得极值的采样点，并根据采样点信息更新代理模型。经过不断的迭代更新，最终从搜索空间中得到一组满足全局最优的超参数。

2.3 模型应用

2.3.1 SHAP解释框架

可解释人工智能（Explainable Artificial Intelligence，XAI）[34]旨在帮助人们理解模型如何在预测过程中进行决策，提升模型的透明度，为特征选择和模型优化等提供指导。本文选用Shapley加法解释（Shapley Additive exPlanation，SHAP）[21]框架来对CatBoost匹配模型进行解释。SHAP是一个事后解释框架，借鉴了合作博弈论的思想，将机器学习模型预测值解释为每个输入特征的贡献之和，SHAP通过一个简单的加法模型 g来拟合和解释某预测模型 f，即：
$f\left( x \right)=g\left( {{x}'} \right)={{\phi }_{0}}+\underset{i=1}{\overset{p}{\mathop \sum }}\,{{\phi }_{i}}{{{x}'}_{i}}$
式中：p为特征向量x中特征的数量； x ' i是第i个特征 x i的映射，当特征 x i存在时 x ' i取1，当特征 x i缺失时 x ' i取0。 ϕ i指特征 x i的SHAP值，表示对模型预测值的平均边际贡献； ϕ 0表示所有的输入值都缺失时模型输出的基准值；SHAP值的绝对值越大，表示该特征对模型预测值的影响越大，其正负则代表影响的方向。
SHAP借助每个特征所有SHAP值的绝对值的平均值来衡量每个特征的重要度，通过式（10）计算。
${{I}_{j}}=\frac{\mathop{\sum }_{n=1}^{N}\left| \phi _{j}^{\left( n \right)} \right|}{N}$
式中： I j表示第 j个特征的重要度； N代表样本数； ϕ j n代表第n个样本中第 j个特征对应的SHAP值绝对值。

2.3.2 性能评价指标

将匹配实体对的标签值设为1，不匹配实体对的标签值设为0，采用查准率（Precision）、查全率（Recall）和F1-score作为模型性能评价指标，各指标的计算方法如式（11）—式（13）所示。
$Precision=\frac{TP}{TP+FP}$
$Recall=\frac{TP}{TP+FN}$
$F1-score=\frac{2Precision\times Recall}{Precision+Recall}$
式中：TP和TN表示正确分类的匹配样本和不匹配样本数量；FP和FN表示错误分类的匹配样本和不匹配样本数量。

3 实验与结果分析

3.1 实验数据来源与处理

本文的实验数据分别来自于青藏高原湖泊数据集[35]和OSM数据，分别包含230个和992个面实体，青藏高原湖泊数据集由国家青藏高原科学数据中心提供，根据卫星影像矢量化生产得来。图4中蓝色填充实体表示OSM数据，红色实线包围的实体来自青藏高原湖泊数据集。
图4 实验区域

Fig. 4 Experimental area

基于Python 3.7完成本文实验，首先对两组数据进行预处理，接下来从2个数据集中随机选取50对匹配实体和500对不匹配实体作为原始训练样本，训练样本仅用于模型训练，不与后续的待匹配样本重叠，部分训练样本如图5所示。图5（a）中是一对一的匹配样本，图5（b）是一对二的匹配样本，图5（c）和图5（d）都是不匹配样本。根据定义计算各个几何特征的相似度（表1）。原始训练样本的类别不平衡度达到10，经采用混合重采样技术对原始训练样本进行处理后，样本中匹配实体和不匹配实体的数量分别为200对和400对，类别不平衡度明显减小。将处理后的训练样本划分为两部分：其中80%的样本作为训练集，剩余的20%作为测试集。
图5 部分训练样本示例

Fig. 5 Example of partial training samples

表1 图5中训练样本相似度与标签值

Tab. 1 The similarity and label value of training samples in Fig. 5

序号 方向 面积 位置 形状 标签值
a1-b1 0.9959 0.9526 0.9930 0.9083 1
a2-b2 0.9578 0.5363 0.8441 0.7988 1
a2-b3 0.8887 0.3313 0.6499 0.7934 1
a3-b4 0.8014 0.0603 0.2039 0.8093 0
a4-b5 0.9252 0.0062 0.5855 0.8070 0

3.2 模型训练

CatBoost模型具有众多超参数，在实际操作中对所有超参数同时进行优化难度极大，为此选取对模型性能影响较大的6个超参数生成搜索空间，选取AUC值即ROC曲线下面积作为模型评估函数，基于分层10折交叉验证实现搜索空间内各超参数的贝叶斯优化，最终的优化结果如表2所示。
表2 待优化参数搜索空间及优化结果

Tab. 2 Search space of parameters to be optimized and optimization results

序号 名称 含义 搜索范围 贝叶斯优化结果
参数1 iterations 最大树数 (10, 1000) 420
参数2 depth 树的深度 (1, 10) 4
参数3 learning_rate 学习率 （0.01,1.0） 0.016
参数4 bagging_temperature 贝叶斯套袋控制强度 (0.0, 1.0) 0.617
参数5 l2_leaf_reg L2正则参数 (2, 30) 17
参数6 scale_pos_weight 类别调整权重 （0.01, 1.0） 0.874
在超参数优化结果的基础上绘制模型的学习曲线（图6），可以看出随着模型训练样本的增加，训练集分数和验证集分数逐渐收敛。将训练完毕的模型在测试集上进行测试，图7的混淆矩阵表明模型取得了较好的测试结果，拟合效果良好，具有较强的学习能力和优异的泛化能力。
图6 模型学习曲线

Fig. 6 Model learning curve

图7 测试集混淆矩阵

注：图中数字表示测试集数量/个。

Fig. 7 Confusion matrix of test set

3.3 模型解释

CatBoost是一个树集成模型，因此本文选用SHAP中的树模型解释器TreeExplainer[36]来对CatBoost匹配模型进行全局和局部解释，以分析模型如何做出预测。

3.3.1 全局解释

首先利用SHAP摘要图（SHAP Summary Plots）从全局角度解释各个输入特征如何影响模型预测。图8中纵轴方向的每一行代表一个特征，按特征重要度从上到下进行降序排列，横轴表示SHAP值，图中每个点都代表一个样本的一个特征，颜色越红表示该点的特征值越大，当点重合时将在垂直方向上进行堆叠。图8显示对模型预测影响最大的特征是位置，然后依次是面积、形状，影响最小的特征是方向。
图8 SHAP摘要图

Fig. 8 SHAP Summary Plot

根据式（10）将图8中的特征重要度进行量化，图9中量化后的特征重要度排序的顺序和图8相一致。排在首位的的特征是位置，其重要度是面积的约1.65倍、形状的约3.63倍、方向的约4.06倍。形状和方向两个特征的重要度分别位列第三和第四位，对模型预测值的影响程度比较接近。
图9 基于SHAP平均绝对值的特征重要度排序

Fig. 9 Feature importance ranking based on mean absolute SHAP value

此外从SHAP摘要图中还可以看出特征值的大小与其对模型预测的贡献可能存在相关关系，例如对于位置特征，从点的颜色分布可以看出特征值越小其对应的SHAP值越小，特征值越大其对应的SHAP值越大。接下来借助SHAP依赖图（SHAP dependence plot）将各个特征与其对应的SHAP值之间存在的关系进行更详细的分析，SHAP依赖图的纵轴代表SHAP值，横轴代表特征值大小。
从图10可以看出，当方向相似度处于0.1~0.9左右的区间时，SHAP值小于0，对模型预测值呈负向贡献，当相似度大于0.8时，相似度值与SHAP值呈正相关；当面积相似度小于0.1时，对模型预测值主要呈负向贡献，当相似度值大于0.1时，对模型预测值呈正向贡献，在相似度值小于0.3时，相似度值与SHAP值之间的正相关关系较强，相似度值大于0.3后SHAP值的单调性不明显；位置相似度与SHAP值之间呈正相关，整体上来讲SHAP值单调递增，当位置相似度小于0.5时，对模型预测值呈负向贡献，当位置相似度大于0.5时，对模型预测值呈正向贡献；当形状相似度小于约0.84时，对模型预测值的贡献是负向的，当相似度大于约0.84时，对模型预测值的贡献是正向的，在相似度值达到约0.9以后，SHAP值不再继续增长，保持相对稳定。
图10 SHAP特征依赖图

Fig. 10 SHAP dependence plot

3.3.2 局部解释

接下来从单个样本的角度来解释CatBoost模型如何做出预测，挑选一个正例样本和一个负例样本，分别对应“匹配”和“不匹配”2种情况。 图11解释了负例样本的预测过程，图11中f（x）代表模型输出的SHAP值，base value表示基准值，该数值由模型本身决定。红色代表该特征值将会推高样本被预测为正例样本的概率，蓝色代表该特征值将会降低样本被预测为正例样本的概率，图11中方向相似度的值为0.943，对模型预测值起到了正向作用，但其正向推动作用远小于其余3个特征对模型产生的负向抑制作用总和，最终输出的SHAP值为-8.86，小于基准值-4.076，该样本被预测为负例样本，即“不匹配”。图12中，4个特征均对模型预测产生正向推动作用，最终输出的SHAP值为8.80，远大于基准值-4.076，该样本被预测为正例样本，即“匹配”。
图11 负例样本的预测解释

Fig. 11 Predictive interpretation of negative samples

图12 正例样本的预测解释

Fig. 12 Predictive interpretation of positive samples

3.4 匹配结果与分析

将训练好的CatBoost模型用于匹配实验，最终输出匹配实体159对，其中正确匹配实体158对，误匹配实体1对，另外还有4对实体漏匹配，计算得到查准率为0.9937，查全率为0.9753，F1-score为0.9844。部分输出样例如图13所示，从中可以看出，A1与B1、B2之间是一对二的匹配情形；A2与B3、B4之间应是一对二的匹配情形，但输出结果中A2与B3两个实体出现漏匹配；A3与B5、B6、B7之间应是一对三的匹配情形，但输出的结果只有A3与B5、B6匹配，A3与B7之间出现了漏匹配；A4与B8不存在匹配关系，但匹配模型错误地将二者识别为一对匹配实体。
图13 部分匹配结果示例

Fig. 13 Example of partial matching results

分析可知，出现漏匹配的原因是图形大小和形状相差过大，计算得到的相似度值较小，从而影响模型判断。而出现误匹配的原因则是由于2个距离较近的面实体在主轴方向或大小上也较为接近，由此导致模型在进行分类时出现错误。

3.5 算法对比

多指标融合的双向匹配是常用的面实体匹配方法，以本文提出的相似度指标为基础，采用双向匹配方法作为对比。表3展示了5组双向匹配实验，其中双向匹配1实验的参数设置方法参考文献[9]，不设置总相似度阈值。双向匹配2实验至双向匹配5实验的权重设置方法参考文献[27]，总体相似度阈值设置参考文献并无说明。
表3 双向匹配方法参数

Tab. 3 Bidirectional matching method parameters

匹配方法 形状相
似度		 面积相
似度		 方向相
似度		 位置相
似度		 总相似
度阈值
双向匹配1 0.25 0.25 0.25 0.25 —
双向匹配2 0.44 0.11 0.23 0.24 0.8
双向匹配3 0.44 0.11 0.23 0.24 0.7
双向匹配4 0.44 0.11 0.23 0.24 0.6
双向匹配5 0.44 0.11 0.23 0.24 0.5
本文对总体相似度阈值设置进行了进一步的实验和分析，分析发现，较高的阈值易导致漏匹配，较低的阈值易导致误匹配，根据实验我们分别设置了0.8、0.7、0.6和0.5的总相似度阈值，得到的参数值如表3所示。
此外还分别采用逻辑回归[37]、K近邻[38]、CART决策树[39]、BP神经网络[14]和随机森林[40]5种常用的机器学习分类算法与本文CatBoost算法作为对比，其中BP神经网络也是文献[14]进行面实体匹配时所用的方法。由于高性能的匹配模型需要一个较为优异的决策边界，匹配过程中创建匹配候选集在减少计算负荷的同时，也引起了一个问题：模型的最终预测结果是直接由模型的决策边界得出，还是又受到了候选集的影响?于是我们又在对比实验中移除了创建匹配候选集的步骤。
对比实验结果如表4所示。由于双向匹配1实验并未设置总相似度阈值，而是在匹配过程中取相似度最大的一对面实体作为匹配实体，虽然识别出全部的162对匹配面实体，但出现了8对误匹配面实体。双向匹配2实验共输出146对面实体，其中正确匹配面实体为145对，误匹配面实体仅为1对，但有17对面实体出现了漏匹配。
表4 各模型匹配实验结果评价指标对比

Tab. 4 Comparison of evaluation indicators for the matching results of various models

候选集
操作		 匹配方法 输出结
果数量/对		 正确匹
配数量/对		 误匹配
数量/对		 漏匹配
数量/对		 Precision Recall F1-score
创建候
选集		 双向匹配1 170 162 8 0 0.9529 1.0000 0.9759
双向匹配2 146 145 1 17 0.9931 0.8951 0.9416
双向匹配3 160 157 3 5 0.9812 0.9691 0.9752
双向匹配4 168 162 6 0 0.9643 1.0000 0.9818
双向匹配5 169 162 7 0 0.9586 1.0000 0.9788
CatBoost 159 158 1 4 0.9937 0.9753 0.9844
不创建
候选集		 逻辑回归 212 154 58 8 0.7264 0.9506 0.8235
BP神经网络 179 157 22 5 0.8771 0.9691 0.9208
K近邻 163 151 12 11 0.9264 0.9321 0.9292
CART决策树 169 157 12 5 0.9289 0.9691 0.9486
随机森林 165 157 8 5 0.9515 0.9691 0.9602
CatBoost 161 158 3 4 0.9814 0.9753 0.9783
CatBoost* 170 157 13 5 0.9235 0.9691 0.9457

注：*训练样本不经过混合采样处理。

随着总相似度阈值的减小，误匹配面实体的数量逐渐增加，漏匹配面实体的数量逐渐减少。当阈值减小至0.5时，共输出169对面实体，无漏匹配面实体，但出现了7对误匹配面实体，可见阈值的大小对匹配结果有较大的影响。本文方法共输出159对面实体，其中误匹配数量为1对，漏匹配数量为4对，从F1-score看出，相较于双向匹配方法，本文方法的综合性能也较出色。
在不创建候选集的情况下，基于CatBoost的匹配方法共输出161个实体对，其中正确匹配实体158对，误匹配实体3对，漏匹配实体4对，证明CatBoost在不依赖候选集约束的情况下，仅依靠自身的决策边界仍能在匹配过程中取得较好的表现。作为对比的其他机器学习算法的召回率都在0.90以上，逻辑回归算法的表现较差，其查准率和F1-score在所有算法中最低。
集成学习算法的表现优于常规分类算法，在2种集成学习算法中，基于boosting的CatBoost算法的查准率、查全率和F1-score分别为0.9814、0.9753和0.9783，比基于bagging的随机森林表现更好。对比实验又验证了训练样本混合重采样处理的有效性，相比于直接使用类别不平衡样本进行模型训练，重采样处理使得模型在查准率、查全率和F1-score上分别提高了5.8%、0.6%和3.3%。从结果可以看出，本文所提方法在匹配过程中表现出了优异的性能。

3.6 傅里叶系数数量的确定

在进行形状相似度计算时，为减少傅里叶高频系数带来的噪声影响及减少计算量，一般只前M项低频系数。通过形状匹配实验来确定需保留的傅里叶系数数量。
从青藏高原OSM湖泊数据集中选取357个湖泊，首先使用道格拉斯-普克算法对每个面实体的边界进行化简，化简效果如图14所示。然后使用本文方法计算化简前后两个数据集中任意一对面实体的形状相似度，得到一个相似度矩阵，取矩阵每行最大值所对应的一对面实体作为匹配实体。最后，统计匹配正确的实体数量并计算匹配准确率。
图14 不同阈值下的图形化简效果

Fig. 14 Graphical simplification effects under different thresholds

不同化简阈值下匹配准确率与傅里叶系数数量M的关系如图15 所示，可以看出随着M的增大，匹配准确率先迅速增大，之后趋于平稳，因此将最终M的取值确定为7，在不损失算法性能的前提下又可以提高计算效率。
图15 傅里叶系数数量-准确率曲线

Fig. 15 Number of Fourier coefficients-accuracy curves

4 结论与讨论

针对面实体匹配过程中的相似度指标权重和阈值难以确定的问题，提出了一种基于集成学习CatBoost算法的面实体匹配方法，该方法将匹配问题转化为机器学习领域的二分类问题。提出了一种计算形状相似度的多尺度角度方法，将其应用于面实体形状相似度计算，并结合面积、方向和位置构建模型分类特征，利用混合重采样技术减小训练样本类别不平衡对模型训练的影响，采用贝叶斯优化技术对模型超参数进行选取，引入SHAP框架对模型进行解释，主要结论如下：
（1）将面实体匹配问题转换为机器学习领域的分类问题是一个可行的方法，此举能有效避免匹配过程中人为因素带来的不确定性影响。匹配实验中，本文CatBoost方法的查准率、查全率和F1-score分别为0.9937、0.9753和0.9844。在不创建候选集而仅依赖机器学习模型自身决策边界的条件下，相比于常规机器学习方法（逻辑回归、BP神经网络、K近邻和决策树），CatBoost方法在查准率、查全率和F1-score上分别有约5.2%~25.5%、0.6%~4.3%和2.9%~15.4%之间的性能提升，同时以上3个指标也均优于bagging集成类型的随机森林方法。另外对非一对一的匹配类型也能进行有效识别。
（2）在两个待匹配数据集规模较小的情况下，训练样本混合重采样处理能有效改善原始训练样本类别不平衡度，扩充少数类样本容量，提高模型的分类性能。实验表明，相较于直接使用类别不平衡度较高的训练样本，使用经混合重采样处理的训练样本训练出的CatBoost匹配模型在查准率、查全率和F1-score上分别提高了约5.8%、0.6%和3.3%。
（3）通过SHAP框架对模型的解释可知，位置相似度是本次实验中对模型分类结果影响最大的特征，其次是面积相似度和形状相似度，方向相似度对模型分类结果的影响最小。位置相似度的重要度是面积相似度的约1.65倍、形状相似度的约3.63倍、方向相似度的约4.06倍。位置相似度的值与其对模型分类结果的贡献值之间存在着较为明显的正相关关系。
本文研究仍存在不足，在未来的研究中，将考虑构建更多的几何指标并结合模型解释结果和特征选择方法对模型输入特征进行优化。由于面实体匹配类型较多，将通过实验进一步验证把面实体匹配从二分类问题转化为多分类问题的可行性，此外在训练样本数量和类型方面也有待进一步丰富。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
廖小罕. 中国对地观测20年科技进步和发展[J]. 遥感学报, 2021, 25(1):267-275.

[ Liao X H. Scientific and technological progress and development prospect of the earth observation in China in the past 20 years[J]. National Remote Sensing Bulletin, 2021, 25(1):267-275. ] DOI:10.11834/jrs.20211017

DOI

[2]
赵文波. “中国高分”科技重大专项在对地观测发展历程中的阶段研究[J]. 遥感学报, 2019, 23(6):1036-1045.

[ Zhao W B. Phase research and practice of upgrading earth observation from test application to system effectiveness in China[J]. National Remote Sensing Bulletin, 2019, 23(6):1036-1045. ] DOI:10.11834/jrs.20199162

DOI

[3]
赵文波, 李帅, 李博, 等. 新一代体系效能型对地观测体系发展战略研究[J]. 中国工程科学, 2021, 23(6):128-138.

[ Zhao W B, Li S, Li B et al. Development strategy of the new-generation effectiveness-oriented earth-observation system[J]. Strategic Study of Chinese Academy of Engineering, 2021, 23(6):128-138. ] DOI:10.15302/J-SSCAE-2021.06.020

DOI

[4]
姜晶莉, 郭黎, 李豪, 等. 面向空间关联的多源矢量数据空间实体匹配方法[J]. 测绘科学, 2020, 45(4):183-191.

[ Jiang J L, Guo L, Li H, et al. Spatial entities matching technology of multi-source spatial vector data for spatial association[J]. Science of Surveying and Mapping, 2020, 45(4):183-191. ] DOI:10.16251/j.cnki.1009-2307.2020.04.026

DOI

[5]
马京振. 顾及尺度变化的道路和居民地融合处理理论与方法研究[D]. 郑州: 战略支援部队信息工程大学, 2020.

[ Ma J Z. Research on theory and methodology of road and settlement fusion considering scale variation[D]. Zhengzhou: PLA Strategic Support Force Information Engineering University, 2020. ]

[6]
孙群. 多源矢量空间数据融合处理技术研究进展[J]. 测绘学报, 2017, 46(10):1627-1636.

[ Sun Q. Research on the progress of multi-sources geospatial vector data fusion[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10):1627-1636. ] DOI:10.11947/j.AGCS.2017.20170387

DOI

[7]
郭黎, 崔铁军, 郑海鹰, 等. 基于空间方向相似性的面状矢量空间数据匹配算法[J]. 测绘科学技术学报, 2008, 25(5):380-382.

[ Guo L, Cui T J, Zheng H Y, et al. Arithmetic for area vector spatial data matching on spatial direction similarity[J]. Journal of Geomatics Science and Technology, 2008, 25(5):380-382. ]

[8]
刘凌佳. 多尺度面实体匹配方法及其融合应用研究[D]. 武汉: 武汉大学, 2018.

[ Liu L J. Research on methods and integration applications of polygonal object matching on multi-scale datasets[D]. Wuhan: Wuhan University, 2018. ]

[9]
郝燕玲, 唐文静, 赵玉新, 等. 基于空间相似性的面实体匹配算法研究[J]. 测绘学报, 2008(4):501-506.

[ Hao Y L, Tang W J, Zhao Y X, et al. Areal feature matching algorithm based on spatial similarity[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4):501-506. ] DOI:10.3321/j.issn:1001-1595.2008.04.017

DOI

[10]
汪汇兵, 唐新明, 邱博, 等. 运用多算子加权的面要素几何匹配方法[J]. 武汉大学学报·信息科学版, 2013, 38(10):1243-1247.

[ Wang H B, Tang X M, Qiu B, et al. Geometric matching method of area feature based on multi-weighted operators[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10):1243-1247. ] DOI:CNKI:SUN:WHCH.0.2013-10-025

DOI

[11]
郭敏, 刘闯, 钱海忠, 等. 利用层次分析法匹配面状居民地[J]. 测绘与空间地理信息, 2018, 41(8):130-134.

[ Guo M, Liu C, Qian H Z, et al. A matching method of habitation features based on analytic hierarchy process[J]. Geomatics & Spatial Information Technology, 2018, 41(8):130-134. ] DOI:CNKI:SUN:DBCH.0.2018-08-034

DOI

[12]
黄宝群, 盛业华, 郭宁宁, 等. 同名边界点的面状居民地要素匹配[J]. 测绘科学, 2018, 43(2):108-113.

[ Huang B Q, Sheng Y H, Guo N N, et al. Residential polygon features matching based on identical boundary points[J]. Science of Surveying and Mapping, 2018, 43(2):108-113. ] DOI:10.16251/j.cnki.1009-2307.2018.02.019

DOI

[13]
刘立恒, 钱新林, 张福浩, 等. 同名居民地在多尺度下的匹配分析[J]. 测绘科学, 2019, 44(11):123-128.

[ Liu L H, Qian X L, Zhang F H, et al. Matching analysis of residential areas of the same name at multiple scales[J]. Science of Surveying and Mapping, 2019, 44(11):123-128. ] DOI:10.16251/j.cnki.1009-2307.2019.11.018

DOI

[14]
许俊奎, 武芳, 魏慧峰. 人工神经网络在居民地面状匹配中的应用[J]. 测绘科学技术学报, 2013, 30(3):293-298.

[ Xu J K, Wu F, Wei H F. Areal settlements matching algorithm based on artificial neural network technique[J]. Journal of Geomatics Science and Technology, 2013, 30(3):293-298. ] DOI:10.3969/j.issn.1673-6338.2013.03.017

DOI

[15]
Wang Y X, Chen D, Zhao Z Y, et al. A back-propagation neural network-based approach for multi-represented feature matching in update propagation[J]. Transactions in GIS, 2015, 19(6):964-993. DOI:10.1111/tgis.12138

DOI

[16]
刘凌佳, 朱道也, 朱欣焰, 等. 基于MBR组合优化算法的多尺度面实体匹配方法[J]. 测绘学报, 2018, 47(5):652-662.

[ Liu L J, Zhu D Y, Zhu X Y, et al. A multi-scale polygonal object matching method based on MBR combinatorial optimization algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(5):652-662. ] DOI:10.11947/j.AGCS.2018.20160625

DOI

[17]
Jordan M I, Mitchell T M. Machine learning: Trends, perspectives, and prospects[J]. Science, 2015, 349(6245):255-260. DOI:10.1126/science.aaa8415

DOI

[18]
肖湘文, 沈校熠, 柯长青, 等. 基于Sentinel-1A数据的多种机器学习算法识别冰山的比较[J]. 测绘学报, 2020, 49(4):509-521.

[ Xiao X W, Shen X Y, Ke C Q, et al. Comparison of machine learning algorithms based on Sentinel-1A data to detect icebergs[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(4):509-521. ] DOI:10.11947/j.AGCS.2020.20190174

DOI

[19]
龙玉洁, 李为乐, 黄润秋, 等. 汶川地震震后10 a绵远河流域滑坡遥感自动提取与演化趋势分析[J]. 武汉大学学报·信息科学版, 2020, 45(11):1792-1800.

[ Long Y J, Li W L, Huang R Q, et al. Automatic extraction and evolution trend analysis of landslides in Mianyuan river basin in the 10 years after Wenchuan earthquake[J]. Geomatics and Information Science of Wuhan University, 2020, 45(11):1792-1800. ] DOI:10.13203/j.whugis20200180

DOI

[20]
方秀琴, 郭晓萌, 袁玲, 等. 随机森林算法在全球干旱评估中的应用[J]. 地球信息科学学报, 2021, 23(6):1040-1049.

DOI

[ Fang X Q, Guo X M, Yuan L, et al. Application of random forest algorithm in global drought Assessment[J]. Journal of Geo-information Science, 2021, 23(6):1040-1049.] DOI:10.12082/dqxxkx.2021.200474

DOI

[21]
Lundberg S M, Lee S-I. A unified approach to interpreting model predictions[C]// Proceedings of the 31st International Conference on Neural Information Processing Systems. Curran Associates Inc., California, 2017:4768-4777.

[22]
Friedman J H. Greedy function approximation: a gradient boosting machine[J]. Annals of statistics, 2001:1189-1232. DOI:10.2307/2699986

DOI

[23]
Prokhorenkova L, Gusev G, Vorobev A, et al. CatBoost: unbiased boosting with categorical features[C]// Proceedings of the 32nd International Conference on Neural Information Processing Systems. Curran Associates Inc., Montréal, Canada, 2018:6639-49.

[24]
Dorogush A V, Ershov V, Gulin A. CatBoost: Gradient boosting with categorical features support[J]. arXiv preprint arXiv:1810.11363, 2018.

[25]
Friedman J H. Stochastic gradient boosting[J]. Computational Statistics & Data Analysis, 2002, 38(4):367-378. DOI:10.1016/S0167-9473(01)00065-2

DOI

[26]
安晓亚, 孙群, 肖强, 等. 一种形状多级描述方法及在多尺度空间数据几何相似性度量中的应用[J]. 测绘学报, 2011, 40(4):495-501.

[ An X Y, Sun Q, Xiao Q, et al. A shape multilevel description method and application in measuring geometry similarity of multi-scale spatial data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4):495-501. ] DOI:CNKI:SUN:CHXB.0.2011-04-018

DOI

[27]
马京振, 孙群, 肖强, 等. 利用多级弦长拱高复函数进行面实体综合相似性度量研究[J]. 中国图象图形学报, 2017, 22(4):551-562.

[ Ma J Z, Sun Q, Xiao Q, et al. Measurement of the comprehensive similarity of area entities using a multilevel arc-height complex function[J]. Journal of Image and Graphics, 2017, 22(4):551-562. ] DOI:10.11834/jig.20170415

DOI

[28]
Xu G, Li C, Wang Q. Unified multi-scale method for fast leaf classification and retrieval using geometric information[J]. IET Image Processing, 2019, 13(12):2328-2334. DOI:10.1049/iet-ipr.2018.6551

DOI

[29]
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.

[ Zhou Z H. Machine learning[M]. Beijing: Tsinghua University Press, 2016. ]

[30]
李艳霞, 柴毅, 胡友强, 等. 不平衡数据分类方法综述[J]. 控制与决策, 2019, 34(4):673-688.

[ Li Y X, Chai Y, Hu Y Q, et al. Review of imbalanced data classification methods[J]. Control and Decision, 2019, 34(4):673-688. ] DOI:10.13195/j.kzyjc.2018.0865

DOI

[31]
Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16(1):321-357. DOI:10.1613/jair.953

DOI

[32]
方昊, 李云. 基于多次随机欠采样和POSS方法的软件缺陷检测[J]. 山东大学学报(工学版), 2017, 47(1):15-21.

[ Fang H, Li Y. Random undersampling and POSS method for software defect prediction[J]. Journal of Shandong University (Engineering Science), 2017, 47(1):15-21. ] DOI:10.6040/j.issn.1672-3961.0.2016.304

DOI

[33]
Dewancker I, McCourt M, Clark S. Bayesian optimization for machine learning: A practical guidebook[J]. arXiv preprint arXiv:1612.04858, 2016.

[34]
Gunning D, Aha D. DARPA's explainable artificial intelligence (XAI) program[J]. AI Magazine, 2019, 40(2):44-58. DOI:10.1609/aimag.v40i2.2850

DOI

[35]
Zhang G, Yao T, Piao S, et al. Extensive and drastically different alpine lake changes on Asia's high plateaus during the past four decades[J]. Geophysical Research Letters, 2017, 44(1):252-260. DOI:10.1002/2016GL072033

DOI

[36]
Lundberg S M, Erion G G, Lee S. Consistent individualized feature attribution for tree ensembles[J]. arXiv preprint arXiv:1802.03888, 2018.

[37]
Xiong Y, Zuo R. GIS-based rare events logistic regression for mineral prospectivity mapping[J]. Computers & Geosciences, 2018, 111:18-25. DOI:10.1016/j.cageo.2017.10.005

DOI

[38]
Dino H I, Abdulrazzaq M B. Facial expression classification based on SVM, KNN and MLP classifiers[C]// 2019 International Conference on Advanced Science and Engineering (ICOASE). IEEE. Zakho-Duhok, Iraq. 2019:70-75. DOI:10.1109/ICOASE.2019.8723728

DOI

[39]
童新华, 张郭秋晨, 韦燕飞. 区域碳收支能力估算的面向对象遥感分类方法[J]. 地球信息科学学报, 2016, 18(12):1675-1683.

DOI

[ Tong X H, Zhang-Guo Q C, Wei Y F. Remote sensing estimation of the carbon balance ability based on the object-oriented method for Guangxi Youjiang district[J]. Journal of Geo-information Science, 2016, 18(12):1675-1683. ] DOI: 10.3724/SP.J.1047.2016.01675

DOI

[40]
Sheykhmousa M, Mahdianpari M, Ghanbari H, et al. Support vector machine vs. random forest for remote sensing image classification: a meta-analysis and systematic review[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13:6308-6325. DOI:10.1109/JSTARS.2020.3026724

DOI

Options
文章导航

/

〈 〉