EN中文

地球信息科学学报 >

2022 , Vol. 24 >Issue 12: 2297 - 2308

DOI: https://doi.org/10.12082/dqxxkx.2022.220209

地球信息科学理论与方法

顾及DEM误差空间自相关的地形变化检测方法

  • 代文 , 1 ,
  • 陈凯 1 ,
  • 王春 , 1, 2, 3, * ,
  • 李敏 2 ,
  • 陶宇 2
展开
  • 1.南京信息工程大学地理科学学院，南京 210044
  • 2.滁州学院地理信息与旅游学院，滁州 239000
  • 3.实景地理环境安徽省重点实验室，滁州 239000
* 王春（1975— ），男，宁夏固原人，教授，研究方向为实景三维建模。E-mail:

代文（1995— ），男，贵州毕节人，讲师，研究方向为实景三维建模与数字地形分析。E-mail:

收稿日期: 2022-04-20

  修回日期: 2022-07-15

  网络出版日期: 2023-02-25

基金资助

安徽高校省级自然科学研究重大项目(KJ2021ZD0130)

实景地理环境智能科技滁州市“113”产业创新团队

江苏省高等学校自然科学研究项目(22KJB170016)

国家自然科学基金项目(41930102)

国家自然科学基金项目(42171402)

南京信息工程大学科研启动经费(2022r019)

收起

Topographic Change Detection that Considers the Spatial Autocorrelation of DEM Errors

  • DAI Wen , 1 ,
  • CHEN Kai 1 ,
  • WANG Chun , 1, 2, 3, * ,
  • LI Min 2 ,
  • TAO Yu 2
Expand
  • 1. School of Geographical Sciences, Nanjing University of Information Science and Technology, Nanjing 210044, China
  • 2. School of Geographic Information and Tourism, Chuzhou University, Chuzhou 239000, China
  • 3. Anhui Province Key Laboratory of Physical Geographical Environment, Chuzhou 239000, China
* WANG Chun, E-mail:

Received date: 2022-04-20

  Revised date: 2022-07-15

  Online published: 2023-02-25

Supported by

Major Project of Natural Science Research of Anhui Provincial Department of Education(KJ2021ZD0130)

Chuzhou "113" Industrial Innovation Team

Natural Science Foundation of the Jiangsu Higher Education Institutions of China(22KJB170016)

National Natural Science Foundation of China(41930102)

National Natural Science Foundation of China(42171402)

Nanjing University of Information Science & Technology Research start-up fund(2022r019)

Fold

摘要

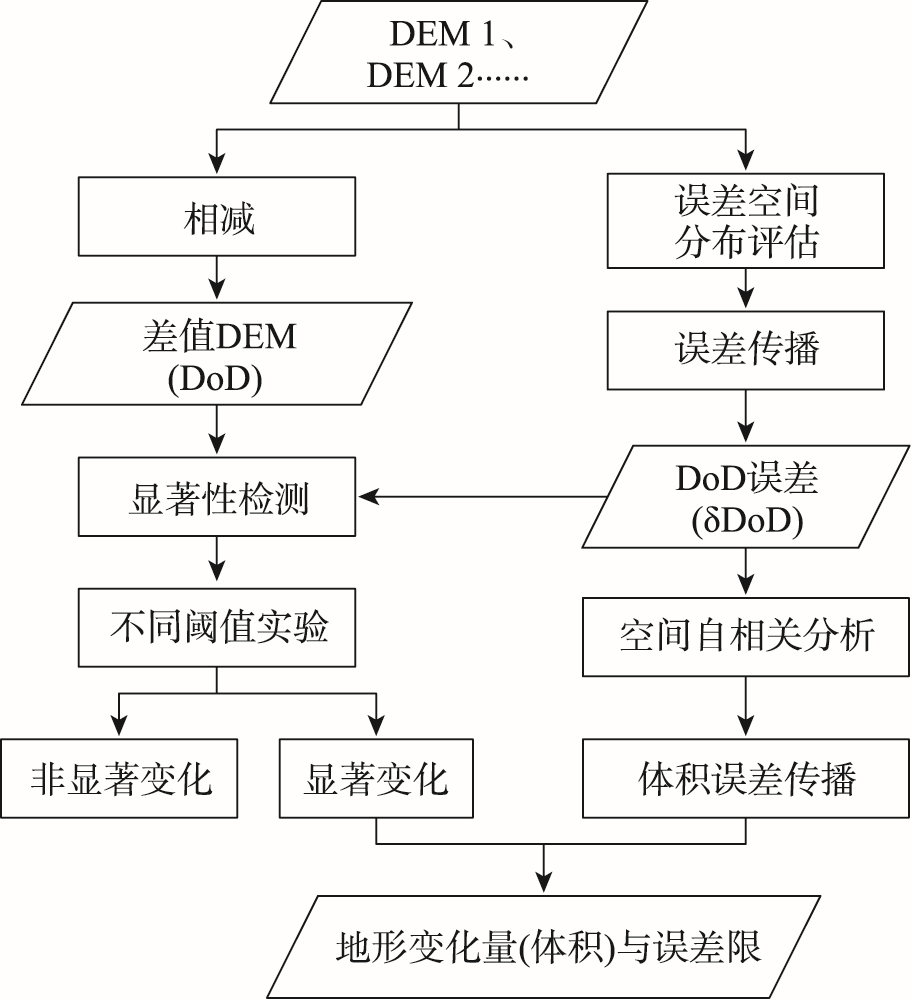
传统的地形变化检测方法忽略了DEM误差的空间自相关性，针对此问题，本文提出了顾及DEM误差空间自相关的地形变化检测方法。首先，通过2期DEM相减得到差值DEM（DoD），并通过蒙特卡罗方法评估DEM的误差空间分布；其次，基于DEM误差空间分布图，通过误差传播公式计算DoD误差，并使用半变异函数分析其空间自相关程度；最后，在误差空间自相关分析和显著性检测的基础上计算地形变化量（体积）和对应的误差限。本文在4个黄土小流域进行了实验，结果表明：无人机摄影测量DEM的高程误差存在一定程度的空间自相关，通过光束平差蒙特卡罗方法可以模拟无人机摄影测量DEM的误差空间分布；在进行地形变化检测时，使用误差空间分布代替中误差进行地形变化检测有效降低了检测结果对显著性阈值的敏感性；显著性阈值从68%提高到95%时，使用误差空间分布的检测结果损失的观测值比使用中误差低5.39%~6.75%。顾及空间自相关的地形变化检测方法能够更加科学、精确地量化地形变化特征，也可有效地应用于地表变形监测、流域侵蚀监测、输沙量评估等领域。

关键词： 地形变化检测; 显著性检测; DEM误差空间分布; 蒙特卡罗方法; 土壤侵蚀监测; 差值DEM

本文引用格式

代文 , 陈凯 , 王春 , 李敏 , 陶宇 . 顾及DEM误差空间自相关的地形变化检测方法[J]. 地球信息科学学报, 2022 , 24(12) : 2297 -2308 . DOI: 10.12082/dqxxkx.2022.220209

Abstract

Traditional topographic change detection methods often ignore the spatial autocorrelation of DEM errors. To solve this problem, a topographic change detection method that considers the spatial autocorrelation of DEM errors is proposed in this paper. Firstly, the DEM of Difference (DoD) is obtained from two original DEMs, and the spatial distribution of DEM errors is evaluated by the Monte Carlo method. Secondly, based on spatially distributed DEM errors, DoD errors are calculated by error propagation and their spatial autocorrelation degree is analyzed using the semi-variance function. Finally, topographic changes (erosion, deposition, and net changes) are calculated based on the spatial autocorrelation analysis and significance detection. The results in four small catchments show that the elevation errors of UAV-photogrammetry DEM are spatially autocorrelated, which can be simulated by the Monte Carlo method. The use of spatially distributed error instead of RMSE for topographic change detection effectively reduces the sensitivity of the detection results to the significance threshold. When the significance threshold is increased from 68% to 95%, the loss of observations using the spatially distributed error is 5.39%~6.75% lower than that using the RMSE. The proposed method can be effectively used in the fields of surface deformation monitoring, erosion monitoring, sediment transport assessment, and so on.

Key words： topographic change detection; level of detection; spatial distribution of DEM errors; Monte Carlo method; soil erosion monitoring; DEM of difference

1 引言

地形变化检测是地表过程研究的重要基础，其不仅可以反映滑坡、崩塌等大型地质灾害[1]，还可以量化水土流失、流域侵蚀的微小变化过程[2]，在各学科中发挥着重要的作用[3-4]。地形变化检测的方法目前主要有3类：① 基于点的大地测量方法；② 基于合成孔径雷达干涉测量（InSAR）的方法；③ 基于2期DEM相减（DEM of Difference, DoD）的方法。
基于点的大地测量方法是常用的地形变化检测方式，如使用全站仪、水准仪或者GNSS等测量手段对特定的检测点进行变化检测[5⇓⇓-8]。但是这种方法工作量大、作业效率低，难以开展面上的地形变化检测。基于InSAR的地形变化检测技术具有覆盖范围广、形变探测精度高等优点。随着研究的深入，后面还出现差分雷达干涉测量[9-10]（D-InSAR）、永久散射体合成孔径雷达干涉测量[11-12]（PS-InSAR）、和小基线合成孔径雷达[13-14]（SBAS-InSAR）等技术。上述技术已在城市地表形变监测[11⇓-13]、滑坡灾害隐患早期识别[15]、地震形变监测[16]等地质灾害领域得到了广泛应用。但是，基于InSAR的地形变化检测技术在黄土小流域应用时，由于植被和土壤侵蚀的影响，InSAR时序影像相干性低，难以满足应用的需求。
2期DEM相减得到差值DEM（DoD）是传统也是直接的地形变化检测方法[17-18]。但是，这种方法忽略了地形测量误差的影响[19]。为了排除误差的影响，学者们提出了显著性阈值分割的方法。显著性阈值检测的核心思想是把误差引起的变化和真实地形变化区分开，假设小于显著性阈值的变化均为误差引起[20]。通过地形误差传播和统计学t检验确立一定的显著性阈值将DOD分割为显著变化和非显著变化。然后，保留显著变化的区域作为“真实”地形变化量。这种方法已经在河床侵蚀监测、冰川变化检测中得到应用[21-22]。但是，已有学者意识到这种方法可能会丢失小于分割阈值的真实变化值，从而引起检测结果的系统性偏差。显著性阈值分割对侵蚀量、沉积量和地形净变化量有何影响，什么时候应该使用显著性阈值分割等问题还缺乏系统性研究。
此外，现有的研究均使用均方根误差（RMSE）作为误差传播指标。但RMSE是一个整体精度指标，无法反映误差的空间分布。已有研究表明DEM误差往往是空间上变化分布的[23]，当前亟需在误差传播和地形变化检测中考虑空间相关性。因此，本文首先通过数值模拟实验评估显著性阈值分割的适用条件；然后，以4个典型黄土小流域为研究区，利用无人机摄影测量建立研究样区DEM，通过蒙特卡洛方法评估研究区DEM的误差空间分布，最后，在误差空间分布图的基础上进行误差传播和地形变化检测，并讨论了不同检测方式和显著性阈值对检测结果的影响。

2 研究方法

2.1 技术路线

本文所提出方法的技术路线如图1所示。首先，通过2期DEM相减得到DoD，并通过蒙特卡罗方法评估DEM的误差空间分布；其次，通过误差传播计算DoD误差，并使用半变异函数分析其空间自相关程度；最后，在误差空间自相关分析和显著性检测的基础上计算地形变化量（体积）和对应的误差限。
图1 全文技术路线

Fig. 1 Work flow of this study

2.2 误差空间分布评估方法

本文通过光束平差蒙特卡洛模拟方法[24]来模拟摄影测量的误差空间分布。其基本思想是在摄影测量过程中，模拟控制点和相机位置网络的误差，通过多次重复光束平差过程查看加密点（特征点）坐标的误差（不确定性），具体步骤如下：
（1）摄影测量预处理。在PhotoScan软件中完成刺点和空中三角测量等基本处理。
（2）误差模拟。把使用全部控制点优化空三之后得到的相机位置网络作为初始网络。然后，根据控制点的测量精度和相机位置（POS）测量精度分别构建正态分布误差模型。控制点测量精度与测量手段有关，如GNSS-RTK一般为平面1 cm，高程3 cm。相机位置测量精度与飞行器平台有关。
（3）重复光束平差。对于每次光束平差，在原始的空三网络中添加步骤（2）中模拟的随机误差，记录每一次光束平差结果。
（4）计算加密点点位误差。由于每次空三网络中均会添加一定的随机误差，其每次平差后的加密点点位也不同。当模拟次数达到一定的次数时，每个加密点的点位标准差将趋近于稳定。此时的点位标准差即加密点误差。由于加密点数量大而且是空间上分布的，将其高程误差通过插值转栅格即可得到DEM高程误差的空间分布。

2.3 误差空间自相关量化方法

量化误差空间自相关所用为半变异函数，其计算公式如下[25]：
γ ( x , h ) = 1 2 V a r [ Z ( x ) - Z ( x + h ) ]
式中： γ ( x , h )是半变异函数值； Z ( x )是区域变量Z在x位置的值； Z ( x + h )是区域变量Z在距x点距离为h处的值。半变异函数难以直接求解，通常选取特定的半变异函数模型拟合半变异函数值。本文采用高斯模型和多项式回归法拟合半变异函数[26]。块金、基台和变程是半变异函数的3个重要参数。影响空间自相关误差传播的主要是变程，地域不同变程也随之改变。变程为0时，可认为误差是空间上完全随机分布，空间自相关性为0；当变程增大时，空间相关性增强。

2.4 误差传播方法

（1）地形误差传播
2期DEM相减可以计算地形（高程）变化量（DoD）。但是，DEM中难以避免地存在测量误差。在计算地形变化量时，往往需要对地形误差进行传播。2个观测量进行加减时的误差传播定律如下[27]：
σ D o D = ± σ 1 2 + σ 2 2 + 2 p σ 1 σ 2
式中： σ D o D是DOD的中误差； σ 1、 σ 2分别为观测量1期和2期的中误差； p表示两期之间的相关系数，范围在0~1之间；若2个观测量之间是独立测量，则p值为0；若两个观测量之间完全相关，则p值为1。由于计算地形变化量的2期DEM通常是独立观测，因此p值为0。传统的方法用RMSE直接进行传播，但是当知道误差的空间分布时，每个像元值即高程误差，此时，式（2）变为：
σ D o D i = ± ( σ D E M 1 i ) 2 + ( σ D E M 2 i ) 2
式中： σ D o D i是DOD第i个像元的误差； σ D E M 1 i 和 σ D E M 2 i表示对应DEM中第i个像元处的误差。
（2）体积误差传播
体积变化量等于面积与地形变化量的乘积。对于单个像元，其体积变化量误差 σ v为[20]：
σ v = L 2 σ D o D
式中：L表示像元大小。
对于整个样区而言，体积变化量等于每个像元变化量的累加。根据误差传播定律，总体积变化量误差 σ V为[23]：
σ V = ∑ i = 1 n   L 4 σ D o D i 2 + 2 ∑ i = 1 n   ∑ j ≠ i n   L 4 p i , j σ D o D i σ D o D j
式中：L表示像元大小；n表示整个样区的像元个数； σ D o D i表示第i个DoD的误差； p i , j表示第i和第j个DoD之间的相关性。
若 σ D o D是随机误差，不存在空间自相关，式（5）可化为：
σ V = n L 2 σ D o D
若 σ D o D是随机误差，但在空间上存在自相关，根据Rolstad等的研究[28]，式（5）可化为：
σ V = n L 2 σ D o D π a i 2 5 L 2
式中：ai为 σ D o D半变异函数的变程。式（7）相当于式（6）乘以空间自相关因子 π a i 2 5 L 2。
若 σ D o D是系统误差，即在空间上完全相关，任意 p i , j均为1，则式（5）可化为式（8），即体积误差等于样区面积乘以地形变化量的中误差。
σ V = n L 2 σ D o D

2.5 地形变化检测

（1）地形变化显著性检验
在得到地形误差后，可以将地形误差传播到地形变化量中并进行显著性检测。根据统计学t检验的原理，一个标准差范围内的显著性（或置信度）约为68%；同理，此时计算出的 σ D o D i在统计学上的显著性也约为68%。对于地形变化检测，一般希望得到在更高显著性或给定显著性水平下的真实地形变化。因此，需要将地形变化量转换成相应的t统计量（假设误差随机分布）并进行显著性检测。根据t检验原理，地形变化量对应的t统计量为[20]：
t = Z D E M 1 - Z D E M 2 σ D o D i
式中： Z D E M 1、 Z D E M 2分别表示第一期DEM和第二期DEM的高程。
得到地形变化的t统计量之后，可以通过界值表查看其对应的显著性。使用一定的显著性阈值将DoD分为显著变化和不显著变化2个区域，在进一步计算体积变化量时，仅需要考虑显著变化的区域。
（2）显著性阈值分割对地形变化检测的影响
地形变化量显著性的重要应用之一是根据给定的显著性阈值分为显著变化和非显著性变化区域，简称显著性阈值分割。68%和95%是常用的 2个显著性检验阈值。此处简略介绍这2个显著性下的检测公式。根据t检验界值表，使用68%和95%显著性阈值时，阈值分割公式分别为：
Z D E M 1 i - Z D E M 2 i > σ D o D i
Z D E M 1 i - Z D E M 2 i > 1.96 × σ D o D i
2期DEM之差分别大于1倍和1.96倍 σ D o D i时，可认为地形分布在68%和95%显著性水平下发生了变化。
为了讨论显著性阈值分割对累计体积变化量的影响，本文设计了一个数值模拟实验（表1）。数值模拟实验分为无地形变化、净堆积、净侵蚀和混合变化3个组。前三组每组模拟一个40×40（即观测数）的栅格，初始像元值代表地形变化量的真值，无地形变化、净堆积和净侵蚀的初始像元值分别为0、1和-1。在每组中分别添加一个空间随机分布的白噪声（半变异函数变程=0），和一个空间上自相关的白噪声作为观测值（半变异函数变程=10），然后分别在有阈值分割和无阈值分割的条件下计算观测到的毛侵蚀量，毛沉积量和净侵蚀（沉积）量。混合变化组的模拟观测数为300个，真实变化量在-1 ~ 1之间线性变化，其他操作和前三组一样。
表1 误差模拟实验

Tab. 1 Error simulation experiment

真实变化量 误差特征 观测数
无地形变化组 0 正态分布
u=0
σ=0.4		 40×40
净侵蚀组 1
净沉积组 -1
混合变化组 -1 ~ 1 300
（3）误差空间自相关对地形变化检测的影响
除数值模拟试验外，本文利用光束平差蒙特卡洛Python程序得到野外实测样区的高程误差空间分布图。然后，在野外实测样区分别使用中误差68%和95%显著性检测和误差空间分布图68%和95%显著性检测4种检测方法分析样区地形变化及精度比较。

3 实验与分析

3.1 研究区与数据

本文研究区选择沟壑侵蚀较为严重的4个黄土小流域作为实验样区（图2）。样区均位于陕西省绥德县，A1（110°15′16.7″E，37°31′33.8″N）和A2（110°15′31.5″E，37°31′40.5″N）位于清水沟村，B1（110°21′58.6″E，37°34′59.5″N）和B2（110°21′50.6″E，37°35′01.5″N）位于王茂庄村。4个样区均是典型的水土流失区，区域内植被稀疏、沟壑侵蚀剧烈，最大高差均在150~200 m之间，是用于研究地形变化检测的理想样区。4个样区第一期地形数据为2016年全数字摄影测量采集，分辨率为1 m，高程中误差A1、A2为0.11 m，B1、B2为0.16 m；A1、A2样区第二期地形数据是2019年由大疆工业级四旋翼无人机Metric 210无人机摄影测量获得，分辨率为1 m，高程中误差为0.15 m；B1、B2样区第二期地形数据为2021年由大疆消费级四旋翼无人机精灵4 Pro采集，分辨率为1 m，高程中误差为0.06 m。
图2 4个典型流域的地形特征

Fig. 2 Topography of the study area

3.2 模拟实验结果

随机误差对毛侵蚀量、毛沉积量的影响较大，随着观测（像元）数的增加，毛侵蚀量、毛沉积量的误差不断累积（图3（e））。但随机误差对净变化量的影响不大（图3（e））。这是因为随机误差服从正态分布，在算净变化量时，正误差和负误差往往能互相抵消。有空间自相关的随机误差对整体毛侵蚀量、毛沉积量和净变化量的影响和无自相关随机误差的影响相似。但是，其净变化量的波动更大（图3（f））。有空间自相关时，误差聚集分布，高值误差的周围也是高值误差（图3（b）），在进行累加时，误差会累计，直到遇到低值区域误差才会抵消，所以其净变化量的波动较大。
图3 真实变化为0时随机误差对地形变化检测的影响

Fig. 3 Influence of random error on topographic change detection when the real change is 0

误差空间自相关对净变化量的影响不大（图3（f）），这由于其直方图仍满足正态分布（图3（b））。但其对变化量的空间分布影响很大（图3（b））。在实际应用时，纯随机误差由于在空间上随机分布，研究者一般不会认为局部区域发生了侵蚀或者沉积；但是，有空间自相关的随机误差往往会造成成片区域侵蚀或沉积的误判。使用显著性阈值分割可以降低随机误差的空间自相关模式，当使用的显著性阈值达90%时，相对于原始观测值，误差的空间分布已经不明显（图3（d）），降低了误判的可能性。
由于误差空间自相关对整体毛侵蚀量、毛沉积量和净变化量的影响和无空间自相关的相似，主要影响其空间分布，后续讨论毛侵蚀量、毛沉积量和净变化量的计算时仅以纯随机误差为例。当真实高程变化量为0时，显著性阈值分割对净变化量的影响不大，其净变化量累计曲线与不分割时几乎重叠（图3（e）和（f））。整个模拟区域的净变化量观测值如表2所示，使用阈值分割或不使用阈值分割的观测值均在真值的误差限内。在毛侵蚀量和毛沉积量方面，显著性阈值分割不能完全消除误差，但能在一定程度上降低误差的累积效应，且显著性阈值越高，越能降低毛侵蚀和毛沉积量的误差累计（图3（e）和（f））。
表2 不同条件下地形净变化量观测值

Tab. 2 Observations of net topographic change under different conditions

真实值 观测值（无分割） 观测值（显著性阈值分割）
无变化组 0 2.65±16 1.75±16（68%）
净侵蚀组 1600 1602.65±16 1498.28±16（95%）
净沉积组 -1600 -1597.34±16 -1460.70±16（95%）
当真实地形变化量表现为净侵蚀或净沉积时，此时毛侵蚀（沉积）量即是净变化量。从表2可以发现，当真实地形净侵蚀或净沉积时，无显著性阈值分割的净变化量观测结果更接近于真实值，使用显著性阈值分割的净变化量观测结果偏差较大。这与随机误差的补偿效应有关，当地形净侵蚀（沉积）时，由于误差的影响，一部分区域的侵蚀（沉积）量会被高估，相应地，会有另一部分的侵蚀（沉积）量被低估。因此，误差对整体的净变化量影响不大。而使用阈值分割会忽略一部分像元的变化量，导致计算净变化量时信息损失。
理论上，在地形较为稳定（或变化量非常小）的区域，计算毛侵蚀或毛沉积量时，应当使用显著性阈值分割减少累计误差；计算净变化量时，一般不使用显著性阈值分割。在侵蚀或沉积为主（变化量较大）区域，计算毛侵蚀、毛沉积量和净变化量时可以不使用显著性阈值分割；但在查看局部区域变化情况、或变化量空间分布情况时建议使用显著性阈值分割。在实际应用中，往往既有地形稳定的区域，又有侵蚀和沉积区域。这种时候一般考虑把样区分割，分为稳定区、侵蚀区和沉积区来分别计算。
小流域作为天然的地理单元，在进行地理研究和分析时，学者们通常希望得到以流域为单元的特征值。因此，在以流域为单元进行地形变化检测时，需要考虑误差对其整体的影响，而不是分割计算。当样区中既存在稳定区域，又存在侵蚀和沉积区域时，模拟实验结果如图4所示。可以发现，毛侵蚀量和毛沉积量一直在增加，但增加的速率不同；毛侵蚀量先增加后趋于稳定，毛侵蚀量先不变后加速增加，这与累加时侵蚀和沉积区域的分布有关。净侵蚀量先增加后减少也和侵蚀和沉积区域的分布有关，当累计遍历完整个样区时，趋近于0。整个样区的各变化量观测结果如表3所示。当使用原始观测值直接累加计算毛侵蚀和毛沉积量时，误差较大；而使用95%显著性分割之后，误差较小。这一结果说明，由于稳定区域的存在，在对小流域整体计算毛侵蚀和毛沉积量时应当使用显著性阈值分割。
图4 随机误差对地形混合变化区的影响

Fig. 4 Influence of random error on terrain mixed change area

表3 地形混合变化下侵蚀量、沉积量和净变化量观测值

Tab. 3 Observations of erosion, deposition and net change under mixed topographic changes

真实值 观测值（无分割） 观测值（95%显著性分割）
毛侵蚀 50 76.18±4.89 46.9±4.89
毛沉积 -50 -76.03±4.89 -46.17±4.89
净变化 0 0.15±6.92 -0.72±6.92

3.3 实测小流域地形变化检测结果

通过蒙特卡罗模拟得到4个实测小流域的高程误差空间分布如图5所示。从图中可以发现，高程误差较大的区域多分布在沟谷区域，坡顶和山脊区域的误差相对较小。这一结果与摄影测量原理相符。由于沟谷地有两侧山坡遮挡，航片在该区域重叠率低，导致特征点解算的不确定度高。而沟间地视野开阔，无遮挡，能被更多的航片所拍到，相对精度高。
图5 实测小流域误差空间分布

Fig. 5 Spatial distribution of errors in the four small watersheds

以A1样区为例，将第一期DEM减去第二期DEM得到地形变化量（图6）。A1样区的地形变化较大，平均地形变化量约为0.5 m。其中，在南边出水口处出现了最大负变化，对比遥感影像可知该处修筑了淤地坝并且有人工回填；在最南边右侧山坡出现了两处极大正变化，对比遥感影像发现该处存在人工的山体开挖；同时在有新修道路和梯田的下游区域沉积（或回填）明显。分别使用中误差和误差空间分布图进行了误差传播和显著性检测（图7）。可以发现，地形变化量较小的区域的显著性均较低，如流域最左侧山顶区域；而地形变化量大的区域的显著性非常高，如流域南侧的几个剧烈变化区域的显著性均接近1。
图6 A1样区地形变化情况

Fig. 6 Topographic changes in the A1 area

图7 A1样区地形变化显著性

Fig. 7 Significance of topographic changes in the A1 area

整体上看，使用误差空间分布图进行误差传播检测出来的地形显著变化区域更多。特别是在正地形坡面区域，许多使用中误差检测时显著性较低的区域在使用误差空间分布图进行检测时显著性明显变高。这跟误差的空间分布有关，从图5可知在正地形区域误差更低，因此，进行显著性检测时，较小的变化量也能表现出较高的显著性。
分别使用中误差和误差空间分布图，并分别在68%和95%的置信度水平下进行了地形变化检测。4种不同方式检测到的变化区域面积不同（表4）。在4个样区中，使用中误差检测到的变化面积均小于使用误差空间分布图时检测到的变化面积。当使用中误差检测，显著性阈值从68%提高到95%时，4个样区检测到的面积下降了17.21%~36.72%；而使用误差空间分布图检测时，其下降程度较低，下降范围在11.82%~29.97%之间；说明使用误差空间分布图的检测结果损失的观测值比使用中误差低5.39%~6.75%。随着置信度的提高，不论使用哪种方式，检测到的变化区域均有一定程度的下降。但是，使用误差空间分布时，下降程度更低，说明使用误差空间分布图进行检测时对置信度水平的敏感性更低，即尽管使用不同的置信度检测水平，发生真实变化的区域总能被识别。因此，在后续研究中使用误差空间分布图代替中误差进行地形变化检测。
表4 不同检测方式下检测的地形变化面积

Tab. 4 Detected topographic change areas under different detection methods （%）

样区 中误差检测 误差空间分布图检测
68%显著性 95%显著性 下降程度 68%显著性 95%显著性 下降程度
A1 82.46 61.26 21.20 87.12 74.35 12.77
A2 84.74 67.53 17.21 88.26 76.45 11.82
B1 57.41 20.69 36.72 66.27 36.30 29.97
B2 57.72 27.14 30.58 63.95 35.95 28.00
为了查看地形变化量的空间分布和计算毛侵蚀量、毛沉积量，此处选择统一使用95%显著性阈值进行地形变化检测（图8、图9）。可以发现A1和A2样区中显著变化的区域明显比B1和B2样区多。这和地形变化量的数量级有关，A1和A2样区的2次测量，间隔了13年，这13年里地形的累计变化量最高超过10 m。而B1和B2样区两次测量间隔仅5年，累计变化量最高仅1 m左右。在进行显著性检测时，由于A1和A2样区变化量均很大，显著性均很高，误差的影响较小；而B1和B2样区变化量较小，许多区域的变化量量级和误差量级相当，显著性低，以95%显著性为界时被认为无显著变化。
图8 A1和A2样区地形变化检测结果

Fig. 8 Topographic changes in the A1 and A2 area

图9 B1和B2样区地形变化检测结果

Fig. 9 Topographic changes in the B1 and B2 area

得到地形变化量之后可以计算整个流域相应的毛侵蚀量、毛沉积量和净变化量。这里要注意的是，4个样区的高程误差具有一定的空间自相关，根据地形变化量计算体积时，误差传播需要考虑空间自相关。通过半变异函数拟合，A1、A2、B1、B2样区的变程分别为100、95、80、85 m。将半变异函数拟合得到的变程代入式7中进行误差传播得到各样区的体积误差。这里将体积和体积误差直接乘以各样区的土壤容重，得到质量和质量误差。
4个样区的毛侵蚀量、毛沉积量、净变化量分别在14 642.17~215 870.70 t，964.96~43 088.44 t，11 095.11~ 172782.26 t之间（表5）。毛侵蚀量均远大于毛沉积量，说明各样区均以侵蚀为主，此时的净变化量即输沙量。将净变化量除以时间得到4个样区的输沙率在2219.02~12 341.59 t/yr之间。高海东在王茂沟流域根据关地沟4号淤地坝和背塔沟淤地坝的淤积信息计算了2个与B1和B2样区相似大小的流域的产沙量在1904~2689 t/yr之间[29]。这与本文的计算结果相近，说明根据无人机摄影测量监测小流域的输沙率是可行的。A1和A2样区还没有关于侵蚀产沙方面的前人文献，但是这2个样区与B1和B2样区相隔不远，土地利用类型也基本一致，4个样区的产沙模数一般相差不大。由于A1和A2的面积约是B1和B2样区的5倍，所以其年均输沙率算出来也约是另外2个样区的5倍。
表5 实测小流域地形变化量及输沙率

Tab. 5 Measured topographic variation and sediment transport rate of small watershed

样区 毛侵蚀量/t(误差) 毛沉积量/t(误差) 净变化量/t(误差) 输沙率/(t/yr)(误差) 输沙率相对误差/%
A1 210 709.34 -41 395.90 169 313.44 12 093.82 6.62
(±10 173.24) (±4703.33) (±11 207.86) (±800.56)
A2 215 870.70 -43088.44 172 782.26 12 341.59 6.24
(±9685.18) (±4733.91) (±10 780.20) (±770.01)
B1 15 523.22 -964.96 14 558.26 2911.65 26.50
(±3589.14) (±1415.46) (±3858.16) (±771.63)
B2 14 642.17 -3547.07 11 095.11 2219.02 29.96
(±3196.08) (±912.49) (±3323.79) (±664.76)
4个样区的输沙率绝对误差在664.76~800.56 t/a之间，相对误差在6.24%~29.96%之间，说明使用无人机摄影测量计算小流域年均输沙率是可行的。其相对误差与小流域的绝对变化量和地形测量误差有关。地形变化量数量级越大，地形测量精度越高，相对误差越小。

4 结论与讨论

本文提出了顾及DEM误差空间自相关的地形变化检测方法，并在黄土高原4个小流域进行了实验。首先，通过2期DEM相减得到DoD，并通过蒙特卡罗方法评估DEM的误差空间分布；其次，基于误差空间分布图，通过误差传播公式计算DoD误差，并使用半变异函数分析其空间自相关程度；最后，在误差空间自相关分析和显著性检测的基础上计算地形变化量（体积）和对应的误差限。实验结果表明：无人机摄影测量DEM的高程误差存在一定程度的空间自相关，通过光束平差蒙特卡罗方法可以模拟无人机摄影测量DEM的误差空间分布；在进行地形变化检测时，使用误差空间分布代替中误差进行地形变化检测有效降低了检测结果对显著性阈值的敏感性；显著性阈值从68%提高到95%时，使用误差空间分布的检测结果损失的观测值比使用中误差低5.39%~6.75%。
同时，本文讨论了显著性阈值分割对地形变化检测的影响。显著性阈值分割对地形净变化量影响不大，但对毛侵蚀量和毛沉积量的影响明显；特别是在地形稳定区域，显著性阈值分割能有效降低对侵蚀或沉积的误判。由于自然流域中往往存在地形稳定区域，在对流域整体进行地形变化检测时建议使用显著性阈值分割。本文使用95%显著性阈值分割计算了4个样区的侵蚀、沉积量和输沙率，得到输沙率相对误差在6.24%~29.96%之间。相对误差大小与小流域的绝对变化量和地形测量误差有关。地形变化量数量级越大，地形测量精度越高，相对误差越小。
本文提出方法的检测效果还受到样区地形变化特征的影响。在不同样区中，地形变化的混合情况不同（如：侵蚀和沉积所占的比例和空间分布等）。这将在一定程度上影响显著性阈值的选择，进一步地形变化检测效果。在后续研究中，可以通过更多地形变化（混合）情况不同的样区进行深入分析，量化这一具体影响。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
贺礼家, 冯光财, 冯志雄, 等. 哨兵-2号光学影像地表形变监测:以2016年MW7.8新西兰凯库拉地震为例[J]. 测绘学报, 2019, 48(3):339-351.

[ He L J, Feng G C, Feng Z X, et al. Coseismic displacements of 2016 MW7.8 Kaikoura, New Zealand earthquake, using Sentinel-2 optical images[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(3):339-351. ]

[2]
代文, 汤国安, 胡光辉, 等. 基于无人机摄影测量的地形变化检测方法与小流域输沙模型研究[J]. 地理科学进展, 2021, 40(9):1570-1580.

DOI

[ Dai W, Tang G A, Hu G H, et al. Modelling sediment transport in space in a watershed based on topographic change detection by UAV survey[J]. Progress in Geography, 2021, 40(9):1570-1580. ]

DOI

[3]
李德仁, 夏松, 江万寿, 等. 一种地形变化检测与DEM更新的方法研究[J]. 武汉大学学报·信息科学版, 2006, 31(7):565-568.

[ Li D R, Xia S, Jiang W S, et al. Approach for terrain change detection and DEM updating[J]. Geomatics and Information Science of Wuhan University, 2006, 31(7):565-568. ] DOI:10.3321/j.issn:1671-8860.2006.07.001

DOI

[4]
Meinen B U, Robinson D T. Mapping erosion and deposition in an agricultural landscape: Optimization of UAV image acquisition schemes for SfM-MVS[J]. Remote Sensing of Environment, 2020, 239:111666. DOI:10.1016/j.rse.2020.111666

DOI

[5]
张绍成, 殷飞, 明祖涛, 等. 先验形变约束的实时动态载波相位差分变形监测[J]. 测绘科学, 2020, 45(11):8-12.

[ Zhang S C, Yin F, Ming Z T, et al. Real-time kinematic deformation monitoring with prior deformation constraint[J]. Science of Surveying and Mapping, 2020, 45(11):8-12. ] DOI:10.16251/j.cnki.1009-2307.2020.11.002

DOI

[6]
李治洪. GNSS系统在黄金峡坝肩边坡变形监测中的应用[J]. 人民黄河, 2021, 43(1):125-128.

[ Li Z H. Application of the automatic GNSS deformation monitoring system in Huangjinxia hydro junction project[J]. Yellow River, 2021, 43(1):125-128. ]

[7]
李瑞峰, 常乐, 秦海. InSAR监测技术与水准测量技术对比研究[J]. 工程质量, 2021, 39(3):72-76.

[ Li R F, Chang L, Qin H. Comparative study on InSAR monitoring technology and leveling technology[J]. Construction Quality, 2021, 39(3):72-76. ]

[8]
郭保. GPS技术在水库大坝变形监测中的应用[J]. 测绘与空间地理信息, 2020, 43(12):103-106.

[ Guo B. Application of GPS technology in reservoir dam deformation monitoring[J]. Geomatics ＆ Spatial Information Technology, 2020, 43(12):103-106. ]

[9]
殷硕文, 邵茜. 基于地形匹配的InSAR地形变化检测方法研究[J]. 武汉大学学报·信息科学版, 2010, 35(1):118-121.

[ Yin S W, Shao Q. A method of topographic change detection base InSAR terrain matching technology[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1):118-121. ] DOI:10.13203/j.whugis2010.01.015

DOI

[10]
Tomiyama N, Koike K, Omura M. Detection of topographic changes associated with volcanic activities of Mt. Hossho using D-InSAR[J]. Advances in Space Research, 2004, 33(3):279-283. DOI:10.1016/S0273-1177(03)00483-6

DOI

[11]
董雅竹, 谭颖, 张朋辉, 等. 利用PS-InSAR研究合肥地区活动构造变形[J]. 地球物理学进展, 2021, 36(5):1822-1833.

[ Dong Y Z, Tan Y, Zhang P H, et al. Using PS-InSAR to study active tectonic deformation in Hefei area[J]. Progress in Geophysics, 2021, 36(5):1822-1833. ]

[12]
Lyu M Y, Ke Y H, Li X J, et al. Detection of seasonal deformation of highway overpasses using the PS-InSAR technique: A case study in Beijing urban area[J]. Remote Sensing, 2020, 12(18):3071. DOI:10.3390/rs12183071

DOI

[13]
许强, 蒲川豪, 赵宽耀, 等. 延安新区地面沉降时空演化特征时序InSAR监测与分析[J]. 武汉大学学报·信息科学版, 2021, 46(7):957-969.

[ Xu Q, Pu C H, Zhao K Y, et al. Time series InSAR monitoring and analysis of spatiotemporal evolution characteristics of land subsidence in Yan'an new district[J]. Geomatics and Information Science of Wuhan University, 2021, 46(7):957-969. ] DOI:10.13203/j.whugis20200146

DOI

[14]
Shi M Y, Yang H L, Wang B C, et al. Improving boundary constraint of probability integral method in SBAS- InSAR for deformation monitoring in mining areas[J]. Remote Sensing, 2021, 13(8):1497. DOI:10.3390/rs13081497

DOI

[15]
郭延辉, 杨溢, 杨志全, 等. 国产GB-InSAR在特大型水库滑坡变形监测中的应用[J]. 中国地质灾害与防治学报, 2021, 32(2):66-72.

[ Guo Y H, Yang Y, Yang Z Q, et al. Application of GB-InSAR in deformation monitoring of huge landslide in reservoir area[J]. The Chinese Journal of Geological Hazard and Control, 2021, 32(2):66-72. ] DOI:10.16031/j.cnki.issn.1003-8035.2021.02.09

DOI

[16]
孙建宝, 梁芳, 沈正康, 等. 汶川MS8.0地震InSAR形变观测及初步分析[J]. 地震地质, 2008, 30(3):789-795.

[ Sun J B, Liang F, Shen Z K, et al. Insar deformation observation and preliminary analysis of the ms 8 Wenchuan earthquake[J]. Seismology and Geology, 2008, 30(3):789-795. ] DOI:10.3969/j.issn.0253-4967.2008.03.017

DOI

[17]
Liu X J, Tang G A, Yang J Y, et al. Simulating evolution of a loess gully head with cellular automata[J]. Chinese Geographical Science, 2015, 25(6):765-774. DOI:10.1007/s11769-014-0716-z

DOI

[18]
曹敏, 汤国安, 张芳, 等. 基于元胞自动机的黄土小流域地形演变模拟[J]. 农业工程学报, 2012, 28(22):149-155,294.

[ Cao M, Tang G A, Zhang F, et al. Simulation of terrain evolution in small loess watershed based on cellular automata[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(22):149-155,294. ] DOI:10.3969/j.issn.1002-6819.2012.22.022

DOI

[19]
王清. 数字地形分析中表面积与体积计算的不确定性建模与分析[D]. 武汉: 华中师范大学, 2016.

[ Wang Q. Uncertainty modelling and analysis of surface area and earthwork calculation based on regular grid digital elevation model(DEM)[D]. Wuhan: Central China Normal University, 2016. ]

[20]
Lane S N, Westaway R M, Murray Hicks D. Estimation of erosion and deposition volumes in a large, gravel-bed, braided river using synoptic remote sensing[J]. Earth Surface Processes and Landforms, 2003, 28(3):249-271. DOI:10.1002/esp.483

DOI

[21]
Heckmann T, Vericat D. Computing spatially distributed sediment delivery ratios: Inferring functional sediment connectivity from repeat high-resolution digital elevation models[J]. Earth Surface Processes and Landforms, 2018, 43(7):1547-1554. DOI:10.1002/esp.4334

DOI

[22]
Antoniazza G, Bakker M, Lane S N. Revisiting the morphological method in two‐dimensions to quantify bed‐material transport in braided rivers[J]. Earth Surface Processes and Landforms, 2019, 44(11):2251-2267. DOI:10.1002/esp.4633

DOI

[23]
Anderson S W. Uncertainty in quantitative analyses of topographic change: Error propagation and the role of thresholding[J]. Earth Surface Processes and Landforms, 2019, 44(5):1015-1033. DOI:10.1002/esp.4551

DOI

[24]
James M R, Robson S, Smith M W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys[J]. Earth Surface Processes and Landforms, 2017, 42(12):1769-1788. DOI:10.1002/esp.4125

DOI

[25]
Curran P J. The semivariogram in remote sensing: An introduction[J]. Remote Sensing of Environment, 1988,24(3):493-507. DOI:10.1016/0034-4257(88)90021-1

DOI

[26]
舒彦军, 张立亭. 求解半变异函数的常用方法与新方法研究[J]. 测绘与空间地理信息, 2012, 35(5):24-27.

[ Shu Y J, Zhang L T. Study of the commonly used methods and new methods of solving semi-variogram[J]. Geomatics ＆ Spatial Information Technology, 2012, 35(5):24-27. ] DOI:10.3969/j.issn.1672-5867.2012.05.008

DOI

[27]
Taylor J R. An introduction to error analysis: the study of uncertainties in physical measurements[M]. 2nd ed. Sau salito, Calif.: University Science Books, 1997

[28]
Rolstad C, Haug T, Denby B. Spatially integra ted geodetic glacier mass balance and its uncertainty based on geostatistical analysis: Application to the western Svartisen ice cap, Norway[J]. Journal of Glaciology, 2009, 55(192):666-680. DOI:10.3189/002214309789470950

DOI

[29]
高海东. 黄土高原丘陵沟壑区沟道治理工程的生态水文效应研究[D]. 北京: 中国科学院研究生院(教育部水土保持与生态环境研究中心), 2013.

[ Gao H D. Hydro-ecological impact of the gully erosion control works in loess hilly-gully region[D]. Beijing: Research Center for Eco-Environmental Sciences,Chinese Academy of Sciences, 2013. ]

Options
文章导航

/

〈 〉