EN中文

地球信息科学学报 >

2022 , Vol. 24 >Issue 12: 2373 - 2388

DOI: https://doi.org/10.12082/dqxxkx.2022.220158

地球信息科学理论与方法

基于特征筛选与差分进化算法优化的滑坡危险性评估方法

  • 周侯伯 , 1, 2 ,
  • 肖桂荣 , 1, 2, * ,
  • 林炫歆 1, 2 ,
  • 尹玉环 1, 2
展开
  • 1.福州大学 数字中国研究院（福建），福州 350108
  • 2.福州大学 空间数据挖掘与信息共享教育部重点实验室，福州 350108
*肖桂荣（1972— ），男，福建龙岩人，博士，研究员，主要从事地理信息系统、空间信息网络服务、政务数据可视化研究。E-mail:

周侯伯（1997— ），男，福建泉州人，硕士研究生，主要从事数据挖掘、机器学习与突发性地质灾害风险评估研究。E-mail:

收稿日期: 2022-04-04

  修回日期: 2022-05-18

  网络出版日期: 2023-02-25

基金资助

中央引导地方科技发展专项(2020L3005)

中国科学院A类战略性先导科技专项(XDA23100504)

收起

Landslide Hazard Assessment Method based on Feature Screening and Differential Evolution Algorithm Optimization

  • ZHOU Houbo , 1, 2 ,
  • XIAO Guirong , 1, 2, * ,
  • LIN Xuanxin 1, 2 ,
  • YIN Yuhuan 1, 2
Expand
  • 1. The Academy of Digital China (Fujian), Fuzhou University, Fuzhou 350108, China
  • 2. Key Laboratory of Spatial Data Mining and Information Sharing of Ministry of Education, Fuzhou University, Fuzhou 350108, China
*XIAO Guirong, E-mail:

Received date: 2022-04-04

  Revised date: 2022-05-18

  Online published: 2023-02-25

Supported by

Central Guided Local Development of Science and Technology Project(2020L3005)

Strategic Priority Research Program of the Chinese Academy of Sciences（Class A）(XDA23100504)

Fold

摘要

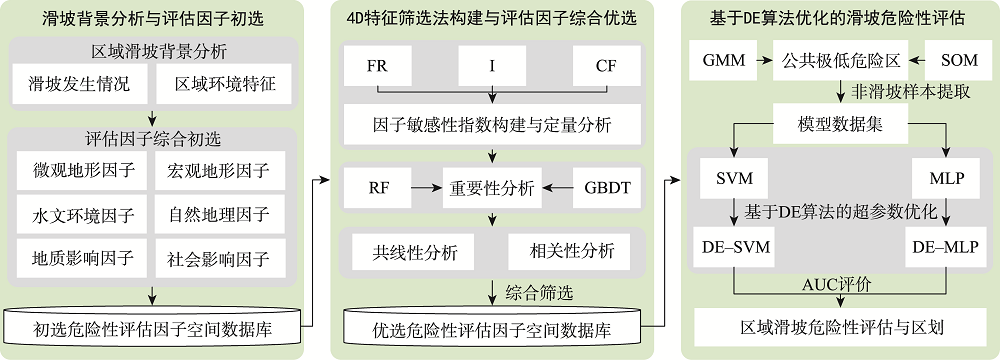
突发性地质灾害危险性评估对灾害防治与风险管理具有重要意义。由于不同地区影响灾害发生的因子各不相同，实际评估过程中难以全面客观地选取适宜的评估因子。机器学习对处理灾害系统的高维非线性问题独具优势，但因模型难以调优而评估效果有限。本文尝试提出一种双向优化的滑坡危险性评估方法：在构建因子敏感性指数开展定量敏感性分析的基础上，结合重要性分析、相关性分析、共线性分析构建四维(Four-Dimensional, 4D)特征筛选法用于评估因子综合优选；为克服模型难以调优的问题，引入差分进化(Differential Evolution, DE)算法优化支持向量机(Support Vector Machine, SVM)与多层感知机(Multi-Layer Perceptron, MLP) 2种推广能力较强的机器学习模型。最后，以福建省滑坡为例，开展评估方法研究。研究表明：4D特征筛选法能更加客观全面地选取适宜性更高的危险性评估因子，从而降低数据维度、减少信息冗余以提升评估模型性能；DE算法对SVM与MLP具有显著的优化效果，有益于增强模型滑坡危险性的评估准确度，DE-SVM、DE-MLP相较于未优化前模型的AUC值分别提升了4.43%与4.37%；基于双向优化的滑坡危险性评估结果表明，降雨与土地利用类型对福建省滑坡发生具有重要影响作用，福建省滑坡极高危险区普遍年均降雨较高、地形复杂多变，极低危险区主要位于东南沿海一带及闽江流域两侧。本研究为滑坡危险性评估中的影响因子客观选取与机器学习模型调优提供了一定思路。

关键词： 滑坡; 危险性; 因子敏感性指数; 四维特征筛选法; 差分进化算法; 支持向量机; 多层感知机; 福建省

本文引用格式

周侯伯 , 肖桂荣 , 林炫歆 , 尹玉环 . 基于特征筛选与差分进化算法优化的滑坡危险性评估方法[J]. 地球信息科学学报, 2022 , 24(12) : 2373 -2388 . DOI: 10.12082/dqxxkx.2022.220158

Abstract

Hazard assessment of sudden geological disasters is of great significance for disaster prevention and risk management. Due to different factors affecting the occurrence of disasters in different regions, it is difficult to select appropriate factors comprehensively and objectively in an actual evaluation process. Machine learning has unique advantages in dealing with high-dimensional nonlinear problems of disaster systems, but its evaluation performance is limited because the model is difficult to tune. This paper attempted to propose a two-way optimization method for landslide hazard assessment. Based on a factor sensitivity index built for quantitative sensitivity analysis, combining importance analysis, correlation analysis, and collinearity analysis, and following the principle of “guarantee sensitivity, retain importance, eliminate correlation, and avoid collinearity", a four-dimensional (4D) feature screening method was constructed to evaluate the comprehensive optimization of factors. In order to overcome the problem that the model is difficult to tune, the Differential Evolution (DE) algorithm was further introduced. Two machine learning models with strong generalization ability, i.e., Support Vector Machine (SVM) and Multi-Layer Perceptron (MLP), were optimized. Finally, we took the landslide in Fujian Province as an example to verify the proposed evaluation method. We found that the 4D feature screening method can more objectively and comprehensively select suitable hazard assessment factors, thereby reducing the data dimension and reducing information redundancy to improve the performance of the assessment model. Ten suitability assessment factors were finally used for landslide hazard assessment in Fujian Province including aspect, variance coefficient in elevation, land use type, average annual rainfall, surface cutting depth, distance to river, distance to road, engineering geological rock group, topographic wetness index, and stream power index. The DE algorithm can obtain better hyperparameters from global search and has a significant optimization effect on SVM and MLP, which is beneficial to improve the evaluation accuracy of the landslide hazard of the model. Compared with the unoptimized models, the AUC values of DE-SVM and DE-MLP increased by 4.43% and 4.37%, respectively. The results of landslide hazard assessment based on two-way optimization show that rainfall and land use types have an important impact on the occurrence of landslides in Fujian Province. Terrain curvature elements, terrain variability elements, and fault structures have little impact on landslide occurrence. The extremely high-hazard areas generally have high annual rainfall and complex and changeful terrain. The extremely low-hazard areas are mainly located along the southeast coast and on both sides of the Minjiang River Basin. This research provides some ideas for objective selection of influencing factors in landslide hazard assessment and machine learning model tuning.

Key words： landslide; hazard; four-dimensional feature screening method; factor sensitivity index; differential evolution algorithm; Support Vector Machine; Multi-Layer Perceptron; Fujian

1 引言

中国是世界上突发性地质灾害最为频发的国家之一，且受灾地域广、受灾人数多、经济损失大。在全球气候剧变与经济发展加速的双重刺激下，灾害治理与风险管理形势愈加严峻。灾害危险性评估研究既是灾害风险评估的重要基础，也是区域发展的必要参考。在第一次全国自然灾害综合风险普查背景下，全面评估突发性地质灾害的危险性，能更好地对灾害风险进行度量，从而为规划和决策提供更加客观准确的信息支持。
突发性地质灾害危险性评估研究本质是对特定灾情危险程度的度量，实现过程一般是结合典型影响因子构建评估指标体系进行灾害危险性指数的复合计算[1]。由于不同区域的地理环境、地质特征、社会概况各不相同，即使是同一类型的灾害在不同区域的影响因子也会存在差异。因此，有效开展灾害危险性评估的前提是有效选取影响因子。根据影响来源，危险性评估因子通常包括地理影响因子，断裂构造、地层岩性等地质影响因子，交通道路、土地利用等社会影响因子3大类，地理影响因子根据尺度和类型可进一步划分出坡度、坡向、曲率等微观地形因子，地形起伏度、地表粗糙度等宏观地形因子，地形湿度指数、径流强度指数等水文环境因子，降雨分布、植被覆盖等自然地理因子[1⇓⇓-4]。目前危险性评估中所使用的影响因子大多是根据已有研究成果或经验选取的，虽然部分研究经敏感性分析[5]或重要性分析[6]后结合相关性或共线性分析进行评估因子筛选，但在实际危险性评估中仍缺乏较为客观全面的评估因子选取方法。
目前，国内外滑坡危险性评估常用的模型主要有经验评估模型、统计分析模型、机器学习模型3大类[7-8]：层次分析法[9]等经验评估模型原理简单、易于计算，但主观性较强；信息量法[10]等统计分析模型在一定程度上能客服评估过程中因子的量化与误差影响，但也难以揭示各评估因子在高维空间中与滑坡灾害的关系；机器学习模型凭借其出色的高维非线性问题处理能力，在突发性地质灾害研究领域中应用广泛，常用模型主要有逻辑回归模型[11]、随机森林[12]、决策树[13]、支持向量机[14]、人工神经网络[15⇓-17]等，以及复合模型[8,18]或其他复杂模型[19-20]等。由于机器学习模型最优超参数难以搜索确定，在实际危险性评估中难以真正发挥效用，模型构建时一般使用默认参数或通过网格搜索获取较优值，部分研究者也尝试使用了遗传算法与粒子群算法[21-22]等进化算法进行超参数的率定并取得一定效果，但总体上优化效率较低。而差分进化算法相较于上述优化算法具有控制参数少、优化效率高、并行性能好、收敛速度快的优势[23]，受到了国内外学者的广泛关注，在信号处理、卫星通信、图像处理等领域应用甚广[24]，但在滑坡危险性评估研究中还鲜有应用。
本文综合四个维度的分析结果构建因子综合选取方法，引入优化算法对具备推广优势的机器学习模型进行优化，对灾害危险性评估方法进行双向优化研究。以福建省滑坡为例，结合灾害背景与研究成果初步选取21个评估因子，针对评估因子难以选取问题，提出因子敏感性指数(Factor Sensitivity Index, FSI)构建方法用于开展定量敏感性评估，结合重要性分析、相关性分析与共线性分析构建四维(Four-Dimensional, 4D)特征筛选法选出适宜性与有效性更强的评估因子用于模型构建；针对机器学习模型难以调优问题，引入差分进化(Differential Evolution, DE)算法对支持向量机(Support Vector Machine, SVM)与多层感知机(Multi-Layer Perceptron, MLP) 2种推广能力较强的评估模型进行调优；对优化后的评估模型进行评价，分析模型的区划效果与评估精度，根据结果总结福建省滑坡危险性规律，为灾害治理与风险管理提供决策支持。

2 研究思路与主要方法

双向优化的滑坡危险性评估方法主要包括滑坡背景分析与评估因子初步选取、评估因子综合优选、基于机器学习的滑坡危险性评估模型构建3个部分。本文以福建省滑坡为例开展危险性评估方法研究，并根据AUC值等指标进行精度评估。具体技术路线如图1所示。
图1 基于双向优化的滑坡危险性评估方法技术路线

Fig. 1 Technology roadmap for a bidirectional optimization-based landslide hazard assessment method

2.1 滑坡背景分析与评估因子初选

结合区域滑坡灾害背景与已有研究成果，考虑数据获取难易情况，从地理影响因子（如坡度等微观地形因子、地形起伏度等宏观地形因子、地形湿度指数等水文环境因子、降雨量等自然地理因子）、地质影响因子（如岩性、断裂等）、社会影响因子（如土地利用类型、道路等）3大类影响因素中初步选取影响区域滑坡发生的相关因子，并根据初选因子构建区域滑坡危险性评估因子数据库。

2.2 用于评估因子优选的四维特征筛选法构建

针对评估因子难以选取，在初步选取评估因子的基础上构建并计算FSI用于因子敏感性分析，结合因子重要性分析、相关性与共线性分析，根据“保证敏感性、保留重要性、剔除相关性、避免共线性”原则构建四维特征筛选法，依据4个维度的定量分析结果综合优选最终输入模型的评估因子。

2.2.1 基于因子敏感性指数的定量分析

目前灾害研究中评估因子的适宜性量化分析模式主要有3种：① 用因子各状态分级对应量化指数逐级合并值表征[5]；② 用因子各状态分级对应量化指数的平均值表征[25]；③ 用因子各状态分级对应量化指数的极差表征[26]。用合并值与平均值表征因子对灾害的影响强度，会使因子状态分级中对灾害影响大的类别影响力被削弱、对灾害影响小的类别影响力被增强，导致正负影响结果相互抵消，削弱了因子对灾害的实际影响力，而极差能较好地揭示因子对灾害影响的总体强度。
因此，本文在已有研究基础之上，将基于频率比系数（Frequency Ratio, FR）、信息量指数（Information Value, I）、确定性系数（Certainty Factor, CF）等量化指数的计算结果统称为确定系数（Determination Coefficient, DC），提出用因子敏感性指数（Factor sensitivity index, FSI）从整体上反应某一种评估因子对灾害发生的影响程度，计算方法如下：
F S I i = D C ( i , m a x ) - D C ( i , m i n )
式中：i表示第i个评估因子；FSIi表示第i个评估因子的敏感性指数； D C ( i , m a x )表示第i个评估因子各状态分级中确定系数的最大值； D C ( i , m i n )表示第i个评估因子各状态分级中确定系数的最小值。此外，计算中还引入判断阈值 μ，当 F S I i > μ时，认为评估因子i对滑坡发生具有较强的影响作用，适合引入研究中进行分析。已有研究的判断阈值一般取1，现根据研究尺度与区域特征设定判断阈值 μ=0.5。
为了避免单一算法的偶然性，本文基于状态分级结果分别计算各因子各个状态分级的频率比系数、信息量指数、确定性系数，取三类确定系数的平均值作为各个因子最终的敏感性指数。根据计算结果，开展敏感性定量分析。

2.2.2 因子特征重要性分析

重要性分析是对有效数据集进行学习后获得各个输入特征重要性相对大小的过程[6,27]。为避免单一模型的偶然性，采用具备bagging集成策略的随机森林[13]与具备boosting集成策略的梯度提升树[28]共同开展因子重要性分析。最终，根据分类正确率对特征重要性表征值进行加权计算，获得各个因子的复合重要性特征值。
评估因子的特征重要性表征值是一具体数值，目前尚未有明确的标准来衡量因子的重要与否，只能根据该数值的相对大小来判断因子对模型结果的贡献程度。因此本文设定一特征重要性的判断阈值d用于剔除对模型贡献过小的因子。令d=1/2n（n为评估因子个数），当表征值>d时，认为该因子对模型结果贡献较大，应予以保留；当表征值<d时，认为该因子对模型结果贡献较为小，应予以剔除。

2.2.3 因子相关性与共线性分析

为降低因子相关性、提高模型稳定性与准确性，考虑到因子相关性较低时不能排除共线性存在，本文同时结合相关性[5]与共线性[6]分析结果进行综合考虑。本文采用皮尔逊相关系数对因子之间的相关性程度进行分析，当2个因子的相关系数绝对值大于0.40时认为存在明显相关性，应予以剔除。共线性分析中，当TOL小于0.10、VIF大于10时认为该因子共线性严重，应予以剔除[6]。

2.3 基于差分进化算法优化的滑坡危险性评估

为消除量纲影响，对最终筛选获得的危险性评估因子进行归一化处理：离散型数据采用独热编码处理，连续型数据采用线性归一化处理。最终构建模型时先采用自组织映射（Self-Organizing Map, SOM）神经网络与高斯混合模型（Gaussian Mixture Model, GMM）对研究区所有栅格单元进行无监督滑坡危险性聚类，再从滑坡危险性最低的聚类公共区中进行负样本提取，同已知滑坡样本构建机器学习数据集。最后，使用DE算法对SVM与MLP 2种代表模型的主要超参数进行全局搜索优化，并将获得的超参数优化结果代入模型进行滑坡危险性评估。

2.3.1 支持向量机（SVM）

支持向量机[7,29]是一种建立在结构风险最小化和VC维理论基础之上的经典机器学习算法，在滑坡危险性评估这一非线性高维模式识别问题上具备特有优势，比其他传统方法更好的评估能力与推广能力。
当滑坡数据集M中存在1组样本 X i ( i = 1,2 , ⋯ , n )， X i表示包含i个滑坡评估因子的输入向量， y i = 1表示发生滑坡， y i = - 1表示不发生滑坡，n为滑坡数据集样本数量。当问题为二分类时，SVM的最终目标是要寻找一个最优超平面将训练数据分成两类。则该超平面方程可表示为：
w x + b = 0
式中： w表示法向量； x表示超平面上的点； b表示常数。当 w和 b达到最优时，所找到的最优超平面将使得正样本与负样本之间的距离最大。在非线性问题中，还引入核函数、松弛变量和惩罚因子，则最优超平面的求解公式如下：
m i n i m i z e W , b , ξ : 1 2 W T W + C ∑ i = 1 h   ξ i
式中： W表示确定超平面方向的权重向量，用于确定分割平面方向；常数项 b表示位移量；h表示支持向量点数量； ξ i表示松弛变量，代表样本点离群的远近； C ( C > 0 )表示惩罚参数，代表对错误分类样本的惩罚程度。式（3）受约束于：
y i w T x + b ≥ 1 - ξ i
经拉格朗日乘子约束后，优化问题便可用二次规划算法求解。

2.3.2 多层感知机（MLP）

多层感知机[30-31]是一种按单向误差传播的多层前馈网络模型，是目前应用最广泛、研究最基本的网络模型之一。MLP可以在整个数据中识别不同的数据集，不需要预先存在的知识或经验，也不需要预先存在的统计模型来训练数据，可有效解决非线性数据的二元分类问题，因此适合应用于滑坡危险性评估。MLP由相似神经元组成的输入层、隐藏层和输出层组成，输入层神经元与隐藏层神经元通过联结关系构成处理对象的联想矩阵，隐藏层神经元与输出层神经元之间的联结构成对处理对象的决策矩阵，三层神经元通过一定权值连接起来，从而构成具有决策能力的稳定网络结构。
经诸多研究表明，隐含层数为1层时模型通常就可获得较好的结果，当隐含层数过多时，容易出现计算消耗过大、过拟合等问题，因此本文构建MLP时将隐含层固定为1层，重点关注隐含层节点数的优化问题。神经网络的隐含层神经元节点数经验取值可根据下式计算获得[32]：
S = m + n + a
式中： S为隐含层神经元个数； m为输入层神经元个数； n为输出层神经元个数； a为1~10的调节常数。

2.3.3 差分进化算法

差分进化算法[23,33]是一种基于群体差异的启发式高效随机搜索全局并行优化算法，具有原理简单、参数较少、运算更快、鲁棒性好等优良特性，是进化算法研究的重要分支。DE算法在滑坡危险性评估中还少有应用案例，因此本文引入DE算法对机器学习模型进行优化研究。
DE算法的新种群生成方案与其他进化算法不同，其本质是一种基于实数编码的具有保优思想的贪婪遗传算法。DE/rand/1/bin变异策略使得变异个体由3个互不相同的随机个体产生，具有全局搜索能力强的特点，更有利于保持种群多样性。设在优化迭代过程中采用 N p个D维向量 x i g = x i , 1 g , x i , 2 g , ⋯ , x i , D g， i = 1,2 , ⋯ , N p分别作为每一代 g = 0,1 , 2 , ⋯ , G m a x的种群，总迭代次数设为 G m a x，群体内所有个体均是一个候选解，则DE算法实现流程如图2所示。
图2 差分进化算法实现流程

Fig. 2 Differential evolution algorithm implementation process

（1）种群初始化。当初始进化代数g=0时，令 x m a x , j和 x m i n , j为解空间中第 j ( j = 1,2 , ⋯ , D )维的上界和下界，rand()函数用于产生[01]的随机数，则初始种群生成表达式为：
x i , j 0 = x m i n , j + r a n d ( j ) × x m a x , j - x m i n , j
（2）变异操作。对第g代种群的个体 x i g i = 1,2 , ⋯ , N p，随机选取3个不同的个体 x r 1 g , x r 2 g , x r 3 g r 1 , r 2 , r 3 ∈ 1 , N p 且 r 1 , r 2 , r 3 ≠ i，则新生成的变异个体表达式为：
ν i g + 1 = x r 3 g + F × x r 1 g - x r 2 g
式中：F为变异因子（0≤F≤2），其作用是控制差分矢量 x r 1 g - x r 2 g对个体 x r 3 g的影响。
（3）交叉操作。父代个体 x i g和变异个体 ν i g + 1的交叉操作由式（8）完成。这一操作方式能确保种群多样性，在生成实验个体 μ i g + 1的同时，保证至少有一位变量取自 ν i g + 1。
μ i , j g + 1 = ν i , j g + 1   r a n d ( ) ≤ C R 或 j = r a n d ( 1 , n ) x i , j g   r a n d ( ) > C R 且 j ≠ r a n d ( 1 , n )
式中： r a n d ( 1 , n )函数用于产生[1, n]的随机整数，从而确保 ν i , j g + 1至少为 μ i , j g + 1提供一个决策变量，维持种群的多样性分布；交叉因子 C R（0≤F≤1）对变异个体 ν i , j g + 1代替目标个体 x i , j g的概率起决定作用。交叉因子越大则收敛速率越快，交叉因子越小则越有利于维持种群多样性。
（4）选择操作。采用“贪婪”策略，从 x i g和 μ i g + 1之间选择适应度较优的个体作为下一代种群，具体操作方程如下：
x i g + 1 = μ i g + 1   μ i g + 1   优 于 x i g μ i g 其 他

3 研究区概况及数据源

3.1 研究区概况

福建省地处中国东南部、东海之滨，东隔台湾海峡与台湾省隔海相望，周临浙江、江西、广东三省，与长江三角洲和珠江三角洲相连，地理位置坐标介于23°33′N—28°20′N、115°50′E—120°40′E。福建省山地、丘陵连绵不绝，占全省总面积的80%以上，河谷、盆地穿插其间，地形起伏较大，气候温暖湿润、雨量充沛，植被茂盛、水系密布、河流众多，地层丰富、岩性复杂、断裂发育，交通道路延伸形成了许多边坡与路堑，房屋依山而建、矿区开山而采，坡后垦植、灌溉、堆载及坡脚切挖等活动频繁[34-35]。
福建省突发性地质灾害十分发育，并以滑坡最为常见，对人民生活与社会发展造成了巨大威胁[4]。福建省地质灾害防治信息网灾情速递信息显示，1990—2019年福建省共通报地质灾情6285起，突发性地质灾害发生数量约占灾情总数的90%，其中滑坡共通报4106起，约占灾情总数的65.33%。

3.2 数据源

本文所使用的6156个福建省2019年之前滑坡点空间分布数据（图3）、2000—2019逐年归一化植被指数数据均来自于资源环境科学与数据中心[36-37]，数字高程模型数据ASTER GDEM V003从Earthdata获取[38]，道路、河流等基础地理信息数据来源于全国地理信息资源目录服务系统[39]，岩性、断裂等地质数据从地质科学数据出版系统的公开数据库提取[40]，土地利用类型数据来源于2020年发布的GLOBELAND30数据[41]，气象站点观测数据来源于温室数据共享平台[42]。
图3 福建省滑坡分布情况

Fig. 3 Distribution of landslides in Fujian Province

4 四维特征筛选方法构建与实现

4.1 评估因子初步选取与处理

对福建省滑坡进行灾情背景分析，初步选取了21个危险性评估因子（表1）。其中：坡向、坡度、地形曲率、平面曲率、剖面曲率、坡度变率、坡向变率直接由Arc GIS空间分析工具提取，地表粗糙度使用栅格计算器根据坡度计算获得，地形起伏度、地表切割深度、高程变异系数结合均值变点法[43]提取，由SAGA GIS计算地形湿度指数与径流强度指数[4]，年平均降雨量由1980—2019年福建省70个气象站点降雨量数据空间插值获得，年平均归一化植被指数由逐年NDVI数据空间插值获得，经距离分析获取到水系距离、到断裂距离、到道路距离，工程地质岩组依据《工程岩体分级标准（GBT50218-2014）》[44]经岩性合并获得。
表1 危险性评估因子初步选取结果

Tab. 1 Preliminary selection results of hazard assessment factors

危险性评估因子类型 初选评估因子
微观地形因子 高程、坡向、坡度、地形曲率、平面曲率、剖面曲率、坡度变率、坡向变率
宏观地形因子 地形起伏度、地表切割深度、高程变异系数、地表粗糙度
水文环境因子 地形湿度指数、径流强度指数
自然地理因子 年均降雨量、年均归一化植被指数、到河流距离
地质影响因子 工程地质岩组、到断裂距离
社会影响因子 土地利用类型、到道路距离
影响因子状态分级方案如下：对于离散型因子，直接重新赋予连续值进行区分；对于连续型因子，到道路距离与到河流距离均以400、800、1200、1600、2000 m划分为6个等级，到断裂构造距离以600、1200、1800、2400、3000 m划分为6个等级，坡向以平地及8个坡向方位划分为9类，地表曲率以<0、=0、>0划分为3级，其余因子均根据已知滑坡样本点对连续型评估因子进行采样，基于采样结果采用自然间断点法将因子分为9类，从而使得状态分级结果更符合研究区域内的滑坡分布特征。
为便于计算与分析，根据区域大小与数据情况将研究区按照30 m×30 m进行格网单元划分，共计134 288 470个评估单元。

4.2 评估因子敏感性指数计算与分析

各初选评估因子的敏感性指数计算结果如表2所示。由表2可知：土地利用类型对滑坡的影响最大、地形曲率对滑坡的影响最小；剖面曲率、平面曲率、坡度变率、坡向变率、断裂构造、地形曲率等6个因子的平均敏感性指数低于判断阈值0.5，对福建省滑坡的影响作用较小；土地利用类型、地表切割深度的平均敏感性指数大于2，对福建省滑坡的影响作用较为显著；总体上，宏观地形因子对滑坡的影响作用明显高于微观地形因子，说明宏观地形地貌特征更有利于揭示滑坡背景或影响滑坡的形成。
表2 危险性评估因子敏感性分析计算结果

Tab. 2 Calculation results of sensitivity analysis of hazard assessment factors

敏感性排序 危险性评估因子 F S I F R F S I I F S I C F F S I ¯
1 土地利用类型 3.09 2.02 1.25 2.12
2 地表切割深度 2.03 2.85 1.41 2.10
3 工程地质岩组 1.40 2.33 1.21 1.65
4 地形起伏度 1.62 2.05 1.22 1.63
5 地表粗糙度 1.19 2.15 1.10 1.48
6 年均降雨量 1.26 1.67 1.06 1.33
7 年均归一化植被指数 1.31 1.57 1.05 1.31
8 坡向 1.01 1.80 0.98 1.26
9 高程 1.03 1.53 0.95 1.17
10 坡度 0.95 1.17 0.85 0.99
11 高程变异系数 0.98 1.05 0.81 0.95
12 到道路距离 1.13 0.91 0.71 0.92
13 到河流距离 0.76 0.69 0.57 0.67
14 径流强度指数 0.49 0.64 0.49 0.54
15 地形湿度指数 0.57 0.56 0.49 0.54
16 平面曲率 0.46 0.54 0.45 0.48
17 剖面曲率 0.46 0.51 0.44 0.47
18 坡度变率 0.44 0.50 0.43 0.46
19 坡向变率 0.20 0.20 0.19 0.20
20 到断裂构造距离 0.19 0.18 0.17 0.18
21 地形曲率 0.07 0.07 0.07 0.07

4.3 评估因子特征重要性分析

进行因子重要性分析时，首先要构建一份模型数据集：正样本为6156个已知滑坡点数据，以滑坡点为圆心生成半径为5 km的圆形缓冲叠加区，在叠加区外随机采样获取同等数量的负样本。经模型构建，计算获得本文各初选评估因子的复合重要性特征值如表3所示。根据表3可知，特征重要性最高的评估因子为年均降雨量，且显著高于其他因子，说明降雨对于预测福建省的滑坡危险情况具有较大的价值，与实际灾害发生情况吻合。特征重要性划分阈值d为0.02，则重要性过低的因子仅有地形曲率。
表3 危险性评估因子重要性分析计算结果

Tab. 3 Calculation results of importance analysis of hazard assessment factors

重要性排序 危险性评估因子 GBDT重要性特征值 RF重要性特征值 复合重要性特征值
1 年均降雨量 0.29 0.10 0.35
2 年均归一化植被指数 0.12 0.08 0.19
3 高程 0.12 0.08 0.19
4 地表切割深度 0.10 0.09 0.17
5 土地利用类型 0.13 0.06 0.17
6 地形起伏度 0.10 0.07 0.16
7 到道路距离 0.04 0.05 0.08
8 高程变异系数 0.01 0.05 0.07
9 工程地质岩组 0.04 0.03 0.06
10 到河流距离 0.01 0.04 0.05
11 到断裂距离 0.01 0.04 0.05
12 地表粗糙度 0.00 0.04 0.04
13 坡度变率 0.00 0.04 0.04
14 坡度 0.01 0.04 0.04
15 地形湿度指数 0.01 0.03 0.04
16 平面曲率 0.00 0.03 0.04
17 径流强度指数 0.00 0.04 0.04
18 坡向变率 0.00 0.03 0.04
19 剖面曲率 0.00 0.03 0.03
20 坡向 0.00 0.03 0.03
21 地形曲率 0.00 0.01 0.01

4.4 评估因子综合优选与结果分析

完成敏感性分析与重要性分析后，还需对21个初选评估因子进行相关性分析（图4）与共线性诊断（表4）。最后，根据4D特征筛选法的构建原则，结合敏感性、重要性、相关性、共线性的定量计算结果，进行福建省滑坡影响因子的综合优选。筛选过程如下：
图4 影响因子相关性矩阵

Fig. 4 Correlation matrix of influencing factors

表4 危险性评估因子共线性分析计算结果

Tab. 4 Calculation results of collinearity analysis of hazard assessment factors

危险性评估因子 TOL VIF 危险性评估因子 TOL VIF
坡度 0.07 14.00 年均降雨量 0.56 1.79
地形起伏度 0.09 10.61 高程变异系数 0.62 1.62
地表切割深度 0.10 9.90 坡度变率 0.75 1.33
地表粗糙度 0.12 8.71 土地利用类型 0.83 1.21
年均归一化植被指数 0.37 2.69 到河流距离 0.84 1.19
地形曲率 0.40 2.51 到道路距离 0.85 1.18
高程 0.47 2.13 到断裂构造距离 0.87 1.15
平面曲率 0.50 1.99 工程地质岩组 0.90 1.12
坡向变率 0.52 1.92 径流强度指数 0.91 1.10
剖面曲率 0.53 1.90 坡向 1.00 1.01
地形湿度指数 0.55 1.81
（1）根据敏感性分析与重要性分析结果，直接剔除剖面曲率、平面曲率、坡度变率、坡向变率、到断裂构造距离、地形曲率6个因子；
（2）降雨对福建滑坡具有显著影响作用，且年均降雨量具有最高特征重要性，故保留；考虑因子相关性，故剔除年均归一化植被指数、高程2个因子；
（3）地表切割深度对揭示福建滑坡特征最具敏感度，故保留；考虑因子相关性与共线性，故剔除坡度、地表粗糙度、地形起伏度等3个因子。
为验证4D特征筛选法的有效性，分别以初选的21个评估因子与优选的10个评估因子设置对照组进行对比实验与分析，并通过ROC曲线进行模型精度评估（表5）。由表5可知，分别根据敏感性分析、重要性分析、敏感性与重要性分析剔除部分因子后，SVM与MLP的ROC曲线AUC值均没有明显变化，表明重要性分析与敏感性分析筛选出的因子更具有典型性，以更少的因子获得了几乎一致的模型精度；保留年均降雨量与保留地表切割深度的评估精度在整体上要优于保留其他相关性较强的因子，说明根据原则保留的评估因子相对较优。因此，剔除上述11个因子后，剩余因子均具有较高的敏感性与重要性，并且相对独立，则最终用于建模的10个适宜性评估因子分别是：坡向、高程变异系数、土地利用类型、年均降雨量、地表切割深度、到河流距离、到道路距离、工程地质岩组、地形湿度指数、径流强度指数。
表5 基于4D特征筛选法的模型对比计算结果

Tab. 5 Results of model comparison calculations based on 4D feature screening method

实验组别 输入因子说明 ROC曲线AUC值
SVM MLP
初始对照组 21个初选因子 0.83 0.84
敏感性实验组 15个保留因子 0.83 0.84
重要性实验组 20个保留因子 0.83 0.84
重要性与敏感性实验组 15个保留因子 0.83 0.84
4D特征筛选结果对照组 10个优选因子 0.80 0.81
年均降雨量实验组Ⅰ NDVI与其他9个优选因子 0.79 0.80
年均降雨量实验组Ⅱ DEM与其他9个优选因子 0.80 0.82
地表切割深度实验组Ⅰ Slope与其他9个优选因子 0.78 0.79
地表切割深度实验组Ⅱ Rough与其他9个优选因子 0.78 0.79
地表切割深度实验组Ⅲ RA与其他9个优选因子 0.80 0.81

注：NDVI表示年均归一化植被指数；DEM表示高程；Slope表示坡度；Rough表示地表粗糙度；RA表示地形起伏度。

5 滑坡危险性评估模型优化与构建

考虑到研究区评估单元较多、滑坡样本较少，最终模型构建过程中均按照8:2的比例划分训练集和测试集，训练集与测试集中的正、负样本比例均为1:1。用于超参数优化的DE算法基于Python实现，种群规模均设为20、最大进化次数均设为50，其余参数均为一般默认值。最后，将所有评估栅格样本的滑坡发生概率作为危险性指数（取值为0~1），并将其从高到低排序按照1:2:4:2:1的面积比划分出极高滑坡危险区、较高滑坡危险区、中等滑坡危险区、较低滑坡危险区、极低滑坡危险区5个区划等级[8]，进行滑坡危险性区划研究。

5.1 支持向量机评估模型构建及优化

在非线性问题先验知识不足的情况下，径向基函数能够将样本映射到一个更高维的空间[29]，因此本文选用径向基函数作为核函数。使用DE算法对SVM的主要超参数惩罚因子C与gamma进行优化，设定惩罚因子C与gamma均在区间[0.110]内通过连续搜索的方式寻找最优超参数，最终获得最优超参数组合为C=10.00、gamma=0.2318，并代入SVM对其进行优化。
对模型计算结果进行空间区划，获得滑坡危险性分级图（图5）与滑坡危险性分级统计结果（表6）。根据表6可知，初始SVM评估获得的极高与较高危险区频率比分别为1.57、1.66，极低与较低危险区频率比分别为0.21、0.44，极高与较高危险区包含了48.93%的滑坡点，极低与较低危险区仅包含10.93%的滑坡点；DE-SVM评估获得的极高与较高危险区包含了47.87%的滑坡点，极低与较低危险区则包含10.41%的滑坡点。经比较，由DE-SVM评估获得的极低危险区滑坡占比略低于SVM，极高与较高危险区的频率比与滑坡占比也均略低于SVM，这是因防止过拟合而根据经验值设置了较小的惩罚因子搜索范围所致。
图5 SVM与DE-SVM福建省滑坡危险性评估分级

Fig. 5 SVM and DE-SVM landslide hazard assessment classification charts for Fujian Province

表6 SVM与DE-SVM滑坡危险性分级统计结果

Tab. 6 Results of SVM and DE-SVM landslide hazard classification statistics

评估模型 栅格单元数量/个 栅格单元面积占比/% 滑坡数量/个 滑坡数量占比/% 频率比 危险性等级
SVM 13 428 847 10 132 2.14 0.21 极低
26 857 694 20 541 8.79 0.44 较低
53 715 388 40 2471 40.14 1.00 中等
26 857 694 20 2048 33.27 1.66 较高
13 428 847 10 964 15.66 1.57 极高
DE-SVM 13 428 847 10 167 2.71 0.27 极低
26 857 694 20 474 7.70 0.38 较低
53 715 388 40 2568 41.72 1.04 中等
26 857 694 20 2026 32.91 1.65 较高
13 428 847 10 921 14.96 1.50 极高

5.2 多层感知机评估模型构建及优化

在构建MLP时，输入层是10个归一化的评估因子，因离散型数据经独热编码处理，所以实际上有30个输入神经元，隐含层为1层，输出层即为滑坡危险性指数。根据式（5）计算获得MLP隐含层神经元个数的经验值为6~16，因此本文结合DE算法设定隐含层节点数S在区间[6,16]内通过离散搜索的方式寻找最优超参数，初始学习率（learning_rate_init，LRI）则在区间[0.1]内通过连续搜索的方式寻找最优超参数，最终计算获得的最优超参数组合为S=14、LRI=0.0095，将其代入MLP对其进行优化。对计算结果进行滑坡危险性区划，获得滑坡危险性分级图（图6）与滑坡危险性分级统计结果（表7）。
图6 MLP与DE-MLP福建省滑坡危险性评估分级

Fig. 6 MLP and DE-MLP landslide hazard assessment classification charts for Fujian Province

表7 MLP与DE-MLP滑坡危险性分级统计结果

Tab. 7 Results of MLP and DE-MLP landslide hazard classification statistics

评估模型 栅格单元数量/个 栅格单元面积占比/% 滑坡数量/个 滑坡数量占比/% 频率比 危险性等级
MLP 13 428 847 10 153 2.49 0.25 极低
26 857 694 20 584 9.49 0.47 较低
53 715 388 40 2328 37.82 0.95 中等
26 857 694 20 1816 29.50 1.47 较高
13 428 847 10 1275 20.71 2.07 极高
DE-MLP 13 428 847 10 146 2.37 0.24 极低
26 857 694 20 570 9.26 0.46 较低
53 715 388 40 2264 36.78 0.92 中等
26 857 694 20 1885 30.62 1.53 较高
13 428 847 10 1291 20.97 2.10 极高
根据表7可知，初始MLP评估获得的福建省滑坡极高与较高危险区的频率比分别为2.07、1.47，极低与较低危险区的频率比分别为0.25、0.47，极高与较高危险区共包含50.21%的滑坡点，极低与较低危险区共包含11.97%的滑坡点；DE-MLP评估获得的极高与较高危险区频率比分别为2.10、1.53，极低与较低危险区频率比分别为0.24、0.46，极高与较高危险区包含了51.59%的滑坡点，极低与较低危险区仅含有11.63%的滑坡点。经比较，由DE-MLP获得的极高与较高危险区的滑坡比及频率比均高于MLP评估结果，由DE-MLP获得的极低与极低危险区的滑坡比及频率比均低于MLP评估结果，因此DE-MLP能更为有效地区划福建省的滑坡危险性。

5.3 模型评估结果评价与分析

本文对训练集、测试集、完整集数据的分类准确率及ROC曲线的AUC值进行计算（表8），并结合各个模型的混淆矩阵（表9）对模型精度进行初步评估。由表8可知：基于3类数据集构建的各模型分类准确率均高于0.85且基本一致，表明模型拟合效果较为合理；基于3类数据集构建的DE-SVM分类准确率与AUC值均明显高于SVM，基于3类数据集构建的DE-MLP分类准确率与AUC值与MLP基本一致，表明DE算法对SVM的分类精度提升效果较为显著，而MLP的分类效果则提升不够明显。由表9可知：DE-SVM中2类样本的召回率均高于SVM，且DE-SVM总体准确率比SVM高了4%，这也再次说明了DE算法有益于提升SVM的分类精度；DE-MLP与MLP的总体准确率一致，但DE-MLP滑坡样本的召回率要高于MLP，表明了经DE算法优化后的MLP也能更有效地识别滑坡。
表8 各类数据集分类准确率及ROC曲线计算结果

Tab. 8 Classification accuracy and ROC curve calculation results for various datasets

项目 SVM DE-SVM MLP DE-MLP
训练集准确率 0.85 0.89 0.85 0.85
测试集准确率 0.86 0.89 0.86 0.85
完整集准确率 0.85 0.89 0.85 0.85
训练集AUC值 0.92 0.95 0.92 0.92
测试集AUC值 0.92 0.95 0.93 0.92
完整集AUC值 0.92 0.95 0.92 0.92
表9 各个模型混淆矩阵计算结果

Tab. 9 Results of confusion matrix calculations for each model

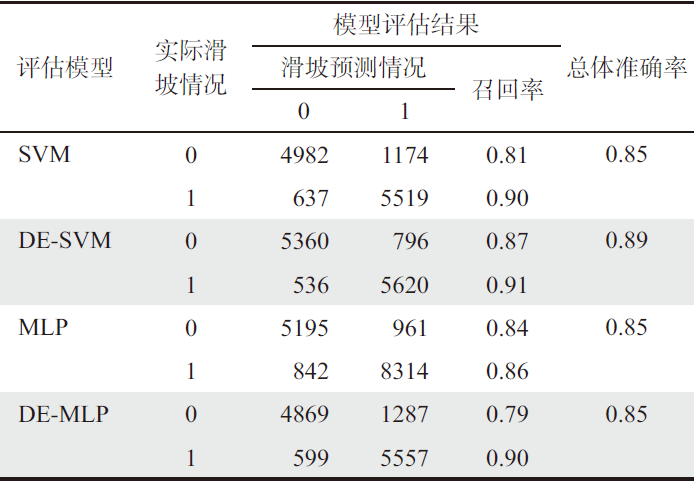注：0表示滑坡不发生；1表示滑坡发生。

为更好地对2种滑坡危险性评估模型的实际评估改进效果进行对比评价，主要使用成功率曲线对基于训练集、测试集、完整集数据计算获得的危险性指数与所有已知滑坡样本的拟合程度进行分析[45⇓-47]，结果见表10与图7。由表10与图7可知：同一模型3类数据集成功率曲线的AUC值基本一致，表明使用上述数据集构建的模型评估效果较为稳定；基于3类数据集经DE算法调优后的SVM与MLP成功率曲线AUC值均显著提升。根据完整数据集的成功率曲线计算结果（图7）可知：DE-SVM的AUC值为0.8208，相较于未经DE算法优化的SVM提高了4.43%；DE-MLP的AUC值为0.7750，相较于未经DE算法优化的MLP提高了4.37%。模型评价结果表明，DE算法具有较强的全局搜索能力，使用DE算法优化SVM与MLP能显著提升模型的滑坡危险性评估准确度。
表10 各类数据集成功率曲线计算结果

Tab. 10 Calculation results of success rate curves of various data sets

数据集类别 SVM DE-SVM MLP DE-MLP
训练数据集 0.78 0.82 0.73 0.77
测试数据集 0.78 0.82 0.74 0.78
完整数据集 0.78 0.82 0.73 0.78
图7 福建省滑坡危险性评估模型成功率曲线

Fig. 7 Success rate curve of landslide hazard assessment model in Fujian Province

由图5与图6可知，虽然各个模型区划结果局部存在细微差异，但滑坡危险性的空间分布规律较一致：福建省滑坡极高危险性地区主要分布在东北部、西部及西北部，小部分位于中部及南部，这些地区普遍年均降雨量较高、地形复杂多变，山区人类活动也更容易为滑坡发生营造条件，故显现出更高危险性；滑坡危险性极低地区主要位于东南沿海一带及闽江流域两侧，其地势均较为平坦、经济水平较高。

6 结论

本文以福建省滑坡为例开展双向优化的滑坡危险性评估方法研究，在构建因子敏感性指数开展敏感性分析的基础上，结合重要性分析、相关性分析、共线性分析构建4D特征筛选法用于评估因子的综合定量筛选，并引入DE算法对SVM与MLP的主要超参数进行全局搜索优化，经分析得出以下结论：
（1）遵循“保证敏感性、保留重要性、剔除相关性、避免共线性”原则构建的4D特征筛选法，能更加客观全面地选取适宜性更高的危险性评估因子，从而降低特征维度、减少信息冗余以提升评估模型性能。
（2）DE算法对SVM与MLP具有显著的优化效果，有益于提升滑坡危险性评估准确度。DE算法能从全局搜索获得更优的超参数，DE-SVM、DE-MLP的AUC值相较于未优化前的模型分别提升了4.43%、4.37%，评估精度均有了较大幅度的提高。
（3）降雨与土地利用类型对福建省滑坡发生具有重要影响作用，地形曲率要素与变率要素、断裂构造对滑坡发生影响较小。福建省滑坡极高危险区普遍年均降雨较高、地形复杂多变，极低危险区主要位于东南沿海一带及闽江流域两侧。
由于滑坡数据难以获取等问题，研究中缺乏使用其他滑坡数据集进行验证分析，未来可以进一步收集有效数据进行研究，并就优化效果同其他机器学习模型进行对比，为今后的滑坡危险性评估研究提供思路。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
张洪吉, 赵铮, 陈建华, 等. 面向滑坡危险性评价的深度一维卷积神经网络方法——以四川省芦山县为例[J]. 自然灾害学报, 2021, 30(3):191-198.

[ Zhang H J, Zhao Z, Chen J H, et al. A deep one-dimensional convolutional neural network method for landslide risk assessment: A case study in Lushan, Sichuan, China[J]. Journal of Natural Disasters, 2021, 30(3):191-198. ] DOI:10.13577/j.jnd.2021.0321

DOI

[2]
Dou J, Yunus A P, Bui D T, et al. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan[J]. Landslides, 2020, 17(3):641-658. DOI:10.1007/s10346-019-01286-5

DOI

[3]
Wang Y, Fang Z C, Hong H Y. Comparison of convolutional neural networks for landslide susceptibility mapping in Yanshan County, China[J]. The Science of the Total Environment, 2019, 666:975-993. DOI:10.1016/j.scitotenv.2019.02.263

DOI PMID

[4]
杨城, 林广发, 张明锋, 等. 基于DEM的福建省土质滑坡敏感性评价[J]. 地球信息科学学报, 2016, 18(12):1624-1633.

DOI

[ Yang C, Lin G F, Zhang M F, et al. Soil landslide susceptibility assessment based on DEM[J]. Journal of Geo-Information Science, 2016, 18(12):1624-1633. ] DOI:10.3724/SP.J.1047.2016.01624

DOI

[5]
牛全福, 冯尊斌, 党星海, 等. 黄土区滑坡研究中地形因子的选取与适宜性分析[J]. 地球信息科学学报, 2017, 19(12):1584-1592.

DOI

[ Niu Q F, Feng Z B, Dang X H, et al. Suitability analysis of topographic factors in loess landslide research[J]. Journal of Geo-Information Science, 2017, 19(12):1584-1592. ] DOI:10.3724/SP.J.1047.2017.01584

DOI

[6]
王毅, 方志策, 牛瑞卿, 等. 基于深度学习的滑坡灾害易发性分析[J]. 地球信息科学学报, 2021, 23(12):2244-2260.

DOI

[ Wang Y, Fang Z C, Niu R Q, et al. Landslide susceptibility analysis based on deep learning[J]. Journal of Geo-information Science, 2021, 23(12):2244-2260. ] DOI:10.12082/dqxxkx.2021.210057

DOI

[7]
李远远, 梅红波, 任晓杰, 等. 基于确定性系数和支持向量机的地质灾害易发性评价[J]. 地球信息科学学报, 2018, 20(12):1699-1709.

DOI

[ Li Y Y, Mei H B, Ren X J, et al. Geological disaster susceptibility evaluation based on certainty factor and support vector machine[J]. Journal of Geo-Information Science, 2018, 20(12):1699-1709. ] DOI:10.12082/dqxxkx.2018.180349

DOI

[8]
黄发明, 殷坤龙, 蒋水华, 等. 基于聚类分析和支持向量机的滑坡易发性评价[J]. 岩石力学与工程学报, 2018, 37(1):156-167.

[ Huang F M, Yin K L, Jiang S H, et al. Landslide susceptibility assessment based on clustering analysis and support vector machine[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1):156-167. ] DOI:10.13722/j.cnki.jrme.2017.0824

DOI

[9]
黄锦林, 赵吉国, 张婷, 等. 基于层次分析法的库岸高速滑坡危险度评价[J]. 自然灾害学报, 2011, 20(5):95-99.

[ Huang J L, Zhao J G, Zhang T, et al. AHP-based hazard degree assessment of high-speed landslide of reservoir bank[J]. Journal of Natural Disasters, 2011, 20(5):95-99. ] DOI:10.13577/j.jnd.2011.0515

DOI

[10]
张钟远, 邓明国, 徐世光, 等. 镇康县滑坡易发性评价模型对比研究[J]. 岩石力学与工程学报, 2022, 41(1):157-171.

[ Zhang Z Y, Deng M G, Xu S G, et al. Comparison of landslide susceptibility assessment models in Zhenkang County, Yunnan Province, China[J]. Chinese Journal of Rock Mechanics and Engineering, 2022, 41(1):157-171. ] DOI:10.13722/j.cnki.jrme.2021.0360

DOI

[11]
Aditian A, Kubota T, Shinohara Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia[J]. Geomorphology, 2018, 318:101-111. DOI:10.1016/j.geomorph.2018.06.006

DOI

[12]
Liang Z, Wang C M, Zhang Z M, et al. A comparison of statistical and machine learning methods for debris flow susceptibility mapping[J]. Stochastic Environmental Research and Risk Assessment, 2020, 34(11):1887-1907. DOI:10.1007/s00477-020-01851-8

DOI

[13]
Chang Z L, Du Z, Zhang F, et al. Landslide susceptibility prediction based on remote sensing images and GIS: Comparisons of supervised and unsupervised machine learning models[J]. Remote Sensing, 2020, 12(3):502. DOI:10.3390/rs12030502

DOI

[14]
Đurić U, Marjanović M, Radić Z, et al. Machine learning based landslide assessment of the Belgrade metropolitan area: Pixel resolution effects and a cross-scaling concept[J]. Engineering Geology, 2019, 256:23-38. DOI:10.1016/j.enggeo.2019.05.007

DOI

[15]
Wang Y, Fang Z C, Wang M, et al. Comparative study of landslide susceptibility mapping with different recurrent neural networks[J]. Computers & Geosciences, 2020, 138:104445. DOI:10.1016/j.cageo.2020.104445

DOI

[16]
Bragagnolo L, da Silva R V, Grzybowski J M V. Landslide susceptibility mapping with r.landslide: A free open-source GIS-integrated tool based on Artificial Neural Networks[J]. Environmental Modelling & Software, 2020, 123:104565. DOI:10.1016/j.envsoft.2019.104565

DOI

[17]
Thi Ngo P T, Panahi M, Khosravi K, et al. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran[J]. Geoscience Frontiers, 2021, 12(2):505-519. DOI:10.1016/j.gsf.2020.06.013

DOI

[18]
Zhu L, Huang L H, Fan L Y, et al. Landslide susceptibility prediction modeling based on remote sensing and a novel deep learning algorithm of a cascade-parallel recurrent neural network[J]. Sensors, 2020, 20(6):1576. DOI:10.3390/s20061576

DOI

[19]
Huang F M, Zhang J, Zhou C B, et al. A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction[J]. Landslides, 2020, 17(1):217-229. DOI:10.1007/s10346-019-01274-9

DOI

[20]
Huang F M, Yin K L, Zhang G R, et al. Landslide displacement prediction using discrete wavelet transform and extreme learning machine based on chaos theory[J]. Environmental Earth Sciences, 2016, 75(20):1-18. DOI:10.1007/s12665-016-6133-0

DOI

[21]
胡安龙, 王孔伟, 李建林, 等. 基于智能算法优化支持向量机模型的滑坡稳定性预测[J]. 自然灾害学报, 2016, 25(5):46-54.

[ Hu A L, Wang K W, Li J L, et al. Prediction of landslide stability based on SVM model optimized by intelligent algorithm[J]. Journal of Natural Disasters, 2016, 25(5):46-54. ] DOI:10.13577/j.jnd.2016.0506

DOI

[22]
Zhu C H, Zhang J J, Liu Y, et al. Comparison of GA-BP and PSO-BP neural network models with initial BP model for rainfall-induced landslides risk assessment in regional scale: A case study in Sichuan, China[J]. Natural Hazards, 2020, 100(1):173-204. DOI:10.1007/s11069-019-03806-x

DOI

[23]
邹强. 洪灾风险综合分析与智能评价的理论与方法[D]. 武汉: 华中科技大学, 2013.

[ Zou Q. Study on the theory and method of comprehensive analysis and intelligent assessment of flood disaster risk[D]. Wuhan: Huazhong University of Science and Technology, 2013. ] DOI:10.7666/d.D409168

DOI

[24]
丁青锋, 尹晓宇. 差分进化算法综述[J]. 智能系统学报, 2017, 12(4):431-442.

[ Ding Q F, Yin X Y. Research survey of differential evolution algorithms[J]. CAAI Transactions on Intelligent Systems, 2017, 12(4):431-442. ] DOI:10.11992/tis.201605015

DOI

[25]
唐川. 德国波恩地区滑坡特征与危险性评价[J]. 水土保持学报, 2000, 14(1):48-53,81.

[ Tang C. Characteristics of landslides and its hazard assessment in Boon area, Germany[J]. Journal of Soil Water Conservation, 2000, 14(1):48-53,81. ] DOI:10.13870/j.cnki.stbcxb.2000.01.010

DOI

[26]
李益敏, 谢亚亚, 蒋德明, 等. 怒江州斜坡地质灾害孕灾环境因素敏感性研究[J]. 水土保持研究, 2018, 25(5):300-305.

[ Li Y M, Xie Y Y, Jiang D M, et al. Study on sensitivity in disaster-pregnant environmental factors of slope geological hazards in Nujiang prefecture[J]. Research of Soil and Water Conservation, 2018, 25(5):300-305. ] DOI:10.13869/j.cnki.rswc.2018.05.043

DOI

[27]
林荣福, 刘纪平, 徐胜华, 等. 随机森林赋权信息量的滑坡易发性评价方法[J]. 测绘科学, 2020, 45(12):131-138.

[ Lin R F, Liu J P, Xu S H, et al. Evaluation method of landslide susceptibility based on random forest weighted information[J]. Science of Surveying and Mapping, 2020, 45(12):131-138. ] DOI:10.16251/j.cnki.1009-2307.2020.12.020

DOI

[28]
宋英旭. 基于空天地一体化监测的滑坡风险动态评价研究[D]. 武汉: 中国地质大学, 2019.

[ Song Y X. Dynamic evaluation of landslide risk based on integrated monitoring of satellite,airborne and ground-based data[D]. Wuhan: China University of Geosciences, 2019. ] DOI:10.27492/d.cnki.gzdzu.2019.000169

DOI

[29]
徐胜华, 刘纪平, 王想红, 等. 熵指数融入支持向量机的滑坡灾害易发性评价方法——以陕西省为例[J]. 武汉大学学报·信息科学版, 2020, 45(8):1214-1222.

[ Xu S H, Liu J P, Wang X H, et al. Landslide susceptibility assessment method incorporating index of entropy based on support vector machine: A case study of Shanxi Province[J]. Geomatics and Information Science of Wuhan University, 2020, 45(8):1214-1222. ] DOI:10.13203/j.whugis20200109

DOI

[30]
王志恒, 胡卓玮, 赵文吉, 等. 基于多层感知器模型的区域滑坡敏感性评价研究——以四川低山丘陵区为例[J]. 防灾减灾工程学报, 2015, 35(5):691-698.

[ Wang Z H, Hu Z W, Zhao W J, et al. Research on regional landslide susceptibility assessment based on multiple layer perceptron:Taking the hilly area in Sichuan as example[J]. Journal of Disaster Prevention and Mitigation Engineering, 2015, 35(5):691-698. ] DOI:10.13409/j.cnki.jdpme.2015.05.021

DOI

[31]
刘杰, 武震. 基于GIS的白龙江流域舟曲—武都段的滑坡危险性评价[J]. 地震工程学报, 2020, 42(6):1723-1734.

[ Liu J, Wu Z. Landslide risk assessment of the Zhouqu-Wudu section of bailong river basin based on geographic information system[J]. China Earthquake Engineering Journal, 2020, 42(6):1723-1734. ] DOI:10.3969/j.issn.1000-0844.2020.06.1723

DOI

[32]
施紫越, 朱海燕, 王晶菁, 等. 耦合模型视角下的湘西州土质滑坡易发性探讨[J]. 水土保持研究, 2021, 28(3):377-383.

[ Shi Z Y, Zhu H Y, Wang J J, et al. Analysis on susceptibility assessment of soil landslide in Xiangxi Prefecture from the perspective of coupling model[J]. Research of Soil and Water Conservation, 2021, 28(3):377-383. ] DOI:10.13869/j.cnki.rswc.20210111.001

DOI

[33]
Storn R, Price K. Differential evolution - A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4):341-359. DOI:10.1023/A:1008202821328

DOI

[34]
狄靖月, 许凤雯, 李宇梅, 等. 东南地区引发地质灾害降水分型及阈值分析[J]. 灾害学, 2019, 34(1):62-67,93.

[ Di J Y, Xu F W, Li Y M, et al. Precipitation type and threshold analysis of geological disasters in southeast[J]. Journal of Catastrophology, 2019, 34(1):62-67,93. ] DOI:10.3969/j.issn.1000-811X.2019.01.013

DOI

[35]
叶龙珍, 柳侃, 黄国平, 等. 福建重大地质灾害特征及其影响因素[J]. 中国地质灾害与防治学报, 2015, 26(1):98-102.

[ Ye L Z, Liu K, Huang G P, et al. The characteristics and influence factors of catastrophic geological disaster in Fujian Province[J]. The Chinese Journal of Geological Hazard and Control, 2015, 26(1):98-102. ] DOI:10.16031/j.cnki.issn.1003-8035.2015.01.017.

DOI

[36]
地质灾害点空间分布数据[DB/OL]. 2019. https://www.resdc.cn/data.aspx?DATAID=290

[Data on the spatial distribution of geological hazard sites[DB/OL]. 2019. https://www.resdc.cn/data.aspx?DATAID=290 ]

[37]
徐新良. 中国年度植被指数(NDVI)空间分布数据集.资源环境科学数据注册与出版系统(http://www.resdc.cn/DOI), 2018.

[ Xu X L. Annual vegetation index (NDVI) spatial distribution dataset for China. Resource and environmental science data registration and publication system(http://www.resdc.cn/DOI), 2018. ] DOI:10.12078/2018060601

DOI

[38]
ASTER Global Digital Elevation Model V003[DB/OL]. 2019. https://search.earthdata.nasa.gov/search

[39]
1:100万公众版基础地理信息数据[DB/OL]. 2021. https://www.webmap.cn/commres.do?method=result100W

[1:1 million public version of basic geographic information data[DB/OL]. 2021. https://www.webmap.cn/commres.do?method=result100W ]

[40]
庞健峰, 丁孝忠, 韩坤英, 等. 1:100万中华人民共和国地质图空间数据库[DB].地质科学数据, http://dcc.ngac.org.cn/geologicalData/rest/geologicalData/geologicalDataDetail/402881f75d9bc10e015d9bc11be70000

[ Pang J F, Ding X Z, Han K Y, et al. 1:1 million spatial database of geological maps of the People's Republic of China[DB]. Geoscience data, http://dcc.ngac.org.cn/geologicalData/rest/geologicalData/geologicalDataDetail/402881f75d9bc10e015d9bc11be70000. ] DOI:10.23650/data.H.2017.NGA105570.T1.64.1

DOI

[41]
30米全球地表覆盖数据[DB/OL]. 2020. http://www.globallandcover.com/defaults.html?src=/Scripts/map/defaults/download.html&head=download&type=data

[30m global ground cover data[DB/OL]. 2020. http://www.globallandcover.com/defaults.html?src=/Scripts/map/defaults/download.html&head=download&type=data ]

[42]
温室数据共享平台气象数据[DB/OL]. 2019. http://data.sheshiyuanyi.com/

[Meteorological data[DB/OL]. 2019. http://data.sheshiyuanyi.com/. ]

[43]
陈学兄, 常庆瑞, 郭碧云, 等. 基于SRTM DEM数据的中国地形起伏度分析研究[J]. 应用基础与工程科学学报, 2013, 21(4):670-678.

[ Chen X X, Chang Q R, Guo B Y, et al. Analytical study of the relief amplitude in China based on SRTM DEM data[J]. Journal of Basic Science and Engineering, 2013, 21(4):670-678. ] DOI:10.3969/j.issn.1005-0930.2013.04.009

DOI

[44]
工程岩体分级标准: GBT50218-2014[S]北京: 中国计划出版社, 2014.

[Standard for engineering classification of rock mass: GBT50218-2014[S]. Beijing: China Planning Press, 2014. ]

[45]
Pourghasemi H R, Jirandeh A G, Pradhan B, et al. Landslide susceptibility mapping using support vector machine and GIS at the Golestan Province, Iran[J]. Journal of Earth System Science, 2013, 122(2):349-369. DOI:10.1007/s12040-013-0282-2

DOI

[46]
Pradhan B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS[J]. Computers & Geosciences, 2013, 51:350-365. DOI:10.1016/j.cageo.2012.08.023

DOI

[47]
Chung C J, Fabbri A G. Predicting landslides for risk analysis: Spatial models tested by a cross-validation technique[J]. Geomorphology, 2008, 94(3/4):438-452. DOI:10.1016/j.geomorph.2006.12.036

DOI

Options
文章导航

/

〈 〉