EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 1: 131 - 141

DOI: https://doi.org/10.12082/dqxxkx.2023.220458

地球信息科学理论与方法

基于SAR和AIS的角度最近邻数据关联方法

  • 李可欣 , 1 ,
  • 郭健 , 1, * ,
  • 王宇君 1 ,
  • 李宗明 2 ,
  • 缪坤 3 ,
  • 陈辉 4
展开
  • 1.信息工程大学，郑州 450001
  • 2.31682部队，兰州 730000
  • 3.陆军特种作战学院，桂林 541000
  • 4.31438部队，沈阳 110031
*郭健（1964—），女，安徽安庆人，教授，硕士生导师，主要从事地理空间数据及地理信息系统应用研究。E-mail:

李可欣（1998—），女，湖北孝感人，硕士研究生，主要从事地理信息系统应用研究。E-mail:

收稿日期: 2022-06-29

  修回日期: 2022-08-29

  网络出版日期: 2023-03-25

收起

A method of Angular Nearest Neighbor Data Association based on SAR and AIS

  • LI Kexin , 1 ,
  • GUO Jian , 1, * ,
  • WANG Yujun 1 ,
  • LI Zongming 2 ,
  • MIU Kun 3 ,
  • CHEN Hui 4
Expand
  • 1. Information Engineering University, Zhengzhou 450001, China
  • 2. 31682 Troops, Lanzhou 730000, China
  • 3. Army Special Operations College，Guilin 541000, China
  • 4. 31438 Troops, Shenyang 110031, China
*GUO Jian, E-mail:

Received date: 2022-06-29

  Revised date: 2022-08-29

  Online published: 2023-03-25

Fold

摘要

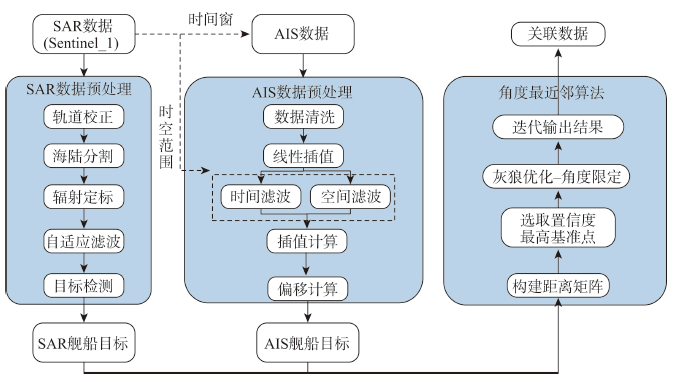
提升海上态势感知能力是构建智慧海洋的重要环节。针对目前海上目标研究单源传感器存在感知盲区，多源传感器数据关联易受杂波干扰、在密集区表现不佳等问题，本文基于合成孔径雷达(SAR)和船舶自动识别系统(AIS)数据，提出一种抗干扰性强的角度最近邻数据关联方法，充分利用SAR与AIS船舶目标的空间角度关系，提高船舶目标在密集区域点迹关联的准确性。首先，对AIS数据进行时空滤波，实现数据粗关联，构建关联分析的数据候选集；然后，从时空数据的空间关系角度出发，在灰狼优化和匈牙利算法的启发下，利用点迹对特征向量矩阵进行运算，实现对多源空间数据的优化关联；最后结合数据几何关系对结果进行置信度评估。本文选取5幅SAR影像与AIS数据进行实验，并基于SAR影像数据及船舶轨迹点分布密度设计仿真实验，结果表明，本文所提出的角度最近邻数据关联方法，在密集分布情况下，关联精度为传统NN、GNN算法的3.62和4.61倍，运行时间为1.69 s，相较于NN算法仅增长1.36 s，仅占GNN运行时间的0.49 %，在运行时间增长不大的情况下具有更强的抗干扰能力，在密集区域仍能取得较好的关联效果。

关键词： 海上目标; 数据关联; 角度最近邻; 灰狼优化; 匈牙利算法; 空间数据; AIS; SAR

本文引用格式

李可欣 , 郭健 , 王宇君 , 李宗明 , 缪坤 , 陈辉 . 基于SAR和AIS的角度最近邻数据关联方法[J]. 地球信息科学学报, 2023 , 25(1) : 131 -141 . DOI: 10.12082/dqxxkx.2023.220458

Abstract

Improving maritime situation awareness is important for building an intelligent ocean. In order to solve the problems of perception blind area of single source sensor and poor performance of multi-source sensor data association in dense area, this paper proposes an angle nearest neighbor data association method with strong anti-interference based on Synthetic Aperture Radar (SAR) and Automatic Identification System (AIS) data. The spatial angle relationship between SAR and AIS is utilized to improve the accuracy of point trace correlation of ship targets in dense areas. Firstly, the spatiotemporal filtering is performed on AIS data to realize data coarse association, and a data candidate set for association analysis is constructed. Then, from the perspective of spatial relationship of spatiotemporal data, inspired by gray wolf optimization and Hungarian algorithm, the eigenvector matrix of point trace pair is operated to achieve the optimal association of multi-source spatial data. Finally, the confidence of the results is evaluated by combining the geometric relationship of the data. In this paper, five SAR images and AIS data are selected for experiments, and simulation experiments are designed based on SAR image data and the distribution density of ship trajectory points. The results show that, in the case of dense distribution, the correlation accuracy of the angular nearest neighbor data association method proposed in this paper is 3.62 and 4.61 times that of the traditional nearest neighbor algorithm and global nearest neighbor algorithm, respectively. The running time of our proposed method is 1.69 s, which is only 1.36 s longer than nearest neighbor algorithm and only accounts for 0.49 percent of global nearest neighbor algorithm’s running time. By comparison, our proposed method has stronger anti-interference ability and can achieve good correlation accuracy in dense areas with little increase in the running time.

Key words： maritime target; data association; gray wolf optimization; hungarian algorithm; angular nearest neighbor; spatial data; AIS; SAR

1 引言

随着卫星定位技术、遥感技术等信息处理技术的飞速发展以及空天地一体化基础建设的全面深入，全方位多维度的海上监视和海洋态势感知成了高端海洋技术战略布局中的重要一环，多基协同多源融合已经成为海洋应用的重要研究方向。通过多源数据融合，不仅可以消除单一传感器的海上态势感知盲区，提升感知精度，还能最终实现空天地一体化全方位协同感知。因此，开展海上多源传感器数据有效融合的研究，具有重要的理论指导和工程实践价值，也是目前海上目标分析应用领域的研究热点之一。
数据关联作为多源数据融合研究的核心与关键环节，其实质就是在传感器校准的基础上寻找最优的关联目标。相关研究中，数据关联的常见方法有最近邻[1]，神经网络[2]，全局最近邻[3]，概率数据关联算法[4]，联合概率密度关联算法[5]等。最近邻算法[6](Nearest Neighbor, NN)计算复杂度低，在目标稀疏场景和少杂波环境下比较适用，但在目标分布密集以及干扰杂波大的场景下容易出现错连、漏连。基于最近邻算法，学者们提出了全局最近邻算法(Global Nearest Neighbor, GNN)，其本质上是一种穷举式的贪婪算法，根据不同的代价方案构建代价矩阵，选取全局代价最小的分配方案作为结果，常用的分配算法有Munkres算法[7]、Jonker-Volgenant算法[8]等，该方法通常能实现全局距离最优，但时间开销随数据集增长急剧增加。概率数据关联算法（PDA）和联合概率密度关联算法（JPDA）通过对点迹对进行排列联合假设，通过估计方程利用观测区域内的观测值更新目标状态，根据关联概率进行加权运算实现目标关联，二者的区别是对于概率的计算不同，适用于杂波环境下的多目标跟踪问题，但当数据量以及杂波增多时，会出现组合爆炸问题，导致计算量激增。
本文主要探讨AIS和SAR数据2种主被动式传感器的数据关联分析方法，实质上就是建立某一时刻二者量测数据间的关系，确定数据是否来自同一目标，属于单目标跟踪问题。Park等[9]首次将AIS、SAR、光学遥感等卫星技术结合起来，实现对于朝鲜海域的大规模非法捕捞活动的发现。Galdelli 等[10]整合AIS和SAR数据的方法，监测渔业异常活动。李斐等[11]基于SAR和AIS数据自动检测冰架，分析有无浮冰。针对AIS和SAR数据关联问题，张蒙蒙[12]引入Munkres算法，基于点迹经纬度坐标构建代价函数设计全局最优分配航迹关联算法，但该方法只将空间数据距离作为关联特征，在密集区域检测效果差。为解决AIS和SAR数据统一坐标系时，由于多普勒位移产生的误差，孟大寓[13]使用相干性点飘移算法匹配空间拓扑结构，相较于NN、GNN算法，在噪声较少的情况下关联精度有显著提升，但随着噪声增多，关联精度明显下降，仅适用于噪声较少时的数据关联问题。为了进一步挖掘数据深层特征属性，Rodger等[14]基于AIS数据训练分类模型，通过迁移学习实现对SAR影像船舶类型的预测，随后利用排序分配技术实现数据间的鲁棒性匹配，但该方法精度依赖于SAR影像分辨率，对于低分辨率的影像识别效果较差。李浩然等[15]设计特征学习网络挖掘数据模态信息间的语义相关性，通过特征映射和关联学习实现SAR和AIS数据关联，但是该方法需要人工对数据集进行标注，难以覆盖多类型的复杂场景，耗时长且普适性较差。以上针对SAR和AIS数据关联的方法，通常只关注数据中的位置信息或基于深度学习实现对深层语义信息的挖掘，方法通常只关注某一具体场景，普适性较差，难以兼顾算法的时效性和准确率，这使得SAR和AIS目标关联模型的建立更具挑战性。
为了构建具有普适性、高效性和准确性的SAR和AIS数据关联模型，充分利用数据特征属性，解决多场景数据关联、关联时效性差、噪声点干扰等问题，本文充分考虑SAR和AIS时空数据的空间角度关系，在灰狼优化和匈牙利算法的启发下，设计了一种角度最近邻的数据关联方法，在保证全局最大关联的基础上最小化全局距离和空间角度误差，以提高关联的准确性，实现SAR和AIS数据之间的优化关联。灰狼种群中的每个个体表示点迹对距离和角度特征，在种群中3个最优个体的引导下，其他灰狼个体不断向最优解靠近，通过构建AIS和SAR的二分矩阵，用匈牙利算法优化点迹关联问题，完成AIS和SAR的优化关联，进而实现AIS、SAR数据的融合分析，选用真实数据集并通过仿真实验模拟各类型场景，验证了方法的普适性、高效性和准确性。

2 角度最近邻数据关联方法

常见的点迹关联方法如最近邻、全局最近邻等，通常只考虑距离最优，忽略了数据间的空间关系，而在实际应用中，不同传感器的船舶轨迹数据间存在空间制约关系，本文在灰狼优化和匈牙利算法的启发下，针对常见数据关联算法的不足，提出了角度最近邻数据关联算法（Angle Nearest Neighbor, ANN）。该算法对匈牙利算法进行改良，添加空间角度限制条件，利用灰狼寻优的思路寻找最优解，在保证运算效率的同时提高了关联准确率，使之更具实用价值。角度最近邻数据关联方法的流程如图1所示。
图1 角度最近邻数据关联方法

Fig. 1 Angle nearest neighbor data association method

2.1 数据预处理

2.1.1 SAR数据关联分析预处理

使用SNAP软件对SAR影像数据进行处理，将SAR图像数据由距离方位坐标映射到经纬度坐标。首先进行轨道校正，用高精度轨道信息替换元数据中的轨道信息；基于海杂波建模算法，对海洋与陆地区域进行分割，移除陆地区域以加速后续阶段的计算和降低误报概率；然后进行辐射定标，将接收的不同单元的后向散射信号转化为有单位的物理量或者没有单位的比例值，将SAR影像的亮度从灰度转化为绝对辐射亮度；最后采用自适应算法更新自适应滤波器的系数，使得输出信号可以达到最佳滤波特性，实现对SAR影像中相干斑的去除。
在进行舰船目标检测时，回波信号除了目标回波也包含海杂波、地杂波、天气杂波、脉冲影像以及接收机干扰等多种杂波干扰。恒虚警率(Constant False-Alarm Rate, CFAR)算法从邻近单元中估计待测单元的干扰杂波特性，根据分布模型和恒虚警率计算得到检测阈值，即通过输入噪声计算阈值。虚警概率 P f和检测概率 P d是雷达信号检测性能判断的2个重要指标，计算公式如下：
P f = P X > X 0 | H 0 = ∫ Y 0 ∞ P x | H 0 d x = ∫ Y 0 ∞ 1 μ e - x μ d x
P d = P X > X 0 | H 1 = ∫ Y 0 ∞ P x | H 1 d x = ∫ Y 0 ∞ 1 μ ( 1 + λ ) e - x 1 μ ( 1 + λ ) d x
式中： H 0为假设检测值均为干扰； λ表示干扰功率平均值， λ = μ； H 1为假设检测值包含干扰和目标， λ = μ ( 1 + λ )。
CFAR采用检测概率最大准则（Neyman-Pearson准则），检测时使用目标窗口、保护窗口和背景窗口按照一定步长进行滑动，通过检测阈值对雷达回波进行判断，当检测概率大于虚警率时，则判定目标窗口内的点为目标点，小于则视为噪声或干扰，然后根据SAR图像的分辨率和标记出的目标，实现船船以及船舶位置、尺度等特征信息的识别及提取。

2.1.2 AIS数据关联分析预处理

由于不同传感器的地理空间坐标以及时间信息等存在差异，需要对AIS数据进行预处理，使得AIS和SAR平台传感器数据在时空上实现统一，流程如图2所示。
图2 AIS数据融合分析预处理流程

Fig. 2 AIS data fusion analysis pretreatment process

以SAR数据产品成像时间为基准，根据AIS数据更新时间分布特点，选取时间t构建时间窗对AIS数据进行粗筛，得到AIS数据产品；对粗筛产品进行插值处理，根据AIS数据报告时间与SAR成像时间的关系，考虑埃米尔特三次样条插值或线性插值，轨迹插值考虑以下3种情况：
T r a j i = ( P 0 , … , P N )
P i = { L A T i , L O N i , S O G i , C O G i , H e a d i n g i }
t P 0 ≥ T S A R 线 性 插 值 t P n ≤ T S A R 线 性 插 值 t P 0 < T S A R < t P n 三 次 埃 米 尔 特 样 条 插 值
式中： T r a j i表示某一段轨迹； P i为第 i个轨迹点； L A T i , L O N i , S O G i , C O G i , H e a d i n g i分别为第i个点的纬度、经度、航速、航向以及船首向； t P 0和 t P n分别为某一段轨迹的起始时间； T S A R为SAR产品的成像时间。由于角度存在限制条件，即[0°, 360°]，当插值求解得到的角度超过限定范围时，取相应限定范围的极值0°或360°。
插值完成后，仅保留所有SAR成像时刻的轨迹点构成数据集。通过偏移计算校正由于多普勒频移所导致的位置误差，移动船舶的方位角位移 ∆ y计算公式如下，经过偏移校正后，将新的图上坐标转换为经纬度坐标。
∆ y = H ∙ V A I S ∙ t a n θ ∙ c o s β V S A R
V A I S = S O G × 0.514
V S A R = G M H + R = 7508.96 m / s
式中：H是sentinel_1卫星的轨道运行高度，为 693 000 m； V A I S和 S O G是船舶AIS系统的报告航速， V A I S / ( m / s )； θ是AIS报告位置对应SAR影像的入射角/°； β是船舶AIS系统报告的对地航向角/°；G为万有引力常量，值为6.67×1011 N·m2/kg2；M为地球质量，值为5.965×1024 kg。

2.2 角度最近邻关联方法

在SAR和AIS关联问题中，由于SAR影像目标检测存在误检，且AIS数据存在非法关闭等现象，因此在数据关联时，SAR影像中的船舶数目通常较AIS数据多。常见的数据关联策略通常只考虑距离因素，以图3为例，只考虑距离最优A_P3可以和2个SAR数据点S_P'、S_P''关联，但是这2个点相较于S_P1的方位角明显不同，距离最优不等于最佳关联，因此在寻找关联点迹时，除了考虑点间的距离外，还需要考虑相应点迹的方位角。为了在节省计算资源的同时，实现全局最优关联，本文综合考虑相对位置关系与最短距离关联，引入灰狼优化和匈牙利算法，提出了一种角度最近邻的AIS-SAR关联策略。
图3 点迹关联示意

注: S_ P1、S_ P2、S_ P3'、S_ P3"表示SAR影像检测船舶目标;A_P1、A_P2、A_P3表示AIS检测船舶目标。

Fig. 3 Schematic diagram of point trace association

2.2.1 算法原理

匈牙利算法[16]是一种多项式求解任务分配问题的组合优化方法，其核心思想是不断寻求增广路径从而求解二分图的最大关联，本质是一个求解多种形式关联问题的递归算法，本文中就是使得尽可能多的AIS轨迹点与SAR中轨迹点关联成功。基于匈牙利算法，学者提出了Kuhn-Munkres算法[7]，相较于匈牙利算法将每个目标的关联对象视为相同级别，KM算法引入权值的概念解决带权二分图的最优关联问题。神经网络[8]、Deep SORT[15,17]等多目标跟踪研究方法均使用匈牙利算法解决数据关联问题。灰狼优化算法是2014年Mirjalili等提出的一种群智优化算法，收敛速度快，能够实现局部寻优与全局搜索之间的平衡，其基本思想是构建灰狼社会等级层次模型，将灰狼种群划分为由高到低4个等级，通过最优解指导候选解，实现目标位置的更新，从而找到更好的解决方案。灰狼优化算法[18-19]被引用到制造业、配电网、舰载机等的调度问题研究中。
匈牙利算法将匹配对象视为同一优先级，只有当输入置信度较高的边进行匹配时才能取得较好的结果。KM算法引入权重概念，基于边的权重，采用贪心思路进行数据匹配解决冲突问题。基于以上思路，在利用匈牙利算法进行数据匹配前，基于灰狼寻优的思路，根据距离特征和空间角度特征，找到可靠度较高的数据输入匈牙利算法模型，以解决SAR和AIS数据的最优关联问题。

2.2.3 角度最近邻数据关联方法求解

利用距离及空间角度关系作为相似性度量来进行数据关联。假设有M个AIS对象，N个SAR对象，首先用半正矢公式计算二者间每个对象的距离关系，构建距离矩阵 D I S M × N，计算公式如下：
D I S M × N = D I S 11 , ⋮ , D I S 1 N ⋮ ⋮ , ⋮ D I S M 1 , ⋯ , D I S M N
D I S i , j = 2 R s i n - 1 s i n L A T A i - L A T S j 2 2 + c o s L A T A i c o s L A T S j s i n L O N A i - L O N S j 2 2
式中： D I S i , j为AIS中的第i个对象与SAR中第j个对象间的距离；R为地球半径，这里取平均半径6371 km。
按照增加成本的顺序对距离矩阵 D I S M × N进行排序，基于灰狼优化的思想，将狼群中点迹距离最短的三匹灰狼，根据社会等级从高到低依次标记为α、β、δ，其余对象标记为一般种群Ω，使用匈牙利算法来寻找最优解。根据角度关系确定数据间的相对位置，限定数据关联条件，根据与基准点的角度差，引导其选择相对最优距离，相关关系和角度限定条件如图4所示。
图4 角度限定相关条件

注: S_ P0、A_ P0分别表示SAR、AIS检测船舶目标，为检测区域中距离最近的一对关联目标点，设为基准关联点;A_ Pi为某一待匹配AIS检测船舶目标; S_ Pα、S_Pβ、S_ _Pθ表示与A_ Pi距离最近的3个SAR检测船舶; D_α、D_β、D_θ表示待匹配点间距离; angle_ A、angle_ S为AIS和SAR中的基准关联点与待匹配点间的角度。

Fig. 4 Related conditions of Angle qualification

设定距离最优点为基准点，对于给定灰狼个体，返回距离最优的3个值，将两个传感器的对于某一目标的信息定义为一个目标的相似性向量 O k。通过灰狼寻优确定最优种群，利用空间角度关系和距离特征计算 S c o r e k， S c o r e k越小则可靠度越高，从而得到可靠的数据关联对，将可靠度高的关联对输入模型进行分配，经过排序分配后确定AIS与SAR数据的最佳关联关系。计算公式如下：
F o r α , β , δ : O k = { D I S , L A T , L O N , A n g l e , H e a d i n g )
A n g l e k = | a n g l e A - a n g l e S | = | t a n - 1 D I S [ L A T A I S k , L O N A I S k ] , L A T A I S k , L O N A I S 0 D I S [ L A T A I S k , L O N A I S 0 ] , [ L A T A I S 0 , L O N A I S 0 - t a n - 1 D I S [ L A T S A R k , L O N S A R k ] , L A T S A R k , L O N S A R 0 D I S [ L A T S A R k , L O N S A R 0 ] , [ L A T S A R 0 , L O N S A R 0 |
S c o r e k = D I S k m a x D I S α , D I S β , D I S δ - m i n D I S α , D I S β , D I S δ + A n g l e k m a x A n g l e α , A n g l e β , A n g l e δ - m i n A n g l e α , A n g l e β , A n g l e δ
对于完成关联的数据对，选择数据中的可靠静态字段：船舶长度、宽度、船首向等，根据船舶特征分布以及经验值设定长度阈值、距离误差阈值、角度误差阈值以及长度比例阈值作为点迹关联结果验证的几何限定条件，去掉不符合阈值要求的关联点迹，得到准确可靠的关联点迹对，实现AIS和SAR的优化关联。

3 实验及结果分析

为了验证本文算法的普适性、高效性和准确性，分别引入真实数据集并设计仿真实验与常见数据关联算法对比评估模型的优势。选取算法运行时间和关联准确率作为评价指标，实验基于Windows10系统jupyter lab平台运行。

3.1 真实数据集

本文使用的真实数据主要包括择SAR遥感影像以及AIS数据，均通过网络公开数据源下载获得。
sentinel_1遥感影像数据。sentinel_1卫星是欧洲航天局哥白尼计划(GMES)发射的地球观测卫星，由两颗极轨卫星组成，搭载的传感器为C波段的合成孔径雷达，属于主动微波遥感卫星，采集平台的关键参数如表1所示。
表1 Sentinel-1 C-SAR仪器的关键参数

Tab. 1 Key parameters of Sentinel-1 C-SAR instrument

关键参数 范围
中心频率 5.405 GHz (对应波长~5.5465763cm)
带宽 0~100 MHz
极化方式 HH+HV, VV+VI-1, VV, HH
入射角 20°~ 46°
视角 右视
AIS数据。AIS是一种国际海事组织强制要求国际航行船舶以及500吨以上货船、客船等安装的进行船岸、船船间海事安全与通信的助航系统，可以结合甚高频和全球定位系统获取并报告船舶的动态、静态信息，实现自动应答，AIS数据是海上交通监管和海上监视等研究的重要研究数据源，AIS数据的关键字段如表2所示。
表2 AIS数据源关键字段

Tab. 2 AIS data source key fields

信息类型 关键字段
静态信息 MMSI、呼号、船名、船舶类型、船舶状态、船长、船宽
动态信息 记录时间、经度、纬度、速度、船艏向、航向
本文所选取的AIS数据集覆盖范围为美国沿岸，为了验证方法的普适性，选取美国西海岸、东海岸以及墨西哥湾船舶分布密集程度不一的区域展开研究。选取2021年1月1日3个区域的5幅sentinel_1卫星记录的SAR影像数据以及2020年12月31日—2021年1月2日的AIS数据进行分析，研究的区域范围如图5所示。
图5 SAR产品数据范围

注:该图基于自然资源部标准地图服务网站下载的审图号为GS(2020) 4397号的标准地图制作，底图无修改。

Fig. 5 Scope of SAR product data

以SAR成像时间为中心，选取2020年12月31日到2021年1月1日的AIS数据进行分析。根据船载AIS对于报告的发送时间间隔规定，静止状态下，AIS应在6 min以内或接收到消息时进行报告；在运动状态下，根据不同的运行状态，规定的报告时间间隔不同，如表3所示。为了探索AIS实际报文更新频率，对实际AIS数据进行分析，得到AIS数据报告更新时间统计表如表4所示。
表3 船载AIS自主工作模式的消息发送标准

Tab. 3 Message sending standards of autonomous working mode of AIS on board

船舶航行状态 停泊
(抛锚)		 船速
0~14节		 船速
0~14节
且航向改变		 船速
14~23节		 船速
14~23节
且航向改变		 船速
>23节		 船速>23节
且改变航向
报告时间间隔 3 min 12 s 4 s 6 s 2 s 3 s 2 s
表4 AIS实际工作汇报时间

Tab. 4 Actual reporting time of AIS work

时间间隔/s (0,60] (60,180] (180,360] (360,600] (600,1200] (1200，+∞]
轨迹条数/条 14 723 170 593 13 568 391 1 006 416 114 794 35 980
占比/% 0.0985 1.1418 90.8146 6.7360 0.7683 0.2408
通过分析可以发现，实际运行中AIS报告更新时间与规定相差较大，99 %以上的船舶报告更新时间不超过20 min，因此在AIS与SAR关联处理时，选择20 min时间窗进行时间滤波以保证点迹的完整性。5个研究区域的SAR和AIS数据产品的具体信息如表5所示。
表5 研究区域数据产品信息

Tab. 5 Study area data product information

SAR数据产品 AIS数据产品
产品
位置		 成像时间 经纬度范围 方位角/° 检测舰船
/艘		 原始数据/条 清洗数据/条 滤波后数据/条 舰船数/艘
区域1 2021-01-01
14:28:49		 LON (123.01°W— 126.43°W)
LAT (48.09°N— 49.98°N)		 -169.81 2284 19 944 119
(15 874)		 14 949 365
(8391)		 10 262 258
区域2 2021-01-01
14:30:16		 LON (112.87°W— 127.10°W)
LAT (43.59°N— 45.49°N)		 -169.98 31 2650 125
区域3 2021-01-01
00:02:09		 LON(88.19°W— 91.10°W)
LAT(27.95°N— 29.87°N)		 -10.36 1258 7019 1274
区域4 2021-01-01
23:02:44		 LON (72.66°W— 75.12°W)
LAT (22.15°N— 24.08°N)		 -10.47 311 1096 53
区域5 2021-01-01
22:18:44		 LON(64.46°W— 67.95°W)
LAT(43.15°N— 44.65°N)		 -10.04 695 56 5

3.2 实验结果及分析

将本文提出的角度最近邻算法（ANN）和常见数据关联算法（NN，GNN)作对比，选择原始数据中的可靠静态字段（船舶长度、宽度、船首向等），设定长度阈值、距离误差阈值、角度误差阈值以及长度比例阈值作为点迹关联程度的置信度评估标准，对算法的数据关联结果进行置信度评估，去除不满足条件的关联点迹对，从而得到可靠的数据关联结果。每种方法重复运行10次取平均值，实验结果如表6所示。实验结果表明，ANN算法虽然无法实现全局最优距离，但是该算法在运行时间无显著增长的情况下，关联准确率相较于其他方法有所提高。
表6 数据关联算法对比

Tab. 6 Comparison of data matching algorithms

区域 关联方法 运行时间/s 全局距离/m 关联点迹/对
1 NN 1.2977 3.768E+07 169
GNN 644.6883 3.766E+07 172
ANN 1.6547 3.771E+07 177
2 NN 0.0005 6.742E+05 2
GNN 0.0026 6.742E+05 2
ANN 0.0041 7.034E+05 2
3 NN 2.1926 1.224E+08 273
GNN 1192.0768 1.223E+08 278
ANN 2.6385 1.224E+08 291
4 NN 0.0592 1.575E+07 23
GNN 23.7882 1.574E+07 25
ANN 0.1524 1.575E+07 33
5 NN 0.0006 3.060E+08 6
GNN 0.0124 3.059E+08 7
ANN 0.0216 3.069E+08 9
由于小规模的真实数据集难以覆盖各种极端情况，并且缺乏对SAR数据可靠性的判断，从而无法进一步对算法性能进行探究。因此，为了验证本文算法的普适性、高效性和准确性，证明距离不是影响数据关联的唯一因素，设计对比实验如下：取地球平均半径R=6371 km，当不考虑角度变形时，经纬度1°≈111 km，根据SAR影像图幅设置经纬度取值范围为0~8334”，随机取值构建基础轨迹点。
AIS轨迹点记为： A I S = { A I S 1 , A I S 2 , ⋯ , A I S m }，统一生成偏移量生成对应关联的SAR轨迹点，并随机添加干扰点，构建对照组，记为 S A R = { S A R 1 , S A R 2 , ⋯ , S A R m , S A R 1 ' , S A R 2 ' , ⋯ , S A R n ' } ,其中 S A R 1~ S A R m为AIS数据点对应的点迹， S A R ' 1~ S A R " n为随机生成的干扰点。构建不同量级的基础数据集并不断变化干扰点数目，验证不同方法在点迹稀疏、密集以及干扰点多少等情况的关联结果。
为了更加直观的验证距离是否是影响点迹关联的唯一因素，基于NN算法，将每一步随机选择初始点改成了每一步选择当前距离最优点作为初始点，设计局部最优最近邻方法（I-NN）；为了验证基于灰狼优化的关联思路，设计基于全局最近邻的角度关联方法（G-ANN），该方法与ANN算法在进行数据关联时均考虑角度因素，但不同于ANN方法采用灰狼优化的思路实现寻优，G-ANN方法采用与GNN类似的贪婪式思路进行穷举寻优。将本文提出的角度最近邻方法(ANN)和最近邻算法(NN)，局部最优最近邻算法（I-NN)，全局最近邻算法(GNN)以及全局角度最近邻方法（G-ANN）作对比，设计对照实验如下。
对照实验一：为了探究参与关联的数据量M与算法性能之间的关系，设置干扰点数量N=0，设置不同的关联数据量M以对比不同算法的性能。为提升实验的可靠性，充分考虑数据分布的各种极端情况，每种方法运行10次，分别观察不同算法的最大关联精度、最小关联精度、平均关联精度与关联数据量M的关系，实验结果如图6所示。
图6 算法关联精度与关联点数量关系

Fig. 6 Relation between algorithm matching precision and number of matching points

随着参与关联的数据集的扩大，关联精度逐渐降低。当数据集较小时，各个方法都能取得较好的关联结果；但是随着数据集增大，传统的NN、GNN算法，无法很好地处理密集分布状态下的数据关联问题，关联精度显著下降；而考虑角度因素的ANN、G-ANN算法对于密集数据集均有较好表现。
对照实验二：在实际应用中，为了更好的分析和利用关联数据，关联方法的时效性非常重要。为了探究各个方法的实验效率，统计各个方法的运行时间与关联数据量M间的关系，每个实验重复运行10次，取平均运行时间，实验结果如图7所示。
图7 算法运行时间对比

Fig. 7 Comparison of algorithm running time

NN、I-NN、ANN算法运行时间呈线性增长，GNN算法和G-ANN算法运行时间则呈几何增长。在数据量M较小时，算法运行时间相差不大；随着数据量增长，以关联数据量M=1000为例， NN算法的运行时间为0.33 s，而GNN算法则达到了342.64 s， 本文所提出的ANN算法为1.69 s，仅为GNN算法的0.49 %。
对照实验三：在实际应用场景中，AIS存在非法关闭、SAR存在虚警情况，通常SAR数据会比AIS数据多，为了检验算法在干扰点存在情况下的关联准确率，对指定关联数量M的数据集分别添加不同的干扰点数量N，实验结果如图8所示。
图8 关联精度与干扰点的关系

Fig. 8 Relationship between matching accuracy and interference points

随着干扰点数目的增加，各个算法的关联精度均有不同程度的下降，且随着数据集扩大，关联精度受干扰点的影响也不断增大。在匹配数据量M较小的时候，关联精度受干扰点影响较小，各方法均有较高准确度，其中G-ANN算法的关联精度最高；随着匹配数量M增大，关联精度受干扰点影响逐渐下降，ANN和G-ANN两种基于角度的方法相较于其他算法，算法的匹配精度更高、抗干扰能力更强；且相较于G-ANN算法，ANN算法在数据密集情况下的抗干扰能力更强。

3.3 讨论

本文算法的改进之处，充分利用SAR和AIS的原始特征信息构造新属性特征，实现对空间数据空间关系的挖掘，显著提升了数据关联精度；同时受灰狼寻优思路启发，实现对数据对的高效关联匹配。在保证运算效率的情况下，显著提高了算法在多干扰以及密集分布等情况下的关联效率。
本文算法的不足之处，初始基准关联对的选取只考虑了距离因素，而整体关联精度依赖于初始关联对的选取，因此在对照实验一中，ANN算法关联精度最小值在数据量较小时表现较差（实验结果见图6(c)）。未来在确定初始关联对时，可以构造多属性特征，确保初始关联对的准确性，从而实现整体算法精度的进一步提高。
本文通过3组对照实验，分别探究了关联数据量对关联精度的影响、关联数据量对算法运行时间的影响以及干扰点数量对关联精度的影响。通过不同尺度的数据集分析对比，ANN算法在数据稀疏时，由于初始基准关联对的选取具有一定的随机性，关联精度会有一定程度的降低，但整体的平均关联精度仍相对较高；随着数据量增加以及干扰点增多，ANN算法的关联准确率和运行时间相比于其他算法有着明显的优势，适用于船舶密集分布以及噪声点多的极端情况。

4 结论与展望

海洋数据来源广泛，但多源数据融合应用水平较低，尚未形成全面、多维度的海洋监测体系。AIS数据由于非法篡改、关闭等现象，存在监视盲区，而SAR影像数据覆盖监视范围广，但包含可利用船舶信息较少，且无法进行时序分析。本文以AIS和SAR两种主被动式传感器为例，从多源数据融合分析与利用角度，创新性地引入空间角度关系对SAR和AIS数据进行关联，实验结论如下：
（1）从全局距离上来看，全局最近邻方法总能得到全局距离最小值，但是时间开销随着数据量的增加成比例增长；通过对关联结果分析，全局距离最优无法保证实现关联结果最优，证明距离不是影响关联结果的唯一因素，只考虑距离因素容易陷入局部最优。
（2）本文所提出的角度最近邻方法，由于考虑了数据的空间关系，当关联数据量M分别为100、500、1000时，平均点迹关联精度为GNN的1.26、1.85、3.18倍，说明角度相关关系的引入可以提升航迹点间的关联准确率，实现点迹关联优化。在添加角度限定条件后，关联方法的关联精度得到了显著的提高，算法的抗干扰能力显著增强，在数据分布密集的情况下仍能有较好表现，证明考虑空间关系能显著提升关联精度。
（3）综合考虑算法的关联精度和时间开销，ANN和G-ANN算法在匹配精度上均有较好的表现，但ANN的运行时间显著低于G-ANN算法，当M=1000时，NN、GNN、G-ANN、ANN算法的运行时间分别为0.340、342.640、2126.408、1.690 s， ANN、G-ANN算法精确度相较于GNN提升3.18和4.94倍，但ANN的运行时间仅为G-ANN的0.079 %，证明ANN方法使用的灰狼优化策略可以在保证计算精度的同时提升计算效率；同时ANN算法的抗干扰能力更强，算法的鲁棒性优于其他算法。
综上所述，本文所提出的角度最近邻数据关联方法具有较好的普适性，综合利用SAR和AIS两种传感器信息，弥补了单一传感器的信息缺陷，能以较小的时间开销实现关联精度的显著提高，适用于船舶分布密集，干扰杂波多等非理想场景的数据关联任务。本文方法综合利用多源传感器信息，有效提高了SAR和AIS数据关联的准确率，为提升海上态势感知能力和加强海上执法监督提供方法支撑。除海上目标分析研究外，还可拓展至陆地、空中等多源传感器的交通管理与分析领域中。在今后的研究中，可以结合更多传感器的信息，在更为广域的范围进行系统性海上目标分析，形成全面、系统性的海上态势感知能力，为提升SAR和AIS数据综合信息利用和海上态势感知能力以及构建海洋多源数据分析平台奠定基础，维护海上安全稳定、加强海上执法监督力度，同时也能够为海上经济的发展和相关政策的制定提供参考。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Sandirasegaram N, Vachon P W. Validating targets detected by SAR ship detection engines[J]. Canadian Journal of Remote Sensing, 2017, 43(5):451-454. DOI:10.1080/07038992.2017.1342204

DOI

[2]
Yoon K, Kim D Y, Yoon Y C, et al. Data association for multi-object tracking via deep neural networks[J]. Sensors (Basel, Switzerland), 2019, 19(3):559. DOI:10.3390/s19030559

DOI

[3]
Pelich R, Chini M, Hostache R, et al. Large-scale automatic vessel monitoring based on dual-polarization sentinel-1 and AIS data. Journal of Remote Sensing. 2019, 11(9):1078. DOI:10.3390/rs11091078

DOI

[4]
王琪, 廖志忠, 燕飞. 基于概率数据关联的雷达导引头抗速度拖引干扰算法[J]. 系统工程与电子技术, 2022, 44(2):448-454.

[Wang Q, Liao Z Z, Yan F. Algorithm for countering velocity gate pull-off jamming of radar seeker based on probability data association[J]. Systems Engineering and Electronics, 2022, 44(2):448-454. ]

[5]
盛涛, 夏海宝, 杨永建, 等. 密集杂波环境下的简化JPDA多目标跟踪算法[J]. 信号处理, 2020, 36(8):1280-1287.

[Sheng T, Xia H B, Yang Y J, et al. A simplified JPDA multi-target tracking algorithm for dense clutter environment[J]. Journal of Signal Processing, 2020, 36(8):1280-1287. ] DOI:10.16798/j.issn.1003-0530.2020.08.011

DOI

[6]
Singer R A, Stein J J. An optimal tracking filter for processing sensor data of imprecisely determined orign in surveillance system[C]// 1971. IEEE Conference on Decision and Control, MiamiBeach, IEEE: 171-175. DOI:10.1109/CDC.1971.270971

DOI

[7]
张湘毅, 丁兴如, 朱志明. Kuhn-Munkres算法在仓储排班中的应用研究[J]. 物流工程与管理, 2021, 43(6):162-166.

[Zhang X Y, Ding X R, Zhu Z M. Research on the application of Kuhn-munkres algorithm in warehouse scheduling[J]. Logistics Engineering and Management, 2021, 43(6):162-166. ]

[8]
毛仁祥, 常建华, 张树益, 等. 基于3D-MobileNetv2的多目标实时跟踪框架[J]. 量子电子学报, 2022, 39(3):364-372.

DOI

[Mao R X, Chang J H, Zhang S Y, et al. Multi-target real-time tracking framework based on 3D-MobileNetv2[J]. Chinese Journal of Quantum Electronics, 2022, 39(3):364-372. ]

[9]
Park J, Lee J, Seto K, et al. Illuminating dark fifishing fleets in North Korea[J]. Science Advances, 2020, 6(30):1197. eabb1197. DOI:10.1126/sciadv.abb1197

DOI

[10]
Galdelli A, Mancini A, Ferrà C, et al. A synergic integration of AIS data and SAR imagery to monitor fisheries and detect Suspicious activities[J]. Sensors (Basel, Switzerland), 2021, 21(8):2756. DOI:10.3390/s21082756

DOI

[11]
李斐, 王振领, 张宇, 等. 基于Sentinel-1 SAR的埃默里冰架前端位置自动检测研究[J]. 武汉大学学报·信息科学版, 2018, 43(12):2012-2022.

[Li F, Wang Z L, Zhang Y, et al. Amery ice shelf frontal position automatic detection from sentinel-1 SAR imagery[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12):2012-2022. ] DOI:10.13203/j.whugis20180171

DOI

[12]
张蒙蒙. 船只目标多传感器数据融合算法研究[D]. 呼和浩特: 内蒙古大学, 2021.

[Zhang Mengmeng. Research on multi-sensor data fusion algorithm for ship target detection[D]. Hohhot: Inner Mongolia University, 2021. ]

[13]
孟大寓. 基于数据融合的SAR图像中海上目标检测与跟踪技术研究[D]. 成都: 电子科技大学, 2022.

[Meng D Y. Research on technologies for sea target recognition and tracking in SAR images based on data fusion[D]. Chengdu: University of Electronic Science and Technology of China, 2022. ]

[14]
Rodger M, Guida R. Classification-aided SAR and AIS data fusion for space-based maritime surveillance[J]. Journal of Remote Sensing, 2020, 13(1):104. DOI:10.3390/rs13010104

DOI

[15]
李浩然, 熊伟, 崔亚奇. 基于深度特征融合的SAR图像与AIS信息关联方法[J/OL]. 系统工程与电子技术, 2022(8):1-10.

[Li H R, Xiong W, CUI Y Q. SAR image and AIS information association method based on deep feature fusion[J/OL]. Systems Engineering and Electronics, 2022(8):1-10. ]

[16]
Kuhn H W. The Hungarian method for the assignment problem[J]. Naval Research Logistics, 2005, 52(1-2):7-21. DOI:10.1002/nav.20053.

DOI

[17]
范婉舒, 赖际舟, 吕品, 等. 基于改进DeepSORT的视觉/激光雷达目标跟踪与定位方法[J]. 导航定位与授时, 2022, 9(4):77-84.

[Fan W S, Lai J Z, Lv P, et al. Vision/Lidar object tracking and localization method based on improved DeepSORT[J]. Navigation Positioning and Timing, 2022, 9(4):77-84. ] DOI:10.19306/j.cnki.2095-8110.2022.04.009.

DOI

[18]
李开言, 王亚刚, 张涛. 基于改进灰狼算法的边缘计算任务调度方法[J]. 信息与控制, 2022(6):1-8.

[Wang Y G, Zhang T. Edge computing task scheduling method based on improved gray wolf algorithm[J]. Information and Control, 2022(6):1-8. ]

[19]
李竹根, 刘波峰, 张晓飞, 等. 基于改进灰狼算法与隐枚举法的配电网分区故障定位研究[J]. 电测与仪表, 2022(6):1-10.

[Li Z, Liu B F, Zhang X F, et al. Research on fault location of distribution network partition based on improved gray wolf algorithm and implicit Enumeration Method[J]. Electrical Measurement and Instrumentation, 2022(6):1-10. ]

[20]
刘玉杰, 韩维, 苏析超, 等. 基于改进灰狼优化算法的舰载机着舰调度[J]. 北京航空航天大学学报, 2022(6):1-15.

[Liu Y J, HAN W, SU X C, et al. Carrier aircraft landing scheduling based on improved grey wolf optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2022(6):1-15. ]

Options
文章导航

/

〈 〉