EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 1: 40 - 48

DOI: https://doi.org/10.12082/dqxxkx.2023.220475

地球信息科学理论与方法

地形扫描数据TIN模型生成DEM的误差计算方法

  • 师长兴 , *
展开
  • 中国科学院地理科学与资源研究所 陆地水循环及地表过程院重点实验室，北京 100101

师长兴（1963— ），男，河北正定人，博士，研究员，主要从事河流地貌、流域物质迁移与环境变化等研究。E-mail:

收稿日期: 2022-07-04

  修回日期: 2022-08-31

  网络出版日期: 2023-03-25

基金资助

国家自然科学基金项目(41971008)

国家自然科学基金项目(41671004)

收起

A Method of Estimating Errors of DEM Constructed from Topographic Scanning Data by TIN Model

  • SHI Changxing , *
Expand
  • Key Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
*SHI Changxing, E-mail:

Received date: 2022-07-04

  Revised date: 2022-08-31

  Online published: 2023-03-25

Supported by

National Natural Science Foundation of China(41971008)

National Natural Science Foundation of China(41671004)

Fold

摘要

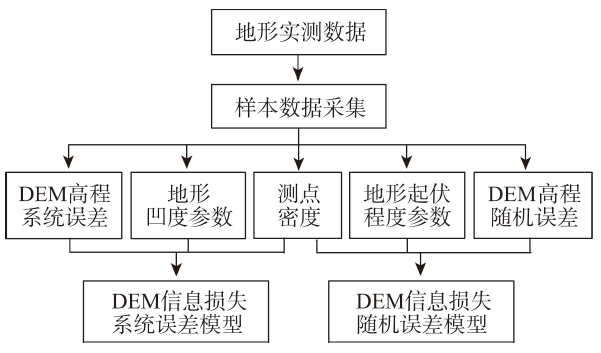
由地表三维空间数据生产的数字高程模型(DEM)的误差包括从数据误差传递来的误差和因数据数量不足以反映地形起伏造成的信息损失误差。本文给出了由三维空间数据的不规则三角网(TIN)模型栅格化为DEM过程中，通过线性插值将数据随机误差传递到DEM栅格上的随机误差的解析解，同时利用地基激光扫描仪测量的冲沟地形数据点云，分析得出因信息损失产生的DEM系统和随机误差的估算方法。结果显示信息损失产生的DEM平均高程系统误差和随机误差都与有效测点密度有关，其中有效测点由TIN中包含DEM栅格中心点的所有三角面的3个顶点组成；信息损失产生的DEM平均高程系统误差和随机误差除与有效测点密度相关外，还与地形特征有关，平均高程系统误差与地形整体凹度参数有关，随机误差与地形整体起伏程度参数有关。建立了分辨率为0.1 m×0.1 m 的DEM误差估算模型。

关键词： 地形扫描; DEM; 插值传递误差; 信息损失误差; 全局误差; TIN模型

本文引用格式

师长兴 . 地形扫描数据TIN模型生成DEM的误差计算方法[J]. 地球信息科学学报, 2023 , 25(1) : 40 -48 . DOI: 10.12082/dqxxkx.2023.220475

Abstract

The errors of DEM derived from scattered topographic scanning data can be divided into errors propagated from topographic data to raster nodes and errors caused by information loss owing to scattered measuring data being incapable of completely reproducing the terrain surface. This study gave an analytical solution of DEM random errors propagated from data random errors in rasterizing the Triangulated Irregular Network (TIN) model by linear interpolation. Moreover, using the topographic scanning data of gullies recorded by a Terrestrial Laser Scanner (TLS), a method was derived for estimating the systematic and random errors caused by information loss in constructing DEM from the TIN model. The results show that both the mean systematic error and random error resulting from information loss are related to the density of effective measuring points which are located at the vertexes of triangles of the TIN model with at least a node of DEM inside them. Besides, the two kinds of errors are also related to terrain characteristics, among which the mean concavity has an impact on the mean systematic error and the terrain roughness affects the random error. For the DEM with a resolution of 0.1 m×0.1 m, the mean systematic error (Hd, in meter) can be estimated by H d = 0.0580 C m D e p + 0.000 001, and the random error at a DEM node (σt, in meter) can be calculated as σ t 2 = σ z 2 + ( 0.1593 D e p - 1.049 C s d 0.9811 ) 2, where Cm is the mean concavity defined as the mean of total height difference (ΔZd, in meter) between surrounding eight grids and the middle grid in a 3×3 sliding window, Dep is the density of effective points (points/dm2), σz is the analytical solution of the random error at a DEM node propagated from data random errors, and Csd is the terrain roughness defined as the standard deviation of the parameter ΔZd.

Key words： topographic measurement; DEM; propagation error; information loss error; global random error; TIN model

1 前言

地基激光地形扫描或无人机地形测量可以在短时间内方便地获取大量地表三维空间数据，近年来被大量应用于河流和沟道冲淤变化、坡地侵蚀等地貌过程研究[1⇓⇓⇓⇓⇓⇓⇓-9]。利用地形三维数据进行地表形态变化的分析过程中，为方便不同时间观测数据对比和编程计算，通常先用数据点云生成数字高程模型（Digital Elevation Model, DEM）。但是，扫描数据存在各种来源的误差（如果不特别指出，本文用误差代指随机误差），生成DEM也会产生误差，为监控和识别地形的变化尤其是微小的变化，需要了解误差的来源和大小，这样才能从数据内在的不确定性中识别出真正的变化[5]。
由地基激光地形扫描和无人机地形测量数据生成的DEM误差来源包括与测量设备精度和影响观测精度的大气条件以及与扫描仪站位位置和数量或无人机飞行高度和地面控制点布设、地表组成、地形复杂程度等有关的测量数据误差，还有由测量数据插值生成DEM时导致的误差[9⇓-11]。在已有估计DEM误差的方法中，有的直接通过高精度样点与DEM的高程差值或不变地形重复测量的数据所得DEM的高差值确定误差[1⇓⇓⇓-5]，这也是大多数评价DEM精度常用的方法，或将DEM栅格内测点去趋势高程的均方差定义为误差[8]，这些方法得到的误差包含了数据误差和生成DEM的误差。一些研究将测量误差和插值生成DEM误差分开来加以分析。对于测量数据误差，尽管有些研究针对不同来源的数据误差提出了控制方法和部分来源误差的计算方法[12⇓-14]，但是因为测量数据误差来源复杂，计算出可靠的数据点位综合误差仍比较困难, 因此如果能够按照仪器适用范围控制其他来源误差水平，可以将仪器标称精度用于估计测量数据误差，而在不能控制多种来源误差情况下，往往通过检验点坐标观测值和真值之差或进行测量数据与高精度数据对比估计数据误差[5⇓-7,11-12]。至于测量数据插值生成DEM时导致的误差，可以分为插值传递误差和信息损失误差[15-16]。其中，插值传递误差是指数据误差传递到DEM栅格点的误差；信息损失误差或称为地形糙度误差或地形描述精度[16-17]，是由于测点数量较少，不足于反映地形起伏变化所产生的误差。由地形观测数据生产DEM可以通过统计方法，也可通过插值方法，其中插值方法又有很多种，各类方法得到的DEM误差也将有所不同。虽然已有插值传递误差和信息损失误差计算公式，但都存在参数不易确定或应用范围限制。
本文利用典型沟道激光扫描数据，对已知数据误差情况下，由一种常用的不规则三角网（Triangulated Irregular Network, TIN）模型插值产生一定分辨率的DEM的误差与主要影响因素的关系进行了分析，为目前应用地基激光地形扫描或无人机地形测量进行地形分析提供一个比较可靠且简单易行的DEM误差估算方法。

2 研究方法

本文主要分析采用TIN模型法插值生成DEM的插值传递误差和信息损失误差。TIN模型法是一种常用的将三维空间点云数据生成DEM的方法。其中，插值传递误差可根据插值点高程计算公式，按照误差传递计算方法求取。由(x1, y1, z1), (x2, y2,z2), (x3, y3, z3)组成的三角平面内插点(x, y)的高程值z为：
z = z 1 - x - x 1 y 21 z 31 - y 31 z 21 - ( y - y 1 ) z 31 x 21 - z 21 x 31 x 21 y 31 - x 31 y 21
式中：x21 = x2-x1； y21 = y2-y1；z21 = z2-z1； x31 =x3-x1；y31 = y3-y1； z31 = z3-z1。
计算信息损失误差需要确定影响信息损失的因素。已有研究结果揭示，插值生成的一定分辨率DEM的信息损失误差主要与地形起伏特征和数据密度有关[15-16]。本文将按照图1所示步骤，依据实测数据，生成样本数据，从中提取地形特征参数和数据密度，再通过统计分析，建立影响要素与信息损失误差的回归关系。
图1 信息损失误差分析路线

Fig. 1 Road map of analysis of information loss errors

2.1 样本数据采集

建立计算信息损失误差的模型，需要获取对应不同地形特征和采样密度的DEM误差数据样本组。因为这里只涉及信息损失误差，所以样本中所有数据点的误差应为0。为此，本文采用观测典型沟道得到的数据点云，利用TIN模型插值生成地表分辨率为0.01 m×0.01 m的DEM。假设这一DEM代表真实的地表。在此基础上，为产生较宽点密度范围的数据，可从约10 pts/dm2开始在3个数量级内由大到小生成不同密度的随机分布点，从该DEM提取高程数据。然后利用不同密度的随机数据点和提取的高程，生成0.1 m×0.1 m的DEMi。计算各DEMi与代表真实地表的DEM的高差。

2.2 DEM高程系统误差和随机误差

为分析地形起伏的影响，按其空间变化，将沟道进行分区。统计得到各分区DEMi与代表真实地表的DEM的高差，这一高差可视为一次测量结果的平均高程误差。在每个采样密度下，进行多次（本文设为30次）随机采样，计算各分区高差的平均值（Hd）和均方差(SHd)。按误差定义，其中高差的平均值表示某分区同一采样密度下逐测次所得DEM的平均高程的系统误差；高差的均方差表示栅格高程的随机误差，也称为中误差。

2.3 测点密度定义

测点密度一般定义为单位面积内测点数。然而，用TIN模型法插值时，与某一插值点有关的测点只是三角网中包含该插值点的某个三角面的3个顶点，因此当测点密度较大时，有些测点与插值结果无关。为此，本文定义一个新的测点密度指标，即与插值产生一定分辨率（此处为0.1 m×0.1 m）的DEM有关的数据测点的密度，称为有效（测）点密度，表示为Dep。可以由0.1 m×0.1 m的DEM转出的格点，从TIN网三角面选出包含插值点的所有三角面，再用这些三角面从测点中选出参与插值的测点，即位于这些三角面顶点的测点。考虑到本文DEM的栅格尺度，这里用每平方分米内的有效测点数，即pts/dm2，作为有效点密度单位。

2.4 地形起伏特征参数

为建立一个较好反映地形起伏特征对DEM误差影响的参数，首先需要考虑所涉及地形的整体特征。如果地面整体无凸凹，DEM与真实地面的高差平均值，即Hd，应该接近于0，但对于一条沟道或者山体，边缘相对内部存在高差的形体，即整体上凸或下凹的形体，利用TIN模型法插值生成的DEM将存在系统误差。以上凹的曲面为例，构成TIN的每个三角平面上的各点都将高于曲面上的点，因此生成的DEM平均高程将高于真实凹形地面。这一系统误差与测点密度、DEM栅格分辨率以及地形整体凸凹程度有关。为此，需要针对这一地形特征，定义反映地形整体凸凹程度参数。这里，以Cm表示地形整体凹度/m，定义为ΔZd的平均值。
C m = 1 n ∑ i = 1 n ∆ Z d i
式中：n为栅格数； ΔZdi为栅格i的ΔZd值)； ΔZd是非重叠3×3滑动窗中心栅格高度与周围8个栅格的高差之合。
Δ Z d = ∑ k = 1 8 ( Z k - 8 Z p )
式中：Zp为滑动窗中心栅格高度；Zk表示周围8个栅格中编号为k的栅格高度。地形起伏除了可能导致DEM存在系统误差，也会增加DEM的随机误差[15-16]。式（3）定义的ΔZd不仅可以表征地表整体凸凹程度，其空间变化还可以表征地形的起伏程度，为此定义ΔZd的均方差为一个地形起伏程度参数，以Csd表示：
C s d = 1 n - 1 ∑ i = 1 n ∆ Z d i - ∆ Z d ¯ 2
式中： ∆ Z d ¯为ΔZdi平均值，即上面定义的Cm值/m，其他符号同上）。
地形起伏程度还可以定义为其他多种参数。Aguilar 等[16]列举并分析了5种地形起伏程度参数与平均高程误差的关系，结果得出由高差均方差(Standard Deviation of the Height Difference, SDHD)定义的起伏程度与DEM的平均高程误差关系比其他起伏程度参数更密切。鉴于其在与DEM误差的关系中表现突出，本文也将利用该参数，确定其与DEM误差的关系，比较Csd与SDHD各自预测DEM误差能力的优劣，确定估算信息损失误差公式。SDHD定义为ΔZp的均方差：
S D H D = 1 n - 1 ∑ i = 1 n ∆ Z p i - ∆ Z p ¯ 2
式中： ΔZpi为栅格i的ΔZp值； ∆ Z p ¯为ΔZpi平均值）； ΔZp是3×3滑动窗中心栅格高度（Zp）与周围8个栅格高度（Zk）差值绝对值的平均值：
∆ Z p = ∑ k = 1 8 Z p - Z k 8

3 数据来源

为建立信息损失误差估算模型，本文利用了作者与研究组成员用FARO三维激光扫描仪实地测量得到的2条沟的地形扫描数据：① 黄河上游东柳沟的一条冲沟；②皇甫川流域的一条冲沟。其中将东柳沟冲沟用于建立误差估算模型，皇甫川冲沟用于检验模型。2条冲沟地形见图2，冲沟及其观测数据概况列于表1。由数据误差传递到DEM的误差可直接用数据误差计算。用TIN模型法从点高程数据插值生成DEM时，如果仅考虑均匀分布且相互独立的高程测量误差，则所生成的DEM栅格平均插值传递误差(σz)可以表示为测点高程误差的（1/2）1/2 [18]。如果进一步考虑测点数据的X，Y，Z误差，而且在X, Y, Z 3个方向误差相互独立条件下，根据式（1）和误差传递公式， DEM每个栅格点上的插值传递误差见式（7）。
σ z 2 = σ x 1 2 ∂ z ∂ x 1 2 + σ y 1 2 ∂ z ∂ y 1 2 + σ z 1 2 ∂ z ∂ z 1 2 + σ x 2 2 ∂ z ∂ x 2 2 + σ y 2 2 ∂ z ∂ y 2 2 + σ z 2 2 ∂ z ∂ z 2 2 + σ x 3 2 ∂ z ∂ x 3 2 + σ y 3 2 ∂ z ∂ y 3 2 + σ z 3 2 ∂ z ∂ z 3 2 = σ x 1 2 y 10 z 32 + C y z C x y + C x y z y 32 C x y 2 2 + σ y 1 2 x 10 z 32 + C x z C x y + C x y z x 32 C x y 2 2 + σ z 1 2 C x y + x 10 y 32 - y 10 x 32 C x y 2 + σ x 2 2 y 10 z 31 C x y + C x y z y 31 C x y 2 2 + σ y 2 2 x 10 z 31 C x y + C x y z x 31 C x y 2 2 + σ z 2 2 y 10 x 31 - x 10 y 31 C x y 2 + σ x 3 2 y 10 z 21 C x y + C x y z y 21 C x y 2 2 + σ y 3 2 x 10 z 21 C x y + C x y z x 21 C x y 2 2 + σ z 3 2 x 10 y 21 - y 10 x 21 C x y 2
式中：σ为以均方差表示的误差，下标表示其所属坐标，x10 =x1-x，x32 =x3-x2，y10 =y1-y，y32 =y3-y2，z32 =z3 -z2，Cxy =x21y31 -x31y21，Cyz=y21z31-y31z21，Cxz=x21z31-x31z21， Cxyz = x10Cyz-y10Cxz，其他符号同式（1）。
图2 黄河支流东柳沟和皇甫川流域中2条冲沟晕渲地形

Fig. 2 Shaded-relief of the measured two gullies in the Dongliugou and Huangfuchuan watersheds in the Yellow River basin

表1 黄河支流东柳沟和皇甫川流域中2条冲沟和观测数据简况

Tab. 1 Briefs of the measured two gullies in the Dongliugou and Huangfuchuan watersheds in the Yellow River basin and the topographic scanning data

冲沟面积/m2 沟头至沟口高差/m 冲沟内测点总数/pts 测点平均密度/(pts/dm2) 站位配准误差/m
东柳沟冲沟 547.3 13.0 670 797 12.26 0.0052
皇甫川冲沟 3011.6 37.6 2 512 519 8.34 0.0011
值得一提的是，当测点数较少时，由于部分DEM栅格点的误差插值来自同样的测点，意味着这些误差相互不独立。因此求插值传递全局误差时应采用有效测点数(N)，并且每个插值来自三角网中的3个测点，所以插值传递全局误差应是栅格误差的(N/3)-0.5倍。

4.2 信息损失误差

如上所述，地形起伏是信息损失误差产生的一个主要因素。为了利用东柳沟的地形扫描数据分析地形起伏对误差的影响，本研究利用0. 1 m×0.1 m的DEM计算了3×3栅格的ΔZd值，按其空间分布，本着分区间起伏程度参数差异大，而且保持各分区有足够的样本量，将该沟道划分为7个区（图3）。
图3 东柳沟冲沟分区和ΔZd值分布

Fig. 3 Subdivisions of the gully in the Dongliugou watershed and distribution of ΔZd values

4.2.1 系统误差

图4点绘了东柳沟冲沟同一点密度下30次采样计算的各分区Cm与高差均值Hd的关系，可见二者在有效测点密度较低时呈现线性关系，密度较大时，二者关系变得不显著。其中，因为是随机采样，随有效测点密度增加，二者相关关系的决定系数在总的下降趋势中存在起伏变化。图5点绘了各分区高差均值与有效测点密度倒数的关系，可见二者大致呈现线性关系。
图4 不同有效点密度下高差均值Hd与地形凹度参数Cm均值的关系

注:不同点符号代表不同的有效点密度/( pts/dm2)。

Fig. 4 The relations between mean elevation difference (Hd) and terrain concavity parameter (Cm) under different effective point densities (pts/dm2) represented by different symbols in each sheet

图5 高差均值Hd与有效点密度倒数1/Dep的关系

Fig. 5 The relation between mean elevation difference (Hd) and the reciprocal of effective point density (1/Dep)

考虑到高差均值与有效点密度及其与Cm间存在不同的函数关系，构建综合变量Cm/Dep，并建立其与高差均值的线性回归方程：
H d = 0.0580 C m D e p - 0.000   0024                   ( n = 77 ,   R 2 = 0.981 )
由式（8），可以依据有效点密度和地形凹度，计算所生产的DEM的平均高程系统误差。值得一提的是，如图4所示，在有效点密度接近1 pts/dm2情况下，高差均值与地形凹度Cm的关系不再显著，高差均值较小，可以忽略DEM的系统误差。

4.2.2 随机误差

高差均方差或信息损失随机误差与有效点密度间存在着幂指数关系，随有效点密度增大而减小（图6）。在同样有效点密度下，高差均方差与SDHD和Csd之间都存在线性关系，亦或幂指数关系（图7）。比较SDHD和Csd二者各自与高差均方差的关系，高差均方差与地形起伏程度指标Csd的关系更为显著；而且多数情况下高差均方差与Csd幂指数关系比线性关系略微更显著（表2）。构建高差均方差(SHd)与有效点密度及地形起伏程度指标之间关系如下：
S H d = 1.289 D e p - 0.9135 S D H D 1.087     ( n = 77 ,   R 2 = 0.982 )    
    S H d = 0.1593 D e p - 1.049 C s d 0.9811             ( n = 77 ,   R 2 = 0.991 )  
可见，式（10）相关性比式（9）更为显著。
图6 高差均方差SHd与有效测点密度Dep的关系

Fig. 6 The relation between standard deviation of mean elevation difference (SHd) and effective point density (Dep)

图7 不同有效点密度下高差均方差SHd与SDHD及其与Csd的关系

注:不同点符号代表不同的有效点密度/(pts/dm2)。

Fig. 7 The relations of standard deviation of mean elevation difference (SHd) with terrain roughness parameters SDHD and Csd under different effective point densities (pts/dm2) represented by different symbols in each sheet

表2 高差均方差SHd与SDHD及其与Csd的相关关系决定系数

Tab. 2 The determination coefficients of relations of standard deviation of mean elevation difference (SHd) with terrain roughness parameters SDHD and Csd under different effective point densities

有效点密度/(pts/dm2) SHd~SDHD SHd~Csd
线性关系 幂指数关系 线性关系 幂指数关系
0.014 0.783 0.792 0.834 0.836
0.027 0.635 0.642 0.841 0.839
0.054 0.849 0.857 0.985 0.984
0.109 0.906 0.898 0.914 0.917
0.217 0.908 0.913 0.979 0.982
0.429 0.890 0.890 0.966 0.971
0.830 0.866 0.865 0.980 0.981
1.50 0.843 0.833 0.936 0.925
2.33 0.722 0.717 0.874 0.867
2.87 0.685 0.684 0.738 0.740
2.99 0.859 0.873 0.895 0.906

4.3 验证

利用皇甫川冲沟数据生成0.01 m×0.01 m 的DEM作为真实地形，同样进行不同密度的重复随机布点，并从该DEM读取地面高程，再生成0.1 m×0.1 m的DEM。将该冲沟分6个区块，其中沟道下部较平坦的沟底分为一个区，其他为任意把沟道分段得到的区块，计算每次抽样所得DEM分区块的地形凹度和起伏度参数，以及与代表真实地形DEM的高差的平均值或信息损失系统误差、高差均方差或信息损失随机误差。最后利用有效点密度、地形凹度和起伏度参数，以及上面由东柳沟冲沟数据得到的式（8）和式（10），计算皇甫川冲沟DEM分区块的平均高差、高差均方差。点绘高程系统误差与由式（8）计算的平均高差，以及随机误差与由式（10）计算的高差均方差关系，如图8。可见，二者基本吻合。平均高程系统误差和随机误差各自实测值和计算值之间回归关系的决定系数分别为0.992 和0.956，纳什效率系数分别为0.992 和0.931。
图8 皇甫川冲沟DEM平均高程系统误差和随机误差实测值与计算值的关系

Fig. 8 The relations between measured and calculated systematic errors of mean DEM elevation and between measured and calculated random errors of mean DEM elevation for the measured gully in the Huangfuchuan River

5 DEM全局误差和讨论

上面分析得到了利用TIN模型插值生成DEM时，由地形数据测点误差传递到DEM栅格点上的误差。同时，利用沟道地形三维激光扫描数据，建立了利用TIN模型插值生成DEM的信息损失误差的统计模型。值得一提的是，由于所涉及的沟道既存在不同坡度的沟坡，又有较平坦的沟底，地表起伏程度变化范围大，统计模型的样本值域宽，所以本文建立的模型对于其他地貌类型同样适用。
与信息损失误差中的随机误差一样，插值传递误差也属于随机误差。将两者合并，得到DEM全局（随机）误差计算式：
σ t 2 = σ z 2 + ( 0.1593 D e p - 1.049 C s d 0.9811 ) 2
式中：σt为DEM栅格高程误差/m，其他符号同上。
需要说明的是，式(11)中σt是利用测量数据通过TIN模型插值得到的DEM的误差，因此不包括测量仪器和测量过程中产生的系统误差，以及像植被覆盖、地形遮蔽等原因产生的不能在测量数据随机误差中体现的误差。另外，本研究针对典型冲沟地形测量数据分析得出了计算分辨率为0.1 m×0.1 m的DEM信息损失误差回归关系式，从关系式的决定系数（式（8）为0.981；式（10）为0.991）和验证结果看，它们具有较好的普适性。但是，对于更大或更小的测量范围，需要生成其他分辨率的DEM，可依照本文提出的方法，重新建立信息损失误差估算模型。

6 结论

地形测量数据插值生成DEM的误差可以分为插值传递误差和信息损失误差。本文利用三角平面高程内插公式和误差传递公式得出TIN模型插值生成DEM的栅格点插值传递误差的解析解，即式（7）。进一步利用沟道地形三维激光扫描数据，提取不同密度数据样本，计算有效测点密度和地形特征参数，统计分析得出信息损失误差与有效测点密度和地形特征参数关系，结果显示：
（1）用TIN模型法由三维空间测点数据线性插值生成的DEM平均高程将存在一个系统偏差，可用测点有效密度和凹度参数由式（8）计算这一系统偏差，DEM的平均高程应扣除系统偏差计算值。但是，对于生成分辨率为0.1 m×0.1 m的DEM，在测点有效密度大于1 p/dm2情况下，DEM的系统偏差可以忽略。
（2）DEM的信息损失随机误差与测点有效密度和地形起伏程度参数有关，0.1 m×0.1 m的DEM的信息损失误差可由式（10）计算。DEM的信息损失随机误差与插值传递误差一起构成DEM的全局误差，可由式（11）计算。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Milan D J, Heritage G L, Hetherington D. Application of a 3D laser scanner in the assessment of erosion and deposition volumes and channel change in a proglacial river[J]. Earth Surface Processes and Landforms, 2007, 32(11):1657-1674. DOI:10.1002/esp.1592

DOI

[2]
Blasone G, Cavalli M, Marchi L, et al. Monitoring sediment source areas in a debris-flow catchment using terrestrial laser scanning[J]. CATENA, 2014, 123:23-36. DOI:10.1016/j.catena.2014.07.001

DOI

[3]
Williams R D, Brasington J, Vericat D, et al. Hyperscale terrain modelling of braided rivers: Fusing mobile terrestrial laser scanning and optical bathymetric mapping[J]. Earth Surface Processes and Landforms, 2014, 39(2):167-183. DOI:10.1002/esp.3437

DOI

[4]
Kinsey-Henderson A, Hawdon A, Bartley R, et al. Applying a hand-held laser scanner to monitoring gully erosion: Workflow and evaluation[J]. Remote Sensing, 2021, 13(19):4004. DOI:10.3390/rs13194004

DOI

[5]
Goodwin N R, Armston J, Stiller I, et al. Assessing the repeatability of terrestrial laser scanning for monitoring gully topography: A case study from Aratula, Queensland, Australia[J]. Geomorphology, 2016, 262:24-36. DOI:10.1016/j.geomorph.2016.03.007

DOI

[6]
周小荃, 余宏亮, 魏玉杰, 等. 无人机倾斜航空摄影监测崩岗侵蚀量变化的方法[J]. 农业工程学报, 2019, 35(21):51-59.

[Zhou X Q, Yu H L, Wei Y J, et al. Method for monitoring change in Benggang erosion based on oblique aerial images of UAV[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(21):51-59. ] DOI:10.11975/j.issn.1002-6819.2019.21.007

DOI

[7]
Wells R R, Momm H G, Castillo C. Quantifying uncertainty in high-resolution remotely sensed topographic surveys for ephemeral gully channel monitoring[J]. Earth Surface Dynamics, 2017, 5(3):347-367. DOI:10.5194/esurf-5-347-2017

DOI

[8]
Vericat D, Smith M W, Brasington J. Patterns of topographic change in sub-humid badlands determined by high resolution multi-temporal topographic surveys[J]. CATENA, 2014, 120:164-176. DOI:10.1016/j.catena.2014.04.012

DOI

[9]
Wheaton J M, Brasington J, Darby S E, et al. Accounting for uncertainty in DEMs from repeat topographic surveys: improved sediment budgets[J]. Earth Surface Processes and Landforms, 2010, 35:136-156.

[10]
王江涛. 地面三维激光扫描数据的DEM重建精度分析[J]. 地理空间信息, 2019, 17(12):99-102,117,11.

[Wang J T. Accuracy analysis of DEM reconstruction of ground 3D laser scanning data[J]. Geospatial Information, 2019, 17(12):99-102,117,11. ] DOI:10.3969/j.issn.1672-4623.2019.12.028.

DOI

[11]
贾雨欣, 李剑南, 张磊, 等. 复杂地形区像控点布设对低空无人机遥感成图的精度影响研究[J]. 北京测绘, 2020, 34(7):890-894.

[Jia Y X, Li J N, Zhang L, et al. Research on the influence of control points' layout of complex terrain areas on remote sensing mapping of low altitude UAV[J]. Beijing Surveying and Mapping, 2020, 34(7):890-894. ] DOI:10.19580/j.cnki.1007-3000.2020.07.003

DOI

[12]
兰寒玉. 低空无人机摄影测量精度分析[J]. 测绘与空间地理信息, 2021, 44(12):167-171.

[Lan H Y. Analysis of photogrammetric accuracy of low altitude UAV[J]. Geomatics ＆ Spatial Information Technology, 2021, 44(12):167-171. ]

[13]
黄小川, 郑慧. 地面三维激光雷达点云误差分析及校正方法[J]. 地理空间信息, 2009, 7(5):95-97.

[Huang X C, Zheng H. Analysis of TLS point cloud data error and a modifing method[J]. Geospatial Information, 2009, 7(5):95-97. ] DOI:10.3969/j.issn.1672-4623.2009.05.031.

DOI

[14]
杨忞婧. 地面三维激光扫描仪的测量误差分析[J]. 东华理工大学学报(自然科学版), 2013, 36(2):228-232.

[Yang M J. The measurement error analysis of a terrestrial 3D laser scanner[J]. Journal of East China Institute of Technology (Natural Science), 2013, 36(2):228-232. ] DOI:10.3969/j.issn.1674-3504.2013.02.020

DOI

[15]
Li Z L. Mathematical models of the accuracy of digital terrain model surfaces linearly constructed from square gridded data[J]. The Photogrammetric Record, 1993, 14(82):661-674. DOI:10.1111/j.1477-9730.1993.tb00776.x

DOI

[16]
Aguilar F J, Aguilar M A, Agüera F, et al. The accuracy of grid digital elevation models linearly constructed from scattered sample data[J]. International Journal of Geographical Information Science, 2006, 20(2):169-192. DOI:10.1080/13658810500399670

DOI

[17]
徐志敏, 王利双. DEM地形描述精度的幂函数定量模型[J]. 遥感信息, 2021, 36(3):39-43.

[Xu Z M, Wang L S. Power function based quantitative model of DEM terrain representation accuracy[J]. Remote Sensing Information, 2021, 36(3):39-43. ] DOI:10.3969/j.issn.1000-3177.2021.03.006

DOI

[18]
李国重, 张国芹, 朱长青. DEM线性建模过程中的高程误差传播[J]. 测绘科学技术学报, 2009, 26(4):283-287.

[Li G Z, Zhang G Q, Zhu C Q. Elevation error propagation in linear modeling on DEM[J]. Journal of Geomatics Science and Technology, 2009, 26(4):283-287. ] DOI:10.3969/j.issn.1673-6338.2009.04.014

DOI

Options
文章导航

/

〈 〉