EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 1: 77 - 89

DOI: https://doi.org/10.12082/dqxxkx.2023.220662

地球信息科学理论与方法

CLAB模型：一种乘客出租出行需求短时预测的深度学习模型

  • 周榆欣 , 1, 2, 3 ,
  • 邬群勇 , 1, 2, 3, *
展开
  • 1.福州大学 空间数据挖掘与信息共享教育部重点实验室，福州 350108
  • 2.卫星空间信息技术综合应用国家地方联合工程研究中心，福州 350108
  • 3.数字中国研究院（福建），福州 350003
*邬群勇（1973— ），男，山东诸城人，博士，研究员，研究方向为时空数据挖掘和地理信息服务。E-mail:

周榆欣（1997— ），女，福建长乐人，硕士生，研究方向为时空数据挖掘。E-mail:

收稿日期: 2022-09-06

  修回日期: 2022-10-05

  网络出版日期: 2023-03-25

基金资助

国家自然科学基金项目(41471333)

福建省科技计划引导项目(2021H0036)

收起

CLAB Model: A Deep Learning Model for Short-term Prediction of Passenger Rental Travel Demand

  • ZHOU Yuxin , 1, 2, 3 ,
  • WU Qunyong , 1, 2, 3, *
Expand
  • 1. Key Lab of Spatial Data Mining and Information Sharing of Ministry of Education, Fuzhou University, Fuzhou 350108, China
  • 2. National & Local Joint Engineering Research Center of Satellite Geospatial Information Technology, Fuzhou 350108, China
  • 3. The Academy of Digital China (Fujian), Fuzhou 350003, China
*WU Qunyong, E-mail:

Received date: 2022-09-06

  Revised date: 2022-10-05

  Online published: 2023-03-25

Supported by

National Natural Science Foundation of China(41471333)

Fujian Science and Technology Plan Guidance Project(2021H0036)

Fold

摘要

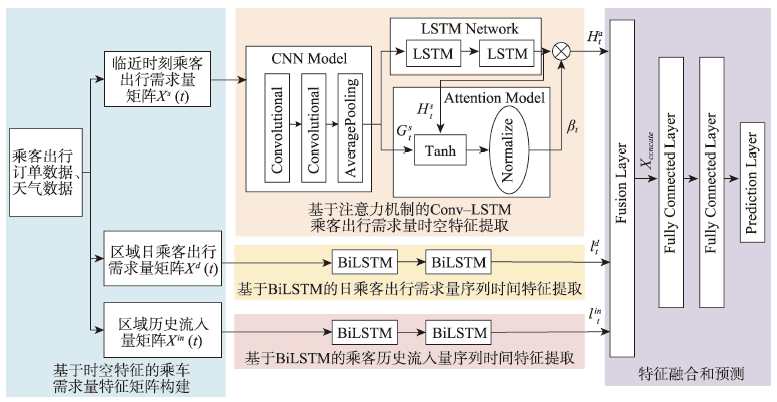
乘客出行需求预测是智能交通系统的组成部分，准确的出行需求预测，对于车辆调度具有重要的意义；然而现有的预测方法无法准确的挖掘其潜在的时空相关性，且大都忽略历史流入量对出行需求的影响。为了进一步挖掘时空大数据中的时空特性及提升模型预测乘客出行需求的精度，本文提出了一种乘客出租出行需求短时预测CLAB(Conv-LSTM Attention BiLSTM)模型。CLAB模型设置了3个模块分别为基于注意力机制的Conv-LSTM模块和2个BiLSTM模块，基于注意力机制的Conv-LSTM模块提取临近时刻乘客出行需求量中的空间特征和短时时间特征，其中注意力机制能自动分配不同的权重来判别不同时间的需求量序列重要性；为了探索长期时间特征，用2个BiLSTM模块来提取历史流入量序列时间特征和日乘客需求量序列的时间特征。采用厦门岛的网约车和巡游车的订单数据进行实验，结果表明：① CLAB模型更适用于使用30 min历史数据预测未来5 min短时乘客出行需求；② 与基准预测模型相比，CLAB模型的整体的效果误差更低，具有更好的预测效果，CLAB模型比CNN-LSTM、LSTM、BiLSTM、CNN和Conv-LSTM的平均绝对误差（MAE）分别降低了33.179%、33.153%、33.204%、5.401%和5.914%，均方根误差（RMSE）分别降低了34.389%、34.423%、34.524%、6.772%和6.669%；③ 同时发现CLAB模型在规律性较高的工作日预测效果优于非工作日，且工作日早高峰预测效果最佳。

关键词： 交通大数据; 出行需求预测; 深度神经网络; 注意力机制; 组合预测模型; 时空融合; 厦门岛; LSTM

本文引用格式

周榆欣 , 邬群勇 . CLAB模型：一种乘客出租出行需求短时预测的深度学习模型[J]. 地球信息科学学报, 2023 , 25(1) : 77 -89 . DOI: 10.12082/dqxxkx.2023.220662

Abstract

Passenger travel demand prediction is an integral part of intelligent transportation systems, and accurate travel demand prediction is of great significance for vehicle scheduling. However, existing prediction methods are unable to accurately explore its potential spatiotemporal correlation and mostly ignore the impact of historical inflow on travel demand. In order to further exploit the spatiotemporal characteristics of spatiotemporal big data and improve the accuracy of the model in predicting passenger travel demand, this paper proposes a Conv-LSTM Attention BiLSTM (CLAB) model for short-time prediction of passenger rental travel demand. The attention-based Conv-LSTM module extracts spatial features and short-term temporal features of passenger travel demand at the near moment, where the attention mechanism automatically assigns different weights to discriminate the importance of demand sequences at different times. To explore long-term temporal features, two BiLSTM modules are used to extract temporal features of historical inflow sequences and temporal features of daily passenger temporal features of the demand series. Experiments are conducted using the order data of online and cruising taxis on Xiamen Island, and the results show that: (1) the CLAB model is more suitable for predicting the future 5-min short-time passenger travel demand using 30-min historical data; (2) the overall effect error of the CLAB model is lower and has better prediction results compared with the benchmark prediction model. The CLAB model is more effective than the CNN-LSTM, LSTM, BiLSTM, CNN, and Conv-LSTM by 33.179%, 33.153%, 33.204%, 5.401%, and 5.914% in mean absolute error (MAE) and 34.389%, 34.423%, 34.524%, 6.772%, and 6.669% in Root Mean Square Error (RMSE), respectively; (3) the CLAB model performs better for weekday prediction with higher regularity than non-working day prediction, with best prediction for weekday morning peaks.

Key words： traffic big data; travel demand forecasting; deep neural network; attention mechanism; combined forecasting model; spatiotemporal fusion; Xiamen Island; LSTM

1 引言

大城市乘客出行服务通常存在着供需失衡[1]，这种不平衡会导致过长的等待时间、收入损失和能源浪费[2]。因此准确预测乘客的出行需求，成为解决供需失衡和资源（如汽车、自行车）调度策略的重要一步。乘客出租出行需求存在波动性和随机性的特征，在时间和空间维度上存在复杂的依赖关系，且受多种因素（如气象数据和时间属性）影响，准确的出租需求预测比普通需求预测更具挑战性。
目前，对出行需求的预测方法主要有基于统计理论的预测模型、基于深度学习的预测模型和基于多种模型结合的组合模型。对于基于统计理论的预测模型，传感技术的发展为通过挖掘数据中的模式进行短时需求预测提供了巨大的机会[3⇓⇓⇓-7]。Li等[8]将乘客需求作为时间序列数据，采用自回归综合移动平均(ARIMA)及其变量等时间序列模型预测出行量。Moreira-Matias等[9]综合了即时变泊松模型、ARIMA模型和加权变泊松模型3种时间序列分析技术聚合GPS数据以预测30 min出租车乘客需求。Tong[10]等提出了一个名为UOTD的线性回归模型来预测大规模出租车需求。Faghih等[11]引入了一种新的时空自回归模型来预测新城的短期优步需求。Li等[12]提出了一种基于最小二乘支持向量机(LS-SVM)的短期交通需求预测模型。该方法模型简单，计算较快，但是只适用于平稳性交通状况且难以处理出行需求数据的时间和空间相结合的依赖关系。随着深度学习方法的快速发展和数据处理能力的不断提升，基于深度学习的乘客出行需求预测方法成为研究的热点[13⇓-15]。Xu等[16]采用高斯核LSTM模型预测新城不同地区的出租车需求。Jiang等[17]将地理空间数据处理为图像，并应用残差网络同时预测出租车接送需求。Zhang等[18]以多个时间尺度的历史出租车需求数据作为输入，提出了一种用于城市范围人群流量预测的深度时空残差网络。该方法学习能力强、考虑了非线性及不确定性且预测精度高，但是存在可移植性不高且大多只考虑单一时间特征或是空间特征对出行需求的影响。基于多种模型组合的组合模型是目前使用最广泛的乘客出行需求预测方法。组合模型可以利用多种模型优势互补，但是增加了计算量和复杂度，且组合不当预测效果反而更差。为了捕捉城市范围内的历史需求的时空关系，研究人员使用CNN作为前端层对输入数据进行特征提取，并将特征信息传递给LSTM进行序列学习和短期出行需求预测[19⇓-21]。Bai等[22]通过区域相似性组织需求数据，通过级联的CNN-LSTM网络提取时空相关性。Shi等[23]将CNN和LSTM创新地集成在一个端到端的DL结构中,命名为ConvLSTM，为解决时空序列问题提供了新的思路。Wu等[24]利用一维CNN捕捉交通流的空间特征，利用2个LSTM来挖掘交通流量的短期变化性和周期性，研究表明，交通具有短期，每日和每周的周期性。这些模型通过建模数据的时空相关性对出行需求数据进行预测；但是，以上方法没有有效的建模数据的时空相关性，且未采用注意力机制自适应地对相关部分予以关注。
在预测乘客出租出行需求时既要考虑区域间的空间依赖性，也需考虑历史数据的时间依赖性，若仅仅单独的考虑空间或时间关系会丢失对预测结果起重要作用的信息。虽然大多数研究使用CNN和LSTM来提取时空数据中的时空特性，但鲜有研究考虑历史入流量对乘客出行需求预测的影响。因此，本文提出一种融合CNN、LSTM、注意力机制和BiLSTM网络的组合模型，该模型可以更有效地捕获出行需求中的时空特征，且引入注意力机制可以自动区别不同时间下出行需求的重要性。

2 乘客出租出行需求预测模型

本文提出了一种用于乘车需求量预测的CLAB模型（Conv-LSTM Attention BiLSTM, CLAB），如图1所示，该模型由3个模块组成，即时空特征提取模块、历史流入量序列时间特征提取模块和日乘客出行需求序列时间特征提取模块。乘客出行需求具有时空依赖性，包括区域空间依赖性、历史出行需求序列和历史流入量序列的时间依赖性。带有注意力机制的Conv-LSTM作为乘客出行需求时空特征提取模块来获取临近时刻出行需求的时空特征，使用2个BiLSTM分别提取出行需求数据中历史流入量序列及日乘客出行需求序列时间特征。考虑天气状况、温度和星期属性等其他因素对出行需求的影响，因此从乘客订单数据和天气数据中提取临近时刻乘客出行需求量矩阵 X s t ,区域日乘客出行需求量矩阵 X d t和区域历史流入量矩阵 X i n t，以矩阵形式输入到模型中；再通过融合层对以上3个模块输出向量进行融合，从而对每个网格研究区域的乘客出租出行需求量进行单步预测。
图1 基于CLAB组合模型的乘客出租出行需求量短时预测技术流程

Fig. 1 Technical process of short-term forecasting of passenger rental travel demand based on CLAB composite model

2.1 基于时空特征的乘车需求量特征矩阵

假设研究区域中有m个网格，每个网格代表一个交通区域, F i = f i 1 ,   f i 2 , … ,   f i m ∈ R N × 1表示为当前时刻为i时m个网格的乘客出行需求量， f i j代表为i时刻网格编号为j的乘客出行需求量。 X i由乘车出行需求量 F i和其它因素影响量 E i组成 X i = F i , E i，其它因素影响量 E i包括i时刻的风速、温度、天气、时间片、星期属性和周期属性。
预测的目标是解决一个包含空间层次和时间序列结构的问题，即在给定前n-1个时刻的历史需求量和其他因素影响量 X t | t = 1 ,   2 ,   … ,   n - 1，预测第n个时刻乘客出行需求量 F n。
（1）临近时刻乘客出行需求量矩阵 X s t
乘客在短时间内的出行需求量变化受到临近需求量的影响。记 X t s包含当前时间切片乘客出行需求量 F t s和其它因素影响量 E t s，则 X t - 1 s包括t-1时刻的乘客出行需求量 F t - 1 s和其它因素影响量 E t - 1 s，以此类推。预测第t个时刻的乘客出行需求量 F t时，用前n-1个临近时刻乘客出行需求量和其他因素影响量构成临近时刻出行需求量矩阵 X s t。
X s t = X t - n s X t - n - 1 s ⋮ X t - 1 s T = F t - n s , E t - n s F t - n - 1 s , E t - ( n - 1 ) s ⋮ ⋮ F t - 1 s , E t - 1 s T = f t s - n , 1 f t s - n - 1 1 , ⋮ , f t s - 1 1 f t s - n 2 , f t s - n - 1 , 2 ⋮ , f t s - 1 2 ⋮ ⋮ ⋮ ⋮ f t s - n m , f t s - n - 1 m , … , f t s - 1 m E t - n s , E t - n - 1 s , … , E t - 1 s
式中： t s-1表示时间t-1时刻， X t - 1 s=[ f t - 1 1 ,   f t - 1 2 , … , f t - 1 m, E t - 1 s]表示t-1时刻m个网格的乘客需求量以及t-1时刻对应的其它影响因素，以此类推。
（2）区域历史流入量矩阵 X i n t
区域的乘客出行需求不仅会受到历史出行需求的影响，而且会依赖于区域历史乘客流入量。乘客出行需求在一定程度上反映了区域人流量的变化情况，区域人流量的变化也会影响区域乘客出行变化，当一个区域一段时间吸引入了大量的人流量，可能会导致人流量未来一段时间内乘车从区域离开[25]。记 X t i n包括当前时间切片乘客流入量 F t i n和其它因素影响量 E t i n，则 X t - 1 i n包括t-1时刻的乘客流入量 F t - 1 i n和其它因素影响量 E t - 1 i n，以此类推。预测第t个时刻的乘客出行需求量 F t时，用前n-1个临近时刻网格研究区的历史流入量和其他因素影响量构成历史流入量序列矩阵 X i n t。
X i n t = X t - n i n X t - ( n - 1 ) i n ⋮ X t - 1 i n T = F t - n i n , E t - n i n F t - n - 1 i n , E t - ( n - 1 ) i n ⋮ ⋮ F t - 1 i n , E t - 1 i n T = f t i n - n 1 , f t i n - ( n - 1 ) 1 , … , f t i n - 1 1 f t i n - n 2 , f t i n - ( n - 1 ) 2 , … , f t i n - 1 2 ⋮ ⋮ ⋮ ⋮ f t i n - n m , f t i n - ( n - 1 ) m , … , f t i n - 1 m E t - n i n , E t - n - 1 i n , … , E t - 1 i n
式中： t i n-1表示时间t-1时刻， X t - 1 i n=[ f t i n - 1 1 ,   f t i n - 1 2 , … ,   f t i n - 1 m ,   E t - 1 i n]表示t-1时刻m个网格的乘客的历史流入量和t-1时刻其它因素影响量，以此类推。
（3）区域日乘客出行需求量矩阵 X d t
为了预测乘车需求量，将前一天相同时间的历史需求量作为每日特征。区域日乘客出行需求矩阵 X d t由与t时刻相同时间前一天的乘客出行需求量 F t d和其它因素影响量 E t d组成。
X d t = F t d ,   E t d = f t d 1 ,   f t d 2 , … ,   f t d m ,   E t d
式中： t d表示与前一天的时间t相同的时刻。 X d t= f t d 1 ,   f t d 2 , … ,   f t d m ,   E t d表示为前一天相同时间t时刻的m个网格的乘客出行需求量和其它因素影响量。

2.2 基于Conv-LSTM的乘客出行需求量时空特征提取

在现有研究中空间特征提取多使用CNN，而时间特征提取多使用LSTM，而Conv-LSTM是时空融合模块，将空间特征提取的输出作为时序特征提取的输入。Conv-LSTM模块[26]是该模型的主要组成部分，用于提取乘客出行需求数据中的区域空间依赖性和临近时间依赖性，主要包括CNN和LSTM网络。CNN网络由2个卷积层组成，LSTM网络包含2个LSTM层。将临近时刻乘客出行需求量矩阵 X s t输入Conv-LSTM模块中，对每个时间窗执行卷积运算提取空间特征，使用卷积核滤波器通过滑动滤波器获取局部感知域。
Y t s = σ W s * X s t + b s
式中： W s是滤波器的权重； b s是偏差； X s t是需求量；*表示卷积运算； σ为激活函数； Y t s为卷积层的输出。空间信息经过2个卷积处理后进行池化，将 G t s表示为池化后的输出结果，输出连接到LSTM网络中。
LSTM利用三门输入门、忘记门和输出门来控制信息流。在每个时间间隔内，LSTM考虑 C t - 1 ,   h t - 1和 X t作为输入，其中输入门决定先前信息传递到单元状态。如果忘记门 f t被激活，LSTM将忘记之前存储单元 C t - 1,输出门 O t控制存储单元的输出。在本文中，使用多个LSTM层堆叠到模型中，每个LSTM层接收前一层的隐藏状态作为输入，如图1所示，第一层LSTM处理来自CNN模块的序列输出张量 G t s = G t - n s , G t - ( n - 1 ) s , … , G t - 1 s，计算每个时间步长的隐藏状态张量 H 1 , t s = [ H 1 , t - n s , H 1 , t - ( n - 1 ) s , … , H 1 , t - 1 s ]，将 H 1 , t s作为第二层LSTM的输入以计算时间步长t的隐藏状态张量 H 2 , t s。每个LSTM层计算公式如下：
i t = σ W g i I t s + W h i H t - 1 s + W c i ⊙ C t - 1 + b i
f t = σ W g f I t s + W h f H t - 1 s + W c f ⊙ C t - 1 + b f
C t = f t ⊙ C t - 1 + i t   t a n h W g c I t s + W h c H t - 1 s + b c
o t = s i g m a W g o I t s + W h o H t - 1 s + W c o ⊙ C t + b o
H t s = o t ⊙ t a n h C t
式中： I t s是LSTM层在时间步长t的输入； σ是激活函数； i t , f t , o t分别是时间t的输入门、忘记门和输出门； C t是单元状态； ⊙表示矩阵元素的乘积，W和b分别是权重和偏差。LSTM层 H t s的最终输出由输出门和更新单元确定。两层LSTM的输入分别为张量 G t s和张量 H 1 , t s。第1层和第2层的LSTM输出 H t s分别对应于 H 1 , t s和 H 2 , t s。最后，我们获得了时间步长t的时空特征张量 H t s。临近时刻乘客出行需求量矩阵 X s t经过两层CNN和池化层后再进入两层LSTM中进行计算。

2.3 基于注意力机制的需求量序列重要性的判别

考虑不同时刻对预测时刻出行需求的影响并不相同，为了对所提取不同时间步的出行需求特征按照重要程度予以不同权重的关注，在Conv-LSTM模块设计了一种注意力机制，以判别不同时间下需求量序列的不同重要性级别。
图2显示了带有注意力机制的Conv-LSTM模块，每个时间步长t的Conv-LSTM的输出 H t a为LSTM中 H t s输出的加权总和，如下所示：
H t a = ∑ k = 1 n β k H t - k - 1 s
β k = e x p s k ∑ k = 1 n e x p s k
s t = V s T t a n h W h s G t s + W l s H t s
式中：n表示时间窗的长度； β k是时间步长t-(k-1)的时间注意力机制。分数 s = s 1 , s 2 , … , s n T表示时间窗中各部分的重要性； V s、 W h s、 W l s是可学习参数， H t s是Conv-LSTM隐藏输出张量。从公式可以看出，时间步长t的注意力机制 β取决于前n-1个时间步长卷积层输出的 G t s和隐藏变量 H t s。注意力机制的输入为CNN层和LSTM层的输出，获得判别分数从而判别不同时间下乘客出行需求量序列的重要性。
图2 带有注意力机制的Conv-LSTM结构示意

注: xst-n,…, xst-2和xst-1 为t时刻临近时刻乘客出行需矩阵Xs(t)中的n个输人数据;Hst-n，…, Hst-2和Hst-1为求量输人数据经过Conv-LSTM网络处理得到的隐藏变量; βn，…, β2和β1为对应时间步长的时间注意力机制; Hat为带有注意力机制的Conv-LSTM模块在时刻的输出变量。

Fig. 2 Schematic diagram of the Conv-LSTM structure with attention mechanisms

2.4 基于BiLSTM的历史流入量序列和日乘客需求量序列时间特征提取

出租车出行时间序列存在周期性，周期为一周，在工作日波动特征相似，而工作日、周末之间存在差异[27]；这导致工作日每天的需求量相似；在给定时间的乘客需求量不仅取决于其前一时间段的乘客需求量，而且反过来影响下一时间段。BiLSTM既保留了LSTM能够处理长时间序列的特点，又考虑了前后数据变换的影响，提高了特征提取的全局性，对于复杂的回归问题具有较好的拟合性。本模型使用两个BiLSTM来分别提取历史流入量序列和日乘客出行需求序列时间特征，用于提取历史流入量序列的时间特征的BiLSTM输入序列为以当前时刻为中心，向前和向后各扩展相应的n个时间间隔，即考虑此时刻以及相邻时间间隔的历史流入量对此时刻研究区出行需求的影响；用于提取日乘客出行需求序列的时间特征的BiLSTM输入序列为以昨日此时刻为中心，向前向后个扩展n个时间间隔，即考虑昨日此时刻以及相邻时间时间的出行需求对该时刻出行需求预测的影响。
BiLSTM通过Forward层与Backward层的LSTM，使用式(13)和(14)分别对过去和未来的需求量信息进行提取与保存，单层BiLSTM网络结构 如图3所示。假设Forward层按时间顺序，Backward层按时间逆序， t时刻的隐层状态定义为 h t 1和 h t 2，根据2个方向的隐层状态计算t时刻双向长短时记忆层输出向量 l t，如式（15）。
h t 1 = f U 1 h t - 1 1 + W 1 X t + b 1
h t 2 = f U 2 h t - 1 2 + W 2 X t + b 2
l 2 = W t 1 h t 1 + W t 2 h t 2 + b 0
式中： W 1和 W 2为对应时刻权重矩阵， U 1和 U 2分别为上一时刻与下一时刻权重矩阵， f代表隐藏层激活函数， W t 1和 W t 2为对应隐层状态权重矩阵， b 1 、 b 2和 b 0为偏置向量。将区域历史流入量矩阵 X i n t和区域日乘客出行需求量矩阵 X d t分别输入到双层BiLSTM中，识别过去和未来的历史流入量和日乘客需求量的信息得到向量 l i i n 和 l t d，利用历史流入量和日乘客需求对乘客出行需求量的影响增加预测的精确性。
图3 双向长短时记忆神经网络结构示意

注: Xt-1、Xt、Xt+1为不同时刻的输入(Input); h1t-1、h1t、h1t+1为不同时刻正向(Forward)LSTM的输出; h2t-1、h2t、h2t+1为不同时刻反向(Backward)LSTM的输出;lt-1、lt、lt+1对应不同时刻正向LSTM和反向LSTM输出拼接得到输出向量(Output)。

Fig. 3 Schematic diagram of the structure of a bidirectional long-and short-term memory neural network

2.5 特征融合和预测

通过Conv-LSTM模块可以得到乘客出行需求时空特征，使用2个BiLSTM模块分别提取历史流入量序列的时间特征和日乘客出行需求序列的时间特征。融合层(Fusion Layer)使用Concatenate()函数可将多个模块提取的特征进行融合，Concatenate()函数将上述3个模块提取的特征在一维上进行拼接后得到特征向量 X c o n c a t e。
X c o n c a t e = C o n c a t e n a t e H t a , l i i n , l t d
式中： H t a代表为所提取的乘客出行需求时空特征， l i i n 和 l t d分别代表所提取的历史流入量序列的时间特征和日乘客出行需求序列的时间特征； X c o n c a t e代表经过特征融合所得的特征向量。
全连接层(Fully Connected Layer)中的每一个神经元都与上一层所有的神经元进行连接，结合所有单元信息进行高层的抽象思维，通过向前计算和反向传播的方式来不断更新权重系数，提高网络识别结果与提取特征的关联程度，使得模型达到预先设计的阈值。本文将 X c o n c a t e特征向量作为输入向量经过两层全连接层后使用一个具有N个神经元的全连接层作为最后的输出预测层（N代表划分网格研究区总数）得到预测结果。全连接层表达式如下：
D t = f W D X D + b D
式中： X D表示全连接层的输入向量； D t表示全连接的输出向量； W D和 b D分别表示对应的权重和偏置； f ·为激活函数。

2.6 损失函数

在训练阶段，设置一个损失函数来更新模型中的参数，包括均方误差、 l 1权重正则化和 l 2权重正则化。损失函数中包含 l 1正则化的目标是获得稀疏模型，可以防止深度模型的过度拟合。损失函数的 l 2正则化可以防止模型中出现数值过大参数，并避免特定特征主导模型的预测性能。损失函数定义如下：
L o s s = 1 n ∑ t = 1 n F P - F t 2 + λ 1 n w 1 + λ 2 n w 2 = 1 n ∑ t = 1 n F P - F t 2 + λ 1 ∑ i = 1 n W i + λ 2 ∑ i = 1 n W i 2
式中： F P是预测需求量； F t是真实需求量； n是数据集数量； λ 1 、 λ 2是正则化参数； w、 W i是权重。

2.7 评价指标

对于多个区域预测出行结果的评价采用平均绝对值误差MAE和均方根误差RMSE作为标准对模型进行评价，评价指标计算原理如式所示：
M A E = 1 n ∑ i = 1 n Y i - y i
R M S E = 1 n ∑ i = 1 n Y i - y i 2
式中： Y i为预测区域的真实值； y i为预测区域的模型预测值；n为所有预测区域网格的个数。评价指标为值越小，模型精度越好，预测误差越小，证明模型效率越高。

3 实验及分析

3.1 实验数据与预处理

本研究选取了厦门岛（不包括鼓浪屿）为研究区。厦门岛是厦门市居民的主要活动聚集区，根据厦门2021年统计年鉴显示[28]，厦门岛土地面积占厦门市的9.3%，而厦门岛常驻人口占厦门市的41.8%，从人数以及面积的占比可以看出，厦门岛的交通承载着巨大的压力，岛内居民的出行需求较大。
本研究所需要数据包括订单数据（巡游车和网约车订单数据总计）和天气数据。其中订单数据来源于2020年数字中国创新大赛公开的2019年5月31日—2019年6月9日，2020年6月18日—2020年6月27日端午节及前一周厦门岛巡游车和网约车订单数据，总计20 d，订单数据主要包括车牌号、出行开始时间、出行结束时间、上车的经纬度位置和下车经纬度位置。天气数据在公开数据Weather Underground网站获取，包括温度、风速、天气类型以小时为单位的数据，其中天气类型分晴、多云、雾、雨依次标记为0~3类。为了提高模型的预测精度，在模型中加入其它数据集，包括星期属性、周期属性和每一天相应时间划分对应的时间片编号；周期属性表示是否为周末，订单数据中包括了端午节的特殊节假日，因此工作日赋值为0，休息日赋值为1，端午节赋值为2。
根据Luo等[29]研究采用基于网格的区域划分方法将厦门岛研究区划分为一定大小的规则网格，将厦门岛研究区域划分为500 m×500 m的网格单元（图4(a)），在641个网格中筛选去掉落在森林、水域以及网格中的需求量总数相对较少的网格，最后将220个网格单元作为最后研究对象（图4(b)），将一天分成相应的时间片段，统计每个时间段各个网格研究区的乘客上车量和下车量。
图4 厦门岛乘客出行需求总量空间分布

Fig. 4 Spatial distribution of the total travel demand of passengers on Xiamen Island

将数据集输入模型之前，使用独热编码对其它数据集中分类特征（一天24 h时间划分对应的时间片、星期属性和周期属性）进行转换；利用Min-Max归一化方法对其它数据集中风速、温度等连续特征进行尺度化处理。对于不同模型预测结果对比、模型消融实验和工作日与非工作日高峰期预测对比的实验中，以5 min划分需求量为准，用前30 min的历史数据预测未来5 min研究区域的需求量，进行单步预测。

3.2 实验参数设置

本文实验环境如下：操作系统Window10，CPU 是Intel(R) Xeon(R) Gold 5118，采用python语言，深度学习框架TensorFlow，GPU为NVIDIA GeForce RTX 2080 Ti。在实验中，将2019年5月31日—2019年6月5日、2019年6月7日（端午节）—2019年6月8日，2020年6月18日—2020年6月23日、2020年6月25日（端午节）日—2020年6月26日作为训练数据，将2019年6月6日（周四），2019年6月9日（周日），2020年6月24日（周三）和2020年6月27日（周六）作为测试数据。对于日乘客需求量特征输入如图5所示，为了预测周一的需求量，使用上周五（而不是周日）的相同时间间隔的历史需求量作为特征输入；预测周六的需求量，将上周日同一时间的历史需求量数据作为特征输入；对于一周中的任何其他一天，将前一天同一时间的历史需求量数据作为日乘客需求量特征输入。
图5 日乘客需求量特征输入构造示例

Fig. 5 Example of daily passenger demand characteristic input construction

CLAB模型中Conv-LSTM模块CNN层有20个滤波器filter，卷积核大小kernel_size为4，滑动窗口步长设置为1，LSTM层的隐藏单元units为20；BiLSTM模块中的BiLSTM层的隐藏单元units为20。使用Adam优化算法优化模型参数，自适应调整学习速率；激活函数采用线性激活单元ReLU，训练轮数epochs设置为100轮。在训练集中，随机选择85%的数据对模型进行训练，15%的数据作为验证集。在临近时刻乘客出行需求量和历史流入量特征矩阵中用30 min内的历史数据作为训练单元，根据不同的时间片划分需求量设置对应的时间窗口，例如5 min为单位划分时间片时,时间窗口设置为6。为了选择最合适的组件层数和训练批量大小，使用5 min划分的需求数据设计相关实验。
为了得到预测模型合适的批量大小，分别将批量大小batch_size设置为16、32、60、128进行实验，测试模型的预测性能。不同批量大小batch_size的实验结果如表1所示。随着批量大小从16增加到60， MAE和RMSE的值逐渐减小，训练效果越好；但是，当批量大小增加到128时， MAE和RMSE值反而增大，说明选择适当的批量大小，对模型预测性能的提升有显著的效果，批量大小数值设置太小或者太大都会导致模型预测性能的下降。从训练的误差效果考虑，CLAB模型的批量大小batch_size选择为60。
表1 不同批量大小的实验结果

Tab. 1 Experimental results for different batchsizes

batch_size MAE RMSE
16 1.756 2.575
32 1.737 2.564
60 1.734 2.547
128 1.742 2.589
CLAB模型是组合模型主要包括Conv-LSTM模块和2个BiLSTM模块，Conv-LSTM模块中CNN、LSTM层数和BiLSTM模块中BiLSTM层数的设计影响模型的性能。同时调整CNN、LSTM和BiLSTM网络层数的取值，使CLAB模型能达到更高的乘客出行需求预测精确度。表2为CLAB模型中CNN、LSTM和BiLSTM网络不同组件层数的实验结果。可以看出，组件层数从1增加到2时候，MAE和RMSE值减少；但从2增加到4时，MAE和RMSE值增加。为了获取最佳的模型预测精度，将CLAB模型中的各组件层数设置为2。Conv-LSTM模块中分别有2层CNN和LSTM网络，BiLSTM模块模块中有2层的BiLSTM网络时，模型的预测效果更加精准MAE和RMSE取最小值分别为1.734和2.547。
表2 不同组件层数的实验结果

Tab. 2 Experimental results for different component layers

组件层数 MAE RMSE
1 1.750 2.571
2 1.734 2.547
3 1.747 2.571
4 1.750 2.589

3.3 不同时间片划分对比实验

探寻不同时间划分下模型的可适用性，对5 、10、15 min划分的乘客出行的需求量进行单步预测，对临近时刻乘客出行需求量和历史流入量矩阵分别使用30 min和60 min的历史数据作为训练单元，实验结果如表3所示。从整体上看，模型的预测精度随着时间片划分时长的增加而降低，5 min划分时间片的乘客出行需求量模型预测精度最高， 15 min划分时间片的乘客出行需求量模型预测精度最低。越细致的时间片划分，信息量越大，模型能从中学习的规律越多，模型预测效果越好。分别用前30 min分钟和前60 min历史数据预测下一时间片的乘客出行的出行需求量，结果表明，用前 30 min的历史数据预测下一时间片的乘客出行的需求量CLAB模型预测的精度更高。因此，选用 5 min划分的乘客出行需求量，临近时刻乘客出行需求量和历史流入量特征矩阵用30 min内的历史数据作为训练单位来进行不同模型预测结果对比、模型消融实验和工作日与非工作日高峰期预测对比的实验。
表3 CLAB模型不同时间片划分对比实验

Tab. 3 CLAB model different time slice division comparison experiment

时间/min 30 min 60 min
MAE RMSE MAE RMSE
5 1.734 2.547 1.753 2.581
10 2.664 4.122 2.714 4.158
15 3.660 5.741 3.667 5.671

3.4 不同模型预测结果对比

为评估本文提出CLAB模型预测效果，将选取一些基准模型在同等环境下进行对比。本文选取的基准模型具体如下：① ConvLSTM[30]：具有LSTM的时序建模能力，还可以通过CNN捕获局部特征，因而能够对时空数据的时空特征进行学习； ② CNN[13]：双层卷积层，1个卷积层可以很好地描述空间区域的近地依赖性，2个卷积层可以进一步描述远地的依赖性。深层卷积层，可以模拟城市中任何2个地区之间的附近和遥远的空间依赖关系；③ CNN_LSTM[31]：单层CNN_LSTM，CNN捕获空间特征，LSTM获取时间特征；④ LSTM[32]：双层LSTM，利用LSTM捕获乘客需求量中的时间特征；⑤ BiLSTM[33]：双层BiLSTM，利用BiLSTM捕获乘客需求量中的上下时间特征联系。
本文所提出的CLAB模型与其他几种神经网络模型方法在乘客出行需求预测的实验结果如表4所示。由实验结果可知，BiLSTM模型的实验结果与LSTM模型相近，2个模型的实验结果差距十分微小。ConvLSTM和CNN-LSTM模型相比较，都考虑了需求预测的空间特征和时间特征，但CNN-LSTM空间数据是输入卷积神经网络以提取空间特征，而时间数据单独输入LSTM网络中提取时间特征,空间特征和时间特征在全连接层中融合，但在本实验乘客出行需求预测中ConvLSTM的精度远高于CNN-LSTM。双层CNN能很好捕捉数据中的空间依赖信息，相较于单层CNN-LSTM精度大幅度提升。可以看出，CLAB模型在所有指标上都优于上述所有算法，CLAB模型相比于CNN-LSTM、LSTM、BiLSTM、CNN和ConvLSTM的平均绝对误差（MAE）分别降低了33.179%、33.153%、33.204%、5.401%和5.914%，均方根误差（RMSE）分别降低了34.389%、34.423%、34.524%、6.772%和6.669%，表明使用该模型得到的预测值与真实值之间的差距更小，出现较大偏差可能性更低，可以更准确的对乘客出行需求量进行预测。
表4 不同方法在预测时长为5 min下的性能对比

Tab. 4 Comparison of the performance of different methods at a prediction duration of 5 min

模型 MAE RMSE
CNN-LSTM 2.595 3.882
LSTM 2.594 3.884
BiLSTM 2.596 3.890
CNN 1.833 2.732
ConvLSTM 1.843 2.729
CLAB 1.734 2.547

3.5 模型消融实验

为进一步探究本文所提出的CLAB模型各部分的有效性，展开了消融实验。将CLAB模型进行了分解分别移除了BiLSTM、Attention机制等，以此验证被去除部分的有效性，为控制参数对实验的影响，每组实验超参数设置相同，加入其它影响因素和无其它影响因素的区别是在模型中加入了温度、风速、天气类型、星期属性、周期属性和时间片数据，实验结果如表5所示。
表5 CLAB模型在预测时长为5 min下消融实验

Tab. 5 CLAB model ablation experiment at a predicted duration of 5 min

模型 加入其它影响因素 无其它影响因素
MAE RMSE MAE RMSE
A去掉注意力机制 1.735 2.587 1.740 2.569
B去掉历史流入量 1.744 2.587 1.761 2.624
C去掉日乘客需求量 1.742 2.558 1.766 2.618
D 去掉历史流入量和日乘客需求量 1.752 2.596 1.740 2.582
E 去掉流入量、日乘客需求量和注意力机制 1.738 2.579 1.748 2.592
CLAB 1.734 2.547 1.739 2.565
从表5可以看出模型的每一个部分对于模型的性能均有明显的提升。在加入其他因素特征实验中，CLAB模型与A、B、C、D、E模型相比，平均绝对误差（MAE）分别降低了0.057%、0.573%、0.459%、1.027%和0.231%，均方根误差（RMSE）分别降低了1.546%、1.546%、0.430%、1.888%和1.241%，预测效果显著提升。这说明历史流入量、日乘客需求量、注意力机制都对提高模型预测精度有一定的影响，表明融入这些因素的有效性。对比将其它因素特征加入模型中，对模型预测效果的影响，加入其它因素特征的CLAB模型比不加入其他因素特征的CLAB模型的预测效果平均绝对误差（MAE）降低了0.288%，均方根误差（RMSE）降低了0.702%。CLAB模型聚集了注意力机制对临近时刻需求量序列重要性级别判断，BiLSTM充分考虑历史流入量数据和日乘客需求量数据前后向数据的影响。

3.6 工作日和非工作日高峰期预测对比实验

人们对于高峰期的乘车需求更加在意，将工作日和非工作日的高峰期数据进行测试，根据图6数据集中订单日变化量的变化趋势，将时间范围在 7:00—9:00为早高峰，时间范围在11:00—14:00为午高峰，时间范围在17:00—20:00为晚高峰。
图6 2020年6月18日—2020年6月27日厦门岛乘客出行订单日变化量

Fig. 6 Daily change in passenger travel orders on Xiamen Island from June 18, 2020 to June 27, 2020

由表6可看出工作日的整体预测结果更好，因为在工作日，人们通常有规律的生活方式，而在节假日，人们生活方式各不相同，很难预测乘客的出行需求。即相比于工作日的需求模式，非工作日的需求模式要更加不规则，规则的需求模式更加有利于模型去学习。对比CLAB模型在工作日和非工作日早、午、晚高峰的乘客出行的预测效果,早、午高峰预测的精度高于晚高峰预测精度；而工作日的早、晚高峰预测精度高于非工作日的早、晚高峰。
表6 CLAB模型在工作日和非工作日高峰期性能对比

Tab. 6 Comparison of CLAB model performance during peak weekday and non-weekday periods

MAE RMSE
全天 早高峰 午高峰 晚高峰 全天 早高峰 午高峰 晚高峰
工作日 1.780 1.444 1.879 2.138 2.544 1.946 2.548 2.910
非工作日 1.688 2.158 1.810 2.164 2.550 2.862 2.505 3.230

4 结论与讨论

4.1 结论

为了更好地挖掘出行数据复杂的时空相关性，准确预测未来出行需求，本文提出了一种乘客出行需求短时预测CLAB模型。CLAB模型考虑出行需求区域空间依赖性，临近时刻出行需求时间依赖性，历史流入量序列时间依赖性和日乘客出行需求序列时间依赖性来进行混合建模。并以厦门岛为例，对厦门岛的乘客短时出行需求进行单步预测。研究结论为：
（1） 基于注意力机制的Conv-LSTM模块能有效提取历史需求数据中的时空特征，注意力的引入为重要且相关性更强的隐含特征向量分配更多权重，降低历史需求数据对预测精度引起的误差；2个BiLSTM模块分别提取历史流入量序列和日乘客出行需求序列的时间特征。以上3个子模块组合构成CLAB模型大大提升模型预测性能且全面考虑时空特征对出行需求预测的重要性，可为交通调度动态管理提供决策依据。
（2） CLAB模型在乘客出行需求预测方面性能优于CNN-LSTM、LSTM、BiLSTM、CNN和ConvLSTM五种基准模型，具有更高的预测精度，平均绝对误差（MAE）分别降低了33.179%、33.153%、33.204%、5.401%和5.914%，均方根误差（RMSE）分别降低了34.389%、34.423%、34.524%、6.772%和6.669%，说明CLAB模型可以更好地探索和学习出行需求时空数据之间的时空依赖性。
（3） 本文分别使用30 min和60 min临近时刻乘客出行需求数据和历史流入量数据，对比5、10 和15 min共3个不同时间片划分的乘客出行需求预测结果，发现CLAB模型更适用于使用30 min历史数据预测未来5 min短时乘客出行需求。
（4）对比CLAB模型在工作日与非工作日高峰期的预测结果，总体来看工作日高峰预测效果优于非工作日高峰，在工作日人们活动更有规律，模型对于周期规律性学习较好，使得预测效果较好。

4.2 讨论

本文提出的CLAB模型能够有效的捕获乘客出行数据中的时空特征，使用历史需求数据、历史流入量数据和其它数据进行乘客需求短时预测。从理论意义上看，本研究证明了充分的挖掘出行需求数据中的时空特征对提高模型预测精度的重要性，从现实意义上来看，本文提出模型可作为出行需求预测的有效手段，其预测结果可以有效的服务车辆与乘客间的供需不均的问题，提升服务车辆的运营效率和利润，同时降低乘客等待时间并改善其对服务平台的满意度。
本研究仍存在一定的不足：
（1）数据的有限性，只使用了20 d的数据训练模型，如果使用多个月的实验数据可以进一步的提高模型的精确性。
（2）将厦门岛研究区域划分为规则网格忽略了道路网络和城市行政区等语义信息且本研究侧重于预测近期（即下一时间步）的乘客需求，然而预测较长时间范围内的乘客需求（即多步时间预测）对于运输服务运营商设计车辆部署策略更有价值。
下一步的研究将考虑复杂的道路路网相关信息，对城市具体的路段和功能区（娱乐区、工业区、旅游景点等）分类研究乘客出租出行需求，从而增强预测模型的泛化能力。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Zhan X Y, Qian X W, Ukkusuri S V. A graph-based approach to measuring the efficiency of an urban taxi service system[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(9):2479-2489. DOI:10.1109/TITS.2016.2521862

DOI

[2]
Jia R, Jiang P C, Liu L, et al. Data driven congestion trends prediction of urban transportation[J]. IEEE Internet of Things Journal, 2018, 5(2):581-591. DOI:10.1109/JIOT.2017.2716114

DOI

[3]
Wang F Y. Parallel control and management for intelligent transportation systems: Concepts, architectures, and applications[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(3):630-638. DOI:10.1109/TITS.2010.2060218

DOI

[4]
Huang Z R, Ling X M, Wang P, et al. Modeling real-time human mobility based on mobile phone and transportation data fusion[J]. Transportation Research Part C: Emerging Technologies, 2018, 96:251-269. DOI:10.1016/j.trc.2018.09.016

DOI

[5]
Liu T, Tian B, Ai Y F, et al. Parallel reinforcement learning-based energy efficiency improvement for a cyber-physical system[J]. IEEE/CAA Journal of Automatica Sinica, 2020, 7(2):617-626. DOI:10.1109/JAS.2020.1003072

DOI

[6]
Almalaq A, Hao J, Zhang J J, et al. Parallel building: A complex system approach for smart building energy management[J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(6):1452-1461. DOI:10.1109/JAS.2019.1911768

DOI

[7]
Chen L, Hu X M, Tian W, et al. Parallel planning: A new motion planning framework for autonomous driving[J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(1):236-246. DOI:10.1109/JAS.2018.7511186

DOI

[8]
Li X L, Pan G, Wu Z H, et al. Prediction of urban human mobility using large-scale taxi traces and its applications[J]. Frontiers of Computer Science, 2012, 6(1):111-121. DOI:10.1007/s11704-011-1192-6

DOI

[9]
Moreira-Matias L, Gama J, Ferreira M, et al. Predicting taxi-passenger demand using streaming data[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(3):1393-1402. DOI:10.1109/TITS.2013.2262376

DOI

[10]
Tong Y X, Chen Y Q, Zhou Z M, et al. The simpler the better: A unified approach to predicting original taxi demands based on large-scale online platforms[C]// Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Halifax, NS, Canada. New York: ACM, 2017:1653-1662. DOI:10.1145/3097983.3098018

DOI

[11]
Faghih S S, Safikhani A, Moghimi B, et al. Predicting short-term uber demand in New York City using spatiotemporal modeling[J]. Journal of Computing in Civil Engineering, 2019, 33(3):05019002. DOI:10.1061/(asce)cp.1943-5487.0000825

DOI

[12]
Li Y X, Lu J, Zhang L, et al. Taxi booking mobile app order demand prediction based on short-term traffic forecasting[J]. Transportation Research Record: Journal of the Transportation Research Board, 2017, 2634(1): 57-68. DOI:10.3141/2634-10

DOI

[13]
LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553):436-444. DOI:10.1038/nature14539

DOI

[14]
Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6):84-90. DOI:10.1145/3065386

DOI

[15]
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8):1735-1780. DOI:10.1162/neco.1997.9.8.1735

DOI PMID

[16]
Xu J, Rahmatizadeh R, Bölöni L, et al. Real-time prediction of taxi demand using recurrent neural networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(8):2572-2581. DOI:10.1109/TITS.2017.2755684

DOI

[17]
Jiang W W, Zhang L. Geospatial data to images: A deep-learning framework for traffic forecasting[J]. Tsinghua Science and Technology, 2019, 24(1):52-64. DOI:10.26599/TST.2018.9010033

DOI

[18]
Zhang J B, Zheng Y, Qi D K. Deep spatio-temporal residual networks for citywide crowd flows prediction[C]// Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence. New York: ACM, 2017:1655-1661

[19]
Ke J T, Zheng H Y, Yang H, et al. Short-term forecasting of passenger demand under on-demand ride services: A spatio-temporal deep learning approach[J]. Transportation Research Part C: Emerging Technologies, 2017, 85:591-608. DOI:10.1016/j.trc.2017.10.016

DOI

[20]
Chu K F, Lam A Y S, Li V O K. Travel demand prediction using deep multi-scale convolutional LSTM network[C]// 2018 21st International Conference on Intelligent Transportation Systems (ITSC). IEEE, 2018: 1402-1407. DOI:10.1109/ITSC.2018.8569427

DOI

[21]
Yao H X, Wu F, Ke J T, et al. Deep multi-view spatial-temporal network for taxi demand prediction[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2018, 32(1):2588-2595. DOI:10.1609/aaai.v32i1.11836

DOI

[22]
Bai L, Yao L N, Kanhere S S, et al. Passenger demand forecasting with multi-task convolutional recurrent neural networks[M]// Advances in Knowledge Discovery and Data Mining. Cham: Springer International Publishing, 2019:29-42. DOI:10.1007/978-3-030-16145-3_3

DOI

[23]
Shi X J, Chen Z R, Wang H, et al. Convolutional LSTM Network: A machine learning approach for precipitation nowcasting[C]// Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 1. New York:ACM, 2015:802-810.

[24]
Wu Y K, Tan H C. Short-term traffic flow forecasting with spatial-temporal correlation in a hybrid deep learning framework[EB/OL]. 2016: arXiv: 1612.01022. https://arxiv.org/abs/1612.01022.

[25]
路民超, 李建波, 逄俊杰, 等. 面向出租车需求预测的多因素时空图卷积网络[J]. 计算机工程与应用, 2020, 56(24):266-273.

DOI

[Lu M C, Li J B, Pang J J, et al. Multi-factor spatio-temporal graph convolution network for taxi demand prediction[J]. Computer Engineering and Applications, 2020, 56(24):266-273. ]

DOI

[26]
Zheng H F, Lin F, Feng X X, et al. A hybrid deep learning model with attention-based conv-LSTM networks for short-term traffic flow prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(11):6910-6920. DOI:10.1109/TITS.2020.2997352

DOI

[27]
程静, 刘家骏, 高勇. 基于时间序列聚类方法分析北京出租车出行量的时空特征[J]. 地球信息科学学报, 2016, 18(9):1227-1239.

DOI

[Cheng J, Liu J J, Gao Y. Analyzing the spatio-temporal characteristics of beijing's OD trip volume based on time series clustering method[J]. Journal of Geo-Information Science, 2016, 18(9):1227-1239. ] DOI: 10.3724/SP.J.1047.2016.01227

DOI

[28]
厦门市统计局. 厦门经济特区年鉴[M]. 北京: 中国统计出版社, 2021.

[Bureau of Statistics of Xiamen. Yearbook of Xiamen special economic zone[M]. Beijing: China Statistics Press, 2021. ]

[29]
Luo S H, Liu Y, Du M Y, et al. The influence of spatial grid division on the layout analysis of urban functional areas[J]. ISPRS International Journal of Geo-Information, 2021, 10(3):189. DOI:10.3390/ijgi10030189

DOI

[30]
Chen X Y, Xie X S, Teng D. Short-term traffic flow prediction based on ConvLSTM model[C]// 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference. IEEE, 2020:846-850. DOI:10.1109/ITOEC49072.2020.9141783

DOI

[31]
Cao M M, Li V O K, Chan V W S. A CNN-LSTM model for traffic speed prediction[C]// 2020 IEEE 91st Vehicular Technology Conference. IEEE, 2020:1-5. DOI:10.1109/VTC2020-Spring48590.2020.9129440

DOI

[32]
Wu Y H, Zhang H Y, Li C, et al. MVDLSTM: MultiView deep LSTM framework for online ride-hailing order prediction[J]. The Journal of Supercomputing, 2022, 78(6):8531-8559. DOI:10.1007/s11227-021-04237-x

DOI

[33]
张维, 袁绍欣, 陶建军, 等. 基于多元因素的Bi-LSTM高速公路交通流预测[J]. 计算机系统应用, 2021, 30(6):184-190.

[Zhang W, Yuan S X, Tao J J, et al. Bi-LSTM expressway traffic flow prediction based on multiple factor data[J]. Computer Systems & Applications, 2021, 30(6):184-190. ] DOI:10.15888/j.cnki.csa.007969

DOI

Options
文章导航

/

〈 〉