EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 2: 277 - 287

DOI: https://doi.org/10.12082/dqxxkx.2023.220381

地球信息科学理论与方法

顾及多特征约束的建筑物组合化简方法

  • 马京振 , 1, 2, 3, * ,
  • 周炤 1 ,
  • 张付兵 1
展开
  • 1.信息工程大学地理空间信息学院，郑州 450052
  • 2.智慧中原地理信息技术河南省协同创新中心，郑州 450052
  • 3.时空感知与智能处理自然资源部重点实验室，郑州 450052

马京振（1993— ），男，山东平邑人，博士，讲师，主要从事数字地图制图技术研究。E-mail:

收稿日期: 2022-06-26

  修回日期: 2022-07-28

  网络出版日期: 2023-04-19

基金资助

国家自然科学基金项目(42101454)

河南省中原学者资助项目(202101510001)

智慧中原地理信息技术河南省协同创新中心和时空感知与智能处理自然资源部重点实验室基金资助项目(212102)

收起

Combined Building Simplification Approach Considering Multi-Feature Constraints

  • MA Jingzhen , 1, 2, 3, * ,
  • ZHOU Zhao 1 ,
  • ZHANG Fubing 1
Expand
  • 1. Institute of Geospatial Information, University of Information Engineering, Zhengzhou 450052, China
  • 2. Collaborative Innovation Center of Geo-information Technology for Smart Central Plains, Zhengzhou 450052, China
  • 3. Key Laboratory of Spatiotemporal Perception and Intelligent processing, Ministry of Natural Resources, Zhengzhou 450052, China
* MA Jingzhen, Email:

Received date: 2022-06-26

  Revised date: 2022-07-28

  Online published: 2023-04-19

Supported by

National Natural Science Foundation of China(42101454)

The Fund Project of ZhongYuan Scholar of Henan Province(202101510001)

The Joint Fund of Collaborative Innovation Center of Geo-Information Technology for Smart Central Plains, Henan Province and Key Laboratory of Spatiotemporal Perception and Intelligent processing, Ministry of Natural Resources(212102)

Fold

摘要

建筑物是大比例尺地图中的重要要素，其自动化简是制图综合领域的重要研究内容。针对当前化简方法仅侧重于某一方面的问题，本文提出一种顾及多特征约束的建筑物组合化简方法。首先，对建筑物进行冗余点删除、尖角去除等预处理操作；然后根据化简阈值筛选出需要化简的短边，并对其局部结构进行自动分类识别；然后，充分考虑建筑物的位置、面积、方向和形状等特征约束的影响，针对不同的结构类型采用不同的化简操作，在化简的过程中采用阈值逐渐增大的渐进式确定方法，直到满足化简要求为止；最后，从多个特征角度对化简结果进行评估，对不合理的化简实体进行调整修改。以OpenStreetMap数据为例进行实验，并与其它化简方法进行对比，实验结果表明，本文所提的方法可以有效保持建筑物的面积、形状、直角等基本特征，可以实现建筑物的自动连续化简，具备一定的通用性。

关键词： 制图综合; 建筑物; 化简; 渐进式; 结构识别; 结果评估; 多特征约束

本文引用格式

马京振 , 周炤 , 张付兵 . 顾及多特征约束的建筑物组合化简方法[J]. 地球信息科学学报, 2023 , 25(2) : 277 -287 . DOI: 10.12082/dqxxkx.2023.220381

Abstract

Settlement generalization is an important step for scale transformation, data fusion and integration, data mining, etc. The methods of settlement generalization include selection, simplification, dimension reduction, merging, and typification, among which simplification has been commonly used method. In large scale data, settlement usually exists in the form of building polygon, so the building simplification has always been the focus of settlement generalization. The essence of building simplification is to delete or edit the points that constitute the boundary, and extract the original figure as a simple polygon, while keeping the basic features of the building. In view of the problem that the current simplification method only focuses on one aspect, this paper proposes a combined building simplification method considering multi-feature constraints. Firstly, redundant points and sharp corners are deleted. Then the short edges that need to be simplified are screened according to the simplification threshold, and their local structures are automatically classified and recognized. Furthermore, the influence of the characteristic constraints such as the location, area, direction, and shape of the building is fully considered, and different simplification operations are adopted for different structural types. In the process of simplification, a progressive method with gradually increasing threshold value is adopted until the simplification requirements are met. Finally, the simplification results are evaluated from multiple features and the unreasonable simplification entities are adjusted and modified. Taking OpenStreetMap data as an example, and compared with other simplification methods, the experimental results show that the proposed method can effectively keep the basic features of buildings, such as area, shape, and orthogonal angle, and realize automatic and continuous simplification of buildings, with certain universality.

Key words： cartographical generalization; building; simplification; progressive operation; structure recognition; result evaluation; multi-feature constraints

1 引言

居民地作为一种重要的基础地理信息数据，与人类的生活密切相关，是地图表达的重要内容[1-2]。居民地综合是尺度变换、数据融合集成、数据挖掘等的重要手段，在综合过程中应该正确表示其几何特征（位置、形状等）、语义特征，处理好居民地与其他要素的关系，同时保持不同区域的密度对比和分布特征。居民地综合应遵循的基本原则是“表达主要的、舍弃次要的”，常用方法包括选取、化简、降维、合并和典型化等[3]，其中化简是最为常用的方法之一。在大比例尺数据中，居民地通常以建筑物多边形的形式存在，因此建筑物的综合一直是重点研究的问题，建筑物化简的实质是对构成边界的点进行删除或者移位，以更简单的多边形对原始图形进行抽象表达，同时要保持建筑物的基本特征[4-5]。
建筑物化简可分为传统方法和智能方法，传统方法主要包括经典的邻近四点及其改进方法[6-7]、递归回归方法[8]、最小二乘法[9⇓-11]、模板匹配方法[12-13]、渐进式化简方法[14]、图像化简方法[15]以及其他几何计算方法[4,16]等。其中邻近四点法将多边形上邻近的四点作为基本处理单元，对建筑物的不同局部结构进行化简处理，但存在局部算法的不足；递归回归方法采用递归分割策略对化简进行迭代处理，该方法仅适用于正交型建筑；最小二乘方法是在点分组的基础上，利用平差模型对多边形点进行拟合，进而实现建筑物的化简和直角化，但该方法对化简阈值的设置较为敏感；模板匹配方法通过典型的模板对建筑物进行化简，该方法过度依赖于模板库的完备性；图像化简方法需要将将建筑物转化为栅格图像再进行化简，转换过程中易造成失真。
智能方法包括机器学习方法、深度学习方法等，如Cheng等[17]利用BP神经网络进行样本训练，进而实现建筑物化简；晏雄锋等[18]利用图卷积神经网络对建筑物形状进行深度识别，建立形状表达与化简算法之间的映射关系，实现建筑物的自动化简；Yang等[19]从质量评估的角度出发，通过构建神经网络对同一建筑物实体的不同化简方法进行评估，进而得到最优的化简结果。智能方法需要依赖于样本的选择，而且化简结果不具备可解释性。
通过以上分析可以看出，现有的方法能够在一定程度上解决建筑物化简问题，但是都有各自的局限性，大都仅考虑建筑物的个别特征（如面积、特征点等），没有同时顾及多种特征的约束。考虑到建筑物作为人工地物，具有特定的几何特征，基于此本文提出一种顾及多特征约束的建筑物组合化简方法，首先对建筑物进行预处理，然后筛选需要化简的边并进行结构识别，对不同的局部结构采用不同的化简操作，在化简的过程中注意建筑物特征的保持。

2 研究方法

2.1 建筑物化简的原则及步骤

建筑物化简主要取决于地图比例尺或特定的制图需求，通过用更简单的形式取代原来的建筑物，同时保留甚至增强其主要特征来实现，一般遵循以下几个原则[20-21]：
（1）建筑物化简前后要保持基本形态，需要符合制图规范的要求，同时满足视觉上的清晰性、易读性和一致性。
（2）建筑物属于人工地物，一般情况下具有明显的直角特征，与自然地物（水系、植被等）特征差异较大，化简时要保持建筑物的正交性。
（3）化简前后建筑物面积基本不变，重心位置应大致相同，主方向应基本一致，如图1所示。
图1 建筑物化简的约束特征

Fig. 1 Constraint features of buildings simplification

（4）如果建筑物为矩形时，不可再继续化简。
已有的化简方法大多侧重于保持某个特征，而建筑物化简是多种特征相互影响、制约的过程，在化简的过程中要充分考虑多种特征的影响[22-23]。因此本文提出一种组合化简方法，通过预处理、结构识别、直角化等过程实现建筑物的自动化简，流程如图2所示，主要步骤如下：
图2 本文方法流程

Fig. 2 Framework of the method in this paper

（1）数据预处理。通过冗余点删除、尖角去除、平行垂直关系加强等操作，去除建筑物潜在的异常结点。
（2）化简边分组。根据制图规范，找出小于阈值的边（一般为图上0.3 mm所代表的实际距离[24]），并对这些边进行分组。
（3）结构识别与化简。根据分组情况，识别不同的分类结构，并采用不同的规则进行化简，在化简的过程中采用逐渐增大阈值的渐进化简方法。
（4）化简结果评估，初步化简结束后对化简结果进行自动评估，对不合理的化简建筑物进行修改，直到满足要求为止。

2.2 数据预处理

建筑物数据预处理主要是针对可能出现的数据错误，如重复结点、共线结点、尖锐结点等，消除这些异常值，如图3所示。假设建筑物用结点表示A={p1, p2, …, pn}（p1= pn），则：
图3 建筑物预处理

Fig. 3 Preprocessing for buildings

重复结点：建筑物A中的2个点pm、pn重复或近似重复，可通过距离阈值dt来判定，如果d(pm, pn)<d，则pm、pn为重复结点，如图3中的E、F点，dt可设置为0.1 mm。
共线结点：建筑物A中的某个点pm与前后两点的夹角为平行或近似平行，可通过角度阈值 θ来判定，如果 180 ° - θ m < θ，则pm为共线结点，如图3（a)中的H点， θ可设置为5°。
尖锐结点：建筑物A中的某个点pm与前后两点的夹角为尖锐的角，可通过角度 θ来判定，如果 θ m < θ，则pm为尖锐结点，如图3（a)中的C点， θ可设置为5°。

2.3 结构识别与分类化简

建筑物还可以用边表示为A={e1, e2, …, en}，小于化简阈值的边称为短边，建筑物化简的前提是筛选出小于阈值的短边，并在此基础上进行化简。首先对可能存在最短边的局部结构进行分类，设需要化简的短边为ei，ei与其邻近的2条边ei-1、ei+1构成局部化简分组，这3条边涉及的结点为p1、p2、p3、p4，如图4所示，定义如下：
图4 简单化简结构

Fig. 4 Simple simplification structure

类型1：Z型结构，p1、p4点位于线段p2p3两侧，如图4（a）所示。
类型2：U型结构，p1、p4点位于线段p2p3同侧，可分为凹、凸结构，如图4（b）、图4（c）所示。
类型3：非直角结构，如图4（d）所示，局部结构包含2个非直角，一条短边，但p1p2、p2p3呈直角或近似直角。
在具体计算的过程中，主要根据点的坐标值进行判断，假设p1、p2、p3、p4的坐标为 ( x 1 , y 1 )、 ( x 2 , y 2 )、 ( x 3 , y 3 )、 ( x 4 , y 4 )，判断Z型或U型的公式如下[25]：
t y p e = ( d x 32 d y 12 - d y 32 d x 12 ) ( d x 32 d y 43 - d y 32 d x 43 )
式中： d x 32 = x 3 - x 2； d y 12 = y 1 - y 2； d y 32 = y 3 - y 2； d x 12 = x 1 - x 2； d y 43 = y 4 - y 3； d x 43 = x 4 - x 3， t y p e < 0时，为Z型结构， t y p e > 0时，为U型结构，可进一步再判定其凹凸性。
当存在多条邻近短边时，本文认为这些短边构成复杂化简结构，如图5所示。
图5 复杂化简结构

Fig. 5 Complex simplification structure

类型4：当2条短边相邻时，构成一个复杂拐角，如图5（a）所示，a、b这2条相邻短边构成一个复杂拐角。
类型5：当有大于2条短边相邻，或者有相隔的短边相邻时，如图5（b）中，3条短边a、b、c相邻，图5（c）中，2条相隔的短边a、b构成复杂结构，化简时需要组合起来进行处理。
类型6：其他复杂结构，如阶梯状建筑物或者复杂的凹入等，图5（d）是阶梯状建筑物，a、b、c三条边相隔平行且大致相等，图5（e）中由2个基本凹部复合构成，在化简时要保持其特征。
在对建筑物的结构进行识别时，主要根据结点进行判断。从起始点开始遍历，记录每条边的长度，并判断其是否小于阈值，如图6所示，2—3、5—6、8—9、13—14、15—16为短边，记录起始点为{2,5,8,13,15}，在此基础上，再根据划分的类别判断短边的具体类型。
图6 建筑物示例

Fig. 6 Example of buildings

在建筑物化简结构识别的基础上，针对不同的结构采用不同的化简操作方法。
操作1：Z型结构化简，如图7（a）所示，p2、p3点删除，p1点按照 p 2 p 3 →的方向进行相应的移动，p4点按照相反方向进行移动，根据化简前后面积保持不变的原则，点p2移动的距离Dis为：
D i s = S ( p 2 , p 3 ) × ( S ( p 3 , p 4 ) / ( S ( p 1 , p 2 ) + S ( p 3 , p 4 ) ) )
式中： S为两点之间的距离，同理可得p4点的移动距离。
图7 简单结构化简操作

Fig. 7 Simplification operation of simple structure

操作2：U型结构化简，如图7（b）所示，主要根据凹凸部的面积大小，根据面积变化最小化原则判定是删除还是夸大处理。取 S t为目标比例尺下的长度阈值，如果 S ( p 2 , p 3 ) × S ( p 1 , p 2 ) < S t 2，则删除该结构，将 p 1点按照 p 2 p 3 →的方向延长至A点；如果 S ( p 2 , p 3 ) × S ( p 1 , p 2 ) ≥ S t 2，则需要进行夸大处理，p1、p2、p3分别调整为B、C、D点， S ( C , D )的长度为 S t，且 S ( B , C ) × S ( C , D ) = S t 2。凹部的处理与此类似，不再赘述。
操作3：非直角结构化简，如图7（c）所示，需要填充这种非直角结构，按照p1p2、p4p3的方向延长，相交于A点，并删除p2、p3点，化简后变为p1、A、p4 点。
操作4：对于复杂的拐角，由于其两条边均小于阈值，因此在化简时需要进行填充补偿处理。如图8（a）所示，将与a、d相连的2条边作延长处理，相交于A点，即完成该复杂拐角的化简。
图8 复杂化简结构操作

Fig. 8 Simplification operation of complex structure

操作5：由于多条短边集中在一起，这种情况下，需要将其看作一个复杂区域进行统一化简。如图8（b）所示，a、d为需要化简的相隔短边，与其相邻的长边共同构成复杂区域，如图中红色线段所示，按照面积不变的原则进行化简，如虚线所示。
操作6：对于阶梯状建筑物，在化简时将a、c边按照Z型结构化简，b边变为长边，不需要化简，如图8（c）所示；对于由2个基本凹部构成的建筑物，按照操作2的方法，分别进行化简，如图8（d）所示。
另外，如果建筑物的最长边小于化简阈值，则将建筑物抽象为面积相等的矩形。

2.4 化简阈值的渐进式确定方法

制图综合是一个渐进的过程，也是一个逐渐优化迭代的过程。渐进式化简的每一步只是在局部发生变化，通过多次的操作得到最终的化简结果，易于操作与维护。另外，本文采取的是局部结构化简，通过渐进式化简方法，可以避免出现特别复杂的局部结构，进而得到较好的实验结果。
现有的化简阈值大都是人工设定的，主要通过阈值逐渐增大的方法实现渐进式化简，本文根据化简建筑物的特点，提出一种化简阈值的渐进式自动确定方法。假设建筑物BDi需要渐进化简到目标尺度，中间经过多次化简，将每次化简的建筑物要素和化简阈值分别记为 B D i { B D i 1 ,   B D i 2 ,   … ,   B D i m }、 S C i { S C i 1 ,   S C i 2 ,   … ,   S C i m }，令STn+1为第n次化简后建筑物 B D i n的最短边的长度，CTn为化简尺度 S C i n下的约束阈值，则下一个化简阈值可定义为：
S C i n + 1 = ( S T n + 1 / C T n ) × S T n + 1
化简阈值通过迭代的方法逐渐增大，如果尺度 S C i m小于设定的化简阈值，则化简继续进行，如果尺度 S C i m大于设定的化简阈值，则其对应的 B D i m即为所需的化简要素。
在化简过程中，化简力度大小，即最小可视的实地距离，不仅与目标比例尺有关，而且与源比例尺也有关系，可按照“自然规律”的综合法则来 计算[26]：
D = S t d ( 1 - S o / S t )
式中， D为目标比例尺下图上最小可视距离对应的实地距离（化简阈值）， S t为化简目标比例尺分母， S o为源比例尺分母， d为图上最小可视距离，一般为0.3 mm。

3 建筑物化简结果评估

建筑物化简不可避免会带来基本特征的改变，但这些特征变化应该限定在一定的范围内。合理的建筑物化简不仅需要限制位置误差，还需要保留原有建筑的基本形状、大小、方向和正交性特征，因此本文从位置、面积、方向和形状4个特征对化简结果进行评估。

3.1 位置评估

空间距离可以表达地理实体在位置上的接近程度，是一种重要的几何特征。假设建筑物 B D i的重心点为 P a ( x 1 , y 1 )，化简后建筑物 B D i '的重心点为 P b ( x 2 , y 2 )，采用欧氏距离对位置进行评估，公式如下：
E p = 1 - ( x 1 - x 2 ) 2 + ( y 1 - y 2 ) 2 U
式中： U为建筑物 B D i与 B D i '任意边界点间距离的最大值。

3.2 面积评估

在化简的过程中，应遵循面积基本不变的原则，面积评估主要是计算化简前后面积的化简程度，计算公式如下：
E a = A r e a 1 - A r e a 2 A r e a 1
式中： A r e a 1、 A r e a 2分别为建筑物 B D i及其化简后 B D i '的面积。

3.3 方向评估

方向也是建筑物的重要判别特征，一般采用最小外接矩形的长轴代替。因此，方向评估计算公式如下：
E d = θ 1 - θ 2 π
式中： θ 1、 θ 2分别为建筑物 B D i及其化简后 B D i '的方向。

3.4 形状评估

形状同样也是建筑物的一个重要视觉特征，本文采用转角函数来描述建筑物的形状特征，该方法利用角度和长度特征，其中顶点上的角度是该点的累积切角，对应的长度是该点上多边形的归一化累积长度[27]。如图9所示，从起始点沿逆时针方向，分别记录对应的弧长以及转角累积值，则切角可以看作是归一化累积长度的函数。转角函数形状相似度计算如下：
E s = 1 - ∫   0 1 e a ( l ) - e b ( l ) d l m a x ∫   0 1 e a ( l ) d l ,   ∫   0 1 e b ( l ) d l
式中： e a ( l )和 e b ( l )分别表示建筑物 B D i及其化简后 B D i '的转角累积值。
图9 转角函数示意图

Fig. 9 Schematic diagram of turning function

4 实验及结果分析

4.1 实验介绍

为了验证本文所提方法的有效性，本文利用Python语言进行开发，结合ArcGIS软件，进行了算法的设计与实现。实验数据为OpenStreetMap数据中的建筑物要素层，2个实验区域如图10所示，分别包含43、61个建筑物实体。实验过程中以 1.5 m作为初始化简阈值，以1:25 000作为目标化简尺度（根据制图规范中的0.3 mm原则，对应的化简阈值为7.5 m），进行渐进式化简，化简结果如图10中红色实线所示。由于本文采用局部化简策略，需要对不同的局部结构逐个进行处理，前面的局部结构化简会引起点位的变化，进而影响后面的局部结构化简，因此不同的起算点和方向会得到不同的化简结果。在文献[6]的研究基础上，本文选取建筑物多边形上最长边起点及逆时针作为化简起算点和方向。
图10 本文所提方法的化简结果

Fig. 10 The simplification results of the proposed method

利用第3节所提的评估方法，对目标尺度上化简建筑物的数据质量进行评价，分别比较原始建筑物与化简建筑物在位置、面积、方向和形状的差异，2个实验区域共104个建筑物的评估结果如 图11所示。从图中可以看出，化简后的建筑物与原始建筑物相比，位置相似度在0.95以上；面积相似度在0.90以上；在方向上，由于化简前后其最小外接矩形的主方向大都没有改变，因此绝大部分建筑物的方向保持不变，个别变化程度较大，约为0.50左右；在形状上，形状相似度值大多在0.75以上，有部分复杂的建筑物化简后形状差异较大，在0.50以下。
图11 化简结果评估

Fig. 11 Evaluation of simplification results

4.2 化简结果分析

将本文所提的化简方法与经典的邻近四点方法、递归回归方法进行对比，以1:25 000为目标化简比例尺，化简阈值设置为7.5 m，采用第3节所述的方法进行化简评估，分别统计化简前后建筑物的位置、面积、方向、形状相似度的平均值，如表1所示。从表中可以看出，在位置和方向上，3种方法化简结果差异不大，均在0.97以上，在面积上，邻近四点方法保持的最好，递归回归方法最差；但是在形状方面，3种方法差别较大，本文方法保持的最好，邻近四点方法次之，递归回归方法最差，主要原因是本文方法能有效顾及多种特征，而其他2种方法更侧重某一方面。
表1 与其他方法化简结果对比

Tab. 1 Simplification results comparison with other methods

尺寸 方法 位置 面积 方向 形状
1:25 000 本文方法 0.9871 0.9873 0.9741 0.9020
邻近四点方法 0.9845 0.9930 0.9748 0.5887
递归回归方法 0.9833 0.9597 0.9760 0.4331
图12列出了4个通过不同化简算法得到的建筑物结果，通过详细对比发现，本文所提的方法可以顾及建筑物的多种特征，能够保持建筑物的面积、形状以及直角特征等。相较于其他2种方法， 本文所提的方法对部分结构进行了夸大处理，如建筑物a、建筑物c中的复杂直角，而其他2种方法没进行夸大处理；另外在局部特征的保持上，本文方法也优于其他2种方法，可以化简较为复杂的建筑物，如建筑物b、建筑物d，更符合制图规范，而邻近四点方法存在特征丢失的情况，递归回归方法容易导致过度化简的结果。
图12 不同算法化简结果对比

Fig. 12 Simplification results comparison of different algorithms

理论上来讲，对小于化简阈值的边都可以进行化简，直到所有的边都大于阈值为止，但化简后的建筑物不一定能满足化简需求，即化简结果评估后差异太大，跟实际的化简情况不相符合。例如，某一建筑物为正N边形（N>=5），每条边的长度小于阈值，但实际的面积并不小于化简阈值，此时利用本文所提的渐进式化简方法并不能得到理想的化简结果，需要进行特殊处理，如抽象为圆形等。

4.3 渐进式化简阈值分析

在实验的过程中，以某个建筑物为例，分析渐进式化简的阈值变化情况。假设该建筑物的初始状态为 B D i 0，第m+1次的化简结果 B D i m + 1可由 B D i m得到，该建筑物的最短边为2.35 m，以2.5 m作为初始化简阈值，以7.5 m作为目标化简阈值，渐进式化简过程中的参数变化情况如表2所示。从表中可以发现经过4次化简，化简阈值分别设置为{2.5、2.81、3.29、4.67}，建筑物可进行连续尺度变换，进而实现渐进式化简。第4次化简后，建筑物的最短边为7.52 m，可满足实际化简需求。在实际操作的过程中，需要对某个区域的多个建筑物同时进行化简，可将这些建筑物看作一个整体，设置一个初始阈值，每次化简之后计算最短边，并与目标阈值进行对比，直到满足化简要求为止。
表2 渐进式化简结果统计

Tab. 2 Results statistics of progressive simplification

B D i 0 B D i 1 B D i 2 B D i 3 B D i 0
化简阈值/m 2.5 2.81 3.29 4.67
最短边长度/m 2.35 2.65 3.04 3.92 7.5
是否满足要求 否 否 否 否 是
建筑物表达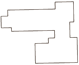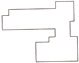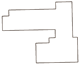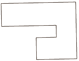

5 结论

本文提出了一种顾及多特征约束的建筑物组合化简方法，该方法考虑了实际的制图需求，将多种方法有机结合起来，通过识别不同的结构进行不同的化简操作。同时在化简的过程中，通过计算化简阈值与最短边的关系，得到不同阈值下的连续表达，进而实现渐进式化简。主要结论如下：
（1）将需要化简的短边分为6种类别，对每种类别的局部结构采用不同的化简操作，可以处理复杂的建筑物结构，适应性较强。
（2）采用化简阈值的渐进式自动确定方法，对化简过程进行优化迭代，通过多次化简可以得到较好的化简结果，易于操作与维护。
（3）化简的过程中充分顾及位置、面积、形状、方向等特征的约束，与其他方法进行对比，本文方法对建筑物的整体和局部特征保持的更好。
但是本文所提的方法主要适用于较大比例尺数据中的建筑物化简，对于尺度变化较大的建筑物化简效果不好，仅考虑了建筑物的几何形状化简，并未顾及化简之后与周围其他地物要素的空间关系。在后续研究中，要进一步将制图知识进行总结概括，以适用于各种跨尺度的化简需求，同时考虑合并、典型化等操作，实现建筑物的智能化综合处理。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
晏雄锋. 深度卷积学习支持下的建筑物模式分析[D]. 武汉: 武汉大学, 2019.

[ Yan X F. Building pattern analysis supported by deep convolutional learning[D]. Wuhan: Wuhan University, 2019. ]

[2]
高晓蓉, 闫浩文, 禄小敏, 等. 利用“计算区”进行建筑物短边结构识别和渐进式化简[J]. 武汉大学学报·信息科学版, 2021, 46(11):1782-1790.

[ Gao X R, Yan H W, Lu X M, et al. Recognition and progressive simplification of short-edge structure of buildings using calculation regions[J]. Geomatics and Information Science of Wuhan University, 2021, 46(11):1782-1790. ] DOI: 10.13203/j.whugis20200698

DOI

[3]
Li Z, Yan H, Ai T, et al. Automated building generalization based on urban morphology and gestalt theory[J]. International Journal of Geographical Information Science, 2004, 18(5):513-534.

DOI

[4]
尹烁, 闫小明, 晏雄锋. 基于特征边重构的建筑物化简方法[J]. 测绘学报, 2020, 49(6):703-710.

[ Yin S, Yan X M, Yan X F. Simplification method of building polygon based on feature edges reconstruction[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(6):703-710. ] DOI:10.1 1947/j.AGCS.2020.20190299

DOI

[5]
Ai T H, Cheng X Q, Liu P C, et al. A shape analysis and template matching of building features by the Fourier transform method[J]. Computers, Environment and Urban Systems, 2013, 41:219-233. DOI:10.1016/j.compenvurbsys.2013.07.002

DOI

[6]
许文帅, 龙毅, 周侗, 等. 基于邻近四点法的建筑物多边形化简[J]. 测绘学报, 2013, 42(6):929-936.

[ Xu W S, Long Y, Zhou T, et al. Simplification of building polygon based on adjacent four-point method[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6):929-936. ]

[7]
连超, 李成名, 殷勇, 等. 改进的邻近四点法建筑物多边形化简算法[J]. 测绘科学, 2016, 41(2):26-29,75.

[ Lian C, Li C M, Yin Y, et al. An improved algorithm of building polygon simplification based on adjacent four-point method[J]. Science of Surveying and Mapping, 2016, 41(2):26-29,75. ] DOI:10.16251/j.cnki.1009-2307.2016.02.005

DOI

[8]
Bayer T. Automated building simplification using a recursive approach[C]. Cartography in Central and Eastern Europe. Berlin, Heidelberg: Springer, 121-146.

[9]
刘鹏程, 艾廷华, 邓吉芳. 基于最小二乘的建筑物多边形的化简与直角化[J]. 中国矿业大学学报, 2008, 37(5):699-704.

[ Liu P C, Ai T H, Deng J F. Simplification and rectangularity of building-polygon based on least squares adjustment[J]. Journal of China University of Mining & Technology, 2008, 37(5):699-704. ]

[10]
Sester M. Optimization approaches for generalization and data abstraction[J]. International Journal of Geographical Information Science, 2005, 19(9):871-897. DOI:10.1080/13658810500161179

DOI

[11]
Sester M. Generalization based on least squares adjustment[J]. International Archives of Photogrammetry & Remote Sensing, 2000, 33:931-938.

[12]
Yan X F, Ai T H, Zhang X. Template matching and simplification method for building features based on shape cognition[J]. ISPRS International Journal of Geo-Information, 2017, 6(8):250. DOI:10.3390/ijgi6080250

DOI

[13]
刘鹏程, 艾廷华, 胡晋山, 等. 基于原型模板形状匹配的建筑多边形化简[J]. 武汉大学学报·信息科学版, 2010, 35(11):1369-1372.

[ Liu P C, Ai T H, Hu J S, et al. Building-polygon simplification based on shape matching of prototype template[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11):1369-1372. ] DOI:10.13 203/j.whugis2010.11.012

DOI

[14]
陈文瀚, 龙毅, 沈婕, 等. 利用约束D-TIN进行建筑物多边形凹部结构识别与渐进式化简[J]. 武汉大学学报·信息科学版, 2011, 36(5):584-587,592.

[ Chen W H, Long Y, Shen J, et al. Structure recognition and progressive Simplification of the concaves of building polygon based on constrained D-TIN[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5):584-587,592. ] DOI:10.13203/j.whugis2011.05.029

DOI

[15]
Shen Y L, Ai T H, Li C M. A simplification of urban buildings to preserve geometric properties using superpixel segmentation[J]. International Journal of Applied Earth Observation and Geo-information, 2019, 79:162-174. DOI:10.1016/j.jag.2019.02.008

DOI

[16]
杨好, 何宗宜, 陈华洋, 等. 顾及路网结构保持的城镇居民地自动综合[J]. 武汉大学学报·信息科学版, 2018, 43(6):965-970.

[ Yang H, He Z Y, Chen H Y, et al. A method for automatic generalization of urban settlements considering road network[J]. Geomatics and Information Science of Wuhan University, 2018, 43(6):965-970. ] DOI:10.13203/j.whugis20160094

DOI

[17]
Cheng B Y, Liu Q, Li X W, et al. Building simplification using backpropagation neural networks: A combination of cartographers' expertise and raster-based local perception[J]. GIScience & Remote Sensing, 2013, 50(5):527-542. DOI:10.1080/15481603.2013.823748

DOI

[18]
晏雄锋, 艾廷华, 杨敏, 等. 地图空间形状认知的自编码器深度学习方法[J]. 测绘学报, 2021, 50(6):757-765.

[ Yan X F, Ai T H, Yang M, et al. Shape cognition in map space using deep auto-encoder learning[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(6):757-765. ] DOI:10.119 47/j.AGCS.2021.20210046

DOI

[19]
Yang M, Yuan T, Yan X F, et al. A hybrid approach to building simplification with an evaluator from a backpropagation neural network[J]. International Journal of Geographical Information Science, 2022, 36(2):280-309. DOI:10.1080/13658816.2021.1873998

DOI

[20]
王辉连, 武芳, 张琳琳, 等. 数学形态学和模式识别在建筑物多边形化简中的应用[J]. 测绘学报, 2005, 34(3):269-276.

[ Wang H L, Wu F, Zhang L L, et al. The application of mathematical morphology and pattern recognition to building polygon simplification[J]. Acta Geodaetica et Cartographic Sinica, 2005, 34(3):269-276. ]

[21]
Buchin K, Meulemans W, Renssen A V, et al. Area-preserving simplification and schematization of polygonal subdivisions[J]. ACM Transactions on Spatial Algorithms and Systems, 2016, 2(1):1-36. DOI:10.1145/2818373

DOI

[22]
Ai T H, Ke S, Yang M, et al. Envelope generation and simplification of polylines using Delaunay triangulation[J]. International Journal of Geographical Information Science, 2017, 31(2):297-319. DOI:10.1080/13658816.2016.1197399

DOI

[23]
Samsonov T E, Yakimova O P. Shape-adaptive geometric simplification of heterogeneous line datasets[J]. International Journal of Geographical Information Science, 2017, 31(8):1485-1520. DOI:10.1080/13658816.2017.1306864

DOI

[24]
Wei Z W, Liu Y, Cheng L, et al. A progressive and combined building simplification approach with local structure classification and backtracking strategy[J]. ISPRS International Journal of Geo-information, 2021, 10(5):302. DOI:10.3390/ijgi10050302

DOI

[25]
周培德. 计算几何算法分析与设计[M]. 北京: 清华大学出版社, 2000.

[ Zhou P D. Computational geometry: analysis and design of algorithms[M]. Beijing: Tsinghua University Press, 2000. ]

[26]
Li Z L, Openshaw S. Algorithms for automated line generalization based on a natural principle of objective generalization[J]. International Journal of Geographical Information Systems, 1992, 6(5):373-389. DOI:10.1080/02693799208901921

DOI

[27]
Fan H C, Zipf A, Fu Q, et al. Quality assessment for building footprints data on OpenStreetMap[J]. International Journal of Geographical Information Science, 2014, 28(4):700-719. DOI:10.1080/13658816.2013.867495

DOI

Options
文章导航

/

〈 〉