EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 5: 896 - 908

DOI: https://doi.org/10.12082/dqxxkx.2023.220536

地球信息科学理论与方法

人口空间化适宜格网评价方法研究

  • 罗永臻 ,
  • 董春 , * ,
  • 张玉
展开
  • 中国测绘科学研究院 自然资源调查监测研究中心，北京 100036
*董 春（1971— ），女，云南红河人，博士，研究员，主要从事人口空间化、国土空间分析与自然资源评价等研究。 E-mail:

罗永臻（1998— ），男，青海西宁人，硕士生，主要从事自然资源与国土空间分析研究。E-mail:

收稿日期: 2022-07-21

  修回日期: 2022-10-13

  网络出版日期: 2023-04-27

基金资助

国家自然科学基金面上项目(71773117)

国家自然科学基金面上项目(71903183)

国家社会科学基金重大项目(18ZDA066)

院基本业务费项目(AR2207)

收起

Study on the Method of Evaluating the Suitable Grid for Population Spatialization

  • LUO Yongzhen ,
  • DONG Chun , * ,
  • ZHANG Yu
Expand
  • Natural Resources Survey and Monitoring Research Centre, Chinese Academy of Surveying and Mapping, Beijing 100036, China
*DONG Chun, E-mail:

Received date: 2022-07-21

  Revised date: 2022-10-13

  Online published: 2023-04-27

Supported by

National Natural Science Foundation of China(71773117)

National Natural Science Foundation of China(71903183)

Major Projects of the National Social Science Foundation of China(18ZDA066)

Basic operating expenses of the institution(AR2207)

Fold

摘要

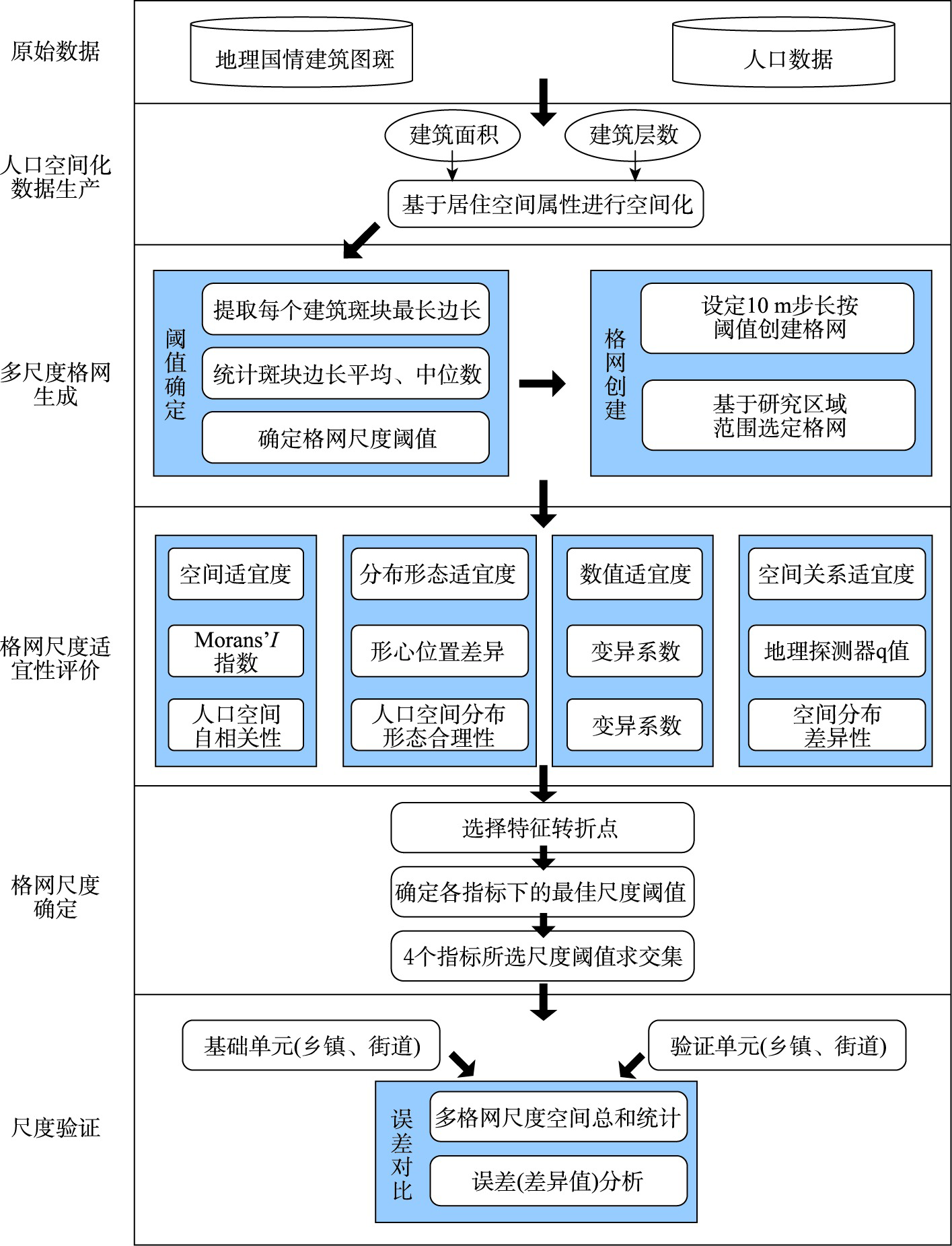
人口在空间上分布的差异较大，统一的格网尺度只能按照一种格网尺度体现人口空间分布，对不同区域更密集或更稀疏人口的空间化表达较差，为了更精准地表达人口空间分布，本文提出一种依据多指标分析的适宜格网尺度确定方法，构建以形心差异距离为创新的指标体系，结合空间适宜度、数值适宜度和空间关系适宜度，利用空间自相关、变异系数与地理探测器模型从空间和数值的角度上摆脱了景观指数自身存在的尺度效应问题。根据各指标特征点变化分析确定各指标下适宜格网尺度阈值，然后采用相对误差绝对值的验证方法，计算与真实人口数值的相对误差绝对值的几何平均值来验证指标分析结果，确定人口格网较适宜尺度。本文将首都经济圈唐山市古冶区作为实证分析区，根据指标体系分析的实验结果表明：随着格网尺度的增大，人口斑块集聚聚类间的差异逐渐变小，其分布形态表现性变差，且人口格网的总体表现能力随尺度增大逐渐降低；从空间适宜度、分布形态适宜度、数值适宜度和空间关系适宜度4个角度进行特征点变化分析，确定90 m、100 m为较适宜格网尺度，在该尺度下进行人口空间化可以得到质量较好的数据结果。通过验证分析可知，该研究区下的人口空间化较适宜格网尺度确定方法存在一定的科学性及合理性。

关键词： 人口空间化; 适宜格网尺度; 空间分析; 指标体系; 形心差异; 人口格网; 空间差异

本文引用格式

罗永臻 , 董春 , 张玉 . 人口空间化适宜格网评价方法研究[J]. 地球信息科学学报, 2023 , 25(5) : 896 -908 . DOI: 10.12082/dqxxkx.2023.220536

Abstract

The spatial distribution of world population varies considerably from region to region due to differences in geography and economic development, which requires a specific scale of population grid for population spatialization in different regions. A uniform grid scale can only represent the spatial distribution of population at one grid scale, which leads to poor representation for more densely or sparsely populated areas. In order to express the spatial distribution of the population more accurately and determine the appropriate scale of the population grid for a given area, this paper proposes a method to determine the scale of suitable grids based on a multi-indicator analysis. We construct an innovative index system based on the shape-centered difference distance, by combining spatial suitability, numerical suitability, and spatial relationship suitability, and use spatial autocorrelation, coefficient of variation, and geographic detector model to get rid of the scale effect of landscape index from the spatial and numerical perspectives. In this paper, the process of population spatialization employs geographic country data combined with occupancy spatial attributes (i.e., number of building floors and floor area). The suitable scale threshold of the grid under each index is determined based on the analysis of the change of the characteristic points of each index, and then the common scale threshold is identified as the overall suitable grid scale. The geometric mean of the absolute relative error against the real population value is calculated to verify the index analysis results and the suitable scale of population grid. This paper takes the Guye District of Tangshan city in the Capital Economic Circle as the empirical analysis area. The results of the index system analysis show that the differences between clusters of population patches gradually become smaller and their distribution patterns become less expressive as the scale of the girds increases, and the overall expressiveness of the population grid gradually decreases as the scale increases. From perspectives of spatial suitability, distribution morphology suitability, numerical suitability, and spatial relationship suitability, 90 m and 100 m are identified as the suitable grid scales, under which the population spatialization could obtain better quality. The validation analysis demonstrates that the method of determining suitable grid scale for population spatialization in this study has a certain degree of validity and reliability.

Key words： population spatialization; appropriate grid scale; spatial analysis; indicator systems; shape-centered differences; population grids; spatial difference

1 引言

人口数据作为表征人类活动最直接的指标之一，与多种社会要素紧密相连[1]，并广泛应用于生态、经济等研究领域[2]。为了发掘和展现人口统计数据中隐含的空间信息，就需要利用空间模型或一定的计算方法，反演出人类活动在一定时间空间下的分布状态，并以多种划分形式再现客观世界的人口分布状况，这一过程即为人口空间化[3]。随着遥感技术的进步，对于人口空间化的研究也日趋完善与多样[4⇓-6]，但以往基于行政单元的人口统计方法尺度统一，只能按一种格网尺度来表示人口的空间分布，在小区域或特定研究范围内不能较好地展现其内部人口分布状况，而规则地理格网单元能够更细致地展现行政区划内部人口空间分布的合理形态，使人口空间化结果更加真实准确[7]，因此根据研究区域选择适宜格网尺度可以提高人口空间化数据质量。
目前得到广泛应用的人口空间化数据多以公里格网为主，如1 km格网数据集：GRUMP[8]、LandScan[9]、中国公里格网[10]（OpenGMS）；5km格网数据集：UNEP/GRID[11]、GPW[12]。该类数据集虽然比传统统计数据有着较高的空间分辨率，但是在更小区域上，其空间化结果还是较为模糊。更小尺度的人口格网数据集则有WorldPop[13]（100 m）等，该类数据虽然保证了一定的空间化精度，但是并没有分析其格网尺度是否适合不同区域。因此针对特定区域分析人口格网数据集的适宜性，能够有效提高人口格网数据集的表现性。
而如何确定适宜格网尺度，目前主要有2类方法。第一类基于源数据进行尺度确定，如精度损失分析法[14]、变异函数[15]、遥感影像响应关系法[16]等；此类方法思路简单，便于实现，但是通过源数据分析，缺乏人口信息协同分析。第二类方法利用人口空间化结果进行分析，如统计学法、半方差函数法等[17]，此类方法综合分析源数据与人口数据，探讨数据尺度特征，但需要以人口数据为前提。也有学者提出指标体系评价法，引入形状指数比等多样性景观生态学指标[18-19]，分析人口分布信息受格网尺度影响的变化趋势并确定相对适宜格网尺度。该类方法虽然取得了具有说服力的结果，但是在指标选取上始终以景观指数作为主要指标，没有摆脱其自身存在的尺度效应[20-21]，这在一定程度上会影响格网尺度的选取。
综上，本文利用地理国情数据，构建空间适宜度、分布形态适宜度、数值适宜度和空间关系适宜度指标体系并借鉴相对误差绝对值的空间人口精度验证方法，综合确定适宜格网尺度。同时该指标体系摆脱景观指数自身的尺度效应，提出以形心差异度为核心的位置一致性表达指标，从空间和数值角度确定适宜人口格网尺度，为特定区域内人口空间化适宜尺度选择提供科学依据，提高人口空间化结果精度。

2 研究方法

本次研究摆脱景观指数自身存在尺度效应的问题，根据已有的研究[4]从空间、位置与数值分析角度建立了以空间适宜度、分布形态适宜度、数值适宜度和空间关系适宜度为主要评价指标的适宜尺度评价体系，而上述4个表达性指标将分别通过Morans'I指数、形心差异度、地理探测器q值以及变异系数来具体体现（图1）。
图1 本文方法技术路线

Fig. 1 Methodological and technical approach

2.1 空间适宜度

人口数据在空间上的分布具有一定的空间自相关性，根据该特性可以明确不同格网尺度下自相关性的表达，因此引入空间适宜度来分析研究区域内人口分布合理性的准确程度，较好的空间适宜度是指在某格网尺度下，人口空间数据能较准确地揭示人口分布的聚集状态，该特定格网即为适宜格网尺度。
Morans'I指数作为典型的空间自相关性指数，其指数大小可以直接体现人口在空间分布上的聚集性特征[22]。Morans'I取值范围为 [ - 1 ,   1 ]  ，若Morans'I >0表示呈正向空间自相关；若Morans'I <0表示呈负向空间自相关性；若Morans'I =0，空间呈随机分布。这也可以证明不同尺度下人口数据的自相关性程度，其计算公式如下所示：
I = n S 0 ∑ i = 1 n ∑ j = 1 n w i , j z i z j ∑ i = 1 n z i 2
式中： z i表示格网 i的人口数值与全部格网的人口平均值的偏差； w i , j表示人口格网 i与格网 j之间的空间权重， n表示格网总数， i = 1,2 , … , n， j = 1,2 , … , n； S 0表示所有空间权重的聚合如式（2）所示。
S 0 = ∑ i = 1 n ∑ j = 1 n w i , j
对于Morans'I值，还存在一个标准统计量Z对其显著性水平进行检验，即Z>0，且通过显著性检验时，表明存在正的空间自相关；当 Z<0，且通过显著性检验时，表明存在负的空间自相关；Z>0时，观察值呈独立的随机分布状态（式3）。
Z = I - E I v a r I

2.2 分布形态适宜度

人口的空间分布形态与居住地的分布有很强的关联性，通过对比不同格网尺度下的人口与居住地的分布形态差异，可以确定人口格网的分布是否准确，因此引入分布形态适宜度来分析研究区内人口分布形态的准确程度。较好的分布形态适宜度是指在某格网尺度下，人口空间数据能较准确地描述人口的空间分布范围，该特定格网即为适宜格网尺度。
本文提出以形心间距离为定级标准，将不同尺度下的人口斑块按照所属房屋区（即按照聚类的思想）进行融合，基于形心公式理念（式（5））计算融合后的人口斑块形心位置[23]与房屋区斑块形心位置，将2个形心进行距离量测，获得每个尺度下形心距离平均值，该值所体现的就是人口栅格斑块与房屋用地斑块在空间位置上的一致性。该值越大表明空间一致性越差；值越小表明空间一致性越小，值最小为0，最大为无限大。
x 0 = M y M = ∫ a b x f x d x ∫ a b f x d x   y 0 = M x M = 1 2 ∫ a b f x 2 d x ∫ a b f x d x
式中： ( x 0 , y 0 )为形心坐标，假设图形是由 y = f x,   x = a , x = b围成的曲边梯形，由此计算多边形形心位置，由于地理图斑是由多个节点组成的面，不是平滑曲线组成，所以基于图斑边缘各节点位置计算其高斯面积（式（5）），然后根据面积和图斑边缘各点位置计算获得形心位置（式（6））。
A = 1 2 ∑ i = 0 n - 1 x i y i + 1 - x i + 1 y i
式中： A为图斑的面积； n是一个图斑上边的个数， x i , y i , i = 1,2 , … , n - 1为图斑边界上节点的坐标。
C x = 1 6 A ∑ i = 0 n - 1 x i + x i + 1 x i y i + 1 - x i + 1 y i C y = 1 6 A ∑ i = 0 n - 1 y i + y i + 1 x i y i + 1 - x i + 1 y i
式中： C x为形心的 x坐标； C y为形心的y坐标。

2.3 数值适宜度

由于地区人口数不是统一标准分布，存在一定的差异性，格网尺度过粗会模糊数值间的差异，降低数据表达性与精度，因此提出数值适宜度来表达研究区范围内人口数值存在的差异程度。较好的数值适宜度是指在某特定格网尺度下，人口空间数据能较准确地揭示研究区内人口数值的差异程度，该特定格网即为适宜格网尺度。
对于数值差异[24]，本研究提出以变异系数（式（7））为判定指标来对人口空间分布的数值信息表达性进行定级评价。首先按面积计算每个格网中的人口密度，然后对不同尺度的人口密度按变异系数公式计算其变异系数。该数值没有确定的大小范围，数值越大，表明人口密度值离散程度越高，该尺度的数据表现性越细致；数值越小，表明人口密度值离散程度越低，该尺度的数据表现性越粗糙。
C v = σ μ
式中： C v为变异系数； σ为标准差； μ为平均值。

2.4 空间关系适宜度

人口的空间分布存在一定的聚集性，而聚落之间会有一定的空间差异，较好的空间差异可以明确人口聚集特征，因此引入空间关系适宜度来分析研究区内人口空间分布差异的程度。较好的空间关系适宜度是指在某特定格网尺度下，人口空间数据能较准确地揭示研究区范围内人口分布差异，该特定格网即为适宜格网尺度。
而在空间差异[25]的表达方面，本研究采用地理探测器[26]检验不同尺度下人口格网数据的空间分异性，因为每个人口格网数据都是由其最邻近房屋图斑内的人口数通过距离权重的线性回归模型计算所得，所以按照其所属于的房屋区域分类（根据聚类的思想）并根据所计算得到的 q值（式（8））评定各尺度下人口格网数据的空间差异性。
q = 1 - ∑ h = 1 L N h σ h 2 N σ 2
式中： h = 1 ,     … ,   L为人口数值空间聚类的分类数； N h和 N分别为区 h和全区的单元数； σ h 2和 σ 2分别是 h和总体人口数值的方差。   q值越大，表明人群分布的空间差异性越明显； q值越小，表明人群分布的空间差异性越不明显， q的值域为[0,1]。

3 实验区概况与数据来源

3.1 实验区概况

唐山市古冶区（图2）位于河北省东部，处于环渤海发展地带，为京津冀“首都经济圈”边缘地区。该地区总面积约248.53 km2，其中北部地区多为低山地区，城镇乡村分布集中，具有明显的聚集性特征；南部地区则以冲积平原为主，村庄城镇分布较少，存在一定的空间间隔。随着社会经济的快速发展，大城市呈现快速向上的发展势头，吸引各类人才的到来，而远离经济中心的地区如华北平原以东持续出现人口流失的现象。古冶区2020年常住人口为317 932人（第七次全国人口普查数据），与六普统计数据相比减少了约40 529人，因此针对该地区进行人口空间化的适宜格网尺度研究，有利于精准把握该地区人口分布状况，分析人口流失严重区域，降低人口空间信息因尺度不适宜而未被发掘的可能性。
图2 研究区地理位置

Fig. 2 Location of the study area

3.2 数据来源

研究区建筑物图斑数据来源于自然资源部国家基础地理信息中心2017年基础性地理国情监测数据，人口统计数据来源于2017区县统计年鉴。人口空间分布参考居住空间属性的人口空间化方案而生成[27]，通过计算不同类型居住建筑的居住人数展现人口空间分布情况。以此为基础，空间化方案为：以居住建筑斑块面积和建筑物层数为人口数量影响因子，以建筑物和行政区划斑块轮廓为分布位置影响因子，求解各类型居住建筑的居住人数（图3）。
图3 2017年古冶区基于建筑物单元人口空间分布

Fig. 3 Spatial distribution of population in Gurye District based on building units in 2017

4 实验及结果与分析

4.1 多尺度人口格网生成

根据研究区域内以建筑物斑块为基础的人口空间分布矢量数据可知，住宅斑块最短边长为 （10±4) m，大斑块的平均边长约为203.34 m，中位数约为162.12 m，总体平均边长为171.66 m。因此按10 m的间隔将格网划分为10、20、30、…、190 、200 m。然后利用ArcGIS“渔网”工具创建不同尺度的格网，然后以距离（网格中心与建筑斑块形心距离）、重叠面积为权重因素，以建筑物图斑内人口数据为基础计算每个格网内的人数（式（9）），最终通过“面转栅格”工具生成多尺度人口格网。
P i = ∑ m = 1 n S m D m                   n ≠ 0 P i = L i D i                                   n = 0
式中： P i为格网 i内的人数； n为格网内的住宅斑块个数； S m为第m个住宅斑块与格网 i相交部分的面积； D m为第m个住宅斑块的人口数； L i为格网 i的中心与邻近住宅斑块形心间的距离； D i为第 i个住宅斑块的人口数。

4.2 人口格网构建

首先建立空间格网，以格网尺度确定阶段的重采样间隔为依据，按照相同步长与大小建立不同尺度的格网，然后以地理国情数据中的人口空间分布数据为源数据，通过线性回归模型法将人口数分配至不同尺度格网当中赋予其人口数值，且随着格网尺度的增大，人口分布在边缘的细致表达程度也在逐渐下降（图4）。
图4 古冶区10~200 m格网尺度下人口空间分布

Fig. 4 Spatial distribution of population at the 10~200 m grid scale in Guye District

4.3 适宜格网尺度确定

基于已经提出的4个适宜性指标及各自代表指数，本研究分别得到了古冶区Morans'I指数、形心差异度、变异系数和地理探测器q值的变化趋势、相对变化以及和格网尺度之间的相关关系。
为了确定适宜格网尺度，依据已得出的4个指标结果，确定各自特征转折点即某格网单元所对应的指标值相对于前一个格网单元所对应的指标值的变化程度，该指标可以反应数值序列的变化程度[28]，即相对变化率绝对值而根据该值，可以将总体格网尺度区间分为指标数值较大和指标数值较小两部分。本文从整体分析，在不使每个指标的表达效果过差的前提下将4个指标结合求其交集，并依据精度验证结果，以4个表达度表达效果较好格网尺度域的交集作为适宜格网尺度域，以此来获取总体较适宜尺度。

4.3.1 空间适宜度较好表达效果阈值范围

计算空间自相关性所得出的 M o r a n s ' I指数（图5），其中 R 2值为0.8009证明该幂函数曲线拟合性很好，且根据幂函数曲线可以看出随着格网尺度增大， M o r a n s ' I指数出现减小的趋势，说明该研究区域格网尺度的增大会降低人口格网数据的空间自相关性，而人口数据作为一种具有较高自相关性的数据，空间自相关性降低说明该数据的无法较好的表现出该地区人口在空间分布上的聚集性。再通过计算其 M o r a n s ' I指数的相对变化率，并求其变化率的几何平均值，通过分析相对变化率可以看出随着格网尺度增大，相对变化越来越不稳定，在40~60 m以及80~110 m为最稳定区域，140 m之后便出现了极大的不稳定变化。通过空间自相关性 M o r a n s ' I指数分析得出适宜尺度为40~60 m和80 ~110 m区间。
图5 10~200 m 人口格网Morans'I指数变化

Fig. 5 Change in Morans' I index of the population grid (10~200 m)

4.3.2 分布形态适宜度较好表达效果阈值范围

计算房屋建筑图斑的形心点，根据每个格网内所分配人口的原所属建筑编号为类别号将不同尺度下的人口格网数据进行聚类分类并转换为矢量图斑，然后提取各个面的形心点，并计算同一个类别下地理国情数据建筑图斑和人口格网图斑的形心距离，并计算相对变化率，其中 R 2值为0.8754趋近于1证明该幂函数曲线拟合性很好。由形心距离值的幂函数曲线可知（图6），随着格网尺度的增大，同一类别下人口图斑与房屋建筑图斑的空间一致性越来越差，然后计算其形心距离相对变化率并计算其几何平均值可以看出在50~100 m区间为平稳变化区间，由形心距离指标分析得出人口空间数据适宜尺度为50~100 m区间。
图6 10~200 m 人口格网形心距离变化

Fig. 6 Variation in distance from the centre of the population grid shape (10~200 m)

4.3.3 数值适宜度较好表达效果阈值范围

将格网数据中的人口数除以格网面积计算人口密度值，根据该值计算其变异系数，其中 R 2值为0.9468趋近于1证明该幂函数曲线拟合性非常好。由变异系数的幂函数曲线可知（图7），随着格网尺度的增大，人口格网数据在数值上的信息表达性差异越来越小，说明人口格网尺度越大，数值之间的差异性越小，计算变异系数相对变化率的几何平均值可以看出60~100 m为平稳变化区间，在50 m尺度以下变异系数变化最大，说明该区间数值信息差异明显，而在130 m尺度以上变异系数变化出现一定波动性，且变异系数持续降低，数值间的差异性持续性降低，所以由变异系数指标分析得出人口空间数据适宜尺度为60~100 m 区间。
图7 10-200m 人口格网变异系数变化

Fig. 7 Variation in the coefficient of variation of the population grid (10~200 m)

4.3.4 空间关系适宜度较好表达效果阈值范围

由于人口空间数据的分布存在一定的聚落式分布，所以按照每个格网所属房屋建筑编号为类别号，提取不同尺度人口格网中的人口数据和类别号，然后利用R工程包处理研究区域范围内的人口数值计算每个尺度下的q值，如图8所示。其中 R 2值为0.6658证明该幂函数曲线拟合性较好，由地理探测器q值的幂函数曲线可知，随格网尺度的变化，q值缓慢增大且无限趋近于0.95，且从图中可知总体q值都保持着一个高值分布，说明不同尺度下的人口格网都具有不错的地理空间差异性。通过计算变异系数相对变化率和几何平均值可以看出 70 ~130 m为平稳变化区间，在140 m之后其相对变化率趋近于0。所以由地理探测器q值指标分析得出人口空间数据适宜尺度为70~130 m区间。
图8 10~200m 人口格网Geodetector q值变化

Fig. 8 Population grid (10~200 m) Geodetector q-value change

4.4 适宜格网尺度合理性验证

本文借鉴董南[19]等提出的相对误差绝对值的平均值验证思路，利用平均值的相对变化量来验证格网尺度合理性，且以研究区内4个乡镇与街道为基本验证单元。然后对不同格网的人口空间数据进行空间统计，获取每个基础单元的统计总人数，然后与基础单元的真实人数进行对比，其中真实人数由原始人口矢量数据获得。通过选用相对误差绝对值的几何平均值进行数值准确性分析，评价格网尺度的合理性（图9）。
图9 验证单元的空间分布及不同格网尺度下相对误差绝对值的平均值相对变化

Fig. 9 The spatial distribution of the validation cells and the relative change in the mean of the absolute values of the relative errors at different grid scales

其中图9(b)可知随着格网尺度的增大，相对误差绝对值的平均值相对变化率也持续增长，即人口空间化数据的精度在逐步降低。且在10~80 m的尺度变化阶段，其相对变化量基本保持在0.006~0.086范围内缓慢增长，表明在该范围内人口空间化数据数值精度损失较小。而随着格网尺度的逐步增大，其精度损失也显著性增长。
由图9(c)分析可知，90 m、100 m格网尺度下的数值为0.123与0.128，虽然其数值大于小尺度格网，但不存在缓慢增长现象，而在100 m之后数据精度逐渐开始大幅度降低。因此，根据综合指标评价与格网尺度合理性分析结果（图9），可以认定90 m与100 m 格网是较适宜格网尺度，证明本文所提出的指标评价体系具有一定的合理性，且在该尺度下生成该研究区域内的人口空间数据可以得到较高质量的结果。

5 讨论

基于地理空间的现象或属性特征值在空间分布上会具有一定的规律，并存在一定的空间关联关系。本文在指标分析当中引入空间自相关性、空间分异性等概念来分析研究区域人口空间分布关联关系在不同格网尺度下的变化，结果表明在格网尺度增大的过程当中，人口空间分布关系的表达受到了一定的影响。而Morans'I指数与地理探测器作为地理学研究当中经典的空间关系研究方法，在空间分析上具有一定的权威性，但仅仅从空间关联关系的角度分析人口格网适宜性不能做到科学、合理。因此本文提出分布形态适宜度，利用形心差异从空间分布形态上分析不同尺度下人口的空间分布与建筑单元的空间分布是否相吻合。实验结果表明，随着格网尺度增加，人口的空间分布形态在边缘上的锐度逐渐降低，其分布形态的形心位置也与建筑斑块的形心距离越远。实验结果与常理相符，即分辨率越低，图像表达性越差，而人口分布形态与建筑斑块分布形态相差越大，说明格网尺度越不合理。本文通过精度验证表明该指标体系评价方法在不引入景观指数的前提下能够实现从空间与数值角度分析人口格网尺度适宜性。
当前实验结果从2个正向指标（分布形态适宜度、空间关系适宜度）与2个逆向指标（空间适宜度、数值适宜度）结合的角度分析格网尺度增大时人口格网的空间表现性。但是本文并未考虑只利用四个指标是否合理，是否需要增加指标数，因为人口的空间分布与城市空间格局高度相关，例如对于地形复杂的地区如重庆市，应当考虑地形因素；对于北京、上海等人口高密度地区，是否应当加入空间经济学指标来分析格网尺度。不同地区有其不同的发展模式，人口的空间分布模式也会不同，在不同类型的研究区域引入何种指标并进行量化使评价方法更具有适用性，是本文未来需要进一步研究的方向。

6 结论

本文提出了基于多指标分析的适宜人口格网尺度评价方法。该方法以地理国情数据和七普人口统计数据为基础，将空间适宜度、分布形态适宜度、数值适宜度和空间关系适宜度作为格网尺度适宜性评价的核心指标，从数值和空间两个角度评价人口格网尺度适宜性。本文以古冶区为研究区域开展了不同尺度下的人口格网适宜性评价实验，实验结果表明：
（1）在适宜人口格网尺度评价方面，研究表明随着格网尺度的增大，人口空间化的人口斑块聚集数值增高，人口集聚聚类间的差异逐渐变小，且人口斑块分布形态与房屋区域重合性变差，即在该研究区内随着格网尺度增大，人口格网的表现能力逐渐降低，误差增大，不能准确的表现地区人口分布状况。
（2）本文从空间和数值2个角度结合地理国情数据，在4个指标之下所确定的人口格网适宜尺度/m 分别为：（40,60）∪（80,110）、（50，100）、（60,100）、（70,130），然后进行格网尺度合理性验证得出90 m与100 m为较适宜格网尺度。
（3）基于适宜格网尺度进行特定区域的人口空间化，以此来进行时空变化分析可以较好的提高空间分析精度，并结合社会经济与地理要素数据能够更加准确地总结地区人口流失因素，降低人口格网尺度不适宜造成空间信息及关系不易被发掘的可能性。
本文针对人口空间化格网尺度的研究摆脱了对于景观指数的依赖，降低了指标自身的尺度效应对研究结果带来的影响，并提出形心差异评价方法，在科学合理的基础上提升了人口空间化较适宜格网尺度分析的研究水平，为确定不同区域适宜人口格网尺度提供了新的研究思路。当前研究仍存在一定的局限性：本文采用较为简单的基于居住建筑属性的人口空间化方法，并未考虑空间化方法可能会对格网尺度的适宜性分析可能造成的误差累积。即在后续的研究当中应从人口空间化方法对格网尺度的影响进行研究。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
董春, 刘纪平, 赵荣, 等. 地理因子与空间人口分布的相关性研究[J]. 遥感信息, 2002, 17(4):61-64.

[ Dong C, Liu J P, Zhao R, et al. An discussion on correlation of geographical parameter with spatial population distribution[J]. Remote Sensing Information, 2002, 17(4):61-64. ]

[2]
柏中强, 王卷乐, 杨飞. 人口数据空间化研究综述[J]. 地理科学进展, 2013, 32(11):1692-1702.

DOI

[ Bai Z Q, Wang J L, Yang F. Research progress in spatialization of population data[J]. Progress in Geography, 2013, 32(11):1692-1702. ]

DOI

[3]
Gallopin G C. Human dimensions of global change: Linking the global and the local processes[J]. International Social Science Journal. 1991, 43(4):707-718.

[4]
董南, 杨小唤, 蔡红艳. 人口数据空间化研究进展[J]. 地球信息科学学报, 2016, 18(10):1295-1304.

DOI

[ Dong N, Yang X H, Cai H Y. Research progress and perspective on the spatialization of population data[J]. Journal of Geo-Information Science, 2016, 18(10):1295-1304. ]

[5]
董春, 尹诗画, 张玉. 多智能体的城市精细尺度人口估算模型[J]. 测绘科学, 2019, 44(8):113-119.

[ Dong C, Yin S H, Zhang Y. A model of urban fine-scale population estimation based on multi-agent[J]. Science of Surveying and Mapping, 2019, 44(8):113-119. ] DOI:10.16251/j.cnki.1009-2307.2019.08.016

DOI

[6]
李泽宇, 董春. 引入兴趣点的地理加权人口空间分布模型研究——以天津市为例[J]. 遥感信息, 2019, 34(2):113-117.

[ Li Z Y, Dong C. Geographically weighted population spatial distribution model with point of interest: Taking Tianjin for an example[J]. Remote Sensing Information, 2019, 34(2):113-117. ]

[7]
廖顺宝, 孙九林. 基于GIS的青藏高原人口统计数据空间化[J]. 地理学报, 2003, 58(1):25-33.

[ Liao S B, Sun J L. GIS based spatialization of population census data in Qinghai-Tibet Plateau[J]. Acta Geographica Sinica, 2003, 58(1):25-33. ]

DOI

[8]
杨晓荣, 陈楠. 基于多源数据的福建省人口数据空间化研究[J]. 贵州大学学报(自然科学版), 2019, 36(2):79-84,95.

[ Yang X R, Chen N. Spatialization of population data for Fujian Province based on multi-source data[J]. Journal of Guizhou University (Natural Sciences), 2019, 36(2):79-84,95. ] DOI:10.15958/j.cnki.gdxbzrb.2019.02.16

DOI

[9]
Bhaduri B, Bright E, Coleman P, et al. LandScan USA: A high-resolution geospatial and temporal modeling approach for population distribution and dynamics[J]. GeoJournal, 2007, 69(1):103-117. DOI:10.1007/s10708-007-9105-9

DOI

[10]
江东, 王乃斌, 刘红辉. 人口数据空间化的处理方法[J]. 地理学报, 2002(B12):70-75.

[ Jiang D, Wang N B, Liu H H. Processing method of population data spatialization[J]. Acta Geographica Sinica, 2002(B12):70-75. ]

[11]
Alegana V A, Atkinson P M, Pezzulo C, et al. Fine resolution mapping of population age-structures for health and development applications[J]. Journal of the Royal Society, Interface, 2015, 12(105):20150073. DOI:10.1098/rsif.2015.0073

DOI

[12]
Balk D L, Deichmann U, Yetman G, et al. Determining global population distribution: Methods, applications and data[J]. Advances in Parasitology, 2006, 62:119-156. DOI:10.1016/S0065-308X(05)62004-0

DOI PMID

[13]
Stevens F R, Gaughan A E, Linard C, et al. Disaggregating census data for population mapping using random forests with remotely-sensed and ancillary data[J]. PLoS One, 2015, 10(2):e0107042. DOI:10.1371/journal.pone.0107042

DOI

[14]
高占慧. 区域生态环境评价中的统计数据空间化方法研究——以山东省为例[D]. 济南: 山东师范大学, 2012.

Gao Z H. Study on spatial distribution of statistical data in regional ecology and environment assessment: A case study of Shandong Province[D]. Jinan: Shandong Normal University, 2012. ]

[15]
Atkinson P, Curran P. Choosing an appropriate spatial resolution for remote sensing investigations[J]. Photogrammetric Engineering and Remote Sensing, 1997, 63:1345-1351.

[16]
叶靖, 杨小唤, 江东. 乡镇级人口统计数据空间化的格网尺度效应分析——以义乌市为例[J]. 地球信息科学学报, 2010, 12(1):40-47.

[ Ye J, Yang X H, Jiang D. The grid scale effect analysis on town leveled population statistical data spatialization[J]. Journal of Geo-information Science, 2010, 12(1):40-47. ]

DOI

[17]
杜国明, 张树文, 张有全. 城市人口分布的空间自相关分析——以沈阳市为例[J]. 地理研究, 2007, 26(2):383-390.

[ Du G M, Zhang S W, Zhang Y Q. Analyzing spatial auto-correlation of population distribution: A case of Shenyang City[J]. Geographical Research, 2007, 26(2):383-390. ]

DOI

[18]
李月娇, 杨小唤, 王静. 基于景观生态学的人口空间数据适宜格网尺度研究——以山东省为例[J]. 地理与地理信息科学, 2014, 30(1):97-100.

[ Li Y J, Yang X H, Wang J. Grid size suitability of population spatial distribution in Shandong Province based on landscape ecology[J]. Geography and Geo-Information Science, 2014, 30(1):97-100. ]

[19]
Dong N, Yang X H, Cai H Y, et al. Research on grid size suitability of gridded population distribution in urban area: A case study in urban area of Xuanzhou District, China[J]. PLoS One, 2017, 12(1):e0170830. DOI:10.1371/journal.pone.0170830

DOI

[20]
刘学录. 我国景观生态学尺度效应研究进展[J]. 甘肃农业大学学报, 2021, 56(6):1-9.

[ Liu X L. Progress of study on scale effect in landscape ecology in China[J]. Journal of Gansu Agricultural University, 2021, 56(6):1-9. ] DOI:10.13432/j.cnki.jgsau.2021.06.001

DOI

[21]
Veldkamp A, Kok K, De Koning G H J, et al. Multi-scale system approaches in agronomic research at the landscape level[J]. Soil and Tillage Research, 2001, 58(3/4):129-140. DOI:10.1016/S0167-1987(00)00163-X

DOI

[22]
王培震, 石培基, 魏伟, 等. 基于空间自相关特征的人口密度格网尺度效应与空间化研究——以石羊河流域为例[J]. 地球科学进展, 2012, 27(12):1363-1372.

DOI

[ Wang P Z, Shi P J, Wei W, et al. Grid scale effect and spatialization of population density based on the characteristics of spatial autocorrelation in Shiyang River Basin[J]. Advances in Earth Science, 2012, 27(12):1363-1372. ]

[23]
郑鹏, 陈伟, 顾媛媛, 等. 基于Voronoi图的多航行器不规则区域搜索规划方法研究[C]// 第四届水下无人系统技术高峰论坛:有人/无人协同技术论文集.陕西,中国: 2021:92-97.

[ Zheng P, Chen W, Gu Y Y, et al. Path Planning Research of Multiple Underwater Vehicles in Irregular Area Based on Voronoi Diagram[C]// 4th Unmanned Underwater Systems Technology Summit:Proceedings of the Manned/Unmanned Collaborative Technology, Xi'an, China: 2021:92-97. ]

[24]
张国俊, 黄婉玲, 周春山, 等. 城市群视角下中国人口分布演变特征[J]. 地理学报, 2018, 73(8):1513-1525.

DOI

[ Zhang G J, Huang W L, Zhou C S, et al. Spatio-temporal characteristics of demographic distribution in China from the perspective of urban agglomeration[J]. Acta Geographica Sinica, 2018, 73(8):1513-1525. ]

DOI

[25]
刘妙龙, 陈鹏, 冯永玖. 上海市人口分形的时空演化与区域差异研究[J]. 中国人口科学, 2005(2):51-60,96.

[ Liu M L, Chen P, Feng Y J. Time-space evolution and regional difference of population fractal in Shanghai[J]. Population Science of China, 2005(2): 51-60,96. ]

[26]
王劲峰, 徐成东. 地理探测器:原理与展望[J]. 地理学报, 2017, 72(1):116-134.

DOI

[ Wang J F, Xu C D. Geodetector: Principle and prospective[J]. Acta Geographica Sinica, 2017, 72(1):116-134. ]

DOI

[27]
杨瑞红, 董春, 张玉. 地理国情普查数据支持下的人口空间化方法[J]. 测绘科学, 2017, 42(1):76-81.

[ Yang R H, Dong C, Zhang Y. Method of population spatialization under the support of geographic national conditions data[J]. Science of Surveying and Mapping, 2017, 42(1):76-81. ] DOI:10.16251/j.cnki.1009-2307.2017.01.015

DOI

[28]
Dong N, Yang X H, Cai H Y, et al. A novel method for simulating urban population potential based on urban patches: A case study in Jiangsu Province, China[J]. Sustainability, 2015, 7(4):3984-4003. DOI:10.3390/su7043984

DOI

Options
文章导航

/

〈 〉