EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 7: 1312 - 1324

DOI: https://doi.org/10.12082/dqxxkx.2023.220769

基于时空组Lasso与分层贝叶斯时空模型的变量选择方法

  • 王玲 , 1, 2, 3, * ,
  • 康子豪 1, 2
展开
  • 1.北京科技大学自动化学院，北京 100083
  • 2.北京科技大学自动化学院工业过程知识自动化教育部重点实验室，北京 100083
  • 3.北京科技大学顺德创新学院，北京 528399

王 玲（1974— ），女，北京人，博士，教授，主要从事数据挖掘、模式识别等研究。E-mail:

收稿日期: 2022-10-10

  修回日期: 2023-02-08

  网络出版日期: 2023-06-30

基金资助

国家自然科学基金项目(62076025)

国家自然科学基金项目(61572073)

广东省基础与应用基础研究基金(2023A1515011320)

收起

Variable Selection Method based on Spatio-temporal Group Lasso and Hierarchical Bayesian Spatio-temporal Model

  • WANG Ling , 1, 2, 3, * ,
  • KANG Zihao 1, 2
Expand
  • 1. School of Automation and Electrical Engineering, University of Science and Technology, Beijing 100083, China
  • 2. Key Laboratory of Knowledge Automation of Industrial Process of Ministry of education, School of Automation and Electrical Engineering, University of Science and Technology, Beijing 100083, China
  • 3. Shunde Innovation School, University of Science and Technology, Beijing 528399, China
*WANG Ling, E-mail:

Received date: 2022-10-10

  Revised date: 2023-02-08

  Online published: 2023-06-30

Supported by

National Natural Science Foundation of China(62076025)

National Natural Science Foundation of China(61572073)

Guangdong Basic and Applied Basic Research Foundation(2023A1515011320)

Fold

摘要

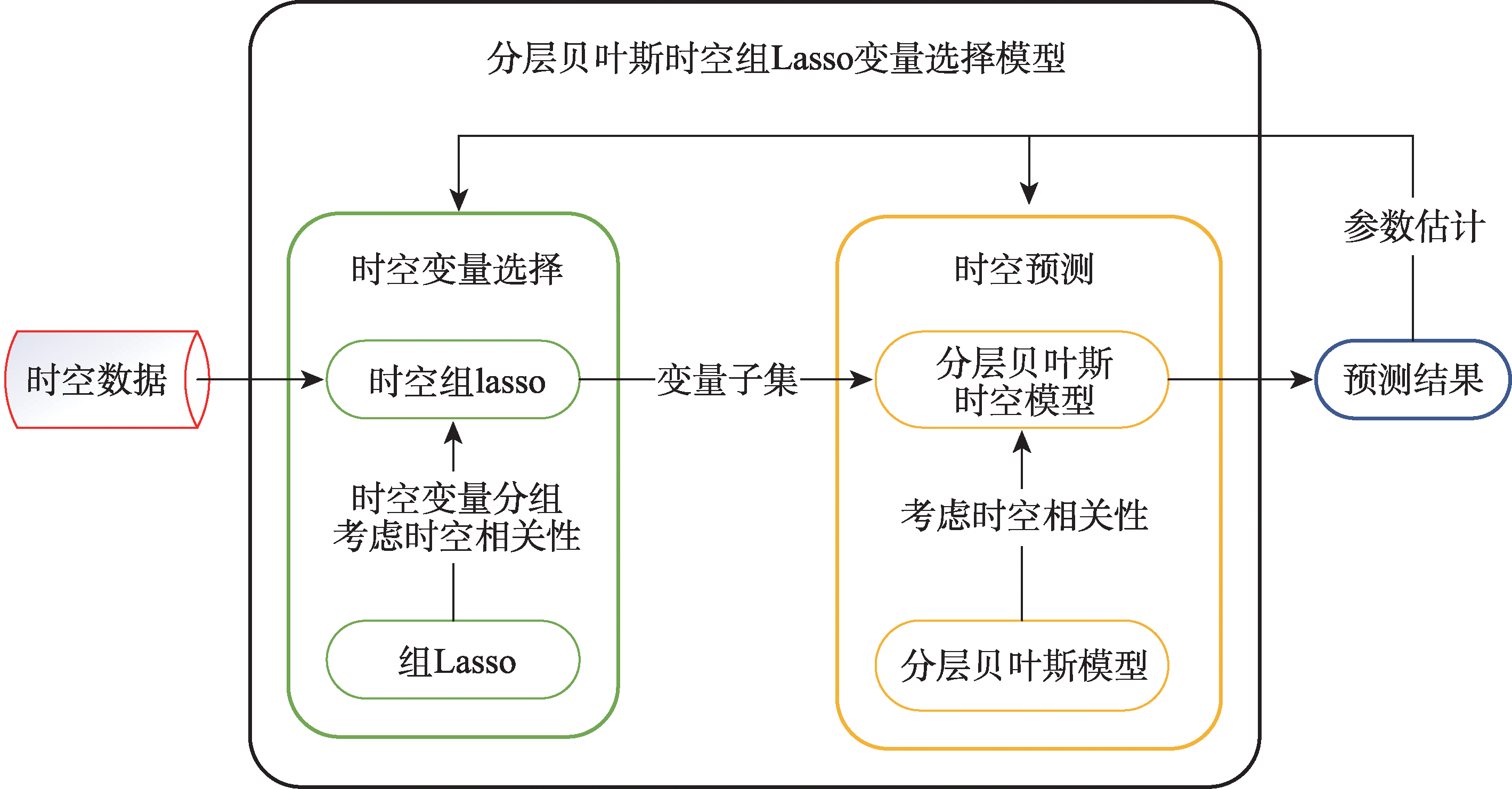
从高维度、大数据量的时空数据中有效选择变量是时空数据领域的重要问题之一，现有的时空数据变量选择的方法在变量选择的过程中未充分考虑时空相关性，时空变量选择阶段与预测阶段分开进行，且往往需要人为设定时空点个数阈值判定变量的取舍，从而无法较为准确的选择对因变量影响最大的变量子集，导致后续预测效果较差。本文针对上述不足，提出了一种基于时空组Lasso与分层贝叶斯时空模型的变量选择方法，称为分层贝叶斯时空组Lasso变量选择模型（Hierarchical Bayesian Spatio-temporal Group Lasso Variable Selection Method， HBST-GLVS)，该方法首先利用时空组Lasso进行变量选择，通过引入最大时间滞后和最大空间邻域充分考虑时空相关性，并根据时空数据连续性，将同一时空变量的时空点进行整体惩罚，避免人为设定时空点个数引起局部片面性。然后，利用分层贝叶斯时空模型对变量选择的效果进行验证，将变量选择过程与模型验证过程置于同一框架下进行参数的调整，从而得到最优的变量子集。实验结果表明，与现有方法相比，本文方法在北京空气质量数据集、波特兰交通流数据集上的RMSE（Root Mean Square Error）和MAE（Mean Square Error）可分别降低9.6%~25.7%以及6.6%~15.9%。

关键词： 时空数据; 变量选择; 时空相关性; 时空组lasso; 最大时间滞后; 最大空间邻域; 分层贝叶斯时空模型

本文引用格式

王玲 , 康子豪 . 基于时空组Lasso与分层贝叶斯时空模型的变量选择方法[J]. 地球信息科学学报, 2023 , 25(7) : 1312 -1324 . DOI: 10.12082/dqxxkx.2023.220769

Abstract

It is one of the important issues in the field of spatio-temporal data analysis to effectively select variables from high-dimensional and large-scale spatio-temporal data. As the most important features of spatio-temporal data, the temporal and spatial correlation of spatio-temporal data must be considered to make effective variable selection. However, existing spatio-temporal data variable selection methods do not fully consider the spatio-temporal correlation, and the variable selection stage is separated from the prediction stage. Moreover, these methods often require manual setting of a threshold of the number of spatiotemporal points to determine variables selection, which may lead to inaccurate selection of the subset of variables that have the greatest impact on the dependent variable, and result in poor prediction performance. In this paper, we propose a variable selection method based on the spatio-temporal group Lasso and the hierarchical Bayesian spatiotemporal model, called the hierarchical Bayesian Spatio-temporal Group Lasso Variable Selection method (HBST-GLVS). In this method, the spatio-temporal expansion is carried out simultaneously in the variable selection stage and prediction stage, and the best nearest neighbor time domain and space domain are determined adaptively through cross validation. In order to obtain the best prediction performance from the selection of variables, the selection of spatio-temporal variables and the prediction of spatiotemporal models are placed under the same framework, so that the selected variables and parameters correspond to the best prediction performance. In order to solve the problem of manual setting of the threshold of the number of spatio-temporal points, the variable selection is processed from the perspective of the entire sequence of spatio-temporal variables, without the threshold of the number of spatio-temporal points. Specifically, this method uses spatio-temporal group Lasso for variable selection, fully considers spatio-temporal correlation by introducing maximum time lag and maximum spatial neighborhood, and applies global penalty to all spatio-temporal points of the same variable based on spatio-temporal data continuity, thus avoiding the lopsidedness caused by artificial setting of thresholds. The effect of variable selection is validated using a hierarchical Bayesian spatio-temporal model, and the variable selection process and the model validation process are placed under the same framework for the adjustment of parameters, so as to obtain the optimal subset of variables. Our results show that the Root Mean Square Error (RMSE) and Mean Square Error (MAE) of the method in this paper can be reduced by 9.6%~25.7% and 6.6%~15.9%, based on Beijing air quality dataset and Portland traffic flow dataset, respectively, compared with the existing methods.

Key words： spatio-temporal data; variable selection; spatio-temporal correlation; spatio-temporal group lasso; maximum time lag; maximum spatial neighborhood; Hierarchical Bayesian spatio-temporal model

1 引言

近年来，时空数据已经逐渐成为数据挖掘领域的热点研究对象。时空数据一般具有数据量大、高维度的特点，因此需要对时空数据进行变量选择提取最优的变量子集，以提高模型的精度和解释性[1]。当下，变量选择的方法众多，如：正向逐步选择法[2]、基于AIC（Akaike Information Criterion）的变量选择法[3]、组Lasso[4]（Group Least Absolute Shrinkage and Selection Operator）、基于遗传算法的变量选择[5]等，它们已经广泛应用于临床医学[6]、工业动态监测[7]、气象学[8]等领域。时空数据最重要的特征是时空相关性，即与相距较远的观测值相比，邻近空间和时间上的观测值更为相似[9]。因此，为了进行有效的变量选择，必须同时考虑时间相关性和空间相关性，目前已有的变量选择方法尚未充分考虑时空数据的时空相关性，因而并不适用于时空数据的变量选择，如何从时空数据中有效的选择变量，已经成为时空领域需要研究的重要问题。
目前，针对时空变量选择的方法主要可以分为三大类：基于统计模型[10]的方法，基于机器学习[11⇓-13]的方法，以及机器学习与统计模型相结合的方法[14]。Fassò等[10]采用与Lasso结合的隐含动态地理统计模型（Least Absolute Shrinkage and Selection Operator-Hidden Dynamic Geostatistical Model，Lasso-HDGM）进行变量选择，考虑到时空相关性，其引入了随近邻时间、空间域变化的随机隐变量，但其只考虑前一历史时刻以及最近空间站点，忽略了近邻时间域和近邻空间域。Chen等[11]提出一种基于混合系数遗传算法优化的LSSVR（最小二乘支持向量机）模型，通过改进的遗传算法选择时空变量，并采用LSSVR预测模型确定最优变量集。Jui等[12]提出一种时空混合蜻蜓优化支持向量回归随机森林(Dragonfly Optimization Algorithm and Support Vector Regression-Random Forest，DRS-RF)算法，首先通过蜻蜓算法优化支持向量回归参数进行时空变量选择，然后构建随机森林模型验证变量选择的效果。Dai等[13]首先采用XGBoost从PM2.5中提取特征，然后使用一维多尺度卷积核（MSCNN）从空气质量数据中提取局部时间和空间特征关系，并进行线性拼接和融合，以获得多特征的时空关系，进而构建LSTM网络预测PM2.5浓度。但上述三种机器学习方法的变量选择阶段与预测阶段分开进行，导致所选时空变量并非对应最佳预测效果。Xu等[14]提出一种基于时空变量选择的支持向量回归（Variable Selection-based Support Vector Regression,VS-SVR）模型，首先采用多元自适应回归样条模型进行变量选择，然后通过支持向量机回归进行交通流的预测以验证变量选择效果。但该方法针对时空点进行变量选择，需通过人为设置时空点个数的阈值选择变量，可能导致变量选择的主观性太强。综上，现有方法主要通过机器学习和统计模型的方法分别进行时空变量选择以及预测，但存在未充分考虑时空相关性、变量选择结果未对应最佳预测效果以及需要人为设置时空点个数阈值的问题。
针对当前时空变量选择所存在的不足，本文提出了分层贝叶斯时空组Lasso变量选择模型（Hierarchical Bayesian Spatio-temporal Group Lasso Variable Selection Method， HBST-GLVS)。该方法具有以下优点：.
（1）为了充分考虑时空相关性，在变量选择阶段和预测阶段同时进行时空拓展，并且通过交叉验证自适应确定最佳近邻时间域和空间域。
（2）为了使变量选择获得最佳预测效果，将时空变量选择，时空模型预测置于同一框架下，从而使得所选变量以及参数对应于最优预测效果。
（3）为了解决人为设置时空点个数阈值的问题，从整个时空变量序列的角度考虑变量选择的过程，无需人为设置时空点个数的阈值。

2 相关理论

2.1 组Lasso

为解决逐个进行变量选择所导致的变量冗余问题，组Lasso[4]作为一种连续、有序的变量选择的方法得到了广泛的应用。组Lasso在变量选择的过程中首先将变量分组，然后在目标函数中通过调整参数惩罚每一组变量的L2范数，当某组变量的系数变为0，该组变量被删除，从而达到变量选择的目的。其表达式如下：
β ˆ = a r g m i n β i 1 2 Y - X β 2 + λ ∑ i = 1 N β i K i
式中： β ˆ为所求得的组Lasso系数； Y为因变量； X为自变量； β为自变量的系数， β = ( β 1 , β 2 , ⋯ , β i , ⋯ , β N )； β i表示第i个变量的系数；N为变量的个数； Y - X β 2为残差的平方； K i为任意的对称正定矩阵； β i K i = ( β i ' K i β i ) 1 / 2为稀疏惩罚，用来对变量进行删除与选择； λ用于调整稀疏惩罚的程度。然而，组Lasso在变量选择的过程中并未考虑时空相关性，对于时空变量选择的效果不佳，因此需对组Lasso进行时空拓展。

2.2 分层贝叶斯模型

为验证变量选择的效果，需要对时空过程进行建模。然而，时空过程除具有时间和空间上的变化外，还包括多变量以及不同系统间的非线性相互作用，通常无法直接表示，但可以通过时空过程的联合分布描述时空过程中所有变量以及变量之间所有可能的相互作用。分层贝叶斯模型[15]能够对一些复杂的环境系统或者物理过程建模，得到其联合分布。其主要过程为将随机变量集合的联合分布分解为一系列条件模型[16]。
一般来说分层贝叶斯模型主要分为3层： ①数据模型： [ D | f ( X ) , ψ ]； ②过程模型： [ f ( X ) | ψ ]； ③参数模型： [ ψ ]， D表示样本观测数据， f ( X )包含自变量与样本观测数据之间的关系， ψ为模型中未知的参数。
第一层关注的是 D的似然分布模型。该过程对观测数据的产生过程进行刻画，即对 D的似然分布进行建模。
第二层关注的是 f ( X )的条件分布模型，这一层通常是构建模型的关键步骤，用于描述所关注的物理过程，对 f ( X )进行建模。
最后一层通过设定参数的分布来考虑参数的不确定性，增强模型后验结果的稳健性。
最终所关注的是通过贝叶斯规则由数据得到的后验分布，如下所示，该分布包含 f ( X )以及参数 ψ的更新：
[ f ( X ) , ψ | D ] ∝ [ D | f ( X ) , ψ ] [ f ( X ) | ψ ] [ ψ ]

3 研究方法

3.1 时空组Lasso

组Lasso通过变量分组解决了逐个进行变量选择所导致的变量冗余问题，但是由于其未考虑时空相关性，并不适用于时空数据的变量选择，为此，在组Lasso的基础上，我们提出了时空组Lasso方法。
令时空数据为 { X , Y }， X为包含 N个自变量的时空数据，可以表示为 X = { D 1 , D 2 , ⋯ , D i , ⋯ D N }， D i = { X 1 i , X 2 i , ⋯ , X s i , ⋯ , X Q i }为第 i个自变量在空间域上的数据， Q为空间点的个数， X t , s = x t , s 1 , x t , s 2 , ⋯ , x t , s i , ⋯ x t , s N为 N个自变量在第 s个空间点和第 t个时刻的值， x t , s i ( i = 1,2 , ⋯ , N )是第 i个自变量在第 s个空间点，第 t个时刻的值。本文的因变量只考虑一个，令 Y = { Y 1 , Y 2 , ⋯ , Y s , ⋯ , Y Q }为因变量在空间域上的数据， Q为空间点的个数， Y s = { y 1 , s , y 2 , s , ⋯ , y t , s , ⋯ , y T , s }为因变量在第 s个空间点的时间序列数据， T为时间域的大小， y t , s表示因变量在第 s个空间点第 t个时刻的值。
考虑到时空数据的时空相关性，本文采用了最大时间滞后和最大空间邻域的概念。最大时间滞后是指每个点都受到其前几个时刻的影响，用 L表示最大时间滞后，即考虑前 L个历史时刻对当前时刻的影响。最大空间邻域是指每个点都受到其近邻域的影响，对于第 s个空间站点，选择距离 s最近的 H个空间点 s 1 , s 2 , ⋯ , s k , ⋯ , s H作为第 s个空间点的最大空间邻域 Ω = { s 1 , s 2 , ⋯ , s k , ⋯ , s H }。为了确定最大时间滞后 L与最大空间邻域数 H，采用SC准则[17]（Schwarz Criterion），如式（3）、（4）所示。
L = a r g m i n l l n y t , s - ∑ i = 1 N ∑ l = 1 L β l i x t - l , s i 2 N + l N l n N
H = a r g m i n h l n y t , s - ∑ i = 1 N ∑ h = 1 H β s k i x t , s k i 2 N + h N l n N
式中： y t , s表示因变量在第 t个时刻；第 s个空间点的值； l表示时间滞后； h表示空间邻域； x t - l , s i表示第 i个自变量在第 t - l个时刻，第 s个空间点的值； x t , s k i表示第 i个自变量在第 t个时刻，空间点 s k处的值； β l i、 β s k i为所对应的系数。
为了在时空数据变量选择时考虑时空相关性以及时空序列的连续性，在式(1)的基础上提出了时空组lasso方法，如式（5）所示。
β G L = a r g m i n β ∑ s = 1 Q ∑ t = L + 1 T y t , s - ∑ i = 1 N ∑ l = 1 L ∑ k = 1 H β l , s k i x t - l , s k i 2 + λ 2 ∑ i = 1 N ∑ l = 1 L ( β l ,       : i ) T Δ ˜ i β l ,       : i ︸ 空 间 惩 罚 + λ 1 ∑ i = 1 N β : i Δ i ︸ 稀 疏 惩 罚  
式中： y t , s表示因变量在第 t个时刻，第 s个空间点的值； Q为空间点的个数； T为时间域的大小； N表示自变量的个数； L为最大时间滞后； H为最大空间邻域； x t - l , s k i表示第 i个自变量在第 t - l个时刻，空间点 s k处的值； β l , s k i为 x t - l , s k i所对应的系数； β l ,       : i = ( β l , s k i ) s k ∈ Ω； β : i = ( β l , s k i ) l ∈ 1 , L , s k ∈ Ω； Δ ˜ i = s 1 - s 0 0 0 0 s 2 - s 0 0 0 0 ⋱ 0 0 0 0 s k - s； Δ i = Δ ˜ i 0 0 0 0 Δ ˜ i 0 0 0 0 ⋱ 0 0 0 0 Δ ˜ i；
β : i △ i = ( ( β : i ) T Δ i β : i ) 1 / 2。 λ 1所对应的惩罚项是一种组Lasso惩罚项，通过 β : 1 Δ i , β : 2 Δ i , ⋯ , β : N Δ i的 l 1范数对属于同一自变量的时空点分组进行统一惩罚，确保自变量的所有时空点能够作为一组来选择或者剔除。 λ 2所对应的惩罚项为空间惩罚项，实现空间正则化，矩阵 Δ ˜ i惩罚基于距离的系数，即与给定位置距离较远的邻域位置受到更多的惩罚， Δ ˜ i可以是对角矩阵，对应于 β l , s k i的对角项等于 s k到第 s个空间点的欧几里得距离，即 s k - s。
设 Y为由 y t , s所组成的长为 ( T - L + 1 ) Q的因变量向量， X为一个空间和时间滞后的自变量矩阵，每一行是由 x t - l , s k i所组成的向量，其维数为 ( ( T - L + 1 ) Q ) × ( N L Ω )。 β是由 β l , s k i所组成的长度为 N L Ω的自变量系数的向量，则时空组Lasso可以改写为式（6）：
β G L = a r g       m i n                                     β L ( λ 1 , λ 2 , β ) =         a r g       m i n Y - X β 2 + λ 2 ∑ i = 1 N β i Δ i 2 + λ 1 ∑ i = 1 N β i Δ i                                  
为了求解公式（6），将其转化为公式（7），
β G L = 1 1 + λ 2 Δ i - 1 S i Τ a r g         m i n                                       β Y ˆ - X ˆ β 2 + γ ∑ i = 1 N β i 2
式中： Δ i ( i = 1 , ⋯ , N )是正定的；令 Δ i = S i Τ S i； C = ( S 1 Τ S 1 ) - 1 S 1 Τ 0 0 0 0 ( S 2 Τ S 2 ) - 1 S 2 Τ 0 0 0 0 ⋱ 0 0 0 0 ( S N Τ S N ) - 1 S N Τ； γ = λ 1 1 + λ 2； Y ˆ = Y 0 ( n )； X ˆ = 1 1 + λ 2 X C λ 2 I；
n为 X的列数。
将该求解问题转化后，所需估计的参数为 λ 1、 λ 2、 γ中的任意2个参数，本文所估计的参数为 λ 2和 γ，不同的 λ 2和 γ对应不同系数 β，将系数为0的变量进行剔除，得到变量选择的结果。

3.2 分层贝叶斯时空模型

为了对时空组Lasso进行参数的估计以及通过时空预测验证其变量选择的效果，需要对时空数据进行准确建模。分层贝叶斯模型虽然能够对一些复杂的环境系统或者物理过程进行建模，得到其联合分布，但没有包含历史时刻、近邻空间自变量对当前时刻、当前空间自变量的影响[18]。为解决上述问题，提出了分层贝叶斯时空模型。
模型的第一级如下：
y t , s = f ( X t , s ) + ε t , s
式中： y t , s表示在第st个空间点和第t个时刻观测到的因变量， s ∈ 1 , Q， t ∈ 1 , T； ε t , s ~ N ( 0 , σ ε 2 )是由高斯白噪声所定义的测量误差，用于说明模型的测量不确定性；为了得到历史时刻、近邻空间自变量对当前时刻、当前空间自变量的影响，对过程模型 f ( X t , s )进行重构，增加了一种时空约束项 ω t , s。
f ( X t , s ) =     X t , s β + ω t , s
式中： β = ( β t , s 1 , β t , s 2 , ⋯ , β t , s N )为对应的自变量系数向量。
ω t , s = ∑ l = 1 L ρ l ω t - l , s + ∑ k = 1 h η t , s k
式中： ∑ l = 1 L ρ l ω t - l , s代表前l时刻自变量对当前时刻自变量的影响；自回归系数 ρ l表示影响大小； ∑ k = 1 h η t , s k代表近邻空间自变量对当前位置自变量的影响，假设 η t , s k是与时间无关的高斯随机场，其空间协方差函数 R ( θ ) = e x p ( - s k - s / θ )，常用于表征空间相关性的模型当中[19]； s k - s是 s k与第 s个空间点之间的欧式距离； θ为反映空间相关性的参数。最终时空模型表达式如（11）所示，
y t , s = X t , s β + ∑ l = 1 L ρ l ω t - l , s + ∑ k = 1 h η t , s k + ε t , s
基于上述模型，所需估计的参数集为：
ψ = { β , σ ε 2 , ρ l , θ , L , h }
为了获得参数集 ψ的最大似然估计（Maximum Likelihood Estimation, MLE），在模型拟合过程中采用期望最大化（Expectation-Maximization Algorithm, EM）算法[20]。
在 E（Expectation）步，以已知观测数据 { Y , X }为条件，基于当前估计值 ψ ˆ ( m - 1 )计算“完整数据”对数似然的期望值 l ( ψ       ; Y , ω )：
Q ψ , ψ ˆ ( m - 1 ) = E ψ ˆ ( m - 1 ) [ l ( ψ       ; Y , ω t , s ) | Y , X ]
式中： Y， X分别代表因变量和自变量； ω = ω t , s 1 , ⋯ , ω t , s 2 , ⋯ , ω t , s i , ⋯ , ω t , s N代表时空约束项； Q ψ , ψ ˆ ( m - 1 )的计算还需要指定约束项 ω以及因变量 Y的条件分布，其可以通过卡尔曼滤波器以及多元正态分布公式获得。
在M（Maximization）步中找到最大似然估计 ψ ˆ的第m次更新：
ψ ˆ ( m ) = a r g       m a x Q ψ ψ , ψ ˆ ( m - 1 )
当对数似然函数的更新值为0或小于给定阈值时，EM算法停止更新。

3.3 HBST-GLVS的整体框架及其实现步骤

基于时空组Lasso和分层贝叶斯时空模型，提出了分层贝叶斯时空组Lasso变量选择模型（Hierarchical Bayesian Spatio-temporal Group Lasso Variable Selection Method， HBST-GLVS)。该模型的整体流程图如图1所示。首先基于时空组Lasso进行时空变量选择，通过引入最大时间滞后与最大空间邻域的概念，获取历史时刻、近邻空间与当前数据的时空相关性，进而获得候选变量子集。然后根据分层贝叶斯时空模型的预测结果调整时空组Lasso的相关参数，获得最佳的变量子集。
图1 HBST-GLVS 的整体框架

Fig. 1 Overall framework of HBST-GLVS

HBST-GLVS的具体实现过程如下：
（1）输入时空数据 { Y , X }，时空组Lasso的空间惩罚项系数 λ 2的候选集 Λ 2 = ( 0 , λ m i n , ⋯ , λ m a x ),求解时空组lasso所需参数 γ的候选集 Γ = ( 0,0.01 γ m a x , 0.1 γ m a x , γ m a x )。
（2）输入数据分区 D 1 ( 1 ) , ⋯ , D 1 ( f ) , ⋯ , D 1 ( 10 ) ⊂ D 0, D 0 = { x t , s , y t , s }表示在所有时间点以及空间点所观测到的值的集合， D 1是 D 0的子集，用于在交叉验证中选择惩罚系数。
（3）初始化 λ 2 = 0， γ = 0。
（4）利用时空组Lasso估计自变量系数 β ( λ 2 , γ )，得到变量子集 A。
（5）将变量子集 A代入分层贝叶斯时空模型，利用 D 0 / D 1 ( f )中的数据,根据EM算法估计分层贝叶斯时空模型的参数集 ψ ( λ 2 , γ )。
（6）将参数集 ψ ( λ 2 , γ )代入时空模型，计算平均 R M S E ( λ 2 , γ )、平均 M S E ( λ 2 , γ )。
（7）若平均 R M S E ( λ 2 , γ )、平均 M S E ( λ 2 , γ )不再降低，则转至步骤（6）；否则根据候选集 Λ 2、 Γ调整 λ 2、 γ，转至步骤（2）。
（8）得到最优变量子集 A。

4 实验及分析

本实验采用两个真实的多元时空数据集来验证算法的性能。实验将提出的算法与组Lasso[4]、Lasso-HDGM[10]、DRS-RF[12] 3种算法进行变量选择与预测对比，分析了不同算法在数据集上的变量选择性能。为统一变量选择标准，对比算法均通过参数调整获得其最优变量子集。为评估变量选择后的预测性能，本文采用均方根误差（RMSE）以及平均绝对误差（MAE）指标。所有实验均是在 1.8 GhzHz 处理器和16.00 GB内存下运行的Python 3.6 环境中执行。

4.1 数据集介绍

为了验证HBST-GLVS的效果，所使用的2个数据集具有明显的时空特征且变量较多，分别包含16和23个候选自变量，其中北京空气质量数据集时间跨度大、空间范围大，候选自变量的数值在相邻时间、相邻站点间变化较小，而波特兰交通数据集时间跨度小、空间范围小，候选自变量的数值在相邻时间、相邻站点间变化较为明显。
北京空气质量数据集[21]来源为北京市环境保护监测中心所管辖的35个空气质量监测站以及中国气象局所监管的北京市的15个气象监测站在2017年1月到2017年12月之间每小时的空气质量监测数据。北京市空气质量监测站和气象监测站的分布如图2所示。本文将PM2.5浓度/（µg/m3）作为因变量，NO2、CO、O3、SO2、CO2、CH4这些气体变量作为PM2.5浓度的候选气体自变量，另外从气象监测站的数据中，选择了气温/℃、露点温度/℃、 湿度/（g/m3）、气压/hPa、风速/（m/s）以及西北、东北、东南、西南4个风向作为PM2.5浓度的候选气象自变量。根据PM2.5的成因分析[22]，上述变量中已确定的无关变量为CO2、CH4、O3。
图2 北京市空气质量监测站和气象监测站分布

Fig. 2 Distribution of air quality monitoring stations and meteorological monitoring stations in Beijing

波特兰交通流数据集[23]是由波特兰市I84公路和I205公路的十字交叉路口构成的路网中的24个检测站的数据组成。该路网的地图及24个检测站的位置及编号如图3所示，其中I84公路上有18个检测站，即1—7、10、13—20、22、24， I205公路上有6个检测站，即8、9、11、12、21、23，检测站用于测量一段时间内所经过的交通工具的交通流量。
图3 检测站在路网中的分布

Fig. 3 Distribution of testing stations in the road network

4.2 北京空气质量数据集实验结果及分析

在该数据集中，为补充缺失数据，对于每个监测点，对缺失不连续超过12 h的变量进行线性插补，如果缺失连续超过12 h，使用距离最近的20%监测站的数据的加权平均值进行插补，权重与距离成反比。本实验中以PM2.5浓度为因变量，其他气体和气象变量为候选自变量。为了评判提出算法变量选择的优越性，实验将不同算法运行到北京空气质量数据集上。

4.2.1 预测结果及分析

图4为不同算法的变量选择后的预测结果。由于PM2.5浓度在4个季节中存在显著的差异，因此对每个季节分别进行讨论。这里仅展示了每个季节各十天（分别为1月、4月、7月、10月的1—10号）的平均PM2.5浓度的预测结果，每个完整季节的平均预测误差如表1、表2所示。
图4 各种方法在每个季节各10天中的预测结果

Fig. 4 Prediction results of various methods for ten days in each season

表1 各种方法在4个完整季节中的RMSE与平均RMSE

Tab. 1 RMSE and average RMSE of various methods in four full seasons

方法 春 夏 秋 冬 平均
组Lasso 27.29 25.22 25.44 28.38 26.58
Lasso-HDGM 21.37 20.90 20.54 20.73 20.89
DRS-RF 14.51 15.73 17.85 16.90 16.50
HBST-GLVS 14.12 14.25 15.77 15.32 14.87
表2 各种方法在4个完整季节中的MAE与平均MAE

Tab. 2 MAE and average MAE of various methods in the four full seasons

方法 春 夏 秋 冬 平均
组Lasso 20.38 21.25 19.02 22.20 20.71
Lasso-HDGM 17.89 18.35 17.25 18.43 17.98
DRS-RF 11.70 12.25 14.23 14.26 13.11
HBST-GLVS 10.89 10.21 12.98 12.01 11.02
通过对比发现，组Lasso的预测效果相对较差，说明如果忽略时空数据的时空相关性，对时空数据的变量选择将产生较大影响。Lasso-HDGM方法虽然在预测阶段考虑了时空相关性，预测效果有一定提升，但考虑的近邻时间和空间范围较小，因此提升的效果并不明显。DRS-RF通过集成学习的方法，能够准确选择有效变量，预测效果比上述两种方法都有提升。相比于其他3种方法，本文的HBST-GLVS方法获得了最好的性能。对于RMSE指标，HBST-GLVS相较于Lasso-HDGM减小了25.7%；相较于DRS-RF减少了9.9%；对于MAE指标，HBST-GLVS相较于Lasso-HDGM减小了33.1%；相较于DRS-RF减少了15.9%。

4.2.2 变量选择结果及分析

为了进一步评估所选变量与目标变量之间的相关程度，我们将变量所对应系数的绝对值表示其贡献度，贡献度为0则表示剔除该变量，贡献度不为0则表示选择该变量。实验中，为量化所选变量贡献度大小，变量均经过标准化处理后使用。不同算法在4个季节中变量选择结果以及变量的贡献度大小如图5所示。
图5 各种方法变量选择结果与变量贡献度大小对比

Fig. 5 Comparison of variable selection results of various methods and contribution of variables

在变量选择的过程中，组Lasso和Lasso-HDGM均可通过调整 λ参数获得不同变量子集，预测误差最低时获得最优的变量选择结果。但由于组Lasso仅通过稀疏惩罚剔除无关变量，并未考虑时空相关性，因此无法有效剔除无关变量，导致选择变量个数较多。相比较于组Lasso，Lasso-HDGM在预测阶段考虑了时空相关性，虽然可以剔除部分无关变量使得变量选择的结果更准确，但所考虑的近邻时间和空间范围较小，仍有已知的无关变量被选择。DRS-RF根据随机森林预测结果确定最终的变量子集，但其并未充分利用时空相关性，仍有少部分无关变量被选择。HBST-GLVS采用时空组Lasso方法，在进行稀疏惩罚时将属于同一自变量的时空点进行统一惩罚，即变量只有在整个时空域内与目标变量相关，才会被选择，从而可以有效的剔除无关变量，同时该方法将变量选择参数确定、预测模型参数确定、预测结果置于同一框架下，因此得到了更准确的变量子集，没有已知的无关变量被选择。

4.3 波特兰交通流数据集实验结果及分析

在波特兰交通流数据集中，为防止异常数据的干扰，将采集的数据去掉了周末和节假日的数据，得到了从2020年4月17日到2020年4月30日共10 d的交通数据。为探究哪些邻近交通流数据对目标检测站交通流数据有影响，在本实验中以任意一个检测站为目标检测站，其交通流数据作为因变量，其他23个检测站交通流数据为候选自变量。为了选择对目标检测站有影响的检测站，评判提出算法变量选择的优越性，实验将不同算法运行到波特兰交通流数据集上进行比较。

4.3.1 单个检测站变量选择及分析

以21号目标检测站为例，变量选择结果如图6所示。HBST-GLVS最终选择结果为5、7、8、11、13、14、18、19、23、24号检测站。这几个检测站主要分为2类：①上游检测站，如5、7、11、13、23、24号检测站；②分流检测站，如在十字路口交叉处，如7、23号检测站的交通量会被18、19等检测站所处的路段分流。可以看到，HBST-GLVS变量选择的结果具有较好的解释性，更为准确。这是由于HBST-GLVS采用了时空组Lasso方法从整个时空变量序列的角度进行变量选择，与其他方法相比，其有效剔除了无关检测站的数据。
图6 21号检测站变量选择结果以及变量贡献度大小对比

Fig. 6 Comparison of the results of variable selection and the magnitude of variable contribution at test station 21

为了验证变量选择的效果，图7给出了不同方法对21号检测站的交通流预测结果，表3给出了其预测误差。可以看到，HBST-GLVS预测误差最小，与预测效果次优的DRS-RF相比，HBST-GLVS的RMSE降低了7.6%，MAE指标降低了8.6%，可知本文方法能够有效选择出对21号检测站有影响的检测站，从而提高预测效果。
图7 不同方法对21号检测站的预测结果对比

Fig. 7 Comparison of the prediction results of different methods on the 21st testing station

表3 不同方法对21号检测站预测误差

Tab. 3 Prediction error of different methods for testing station 21 (%)

方法 RMSE MAE
组Lasso 70.86 84.32
Lasso-HDGM 70.31 78.77
DRS-RF 67.61 66.76
HBST-GLVS 62.47 60.99

4.3.2 所有检测站平均预测效果及分析

为了验证不同方法对所有检测站的变量选择效果，图8给出了平均预测结果，表4给出了其预测误差。同样，HBST-GLVS效果最好，与效果次优的DRS-RF相比，HBST-GLVS的RMSE降低了9.6%，MAE指标降低了6.6%，因此HBST-GLVS能够有效选择出对目标检测站有影响的检测站，降低预测误差。
图8 不同方法对所有检测站的平均预测结果对比图

Fig. 8 Comparison of the average prediction results of different methods for all testing stations

表4 不同方法对所有检测站的平均预测误差

Tab. 4 Average prediction error of different methods for all testing stations （%）

方法 平均 RMSE 平均 MAE
组Lasso 76.02 88.53
Lasso-HDGM 74.86 83.32
DRS-RF 69.13 76.27
HBST-GLVS 62.46 71.23

5 结论与讨论

本文提出了分层贝叶斯时空组Lasso变量选择模型。该方法在变量选择阶段和预测阶段同时考虑时空相关性，并且通过交叉验证自适应确定最佳近邻时间域和空间域；将时空变量选择，时空模型预测置于同一框架下，从而使得所选变量以及参数对应于最佳的预测效果；从整个时空变量序列的角度考虑变量选择的过程，无需人为设置时空点个数的阈值。
实验结果表明，与现有的时空变量选择的方法比较，HBST-GLVS能够对不同特点时空数据进行有效的变量选择，准确剔除了无关变量，选择了有效变量，预测效果更优，预测所得RMSE和MAE可分别降低9.6%~25.7%以及6.6%~15.9%。
本文虽然无需设置时空点个数的阈值，近邻时间与空间域通过交叉验证自适应确定，但需要通过调整惩罚项系数 λ 1和 λ 2的候选集，选择出对应于最佳预测效果的变量子集。同时，本文主要依赖建立数学模型的方法验证变量选择的效果，对模型建立的准确性有一定要求，后续将探究其他验证方法，减少参数选择与模型确定等人为因素对实验结果的影响。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Rowley E K. Comparison of variable selection methods[D]. Chapel Hill, NC, USA: The University of North Carolina at Chapel Hill, 2019. DOI:10.1155/2020/6795392

DOI

[2]
Saha P, Patikar S, Neogy S. A correlation-sequential forward selection based feature selection method for healthcare data analysis[C]// 2020 IEEE International Conference on Computing, Power and Communication Technologies (GUCON). IEEE, 2020:69-72. DOI:10.1109/GUCON48875.2020.9231205

DOI

[3]
Pham H. A new criterion for model selection[J]. Mathematics, 2019, 7(12):1215. DOI:10.3390/math7121215

DOI

[4]
Simon N, Friedman J, Hastie T, et al. A sparse-group lasso[J]. Journal of Computational and Graphical Statistics, 2013, 22(2):231-245. DOI:10.1080/10618600.2012.681250

DOI

[5]
Peres F A P, Fogliatto F S. Variable selection methods in multivariate statistical process control: A systematic literature review[J]. Computers & Industrial Engineering, 2018, 115:603-619. DOI:10.1016/j.cie.2017.12.006

DOI

[6]
Chowdhury M Z I, Turin T C. Variable selection strategies and its importance in clinical prediction modelling[J]. Family Medicine and Community Health, 2020, 8(1):e000262. DOI:10.1136/fmch-2019-000262

DOI

[7]
Xiao B, Li Y, Sun B, et al. Decentralized PCA modeling based on relevance and redundancy variable selection and its application to large-scale dynamic process monitoring[J]. Process Safety and Environmental Protection, 2021, 151:85-100. DOI:10.1016/j.psep.2021.04.043

DOI

[8]
Wells B, Dolwick P, Eder B, et al. Improved estimation of trends in U.S. ozone concentrations adjusted for interannual variability in meteorological conditions[J]. Atmospheric Environment, 2021, 248:118234. DOI:10.1016/j.atmosenv.2021.118234

DOI

[9]
许可, 王雅琼. 时空统计建模方法探讨[J]. 统计与决策, 2021, 37(22):11-14.

[Xu K, Wang Y Q. Discussion on spatio-temporal statistical modeling methods[J]. Statistics & Decision, 2021, 37(22):11-14.] DOI:10.13546/j.cnki.tjyjc.2021.22.002

DOI

[10]
Fassò A, Maranzano P, Otto P. Spatiotemporal variable selection and air quality impact assessment of COVID-19 lockdown[J]. Spatial Statistics, 2022, 49:100549. DOI: 10.1016/j.spasta.2021.100549

DOI

[11]
Chen X B, Wei Z J, Liu X, et al. Spatiotemporal variable and parameter selection using sparse hybrid genetic algorithm for traffic flow forecasting[J]. International Journal of Distributed Sensor Networks, 2017, 13(6):155014771 771337. DOI:10.1177/1550147717713376

DOI

[12]
Jui S J J, Ahmed A A M, Bose A, et al. Spatiotemporal hybrid random forest model for tea yield prediction using satellite-derived variables[J]. Remote Sensing, 2022, 14(3):805. DOI:10.3390/rs14030805

DOI

[13]
Dai H B, Huang G Q, Zeng H B, et al. PM2.5 concentration prediction based on spatiotemporal feature selection using XGBoost-MSCNN-GA-LSTM[J]. Sustainability, 2021, 13(21):12071. DOI:10.3390/su132112071

DOI

[14]
Xu Y Y, Chen H, Kong Q J, et al. Urban traffic flow prediction: A spatio-temporal variable selection-based approach[J]. Journal of Advanced Transportation, 2016, 50(4):489-506. DOI:10.1002/atr.1356

DOI

[15]
Allenby G M, Rossi P E. Hierarchical Bayes models[M]// The Handbook of Marketing Research. 2455 Teller Road, Thousand Oaks California 91320 United States of America: SAGE Publications, Inc., 2006:418-440. DOI:10.4135/9781412973380.n20

DOI

[16]
Cameletti M, Ignaccolo R, Bande S. Comparing spatio-temporal models for particulate matter in Piemonte[J]. Environmetrics, 2011, 22(8):985-996. DOI:10.1002/env.1139

DOI

[17]
Fathurahman M. Pemilihan model regresi terbaik menggunakan metode Akaike's information criterion dan Schwarz information criterion[J]. Informatika Mulawarman: Jurnal Ilmiah Ilmu Komputer, 2016, 4(3):37-41. DOI:10.30872/jim.v4i3.41

DOI

[18]
王雅琼, 徐敏亚, 王菲菲. 隐含动态地理统计校准模型——以PM2.5污染分析为例[J]. 数理统计与管理, 2021, 40(2):191-204.

[Wang Y Q, Xu M Y, Wang F F. Hidden dynamic geostatistical calibration model—With application to PM2.5 pollution[J]. Journal of Applied Statistics and Management, 2021, 40(2):191-204.] DOI:10.13860/j.cnki.sltj.20201205-001

DOI

[19]
Finazzi F, Alessandro Fasso O. D-STEM: A software for the analysis and mapping of environmental space-time variables[J]. Journal of Statistical Software, 2015, 62(6):1-29. DOI:10.18637/jss.v062.i06

DOI

[20]
Sammaknejad N, Zhao Y, Huang B. A review of the Expectation Maximization algorithm in data-driven process identification[J]. Journal of Process Control, 2019, 73:123-136. DOI:10.1016/j.jprocont.2018.12.010

DOI

[21]
Wan Y T, Xu M Y, Huang H, et al. A spatio-temporal model for the analysis and prediction of fine particulate matter concentration in Beijing[J]. Environmetrics, 2021, 32(1):e2648. DOI:10.1002/env.2648

DOI

[22]
Lei, Chen,. Assessing air-quality in Beijing-Tianjin-Hebei region: The method and mixed tales of PM2.5 and O3[J]. Atmospheric Environment, 2018, 193:290-301. DOI: 10.1016/j.atmosenv.2018.08.047

DOI

[23]
陈小波, 刘祥, 韦中杰, 等. 基于GA-LSSVR模型的路网短时交通流预测研究[J]. 交通运输系统工程与信息, 2017, 17(1):60-66,81.

[Chen X B, Liu X, Wei Z J, et al. Short-term traffic flow forecasting of road network based on GA-LSSVR model[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(1):60-66,81.] DOI:10.16097/j.cnki.1009-6744.2017.01.010

DOI

Options
文章导航

/

〈 〉