EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 7: 1448 - 1463

DOI: https://doi.org/10.12082/dqxxkx.2023.220584

融合图自编码器与GRU的城市盗窃犯罪时空分布预测模型

  • 赵丹 , 1, 2, 3 ,
  • 杜萍 , 1, 2, 3, * ,
  • 刘涛 1, 2, 3 ,
  • 令振飞 1, 2, 3
展开
  • 1.兰州交通大学测绘与地理信息学院， 兰州 730070
  • 2.地理国情监测技术应用国家地方联合工程研究中心， 兰州 730070
  • 3.甘肃省地理国情监测工程实验室，兰州 730070
*杜 萍（1976— ），四川营山人，博士，副教授，主要从事应急制图、地理空间语义网及网络GIS方面的研究。E-mail:

赵 丹（1997— ），女，陕西宝鸡人，硕士生，研究方向为犯罪预测与时空数据挖掘。E-mail:

收稿日期: 2022-08-12

  修回日期: 2022-11-29

  网络出版日期: 2023-06-30

基金资助

国家自然科学基金项目(42061060)

兰州交通大学优秀平台支持(201806)

兰州交通大学天佑创新团队(TY202001)

收起

Spatio-temporal Distribution Prediction Model of Urban Theft by Fusing Graph Autoencoder and GRU

  • ZHAO Dan , 1, 2, 3 ,
  • DU Ping , 1, 2, 3, * ,
  • LIU Tao 1, 2, 3 ,
  • LING Zhenfei 1, 2, 3
Expand
  • 1. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China
  • 2. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, Lanzhou 730070, China
  • 3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China
*DU Ping, E-mail:

Received date: 2022-08-12

  Revised date: 2022-11-29

  Online published: 2023-06-30

Supported by

National Natural Science Foundation of China(42061060)

LZJTU EP(201806)

Tianyou innovation team of Lanzhou Jiaotong University(TY202001)

Fold

摘要

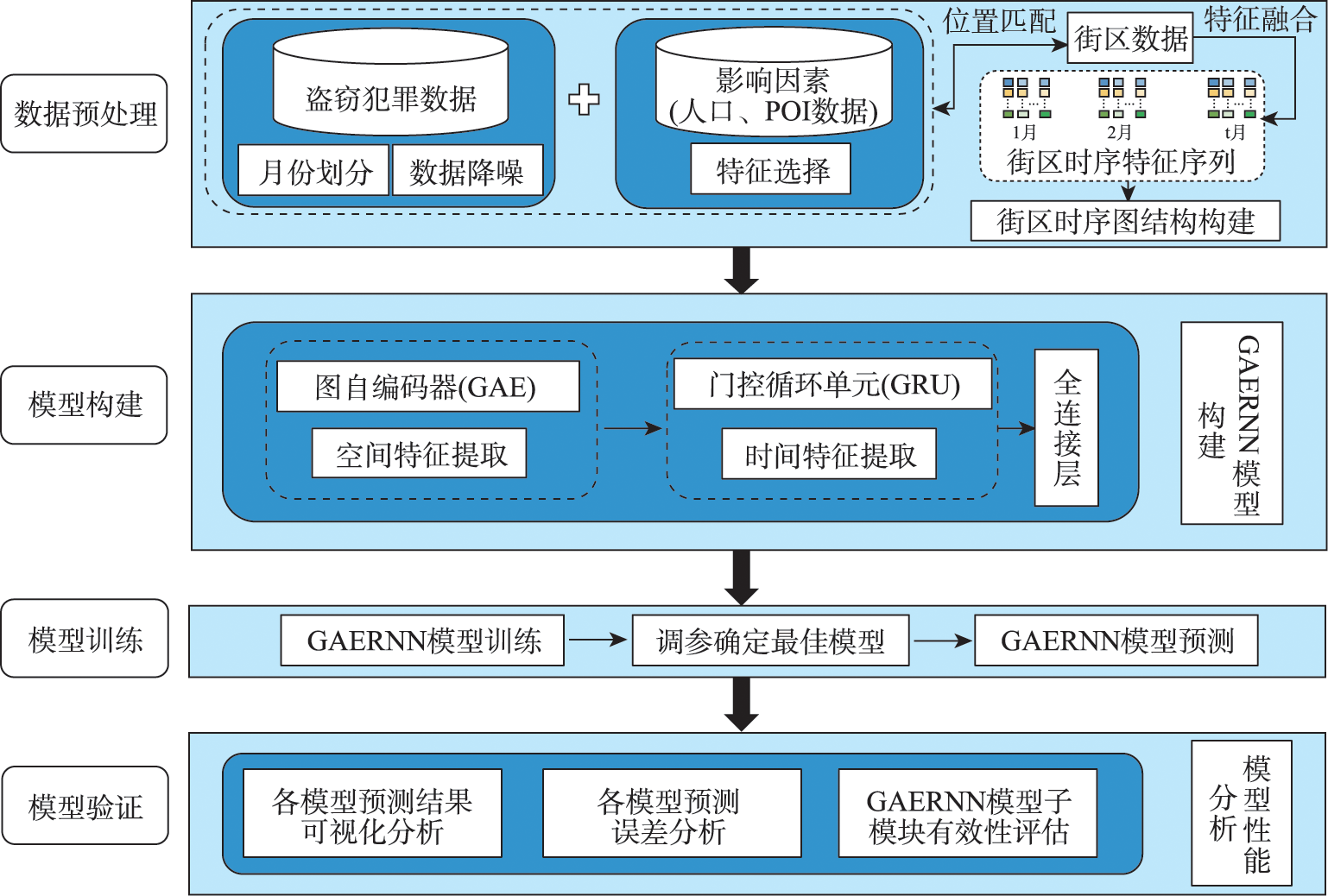
犯罪预测是进行犯罪预防的前提，高效准确的犯罪预测对于提高城市管理效率、保障公共安全都具有重要的意义。当前，关于犯罪预测的已有研究大多采用单一的机器学习方法或深度学习模型，忽略了犯罪的时空依赖关系，往往难以获得准确的预测结果。本文提出一个基于深度学习技术的犯罪时空预测模型—GAERNN：① 利用GAE模型捕获犯罪案件的空间分布特征；② 将带有空间依赖关系的特征经序列化处理后作为GRU模型的输入，进一步提取犯罪序列的时间特征；③ 经全连接层处理获得犯罪时空预测结果，并选取MLP、GCN等基准模型进行对比实验，结合RMSE、MSE等多个指标对模型预测结果进行评估。实验结果表明：对于各模型预测结果可视化分析， GAERNN模型预测的可视化结果与实际数据分布最相符合；在各模型误差分析方面，相比预测性能较差的MLP， GAERNN模型各月份的RMSE分别降低了1.02、3.58、1.29以及0.45；在子模块有效性评估方面，相比其变体模型GAE-LSTM， GAERNN模型在各月份的MAPE分别降低了2.15%、10.07%、1.92%以及2.54%，说明GAERNN模型能显著提高盗窃犯罪时空预测精度，可用于城市盗窃犯罪的积极预防和有效治理。

关键词： 盗窃; 时空分布预测; 城市犯罪; 图神经网络; 深度学习; 门控循环单元; 图自编码器; 兰州市

本文引用格式

赵丹 , 杜萍 , 刘涛 , 令振飞 . 融合图自编码器与GRU的城市盗窃犯罪时空分布预测模型[J]. 地球信息科学学报, 2023 , 25(7) : 1448 -1463 . DOI: 10.12082/dqxxkx.2023.220584

Abstract

Crime prediction is a prerequisite for crime prevention. Forecasting crime efficiently and accurately is of great significance for improving urban management and public safety. At present, it is difficult for most of the existing studies to obtain accurate crime prediction, because they usually utilize a single machine learning or deep learning model, ignoring the spatiotemporal dependence of the crime. In this paper, we propose a spatiotemporal prediction model GAERNN based on deep learning techniques. Firstly, the GAE model is used to capture the spatial distribution characteristics of crime cases. Secondly, the features with spatial dependencies are input into the GRU model after serialization to further extract the temporal features of crime sequences. Then, the spatial and temporal prediction results of theft crime are obtained by the fully connected layer processing. Finally, we select MLP and GCN to carry out contrastive experiments by using several indicators, such as RMSE and MSE, to verify the performance of our model. The results show that our model is significantly superior to other benchmark models in spatiotemporal prediction, and it can be used to prevent and control theft crime effectively.

Key words： theft; spatiotemporal distribution prediction; urban crime; graph neural network; deep learning; gated cyclic unit; graph self-encoder; Lanzhou

1 引言

随着城市化进程的加快，犯罪问题日益突出。在不同的犯罪类型中，盗窃是最常发生的犯罪案件[1]。盗窃罪一般是指非法占有公共财产或他人财产的行为[2]。盗窃案件的频繁发生，给公众造成财产损失的同时，还威胁到城市的健康发展。因此，为了维护社会的和谐稳定，提高公众的生活质量，建立一个精准有效的城市犯罪预测模型显得尤为迫切 [3]。
对犯罪预测的已有研究大致可以分为传统犯罪预测和机器学习预测两类。传统犯罪预测的代表性方法除核密度估计[4⇓-6]外，还包括邻近重复[7-8]、风险地形建模[9-10]等。核密度估计主要利用犯罪案件的空间集聚规律进行犯罪风险制图，能够较好地识别区域犯罪热点[11]。邻近重复[12]是指先前犯罪地点的周边地区在未来一段时间内具有更高的犯罪风险。在此基础上，Mohler等[13]提出了一个自激点过程来模拟犯罪及其近似重复现象，并且取得了较好的效果。然而，上述方法依赖于犯罪案件的时空信息进行犯罪预测，未考虑与犯罪相关的环境特征，且无法保证细小时空尺度上的预测准确性。风险地形建模[14]较好地考虑了各环境因素对犯罪的影响，能够分析微观尺度犯罪行为的生成机理、动力机制及演化规律[15]。然而，该方法主要依靠人工辨识相关风险因子，模型运行效率较低。
随着大数据和机器学习技术的发展，包括K近邻[16]、随机森林[17]、支持向量机[18]以及贝叶斯模型[19]等多种方法被广泛应用于犯罪预测的研究中，如Xia等[20]使用时空随机森林模型预测与毒品犯罪相关的犯罪热点区域；Zhang等[21]使用XGBoost算法进行犯罪可解释性预测。这些预测方法在一定程度上增强了对犯罪信息的挖掘能力，但其模型结构较浅，缺乏深度特征提取能力，因此在一定程度上制约了模型预测的准确性和可靠性。
近年来，深度学习作为一种先进的机器学习方法，引起了各领域的广泛关注，并在各类任务中表现出显著的优势。随后，越来越多的学者开始将其应用到犯罪预测任务中，如Marzan等[22]通过将MLP与不同方法进行对比，探究其在城市犯罪模式预测上的表现情况；Andersson等[23]使用CNN进行犯罪预测并验证了该方法的可行性；Singh[24]使用LSTM、GRU等方法进行犯罪预测，发现GRU能够产生更好的预测结果。此外，也有学者采用不同方法的组合模型进行相应的研究。如Muthamizharasan等[25]使用CNN-LSTM模型对城市犯罪进行预测；John等[26]基于网络新闻数据，采用CNN-GRU模型进行犯罪预测。然而，这些深度学习模型大多适用于规则的二维矩阵，如图像、规则网格等，在处理区域复杂的拓扑结构时具有局限性。随着图深度学习[27]的发展，使得基于拓扑空间的犯罪预测成为了可能，如Zhu等[28]采用图卷积网络（GCN）进行犯罪空间分布预测，并且对于犯罪案件在拓扑空间中的传递取得了较好的预测效果。然而，由于造成犯罪的因素较为复杂，犯罪的发生通常是时空交互作用的结果[29]，使用单一模型往往无法捕捉犯罪的时空依赖特征，也无法反映环境的动态变化，因此，本质上仍难以实现准确的犯罪时空预测。
针对以上问题，本文以兰州市主城区盗窃犯罪、人口及POI等数据为基础，以街区为空间分析单元，按月份对盗窃犯罪数据进行划分，构建街区时序图结构，并结合现有的深度学习预测模型，提出一个用于盗窃犯罪预测的、新的神经网络方法——图自编码循环神经网络（Graph Auto Encoder Recurrent Neural Network，GAERNN）。该方法综合利用图自编码器（Graph Auto Encoder, GAE）在深层次空间特征挖掘中的优势及门控循环单元（Gate Recurrent Unit, GRU）强大的时序处理能力，将GAE与GRU的预测结果通过全连接层实现线性组合，采用梯度下降方法拟合损失，并使用反向传播算法进行权重学习，从而得到更为准确的盗窃犯罪时空预测结果。

2 研究方法

盗窃犯罪成因复杂多变，通常易受外界环境的影响，并伴随有明显的时空依赖，对其进行精确预测具有一定的难度。为此，本文提出一个用于盗窃犯罪时空分布预测的图自编码循环神经网络（GAERNN），在编码器中引入聚合邻域节点的思想，使得图结构中的每个节点可以充分利用周围节点的信息，从而提高了模型图数据嵌入的完整性。在此基础上，考虑到盗窃犯罪具有明显的时空依赖关系，本文在使用GAE进行空间特征提取的同时，结合门控循环单元（GRU）强大的时序处理能力实现盗窃犯罪时空分布预测。具体思路如图1所示，包括数据预处理、模型构建、模型训练以及模型验证4个阶段。
图1 城市盗窃犯罪时空分布预测研究框架

Fig. 1 The framework of spatial and temporal distribution prediction for urban theft

（1）数据预处理。将盗窃犯罪数据以月份为单位进行划分并匹配到街区中，使用卡尔曼滤波对其进行降噪处理，并将处理后的盗窃犯罪数据与选取的人口、POI等特征数据经特征融合得到街区时序特征序列，在此基础上构建街区时序图结构。
（2）模型构建。设计实现一种结合图自编码器（Graph Auto Encoder, GAE）与门控循环单元（Gate Recurrent Unit, GRU）的图自编码循环神经网络（Graph Auto Encoder Recurrent Neural Network，GAERNN）。
（3）模型训练。对GAERNN模型进行训练并选取最优参数组合实现模型预测。
（4）模型验证。结合RMSE、MSE以及MAPE等指标，将GAERNN模型与一系列基线模型进行了各模型预测结果可视化分析、各模型预测误差分析以及GAERNN模型子模块有效性评估，从而验证了模型的预测性能。

2.1 研究区概况、数据来源及处理

2.1.1 研究区域

兰州市总面积为1.31万km2，常住人口为435.94万人，全市下辖三县（榆中县、皋兰县和永登县）、五区（城关区、七里河区、安宁区、西固区及红古区）。主城区总面积占全市总面积的8.49%，却集中了全市69.80%的人口，流动人口多且城市环境复杂，面临的犯罪防范压力较大，因此本文以兰州市主城区作为研究区域，包括城关区、西固区、安宁区以及七里河区4个区级行政区划，共下辖63个街道办事处。

2.1.2 数据来源及预处理

日常活动理论[30]认为潜在的罪犯、合适的犯罪目标以及现场缺乏监护人保护是发生犯罪的3个条件。犯罪模式理论[31]指出罪犯是受日常活动和生活习惯影响的，强调罪犯在寻找犯罪机会时，更倾向于在所熟悉的空间范围内寻找合适的作案目标。犯罪产生地和犯罪吸引地是犯罪模式理论中的概念，是指能够为罪犯提供犯罪机会的特定场 所[32]。犯罪产生地将与所发生的犯罪活动毫无关系的个人由于各种原因聚集到一起，包括购物商场、餐饮服务区等；相比之下，犯罪吸引地[33]就是创造犯罪机会的地方，能够对有动机的罪犯产生吸引作用，如酒吧等娱乐场所。因此，依据日常活动理论和犯罪模式理论并结合相关研究，本文选用人口数据表征合适的犯罪目标，选用犯罪吸引地和犯罪产生地的POI数据表征潜在的罪犯，从而选取与犯罪分布格局呈正相关的影响因子，实验数据清单如 表1所示。
表1 实验数据

Tab. 1 Experimental data

数据名称 采集
时间/年		 数据类型 数据来源
人口数据 2022 文本 兰州市第七次人口普查公报
POI数据 2021 地图 高德地图
犯罪数据 2016—2020 文本 中国裁判文书网
主要数据预处理过程如下：
（1）人口数据
本文使用的人口数据来源于《兰州市第七次人口普查公报》[34]，并将其精确匹配到街区，通过街区内居民总数同居住用地的比值得到各街区的人口密度，如图2所示。
图2 兰州市主城区人口密度分布

Fig. 2 Population density distribution in the main urban area of Lanzhou

（2）POI数据
本文采用的POI数据来源于高德地图，数据属性包括坐标、类型信息等。剔除POI坐标属性不全的数据，本文共使用19 661个兴趣点，并按照《城市用地分类与规划建设用地标准》（GB50137—2011）[35]对其进行分类，分类结果如表2所示。
表2 POI分类

Tab. 2 POI classification

一级类 二级类 三级类
住宅服务 房产建筑 住宅小区、写字楼
商业服务 购物服务 商场、超市、商店
娱乐服务 KTV、酒吧、网吧、会所
餐饮服务 饭馆、快餐店、农家乐
（3）犯罪数据
本文用于模型训练和预测方法评估的犯罪数据来源于中国裁判文书网。犯罪数据为兰州市主城区近5年（2016—2020年）的盗窃犯罪历史数据，包含扒窃、入室盗窃、机动车盗窃三类，数据属性包括案发时间、地点、简要案情等，并通过地理编码得到案发地的地理坐标，对收集到的犯罪数据进行数据清洗、去重[36]等步骤后，共得到3 316条盗窃犯罪历史数据。
将处理后的犯罪数据按月尺度进行划分，并匹配到街区。由于月尺度下的街区盗窃犯罪数据中零值较多，将其直接输入到模型中会产生一定的噪声，因此，本文使用卡尔曼滤波[37-38]对基于月尺度的盗窃犯罪数据进行降噪处理，实现特征增强，优化效果示例如图3所示。
图3 卡尔曼滤波优化效果示例

Fig. 3 Example of Kalman filter optimization effect

2.1.3 街区时序图结构构建

本文将街区时序图结构G定义为G=（ G 1 , G 2 , ⋯ , G t），其中， G t=（ V t, E t）表示t月份的无向连接图； V t=（ v 1 t , ⋯ , v i t , ⋯ , V N t）表示t月份图的节点集合，N为图中街区数量； E t表示图的边集合，连接图中的N个节点。
如图4所示，以街区作为图的节点，以节点之间的连线作为边，将街区时序特征序列嵌入到每张图的节点中，得到由t月份对应的t张图组成的街区时序图结构G=（ G 1 , G 2 , ⋯ , G t）。其中，每个图节点中包含多个特征，节点特征矩阵用X=（ x 1 , x 2 , ⋯ , x t）表示，且X ∈ R N × P， x t = V t，t为月份数量，P表示选取的特征维度。边的权重用连接2个节点之间的欧氏距离表示，这些节点的连接关系用邻接矩阵A表示，且A ∈ R N × N。
图4 街区时序图结构构建

Fig. 4 Construction of block sequence chart structure

2.2 图自编码器

图自编码器（GAE）是一种源于神经网络的图嵌入模型[39]，它使用GCN编码器和内积解码器，通过图数据重构来获得最优表示。由于具有简洁的编解码结构和高效的编码能力，GAE已被广泛应用于人脸识别[40]、生物医药[41]等领域。
如图5所示，编码器采用两层GCN实现，以聚合邻域节点特征，得到节点最优表示，其过程表示如下：
Z = G C N ( X , A )
图5 GAE模型结构

Fig. 5 Structure of GAE

给定节点特征矩阵X ∈ R N × P和邻接矩阵 A ∈ R N × N，将其输入到GCN函数中，输出Z ∈ R N × F，其中， z i ϵ R F为节点的表示向量，F为节点表示维度，GCN的计算过程为：
G C N ( X , A ) = A ˜ R e L U A ˜ X W 0 W 1
式中： A ˜ = D - 1 2 A D - 1 2 ; D 是 节 点 的 度 矩 阵 ; W 0和 W 1是待学习参数。
解码器由邻接矩阵解码和节点特征解码两部分组成，因此GAE的损失函数分别由对应重构邻接矩阵和重构节点特征的损失函数组成。其中，邻接矩阵决定了图的结构，经节点低维表示重构出的邻接矩阵与原始矩阵越相似，说明节点的低维表示越符合图的结构，进而使用交叉熵函数来衡量原始邻接矩阵与重构邻接矩阵之间的差异；节点特征矩阵决定了图的属性，经节点低维表示重构出的节点特征矩阵与原始矩阵越相似，说明节点的低维表示越符合图的属性，进而使用均方根误差来衡量原始节点特征矩阵与重构节点特征矩阵之间的差异。重构矩阵与原始输入的差异越小，则表示得到的节点最优表示Z能够保留更多的空间信息。GAE损失函数的计算公式如下：
L 1 = - 1 N ∑ i = 1 N   y i l o g 1 - y i + y ˆ i l o g 1 - y ˆ i
L 2 = R M S E ( X , X ˆ )
L = L 1 + L 2
式中： y代表邻接矩阵 A中某个元素（0或1）； y ˆ代表重构矩阵 A ˆ中相应元素的值（0到1之间）； X为原始节点特征矩阵； X ˆ为重构后的节点特征矩阵，RMSE代表均方根误差的计算； L 1为重构邻接矩阵的损失函数； L 2为重构节点特征的损失函数； L为总损失函数。

2.3 门控循环单元

门控循环单元[42]（GRU）是循环神经网络（RNN）的一种，同LSTM一样，都是为了解决长期记忆和反向传播中的梯度[43]等问题而提出来的。但LSTM的模型结构较为复杂，神经网络的训练时间较长。同时，随着数据量的增加，其运行效率有所降低。相比之下，GRU的结构更简单、计算量更小、收敛速度也更快，不但解决了传统循环神经网络因数据序列过长导致的梯度消失、训练时间长与过拟合等问题，而且保留了对时间序列数据内在关系的敏感 性[44]。因此，GRU能够有效提升模型的训练速度，优化模型的局部训练能力和网络泛化能力。
GRU的核心结构由重置门和更新门两部分组成（图6）。其中，重置门决定了如何把新的输入与之前的记忆相结合，更新门决定了前一时间步和当前时间步中需要继续传递的信息量。GRU模型的计算公式如下：
z t = σ W z ∙ h t - 1 , x t r t = σ W r ∙ h t - 1 , x t h ˜ t = t a n h W ∙ r t * h t - 1 , x t h t = 1 - z t * h t - 1 + z t * h ˜ t
式中： ∙ 是 矩 阵 乘 法 ; z t为更新门； r t为重置门； h ˜ t为候选隐藏状态， h t - 1 为 上 一 时 刻 的 隐 藏 状 态 ; * 表 示 矩 阵 元 素 乘 积 ; σ为激活函数sigmoid；tanh为双曲正切函数； W 、 W z 、 W r为可学习权重矩阵。
图6 GRU 模型结构

Fig. 6 Structure of GRU

2.4 图自编码循环神经网络模型

本文提出一个基于GAE和GRU的图自编码循环神经网络（GAERNN）模型。由于犯罪预测问题的本质是学习一个函数f，根据给定多维特征数据X=（ x 1 , x 2 , … , x t）和图数据G，预测未来m时间段各街区的犯罪案件数量Y=（ y t + 1 , y t + 2 , … , y t + m）。因此，本文的盗窃犯罪时空预测模型可表示如下：
y t + 1 , y t + 2 , … , y t + m = f x 1 , x 2 , … , x t , G
模型首先使用GAE得到节点最优表示 Z ∈ R N × F，并将其输入到下游的GRU中以获得时间特征，最后经全连接层处理获得犯罪时空预测序列。
GAERNN模型的结构如图7所示。首先，将具有拓扑关系的邻接矩阵A与节点特征矩阵 X=（ x 1 , x 2 , … , x t）依次输入到GAE中，通过编码器对输入数据进行编码，并使用解码器获得重构邻接矩阵 A ˆ与重构节点特征矩阵 X ˆ，同时对模型的参数进行优化，使得重构结果与原始输入尽可能相似，从而获得节点最优表示Z=（ z 1 , z 2 , … , z t）；然后，将带有空间信息的时间序列数据输入到GRU，通过单元之间的信息传递，进一步处理得到犯罪案件的时间依赖；最后通过全连接层获得时空预测特征序列 Y=（ y t + 1 , y t + 2 , … , y t + m）。
图7 GAERNN模型结构

Fig. 7 Structure of the GAERNN model

在训练过程中，目标是尽可能最小化实际犯罪值与预测犯罪值之间的误差。因此， GAERNN模型的损失函数公式如下：
L o s s = M S E ( C t u r e , C p r e ) + L
式中： C t u r e表示实际犯罪值； C p r e表示预测犯罪值； L为重构总损失。

2.5 预测性能评价指标

由于特定区域内的犯罪数量可能为零并很少出现极端值，因此本文选取均方根误差（RMSE）、均方误差（MSE）与平均绝对百分比误差（MAPE）3个指标来衡量不同犯罪预测模型的预测性能。其中，RMSE和MSE用于评估整体绝对预测精度， RMSE与MSE的值越小，表示预测值与真实值越接近，模型的性能越好。MAPE用于测量相对误差， MAPE为0%表示完美模型， MAPE大于100%则表示劣质模型。以上3个指标的计算公式如下：
R M S E = 1 n ∑ i = 1 n   y i - y ˆ i 2
M S E = 1 n ∑ i = 1 n   y i - y ˆ i 2
M A P E = 1 n ∑ i = 1 n   y i - y ˆ i y i × 100 %
式中：n表示样本的数量； y ˆ i表示预测值； y i代表真实值。

3 实验结果与分析

本文使用Python 3.6和Pytorch 1.8.1深度学习框架构建GAERNN模型，并以2016年1月1日至2019年12月31日收集的2 220起盗窃犯罪案件作为训练集，以2020年1月1日至12月31日收集的 1 096起盗窃犯罪案件作为测试集，进行模型训练。

3.1 超参数设置

模型的超参数包括学习率（Learning Rate）、批次数（Batch_size）、隐藏单元（Hidden Units）、训练步数（Epoch）等。经多次测试比较，本文将Batch_size大小设置为20， Epoch设置为300。为了保证预测精度，实验中需要合理设置隐藏单元和学习率的大小。本文基于犯罪历史数据集，选取不同的数值确定二者的取值大小。其中，将隐藏单元设置为hsize={8、16、32、64、128、256} 6种维度，并将学习率的取值分别设置为0.001、0.002、0.025、0.01、0.02与0.1，探讨hsize在不同学习率下的变化趋势，以从中选择最优参数组合。训练结果如图8所示。由图可知，当学习率为0.1时（图8（f）），模型的损失值整体较高，模型训练效果欠缺，说明学习率设置较大会导致模型性能下降；当学习率依次设置为0.001（图8（a））、0.002（图8（b））以及0.025（图8（c））时，损失曲线下降缓慢，并且无法进行准确拟合，说明学习率设置过小也会降低曲线拟合程度；最终将学习率分别设置为0.01、0.02，进行比较之后发现当学习率设置为0.02时，损失曲线下降缓慢；而当学习率设置为0.01时，损失曲线整体具有较好的拟合效果。因此本文将学习率大小设置为0.01。在模型的学习率确定之后，从图8（d）中可以发现，当hsize=64时，曲线损失达到最高，hsize={8、128、256}次之，在 hsize=32时的损失曲线相对平稳且损失值最小，因此考虑到上述因素和训练时间，本文将隐藏单元设置为32。
图8 GAERNN模型的训练损失曲线

Fig. 8 Training loss curve of GAERNN

3.2 各模型预测结果可视化分析

为了评估预测性能，本文从测试集中选取1、5、7、11月4个代表不同季度的月份进行分析（图9），并选取MLP、GCN、CNN-LSTM以及CNN-GRU 4种基准模型作为参照，将它们的预测结果与实际数据集进行对比，以评估GAERNN模型的预测性能。分别将实际数据集、GAERNN以及其他基准模型的预测结果进行可视化，以便更加直观地比较各模型的预测结果，图中颜色的深浅代表犯罪数量的多少，颜色越深，表示该区域的犯罪数量越多，反之则越少。从图9可以看出： MLP模型在不同月份的预测结果与实际数据相差较大； GCN模型各月份预测结果均为大面积分布，区分度较低；CNN-LSTM模型的预测效果次之，模型稳定性有待提高；CNN-GRU模型的预测结果在准确率方面较CNN-LSTM模型有所提升，但该模型对于细小区域仍难以进行准确预测。相较于上述基准模型，GAERNN模型的预测效果最好，能够准确且稳定地识别出存在犯罪行为的区域，预测结果与实际犯罪数据最为接近，但对于颜色最深的犯罪高发区域的预测仍然存在略微偏差，可能是由于模型中的GAE部分需要学习节点周围复杂的邻域关系，而犯罪高发区域的节点分布过于密集，密集的节点分布可能会产生更多邻域结果相似的节点，从而在一定程度上影响了模型的判别能力。总体而言， GAERNN模型的预测结果与真实数据集的时空分布最相符合。
图9 兰州市主城区实际盗窃犯罪分布与各模型预测分布

Fig. 9 The actual distribution of theft and the predicted distribution of each model

3.3 各模型预测误差分析

本文进一步对比分析了各模型对不同月份进行预测的误差表现，如表3所示。从表3可以看出，GAERNN模型具有明显的低误差优势，并且对各月的预测均呈现出优异的预测效果。以2020年5月份的预测任务为例， GAERNN模型的RMSE值为0.83，相较于CNN-LSTM，RMSE值降低了1.69。此外，相比预测性能较差的MLP，GAERNN模型各月RMSE分别降低了1.02、3.58、1.29以及0.45，说明对于不同的预测任务，GAERNN模型都具有更好的预测精度，能够在犯罪预测任务中获得更加准确的结果。
表3 各模型不同月份的预测误差

Tab. 3 Error of each model on different months

方法 1月 5月 7月 11月
RMSE MSE MAPE/% RMSE MSE MAPE/% RMSE MSE MAPE/% RMSE MSE MAPE/%
MLP 2.42 1.50 11.75 4.41 2.49 15.50 3.54 2.13 14.08 1.51 1.28 12.18
GCN 2.16 1.36 10.00 1.93 1.32 12.60 3.19 1.92 13.00 1.38 0.86 7.10
CNN-LSTM 2.11 1.37 10.34 2.52 1.79 13.52 3.23 1.89 12.70 1.48 0.89 7.47
CNN-GRU 1.52 1.12 9.67 1.42 0.83 6.70 2.45 1.52 11.44 1.36 1.02 9.41
GAERNN 1.40 0.95 7.70 0.83 0.50 4.40 2.25 1.54 10.00 1.06 0.78 6.90
GAERNN模型与不同基准模型的误差对比如图10所示。从该图可以看出，GAERNN模型的预测效果明显优于其他基准模型。以2020年7月的预测任务为例，GAERNN模型的MAPE值为10%，较MLP、GCN、CNN-LSTN以及CNN-GRU模型分别降低了4.08%、3.00%、2.70%以及1.44%，说明GAERNN模型捕获时空依赖关系的能力明显优于其他基准模型。
图10 GAERNN与基准模型的盗窃犯罪预测误差对比

Fig. 10 Comparison of theft prediction error between GAERNN and reference model

3.4 GAERNN模型子模块有效性评估

本文对GAERNN模型的子模块也进行了有效性评估，操作方法与控制变量法类似，目的是证明模型中的各个子模块对于模型预测能力具有提升作用。分别使用MLP和LSTM替换GAE和GRU，结果如表4所示。由表4可知，在使用LSTM替换GRU之后，各月份预测误差明显上升，相比GAERNN模型，GAE-LSTM在1、5、7以及11月的MAPE值分别上升了2.15%、10.07%、1.92%以及2.54%，月份平均RMSE、MSE和MAPE值分别上升了1.24、0.64以及4.17%。说明相较于LSTM模型，GRU模型能够更有效的捕获犯罪案件的时间特征，得到更加精确的时空预测结果；对于使用MLP替换GAE的情况，其1月和5月的MAPE值较GAE-LSTM分别降低了0.42%和0.06%，但相较于GAERNN模型， MLP-GRU月份平均RMSE、MSE以及MAPE值仍然上升了0.86、0.68以及4.41%，表明该变体模型的预测误差仍然较大。
表4 GAERNN及其变体模型误差统计

Tab. 4 Error statistics for GAERNN and its variant models

方法 1月 5月 7月 11月
RMSE MSE MAPE/% RMSE MSE MAPE/% RMSE MSE MAPE/% RMSE MSE MAPE/%
MLP-GRU 1.64 1.15 9.43 3.49 2.13 14.41 2.55 2.13 12.69 1.30 1.08 10.11
GAE-LSTM 2.07 1.27 9.85 4.08 2.30 14.47 2.61 1.67 11.92 1.77 1.07 9.44
GAERNN 1.40 0.95 7.70 0.83 0.50 4.40 2.25 1.54 10.00 1.06 0.78 6.90
图11为MLP-GRU与GAE-LSTM这2个变体模型与GAERNN模型预测结果的误差对比图，从图11可以看出， MLP-GRU和GAE-LSTM这2种变体模型在不同月份上的RMSE和MAPE值均高于GAERNN模型。可见，当使用MLP、LSTM分别替换GAE、GRU后，得到的变体模型预测效果较差，说明本文所提模型的子模块（GAE与GRU）在犯罪预测任务中具有十分重要的作用，二者联合训练构成的GAERNN模型能够很好地完成犯罪预测任务并取得满意的结果。
图11 盗窃犯罪预测变体模型误差对比

Fig. 11 Comparison of errors in prediction variants of theft crime models

4 讨论

4.1 基于格网尺度的GAERNN模型预测性能验证

为实现更加精细的犯罪预测，通常需要将小范围的辖区进一步以格网为分析单元进行细分。本文已证实GAERNN模型能够很好地处理街区等不规则结构单元。为探究GAERNN模型在格网尺度的预测性能，本文将研究区域划分为3 km×3 km的格网，基于格网尺度的盗窃犯罪预测结果如图12所示，通过对比实际数据分布以及不同基准模型的预测结果，发现GAERNN模型在格网尺度层面仍然具有最好的预测性能，能够精准地预测出不同月份盗窃犯罪案件的分布情况。进一步将不同模型与GAERNN模型在格网尺度的预测误差进行对比 （图13），从图中可以看出，相较于其他基准模型，GAERNN模型在处理时空关系方面优势明显，模型预测精度较高，能够达到更好的预测效果。
图12 基于格网尺度的实际盗窃犯罪分布与各模型预测分布

Fig. 12 The actual distribution of theft and the predicted distribution of each model based on grid scale

图13 格网尺度下GAERNN与基准模型的盗窃犯罪预测误差对比

Fig. 13 Comparison of theft prediction error between GAERNN and reference model based on grid scale

然而，警务部门往往希望实现小尺度上的犯罪时空预测，以便更精准详细地部署警务工作。本文采用的街区尺度以及3 km × 3km格网尺度对于实际警务工作来说仍然偏大。受当前数据获取条件所限，本文收集的犯罪数据在较小时空尺度上由于犯罪案件分布稀疏，导致犯罪时空分布特征难以识别和提取。

4.2 GAERNN模型的不确定性分析

本文在盗窃犯罪的特征变量选取方面主要考虑了空间特征的影响，并且选取的社会、环境等外部特征均为静态特征。然而，盗窃犯罪往往具有一定的时空交互关系，盗窃犯罪行为也并非静态，因此，未来研究中应加入相关时序特征变量（如工作日、休息日、节假日等），并结合动态人流量等动态数据，以期实现更为精准的犯罪时空预测。此外，本文将所选特征变量视为同等重要，未来工作中若能量化这些特征变量对于盗窃犯罪的影响程度，则可能进一步提高模型的预测性能。再者，对于GAERNN模型，如若研究区域内的节点分布过于密集，可能会产生更多邻域结果相似的节点，从而在一定程度上影响了模型的判别能力，后续研究将对此进行优化。

5 结论

城市化进程的加快使得犯罪问题日益突出，准确、有效地预测犯罪时空分布对于保障城市的健康发展以及人民群众的生命财产安全具有极其重要的意义。
本文基于兰州市盗窃犯罪历史数据、人口数据以及娱乐服务等POI数据，提出融合图自编码器与GRU的图自编码循环神经网络（GAERNN）模型，对兰州市主城区未来的盗窃犯罪行为进行时空分布预测，并通过实验验证了模型在城市盗窃犯罪预测中的可行性和有效性。相较于以往的犯罪预测模型，GAERNN模型不仅能够处理研究区域中复杂的拓扑结构，同时还考虑了盗窃犯罪案件的时间和空间特征，预测效果优于仅考虑时间或空间某一方面的模型。实验表明：
（1）相较于其他基准模型，GAERNN模型的可视化预测结果与真实数据集的时空分布最相符合。
（2）GAERNN模型在不同月份的RMSE、MSE以及MAPE的值均低于其他基准模型，且捕获时空依赖关系的能力明显优于其他基准模型，相比预测性能较差的MLP， GAERNN模型各月份RMSE值分别降低了1.02、3.58、1.29以及0.45，表明该模型具有更好的时空预测能力。
（3）GAERNN模型的预测误差显著低于其变体模型，相比GAE-LSTM，GAERNN模型在1、5、7以及11月的MAPE值分别降低了2.15%、10.07%、1.92%以及2.54%；相比MLP-GRU，GAERNN模型月份平均RMSE、MSE和MAPE值分别降低了0.86、0.68和4.41%，表明GAERNN模型中的各个子模块对于模型预测能力具有提升作用。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Cohen L E, Cantor D. The determinants of larceny: An empirical and theoretical study[J]. Journal of Research in Crime and Delinquency, 1980, 17(2):140-159. DOI:10.1177/002242788001700202

DOI

[2]
Hu J. M. A hybrid GCN and LSTM structure based on attention mechanism for crime prediction[J]. CONVERTER, 2021:328-338. DOI:10.17762/converter.132

DOI

[3]
Jin G Y, Wang Q, Zhu C C, et al. Addressing crime situation forecasting task with temporal graph convolutional neural network approach[C]// 2020 12th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA). IEEE,: 474-478. DOI:10.1109/ICMTMA50254.2020.00108

DOI

[4]
Chainey S, Ratcliffe J. GIS and Crime Mapping[M]. John Wiley & Sons, 2013.

[5]
Kalinic M, Krisp J M. Kernel density estimation (KDE) vs. hot-spot analysis-detecting criminal hot spots in the City of San Francisco[C]// Proceeding of the 21 Conference on Geo-Information Science. 2018.

[6]
Santana-Arias R, George T S, Padrón-Salas A, et al. The relationship between density of drug outlets, crime hot spots and family factors on the consumption of drugs and delinquent behaviour of male adolescent Mexican students[J]. Social Science & Medicine, 2021, 279: 113985.

DOI

[7]
Townsley M, Homel R, Chaseling J. Infectious burglaries. A test of the near repeat hypothesis[J]. British Journal of Criminology, 2003, 43(3):615-633.

DOI

[8]
徐冲, 柳林, 周素红. 基于临近相似性考虑的犯罪热点密度图预测准确性比较——以DP半岛街头抢劫犯罪为例[J]. 地理科学, 2016, 36(1):55-62.

DOI

[Xu C, Liu L, Zhou SH. The comparison of predictive accuracy of crime hotspot density maps with the consideration of the near similarity: A case study of robberies at DP peninsula.[J] Scientia Geographica Sinica, 2016, 36(1):55-62.] DOI:10.13249/j.cnki.sgs.2016.01.007

DOI

[9]
Caplan J M, Kennedy L W. Risk terrain modeling manual: Theoretical framework and technical steps of spatial risk assessment for crime analysis[M]. Rutgers Center on Public Security, 2010.

[10]
Rummens A, Hardyns W. Comparison of near-repeat, machine learning and risk terrain modeling for making spatiotemporal predictions of crime[J]. Applied Spatial Analysis and Policy, 2020, 13(4):1035-1053. DOI:10.1007/s12061-020-09339-2

DOI

[11]
Chainey S, Tompson L, Uhlig S. The utility of hotspot mapping for predicting spatial patterns of crime[J]. Security Journal, 2008, 21(1):4-28. DOI:10.1057/palgrave.sj.8350066

DOI

[12]
Ratcliffe J H, Rengert G F. Near-repeat patterns in Philadelphia shootings[J]. Security Journal, 2008, 21(1/2):58-76. DOI:10.1057/palgrave.sj.8350068

DOI

[13]
Mohler G O, Short M B, Brantingham P J, et al. Self-exciting point process modeling of crime[J]. Journal of the American Statistical Association, 2011, 106(493):100-108. DOI:10.1198/jasa.2011.ap09546

DOI

[14]
Wheeler A P, Steenbeek W. Mapping the risk terrain for crime using machine learning[J]. Journal of Quantitative Criminology, 2021, 37(2):445-480. DOI:10.1007/s10940-020-09457-7

DOI

[15]
张宁, 王大为. 基于风险地形建模的毒品犯罪风险评估和警务预测[J]. 地理科学进展, 2018, 37(8):1131-1139.

DOI

[ Zhang N, Wang D W. Drug-related crime risk assessment and predictive policing based on risk terrain modeling[J]. Progress in Geography, 2018, 37(8):1131-1139.]

DOI

[16]
Zhang X, Liu L, Xiao L Z, et al. Comparison of machine learning algorithms for predicting crime hotspots[J]. IEEE Access, 8:181302-181310. DOI:10.1109/ACCESS.2020.3028420

DOI

[17]
柳林, 纪佳楷, 宋广文, 等. 基于犯罪空间分异和建成环境的公共场所侵财犯罪热点预测[J]. 地球信息科学学报, 2019, 21(11):1655-1668.

DOI

[ Liu L, Ji J K, Song G W, et al. Hotspot prediction of public property crime based on spatial differentiation of crime and built environment[J]. Journal of Geo-information Science, 2019, 21(11):1655-1668.]

[18]
Alwee R, Shamsuddin S M, Sallehuddin R. Modeling of violent crime rates with economic indicators using hybridization of grey relational analysis and support vector regression[J]. Jurnal Teknologi, 2015, 76(1). DOI:10.11113/jt.v76.3899

DOI

[19]
Aldossari B S, Alqahtani F M, Alshahrani N S, et al. A comparative study of decision tree and naive Bayes machine learning model for crime category prediction in Chicago[C]// Proceedings of 2020 the 6th International Conference on Computing and Data Engineering. New York, NY, USA: ACM, 2020:34-38. DOI:10.1145/3379247.3379279

DOI

[20]
Xia Z Y, Stewart K, Fan J C. Incorporating space and time into random forest models for analyzing geospatial patterns of drug-related crime incidents in a major US metropolitan area[J]. Computers, Environment and Urban Systems, 2021, 87:101599. DOI:10.1016/j.compenvurbsys.2021.101599

DOI

[21]
Zhang X, et al. Interpretable machine learning models for crime prediction[J]. Computers, Environment and Urban Systems, 2022, 94:101789. DOI:10.1016/j.compenvurbsys.2022.101789

DOI

[22]
Marzan C S, Baculo M J C, de Dios Bulos R, et al. Time series analysis and crime pattern forecasting of city crime data[C]// ICACS '17:Proceedings of the International Conference on Algorithms, Computing and Systems. 2017:113-118. DOI:10.1145/3127942.3127959

DOI

[23]
Andersson V O, Birck M A F, Araujo R M. Investigating Crime Rate Prediction Using Street-Level Images and Siamese Convolutional Neural Networks[C]// Latin American Workshop on Computational Neuroscience. Springer, Cham: Springer, 2017:81-93. DOI:10.1007/978-3-319-71011-2_7

DOI

[24]
Singh P. Time series forecasting on crime data in amsterdam for a software company[D]. 2018.

[25]
Muthamizharasan M, Ponnusamy R. Forecasting crime event rate with a CNN-LSTM model[M]// Innovative Data Communication Technologies and Application. Springer, Singapore, 2022:461-470.

[26]
John J, Varkey M S, M S. Multi-class text classification and publication of crime data from online news sources[C]// 2021 8th International Conference on Smart Computing and Communications (ICSCC). IEEE, 2021:64-63. DOI:10.1109/ICSCC51209.2021.9528127

DOI

[27]
韩昕格. LSTM与ST-GCN融合的城市盗窃犯罪预测方法[D]. 北京: 中国人民公安大学, 2021.

[Han X G. Prediction method of theft crimes in urban: An integrated model of LSTM and ST-GCN[D]. Beijing: Chinese People's Public Security University, 2021.] DOI:10.27634/d.cnki.gzrgu.2021.000042

DOI

[28]
Zhu Q, et al. Static or dynamic? Characterize and forecast the evolution of urban crime distribution[J]. Expert Systems With Applications, 2022, 190:116115. DOI:10.1016/j.eswa.2021.116115

DOI

[29]
柳林, 刘文娟, 廖薇薇, 等. 基于随机森林和时空核密度方法的不同周期犯罪热点预测对比[J]. 地理科学进展, 2018, 37(6):761-771.

DOI

[Liu L, Liu W J, Liao W W, et al. Comparison of random forest algorithm and space time kernel density mapping for crime hotspot prediction[J]. Progress in Geography, 2018, 37(6):761-771.] DOI:10.18306/dlkxjz.2018.06.003

DOI

[30]
Song G W, Bernasco W, Liu L, et al. Crime feeds on legal activities: Daily mobility flows help to explain thieves’ target location choices[J]. Journal of Quantitative Criminology, 2019, 35(4):831-854. DOI:10.1007/s10940-019-09406-z

DOI

[31]
Brantingham P, Brantingham P. Crime pattern theory[M]// Environmental criminology and crime analysis. Willan, 2013:100-116.

[32]
柳林, 梁斯毅, 宋广文. 基于潜在受害者动态时空分布的街面接触型犯罪研究[J]. 地球信息科学学报, 2020, 22(4):887-897.

DOI

[ Liu L, Liang S Y, Song G W. Explaining street contact crime based on dynamic spatio-temporal distribution of potential targets[J]. Journal of Geo-Information Science, 2020, 22(4):887-897.]

[33]
Madensen T D. Bar management and crime: Toward a dynamic theory of place management and crime hotspots[D]. University of Cincinnati, 2007.

[34]
兰州市统计局兰州市第七次全国人口普查领导小组办公室. 兰州市第七次全国人口普查公报[1]——2021年5月27日[N]. 兰州日报, 2021-05-28(2).

[ Lanzhou City Bureau of Statistics Lanzhou City Seventh National Census Leading Group Office. Lanzhou City Seventh National Census Bulletin[1]——27 May 2021[N]. Lanzhou Daily, 2021-05-28( 2).] DOI:10.28556/n.cnki.nlzrb.2021.001834

DOI

[35]
李萍. 城市复杂路网瓶颈路段路径优化问题研究[D]. 兰州: 兰州交通大学, 2019.

[ Li P. Research on path optimization problem of bottleneck section of urban complex road network[D]. Lanzhou Jiaotong University, 2019.]

[36]
姜昀呈, 孙立坚, 王涛涛, 等. 兰州市中心城区犯罪分布与城市环境的关系[J]. 测绘科学, 2021, 46(5):167-174.

[Jiang Y C, Sun L J, Wang T T, et al. The coupling relationship between crime distribution and urban environment in Lanzhou City center[J]. Science of Surveying and Mapping, 2021, 46(5):167-174.] DOI:10.16251/j.cnki.1009-2307.2021.05.023

DOI

[37]
祝石厚. 基于卡尔曼滤波算法的动态谐波状态估计技术研究[D]. 重庆: 重庆大学, 2008.

[ Zhu S H. Study on dynamic harmonic state estimation technology based on Kalman filter[D]. Chongqing: Chongqing University, 2008.]

[38]
李芳, 戚振东. 超声波流量测量时差改进卡尔曼滤波[J]. 科技信息, 2011(5):484-485.

[ Li F, Qi Z D. Ultrasonic flow measurement time difference improvement Kalman filtering[J]. Science ＆Technology Information, 2011(5):484-485.]

[39]
Kipf T N, Welling M. Variational graph auto-encoders[EB/OL]. 2016: arXiv: 1611.07308. DOI: https://arxiv.org/abs/1611.07308

DOI

[40]
马佳欣. 基于深度学习的人脸正面图像合成方法的研究与实现[D]. 北京: 北京邮电大学, 2019.

[ Ma J X. Research and implementation of frontal face image synthesis based on deep learning method[D]. Beijing: Beijing University of Posts and Telecommunications, 2019.]

[41]
Wu Q W, Xia J F, Ni J C, et al. GAERF: predicting lncRNA-disease associations by graph auto-encoder and random forest[J]. Briefings in Bioinformatics, 2021, 22(5):bbaa391. DOI:10.1093/bib/bbaa391

DOI

[42]
许秀锋, 蒲家坤, 周爱国, 等. 基于门控循环单元的车载控制器局域网络总线入侵检测方法[J]. 科学技术与工程, 2021, 21(16):6786-6793.

[ Xu X F, Pu J K, Zhou A G, et al. Gated recurrent unit-based intrusion detection method for in-vehicle controller area network bus[J]. Science Technology and Engineering, 2021, 21(16):6786-6793.]

[43]
陈修凯, 陆志华, 周宇. 基于卷积编解码器和门控循环单元的语音分离算法[J]. 计算机应用, 2020, 40(7):2137-2141.

DOI

[ Chen X K, Lu Z H, Zhou Y. Speech separation algorithm based on convolutional encoder decoder and gated recurrent unit[J]. Journal of Computer Applications, 2020, 40(7):2137-2141.]

DOI

[44]
周满国, 黄艳国, 段锦锋. 基于GRU-RF模型的太阳辐照度短时预测[J]. 太阳能学报, 2022, 43(7):166-173.

DOI

[Zhou M G, Huang Y G, Duan J F. Short-term prediction of soral irradiance based on gru-rf model[J]. Acta Energiae Solaris Sinica, 2022, 43(7):166-173.] DOI:10.19912/j.0254-0096.tynxb.2020-1091

DOI

Options
文章导航

/

〈 〉