EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 10: 1986 - 1999

DOI: https://doi.org/10.12082/dqxxkx.2023.230299

地球信息科学理论与方法

顾及道路权重的图卷积犯罪时空预测模型

  • 贺日兴 , 1, 2 ,
  • 唐宗棣 1, 2 ,
  • 姜超 3 ,
  • 林艳 4 ,
  • 陆宇梅 1, 2 ,
  • 李欣然 1, 2 ,
  • 龙伟 1, 2 ,
  • 邓悦 , 1, 2, *
展开
  • 1.首都师范大学资源环境与旅游学院，北京 100048
  • 2.首都师范大学三维数据获取与应用教育部重点实验室，北京 100048
  • 3.首都经济贸易大学城市经济与公共管理学院，北京 100070
  • 4.中国人民公安大学信息网络安全学院，北京 100038
* 邓悦（1994—），女，新疆哈巴河人，博士，讲师，主要研究方向为空间数据挖掘、空间分析。 E-mail:

贺日兴（1972—），男，江西安福人，博士，教授，博导，主要从事犯罪地理和警用地理信息技术等研究。E-mail:

收稿日期: 2023-05-31

  修回日期: 2023-08-02

  网络出版日期: 2023-09-22

基金资助

国家重点研发计划项目(2022YFB3903602)

公安部科技强警基础工作专项(2021JC35)

国家自然科学基金青年项目(42001159)

国家自然科学基金项目(41971367)

收起

A Graph Convolution-based Spatio-temporal Crime Prediction Model Considering Road Weights

  • HE Rixing , 1, 2 ,
  • TANG Zongdi 1, 2 ,
  • JIANG Chao 3 ,
  • LIN Yan 4 ,
  • LU Yumei 1, 2 ,
  • LI Xinran 1, 2 ,
  • LONG Wei 1, 2 ,
  • DENG Yue , 1, 2, *
Expand
  • 1. College of Resources Environment and Tourism, Capital Normal University, Beijing 100048, China
  • 2. Key Laboratory of 3D Information Acquisition and Application, MOE, Capital Normal University, Beijing 100048, China
  • 3. College of Urban Economics and Public Administration, Capital University of Economics and Business, Beijing 100070, China
  • 4. Policing Information Technology and Network Security College People's Public Security University of China, Beijing 100038, China
* DENG Yue, E-mail:

Received date: 2023-05-31

  Revised date: 2023-08-02

  Online published: 2023-09-22

Supported by

National Key Research and Development Program(2022YFB3903602)

Special Projects of Ministry of Public Security in Strengthening Basic Police Work(2021JC35)

Youth Fund of the National Natural Science Foundation of China(42001159)

National Natural Science Foundation of China(41971367)

Fold

摘要

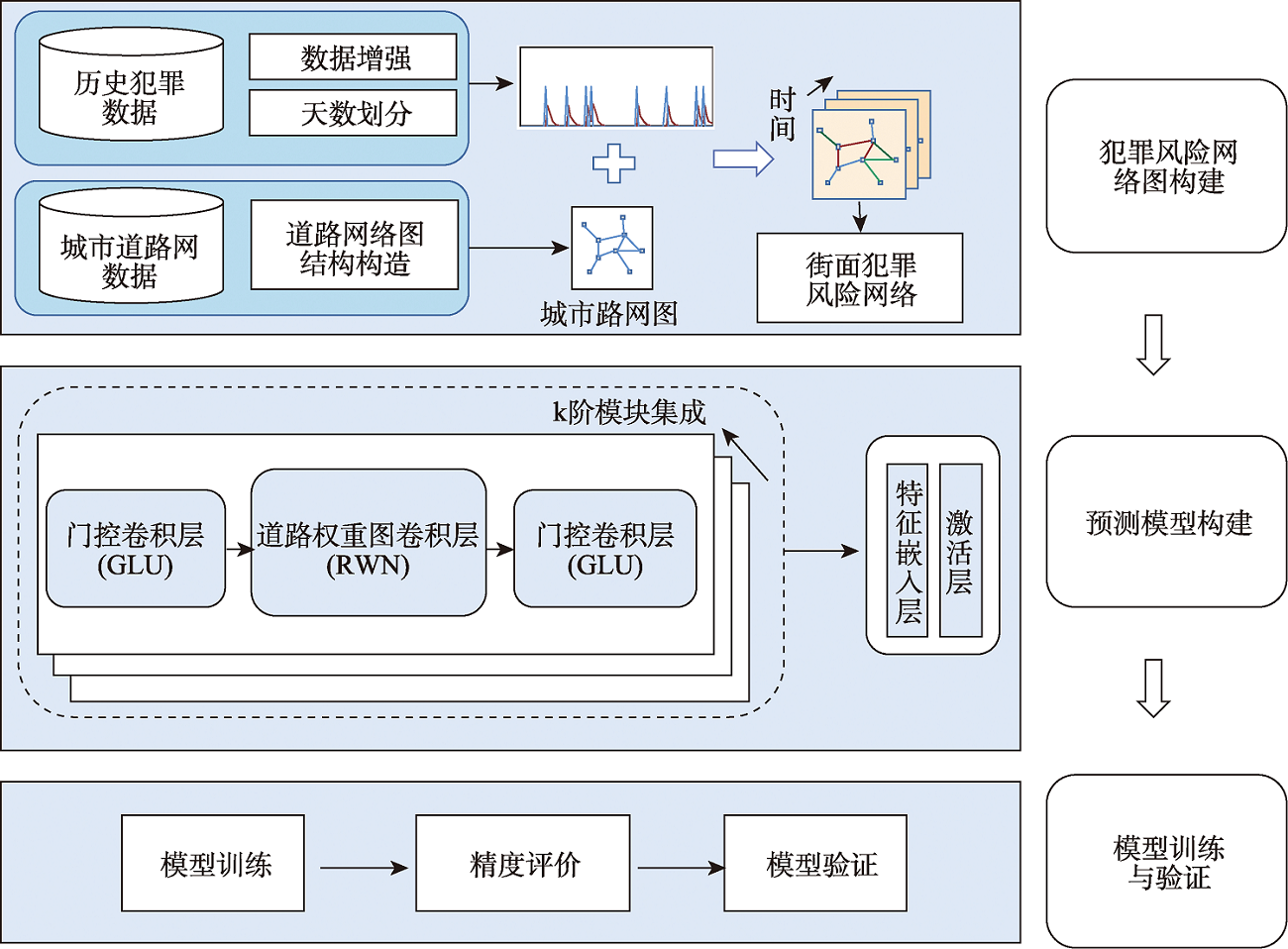
传统的犯罪地理和犯罪时空预测方法主要是以警务辖区或格网为基本单元，分析结果不利于指导精细化的巡防警力规划部署。基于深度学习的图神经网络方法可以自然地与微观尺度下的路网拓扑结构相结合，实现道路尺度下的精细犯罪预测，但现有方法鲜有考虑道路权重对预测结果的影响。本文通过引入道路通达度和距离衰减因子，构建了一种顾及道路权重的图卷积犯罪时空预测模型（Road Weighted Spatio-Temporal Graph Convolutional Network，RW-STGCN），并利用芝加哥2016—2017年街面盗窃犯罪数据对模型进行评估。结果表明： ① 与未考虑道路权重的时空图卷积模型相比，RW-STGCN模型命中率在不同的路网覆盖比例下（1%、5%、10%、20%）的提升均在6.5%以上，且随着覆盖比例的下降，模型命中率的提升更为显著，最大提升超过了50%； ② 模型消融性实验表明，同时考虑2种道路权重的模型比仅考虑距离衰减权重或道路通达度权重单个因子的模型预测性能提升更为明显，命中率最大提升了12.9%。本研究构建的RW-STGCN模型有助于街面类犯罪预测，可为警务部门基于路网进行科学巡逻防控规划与警力部署提供辅助决策支持，此外还可用于以道路作为分析单元的城市计算问题研究。

关键词： 街面犯罪; 时空预测; 图卷积神经网络; 道路权重; 空间句法; 犯罪预测; 预测性警务

本文引用格式

贺日兴 , 唐宗棣 , 姜超 , 林艳 , 陆宇梅 , 李欣然 , 龙伟 , 邓悦 . 顾及道路权重的图卷积犯罪时空预测模型[J]. 地球信息科学学报, 2023 , 25(10) : 1986 -1999 . DOI: 10.12082/dqxxkx.2023.230299

Abstract

Spatiotemporal crime prediction often employs quantitative techniques such as Geographic Information Systems (GIS), geo-statistics, and big data analysis to predict the time and risk area (or location) of crime events that are more likely to occur in the future. In the era of big data, how to dynamically optimize the deployment of limited police forces and successfully improve the effectiveness of crime prevention based on data-driven crime predictions is a research focus in the field of global predictive policing. It is also a main practical direction for law enforcement agencies worldwide to implement modern proactive policing models. Traditional crime geography and spatiotemporal crime prediction methods mainly use police precincts or grids as the basic spatial analysis unit, and the analysis results are not conducive to guiding refined patrol force planning and deployment. The graph neural network based on deep learning can be combined with the topological structure of the road network at the micro scale, enabling precise crime prediction at the street scale. However, existing approaches rarely consider the impact of road weights in model prediction. In this paper, a Road Weighted Spatiotemporal Graph Convolutional Network (RW-STGCN) is constructed for street crime prediction by introducing road network accessibility and distance attenuation factors, and the model is evaluated using street theft crime data of Chicago. The results show that: (1) Compared to the spatiotemporal graph convolutional networks without considering road weights, the hit rate of the RW-STGCN increases by more than 6.5% across various road network coverage ratios (1%, 5%, 10%, and 20%), and the increase becomes more significant as the coverage ratio decreases, with a maximum increase exceeding 50%. This indicates the effectiveness and superiority of the RW-STGCN for smaller units; (2) Model ablation experiments show that the hit rate of the RW-STGCN considering road weights increases by 13.5% compared to the model result without considering road weights, and the model considering both road weights has a more significant improvement in prediction performance than the model considering only a single factor of distance attenuation weight or road network access weight, with a maximum increase of 12.9% in hit rate. This suggests that deep learning methods combined with geographic features can effectively improve the accuracy of crime prediction. The RW-STGCN is helpful for street crime prediction and can provide auxiliary decision support for law enforcement agencies to conduct scientific patrol planning and police force deployment based on road networks. In addition, it is also useful for the study of road-related urban computing problems.

Key words： street crime; spatialtemporal prediction; graph convolutional network; road weights; spatial syntax; crime prediction; predictive policing

1 引言

犯罪活动影响社会和谐稳定和人民群众安全感，并会引发系列社会问题，是仅次于灾害与战争的世界第三大危害[1]。随着当今城市化进程加快，城市犯罪问题凸显，并呈现多发性、智能性、组织性、高流窜性等特征，对警务部门的社会治安防控和犯罪打击提出了严峻挑战。随着大数据时代的到来，如何在有限的警力资源条件下，基于数据驱动的犯罪时空预测技术来动态优化警力部署，以有效提升犯罪防控与打击效率，是当前欧美国家预测性警务领域的研究热点和主要实践方向[2]，也将是我国智慧警务建设所追求的重要目标之一。
犯罪时空预测运用GIS、地理统计、大数据分析等定量技术，对历史犯罪及其相关数据进行分析和建模，通过识别历史犯罪事件隐含的时空分布规律及模式，来有效预测未来犯罪事件可能发生的时间及风险区域（或地点）[2]。在计算机技术的不断发展与推动下，犯罪预测方法从早期的区域分级设色（如四色预警[3]）、格网专题统计[4]、核密度估计[5]等时空统计方法来确定犯罪热点区域[3,6]，向基于地理统计模型[7-8]、大数据分析[9]及机器学习[10]等方法发展[6,11]。空间分析单元的尺度也呈现出由大到小，由宏观（如行政区域[12]、警务辖区[13]、社区[14]）向微观（如网格[15⇓⇓-18]、路段[19-20]）逐步发展的趋势，但主要仍以规则格网为主[2]。由于警务部门的日常巡逻路线主要基于路网来规划与实施，基于人口普查区或规则格网的预测结果不利于警务巡防工作的组织实施。因此，近年来部分学者开始关注道路尺度下的犯罪预测[21⇓⇓-24]。因犯罪空间分布的不均匀性容易导致部分道路单元的犯罪数据十分稀疏，产生零膨胀的问题[21,25-26]，传统的地统计方法在以路网作为空间分析单元时预测效果并不佳。
近年来，随着人工智能应用的兴起，基于深度学习的犯罪时空预测成为新的研究热点[2]。采用深度学习技术可以在微观尺度下有效捕捉传统空间统计方法难以拟合的时空特征，尤其是基于图的深度学习模型可以方便地和城市路网拓扑结构建立映射关系，并有效处理以道路为基本单元的城市计算问题，近年来在道路交通、人口流动等研究中得到广泛应用[27-28]。如Zhao[29]和Yu[27]等通过考虑时间特征的影响分别提出了时间图卷积网络（Temporal Graph Convolutional Network，TGCN）和时空图卷积网络（Spatio-Temporal Graph Convolutional Networks，STGCN）来提取交通数据的时空特征，并取得了不错的效果。但研究[30]也发现常规的图卷积（Graph Convolutional Network, GCN）仍存在一定的局限性，许多研究者先后提出了一些改进模型。如Velickovic等[30]提出了图注意力网络（Graph Attention Networks，GAT），通过分配不同节点间连接的权重，以加强对节点间相关性的考虑；Guo等[31]提出的混合注意力时空图卷积（Attention Based Spatial-Temporal Graph Convolutional Networks，ASTGCN）在城市交通预测中得到了比STGCN更好的预测结果；William等[32]提出图聚合网络（Graph SAmple and aggreGatE，GraphSAGE），采用归纳式学习对邻节点进行采样并聚合，减轻了GCN模型在复杂路网中容易出现的过拟合问题。近年来，Zhang等[26]尝试将图卷积模型引入到对街头盗窃、袭击、入室盗窃等时空预测研究和应用当中，该模型在10%和20%路网覆盖率上的平均命中率分别比最先进的基线模型提高了12%和25%。由于犯罪风险的传递不仅与道路节点的邻接关系密切相关，同时还受路段间距离以及道路通达度等因素的影响，且犯罪活动会沿着路网进行传播[33-34]，道路之间距离越远，影响越弱。同时，城市道路的建成环境和社会环境存在异质性，高通达度的道路段会吸引更多的公共设施分布和人流的聚集，高流动的人群和陌生人的涌入会降低社会监管能力，容易产生街面盗窃犯罪的机会，即通达度高的道路段和盗窃犯罪总是呈现显著的正相关[20,35-36]。而现有犯罪时空预测研究在基于路网建模时并未考虑上述道路权重的影响。为此，本研究对传统时空图卷积模型进行了改进和优化，提出了一种顾及道路权重的图卷积犯罪时空预测模型（Road Weighted Spatio-Temporal Graph Convolutional Network，RW-STGCN）。该模型一方面将犯罪风险分解为固定的背景特征和传递风险的时空特征，在避免模型过拟合的同时，又有效缓解了模型零膨胀的问题；另一方面将利用空间句法获得的道路通达度以及考虑路段间影响获得的道路距离权重因子纳入图卷积模型中，有效提升了犯罪时空预测精度。

2 研究方法

本文的研究框架如图1所示，主要包括犯罪风险网络构建、预测模型构建、模型训练与验证三个部分。首先将犯罪数据以天为单位划分，经过数据处理后映射到最近的城市道路段，并结合时间特征，构建道路网络的时空图结构；然后，设计一种顾及道路权重的图卷积层（Road Weighted Network，RWN）提取犯罪活动的空间特征，同时采用门控卷积层[37]（Gated Linear Unit，GLU）提取犯罪活动的时间特征，以提升模型预测性能；最后，使用均方差损失函数评估预测值和真实值之间的差距，经过反向传播对超参数不断调整，利用精度评价指标与多个基线模型进行比较，分析模型对于时空特征提取能力的敏感性，验证并评估不同道路权重对模型预测结果的影响。
图1 城市街面类犯罪预测研究框架

Fig. 1 Research framework for urban street crime prediction

2.1 研究区概况及数据来源

本文的研究区位于芝加哥南部，由12个辖区组成，面积为95.8 km2，主要包含商业区、工业区及居民区等。研究区人口组成复杂，文化特征多样，人口密度高，差异性较大的社区环境使得该研究区成为芝加哥市街面盗窃犯罪的高发区域之一，具体区位如图2（a）所示。区内街道路网发达，街道设施较为完善和成熟，街面盗窃犯罪的时空特征较为稳定和显著，因此选择该地区作为研究区进行实验具有一定代表性。
图2 研究区位置及区内路网与犯罪热点分布

Fig. 2 Location of the study area and distribution of its road networks and crime hotspots

研究数据主要包括以下2种：① 路网数据，来源于OSM（Open street Map）网站（https://www.openstreetmap.org），经过数据清洗后共包含街道 4 927条，具体分布如图2（b）所示；② 历史街面盗窃犯罪数据，来源于芝加哥市开放数据门户网站（https://data.cityofchicago.org），关键字段包括案发时间、经纬度等，其时间跨度为2016年1月1日至2017年12月31日（共计731 d），经数据清洗后共包含13 316起案件，其分布热力图如2（c）所示。

2.2 街面犯罪风险网络图构建

为了开展基于图的街面犯罪时空预测，首先要对数据进行预处理，主要包括以下2个核心步骤：
（1）城市路网图构造。对已有相关研究统计分析表明，大多数警务部门通常以天为单位来分配与执行巡逻任务[26]，以天为单位的犯罪预测可能更有利于预测性警务的实施[2]，因此，本研究将最小时间单元设置为1 d；本研究的最小空间单元为道路段，将历史犯罪数据映射至最近的道路段，其聚集的历史犯罪数量值作为该道路段的犯罪风险特征。同时将城市道路网络定义为G（V，E，W）的图集合，其中V为图结构中道路节点集合；E代表节点邻接关系表eij，邻接关系表用来表示道路段i和道路段j的相交关系；W为道路段i和道路段j之间联系的权重wij，在2.3节模型构建部分将详细阐述路段节点权重的设计。
（2）历史犯罪数据信息增强。为了解决微观时空单元下易出现的数据零膨胀问题，采用简单指数平滑（Simple Exponential Smoothing，SES）[26]对映射到每条道路上的犯罪风险数据进行增强，如图3所示。SES是一种经验方法，用于平滑时间序列数据，它使用指数加权函数为过去的观测值分配逐渐递减的权重。随着时间的推移，先前观测值的影响逐渐减弱。假设历史犯罪数据的时间序列是从t时刻开始，那么指数平滑的公式为：
S E S t = a · y t - 1 + 1 - a S t - 1
图3 单条道路的信息增强示例

Fig. 3 Example of information enhancement for a single road

式中: S t - 1为t-1时刻的特征值； y t - 1为t-1时刻的实际输入值； S E S t表示t时刻的数据增强后特征的输出； a为平滑因子参数，其范围是0~1，其值越大则具有更强的波动性。

2.3 预测模型构建

在深度学习方法中，图卷积模型由于可以处理非结构化数据，因此在解决以拓扑图为数据结构的城市道路相关的预测问题中具有显著优势。传统的图卷积一般是通过邻节点之间的关系传递信息，但现有犯罪预测研究鲜有考虑真实的道路特征（距离、通达度）对结果的影响。本文引入道路通达度和距离衰减因子，提出了一种顾及道路权重的图卷积犯罪时空预测模型（Road Weighted Spatio-Temporal Graph Convolutional Network，RW-STGCN）。该模型将犯罪风险的权重分解为特征背景权重和道路权重以减少零膨胀问题带来的影响，并在道路权重的计算中结合道路通达度和距离衰减因子，加权求解犯罪风险的传递值，以有效提升模型的空间特征提取能力。
RW-STGCN模型由门控卷积层、道路权重图卷积层和模型集成设计3部分组成。一个道路权重图卷积层连接了2个门控卷积层组成一个基本单元。其中，门控卷积层能够快速提取犯罪时间特征，而道路权重图卷积层则优化了犯罪空间信息的传递过程，因此犯罪风险数据的时空特征能够快速传播并得以提取。同时，为了提取更深层的非线性时空特征，模型采用了集成设计来堆叠集合多个基本单元，通过特征的嵌入合并后输出下一个时刻的预测结果。

2.3.1 门控卷积层

为避免采用递归神经网络[38]（Recurrent Neural Network，RNN）、长短期记忆网络[39]（Long Short Term Memory，LSTM）等常用模型在提取长时序犯罪特征时易出现梯度爆炸、消失以及训练时间过长等问题，本研究采用门控卷积模块[37]，通过一维卷积和并行计算以提高提取犯罪时间特征的效率（图4）。GLU包含一个一维卷积，卷积核为 Γ ∈ R K t × C i × 2 C o，其中 K t为卷积核的宽度， C i为输入的通道数， 2 C o为卷积核的数量。GLU的计算过程如下：
Γ * τ X = P ⊙ σ Q ∈ R M - K t + 1 × C o
σ Q = 1 1 + e - Q
图4 GLU模型结构

Fig. 4 Structure of GLU

式中：输入的犯罪风险值 X划分为相同的两部分x1、x2，分别经过一维卷积后得到P和Q； ⊙是指元素对应相乘的哈达玛积（Hadamard product）； σ Q是sigmoid函数，可以控制输入的犯罪时间特征在该层的信息流动，并利用其门控机制，控制了时间序列中的特定犯罪特征传入下一层； M是输入的时间序列长度。GLU中隐藏层使用激活函数ReLU（式(4)），使得反向传播中梯度下降速度更快，更容易使模型收敛，最终得到犯罪活动在时间维度中的特征变化规律。在多次堆叠后，得到门控卷积层的数学公式（式(5)）：
R e L U X = m a x ( 0 , X )
t n X n = R e L U Γ n × τ X n
式中：n是门控卷积模块的数量; ReLU代表激活函数，通过取得大于0时输入值 X的最大值对模块进行激活， t n用于提取时间特征的输出值。

2.3.2 道路权重图卷积层

以往研究[27⇓-29]主要侧重于利用图神经网络模型提取图结构的空间特征。GCN等模型为了减少训练的复杂度，采用了参数共享的思想，即在每个节点采用了相同的卷积核。但对于微观尺度下的犯罪时空预测，一天当中发生的案件数和研究单元数量的比例相差较大，采用参数共享方法会因部分路段数据分布稀疏而产生零膨胀问题，导致模型训练结果过拟合。此外，图卷积模型未考虑相邻节点间的道路特征，易导致预测结果与真实犯罪在城市中的分布有所差异。为了解决上述问题，本研究模拟自激点过程分解犯罪风险的长期背景差异和影响传播的时空变化，并结合道路距离衰减权重和通达度两种道路权重，构建考虑道路权重的图卷积层（Road Weighted Network，RWN），作为RW-STGCN中犯罪风险空间特征提取层（图5），计算公式如下：
g X = W ˜ × S ˜ × x + η x
图5 RWN模型结构

Fig. 5 Structure of RWN

式中： x是输入的犯罪风险值； W ˜为道路距离衰减的影响； S ˜为道路通达度的影响； η代表犯罪风险的长期背景差异； g X为每条道路受到犯罪活动的影响值。该模型可以更有效避免零膨胀问题，并且通过使用路网加权的方式优化信息传递的过程，还可以减少路段上的异质性问题。道路权重图卷积层构建的详细过程如图5所示。
（1）距离衰减权重计算
城市犯罪活动风险在一定范围内会沿着道路网进行传播，并且随着距离的增加，犯罪风险逐渐减弱，即具有明显的距离衰减效应。因此，本研究以核密度估计中常用的高斯函数为基础，计算犯罪活动影响的距离衰减权重，公式如下：
W i j = k ( d i j r ) = ( - d i j 2 2 r ) e i j = 1 且 0 < d i j ≤ r k ( d i j r ) = 0 d i j > r 或 i = j
式中： W i j为计算后得到的路网节点间距离权重； e i j代表2条路段的邻接关系，取值为0或1，取值为1时表示道路之间相交； d i j是2条路段长度和的一半，即路段中点之间距离；r为搜索半径，已有的研究[40-41]表明500 m是较为舒适的步行距离，符合个体步行活动的微观活动特征，同时也考虑了空间尺度的异质性[42]。因此本研究将搜索半径r设置为500 m。
（2）道路通达度权重计算
现有考虑道路通达度的方法[21,43]通常以路网密度来衡量某区域内的道路网通达程度，但对于微观尺度下的路网系统，往往还需要计算每条路段的通达度。空间句法可以根据集中度的概念来衡量道路的通达度，其定义是某路段到区域内其他路段的难易程度，其值越高表示该路段的中心性越强，对周围的人流、车流、犯罪活动等具有更高的吸引力[44-45]。其计算公式如下：
N Q P D x = ∑ P y d M x , y
式中： R x是相邻路段节点集合； P y是指范围内道路y的长度和搜素半径的比例，代表道路y在搜素半径内的权重，其范围在0~1之间； d M x , y是道路x和道路y之间的最短路网距离。
（3）道路权重计算
图结构中的信息扩散方式主要分为矩阵分解和随机游走2种方式。本研究按照随机游走方式先计算每条道路对下一路段的影响风险，然后再汇总每条路段对相邻路段的影响，最终得到综合考虑距离衰减权重和道路通达度的道路权重，相关公式如下：
W ˜ = w j ∑ j ∈ v i w i j
S ˜ = N Q P D j ∑ j ∈ v i N Q P D i j
W S × x i = ∑ j ∈ v i W ˜ × S ˜ × x i = ∑ j ∈ v i w i j × N Q P D i j × x i ∑ j ∈ v i w i j × N Q P D i j
式中： v i是路段i相邻路段的集合； x i是每条路段上的犯罪特征； W ˜和 S ˜分别是距离衰减权重和路网道路通达度权重； w j和 N Q P D j分别由式(7)和式(8)计算得到。
（4）道路风险传播过程表征
道路风险传播过程综合考虑了背景特征和传递风险的时空特征，本研究通过RWN层表征其过程。在RWN层中，假设 X m ∈ R N × C，其中m是道路加权图卷积神经网络的层数，N是图结构中路网节点的数量，C是节点的特征数，数学公式为：
g m X m = R e L U X m × η m + W S × X m × θ m
式中： η 、 θ分别为模型中学习的参数，隐藏层同样选择ReLU函数； X m × η m代表背景特征； W S × X m代表传递风险的时空特征。

2.4 模型集成设计

为了更好地提取输入数据犯罪时空的特征，本研究采用堆叠的形式对模型进行集成。通过对GLU和道路权重图卷积层RWN的组合，实现对时空特征的非线性拟合，以有效提取犯罪活动时空特征的变化。同时，对模型进行多层叠加，以感知多阶路网节点的犯罪空间特征。RW-STGCN的公式化表达为：
C o n v i X = t i + 1 g i t i X · ω i + b i
R W S T G C N X = Γ × τ ( C o n v k ( C o n v k - 1 ( ⋯ ( C o n v 2 ( C o n v 1 X ) ) ⋯ ) ) ) · ρ + d
式中: ω i 、 b i 、 ρ 、 d是模型训练时需要学习的参数； Γ、 t X和 g X分别由式（2）、式（5）及式（12）得到。
经过SES平滑处理后的数据按照式(13)，输入到2层的GLU和1层的RWN提取每个节点1阶的图结构特征，通过多次堆叠集成，完成k阶的特征提取，并结合一个GLU和全连接层进行特征嵌入，最终使用ReLU激活函数输出预测结果（式(14)），实现对下一个时间段的犯罪风险时空预测。

3 实验设计及结果分析

3.1 实验设计与精度评价

3.1.1 对比模型选择及参数设置

为了验证所构建模型的预测精度，本研究选择GCN、GraphSAGE、GAT等应用较广的图卷积模型进行对比实验。RW-STGCN及其他3个基线模型都基于PyTorch1.12的环境实现。实验的重点在于比较不同道路权重的空间特征提取方法对预测结果的影响，因此3种基线模型在时间特征的提取上采取相同的门控卷积神经网络（GLU），对比实验所使用的3种基线模型及其参数设置如下：
(1) STGCN：该模型采用的是基于切比雪夫多项式的图卷积，并考虑了节点特征及时间相关性对犯罪的影响。本实验中设置时间门控卷积层数为2，图卷积层数为1，隐藏层数为32，全连接层数为1。
(2) STGAT：该模型使用Attention函数计算出对犯罪影响最大的节点，并考虑了时间序列对犯罪的影响。本实验中设置时间门控卷积层数为4，图卷积层数为2，隐藏层数为16，多头注意力机制中头数为3，全连接层数为1。
(3) STGraphSAGE：该模型是一种归纳式的图聚合网络方法，通过对目标节点的邻节点进行采样，利用聚合函数得到邻节点的特征，同时也考虑了目标节点的时间特征。本实验中设置时间门控卷积层数为2，图卷积层数为1，隐藏层数为16，全连接层数为1。

3.1.2 实验数据集设计及相关设置

基于近重复受害理论[46]，并考虑犯罪数据的稀疏性等因素，设置时间窗口为m天，即用前m天数据进行训练来预测后1 d的盗窃犯罪分布。在模型训练时，将数据按时序划分成训练集、验证集以及测试集，比例为4.3:1:1；学习率设置为0.001。采用Adam优化器在训练i个epoch后（i取值范围通常在100~200之间），使模型训练误差逐渐降低并趋于平稳，预测结果达到收敛；同时为了防止过拟合，在验证集中进行预测检验，以筛选出具有最小损失函数值的模型参数，损失函数设置为均方差，其公式如下：
l o s s y ˆ | y = 1 n ∑ y ˆ i - y i 2
式中: y ˆ i代表犯罪风险的预测值； y i代表犯罪风险的真实值。相关参数设定后，通过反复试验以获得模型的最优结果。

3.1.3 精度评价

为了测试模型的预测性能，本研究采用命中率（Hit Rate）[47]来衡量预测结果的准确性。命中率是一种在犯罪地理研究领域广泛应用的精度评价指标，其含义是预测正确的样本占总样本的百分比（式(16)），命中率越高代表预测精度越高。命中率会随着预测区域的扩大而增大，在对比模型保持相同区域比例的前提下，评价指标可以明显地展示不同模型的精度差异及趋势。
H i t R a t e = n N × 100 %
式中：n是预测正确的犯罪数量；N是犯罪发生的总数量。由于不同模型方法计算结果并不相同，因此不能通过预测值的高低进行区域分级，而需要通过每种模型预测值的高低按比例划分热点区域。在现有研究中[16,22,26,48]，衡量犯罪预测精度的格网或者路网的覆盖比例一般在1%~20%，因此本研究选取研究区1%、5%、10%、20%比例的道路覆盖度进行命中率的预测及模型命中率比较。同时考虑到街头盗窃犯罪随机性对模型结果稳定性的影响，使用测试结果时间窗口内的平均命中率作为盗窃犯罪预测的精度评价指标。

3.2 模型预测结果对比分析

为缓解数据稀疏性问题，在将RW-STGCN模型和几种主流的图卷积预测模型进行比较时，对每种模型都采用了简单指数平滑，平滑因子设为0.5。时间窗口m设置为100，测试集的时间段为2017年9月23日—2017年12月31日，即100 d。
图6展示了不同模型在100 d内的平均命中率。结果显示，STGAT在所有时空图卷积模型中命中率最低，相较于之前的一些研究[49]，预测结果不具有优势，原因可能是在微观的时空尺度下，犯罪数据稀疏性被放大以及特征的非平稳性变化，使其难以捕捉邻接边的重要性；而RW-STGCN模型在 4种不同路段覆盖比例下都优于其他模型，取得了最好的精度提升，其中：在覆盖20%的路段下，RW-STGCN相较于其他基线模型的最好预测结果，命中率提升了8.4%；在覆盖10%的路段下RW-STGCN比预测效果最好的基线模型提升了6.5%；在覆盖5%的路段下，RW-STGCN比预测效果最好的基线模型提升了9.4%，而在覆盖1%的路段下RW-STGCN比预测效果最好的基线模型提升了50.8%。在4种不同覆盖比例下，RW-STGCN均取得了最好的精度提升；相较于3个基线模型，RW-STGCN的命中率在预测覆盖较小区域，提升更为显著。模型对比分析结果表明，顾及道路权重的时空图卷积模型能有效提升模型的预测性能。
图6 不同模型的犯罪风险预测结果对比

Fig. 6 Comparison of crime risk prediction results of different models

由于模型的预测精度随时间间隔变大而逐渐降低，需要进一步分析模型命中率的稳定性，图7展示了居于测试期中间日期的预测犯罪风险分布情况。从图7可看出，RW-STGCN和STGAT的预测结果空间分布类似，这可能是因为二者都考虑了模型边的权重对路网节点的影响，但因RW-STGCN考虑了街面犯罪在道路上影响距离衰减效应及路网通达性等因子，所以取得了更高的精度。4种方法都预测正确了一些共同的犯罪热点，但RW-STGCN还准确预测了更多的犯罪热点路段，特别是一些位于研究区边缘的路段，说明顾及道路空间特征有助于优化模型性能。和图2（c）中的犯罪热力图比较，4种模型均能识别一些明显的历史热点区域，但以RW-STGCN识别的路段区域更为集中。
图7 2017年11月18日芝加哥南部不同模型5%道路覆盖下的犯罪风险预测

Fig. 7 Crime risk prediction map for different models under 5% road coverage in the southern part of Chicago on November 18, 2017

3.3 敏感性分析

通常模型的预测精度并不是固定的，会随着时间步长和空间邻阶层数变化而改变。可利用敏感性实验来分析两者变化对模型预测结果的影响，并通过调整参数以获得高精度的预测结果。
对于时态特征，理论上越长的时间步长会提供更多的历史信息，有助于提升模型的拟合能力，但过长的时间步长会使模型的历史信息记忆能力丢失，从而导致预测能力下降、模型过拟合等问题。因此，需要通过实验确定最优的时间步长。
如图8所示，RW-STGCN模型的命中率精度随着时间窗的增长，而呈现出先上升再下降的趋势，模型在时间窗口m为100 d时，精度最高，然后随着时间窗口m值增加，开始下降。因此，在实验中需要选取最佳时间窗口参数，以避免模型难以捕捉犯罪活动快速变化的特征。
图8 RW-STGCN模型中随时间窗变化的犯罪风险预测结果（30~150 d）

Fig. 8 Crime risk prediction results of the RW-STGCN with a time window of 30~150 days

RW-STGCN模型的空间特征捕获方法与其他图卷积模型类似，通过捕获邻阶的节点特征，得到更丰富的特征表示。在一阶卷积中只考虑了节点本身和其一阶相邻节点的特征，而多阶卷积则考虑了更远的节点的特征。因此通过多层卷积扩展节点的感受野，以更全面地捕捉图中信息。
如图9所示，RW-STGCN模型的平均命中率大部分呈现出先上升后下降的趋势。这可能是因为随着卷积深度的增加，远处节点的噪声及无关信息也会制约模型性能的提升。因此在实际应用中，需要为模型确定合适的模型层数。
图9 RW-STGCN模型随道路权重图卷积层数量变化的犯罪风险预测结果

Fig. 9 Crime risk prediction results of the RW-STGCN with different number of convolutional layers of road network weights

3.4 消融分析

为验证RW-STGCN模型中所引入的道路权重模块的有效性，本研究通过修改模型结构建立不同的模型变体（表1）设计了消融实验。具体地，通过计算各模型变体在100 d时间窗口内的街面盗窃犯罪平均命中率，来比较不同模型变体的预测精度，分析不同权重因素对犯罪预测的影响。
表1 不同权重的模型变体

Tab. 1 Model variants with different weights

模型变体 道路距离权重 道路通达度权重
RW-STGCN-T × ×
RW-STGCN-S1 √ ×
RW-STGCN-S2 × √
RW-STGCN-SS √ √
如图10所示，消融实验结果表明，相较于未考虑道路权重影响的模型，顾及了道路权重的3种模型在不同道路覆盖率条件下，命中率都得到了提升。值得注意的是，同时考虑道路的距离权重和集中度，会使命中率获得更大的提升：相比于RW-STGCN-T模型，命中率提升了1.9%~13.5%；相比于仅考虑道路权重的RW-STGCN-S1和RW-STGCN-S2模型，RW-STGCN-SS命中率提升了0.5%~12.9%，实验表明道路权重对模型性能提升起到重要作用。
图10 考虑不同道路权重的RW-STGCN模型变体消融分析结果比对

Fig. 10 Comparison of ablation analysis results of RW-STGCN model variants considering different road weights

4 结论和展望

4.1 结论

本文提出了一种顾及道路权重的图卷积犯罪时空预测模型RW-STGCN用于城市街面盗窃犯罪预测。该模型设计了一种新的犯罪特征传递的结构，同时考虑了道路距离衰减效应和道路通达度因子对犯罪活动的影响，历史犯罪数据作为输入数据，被分解为图结构形式的固定背景特征和传递犯罪风险的空间特征，通过融合门控卷积层来充分挖掘所输入的时空特征，以更好地提升预测精度。以芝加哥南部历史犯罪数据进行的比对实验分析表明，该模型取得了较好的预测效果。主要结论如下：
（1）相较于未考虑道路权重的时空图卷积模型，本研究所提出的RW-STGCN模型命中率在不同路网覆盖比例（1%、5%、10%、20%）下的提升率均在6.5%以上，且在道路覆盖比例较小时，RW-STGCN模型命中率的提升更为显著。
（2）与其他相关图卷积模型对比实验表明，通过图注意力机制考虑模型中连接节点的边权重，对路网节点的影响并未显著提升模型的预测性能，而通过道路对图边加权的RW-STGCN模型不仅预测精度更高、预测路段区域更为集中，还能识别路网边缘的犯罪热点，这表明考虑路网地理空间特征对采用深度学习技术预测城市街道类犯罪具有正向意义。
（3）模型敏感性分析表明，RW-STGCN模型的时间特征信息和空间特征信息提取能力随着时间窗的长度和图卷积层数增加呈现先上升后下降的趋势。究其原因，可能是长时间序列特征和多阶的空间特征有助于模型性能提升，但同时也会受到过拟合和过平滑等问题对预测精度的制约。
（4）对RW-STGCN模型进行的消融实验分析表明，考虑道路权重均能有效提升模型预测精度，并且同时考虑2种道路权重比仅考虑距离衰减权重或路网通达性权重提升更为明显。

4.2 展望

本研究在基于时空图卷积的犯罪预测模型优化方面做了有益探索，但仍存在许多问题及不足，有待后续进一步深入研究：
（1）由于城市道路长度并不完全相等，这将导致在同一条道路的不同位置上仍存在犯罪风险的差异性，未来需要进一步探索顾及路网空间异质性的方法。
（2）不同的街面犯罪类型时空特征存在一定差异性，未来需要进一步对其他街面犯罪类型进行实验，以测试模型的泛化性。
（3）城市路网单元作为一个复杂的社会交互环境，道路权重和通达度仅是其中重要影响因素之一，后续研究还需要考虑更多因素对街面犯罪活动的影响，如道路上的流动人口、周边建成环境等。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
王发曾. 我国城市犯罪空间防控研究二十年[J]. 人文地理, 2010, 25(4):25-30.

[Wang F Z. A review of urban spatial anti-crime study in China from 1980 to 2000[J]. Human Geography, 2010, 25(4):25-30.] DOI:10.13959/j.issn.1003-2398.2010.04.011

[2]
贺日兴, 陆宇梅, 姜超, 等. 近10年来犯罪时空预测国内外研究与实践进展[J]. 地球信息科学学报, 2023, 25(4):866-882.

DOI

[He R X, Lu Y M, Jiang C, et al. Progress in research and practice of spatial-temporal crime prediction over the past decade[J]. Journal of Geo-information Science, 2023, 25(4):866-882.] DOI:10.12082/dqxxkx.2023.220808

[3]
Perry W L, Mcinnis B, Price C C, et al. Predictive policing: the role of crime forecasting in law enforcement operations[M]. Santa Monica, CA: RAND Corporation, 2013.

[4]
Townsley M, Homel R, Chaseling J. Infectious burglaries. A test of the near repeat hypothesis[J]. The British Journal of Criminology, 2003, 43(3):615-633. DOI:10.1093/bjc/43.3.615

[5]
Kafadar K, Bowman A W, Azzalini A. Applied smoothing techniques for data analysis: the kernel approach with S-PLUS illustrations[J]. Journal of the American Statistical Association, 1999, 94(447):982. DOI:10.2307/2670015

[6]
贺日兴. 警用地理信息系统——理论、技术与应用[M]. 北京: 中国人民公安大学出版社, 2022:240-248.

[He R X. Police Geographic Information System - Theory, Technology, and Application[M]. Beijing: China Renmin University Press, 2022:240-248.]

[7]
Kennedy L W, Caplan J M, Piza E. Risk clusters, hotspots, and spatial intelligence: Risk terrain modeling as an algorithm for police resource allocation strategies[J]. Journal of Quantitative Criminology, 2011, 27(3):339-362. DOI:10.1007/s10940-010-9126-2

[8]
Mohler G O, Short M B, Brantingham P J, et al. Self-exciting point process modeling of crime[J]. Journal of the American Statistical Association, 2011, 106(493):100-108. DOI:10.1198/jasa.2011.ap09546

[9]
李卫红, 闻磊, 陈业滨. 改进的GA-BP神经网络模型在财产犯罪预测中的应用[J]. 武汉大学学报·信息科学版, 2017, 42(8):1110-1116,1171.

[Li W H, Wen L, Chen Y B. Property crime forecast based on improved GA-BP neural network model[J]. Geomatics and Information Science of Wuhan University, 2017, 42(8):1110-1116,1171.] DOI:10.13203/j.whugis20160911

[10]
柳林, 刘文娟, 廖薇薇, 等. 基于随机森林和时空核密度方法的不同周期犯罪热点预测对比[J]. 地理科学进展, 2018, 37(6):761-771.

DOI

[Liu L, Liu W J, Liao W W, et al. Comparison of random forest algorithm and space-time kernel density mapping for crime hotspot prediction[J]. Progress in Geography, 2018, 37(6):761-771.] DOI:10.18306/dlkxjz.2018.06.003

[11]
Hardyns W, Rummens A. Predictive policing as a new tool for law enforcement? recent developments and challenges[J]. European Journal on Criminal Policy and Research, 2018, 24:201-218. DOI:10.1007/s10610-017-9361-2

[12]
Baculo M J C, Marzan C S, de Dios Bulos R, et al. Geospatial-temporal analysis and classification of criminal data in Manila[C]//2017 2nd IEEE International Conference on Computational Intelligence and Applications (ICCIA).IEEE, 2017:6-11. DOI:10.1109/CIAPP.2017.8167050

[13]
刘大千. 长春市犯罪空间分析及规划管理防控[D]. 长春: 东北师范大学, 2012.

[Liu D Q. Spatial analysis of crimes in Changchun and crime control from planning and administrative perspective[D]. Changchun: Northeast Normal University, 2012.]

[14]
Han X G, Hu X F, Wu H G, et al. Risk prediction of theft crimes in urban communities: An integrated model of LSTM and ST-GCN[J]. IEEE Access, 2020, 8:217222-217230. DOI:10.1109/ACCESS.2020.3041924

[15]
陈鹏, 林平, 孙菲菲, 等. 风险地形建模在犯罪风险评估中的应用[J]. 测绘与空间地理信息, 2017, 40(12):4-9.

[Chen P, Lin P, Sun F F, et al. The application of risk terrain model in risk assessment of crime[J]. Geomatics & Spatial Information Technology, 2017, 40(12):4-9.] DOI:10.3969/j.issn.1672-5867.2017.12.002

[16]
徐冲, 柳林, 周素红. 基于临近相似性考虑的犯罪热点密度图预测准确性比较——以DP半岛街头抢劫犯罪为例[J]. 地理科学, 2016, 36(1):55-62.

DOI

[Xu C, Liu L, Zhou S H. The comparison of predictive accuracy of crime hotspot density maps with the consideration of the near similarity: A case study of robberies at DP peninsula[J]. Scientia Geographica Sinica, 2016, 36(1):55-62.] DOI:10.13249/j.cnki.sgs.2016.01.007

[17]
毛媛媛, 戴慎志. 犯罪空间分布与环境特征——以上海市为例[J]. 城市规划学刊, 2006(3):85-93.

[Mao Y Y, Dai S Z. Research on spatial and environmental characters of crimes: Case study of Shanghai[J]. Urban Planning Forum, 2006(3):85-93.] DOI:10.3969/j.issn.1000-3363.2006.03.013

[18]
宋广文, 黎晓彐, 肖露子, 等. 交互作用视角下人口流动性与住房类型对城市入室盗窃空间格局的影响[J]. 地理研究, 2022, 41(11):2897-2911.

DOI

[Song G W, Li X X, Xiao L Z, et al. Effects of population mobility and housing type on spatial pattern of urban burglary from the perspective of interaction[J]. Geographical Research, 2022, 41(11):2897-2911.] DOI:10.11821/dlyj020220350

[19]
张延吉, 林钦熙, 朱春武, 等. 可渗透性环境对盗窃犯罪分布的影响及社会解组的调节作用——兼论街道眼理论与防卫空间理论的适用性[J]. 地理科学进展, 2022, 41(6):1041-1052.

DOI

[Zhang Y J, Lin Q X, Zhu C W, et al. The influence of permeable built environment on theft crime pattern and the moderation effects of social disorganization: Applicability of street eyes and defensible place theories[J]. Progress in Geography, 2022, 41(6):1041-1052.] DOI:10.18306/dlkxjz.2022.06.008

[20]
柳林, 杜方叶, 肖露子, 等. 不同类型道路密度对公共空间盗窃犯罪率的影响——基于ZG市的实证研究[J]. 人文地理, 2017, 32(6):32-38, 46.

[Liu L, Du F Y, Xiao L Z, et al. The density of various road types and larceny rate: An empirical analysis of zg city[J]. Human Geography, 2017, 32(6):32-38,46.] DOI:10.13959/j.issn.1003-2398.2017.06.004

[21]
Sadeek S N, Minhuz Uddin Ahmed A J M, Hossain M, et al. Effect of land use on crime considering exposure and accessibility[J]. Habitat International, 2019, 89:102003. DOI:10.1016/j.habitatint.2019.102003

[22]
Rosser G, Davies T P, Bowers K J, et al. Predictive crime mapping: arbitrary grids or street networks?[J]. Journal of Quantitative Criminology, 2017, 33(3):569-594. DOI:10.1007/s10940-016-9321-x

PMID

[23]
Okabe A, Satoh T, Sugihara K. A kernel density estimation method for networks, its computational method and a GIS-based tool[J]. International Journal of Geographical Information Science, 2009, 23(1):7-32. DOI:10.1080/13658810802475491

[24]
Shiode S, Shiode N. Microscale prediction of near-future crime concentrations with street-level geosurveillance[J]. Geographical Analysis, 2014, 46(4):435-455. DOI:10.1111/gean.12065

[25]
Zhou B B, Chen L B, Zhou F X, et al. Dynamic road crime risk prediction with urban open data[J]. Frontiers of Computer Science, 2022, 16(1):161609. DOI:10.1007/s11704-021-0136-z

[26]
Zhang Y, Cheng T. Graph deep learning model for network-based predictive hotspot mapping of sparse spatio-temporal events[J]. Computers, Environment and Urban Systems, 2020, 79:101403. DOI:10.1016/j.compenvurbsys.2019.101403

[27]
Yu B, Yin H T, Zhu Z X. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting[EB/OL]. 2017: arXiv:1709.04875. https://arxiv.org/abs/1709.04875

[28]
Sun J K, Zhang J B, Li Q F, et al. Predicting citywide crowd flows in irregular regions using multi-view graph convolutional networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(5):2348-2359. DOI:10.1109/TKDE.2020.3008774

[29]
Zhao L, Song Y J, Zhang C, et al. T-GCN: A temporal graph convolutional network for traffic prediction[J]. IEEE Transactions On Intelligent Transportation Systems, 2020, 21(9):3848-3858. DOI:10.1109/TITS.2019.2 935152

[30]
Veličković P, Cucurull G, Casanova A, et al. Graph attention networks[EB/OL]. 2017: arXiv:1710.10903. https://arxiv.org/abs/1710.10903

[31]
Guo S N, Lin Y F, Feng N, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[J]. Proceedings of the AAAi Conference on Artificial Intelligence, 2019, 33(1):922-929. DOI:10.1609/aaai.v33i01.3301922

[32]
Hamilton W L, Ying R, Leskovec J. Inductive representation learning on large graphs[EB/OL]. 2017:arXiv:1706.02216. https://arxiv.org/abs/1710.10903.

[33]
Johnson S D, Bowers K J, Birks D, et al. Burglary prediction, theory, flow and friction[M]. CRC Press, 2005:203-223.

[34]
Johnson S D, Bowers K J. Near repeats and crime forecasting[M]. Encyclopedia of Criminology and Criminal Justice, Bruinsma G, Weisburd D, New York, NY: Springer New York, 2014:3242-3254.

[35]
肖露子, 柳林, 宋广文, 等. 基于理性选择理论的社区环境对入室盗窃的影响研究[J]. 地理研究, 2017, 36(12):2479-2491.

DOI

[Xiao L Z, Liu L, Song G W, et al. Impacts of community environment on residential burglary based on rational choice theory[J]. Geographical Research, 2017, 36(12):2479-2491.] DOI:10.11821/dlyj201712017

[36]
Dong H W. Does walkability undermine neighbourhood safety?[J]. Journal of Urban Design, 2017, 22(1):59-75. DOI:10.1080/13574809.2016.1247644

[37]
Dauphin Y N, Fan A, Auli M, et al. Language modeling with gated convolutional networks[EB/OL]. 2016: arXiv: 1612.08083. https://arxiv.org/abs/1612.08083

[38]
Zaremba W, Sutskever I, Vinyals O. Recurrent neural network regularization[EB/OL]. 2014: arXiv:1409.2329. https://arxiv.org/abs/1409.2329

[39]
Shi X J, Chen Z R, Wang H, et al. Convolutional LSTM network: A machine learning approach for precipitation nowcasting[EB/OL]. 2015:arXiv:1506.04214. https://arxiv.org/abs/1506.04214

[40]
谢超. 基于网络分析的地下通道对街区步行可达性影响研究——以广州天河新城为例[C].成都://面向高质量发展的空间治理——2021中国城市规划年会论文集(05城市规划新技术应用), 2021:444-453.

[Xie C. Research on the impact of underground passages on pedestrian accessibility of street blocks based on network analysis: A case study of Tianhe new city in Guangzhou[C]. Chengdu Sichuan//Spatial governance for high-quality development: Proceedings of the 2021 China Urban Planning Annual Conference (05 Urban Planning New Technology Application), 2021:444-453.]

[41]
陈方, 张澄洋, 丁思远. 生活街区轨道站步行易达性测度研究——以深圳和香港为例[J]. 南方建筑, 2021(4):31-38.

DOI

[Chen F, Zhang C Y, Ding S Y. A study on the measurement of pedestrian accessibility of living-block rail transit station: A case study of Shenzhen and Hong Kong[J]. South Architecture, 2021(4):31-38.] DOI:10.3969/j.issn.1000-0232.2021.04.031

[42]
张春霞, 周素红, 柳林, 等. 建成环境对星级酒店内被盗的影响——以ZG市中心城区为例[J]. 地理科学进展, 2020, 39(5):829-840.

DOI

[Zhang C X, Zhou S H, Liu L, et al. Relationship between the built environment and theft cases in star hotels in ZG central city[J]. Progress in Geography, 2020, 39(5):829-840.] DOI:10.18306/dlkxjz.2020.05.011

[43]
何健, 黄启乐, 汪振东. 广州市城市道路网密度提升路径探索[J]. 交通与运输, 2019, 35(4):35-38.

[He J, Huang Q L, Wang Z D. Path of urban road network density enhancement in Guangzhou[J]. Traffic & Transportation, 2019, 35(4):35-38.] DOI:10.3969/j.issn.1671-3400.2019.04.009

[44]
居少捷, 孙琳珊. 基于空间句法的轨交站点人流空间分布研究——以南京新街口为例[J]. 城市建筑, 2023, 20(6):87-89,93.

[Ju S J, Sun L S. Study on spatial distribution of population flow in rail transit station based on space syntax: A case of Nanjing Xinjiekou[J]. Urbanism and Architecture, 2023, 20(6):87-89,93.] DOI:10.19892/j.cnki.csjz.2023.06.24

[45]
姜昀呈, 孙立坚, 王涛涛, 等. 兰州市中心城区犯罪分布与城市环境的关系[J]. 测绘科学, 2021, 46(5):167-174.

[Jiang Y C, Sun L J, Wang T T, et al. The coupling relationship between crime distribution and urban environment in Lanzhou city center[J]. Science of Surveying and Mapping, 2021, 46(5):167-174.] DOI:10.16251/j.cnki.1009-2307.2021.05.023

[46]
Farrell G, Phillips C, Pease K. LIKE TAKING CANDY: Why does repeat victimization occur?[J]. The British Journal of Criminology, 1995, 35(3):384-399. DOI:10.1093/oxfordjournals.bjc.a048523

[47]
Bowers K J, Johnson S D, Pease K. Prospective hot-spotting: The future of crime mapping?[J]. The British Journal of Criminology, 2004, 44:641-658. DOI:10.1093/bjc/azh036

[48]
Hu Y J, Wang F H, Guin C, et al. A spatio-temporal kernel density estimation framework for predictive crime hotspot mapping and evaluation[J]. Applied Geography, 2018, 99:89-97. DOI:10.1016/j.apgeog.2018.08.001

[49]
Song J, Son J, Seo D H, et al. ST-GAT: a spatio-temporal graph attention network for accurate traffic speed prediction[C].//Proceedings of the 31st ACM International Conference on Information & Knowledge Management New York, NY, USA: ACM, 2022:4500-4504. DOI:10.1145/3511808.3557705

Options
文章导航

/

〈 〉