EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 10: 2026 - 2038

DOI: https://doi.org/10.12082/dqxxkx.2023.230152

地理空间分析综合应用

基于随机森林模型的“网格-月”尺度武装冲突风险预测及影响因素分析——以中南半岛为例

  • 杜树坤 , 1 ,
  • 张晶 , 1, 2, * ,
  • 韩志军 1, 2 ,
  • 公茂玉 1, 2
展开
  • 1.信息工程大学地理空间信息学院，郑州 450001
  • 2.智慧中原地理信息技术河南省协同创新中心，郑州 450001
* 张晶（1974—），女，辽宁西丰人，博士，教授，主要从事人文地理学理论与应用研究。E-mail:

杜树坤（1998—），男，山东东营人，硕士生，主要从事人文地理学与地理大数据研究。E-mail:

收稿日期: 2023-03-27

  修回日期: 2023-06-02

  网络出版日期: 2023-09-22

基金资助

国家自然科学基金项目(41301125)

国家社科基金重大项目(20&ZD138)

收起

Armed Conflict Risk Prediction and Influencing Factors Analysis Based on the Random Forest Model at the Grid-month Scale: A Case Study of Indochina Peninsula

  • DU Shukun , 1 ,
  • ZHANG Jing , 1, 2, * ,
  • HAN Zhijun 1, 2 ,
  • GONG Maoyu 1, 2
Expand
  • 1. College of Geospatial Information, Information Engineering University, Zhengzhou 450001, China
  • 2. Collaborative Innovation Center of Geo-information Technology for Smart Central Plains, Zhengzhou 450001, China
* ZHANG Jing, E-mail:

Received date: 2023-03-27

  Revised date: 2023-06-02

  Online published: 2023-09-22

Supported by

National Natural Science Foundation of China(41301125)

National Social Science Foundation of China(20&ZD138)

Fold

摘要

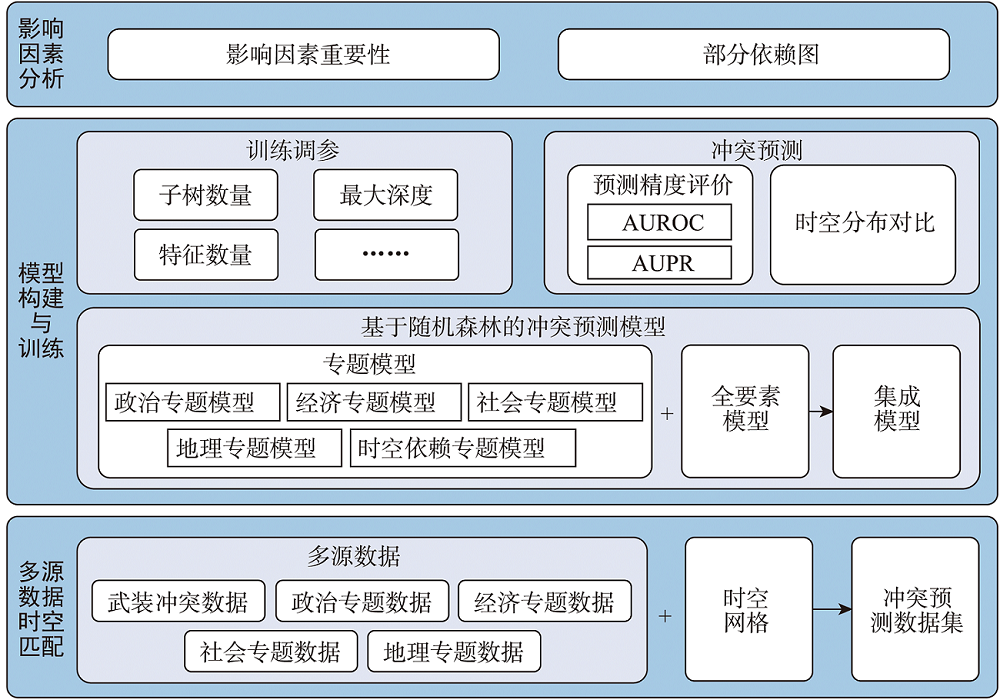
掌握周边地区武装冲突风险形势对我国“一带一路”倡议推进和海外投资建设具有十分重要的意义。由于武装冲突风险涉及的因素众多，很多数据时空精度有限，以往研究的尺度大多集中于“国家-年”层面，未能从次国家尺度上预测武装冲突风险。通过将武装冲突与政治、经济、社会和地理等专题的多源数据匹配到统一的“网格-月”尺度的时空框架中，构建了多个基于随机森林模型的武装冲突风险预测模型，以中南半岛为例，对比各专题模型和集成模型的预测精度，将预测结果与实际的武装冲突风险时空分布情况进行比较与分析，计算各影响因素的权重并分析其影响作用。研究结果表明：① 基于随机森林模型的冲突预测模型比传统的逻辑回归模型预测精度更高，其中集成模型的准确率、ROC曲线下面积和PR曲线下面积分别提高了0.017 7、0.436 2和0.171 2；② 中南半岛武装冲突风险受政治、经济和社会要素影响较高，地理要素的相关性较弱，但随着风险水平发生变化，影响因素的作用程度也在改变；③ 在基础专题数据的支撑下，顾及冲突的时空依赖性可以明显提高模型的预测精度；④ 与大尺度研究相比，“网格-月”尺度的冲突预测结果精度更高，可解释性也更强。本研究可为我国海外投资与当地冲突风险防控与治理等提供参考和依据。

关键词： 武装冲突; 随机森林模型; 风险预测; 影响因素; 中南半岛

本文引用格式

杜树坤 , 张晶 , 韩志军 , 公茂玉 . 基于随机森林模型的“网格-月”尺度武装冲突风险预测及影响因素分析——以中南半岛为例[J]. 地球信息科学学报, 2023 , 25(10) : 2026 -2038 . DOI: 10.12082/dqxxkx.2023.230152

Abstract

A better understanding of the threat of armed conflict in a region is essential to advance the Belt and Road Initiative and overseas investment and construction. Most existing studies have concentrated on a "country-year" level and have limited accuracy in predicting armed conflict risk at the sub-national level, because the armed conflict risk involves numerous influencing factors and many data have limited spatiotemporal accuracy. In our study, we built several models based on random forest methods for armed conflict risk prediction by integrating multi-source armed conflict data with political, economic, social, and geographic thematic information into a unified spatiotemporal framework at "grid-month" scale. Taking the Indochinese Peninsula as an example, we compared the prediction accuracy of each thematic model and the integrated model for armed conflict risk. Then we compared the prediction results against the actual spatiotemporal distribution of armed conflicts, and the weights of each influencing factor were calculated and analyzed. The results show that: (1) compared to the traditional logistic regression model's performance, the accuracy, area under the ROC curve, and area under the PR curve of the integrated random forest model increased by 0.017 7, 0.436 2, and 0.171 2, respectively; (2) the political, economic, and social factors had a significant impact on the risk of armed conflict in the Indochina Peninsula, while geographic factors were less important. However, as the risk level changes, the degree of influence of these factors also changed; (3) the model prediction accuracy of armed conflict risk can be greatly increased by taking into account the spatiotemporal dependence of conflicts, which was supported by the underlying thematic data; (4) the conflict results predicted at the "grid-month" scale were more precise and interpretable compared to large-scale prediction results. This study provides a reference and basis for China's overseas investment as well as local conflict risk prevention, control, and governance.

Key words： armed conflict; Random Forest Model; risk prediction; influence factor; Indochina Peninsula

1 引言

武装冲突问题一直是政治学的研究热点，其主要研究议题包括武装冲突发生机制和武装冲突预测等方面。早期研究主要集中在从经济学视角对武装冲突的爆发进行定性解释，Collier等[1]建立的“动机-成本”分析框架为武装冲突研究奠定了理论基础。随着研究不断深入，经济增长、人均收入、分配不平等和税收等[2]经济因素以外的自然、社会因素也逐步被纳入到解释武装冲突爆发的分析框架中，包括地形地貌[3]、自然资源禀赋[4]、气候变化[5]、自然灾害[6]、人口规模[7]、民族-宗教构成[8]以及粮食援助[9]等。在研究方法方面，传统的统计回归模型也逐渐应用于冲突研究，为解释不同要素的影响作用提供了数学支撑。日益完善的分析框架与逐渐应用的数学模型共同为武装冲突预测提供了扎实的理论和方法基础。
武装冲突预测方面的早期研究更注重影响因素的显著性及相应解释[10-11]，一定程度上忽略了模型的预测效果；而研究尺度多集中在“国家-年”级别，但理想情况下，预测应该在更精细的尺度上进行[12]。Weidmann等[11]较早地利用时空回归模型在“次国家-月”的尺度上开展冲突预测研究，探讨了地理因素在预测冲突方面的作用，并发现冲突具有较强的时空依赖性，为后续冲突预测研究提供了重要参考。但由于数据颗粒度的限制，此后一段时期内的冲突预测研究的主要进展多侧重于使用新的模型、加入新的影响要素对武装冲突进行预测，研究尺度仍主要为“国家-年”层面。如Muchlinski等[13]比较了随机森林模型与罕见事件逻辑回归、正则化逻辑回归对冲突的预测性能，证明随机森林模型不仅预测精度比传统的参数方法更高[14]，并有较好的解释能力；Mueller等[15]采用LDA模型实现利用报纸文本预测冲突事件；Eastin[16]和Mach[17]等则重点评估了气候变化对武装冲突风险的影响。随着数据的扩展与方法的改进，近年来越来越多的研究开始在微观的时空尺度上开展[18]，Hegre等[19]基于随机森林模型开发了一款政治暴力预警系统（ViEWS），通过PRIO-GRID对非洲进行网格化覆盖，实现“网格-月”尺度上的冲突预测，陈冲等[20]重点从空间依赖性视角预测缅甸的武装冲突，Hultman等[21]则在ViEWS的基础上探究了维和数据对冲突预测的改进效果，D'Orazio等[22]利用自动机器学习（autoML）算法在与ViEWS相同的“网格-月”尺度上展开预测，并实现了较高的预测精度。
随着预测模型不断发展，尤其是机器学习和神经网络等技术的引入，使对预测结果的解释逐渐变得困难，而多数针对武装冲突影响因素的研究仍以预测精度较低的传统时空回归模型为主，武装冲突预测与影响因素分析逐渐趋向割裂。但如Muchlinski等[13]强调的，准确的预测与合理的解释缺一不可。近年来，采用机器学习等新方法的影响因素分析也逐渐增多。如D'Orazio等[22]通过评估特征变量重要性对自动机器学习（autoML）的预测结果进行了初步解释。Hao等[23]利用增强回归树（BRT）探究了不同气候-社会-地理模式对武装冲突的影响。
这些研究丰富和拓展了武装冲突预测的思路和方法，但仍存在以下问题：① 较大的研究尺度与有精确时空信息的武装冲突事件不匹配，在“国家-年”层面的研究，容易忽视国家内部冲突态势和影响因素的时空分异，缓慢变化的结构变量也难以满足精准预测的需求[12]；② 解释性模型的预测能力有限，尤其是样本外预测精度不高，难以为其因果关系理论提供支撑[13]；③ 而在小尺度的研究中，许多黑箱模型优化了冲突预测精度，但忽略了预测研究对理论性解释的要求[18]。因此，本文以中南半岛国家内部武装冲突为例，基于现有的武装冲突分析框架，将武装冲突数据与政治、经济、社会、地理等多源专题数据集成到统一的时空框架中，使用随机森林模型在“网格-月”的尺度上评估各专题要素的冲突预测能力，通过专题集成和模型集成的方式预测中南半岛武装冲突风险并进行验证和对比，最后对影响武装冲突风险预测的主要致险因素及其作用规律进行分析。

2 研究区概况、数据来源与研究方法

2.1 研究区域概况

中南半岛国家包括越南、老挝、柬埔寨、泰国和缅甸5个国家。该地区位于亚洲东南部，东西濒临太平洋、印度洋两大洋，南部控扼马六甲海峡，具有重要的战略地位；北部地势较高，山脉呈掌状向南展开，形成山河相间，纵列分布的自然地理格局；自然资源丰富，蕴含大量煤炭、铜、镍等矿产资源，年产丰富的橡胶、稻米等农业资源；人口分布密集，共计约2.47亿人，同时当地民族构成多样，文化宗教多元；经济潜力巨大，2021年经济总量约9 800亿美元，是中国-中南半岛经济走廊建设的主要地区，也是“一带一路”建设的重点地区之一。但该地区地缘环境复杂多变，面临政局动荡、经济发展不平衡、民族和宗教矛盾交织等严重社会问题，导致各国内部武装冲突频发，是全球冲突风险较高的地区之一。因此，该地区一方面因实验数据充足而十分适合开展武装冲突预测等研究，另一方面严峻的现实形势和战略意义导致其也迫切需求相关研究为冲突治理提供决策依据。

2.2 数据来源

本文使用的数据除武装冲突事件外，还包括政治、经济、社会、地理和时空依赖性5类专题数据，具体指标、含义和数据来源如表1所示。
表1 数据来源

Tab. 1 Data sources

专题要素 指标数据 指标含义 数据来源
政治 民众抗议 反映冲突前的局势紧张程度 ACLED[24]
政府与反对群体互动 GDELT[25]
到首都的距离 反映政府对当地的控制能力 PRIO-GRID[26]
到主要城市的距离
到国界的距离
军费开支 反映政府对国家的整体控制能力 World Bank[27]
经济 人均收入 反映民众发起叛乱冲突的机会成本 World Bank[27]
人均收入增长率
国内生产总值 反映国家整体经济发展水平
经济增长率
夜间灯光 反映当地经济发展水平 DMSP[28], EOG[29]
社会 种族歧视 反映族群矛盾 EPR[30]
儿童营养不良率 反映社会不平等程度 PRIO-GRID
新生儿死亡率
毒品种植 反映社会不稳定程度
失业率 World Bank
国家人口数量 反映整体上脱离国家的意愿
国家人口密度
当地人口规模 反映人口导致的资源稀缺情况 World Pop[31]
地理 山区地形 能够作为反叛组织的避风港 PRIO-GRID
森林覆盖
土地贫瘠 反映地区民众发起叛乱冲突的机会成本
自然资源 反映叛乱组织动机程度
自然灾害 增加民众不满情绪，降低机会成本 SEDAC[32]
时空依赖性 历史冲突 反映冲突的时间依赖性 ACLED
邻近冲突 反映冲突的空间依赖性
武装冲突数据是本文的核心数据。数据来源为“武装冲突地点和事件数据项目”（The Armed Conflict Location & Event Data Project，ACLED）。ACLED数据库详细记录了中南半岛国家在2010—2021年发生的各类武装冲突和抗议事件，每个事件均包含具体的冲突双方、冲突类型以及经纬度坐标等信息。
政治专题数据包括民众抗议、政府与反动群体互动[33]、到首都的距离[34]、到主要城市的距离、到国界的距离[35]以及军费开支[1]。经济专题要素包括人均收入及增长率[36]、国内生产总值及增长率[37]。社会专题数据包括种族歧视[38]、儿童营养不良率[39]、新生儿死亡率[37]、毒品种植[8]、失业率[16]、国家人口数量和密度以及当地人口规模[7,39]。地理专题数据包括地区山区地形[7]、森林覆盖[34]、土地贫瘠[23]、自然资源[40]和自然灾害情况[16]。时空依赖专题数据包括历史冲突[2,41-42]与邻近冲突[20,36,39,43]。相关研究表明，暴力冲突在结束后的前两年具有极高的复发性即Collier等[44]提出的“冲突陷阱”论断，因此使用历史冲突来反映暴力冲突的时间依赖性。同时也有大量文献为冲突的空间自相关性和溢出效应提供了证据，说明暴力冲突容易在当地形成聚集效应，同时向周边地区扩散，因此使用邻近冲突来反映其空间依赖性。
需要说明的是，民众抗议包括发生次数与死亡人数，互动事件包括发生次数与事件分值；军费开支为占中央政府财政支出的比例；人均收入和增长率由人均GDP表示；种族歧视、毒品种植、自然资源和自然灾害为逻辑变量，其中自然资源包括石油和稀有矿产等不可再生资源；山区地形、森林覆盖与土地贫瘠为相应类型覆盖率；历史冲突包括当地前1个月、3个月和6个月内发生的冲突与严重冲突的次数与死亡人数，邻近冲突包括四阶Queen邻近地区发生的冲突与严重冲突的次数、死亡人数及相应历史冲突情况。受数据来源所限，除时空依赖指标数据为月度更新外，其他指标数据均为年度更新的数据。

2.3 研究方法

2.3.1 技术路线

本文首先建立“网格-月”尺度的时空框架，再据此将收集的武装冲突和政治、经济、社会和地理等多源专题数据进行预处理和时空匹配融合，而后计算各时空网格对应的时空依赖数据。网格的空间框架选用奥斯陆和平研究所的PRIO-GRID，网格大小为0.5°×0.5°，在赤道地区长约55 km；在进行多源数据时空匹配时，对来自奥斯陆和平研究所的数据，因有对应网格的编码信息，可通过网格的编码进行匹配，栅格数据通过空间位置匹配为相应时间范围内的网格赋值，其他数据因均包含行政信息，因此通过行政区划进行匹配；时间滞后长度参考了ViEWS[19]与陈冲等[20]的预测模型，包括前1个月、 3个月和6个月；空间滞后范围根据Ward 等[45]提出的国际关系中以200 km以内为邻近的标准确定。数据处理完成后，使用随机森林模型构建和训练 5个专题要素模型、1个全要素模型和上述模型的集成模型，其中模型参数采用网格搜索算法进行优化，而后对武装冲突进行预测，比较其预测精度，并分析主要的影响因素。值得注意的是，武装冲突作为一种典型的稀有事件（rare event），在构建的9万多个时空网格中，发生冲突的仅占4.4%，单一指标难以准确反映模型的预测精度，因此采用受试者工作特征（Receiver Operating Characteristic, ROC）曲线下面积（AUROC）与精确率/召回率（Precision/Recall, PR）曲线下面积(AUCPR)相结合的方式评估模型精度[46]。本文所有实验都使用Python语言完成，用到的Python库主要包括3个部分：① sklearn库。使用其进行数据拆分、交叉验证、随机森林等模型的构建和优化以及模型预测精度评价；② pdpbox库。使用其进行重要影响因素的部分依赖分析，并制作部分依赖图；③ geopandas库。使用其进行空间可视化。技术路线如图1所示。
图1 本文技术路线

Fig. 1 Technology frame of this study

2.3.2 随机森林模型

随机森林模型是由Breiman[47]将集成算法和随机子空间方法[48]相结合提出的一种基于决策树的Bagging集成学习算法。随机森林模型对多元线性不敏感，对噪声和异常值有良好的稳健性，大量研究表明其在空间分布预测、稀有事件预测等领域表现良好[33,49-50]。在本文中，通过从构建的冲突预测数据集中抽取不同专题的数据集，分别构建基于随机森林模型的各专题要素模型和全要素模型。各模型在训练过程中，采用Bootstrap抽样方法从专题要素/全要素数据集中抽取n个训练样本集，并针对每个样本集分别构建决策树，同时随机地从全部M个影响因素中选取m个（m <M）用于分割节点。相互独立的决策树单独进行训练，最终判断每个时空网格单元是否发生冲突由各个决策树的结果投票决定。具体过程如图2所示。
图2 随机森林模型示意图

Fig. 2 Diagram of random forest model

模型参数优化方法选择网格搜索算法（GridSearchCV），该算法主要包括网格搜索GridSearch和交叉验证CV，优化的参数包括随机森林中决策树的最大深度、决策树最大深度和分割决策树的特征数量等。由于稀有事件预测的特殊性，选用平均精度（Average Precision），即PR曲线下面积（AUCPR）作为参数优化过程中模型精度的主要评价函数，同时考虑到现实情况中对人们对冲突状态的关注度更高，因此在模型中为冲突类与和平类赋予不同的类别权重，一方面符合现实的基本情况，另一方面可以有效提高模型的预测精度。

2.3.3 影响因素重要性

对影响因素的重要性进行解释是冲突预测重要的理论支撑。随机森林模型可以通过计算基尼指数（Gini Index）评估影响因素重要性，即计算每个影响因素在所有树中节点分裂不纯度的平均改变量。具体公式为：
V I M j G i n i = 1 n ∑ i = 1 n V I M i j G i n i
式中： V I M j ( G i n i )为各专题或全要素模型中输入的影响因素j的重要性； V I M i j ( G i n i )为影响因素j在模型中第i棵树中的重要性；n为模型中决策树数量。
V I M i j G i n i = ∑ m = 1 M V I M j m G i n i = ∑ m = 1 M G I m - G I l - G I r
式中：M为影响因素j在第i棵树中出现的次数； V I M j m ( G i n i )为影响因素j在决策树i的节点m的重要性； G I m为节点m的基尼指数； G I l和 G I r分别为节点m分裂出的2个新节点的基尼指数。
对于本文中对冲突是否发生进行预测的二分类问题：
G I m = 2 p ˆ m 1 - p ˆ m
式中： p ˆ m为某一时空网格单元在节点m是否发生武装冲突的概率估计值。

2.3.4 部分依赖图

部分依赖图（The Partial Dependence Plot，PDP）用于反映某一影响因素对冲突预测模型结果的边际效应[51]，即在控制其他影响因素为观测值的情况下，衡量这一影响因素值的变动对模型预测结果的影响。由此，可以分析各专题要素对武装冲突预测的影响作用，用以验证和补充既有理论。具体公式为：
f ˆ S x S = E X C f ˆ S x S , X C = ∫ f ˆ S x S , X C d P X C
式中： f ˆ S x S为各专题要素或全要素模型中的影响因素 x S的部分依赖函数； X C为模型中的其他影响因素； f ˆ为使用的机器学习模型，即基于随机森林模型的各预测模型。
P X C = ∫ p X a l l d x s
式中： ∫ p X a l l为模型中所有影响因素的边和概率密度函数。

2.3.5 预测精度评估

受试者工作特征（Receiver Operating Characteristic, ROC）曲线是机器学习中二分类问题常用的结果可视化方法，根据预测结果作为可能的判断阈值，由此计算相应的真阳性率（True Positive Rate, TPR）和假阳性率（False Positive Rate, FPR），而后以TPR作为纵坐标，FPR作为横坐标绘制而成[52]。其曲线下面积（AUROC）作为模型预测精度的评估指标，取值范围为[0,1]。AUROC越大，即曲线越靠近左上角，说明模型性能越好。
精确率/召回率（Precision/Recall, PR）曲线以精准率作为纵坐标，召回率作为横坐标绘制曲线，其中精准率代表预测为阳性的样本中真阳性样本的比例即TP/（TP+FP），召回率代表原阳性样本中被正确预测的比例即真阳性率（TPR）。其曲线下面积（AUPR）取值范围为[0,1]，数值越大，即曲线越靠近右上角，说明模型性能越好。指标详细意义可见图3混淆矩阵。
图3 混淆矩阵

Fig. 3 Confusion matrix

由图3可见，因为ROC曲线选用的真阳性率（TPR）、假阳性率（FPR）分别聚焦于阳性和阴性样本，样本的类别分布对其几乎没有影响，使其成为较为均衡的评估方法[53]。但也正因为这种特性，当样本中阴性样本数量增加，ROC曲线并不会发生改变，说明产生了大量假阳性预测，而当样本极度不平衡时，尽管假阳性预测会很多，但假阳性率（FPR）的变化会因阴性样本数量过多而变化缓慢，结果是大量阴性样本被错误预测为阳性，而ROC曲线却无法直观显示出来，导致其呈现出过于乐观的预测效果。相比之下，PR曲线完全聚焦于阳性样本，因此在不平衡样本中，用PR曲线衡量模型的预测精度会更加准确[54]。考虑到现实中，决策者和研究者更关注冲突发生的情况（即阳性样本）以及对其预测的准确性（即召回率和精准率），PR曲线更适宜作为本研究中模型的评价指标，同时也使用ROC曲线作为补充指标。

3 结果与分析

3.1 模型构建与精度分析

按照“网格-月”尺度的时空框架对2010—2021年的中南半岛国家进行划分，而后将得到的时空网格与各专题要素数据和武装冲突数据进行时空匹配，并对相关数据进行计算和处理，最终得到由共计98 208个时空网格组成的冲突预测数据集，其中每个网格均包含78个属性变量。本文以网格当月是否发生武装冲突为因变量，政治、经济、社会、地理和时空依赖性5个专题的特征为自变量，利用随机森林模型构建了各专题要素预测模型和全要素预测模型，并以冲突预测中常用的逻辑回归模型作为基准模型。。
模型具体构建过程为：① 数据准备。将进行时空匹配后的数据集按照7:3的比例拆分，抽取原始数据集中的70%作为训练集，用于训练各个预测模型；② 模型构建。分别将表1中政治要素、经济要素、社会要素、地理要素和时空依赖性对应的指标作为随机森林模型的特征变量分别构建各专题模型以及将全部指标作为特征变量构建全要素模型，使用默认参数进行训练，得到各模型的预测精度；③ 模型优化。使用网格搜索算法对各模型中的子树数量、决策树深度、节点再分割所需最小样本数、叶子结点最小样本数以及最大特征数等超参数进行调参，得到最优模型，计算各模型的AUPR。然后以各要素专题模型和全要素模型的AUPR为权重，采用加权集成的方式构建一个集成模型，并进行训练。为避免结果的随机性，以上各模型共重复训练30次；④ 精度对比。将剩余30%的数据作为验证集，计算上述各模型以及逻辑回归模型的准确率、AUROC与AUPR的平均值及95%置信区间范围，以比较其预测精度。具体结果如表2、图4所示。
表2 预测精度对比

Tab. 2 Comparison of prediction accuracy

模型名称 准确率 AUROC AUPR
逻辑回归模型 0.955 8±0 0.500 0±0 0.522 1±0
政治专题模型 0.969 3±0.000 24 0.918 6±0.000 61 0.620 8±0.001 04
经济专题模型 0.969 0±0.000 39 0.911 4±0.001 64 0.614 1±0.002 83
社会专题模型 0.967 8±0.000 11 0.931 4±0.001 28 0.657 4±0.000 57
地理专题模型 0.963 4±0.000 03 0.898 4±0.000 38 0.508 3±0.000 30
时空依赖性专题模型 0.969 3±0.000 23 0.918 5±0.000 65 0.620 8±0.001 03
全要素模型 0.972 1±0.000 19 0.933 4±0.000 82 0.674 4±0.000 70
集成模型 0.973 5±0.000 17 0.936 2±0.000 87 0.693 3±0.000 86
图4 各模型预测精度

Fig. 4 Prediction accuracy of each model

整体上看，各模型的预测准确率都在0.950 0以上，但逻辑回归模型的AUROC仅为0.5，与随机分类的精度相等，说明对于“网格-月”尺度的冲突预测，因受样本分布极不均衡的影响，传统的逻辑回归模型表现并不好，难以准确识别小概率的武装冲突事件。其他模型的准确率与AUROC均较高，说明其他模型对冲突风险的捕捉能力比逻辑回归模型更优秀，能够识别大多数的武装冲突事件，但对比各模型的AUPR发现，逻辑回归模型与地理专题模型的AUPR值在0.5左右，反映出其在预测过程中存在假阳性的误判比例较高，这无疑为当地的冲突防范增加了成本。
经对比发现，各专题模型表现相对更好，其中社会专题模型精度最高，反映出社会要素在影响武装冲突风险方面的关键作用，地理专题模型精度相对偏低，主要是因为此类要素在空间上相对固定，时间上变化缓慢，即在宏观层面差异大，微观层面差异小，导致在更精细的“网格-月”尺度上，部分样本间数据差别不明显。全要素模型在AUROC与AUPR方面相较各专题模型有了明显提高，3类精度指标平均值分别提高0.002 8~0.008 7、0.002 0~0.035 0和0.017 0~0.166 1，参考其他冲突预测工作，模型精度得到较为明显提高[33]；而由上述模型构建的集成模型，精度有了进一步优化，AUROC达到0.936 2，AUPR接近0.7，已具有较好的现实意义[20]。

3.2 武装冲突风险空间分布

以验证集中2010—2021年每年的6月为例，使用集成模型预测各时空网格的武装冲突风险水平，通过制图得到中南半岛国家内部武装冲突风险在不同时期的空间分布，具体结果如图5所示。
图5 武装冲突风险空间分布示意

Fig. 5 Spatial distribution of armed conflict risk

可以发现，在武装冲突及其风险的空间分布方面，具有较为明显的聚集性，主要分布在缅甸的克钦邦和若开邦以及泰国南部三府一带，这些高发地区面临较为严重的民族宗教矛盾以及社会不平等问题，这种突出的空间相关性也是社会专题模型的预测精度相较其他专题模型更高的主要原因。此外，在泰国东南部、柬埔寨以及越南东北部，也分布有零散的武装冲突，这些爆发冲突的地点靠近各国首都，政治敏感度较高，人员构成复杂，社会不满情绪或反对派武装分子容易在此引发冲突。在2021年缅甸发生政变后，各地暴力抗议活动不断，导致小规模武装冲突在全各各地爆发蔓延。通过对比实际发生冲突的位置与模型预测的风险分布，能够发现在大部分时间段内，高风险网格与实际冲突的位置基本吻合，进一步印证了集成模型具有较高的预测精度。

3.3 影响因素重要性分析

通过计算每个影响因素在随机森林模型中节点分裂不纯度的平均改变量及其基尼系数，得到各影响因素在全要素模型预测中的重要性。具体如图6所示。
图6 影响因素重要性

Fig. 6 Importance of influencing factors

在此基础上计算各专题下所含各影响因素的平均重要性，得到政治专题、经济专题、社会专题、地理专题以及时空依赖性的重要性分别为0.183、0.071、0.068、0.036和0.642。其中时空依赖性在武装冲突预测中重要性最高，政治专题重要性次之，经济专题与社会专题重要性相近，而地理专题在模型中的重要性最低。
各专题要素在全要素模型中的重要性与各专题模型预测能力没有完全匹配，主要是在各专题模型中预测精度较低的时空依赖性专题在全要素模型中的重要性最高，而原本精度最高的社会专题模型在全要素模型中的重要性却一般。主要原因是，时空依赖性专题由武装冲突数据产生，因此数据精度更高，而社会专题数据在理论上对武装冲突有重要影响，其专题模型的预测精度也说明了这一点，但受限于数据自身精度问题，在全要素模型中变化量不明显，导致更高精度的时空依赖性专题数据在关键节点的识别中具有较大优势。而时空依赖性专题模型自身精度较低，也说明仅凭时空依赖性难以实现对武装冲突的高精度预测，主要是因为关键的政治专题、经济专题、社会专题和地理专题等基础性数据的缺失。因此可以说明，从武装冲突的发生机制方面看，各政治、经济、社会和地理专题要素是影响武装冲突风险的根本性因素，这些要素自身及其组合变化影响冲突的发生规律，而时空依赖性则是对已发生的武装冲突时空规律的统计性总结，是武装冲突的自生属性。

3.4 重要影响因素分析

为了进一步分析武装冲突风险各影响因素的作用机制，本文选取除空间依赖性以外的各类专题中重要性较高的要素，计算其部分依赖函数，分析其对武装冲突风险的影响规律。具体如图7所示。
图7 重要影响因素部分依赖

Fig. 7 Partial dependence plot of important factor

社会专题选取的要素是当地人口规模，其与武装冲突风险呈明显正相关，变化率相对稳定，说明中南半岛国家内部武装冲突多发在人口较为稠密的地区，这些地方人员构成复杂，民族宗教矛盾也更为凸显，而且在此处爆发的武装冲突会产生更大的社会冲击，便于武装集团和组织扩大其政治影响力。
经济专题选取的要素是经济增长率，其与武装冲突风险呈负相关，当经济增长率在-5%以下时变化率较大，反之则相对平缓。说明当经济发生较大衰退时，对武装冲突风险的促进作用更为明显，此时底层群众破产、大量青年失业，发起暴乱的机会成本降低，收益明显增加，容易引起强烈动机。
政治专题选取的要素是到国界的距离，其与武装冲突风险呈现U型关系，即在靠近国界的边疆地区与远离国界的内部地区，发生武装冲突的风险均更高，这反映出国家内部武装冲突的2种主要模式，即叛乱与暴动，前者基于分离主义思想而多发在边境地区，这里弱势的少数族群集中居住，中央政府控制力相对较弱，而且容易得到外国势力支援；后者出于夺取政权或政府改革等目的，多发于内地大城市以及首都一带，易于产生较大政治影响以及招募更多人员。
地理专题选取的要素是山区覆盖率，其与武装冲突风险呈正相关，印证了传统理论认为崎岖的山地地形能为武装组织提供庇护地的解释，但在山区覆盖率达到0.7时，武装冲突风险才有明显上升，说明武装组织多藏身于范围较大的山区，一方面利于其躲藏，另一方面便于其实施运动和获取必要补给。

4 结论与讨论

本文基于“网格-月”时空尺度，耦合政治、经济、社会和地理等多源专题数据，使用由随机森林模型构建的各专题要素模型、全要素模型和集成模型来预测2010—2021年中南半岛次国家武装冲突风险，验证了各个模型的预测精度，分析了各影响因素的重要性及其对武装冲突风险的影响规律。研究结果表明：
（1）基于随机森林模型的专题要素模型、全要素模型和集成模型能够比传统的逻辑回归模型更好地预测武装冲突风险。
（2）在各专题要素模型中，社会要素模型预测精度相对最高，地理要素模型精度相对最低，而全要素模型和集成模型的精度均有相应提高。
（3）全要素模型中，时空依赖性要素重要性最高，政治专题、经济专题、社会专题、地理专题要素依次降低，说明在基础数据的支撑下，顾及时空依赖性能够明显提高模型对武装冲突风险的预测精度。
（4）通过对各专题中的重要要素进行部分依赖分析，验证了经典冲突理论，证实人口规模、经济增长、国界距离以及山区覆盖率对武装冲突风险的不同影响作用，进一步分析其影响规律，补充了现有理论的不足。
（5）与“国家-年”或“国家-月”等大尺度的冲突预测研究相比，“网格-月”尺度的冲突预测时空颗粒度更精细，一方面使得分析的数据量更大，因此预测结果更加精确，影响因素分析的可靠性也更高；另一方面，冲突风险分布更加具体，对冲突预防等现实需求有着较强的参考意义。总体而言，本文在武装冲突经典理论框架下，构建的冲突风险预测模型具有良好的精度和现实性意义，与现有研究相比，一方面有效提高了微观时空尺度上的小概率武装冲突风险预测的精度，特别是减少了大量假阳性的预测，另一方面克服了以往预测研究只重视预测精度，但忽视对其预测结果进行合理解释、无法对相关理论进行补充的不足，较好地兼顾了武装冲突风险研究的理论意义与现实需求，也为将来深入探究武装冲突风险预测尤其是对风险预测的解释即风险发生机制奠定了研究基础。
此外，由于本文使用的冲突风险预测指标体系仍存在部分遗漏，许多数据的时空精度也相对有限，因此预测精度仍有进一步提高的空间，而各专题要素时空精度差异较大，也导致各类要素的重要性分析也存在一定误差。因此，后续研究将致力于结合相关理论，丰富武装冲突预测指标体系，提高各专题要素数据的时空精度，以期为后续武装冲突风险分析与应对提供更加精确可靠的参考依据。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Collier P, Hoeffler A. On economic causes of civil war[J]. Oxford Economic Papers, 1998, 50(4):563-573. DOI:10.1093/oep/50.4.563

[2]
Collier P. On the economic consequences of civil war[J]. Oxford economic papers, 1999, 51(1):168-183. DOI:10.1093/oep/51.1.168

[3]
Diehl P F. Geography and war: A review and assessment of the empirical literature[J]. International Interactions, 1991, 17(1):11-27. DOI:10.1080/03050629108434768

[4]
Addison T, Le Billon P, Murshed S M. Conflict in Africa: The cost of peaceful behaviour[J]. Journal of African Economies, 2002, 11(3):365-386. DOI:10.1093/jae/11.3.365

[5]
Hendrix C S, Glaser S M. Trends and triggers: Climate, climate change and civil conflict in Sub-Saharan Africa[J]. Political Geography, 2007, 26(6):695-715. DOI:10.1016/j.polgeo.2007.06.006

[6]
Nel P, Righarts M. Natural disasters and the risk of violent civil conflict[J]. International Studies Quarterly, 2008, 52(1):159-185. DOI:10.1111/j.1468-2478.2007.00495.x

[7]
Brückner M. Population size and civil conflict risk: Is there a causal link?[J]. The Economic Journal, 2010, 120(544):535-550. DOI:10.1111/j.1468-0297.2010.02352.x

[8]
Collier P, Hoeffler A. Greed and grievance in civil war[J]. Oxford Economic Papers, 2004, 56(4):563-595. DOI:10.1093/oep/gpf064

[9]
Nunn N, Qian N. US food aid and civil conflict[J]. American Economic Review, 2014, 104(6):1630-66. DOI:10.1257/aer.104.6.1630

[10]
Caprioli M. Primed for violence: The role of gender inequality in predicting internal conflict[J]. International Studies Quarterly, 2005, 49(2):161-178. DOI:10.1111/j.0020-8833.2005.00340.x

[11]
Weidmann N B, Ward M D. Predicting conflict in space and time[J]. Journal of Conflict Resolution, 2010, 54(6):883-901. DOI:10.1177/0022002710371669

[12]
Ward M D, Metternich N W, Dorff C L, et al. Learning from the past and stepping into the future: Toward a new generation of conflict prediction[J]. International Studies Review, 2013, 15(4):473-490. DOI:10.1111/misr.12072

[13]
Muchlinski D, Siroky D, He J, et al. Comparing random forest with logistic regression for predicting class-imbalanced civil war onset data[J]. Political Analysis, 2016, 24(1):87-103. DOI:10.1093/pan/mpv024

[14]
Montgomery J M, Hollenbach F M, Ward M D. Improving predictions using ensemble Bayesian model averaging[J]. Political Analysis, 2012, 20(3):271-291. DOI:10.1093/pan/mps002

[15]
Mueller H, Rauh C. Reading between the lines: Prediction of political violence using newspaper text[J]. American Political Science Review, 2018, 112(2):358-375. DOI:10.1017/s0003055417000570

[16]
Eastin J. Hell and high water: Precipitation shocks and conflict violence in the Philippines[J]. Political Geography, 2018, 63:116-134. DOI:10.1016/j.polgeo.2016.12.001

[17]
Mach K J, Kraan C M, Adger W N, et al. Climate as a risk factor for armed conflict[J]. Nature, 2019, 571(7764):193-197. DOI:10.1038/s41586-019-1300-6

[18]
Cederman L E, Weidmann N B. Predicting armed conflict: Time to adjust our expectations?[J]. Science, 2017, 355(6324):474-476. DOI:10.1126/science.aal4483

[19]
Hegre H, Allansson M, Basedau M, et al. ViEWS: A political violence early-warning system[J]. Journal of Peace Research, 2019, 56(2):155-174. DOI:10.1177/0022343319823860

[20]
陈冲, 胡竞天. 空间依赖与武装冲突预测[J]. 国际政治科学, 2022, 7(2):86-123.

[Chen C, Hu J T. Spatial dependence and armed conflict prediction[J]. Quarterly Journal of International Politics, 2022, 7(2):86-123.] DOI:10.16513/j.cnki.qjip.2022.0010

[21]
Hultman L, Leis M, Nilsson D. Employing local peacekeeping data to forecast changes in violence[J]. International Interactions, 2022, 48(4):823-840. DOI:10.1080/03050629.2022.2055010

[22]
D'Orazio V, Lin Y. Forecasting conflict in africa with automated machine learning systems[J]. International Interactions, 2022, 48(4):714-738. DOI:10.1080/03050629.2022.2017290

[23]
Hao M M, Ding F Y, Xie X L, et al. Varying climatic-social-geographical patterns shape the conflict risk at regional and global scales[J]. Humanities and Social Sciences Communications, 2022, 9:276. DOI:10.1057/s41599-022-01294-2

[24]
Raleigh C, Linke, Hegre H, et al. Introducing ACLED: An armed conflict location and event dataset[J]. Journal of peace research, 2010, 47(5):651-660. DOI:10.1177/0022343310378914

[25]
GDELT. The GDELT Project[EB/OL]. [2023-03-10]. https://www.gdeltproject.org/.

[26]
Tollefsen A F, Strand H, Buhaug H. PRIO-GRID: A unified spatial data structure[J]. Journal of Peace Research, 2012, 49(2): 363-374. DOI:10.1177/0022343311431287

[27]
World Bank. World Bank Open Data[EB/OL]. [2023-03-10]. https://data.worldbank.org/.

[28]
National Geophysical Data Center. Operational Line scan System-data Description[EB/OL]. (2008-09-06) [2023-03-10]. http://www.ngdc.noaa.gov/dmsp/sensors/ols.html.

[29]
Elvidge C D, Zhizhin M, Ghosh T, et al. Annual time series of global VIIRS nighttime lights derived from monthly averages: 2012 to 2019[J]. Remote Sensing, 2021, 13(5):922. DOI:10.3390/rs13050922

[30]
Wucherpfennig J, Weidmann N B, Girardin L, et al. Politically relevant ethnic groups across space and time: Introducing the GeoEPR dataset[J]. Conflict Management and Peace Science, 2011, 28(5):423-437. DOI:10.1177/0738894210393217

[31]
Stevens F R, Gaughan A E, Linard C, et al. Disaggregating census data for population mapping using random forests with remotely- sensed and ancillary data[J]. PLoS One, 2015, 10(2): e0107042. DOI:10.1371/journal.pone.0107042

[32]
Rosvold E L, Buhaug H. GDIS, a global dataset of geocoded disaster locations[J]. Scientific data, 2021, 8(1):61. DOI:10.1038/s41597-021-00846-6

PMID

[33]
Blair R A, Sambanis N. Forecasting civil wars: Theory and structure in an age of “big data” and machine learning[J]. Journal of Conflict Resolution, 2020, 64(10):1885-1915. DOI:10.1177/0022002720918923

[34]
Buhaug H, Lujala P. Accounting for scale: Measuring geography in quantitative studies of civil war[J]. Political Geography, 2005, 24(4):399-418. DOI:10.1016/j.polgeo.2005.01.006

[35]
Buhaug H, Gates S. The geography of civil war[J]. Journal of Peace Research, 2002, 39(4):417-433. DOI:10.1 177/0022343302039004003.

[36]
Hegre H, Buhaug H, Calvin K V, et al. Forecasting civil conflict along the shared socioeconomic pathways[J]. Environmental Research Letters, 2016, 11(5):054002. DOI: 10.1088/1748-9326/11/5/054002

[37]
Moyer J D, Matthews A S, Rafa M, et al. Identifying patterns in the structural drivers of intrastate conflict[J]. British Journal of Political Science, 2023, 53(2):749-756. DOI:10.1017/S0007123422000229

[38]
Wucherpfennig J, Weidmann N B, Girardin L, et al. Politically relevant ethnic groups across space and time: Introducing the GeoEPR dataset[J]. Conflict Management and Peace Science, 2011, 28(5):423-437. DOI:10.1177/0738894210393217

[39]
Bowlsby D, Chenoweth E, Hendrix C, et al. The future is a moving target: Predicting political instability[J]. British Journal of Political Science, 2020, 50(4):1405-1417. DOI: 10.1017/s0007123418000443

[40]
Wegenast T, Schneider G. Ownership matters: Natural resources property rights and social conflict in Sub-Saharan Africa[J]. Political Geography, 2017, 61:110-122. DOI: 10.1016/j.polgeo.2017.07.007

[41]
Bazzi S, Blair R A, Blattman C, et al. The promise and pitfalls of conflict prediction: Evidence from Colombia and Indonesia[J]. Review of Economics and Statistics, 2022, 104(4):764-779. DOI:10.1162/rest_a_01016

[42]
陈冲. 机会、贪婪、怨恨与国内冲突的再思考——基于时空模型对非洲政治暴力的分析[J]. 世界经济与政治, 2018(8):94-127,158.

[Chen C. Rethinking opportunity, greed, grievance and internal conflict: A spatio-temporal analysis of African political violence[J]. World Economics and Politics, 2018(8):94-127,158.]

[43]
Ward M D, Gleditsch K S. Location, location, location: An MCMC approach to modeling the spatial context of war and peace[J]. Political Analysis, 2002, 10(3):244-260. DOI:10.1093/pan/10.3.244

[44]
Collier P. Breaking the conflict trap: Civil war and development policy[M]. Washington, DC: World Bank, 2003.

[45]
Ward M D, Gleditsch K S. Spatial regression models[M]. London: Sage Publications, 2018.

[46]
Ward M D, Beger A. Lessons from near real-time forecasting of irregular leadership changes[J]. Journal of Peace Research, 2017, 54(2):141-156. DOI:10.1177/0022343316680858

[47]
Breiman L. Random forests[J]. Machine Learning, 2001, 45(1):5-32. DOI:10.1023/A:1010933404324y

[48]
Ho T K. The random subspace method for constructing decision forests[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(8):832-844. DOI: 10.1109/34.709601

[49]
张嘉琪, 杜开虎, 任书良, 等. 多源空间大数据场景下的家装品牌线下广告选址[J]. 武汉大学学报·信息科学版, 2022, 47(9):1406-1415.

[Zhang J Q, Du K H, Ren S L, et al. Site selection of outdoor advertisement for home decoration brands based on multi-source spatial big data[J]. Geomatics and Information Science of Wuhan University, 2022, 47(9):1406-1415.] DOI:10.13203/j.whugis20190468

[50]
刘坚, 李树林, 陈涛. 基于优化随机森林模型的滑坡易发性评价[J]. 武汉大学学报·信息科学版, 2018, 43(7):1085-1091.

[Liu J, Li S L, Chen T. Landslide susceptibility assesment based on optimized random forest model[J]. Geomatics and Information Science of Wuhan University, 2018, 43(7):1085-1091.] DOI:10.13203/j.whugis20160515

[51]
Friedman J H. Greedy function approximation: A gradient boosting machine[J]. Annals of Statistics, 2001, 29(5):1189-1232. DOI:10.1214/aos/1013203451

[52]
王运生, 谢丙炎, 万方浩, 等. ROC曲线分析在评价入侵物种分布模型中的应用[J]. 生物多样性, 2007(4):365-372.

[Wang Y S, Xie B Y, Wan F H, et al. Application of ROC curve analysis in evaluating the performance of alien species'potential distribution models[J]. Biodiversity Science, 2007(4):365-372.] DOI:10.3321/j.issn:1005-0094.2007.04.005

[53]
Fawcett T. An introduction to ROC analysis[J]. Pattern Recognition Letters, 2006, 27(8):861-874. DOI:10.1016/j.patrec.2005.10.010

[54]
Davis J, Goadrich M. The relationship between precision-recall and ROC curves[C]//Proceedings of the 23rd international conference on Machine learning. New York: Association for Computing Machinery, 2006:233-240. DOI: 10.1145/1143844.1143874

Options
文章导航

/

〈 〉