EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 11: 2120 - 2133

DOI: https://doi.org/10.12082/dqxxkx.2023.230206

地球信息科学理论与方法

顾及空间分布的改进薄板样条矢量数据几何精度降低方法

  • 王敏璇 , 1 ,
  • 阳璇 1 ,
  • 查启航 1 ,
  • 孙睿 1 ,
  • 任娜 , 1, 2, *
展开
  • 1.虚拟地理环境教育部重点实验室(南京师范大学)， 南京 210023
  • 2.地理信息安全与应用湖南省工程研究中心，长沙 410000
*任娜（1981— )，女，山东莱西人，博士，教授，研究方向为地理数据安全。E-mail:

王敏璇（2002— ），女，江苏镇江人，本科生，研究方向为地理数据安全。E-mail:

收稿日期: 2023-04-19

  修回日期: 2023-06-05

  网络出版日期: 2023-11-02

基金资助

国家自然科学基金项目(42071362)

国家自然科学基金项目(41971338)

国家重点研发计划项目(2022YFC3803600)

收起

A Vector Data Geometric Accuracy Reduction Method Considering Spatial Distribution Based on the Improved Thin Plate Spline Model

  • WANG Minxuan , 1 ,
  • YANG Xuan 1 ,
  • ZHA Qihang 1 ,
  • SUN Rui 1 ,
  • REN Na , 1, 2, *
Expand
  • 1. Key Laboratory of Virtual Geographic Environment of Ministry of Education, Nanjing Normal University, Nanjing 210023, China
  • 2. Hunan Engineering Research Center of Geographic information security and application, Changsha 410000, China
*REN Na, E-mail:

Received date: 2023-04-19

  Revised date: 2023-06-05

  Online published: 2023-11-02

Supported by

National Natural Science Foundation of China(42071362)

National Natural Science Foundation of China(41971338)

National Key Research and Development Program of China(2022YFC3803600)

Fold

摘要

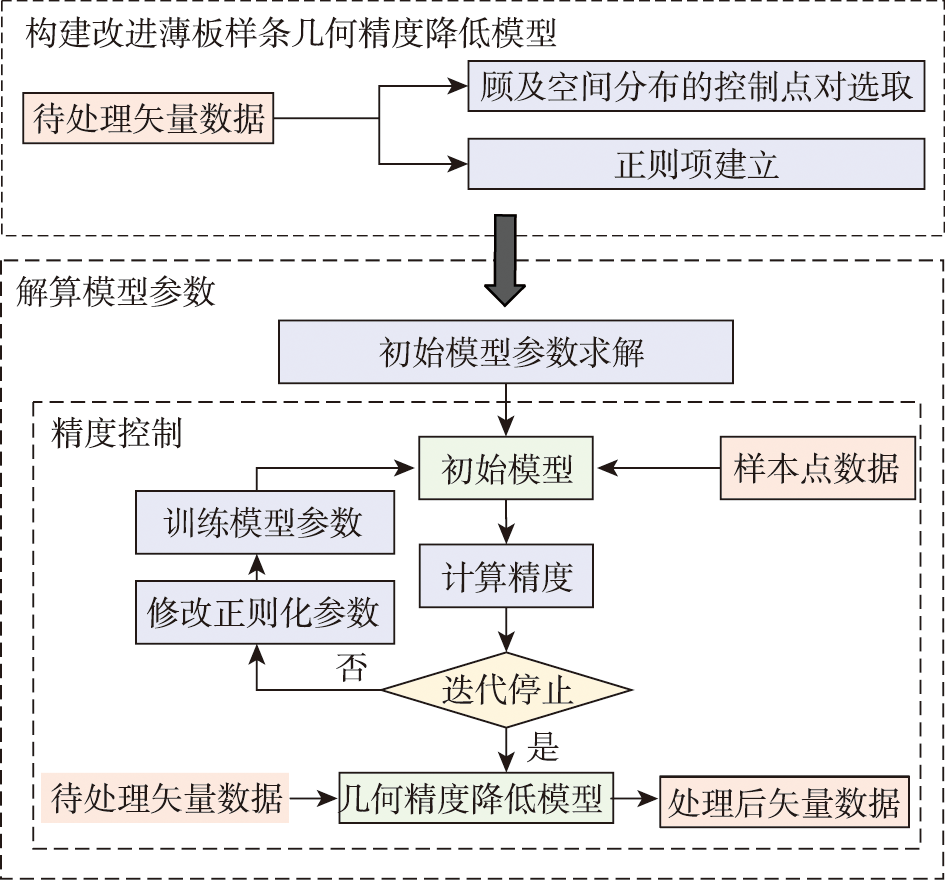
随着测绘地理信息数据的共享应用成为趋势，地理数据的精度降低处理成为数据公开前不可缺少的环节。基于传统薄板样条插值的坐标偏移模型利用本身优势可以实现坐标变换从而降低数据的几何精度，但是该模型受控制点精确程度影响大，抗噪声能力弱，若控制点选取不合理则易产生要素形态畸变的问题，导致数据无法被使用。本文提出了一种顾及空间分布的改进薄板样条矢量数据精度降低方法，首先通过四叉树索引结构进行格网划分，分别在网格内选取控制点，使得选出的控制点对和原始矢量数据在空间分布特征和数量特征上一致。然后基于Tikhonov正则化思想在原始坐标偏移模型中添加正则化项，弱化控制点的约束作用，增强模型抗噪声能力。本文选取不同尺度、不同类型以及多图层数据进行精度降低测试，实验表明： ① 本文算法针对不同实验数据都可以满足自然资源部95号文公开地图精度不高于10 m的要求，模型普适性好且效率较高; ② 本文算法能有效提高模型的稳定性以及减少处理后坐标突变的问题。以南京市鼓楼区线数据为测试数据的计算结果表明，精度降低后数据空间方向一致性为99.62%，图形形态相似性为99.99%，均优于传统薄板样条模型与高斯基函数坐标偏移模型; ③ 本文算法使精度降低后数据的偏移效果实现局部一致性以及全局随机性，精度降低后数据在明攻击或盲攻击的情况下精度仍能保持在10 m左右，说明坐标偏移结果不易被恢复。本研究证明提出的顾及空间分布的改进薄板样条精度降低模型兼顾处理后数据的安全性以及可用性，促进了矢量地理数据的社会化应用。

关键词： 地理信息安全; 几何精度降低; 正则化; 四叉树; 薄板样条模型; 矢量地理数据; 拓扑保持性; 非线性变换

本文引用格式

王敏璇 , 阳璇 , 查启航 , 孙睿 , 任娜 . 顾及空间分布的改进薄板样条矢量数据几何精度降低方法[J]. 地球信息科学学报, 2023 , 25(11) : 2120 -2133 . DOI: 10.12082/dqxxkx.2023.230206

Abstract

With the sharing and application of surveying and mapping geographic information data, the accuracy reduction of geographic data prior to data release has become an essential step to avoid leaks of classified high-precision data that could threaten national security. Geometric accuracy reduction is an important component of geographic data accuracy reduction, which refers to transforming the coordinates of element points and reducing the precision of the publicly available data. The traditional thin plate spline interpolation model can achieve coordinate transformation with its advantages. However, this model is easily influenced by the accuracy of control points and is not robust against noise. For example, if the control points are not selected reasonably, data morphological distortion easily occurs due to noisy control points, resulting in poor data quality. In this article, a vector data accuracy reduction method considering spatial distribution based on the improved thin plate spline model is proposed. Firstly, the grid is divided by quadtree index structure. The control points are selected in each grid, so that the selected control points are consistent with the original vector data in terms of spatial distribution and quantitative characteristics. Then, regularization terms are added to the traditional function based on Tikhonov regularization to weaken the constraint imposed by control points and enhance the anti-noise ability of the model. We choose vector geographic data with different scales and types and multi-layer vector geographic data for experiments. Results show that: (1) Based on different experimental data, our algorithm can meet the requirement that the procerssed data precision should not exceed 10 meters according to the No.95 official document from the Ministry of Natural Resources, which demonstrates the model adaptability and efficiency; (2) The algorithm can effectively improve model stability and reduce abrupt changes in coordinates. The experiment conducted on the line data of Gulou District in Nanjing shows that, the processed data exhibit a spatial directional consistency of 99.62% and a graphical morphological similarity of 99.99%, which outperforms the results based on traditional thin plate spline model and guassian radial basis function model; (3) The offset effect is locally consistent and globally random. The processed of the processed data after either direct attacking or blind attacking remains around 10 meters, indicating the difficulty of recovering processed data to original results. This research proves that the proposed model can balance data's security and availability, promoting social application of vector geographic data.

Key words： geographic information security; geometric accuracy reduction; regularization; quadtree; thin plate spline model; vector geographic data; topology maintenance; nonlinear transformation

1 引言

1.1 公开地图精度降低要求

近年来，测绘地理信息产业不断发展，测绘地理数据作为当今社会化地理数据的基础来源，具有巨大的社会需求。矢量数据作为其中一种重要的地理数据，由于其基础性、普适性和流通性等特点，得到了广泛的应用。然而正是因为其易于被复制和分发，矢量数据中的敏感信息极有可能被泄露，严重威胁国家安全，所以实现地理数据共享必须首先保证其安全。2020年自然资源部95号文中要求公开地图位置精度不得高于10 m、等高距不得小于20 m[1]。因此，在信息交互中如何防止敏感地区信息泄露，既满足安全性要求又满足社会发展需要，成为地理数据共享的研究热点。
地理数据精度降低技术为解决上述问题提供了可行的途径。地理数据精度降低是指按照相关文件的要求过滤、删除涉密信息内容，降低空间精度，形成可在非涉密网环境中使用的公开数据集[2]。对于矢量数据的精度降低方法包括属性处理精度处理和几何精度降低，本文基于几何精度降低展开。
几何精度降低是地理数据精度降低的重要内容，指通过对数据的坐标进行偏移，增加数据误差，从而达到降低数据精度的目的[3]。综合考虑矢量数据特性与实际应用需求，几何精度降低方法应满足以下要求：
（1）满足目标精度要求。精度降低后的数据精度应满足国家保密要求。参照国家安全技术指标，我国现阶段对公开地图要求为位置精度不得高于10 m;
（2）数据可用。为达到社会化应用，合理的精度降低效果应具备以下几点：① 处理后数据应具有光滑渐进效果，避免突变现象产生;② 处理后数据与原始数据具有拓扑一致性，包括空间方向一致性、要素形态相似性，使要素形态与空间关系能够得到维护;
（3）模型可控。能够通过调控模型参数控制几何精度降低效果，满足相应使用需求;
（4）模型安全性高。在对精度降低后数据分别进行明攻击与盲攻击的情况下，数据都应当不易被纠正恢复，从而避免敏感信息泄露;
（5）普适性。对于单图层数据，不同尺度数据经精度处理后应均能够满足目标精度要求;对于多图层数据，各图层采用相同的几何精度降低方法后应能取得统一的偏移效果;
（6）算法高效。精度处理过程应尽量减少人工干预，实现高效高质量几何精度降低。

1.2 几何精度研究背景

针对几何精度降低，目前的精度处理模型主要分为线性变换和非线性变换两类。线性变换是基于一次函数的变换，包括相似变换[4]、射影变换[5]、仿射变换[6]等，是普遍使用的几何纠正方式。白晓春等[7]对矢量数据进行控制点连接和线性变换，校正后的数据满足国家对公众版地图上线要素精度降低的要求且能较好的与遥感影像契合，拓扑关系可以得到保持，但是线性变换处理后易被逆向恢复，安全性较低。
非线性变换指输入值与变换后的输出值之间不存在线性关系，非线性变换包括多项式变换[8,9]、三角函数变换[10]、径向基函数变换[11]等方法，能够有效提高安全性。其中径向基函数是一个取值仅依赖于离原点距离的实值函数，常用的径向基函数有高斯基函数、正定紧支撑函数、薄板样条函数等。于辉[12]利用高斯基函数模型对数据进行精度降低处理，处理结果满足了光滑偏移、控制点精确变换的要求，但图形变换受控制点影响较大，很难控制坐标的整体变换方向;高隆杰[13]利用正定紧支撑径向基对数据进行几何精度降低处理，限制了函数模型节点的作用范围，但精度处理过程中发现函数变化剧烈时会影响数据的视觉效果和可用性。薄板样条函数具有平滑、连续等特点，常用于插值，在曲面拟合、图像配准中具有广泛的应用[14⇓-16]。此外薄板样条函数插值不需要控制点规则排列，适合离散点插值，特别是在复杂环境中也能得到较好的插值结果[17]。因此，本文选择薄板样条函数模型对待处理点集的坐标偏移量进行插值从而降低整体精度。但是，薄板样条函数存在插值结果精确性建立在对应选择点的精确性的基础上的问题[18]。张永军[19]指出在拟合滤波分类面时，普通的薄板样条插值要求插值面严格经过所有的控制点，即使少量异常或噪声点对插值面的构建仍具有明显影响，解决此类问题往往需要手动减少误差或采取相应平滑技术。
为了减少噪声控制点的存在和干扰，使控制点的选择和几何精度降低模型自适应待处理数据，避免发生精度降低后要素形态畸变的问题，本文提出了一种顾及空间分布的改进薄板样条几何精度降低模型。首先利用四叉树索引结构选取控制点对，使控制点对具有原始矢量数据空间上的分布特征和数量特征，然后基于正则化薄板样条函数模型迭代解算参数，最后将求解得到的模型用于全局精度处理，以此提高模型的稳定性，实现数据的高质高效几何精度降低。

2 几何精度降低模型

本文基于薄板样条函数建立从原始坐标(x，y)到偏移后坐标(x'，y')之间的函数映射。通过选取同名点对作为控制点，解算初始参数。然后在图幅范围内选取若干样本点进行迭代处理，更新正则化参数并调整精度处理模型中系数，直至中误差满足目标精度的要求，实现控制精度。建立系数完备的坐标偏移模型后，对待处理要素点的坐标进行插值，得到偏移后结果。技术流程如图1所示。
图1 算法流程

Fig. 1 Technical route in this study

2.1 薄板样条模型概述

薄板样条函数(Thin-Plate Splines，TPS)[20]是一种空间数据插值方法，是基于样条线的平滑技术。薄板样条函数具有明确的物理意义，它描述了给定n个控制点Pi(Xi，Yi) (i=0，1，2，…，n)后，对金属铁板进行刚性变换，最终找到一个穿过所有控制点的曲率最小，即能量最小的连续光滑表面。
薄板样条插值函数模型由局部趋势函数和基本函数组合而成，为待处理点x坐标与y坐标分别设计不同系数的插值模型，坐标偏移表达式如下所示：
x ' = f x ( x , y ) = a + a x x + a y y + ∑ j = 1 n u m [ w j × U ( r ) ]
y ' = f y ( x , y ) = a ' + a x ' x + a y ' y + ∑ j = 1 n u m [ w j ' × U ( r ) ]
式中：(x，y)代表原始点坐标;(x'，y')代表偏移后点坐标;a+axx+ayy 表示局部趋势函数;(a，ax，ay，wj)和(a'，ax'，ay'，wj')是两组待求解的模型系数，确定最逼近所有控制点的线性平面; U(r)为基本样条函数，作用于生成曲率最小的表面，可表示为： U ( r ) = r 2 × l n r;num为插值控制点个数;r为所求点与控制点i之间的欧氏距离;wi为对应各个控制点的权值，求解时具有如下约束条件：
∑ i = 1 n u m w i = 0
∑ i = 1 n u m x i w i = ∑ i = 1 n u m y i w i = 0

2.2 改进薄板样条几何精度降低算法

2.2.1 顾及空间分布的控制点选取方法

基于插值思想的变换模型需要利用已有控制点对作为已知数据来求解插值曲线，控制点对的选取情况直接影响到模型各参数的计算。由于矢量数据具有分布不均与要素量大小不一的特征[21]，若直接使用全局均匀选取控制点的方法，在缺少人工手动减少误差的情况下，控制点偏移量与偏移方向难以根据待处理数据的特征进行控制，局部的插值结果则会可能受到干扰。
因此，本文提出顾及空间分布的控制点选取方法，即考虑待处理矢量数据的数据量以及所包含的要素节点在空间上呈现出数量分布不均的情况，建立四叉树索引结构对图幅进行划分，从而对控制点的设置过程进行相应的约束，实现步骤如图2所示。将矢量数据的所有要素转为点集,并进行遍历，将点集中的点存储至四叉树对应节点中;若该四叉树节点内已存储点数大于限制点数，则对该节点范围进行划分，然后重新判断点与新节点范围的包含关系并进行存储。四叉树每个节点代表一个矩形范围，要素点集存储完毕后，选出存储有点要素的叶子节点，在其四至范围内均匀选择相同个数控制点，并按照叶子节点的遍历顺序设置每一个控制点偏移的方向与距离，使偏移方向在空间上渐进变化，最终构造出用于拟合的同名点对。
图2 改进控制点对选取方法

Fig. 2 Improved control point selection method

图3表示范围内有50个点要素，在分布不均的情况下，根据分布情况以及每个节点最多包含8个点要素的设定条件，对该区域进行多层划分，最终得到如图3所示的多级格网划分结果。
图3 四叉树结构划分格网

Fig. 3 Grid division based on quadtree structure

图4所示，在相同个数的控制点作用下，图4(a)为已有几何精度降低算法中常用的均匀控制点对作用下得到的偏移结果，图4(b)为顾及分布的控制点对插值得到偏移结果。如图所示，图4(a)中的边界处受全局控制点对影响，坐标出现突变，形态发生剧烈变化，边界处更为明显;图4(b)中可以看出局部区域的控制点偏移效果能够得到控制，尤其是要素密集区域，得到结果的几何形态也更趋于稳定。
图4 控制点对选取方法对比

Fig. 4 Comparison of control point selection methods

2.2.2 正则项建立

薄板样条能近似拟合复杂曲线形状，泛化能力弱，当选取的控制点对存在噪声时，会产生局部坐标突变、拓扑关系变化等问题，本文对插值函数进行吉洪诺夫正则化处理，提高模型抗噪能力。吉洪诺夫正则化(Tikhonov regularization)是通过正则化参数和正则化矩阵作用于原病态矩阵来改善矩阵的病态性[22]，从而使求解得到的未知参数更为稳定且可靠。
添加正则化项后的样条基函数为：
U ' ( r i j ) = r i j 2 × l n r i j + λ 2 × c o s ( r i j ) × σ
其中：
λ = 1 n u m 2 ∑ i n u m ∑ j n u m r i j
式中：num表示选取用做插值的控制点个数;λ为正则化固定系数; rij表示控制点i与控制点j之间的欧氏距离。在正则化项中添加余弦项并用两点之间距离作为自变量，使正则化效果具备周期性，同时对此项起数值上的约束作用。正则化项中σ为正则化参数，控制正则化程度，若σ=0，正则化项未起平滑作用，函数模型为普通薄板样条模型;若σ趋向无穷大，则样条函数受控制点间距离的控制作用趋向无穷大，此时正则化项所起的平滑效果也将退化。因此，在求解过程中需要根据目标精度迭代计算，以求得合适的正则化参数。
正则化避免过拟合现象作用效果见图5，其中，图5(a)表示基于普通薄板样条几何精度降低模型的坐标偏移效果，当对控制点进行噪声干扰时，偏移结果存在明显拓扑错误与突变;图5(b)表示在选取相同的控制点对的情况下，基于正则化薄板样条几何精度降低模型的坐标偏移效果。与图5(a)对比可见，在局部突变处有较大改善，整体偏移效果趋于光滑渐进，边界处也更加稳定。此方法在保持局部偏移趋势的同时，有效提高了模型的拓扑保持和特征保持能力。
图5 正则化前后效果对比

Fig. 5 Effect comparison before and after regularization

2.3 解算模型参数

2.3.1 初始模型参数求解

（1）基于目标地图范围以及要素点集的空间分布划分格网;基于划分完各格网的四至范围选取相同个数的控制点Pi(sXi，sYi) (i=0，1，2，…，num)，并赋予相应偏移量，得到偏移后的控制点Ti(tXi，tYi) (i=0，1，2，…，num);
（2）基于模型变量及参数对应关系设置数学矩阵：设控制点i相对于控制点j的正则化基本函数输出值U(rij)为矩阵K;输入原控制点Pi(sXi，sYi) (i=0，1，2，…，num)坐标，并设其为矩阵P;将矩阵K、矩阵P、转置矩阵PT与零矩阵设为矩阵L;输入偏移后控制点Ti(tXi，tYi) (i=0，1，2，…，num)坐标，设为矩阵Y;
K = U ( r 11 ) U ( r 12 ) U ( r 13 ) . . . U ( r 1 n u m ) U ( r 21 ) U ( r 22 ) U ( r 23 ) . . . U ( r 2 n u m ) U ( r 31 ) U ( r 32 ) U ( r 33 ) . . . U ( r 3 n u m ) . . . . . . . . . . . . . . . U ( r n u m 1 ) U ( r n u m 2 ) U ( r n u m 3 ) . . . U ( r n u m n u m )
P = 1 x 1 y 1 1 x 2 y 2 1 x 3 y 3 . . . . . . . . . 1 x n u m y n u m
L = K P P T O
Y = x 1 ' y 1 ' x 2 ' y 2 ' x 3 ' y 3 ' . . . . . . x n u m ' y n u m ' 0 0 0 0 0 0
W = w x 1 w y 1 w x 2 w y 2 w x 3 w y 3 . . . . . . w x n u m w y n u m a a ' a x a x ' a y a y '
（3）采用LU分解法求解矩阵L的逆矩阵L-1，逆矩阵求解速度得到大幅提高;
（4）根据各矩阵间算术关系式，得到求解薄板样条几何精度降低模型各变量前系数及权值矩阵的求解方法： W = L - 1 × Y。
（5）获得权值矩阵W，正则化薄板样条函数初始模型构建完毕。

2.3.2 处理精度控制

本文采用均方误差最小化准则(Minimization Criterion of Mean-square Error)[23]，通过选取样本数据降低几何精度，计算与原数据中误差并与目标中误差比较，更新正则化参数并迭代计算，使处理后中误差逼近目标中误差，由此获得最终正则化参数。此方法对参数进行了优化同时提高了模型处理精度的控制效果。在此过程中对样本点坐标偏移，也对全局几何精度降低效果起到了约束作用。具体求解步骤如下所示：
（1）根据要素空间分布选取样本点SPi(ssXi，ssYi) (i=0，1，2，…，snum);
（2）读取样本点坐标值，输入薄板样条插值模型，进行坐标移位，计算偏移后样本点坐标TPi(tsXi，tsYi) (i=0，1，2，…，snum);
（3）根据中误差计算公式，得到第一次精度降低后与原数据中误差TRMS，具体公式为：
T R M S = 1 s n u m ∑ i = 1 s n u m [ ( s s X i ' - t s X i ) 2 + ( s s Y i ' - t s Y i ) 2 ]
（4）将中误差与目标精度RMS比较，判断是否满足约束条件0<TRMS-RMS<1;如不满足目标中误差要求，则对正则化参数σ进行调整，调整方法为：
σ = σ × R M S T R M S
（5）根据更新后的正则化参数，重复执行2.3.1节第(2)—第(5)步求解系数矩阵;
（6）得到新的系数矩阵后，重复执行本小节第(2)—第(4)步，进行下一轮判断;
（7）当处理后精度在目标允许误差范围内，视为达到终止条件，迭代完成，得到最终正则化参数σ;
（8）保存迭代完成后的正则化参数σ，得到完整薄板样条插值模型，并保存密钥。

3 实验结果及分析

3.1 矢量数据几何精度降低实例

实验以shapefile格式的点、线、面矢量数据为例进行实验说明。测试的矢量数据分别为来源于OpenStreetMap(www.openstreetmap.ie)的全国主要铁路线数据、江苏省景区POI数据、南京市鼓楼区道路线数据以及来源于地理监测云平台(www.dsac.cn)的江苏省南京市绿地面数据四级行政区划范围的数据，具备尺度上的多样性。同时， 4组数据所包含的节点个数也呈现了数值上的变化。因此，本文用作验证的矢量数据在空间上呈现不同的复杂程度，具有代表性。用作测试的矢量数据的数据量、坐标范围等基本信息如表1所示。
表1 待处理数据基本信息

Tab. 1 Basic information of the data to be prcessed

数据 类型 范围 要素节点数/个 坐标范围
1 线要素 全国 47 580 84°42′29″ E—131°12′45″ E， 21°10′26″ N—53°00′16″ N
2 点要素 江苏省 8 222 116°34′42″ E—121°42′15″ E， 30°51′38″ N—34°54′52″N
3 面要素 南京市 22 614 118°29′26″ E—119°06′53″ E， 31°16′58″ N—32°31′47″ N
4 线要素 鼓楼区 6 874 118°42′56″ E—118°46′41″ E，32°02′22″ N—32°05′30″ N
由于测试数据组的坐标采用地理坐标系表示，在精度降低处理之前首先进行投影变换的操作。
基于前文2.2.1节所述的构建四叉树结构选取控制点的方法，得到顾及空间分布的控制点对。图6为4组数据的控制点对空间分布图，红色部分为局部区域放大图。在全局上，控制点对的空间分布与各组原始数据的覆盖范围一致，能够作用于范围内的所有要素进行拟合。在局部上，测试数据要素节点密集区域的控制点选取个数明显增加，而在要素节点相对稀疏的区域，控制点个数也呈现逐渐减少的趋势。
图6 顾及待处理数据空间分布的控制点选取结果

Fig. 6 Results of control points considering spatial distribution of the data to be processed

3.2 几何精度降低结果分析

3.2.1 优化薄板样条模型精度降低效果

对4组矢量数据分别进行精度降低，得到的处理后数据与原数据中误差均满足目标精度10 m的要求，并且算法运行效率较高（表2）。图7为四组数据精度降低前后可视化效果图，红色要素表示原始数据，绿色要素表示精度降低后的数据。红色放大区域显示，精度降低后数据相对于原数据存在明显偏移，同时，局部区域内要素的偏移量与偏移方向均保持统一，处理后数据基本保持原始数据的几何、拓扑特征，未出现明显的畸变问题。
表2 处理后精度及最大最小偏移量统计

Tab. 2 Statistics of RMSE and maximum/minimum offset value of the processed data

数据 精度/m 速度/(kb/s) 最小偏移量/m 最大偏移量/m
1 10.246 1 363.342 0 0.09 13.32
2 10.517 3 644.348 0 0.19 17.71
3 10.756 7 756.551 6 0.54 16.33
4 10.467 6 526.079 4 0.28 12.59
图7 基于改进薄板样条模型的精度降低前后数据可视化

Fig. 7 Data visualization before and after accuracy reduction based on the improved thin plate spline model

图8为对多图层矢量数据进行精度降低可视化效果图，在相同模型的作用之下，局部区域相同坐标的偏移效果相同，要素与要素、点、线、面3个图层之间的拓扑关系保持较好。同时， 3个图层的处理后中误差分别为12.010 1 m、10.655 7 m、10.013 1 m，达到精度要求。综上，验证得到本文几何精度降低模型可以满足不同数据类型、不同数据量以及多个图层的矢量地理数据的精度降低要求，具有良好的普适性。
图8 多图层矢量数据精度降低前后数据可视化效果

Fig. 8 Visualization of multi layer vector geographic data before and accuracy reduction

表3、图9为4组处理后数据相对于原数据的偏移方向统计表与统计图。从全局统计量来看，本文的改进薄板样条模型算法方法能够实现在4个方向上均有偏移且统计个数近似均匀分布的效果，证明本文几何精度降低方法具有全局随机性。表4、 图10为4组精度降低后数据相对于原数据的偏移量统计表与统计图，图10中曲线为对偏移量统计数据拟合的高斯曲线。拟合结果反映偏移量在10 m处较为集中，统计直方图与正态分布曲线基本吻合，且不存在过于剧烈的偏移效果(大于20 m)，稳定性较好。综上，本文方法有效地实现全局随机坐标偏移效果与局部一致坐标偏移效果，保证了数据可用。
表3 精度降低后要素节点偏移方向统计

Tab. 3 Statistics of offset direction of the nodes after accuracy reduction

数据 偏移方向
东北/个 占比/% 东南/个 占比/% 西北/个 占比/% 西南/个 占比/%
1 9 766 20.53 13 009 27.34 14 468 30.41 10 337 21.73
2 2 221 27.01 1 804 21.94 2 028 24.67 2 169 26.38
3 5 502 24.33 5 550 24.54 5 662 25.04 5 900 26.09
4 1 982 28.83 1 453 21.14 1 929 28.06 1 510 21.97
图9 精度降低后要素节点偏移方向统计

Fig. 9 Statistics of offset direction of the nodes after accuracy reduction

表4 精度降低后要素节点偏移量统计

Tab. 4 Statistics of offset value of the nodes after accuracy reduction

数据 偏移量/m
0~2 2~5 5~8 8~11 11~14 14~17 17~20 >20
1 840 3 624 13 553 23 026 6 537 0 0 0
2 107 334 2 669 3 835 1 076 197 4 0
3 438 4 103 7 140 10 001 568 364 0 0
4 165 637 1 808 3 463 801 0 0 0
图10 精度降低后要素节点坐标偏移量统计

Fig. 10 Statistics of offset value of the nodes after accuracy reduction

评价矢量地理数据几何精度降低模型的安全性通过对已降低精度的地理数据进行校正攻击来实现，包括明攻击和盲攻击2种方法。本文通过在ArcGIS软件中对处理后鼓楼区线数据进行仿射变换校正实现盲攻击测试，仿射变换模型是应用于二维平面的一种变换模型，是平移、缩放、翻转、旋转和剪切的组合，在图像图形方面应用广泛。在未知密钥情况下，共选取4组不同个数的同名点对，选取个数分别为50、150、300、500个，进行校正。明攻击是已知密钥与精度降低模型的情况下，将已选取的偏移前后同名控制点交换，然后输入薄板样条模型进行参数解算，对已处理的数据进行校正，计算校正后数据与原数据的中误差判断能否被恢复。
结果显示（表5），校正后精度无明显提高，在目标中误差值附近波动。未知或已知密钥和模型的情况下都无法通过变换实现逆向恢复，模型具备良好抗攻击性，安全性高。
表5 明攻击/盲攻击后数据精度统计

Tab. 5 Statistics of RMSE after clear attacking and blind attacking

攻击方式 数据 同名点/对 精度/m
盲攻击 校正数据1 50 10.222 3
校正数据2 150 10.133 5
校正数据3 300 10.225 6
校正数据4 500 9.955 6
明攻击 校正数据5 33 11.236 4

3.2.2 算法对比

在选取相同控制点对的情况下，以鼓楼区线数据为例，本文将改进薄板样条精度降低模型与传统薄板样条模型、高斯径向基函数模型分别进行测试对比。结果反映（表6），传统TPS模型与高斯基函数模型都可以满足坐标偏移后精度要求，精度分别为10.552 2 m和12.389 0 m。同时基于图形复杂度相似性[24]与空间方向一致性[25]对3组结果进行计算。计算结果显示，在空间方向一致性上，改进薄板样条处理结果明显高于传统薄板样条处理结果与高斯处理结果，具有更好的拓扑保持能力。在图形形态相似性上，3组均保持较好，而改进薄板样条为略高于另外2组，说明精度降低后数据在逼近原始数据的形态特征的同时也存在差异，能够满足有效降低精度与数据可用2个方面的要求。
表6 3种算法降低精度与数据可用性对比

Tab. 6 Comparison of RMSE and data availability after accuracy reduction based on three models

处理模型 处理后
精度/m		 空间方向一致性/% 图形形态相似性/%
改进薄板样条模型 10.467 6 99.62 99.99
传统薄板样条模型 10.552 2 94.10 99.97
高斯函数模型 12.389 0 93.76 99.98
如图11所示，3种精度降低处理方法得到的偏移量都呈现以目标精度为中心的近似正态分布,在8~11 m内较为集中。改进薄板样条处理后坐标偏移区间为0 ~13 m,偏移量在数值上具备良好的稳定性。而传统薄板样条精度降低模型与基于高斯函数的精度降低模型得到的偏移量区间范围较大，最大偏移量均超过30 m，更易在局部区域上发生突变。
图11 3种算法处理后要素节点偏移量统计

Fig. 11 Statistics of value of offset after accuracy reduction based on three models

图12为3种方法处理后的局部区域效果图。图12(b)显示，传统薄板样条处理结果会出现局部几何特征变化的问题。图12(d)为处理后数据边界处，高斯函数处理后数据在此区域的偏移量大于30 m，精度降低效果不稳定，而图12(a)、图12(c)显示的改进薄板样条处理结果均不存在如上问题。以上2种方法因为直接根据已知控制点对进行参数计算，模型不能排除噪声的干扰，因此精度降低后的数据质量不如改进后的薄板样条好。
图12 3种算法局部精度降低效果对比

Fig. 12 Local comparison of the results after accuracy reduction based on three models

4 结论与讨论

4.1 结论

针对矢量数据几何模型处理易出现的突变问题，本文提出一种顾及空间分布的改进薄板样条矢量精度降低方法。首先根据待处理数据的空间分布建立四叉树索引结构选取控制点。然后对函数模型进行正则化处理，并通过选取样本点迭代计算从而获得优化的正则化参数。最后根据获得的正则化参数对矢量数据进行处理。本文以全国主要铁路线数据、江苏省景区POI数据、江苏省南京市绿地面数据、南京市鼓楼区道路线数据四级行政区划范围的数据为例验证本文提出的改进模型并进行分析，研究结论为：
（1）基于本文提出的模型降低模型对不同尺度、数据量的单图层数据、多图层数据坐标进行偏移，中误差均大于10 m，表明本文模型能有效满足精度降低要求且具有普适性;
（2）统计处理后要素节点的偏移量与偏移方向，偏移量呈现出以目标精度10 m为中心正态分布的趋势，单个节点的偏移量不超过20 m;同时要素节点在东南、东北、西南、西北4个方向上均有偏移，表明精度降低后数据稳定性较好，且具有全局上随机偏移的特征，使精度降低后数据难以被恢复。
（3）对比传统薄板样条模型与高斯径向基函数模型，本文提出的改进模型得到结果的空间方向一致性、图形形态相似性最高，分别为99.62%与99.99%，表明改进后的模型可以使精度降低后数据更接近原始数据的形态特征，数据的可用性高。
（4）对精度降低后数据进行明攻击与盲攻击测试，攻击后数据精度保持在10 m左右，无法被恢复为原始数据，验证得到改进后的模型安全性高。

4.2 讨论

本文提出的模型目前也存在不足之处。以目标精度10 m为例，本文在选取控制点并进行偏移时，设置的单个控制点坐标偏移量是在10 m附近波动的随机数，偏移方向在四叉树节点间渐进变化，保证控制点对的整体中误差保持在10 m左右。在此过程中若控制点对的偏移精度与目标精度相差过大，尽管模型经过正则化来减弱其干扰，也会影响迭代计算效率与处理后精度准确性。同时，随机数的存在能够增强全局坐标偏移的随机性，保证了精度处理效果的安全性，但是也导致不同实验下同一数据的处理效果存在不一致，进一步探究控制点偏移效果的设置方法，是未来需要关注的重点内容。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
自然资源部,国家保密局. 测绘地理信息管理工作国家秘密范围的规定[EB/OL].(2020). https://www.gov.cn/zhengce/zhengceku/2020-07/08/content_5525075.htm.

[ Ministry of Natural Resources of the People's Republic of China, National Administration of State Secrets Protection. Regulations on the scope of state secrets in the management of geographic information in surveying and mapping[EB/OL].(2020). https://www.gov.cn/zhengce/zhengceku/2020-07/08/content_5525075.htm. ]

[2]
聂时贵, 刘玫, 王会娜. 基于ArcGIS的江苏省地理信息公共服务平台数据脱密方法[J]. 现代测绘, 2012, 35(6):42-44.

Nie S G, Liu M, Wang H N. A decryption processing method on spatial data in Jiangsu provincial public service platform based on ArcGIS[J]. Modern Surveying and Mapping, 2012, 35(6):42-44. ] DOI:10.3969/j.issn.1672-4097.2012.06.015

[3]
朱长青, 任娜, 徐鼎捷. 地理信息安全技术研究进展与展望[J]. 测绘学报, 2022, 51(6):1017-1028.

DOI

Zhu C Q, Ren N, Xu D J. Geo-information security technology: Progress and prospects[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(6):1017-1028. ] DOI:10.11947/j.AGCS.2022.20220172

[4]
王忠美, 杨晓梅, 顾行发, 等. 投影相似变换的无人机影像拼接[J]. 测绘科学, 2016, 41(9):112-117.

Wang Z M, Yang X M, Gu X F, et al. UAV image mosaic based on projection-similarity transformation[J]. Science of Surveying and Mapping, 2016, 41(9):112-117. ] DOI:10.16251/j.cnki.1009-2307.2016.09.022

[5]
赖明珠, 段志鸣. 基于局部特征射影变换的组织切片图像非刚性配准[J]. 科学技术与工程, 2022, 22(29):12954-12962.

Lai M Z, Duan Z M. Non-rigid registration of tissue section images based on local feature projective transformation[J]. Science Technology and Engineering, 2022, 22(29):12954-12962. ] DOI:10.3969/j.issn.1671-1815.2022.29.031

[6]
胡安文, 张祖勋. 对高分辨率遥感影像基于仿射变换的严格几何模型的讨论[J]. 武汉大学学报·信息科学版, 2006, 31(2):104-107.

Hu A W, Zhang Z X. Discussion on “strict geometric model based on affine transformation for remote sensing image with high resolution”[J]. Geomatics and Information Science of Wuhan University, 2006, 31(2):104-107. ] DOI:10.3969/j.issn.1671-8860.2006.02.003

[7]
白晓春, 戚国辉, 郑树海, 等. 输变电工程地理信息数据脱密处理研究[J]. 矿产勘查, 2019, 10(9):2446-2460.

Bai X C, Qi G H, Zheng S H, et al. Research on Geographic information data densification related to power transmission and transformation engineering[J]. Mineral Exploration, 2019, 10(9):2446-2460. ] DOI:10.3969/j.issn.1674-7801.2019.09.043

[8]
江栋华, 周卫. 一种基于Chebyshev多项式的矢量数据几何精度脱密模型[J]. 测绘科学技术学报, 2018, 35(3):321-325.

Jiang D H, Zhou W. Decryption model for vector geographic data based on Chebyshev polynomials[J]. Journal of Geomatics Science and Technology, 2018, 35(3):321-325. ] DOI:10.3969/j.issn.1673-6338.2018.03.019

[9]
刘宏林, 吕晓华, 江南, 等. 影响地图投影多项式变换精度的若干因素分析[J]. 测绘科学技术学报, 2011, 28(2):108-112.

Liu H L, Lv X H, Jiang N, et al. Analysis of some influencing factors on accuracy of map projective polynomial transformation[J]. Journal of Geomatics Science and Technology, 2011, 28(2):108-112. ] DOI:10.3969/j.issn.16 73-6338.2011.02.008.

[10]
于辉, 周卫, 马心念. 一种基于三角函数的矢栅地理数据可逆几何脱密模型[J]. 测绘通报, 2017(10):89-94.

DOI

Yu H, Zhou W, Ma X N. A reversible decryption model for vector and raster integration based on trigonometric function[J]. Bulletin of Surveying and Mapping, 2017(10):89-94. ] DOI:10.13474/j.cnki.11-2246.2017.0322

[11]
Morelli M, Bellosta T, Guardone A. Efficient radial basis function mesh deformation methods for aircraft icing[J]. Journal of Computational and Applied Mathematics, 2021, 392:113492. DOI:10.1016/j.cam.2021.113492

[12]
于辉. 基于径向基和三角函数的矢栅一体化脱密模型研究[D]. 南京: 南京师范大学, 2016.

Research on decryption model for vector and raster integration based on radial basis function and trigonometric function[D]. Nanjing: Nanjing Normal University, 2016. ] DOI:10.27245/d.cnki.gnjsu.2016.000165

[13]
高隆杰. 基于径向基函数的DLG几何精度脱密模型研究[D]. 南京: 南京师范大学, 2014.

[ Gao L J. Research on DLG geometric accuracy decrypt model based on radial basis functions[D]. Nanjing: Nanjing Normal University, 2014. ]

[14]
Chen C F, Li Y Y, Cao X W, et al. Smooth surface modeling of DEMs based on a regularized least squares method of thin plate spline[J]. Mathematical Geosciences, 2014, 46(8):909-929. DOI:10.1007/s11004-013-9519-5

[15]
黄华峰, 陈飞, 曾勋勋. 基于薄板样条配准和全局相似的图像交互拼接[J]. 南京大学学报(自然科学), 2021, 57(5):828-837.

Huang H F, Chen F, Zeng X X. Image interactive stitching based on thin plate spline registration and global similarity[J]. Journal of Nanjing University (Natural Science), 2021,57(5):828-837. ] DOI:10.13232/j.cnki.jnju.2021.05.013

[16]
Guo H, Hou Y, Zhao Y. An image matching algorithm using Thin Plate Splines (TPS) transformation model[J]. International Journal of Simulation: Systems, Science & Technology, 2016, 17(8):13. DOI:10.5013/ijssst.a.17.08.13

[17]
徐旺, 官云兰, 张钊, 等. 结合薄板样条插值的机载LiDAR渐进形态学滤波算法[J]. 激光与光电子学进展, 2022, 59(10):412-421.

Xu W, Guan Y L, Zhang Z, et al. Progressive morphological filtering algorithm combined with thin-plate spline interpolation for airborne LiDAR[J]. Laser & Optoelectronics Progress, 2022, 59(10):412-421. ] DOI:10.3788/LOP202259.1028002

[18]
张煜, 李树祥, 陈武凡, 等. 薄板样条插值函数的改进与应用[J]. 中国图象图形学报(A辑), 2003, 8(z1):46-49.

Zhang Y, Li S X, Chen W F, et al. The improvement and application for thin-plate Spline[J]. Journal of Image and Graphics, 2003, 8(z1):46-49. ] DOI:10.3969/j.issn.1006-8961.2003.z1.011

[19]
张永军, 黄星北, 刘欣怡. 一种地形自适应的机载LiDAR点云正则化TPS滤波方法[J]. 地球信息科学学报, 2020, 22(4):898-908.

DOI

Zhang Y J, Huang X B, Liu X Y. A terrain-adaptive airborne LiDAR point cloud filtering method using regularized TPS[J]. Journal of Geo-information Science, 2020, 22(4):898-908. ] DOI:10.12082/dqxxkx.2020.190774

[20]
Bookstein F L. Principal warps: Thin-plate splines and the decomposition of deformations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(6):567-585. DOI:10.1109/34.24792

[21]
姚晓闯. 矢量大数据管理关键技术研究[J]. 测绘学报, 2018, 47(3):423.

DOI

Yao X C. Research on key technologies of vector big data management[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3):423. ] DOI:10.11947/j.AGCS.2018.20170385

[22]
林东方, 朱建军, 宋迎春, 等. 正则化的奇异值分解参数构造法[J]. 测绘学报, 2016, 45(8):883-889.

DOI

Lin D F, Zhu J J, Song Y C, et al. Construction method of regularization by singular value decomposition of design matrix[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8):883-889. ] DOI:10.11947/j.AGCS.2016.20150134

DOI

[23]
林东方, 朱建军, 付海强, 等. 均方误差意义下的正则化参数二次优化方法[J]. 测绘学报, 2020, 49(4):443-451.

DOI

Lin D F, Zhu J J, Fu H Q, et al. Optimization of regularization parameter based on minimum MSE[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(4):443-451. ] DOI: 10.11947/j.AGCS.2020.20190148

DOI

[24]
段先云, 邓学雄, 左启阳. 级进模刃孔图形复杂度的研究[J]. 工程图学学报, 2006, 27(5):94-97.

Duan X Y, Deng X X, Zuo Q Y. The research on the complexity of progressive die edge[J]. Journal of Engineering Graphics, 2006, 27(5):94-97. ] DOI:10.3969/j.issn.1003-0158.2006.05.017

[25]
李安波, 吴雪荣, 解宪丽, 等. 精度可控的矢量地理数据脱密方法[J]. 中国矿业大学学报, 2016, 45(5):1050-1057.

Li A B, Wu X R, Xie X L, et al. A precision alterable declassification technique for vector geo-data[J]. Journal of China University of Mining & Technology, 2016, 45(5):1050-1057. ] DOI:10.13247/j.cnki.jcumt.000572

Options
文章导航

/

〈 〉