EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 12: 2340 - 2360

DOI: https://doi.org/10.12082/dqxxkx.2023.230148

SpatialDI 2023 会议优秀论文

工业污染对癌症影响的挖掘方法：改进的空间同位模式

  • 张玲莉 , 1 ,
  • 王丽珍 , 1, 2, * ,
  • 杨培忠 1
展开
  • 1.云南大学信息学院，昆明 650504
  • 2.云南大学滇池学院，昆明 650228
*王丽珍(1962— )，女，山东博兴人，博士，教授，博士生导师，主要研究方向为空间数据挖掘、交互式数据挖掘、大 数据分析及应用等。E-mail:

张玲莉（1997— ），女，云南昆明人，硕士生，主要研究方向为空间数据挖掘。E-mail:

收稿日期: 2023-03-25

  修回日期: 2023-06-22

  网络出版日期: 2023-12-05

基金资助

国家自然科学基金项目(62276227)

国家自然科学基金项目(61966036)

国家自然科学基金项目(62266050)

云南省基础研究计划重点项目(202201AS070015)

云南省创新团队项目(2018HC019)

收起

Mining the Influence of Industrial Pollution on Cancer: An Improved Spatial Co-location Pattern

  • ZHANG Lingli , 1 ,
  • WANG Lizhen , 1, 2 ,
  • YANG Peizhong 1
Expand
  • 1. School of Information Science and Engineering, Yunnan University, Kunming 650504, China
  • 2. Dianchi College of Yunnan University, Kunming 650228, China
*WANG Lizhen, E-mail:

Received date: 2023-03-25

  Revised date: 2023-06-22

  Online published: 2023-12-05

Supported by

National Natural Science Foundation of China(62276227)

National Natural Science Foundation of China(61966036)

National Natural Science Foundation of China(62266050)

Yunnan Fundamental Research Projects(202201AS070015)

Project of Innovative Research Team of Yunnan Province(2018HC019)

Fold

摘要

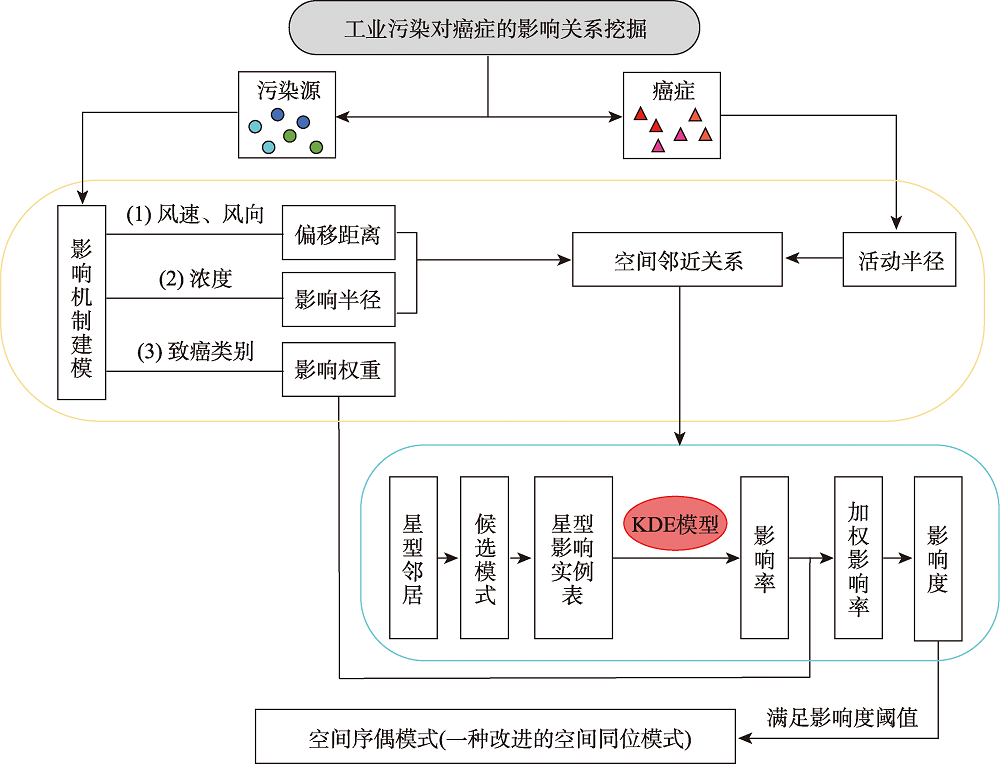
引起人类患癌的原因，环境污染占比60%。空间同位(co-location)模式挖掘算法可以识别其实例在地理空间中频繁邻近的模式，可应用于探究工业排放的室外空气污染物与癌症的潜在联系。传统的空间同位模式挖掘算法在衡量模式兴趣度时通常基于模式实例出现频次计算其频繁性，但污染源实例对癌症实例的影响还与实例之间的距离相关，加之污染源受气象条件、浓度大小、危害程度等因素的影响具有差异性，因此不能只依靠实例出现次数度量其兴趣度。为此，基于高斯核密度估计模型提出了空间序偶模式及相应挖掘算法，高斯核函数可以较好地刻画污染源对癌症病例的影响随距离衰减的过程，为了尽可能地还原污染源在真实世界中的扩散情况，将城市风向、风速以及污染源排放浓度考虑在内定义了新的空间邻近关系度量准则，并且对污染源所属致癌类别进行了归类，对不同致癌类别的污染物进行加权区分，提出了更加新颖的污染源与癌症关系模式的度量和相应的挖掘算法。最后，在真实和合成数据集上验证了所提度量和挖掘算法的有效性和高效率，结果表明，提出的影响度度量较传统参与度度量更能捕获现实生活中更具有现实意义的空间序偶模式，且相较于同类型算法挖掘效率平均提高了60%左右。

关键词： 空间数据挖掘; 空间同位模式; 空间序偶模式; 污染源; 癌症; 核密度估计; 距离衰减; 影响因子

本文引用格式

张玲莉 , 王丽珍 , 杨培忠 . 工业污染对癌症影响的挖掘方法：改进的空间同位模式[J]. 地球信息科学学报, 2023 , 25(12) : 2340 -2360 . DOI: 10.12082/dqxxkx.2023.230148

Abstract

About 60% of all known causes of cancer are related to environmental pollution. Identifying the spatial co-location pattern of prevalent neighbor spatial feature sets in geographical space is important to explore the potential relationship between industrial outdoor air pollutants and cancer risk. The traditional spatial co-location pattern mining algorithms usually calculate the prevalence of co-locations based on the frequency of cancer instances when measuring pattern interest. However, the influence of pollution source on cancer instances is also dependent on their proximity. In addition, pollution sources are also influenced by factors such as meteorological conditions, concentration levels, and the degree of harm. So, the pattern interest cannot be measured by relying solely on the number of instance occurences. To address this issue, a new spatial co-location pattern (called spatial ordered-pair pattern) is defined, and a novel mining algorithm is proposed based on the Gaussian kernel density estimation model. The Gaussian kernel function can well capture the decay of the influence of pollution sources on cancer cases with distance. To better represent the real-world diffusion of pollution sources, a spatial neighbor relationship between pollution source and cancer is defined, which considers urban wind direction, wind speed, and pollution emission concentration. Furthermore, pollution sources are categorized into different carcinogenic groups, and a weighted differentiation method is employed to distinguish pollutants based on their carcinogenic categories. The influence of various pollutants on cancer is calculated by weighting their contributions by the "carcinogenic coefficient." Therefore, a novel metric of the influence of pollution sources on cancer along with corresponding mining algorithm is presented. It not only effectively measures the impact of distance between pollution sources and cancer instances on the prevalence patterns but also models the mechanism of the influence of pollution sources on cancer by incorporating real-world conditions, overcoming the limitations of the traditional methods. Furthermore, this study improves the robustness of the method by using a smoothing factor to mitigate mining anomalies caused by uneven distributions of cancer instances. Finally, the effectiveness and efficiency of the metric and the mining algorithm proposed in this study are tested through experiments on real and synthetic datasets, and insights are also provided for cancer prevention and urban planning for Yunnan Province. The experimental results indicate that both the influence degree and participation index can accurately reflect the pattern interest from both macroscopic and microscopic perspectives. Furthermore, the mining efficiency increases by an average of 60% compared to other algorithms. The proposed influence degree measurement can more effectively capture spatial co-location patterns and can better reflect the impact of pollution sources on the incidence of cancer.

Key words： spatial data mining; spatial co-location pattern; spatial ordered-pair pattern; pollution sources; cancer; kernel density estimation; distance attenuation; influence factor

1 引言

2021年2月，《CA-CANCER J CLIN》发布了《Global Cancer Statistics 2020》[1]，统计了全球185个国家，36种癌症的发病率与死亡率。报告指出中国女性较高的肺癌发病率可能与户外空气污染有关。由于长久以来人们更加关心食物、生活方式、遗传因素等对健康的影响，从而忽略了环境污染带来的风险。早在1960年，Percy Stocks就证明了室外空气中的颗粒物、苯并芘与肺癌、胃癌有显著关系[2]，关于环境污染与癌症的关系研究，现有方法主要表现为两类，一类是通过对患癌人群以及环境污染数据进行数理统计分析[2⇓⇓⇓⇓-7]，一般用于发现发病率和死亡率较高的某类癌症和工业污染的关系；另一类是通过在临床上探究某种污染物对人体细胞基本结构造成的影响[8-9]，研究周期长。2种方式均从不同维度证明了污染物与癌症的发生是存在关联的，但是癌症和环境污染源种类繁多，要对其关联关系进行详尽的分析还存在很大的挑战。因此，在流行病学专家证明了污染源与癌症具备相关性的基础上，本文试图利用改进的空间同位模式挖掘理论来探索工业排放的各类室外空气污染物以及空气污染物组合与各类癌症之间潜在的空间关联，而不是因果关系。从空间数据分布的角度进行分析，希望能为城市规划、癌症筛查提供参考，以及为流行病学专家提供有用的信息，进一步分析污染与癌症的关系。
托布勒第一地理学定律指出，在地理空间中距离较近的事物往往比距离较远的事物更加相关。由此空间同位(co-location)模式挖掘被提出[10]。空间同位模式是空间特征集的一个非空子集，其特征实例在地理空间中频繁邻近。在空间数据中，空间特征用于表示不同种类的空间事物，如物种种类、城市设施等。空间实例是空间特征在具体地理位置上的一个对象，比如学校是一个空间特征，则云南大学是学校这个特征的一个实例。空间同位模式挖掘要求特征实例满足某个给定的距离阈值从而形成邻近关系，使用参与度量化满足邻近关系的实例在地理空间中邻近出现的频率，参与度大于等于用户给定的频繁度阈值即为频繁同位模式。空间同位模式挖掘可以自动提取隐含在海量空间数据中未知但极具指导意义的模式，多年来被广泛应用于物种分布[10]、公共卫生[11]、环境管理[12]等各个领域。但是，参与度的计算往往需要耗费大量的时间，于是便衍生出了一系列改进效率的算法。具有代表性的主要有join-based[13]，Partial-join[14]，joinless[15]，CPI-tree[16]，基于密度的挖掘算法[17]，CPM-Col算法[18]等。针对不同类型的数据，研究专家们提出了多种有效的针对数据多样性的挖掘算法[19⇓-21]。随着空间同位模式挖掘的流行，不少研究工作将该理论运用到实际中，胡添等[22]基于POI数据同位模式挖掘获取了城市服务业空间关联结构。徐振等[23]提出一种不依赖于空间谓词的同位 模式发现方法，有效提取了耕地相关的关联模式。Li等[11]提出了一种基于概率的同位模式挖掘方法探究儿童癌症与污染物之间的关系，该方法将污染源视为不确定性数据，并对其进行真实世界的建模，发现了一些化学污染物的组合与某些癌症存在显著的关联关系，但是挖掘过程对网格粒度的选取较为敏感，不同粒度得到的结果差异很大。谢旺等[24]首次提出空间序偶模式用于挖掘污染源与癌症组成的同位模式，通过单纯地累加污染源对癌症病例的影响进行模式的频繁性度量，挖掘结果受癌症病例数目影响较大，当病例数目分布不均匀时，影响度大的模式几乎集中在病例较少的癌症特征。
以上现有的空间同位模式挖掘方法在污染源与癌症同位关系发掘上还存在以下局限：
（1）对模式的频繁性度量只计算邻近的模式实例的出现次数，只根据一个距离阈值来判断实例间是否邻近。对于污染源和癌症病例来说，癌症病例离污染源越近，患癌的风险也会随之提高，所以模式的频繁性度量既要衡量实例频繁同位的频率，也要考虑污染源实例与癌症实例距离远近不同带来的影响变化。加之企业污染源排放浓度不同，影响范围也存在差异，只用一个距离阈值来决定邻近关系并不合理。
（2）基于参与度的频繁性度量方式要求所有的特征实例平等的对模式做出贡献，污染源实例所属致癌类别不同，致使人类患癌的风险也不相同，所以在计算污染源实例的贡献时，不应该对其一视 同仁。
（3）模式中的特征并不需要满足特定的顺序，例如模式{松茸，松树}与{松树，松茸}都能显示这 2个物种生存空间的同位关系。然而，对于污染源和癌症来说，研究诸如{污染源A，污染源B}、{癌症A，癌症B}此类模式并无实际意义，更倾向研究类似{污染源A，癌症A}共存关系，这就要求在生成模式时须按照一种特定的方式。
核密度估计（Kernel Density Estimation, KDE）模型是概率论中用来估计未知的密度函数，在点空间数据中，KDE模型可以有效提取数据的聚类信息，正态高斯核函数被定义为空间中任一点x到某一中心点xc之间欧氏距离的径向基函数。本文在传统同位模式挖掘方法的基础上，结合核密度估计模型与正态高斯核函数提出了一种新颖的影响度度量方法，主要贡献总结如下：
（1）提出影响度作为模式的有趣性度量准则，既衡量了模式频繁同位的频率，又考虑了实例对之间影响随距离衰减的过程。此外，在计算影响度时，不再生成传统的表实例，而是生成一种新的便于影响度计算的星型影响实例表，可以快速计算候选模式的影响度。
（2）充分考虑污染源实例的差异性。首先根据污染物排放浓度设定不同等级的影响半径，并给定癌症病例活动半径，将二者有机结合以识别污染源实例和癌症病例之间的邻近关系；其次，根据每一类污染源所属致癌类别的不同，在计算影响率时对每一个污染源特征进行了加权区分。
（3）根据大气污染物扩散与气象条件的关系，将风向、风速对于污染物扩散的影响考虑在内，提出了偏移距离的概念，尽可能的还原现实中污染源的扩散过程。

2 形式化定义、分析及算法

本节主要对基于高斯核密度估计的空间序偶模式挖掘算法进行详细的分析与定义。技术路线如图1所示。
图1 技术路线

Fig. 1 Technology roadmap

图1中，首先对污染源实例进行3种因素的影响机制建模，依据污染源实例偏移后的位置和影响半径，结合癌症实例的活动半径确定污染源实例和癌症实例之间的空间邻近关系（浅黄色框），再通过提出的度量计算模式的影响度（浅蓝色框），最后输出满足阈值的空间序偶模式（一种改进的空间同位模式）。根据技术路线图，首先给出空间序偶模式相关概念，然后是污染源影响机制建模的相关内容，之后给出基于核密度估计的模式有趣性度量，最后呈现完整的挖掘算法。

2.1 空间序偶模式

给定一个空间数据集，包含特征集 F = P F , C F，其中污染源特征集 P F = p 1 , p 2 , … , p n，一个污染源实例用 p i . j表示，所有污染源实例构成的集合称为污染源实例集，记为 O P = O p 1 ⋃ O p 2 ⋃ … ⋃ O p n， O p i ( 1 ≤ i ≤ n ))表示污染源特征 p i p i ∈ P F的实例集合。除了特征类型，实例ID和空间位置，每个污染源实例还携带浓度和致癌类别信息，可以用一个五元组唯一标识，即<特征类型，实例ID，浓度，致癌类别，空间位置>。癌症特征集 C F = c 1 , c 2 , … , c m，一个癌症实例用 c s . t表示，所有癌症实例构成的集合称为癌症实例集，记为 O C = O c 1 ⋃ O c 2 ⋃ … ⋃ O c m， O c s 1 ≤ s ≤ m表示癌症特征 c s c s ∈ C F的实例集合，癌症实例可用一个三元组表示，即<特征类型，实例ID，空间位置>。
定义1（空间序偶模式） 给定污染源特征集 P F和癌症特征集 C F，将序偶 c = F p , F c F p ⊆ P F , F c ⊆ C F称为空间序偶模式 S O P P _ c，c中包含的空间特征个数称为阶，记为 s i z e c = F p + F c。
一个特征及其实例空间坐标分布示例如图2 所示，污染源特征集 P F = A , B，实例集 O P = A . 1 , A . 2 , A . 3 , A . 4 , A . 5 , B . 1 , B . 2 , B . 3 , B . 4 , B . 5，癌症特征集 C F = a，实例集 O c = a . 1 , a . 2 , a . 3。
图2 特征实例空间坐标分布示例

注：图中的数字表示实例序号。

Fig. 2 An example of feature instances space coordinates distribution

为了使空间序偶模式反映的污染源对癌症的影响更符合实际，本文考虑了污染源受风向、风速、浓度的干扰作用，以及污染物所属致癌类别。详细定义如下。

2.2 污染源影响机制建模

2.2.1 风向、风速对污染物扩散的影响

污染物在一个地区的分布受多种因素的影响，如污染物类型、释放浓度、天气条件（风、降水）、地形等，本文目标并不是重现复杂的空气污染分布模型，而是在挖掘过程中尽可能地模拟污染物在真实世界中的扩散过程。风向、风速的应用可能有2种情况：①污染物排放地区全年无风，即污染物不发生位置偏移；②在盛行风向下，风速非零。风速、风向直接决定了大气污染物的扩散范围，风速与化学物质传播距离呈正相关。根据典型地域的风向特征研究[25]，云南省盛行风向为西南风，风向年分布形态非常稳定。风向频率表示为：风向频率 =某风向出现次数 /风向的总观测次数 × 100 %，风玫瑰图是根据某一地区多年平均统计的各个风向频率值和风速值按一定比率绘制，玫瑰图上的风向指的是从外面吹向地区中心的方向。云南省风玫瑰图如图3所示。
图3 云南省风玫瑰图

Fig. 3 Wind rose map of Yunnan Province

根据风玫瑰图可知，云南省风向集中为西南风，平均风速不超过15 m/s，受西南风的影响，污染源空间位置逐渐向东北方位发生偏移，产生偏移距离。
定义2（偏移距离） 给定一个污染源实例 p i . j p i . j ∈ O p i，实例 p i . j在风条件影响下，自东北方向发生的偏移距离记为s， s = λ v。其中 λ为拉伸系数，拉伸系数越大，偏移距离越大，v为云南省西南风风速，变化范围 0 ~ 25   m / s，参照大气污染物扩散与气象条件的关系，拉伸系数 λ固定取值300，45°为西南风风向与水平方向和垂直方向的夹角大小。假设污染源实例 p i . j的空间坐标为 x , y， p i . j的偏移坐标 x , , y ,表示如下：
    x ,   =   x   +   λ v c o s 45 °   y ,   =   y   +   λ v s i n 45 °
污染源实例的偏移坐标通过偏移距离s的三角函数关系计算可得，最终根据癌症实例坐标与污染源实例偏移坐标可计算实例之间的欧式距离。如图4所示，癌症实例 a . 1和污染源实例 A . 1之间的实际距离为 d i s t a . 1 , A . 1 '。
图4 污染源实例坐标偏移计算示例

注:图中a.1表示-一个癌症实例，A.1 (x, y)表示-一个污染源实例及其空间坐标，A.1'(x', y')表示A.1发生位置偏移后的实例及其空间坐标，dist( )表示癌症实例与污染源实例间的欧式距离，s表示西南风作用下污染源A.1到A.1'的偏移距离，45°表示西南风与水平方向的夹角。

Fig. 4 Example of calculation of pollution source instance coordinate shift

2.2.2 污染物浓度

每个污染物不同时段的排污浓度越大，排污量越大，影响范围越广。现将浓度与污染源影响范围联系起来，定义了新的与浓度相关的空间邻近关系划分标准，详细定义如下。
定义3（局部平均浓度） 给定一个污染源实例 p i . j p i . j ∈ O p i，实例 p i . j不同时段的浓度值 C o n c p i . j = c o n c 1 , … , c o n c k，局部平均浓度为 C o n c p i . j的平均值，记做 L M C o n c p i . j，计算如下：
L M C o n c p i . j = ∑ t = 1 k c o n c t k
例如 C o n c A . 1 = 0.1,0.2,0.3，单位 m g / N m 3，则 L M C o n c A . 1 = 0.1 + 0.2 + 0.3 / 3 = 0.2   m g / N m 3。
定义4（全局平均浓度） 给定一个污染源特征 p i p i ∈ P F，全局平均浓度表示 p i的实例集 O p i的局部平均浓度和的平均值，记做 G M C o n c p i，计算如下：
G M C o n c p i   = ∑ L M C o n c p i . j n ( O p i )
例如 L M C o n c A = 0.2,0.3,0.5,0.1,0.8 ,  单位 m g / N m 3，则 G M C o n c A = 0.2 + … + 0.8 / 5 = 0.4   m g / N m 3。
定义5（污染源影响半径） 根据污染源局部平均浓度和全局平均浓度的关系，将污染源影响半径划分为3个等级，分别表示为 r m i n、 r m i d、 r m a x。给定一个污染源实例 p i . j   p i . j ∈ O p i，影响半径 r p i . j定义如下：
r p i . j = r m i n                 L M C o n c p i . j < G M C o n c p i r m i d                 L M C o n c p i . j = G M C o n c p i r m a x               L M C o n c p i . j > G M C o n c p i
式中： r m i n、 r m i d、 r m a x为用户自定义阈值，且 r m i n < r m i d < r m a x，且 r m i n、 r m i d、 r m a x分别对应污染源低、中、高等级的浓度。
定义6（癌症病例活动半径） 每个癌症病例通常情况下不会长期呆在同一个位置，由于工作或其他原因存在一个活动范围。为了尽可能的还原现实情况，本文为癌症病例定义了一个活动半径，给定一个癌症实例 c s . t c s . t ∈ O c s，活动半径记为 r c s . t。
定义7（空间邻近关系） 由于人类活动以及污染物扩散运动，人类活动区域与污染源影响区域会发生相交，由此人类便会接触到致癌物，本文根据污染源影响半径和癌症病例活动半径定义相应实例间的空间邻近关系。给定一个癌症实例 c s . t c s . t ∈ O c s，一个污染源实例 p i . j p i . j ∈ O p i，将癌症实例 c s . t与污染源实例 p i . j之间的邻近关系记为 R c _ p，如果 d i s t c s . t   ,   p i . j ≤ r c s . t + r p i . j，则称癌症实例 c s . t与污染源实例 p i . j存在邻近关系 R c _ p，记做 R c _ p c s . t , p i . j ⇔ d i s t c s . t , p i . j ≤ r c s . t + r p i . j。
如图5所示， d i s t a . 2 ,   A . 5 = 2.83 ， r a . 2 + r A . 5 = 2 + 2 = 4， d i s t a . 2 ,   A . 5 < r a . 2 + r A . 5，实例 a . 2和 A . 5满足邻近关系。将所有满足邻近关系的实例对用虚线连接。
图5 实例间空间邻近关系示例

注:图中数字表示实例序号;虚线表示癌症病例活动范围与污染源实例影响范围相交或相切，满足实例间邻近关系; 表示污染源实例影响范围不超过半径为1、2、3的圆; 表示癌症病例活动范围不超过半径为2的圆。

Fig. 5 Examples of spatial neighbor relationship between instances

由此，将污染源浓度合理地应用在空间邻近关系计算过程中。

2.2.3 污染物致癌类别

2021年世界卫生组织国际癌症研究机构公布了最新的致癌物清单，将致癌物分为4个类别，记为 c a t e g o r y 1 , … , c a t e g o r y 4。一类是明确致癌的物质，二类是可能性较高的致癌物质，三类是致癌证据不充分的致癌物，四类是对人体可能不致癌的物质。如果人体长期直接或间接接触这些物质，会使得癌细胞恶性增生从而形成肿瘤。由于污染源一般不会包含第四类致癌物，所以本文仅对前三类致癌物进行讨论。在本研究中，提出“致癌系数”区分企业污染物中不同类别的致癌物，以“致癌类别”划分致癌物对人体的“影响级别”，符合流行病学分类管理和控制的策略。用“致癌系数”作为权重进行加权求和计算各种污染物对癌症的影响，权重越大表示对人类致癌的证据越充分，污染物对癌症的影响也越大。
定义8（致癌系数） 给定一个污染源特征 p i p i ∈ P F，将 p i的致癌系数记为 v p i。
v p i = ε 1                     p i ∈ c a t e g o r y 1 ε 2                   p i ∈ c a t e g o r y 2 ε 3                   p i ∈ c a t e g o r y 3
当污染源特征属于一类致癌物，则将其致癌系数 v p i设置为 ε 1，同理，可对属于二三类致癌物 的污染源设置其致癌系数，其中 0 < ε 3 < ε 2 < ε 1 ≤ 1， ε大小的设置参照世卫组织对致癌物等级的划分标准。

2.3 基于KDE模型的模式有趣性的度量

核密度估计（Kernel Density Estimation）是一种用于估计概率密度函数的非参数估计方法，是分析空间自相关和密度分布的有效数学工具，例如利用KDE模型可以从一组给定的二维空间数据中生成一个光滑的三维钟型曲面，该曲面显示了点空间数据的聚类信息，根据指定的密度阈值即可提取所需的聚类。在点空间数据中，KDE模型可以表示为：
f O x = 1 h 2 ∑ i = 1 t d i s t O x , O i h
式中： f O x是基于数据集 O ' = O 1 , O 2 , … , O t的空间实例 O x的密度估计， O '是以 O x为中心半径为 h的圆内的所有实例， t是 O '的实例数， h是一个平滑参数，称作带宽， d i s t ·用于计算2个空间实例之间的欧几里得距离。K是用于模拟实例对 O x , O i贡献的核函数，距离越大，贡献越小，核函数 K满足非负性并且积分为1，假设 O x是癌症实例， O '是污染源实例集，KDE模型不仅能够考虑 O '与 O x之间距离衰减带来的影响变化，同时通过密度估计也能合理地度量模式的频繁性。
KDE模型有2个重要参数：核函数K和带宽h。K可以选择高斯函数、指数函数、幂函数等，在本研究中，由于高斯核函数变化趋势更符合影响衰减情况，所以选择正态高斯核函数，即：
K x = a × e x p - x - b 2 2 c 2
参数 a决定了曲面的峰高，b决定了峰值在横轴上的位置，c决定了曲线的宽度，在正态高斯核函数中， a = c = 1和   b   =   0。 e x p ∙是以自然常数e为底的指数函数，正态高斯核函数在三维空间中的变化曲线如图6所示。
图6 三维高斯核函数

Fig. 6 The Gaussian kernel function in 3-dimensional space

假设中心点是一个癌症实例，那么满足距离阈值的污染源实例集根据其与癌症实例的欧式距离即可产生一个光滑的三维钟形曲面，该曲面可以清晰的展示出污染源对癌症病例的影响随距离衰减的程度。那么，式（7）可以转换如下：
f O x = 1 h 2 ∑ i = 1 t - d i s t O x , O i 2 2 h 2
基于以上陈述，定义了一种新的有趣性度量准则-影响度，采用星型邻居物化空间数据集的邻近关系，生成符合影响度计算模型的星型影响实例表，从而减少无效候选模式产生。基于KDE模型计算影响度，不仅能够反映污染源对癌症病例的影响随距离的衰减趋势，同时也更加合理的度量了模式的频繁程度。详细定义如下。
定义9（星型邻居） 给定一个癌症实例 c s . t c s . t ∈ O c s， c s . t的星型邻居被定义为一个污染源实例的集合，这些污染源实例均与癌症实例 c s . t满足空间邻近关系。记为 S N c s . t = { p i . j ∈ O p | R c _ p c s . t , p i . j }，其中 O p是污染源实例集，且 p i . j以实例名的字典序排序。
例如图5中癌症实例 a . 1的星型邻居表示为 S N a . 1 = A . 1 , A . 2 , B . 1 , B . 2 , B . 3。
在癌症实例 c s . t的星型邻居中，将单个污染源特征 p i的实例集称为 p i对 c s . t的星型影响实例集，记做 S E I p i c s . t = { O p i | O p i ⊆ S N c s . t }，在图5中，污染源特征A和B对癌症实例 a . 1的星型影响实例集分别为 S E I A a . 1 = A . 1 , A . 2和 S E I B a . 1 = B . 1 , B . 2 , B . 3。
定义10（星型影响实例表）给定一个空间序偶模式 S O P P _ c = F p , F c， F p = p 1 , p 2 , . . . , p k F p ⊆ P F， F c = c s F c ∈ C F， S O P P _ c的星型影响实例表定义为癌症特征 c s的实例子集与其对应污染源特征集 F p的星型影响实例集的集合，记做 I n s T S O P P _ c = { { S E I p i c s . t | p i ∈ F p , 1 ≤ i ≤ k } , c s . t | c s . t ∈ O c s }。
如图5中，所有候选模式的星型影响实例表如表1所示。
表1 候选模式的星型影响实例表示例

Tab. 1 An example of star effect instance table of candidate patterns

候选模式 [A, a] [B, a] [{A, B}, a]
{{A.1, A.2}, a.1} {{B.1, B.2, B.3}, a.1} {{{A.1, A.2}, {B.1, B.2, B.3}}, a.1}
星型影响实例表 {{A.5}, a.2} {{B.3}, a.3} {{{A.3, A.4}, {B.3}}, a.3}
{{A.3, A.4}, a.3}

注：表格中的A,B表示污染源特征，a表示癌症特征，数字代表实例序号，如A.1表示污染源特征A的第一个实例，候选模式星型影响实例表的生成依据定义10与图5中的数据计算得到。

要对空间序偶模式的频繁性进行度量，首先，要考虑单个污染源实例对某个癌症实例造成的影响，进而计算单个污染源特征对某个癌症特征的影响，从而衡量模式的频繁同位程度。现实生活中，往往还存在多种污染源共同作用促使某种癌症的发生，在计算模式的影响度时，也需对此进行合理的考量。
基于KDE模型，将癌症实例 c s . t受到某个星型影响实例集 S E I p i c s . t的影响记为 S E I E p i c s . t。计算如下：
S E I E p i c s . t = 1 n ( p i ) ∑ j = 1 n ( S E I p i c s . t ) e x p - d i s t p i . j , c s . t 2 2 r p i . j + r c s . t 2
式中： n ( p i )表示污染源 p i的实例总数； n ( S E I p i c s . t )表示癌症实例 c s . t对应污染源 p i的星型影响实例数， p i . j ∈ S E I p i c s . t。核函数用于模拟实例 p i . j对   c s . t的影响，距离越大，影响越小。当 2个实例之间的距离为0时，影响最大，否则，污染源实例对癌症实例的影响随距离衰减，当二者之间的距离 d i s t ( p i . j , c s . t ) > r p i . j + r c s . t，影响衰减为0。当且仅当污染源特征 p i的所有实例出现在   c s . t的星型影响实例集中时，   c s . t的核密度估计值为1，即 p i对   c s . t的影响为1，但是现实情况中， p i的实例几乎不可能全部出现在   c s . t周围，所以影响值一般小于1。
在图5中，利用模式[{A, B}, a]的星型影响实例表InsT([{A, B}, a])可进行计算，$SEI{{E}_{\text{A}}}\left( \text{a}.1 \right)=\frac{1}{n\left( \text{A} \right)}\times \left( exp\left( -\frac{dist{{\left( \text{A}.1,\text{a}.1 \right)}^{2}}}{2{{\left( {{r}_{\text{A}.1}}+{{r}_{\text{a}.1}} \right)}^{2}}} \right)+exp\left( -\frac{dist{{\left( \text{A}.2,\text{a}.1 \right)}^{2}}}{2{{\left( {{r}_{\text{A}.2}}+{{r}_{\text{a}.1}} \right)}^{2}}} \right) \right)=\frac{1}{5}\left( exp\left( -\frac{{{1.414}^{2}}}{2{{\left( 1+2 \right)}^{2}}} \right)+exp\left( -\frac{{{2}^{2}}}{2{{\left( 2+2 \right)}^{2}}} \right) \right)$=0.355，同理可得 S E I E A a . 3 = 0.352， S E I E B a . 1 = 0.413， S E I E B a . 3 = 0.144。
定义11（影响率） 将污染源 p i p i ∈ F p对癌症 c s c s ∈ F c的影响率记做 E R p i c s，是癌症特征 c s的实例在模式 S O P P _ c的星型影响实例表中，对应污染源 p i的影响之和，计算如下：
E R p i c s = ∑ n ( c s   ,   I n s T S O P P _ c ) S E I E p i c s . t
这个值与传统方法中的参与率PR值类似，只不过ER更加强调2个特征的单向影响关系，由于计算ER值时，星型影响实例表中的污染源实例影响被重复计算，使得ER值受癌症实例数量的影响具有不确定性，癌症实例数量越多，ER值就越大，可以利用指数函数对其进行改进，以改善由于癌症实例数量差异带来的影响率偏差过大问题，将改进后的影响率记为 E R p i c s ¯，计算如下。
E R p i c s ¯ = E R p i c s × ( n ( c s ) n ( c - a v e ) ) δ
式中： n ( c s )表示癌症 c s的所有实例数； n ( c _ a v e )表示所有癌症特征实例总和的平均值； δ称为平滑因子，且 - 1 < δ < 0， ( n ( c s ) n ( c _ a v e ) ) δ变化图像如图7所示。当 n ( c s ) n ( c _ a v e ) > 1， c s数量较多， ( n ( c s ) n ( c _ a v e ) ) δ < 1， E R p i c s ¯比 E R p i c s略小， n ( c s )越大， E R p i c s ¯值越小。反之，当 n ( c s ) n ( c _ a v e ) < 1， c s数量较少， ( n ( c s ) n ( c _ a v e ) ) δ > 1， E R p i c s ¯比 E R p i c s略大， n ( c s )越小， E R p i c s ¯值越大。就影响率的改进来说，对于同一种癌症，并不影响模式前件的生成和组合，因为同一种癌症的 ( n ( c s ) n ( c _ a v e ) ) δ是相同的。合理地对 δ  进行取值，可有效避免因癌症实例数差异引起的模式挖掘缺陷。
图7 平滑因子变化对 ( n ( c s ) n ( c _ a v e ) ) δ的影响

注: n(cs)为癌症特征cs的实例个数; $\delta$为平滑因子; n(c_ave)为所有癌症特征实例总和的平均值。因为$-1<\delta <0$，所以变化曲线为实线部分。

Fig. 7 The effect of smoothing factor changes on ( n ( c s ) n ( c _ a v e ) ) δ

如图5中，模式[{A, B}, a]的$E{{R}_{\text{A}}}\left( \text{a} \right)=SEI{{E}_{\text{A}}}\left( \text{a}.1 \right)+SEI{{E}_{\text{A}}}\left( \text{a}.3 \right)=0.355+0.352=0.707$，
$\overline{E{{R}_{\text{A}}}\left( \text{a} \right)}=E{{R}_{\text{A}}}\left( \text{a} \right)\times {{\left( \frac{n\left( \text{a} \right)}{n\left( {{\text{c}}_{\_ave}} \right)} \right)}^{-0.6}}=0.707\times {{\left( \frac{3}{3} \right)}^{-0.6}}=0.707$。
定义12（加权影响率） 影响率的计算默认每个污染源特征的影响相同，根据定义8，每个污染源特征的影响程度并不相同，由此提出加权影响率，记为 W E R p i c s。
W E R p i c s = v p i ε 1 + ε 2 + ε 3 × E R p i c s ¯
式中： v p i表示污染源 p i对应的致癌系数； ε 1 + ε 2 + ε 3为3类致癌系数之和。如图5中，模式[{A, B}, a]的 W E R A a = v A ε 1 + ε 2 + ε 3 × E R A a ¯ = 1 1 + 0.7 + 0.3 × 0.707 = 0.353   50，同理， W E R B a = 0.083   55。
定义13（影响度） 空间序偶模式的影响度记为 W E I S O P P _ c。
W E I ( S O P P _ c ) = 1 - Π i = 1 k ( 1 - W E R p i ( c s ) )
如图5所示，$WE{{I}_{\text{AB}}}\left( \text{a} \right)=1-\left( 1-WE{{R}_{\text{A}}}\left( \text{a} \right) \right)\times \left. \left( 1- \right.\text{ }\!\!~\!\!\text{ }WE{{R}_{\text{B}}}\left( \text{a} \right)\text{ }\!\!~\!\!\text{ } \right)=$$1-\left( \text{ }\!\!~\!\!\text{ }1-0.353\text{ }\!\!~\!\!\text{ }50\text{ }\!\!~\!\!\text{ } \right)\times \left( \text{ }\!\!~\!\!\text{ }1-0.083\text{ }\!\!~\!\!\text{ }55 \right)=0.407\text{ }\!\!~\!\!\text{ }50$。所以最终模式[{A, B}, a]的影响度大小为0.407 50。假如影响度阈值 m i n _ p i i = 0.3，则模式[{A, B}, a]为频繁序偶模式。
序偶模式的影响度随着模式阶数的增加， 高阶模式的影响度可能会比低阶模式的影响度 更大。如图5中， W E I B ( a ) = 0.083   55， W E I A B ( a ) =0.407 50。因此，与传统空间同位模式的参与度度量不同，衡量序偶模式频繁性的影响度度量不满足向下闭合性质。

2.4 挖掘算法

本节给出了提出的空间序偶模式的挖掘算法，详见算法1。
算法1 基于KDE模型的空间序偶模式挖掘算法
输入:1污染源空间数据集 P S，癌症空间数据集 C S
2拉伸系数 λ，风速 v
3污染源实例影响半径 r m i n、 r m i d、 r m a x；癌症病人活动半径 r c
4致癌系数 ε 1， ε 2， ε 3
5平滑因子 δ
6影响度阈值 m i n _ p i i
输出:所有频繁空间序偶模式 S O P P _ c
变量： P S _ l m C o n c：带有局部平均浓度信息的污染源实例集
    g m _ C o n c S：污染源实例的全局平均浓度集
    S N S：所有癌症实例的星型邻居集
    k  ：模式的阶数
    C k： k阶候选模式
    i n s _ T k： C k的星型影响实例表集
    P k： k阶频繁模式
步骤:
1 P S= get_wind_influence_PS( λ, v, P S)
2 P S _ l m C o n c = get_local_mean_Concentration( P S)
3 g m _ C o n c S = get_global_mean_Concentration( P S _ l m C o n c)
4 S N S  = gen_star_neighbor_set ( C S , r m i n , r m i d , r m a x , r c , P S _ l m C o n c ,
g m _ C o n c S)
5 C 2= gen_candidate_patterns ( S N S)
6 k=2
7 WHILE( C k ≠NULL)
i n s _ T k = gen_InsTable ( C k, S N S  )
  P k = gen_prev_SOPP ( C k , i n s _ T k , ε 1 , ε 2 , ε 3 , δ , m i n _ p i i)
  S O P P _ c ← S O P P _ c ⋃ P k
    C k + 1= gen_candidate_patterns( S N S)
k=k+1
8 RETURN     S O P P _ c
关于算法1的解释如下：
步骤1：根据输入的拉伸系数λ和风速v计算污染源实例的偏移坐标。
步骤2—步骤3：计算污染源实例的局部平均浓度和全局平均浓度。
步骤4：根据污染源实例局部平均浓度和全局平均浓度的关系判断其对应的影响半径，进而生成癌症实例的星型邻居集。
步骤5：根据星型邻居集生成2阶候选模式。因为与某个癌症对应的模式前件只会在癌症的星型邻居集对应的特征中出现，所以在生成候选模式时，根据星型邻居集即可生成。
步骤6—步骤8：从2阶开始，逐阶循环生成模式的星型影响实例表，再根据实例表计算模式的影响度，保留满足影响度阈值的模式。直至k+1阶候选模式为空，退出循环，输出结果。
算法1的时间复杂度分析，步骤1—步骤3均需要遍历污染源实例集，复杂度为 O n，步骤4每一个癌症实例都需遍历一遍所有污染源实例判断邻近关系，故复杂度为 O m × n， n是污染源实例数， m是癌症实例数。步骤5复杂度与步骤4同等级。在步骤7中，耗时最多的步骤是星型影响实例表 i n s _ T k的生成过程，生成一个候选模式的实例表需要 O S N S，故需要 O C k × S N S。生成频繁模式 P k所需时间为 O C k，生成 k + 1阶候选模式所需时间为 O C k × O C k - 1。算法的距离阈值过大或者实例数过多都会对算法效率产生影响。

3 实验与分析

在本节，通过在真实数据集和合成数据集上进行实验，对本文所提算法的有效性和性能进行评估。实验算法采用C++实现，硬件环境为Inter Core i7、16 G运行内存，运行环境Visual Studio 2019。

3.1 实验数据集

实验基于1个真实数据集和5个人工合成数据集完成，真实数据集包括癌症病例数据和污染源数据两个部分，癌症病例数据主要由云南省某医院提供，有少量其他一些医院的数据，时间为2014—2015年。根据得到的病例数据选取了相应范围的污染企业形成实验数据，主要来自云南省排污单位自行监测信息公开平台(https://wryjc.cnemc.cn/gkpt/mainZxjc/530000)，并且只保留了对人类致癌的空气污染物，真实数据分布如图8所示，小写字母 a-beta为癌症，大写字母A-S为污染源。合成数据集1在真实数据集的基础上将污染源数据在地理空间中的分布修改为随机分布。其他合成数据集是随机产生的，主要用于算法的效率分析，数据均匀分布在97º E—107º E、20º N—30º N的空间中。数据集如表2所示。
图8 真实数据集分布

Fig. 8 Distribution map of the real dataset

表2 数据集

Tab. 2 Data Set

数据集 污染源(特征/实例) 癌症(特征/实例) 数据分布(经度97 °E—107 °E、纬度20 °N—30 °N)
真实数据集 19(A-S)/9294 28(a-beta)/28797 真实地理坐标
合成数据集1 19(A-S)/9294 28(a-beta) /28797 随机分布
合成数据集2 10(A-J)/10000 10(a-j)/10000 随机分布
合成数据集3 10(A-J)/20000 10(a-j)/20000 随机分布
合成数据集4 10(A-J)/30000 10(a-j)/30000 随机分布
合成数据集5 10(A-J)/40000 10(a-j)/40000 随机分布

3.2 影响度度量的有效性分析

由于空间序偶模式挖掘需要对污染源数据和癌症数据进行底层建模，并且模式生成与传统方式并不相同，要将本文算法与传统算法进行比较是困难的，为了证明本文算法的有效性，我们在传统的参与度算法上进行了改进，称为PI_SOPPMA算法。PI_SOPPMA按照Kde_SOPPMA算法的方式生成候选模式，区别主要表现在PI_SOPPMA按照传统方式生成表实例，基于表实例计算候选模式的参与率和参与度进而生成频繁模式。将2个算法进行比较，并从宏观上和微观上证明了算法1应用于挖掘污染源与癌症关系的有效性。
基于真实数据集和合成数据集1进行实验，暂不考虑风向的影响。对距离阈值的选取，以室外大气污染物扩散与气象条件的关系作为先验指导，最大距离阈值不超过小尺度范围 10   k m。算法1中，污染物影响半径 r m i n、 r m i d、 r m a x分别4.5、5.0、 5.5 km，癌症病例的活动半径 r c为4.5 km，一类、二类、三类致癌系数分别取1.0、0.7、0.3，平滑指数取0.6。PI_SOPPMA算法距离阈值同算法1。

3.2.1 宏观分析

表3分别记录了2种方法得到的2阶模式频繁指数最小值，最大值以及平均值。从表3中可以看出，2种方法在相同的数据集和距离阈值下，影响度的大小分布比参与度大，这是因为影响度更加强调污染源对癌症单方面的影响，对于模式的贡献程度，利用邻近对之间的距离加权进行计算，将兴趣度转化为一个密度估计问题；对于参与度来说，除了污染源，还要对癌症的贡献大小进行评估，在我们的物化模型中癌症实例周围总是有污染源分布，污染源参与率和癌症参与率会出现一定的差距，所以计算的参与度值往往比影响度值要小。尽管如此，影响度和参与度的总体变化趋势是一样的，无论是影响度还是参与度，在真实数据集上的最小值、最大值、平均值都比合成数据集1上要小。从宏观上可以看出，基于KDE模型的影响度计算可以反应出模式在空间中的频繁同位关系。
表3 2阶频繁模式频繁指数极值

Tab. 3 The extreme values of the prevalence indices of size-2 patterns

数据集 影响度 参与度
最小值 最大值 平均值 最小值 最大值 平均值
真实数据集 0 0.628 0.211 0 0.443 0.099
合成数据集1 0 1.000 0.253 0 0.518 0.128

3.2.2 微观分析

虽然基于参与度的方法改进后能够有效利用本文对污染源数据底层建模的优势，但是在相同数据集和距离阈值下，2种方法的频繁指数结果分布不同，无法以相同的频繁阈值进行比较，所以本 文采用Top_k频繁模式[26]来比较2种算法的结果。 表4记录了在真实数据集上算法1得到影响度排名前十的2阶频繁空间序偶模式以及相关模式在PI_SOPPMA算法中的等级和参与度大小。
表4 top_10模式对比

Tab. 4 Top_10 patterns comparison

Top_10 Kde_SOPPMA 排序 PI- SOPPMA 排序
[颗粒物，TBL(气管、支气管和肺癌)] 0.628 1 0.443 1
[酸雾，肝癌] 0.610 2 0.074 292
[钴及其化合物，TBL] 0.601 3 0.036 441
[酸雾，TBL] 0.596 4 0.061 343
[烟尘，TBL] 0.575 5 0.166 70
[苯并芘，TBL] 0.569 6 0.023 497
[颗粒物，结直肠癌] 0.563 7 0.341 9
[苯并芘，骨癌} 0.559 8 0.032 463
[颗粒物，子宫癌] 0.550 9 0.367 4
[颗粒物，骨癌] 0.541 10 0.302 22
表4展示了几个信息。① 前10个频繁空间序偶模式中，肺癌和支气管恶性肿瘤分别与颗粒物、钴及其化合物、酸雾、烟尘、苯并芘存在空间关联，除了钴及其化合物，其他均有证据表明与肺癌的发病存在因果关系，这说明本文方法挖掘得到的结果是符合实际的。② 对比2个算法得出的结果，有3个模式{颗粒物，TBL}、{颗粒物，结直肠癌}、{颗粒物，子宫癌}均为top_10模式，{颗粒物，TBL}在2种方法中均排在第一位，说明颗粒物有很大可能性会导致肺癌、气管癌。值得注意的是，{颗粒物，结直肠癌}、{颗粒物，子宫癌} 2个模式在2种方法中获得了不同的等级。图9为2个模式中满足邻近关系的污染源实例与癌症实例之间的欧式距离分布频率直方图，从2个图中可以看出，{颗粒物，结直肠癌}的实例距离分布与{颗粒物，子宫癌}的较为相似，但前者平均值小于后者，前者实例之间比后者更加邻近，算法1能够有效地捕获这种距离远近差异带来的影响，并赋予了该模式相对PI_SOPPMA算法结果更低的频繁等级。③ 诸如{苯并芘，TBL}这类模式，影响度较大，但是参与度却很小，这主要是因为苯并芘实例数相对稀少，苯并芘周围几乎都有肺癌，但是大量的肺癌周围却很少有苯并芘，癌症的参与率相对较低，参与度也会非常低，这就造成了虽然苯并芘对肺癌有较大的影响，但是PI_SOPPMA算法并不能发现这样的模式，算法1却能有效处理这种情况，使得无论污染源实例多或少，都能找到被其潜在影响的癌症。
图9 模式满足邻近关系的污染源实例与癌症实例之间的距离分布频率直方图

Fig. 9 The Distance frequency distribution histogram between pollution source instances and cancer instances satisfying spatial neighbor relationship

综上所述，无论是从宏观还是微观的角度看，本文提出方法相较于传统方法，能够更加有效地发现污染源对癌症的影响。

3.3 风向、风速对模式挖掘结果的影响分析

从真实数据分布可以看出，患癌群体在云南省东北方位较为密集，虽然该地区是云南省经济发达地区，人口居多，患癌人数占比也会偏大，但东北方位的癌症病例密集程度却远超正常水平，城市周围并没有太多排污企业，很难对癌症起因进行分析。结合大气污染物扩散与风力活动的关系，本节分析了风向、风速对频繁模式生成的影响。考虑到现实生活中，出现5种以上化学污染物发生相互作用致癌的情况极少[5]，所以除了效率对比以外，本文最多只对5阶频繁模式挖掘结果进行讨论，后续不再赘述。图10显示了真实数据集和合成数据集1在不同风速下，生成频繁模式的情况，污染物影响半径 r m i n、 r m i d、 r m a x分别为5.0、5.5、6.0 km，癌症病例的活动半径 r c为2 km，一类、二类、三类致癌系数分别取1.0、0.7、0.3，平滑指数取0.6，影响度阈值取0.6，风速范围参照云南省风速玫瑰图，设定为0~25 m/s。
图10 风速变化对挖掘结果的影响

Fig. 10 Effect of wind speed changes on mining results

从图10可发现，无论是真实数据还是合成数据，相同影响度阈值下，随着风速的增大频繁模式逐渐增多，这主要是因为污染源在西南风作用下逐渐向东北方向发生偏移，导致原本污染物稀少的区域污染物逐渐增多。对于真实数据分布来说，风速0~15 m/s增幅较缓慢，从15 m/s以后频繁模式开始急剧增多，说明当风速大于15 m/s时，那些原本远离人类生活区的致癌污染物随着风活动会更接近人类生活区，风速越大，堆积的污染物会越多，人类患癌的风险也越大，符合本文的假设。反观合成数据上的实验，因为数据是均匀分布的，在风力作用下，污染物发生偏移对数据空间分布影响较小，风活动影响后虽然频繁模式会缓慢增加，但是涨幅很小，说明风力作用对均匀分布的污染源致癌情况影响较小。尽管如此，这并不意味着要在云南省内均匀分布的建立企业，因为云南省风速大约90%分布在0~15 m/s，在这个范围内，合成数据产生的频繁模式要比真实数据产生的 更多。

3.4 污染物浓度对模式挖掘结果的影响分析

3.4.1 污染源浓度对应的影响半径梯度差异对模式挖掘结果的影响

根据污染源局部平均浓度和全局平均浓度的关系，可将影响半径分为3个等级，3个等级的影响半径存在梯度变化，梯度不同对应的模式挖掘结果也不相同。图11显示了3个等级的影响半径在不同变化梯度下，对频繁模式挖掘结果的影响。对于影响半径的选取尽可能符合实际，在梯度为3 km时， r m i n = 4.0   k m， r m i d = 7.0   k m， r m a x = 10.0   k m，刚好达到小尺度范围最大值。所以选取 r m i n的范围在0.5 km到4 km之间，癌症病例的活动半径 r c固定为1.0 km，一类、二类、三类致癌系数分别取1.0、0.7、0.3，平滑指数取0.6，影响度阈值取0.3。
图11 半径梯度变化对挖掘结果的影响

Fig. 11 Effect of diameter gradient changes on mining results

无论对于真实数据集还是合成数据集1，在相同条件下，影响半径变化梯度越大，挖掘得到的频繁模式也越多，符合预期。这是由于 r m i n相等，梯度越大 r m i d和 r m a x就越大，具有邻近关系的实例对就越多，所以计算得到的影响度也会越大。

3.4.2 污染源高浓度实例占比不同对模式挖掘结果的影响

本文还对污染源高浓度实例占比不同对频繁模式挖掘结果的影响进行了分析，图12为不同风条件下，真实数据集和合成数据集1上污染源高浓度实例占比由10%增长到100%进行实验的结果。对于实例低中高浓度的划分采用随机选取的方式，除高浓度实例以外，剩下的实例按照1:1的比率随机赋予低浓度和中等浓度。污染物低浓度到高浓度影响半径分别为5.0、6.0、7.0 km，癌症病例的活动半径固定2.0 km，一类、二类、三类致癌系数分别取1.0、0.7、0.3，平滑指数取0.6，影响度阈值取0.6。
图12 高浓度实例占比不同对挖掘结果的影响

Fig. 12 Effect of different ratio of high concentration examples on mining results

可以看出，相同条件下，无论是有风还是无风，污染源高浓度实例占比与频繁模式个数均呈正相关，高浓度实例越多，影响范围大的污染源实例就越多，所以频繁模式也随之增加。值得注意的是，在风条件的影响下，无论是真实数据还是合成数据，频繁模式都比无风时多，真实数据上，频繁模式个数随着高浓度实例的占比增加大幅增多，超出正常水平，说明有风时，污染源高浓度实例越多，人类患癌的风险会大幅增加。

3.5 致癌系数对模式挖掘结果的影响分析

致癌系数主要用于计算加权影响率，给定不同的致癌系数最终都会转化为权重，所以本节直接将致癌系数设置为权重进行实验。图13体现了3类致癌物对应的致癌系数权重变化对模式挖掘结果的影响。在真实数据集上进行实验，污染源影响半径 r m i n范围在1.0~5.0 km，影响半径梯度1.0 km，癌症病例的活动半径 r c固定1.0 km，平滑指数取0.6，影响度阈值取0.35。
图13 致癌系数变化对挖掘结果的影响

Fig. 13 Effect of carcinogenic factors changes on mining results

从整体上看，无论有风还是无风条件下，当一类致癌物致癌系数权重较大时，产生的频繁模式更多，当一类致癌物致癌系数权重相同时，二类致癌系数权重较大时，产生的频繁模式也更多。这说明致癌程度高的污染物权重越大，产生的频繁模式也越多，人类患癌的风险越大。
现有方法中，当影响因素与疾病存在空间线性关系时，可利用空间回归模型进行分析，存在非线性关系时，地理探测器也可应用于探究疾病的致病因素。空间回归模型中最常用的为Logistic回归模型，除了要求自变量与因变量具有线性关系以外，还需要保证自变量之间无多重共线性，因变量一般为二分类量。适用于分析无多重共线性的危险因素与疾病之间的联系以及疾病预测。如利用Logistic回归模型探究胃癌的致病因，因变量为是否患胃癌，自变量包括年龄、性别、饮食习惯、环境等独立因素，通过回归分析可对胃癌的危险因素进行探究。
地理探测器是基于地理学第二定律提出来的一种探测空间分异性以及揭示其背后驱动力的空间分析方法，被广泛用于驱动力分析和因子分析，其核心思想是基于这样的假设：如果某个自变量对某个因变量有重要影响，那么自变量和因变量的空间分布应该具有相似性。在流行病学研究中，地理探测器适用于分析自变量为类型量，因变量为数值量之间的关系，比如利用空间探测器分析环境污染与食道癌死亡率的关系，研究空气污染和乳腺癌发病率的关系等。空间模式挖掘则是在空间距离驱动下寻找与疾病在空间中频繁邻近出现的污染源特征，核心思想是在空间上越接近的事物关联越紧密。适用于自变量为类型量，因变量也为类型量的分析，自变量与因变量须带有空间位置信息，对数据之间是否有线性关系没有要求，两者都可以为多分类量。现实生活中，污染源受多种因素的干扰具有差异性和复杂性，通常情况下和癌症不属于简单的线性关系，综上，空间回归模型以及地理探测器不适用于分析污染物与癌症的空间关联关系，因此在进行对比分析时，本文选用与本文一致的空间序偶模式挖掘算法进行比较。

3.6 比较分析

将本文算法与文献[24]提出的PSSOPP_OA算法在真实数据集上的挖掘结果进行了比较，尽管 2个算法输入参数存在差异，但是仍然可以通过控制PSSOPP_OA算法的参数使其在生成癌症实例的星型邻居集时具有相同的距离阈值，表5显示了本文算法Kde_SOPPMA和PSSOPP_OA在相同距离阈值时挖掘到的Top_100模式的后件中癌症特征及实例数的分布情况。
表5 Top_100模式中癌症特征及实例数分布情况

Tab. 5 Distribution of cancer characteristics and the number of examples in the TOP_100 patterns

排序 Kde_SOPPMA PSSOPP_OA
癌症特征 实例数/个 占比/% 癌症特征 实例数/个 占比/%
1 o 1 592 5.5 w 104 0.3
2 w 104 0.3 t 362 1.2
3 d 1 637 5.6 p 291 1.0
4 g 449 1.5 y 127 0.4
5 x 470 1.6 u 132 0.4
6 alpha 308 1.0 f 359 1.2
7 e 2 032 7.0
8 k 1 065 3.7
在真实数据集上，进行了多组实验，Kde_SOPPMA的top_100模式中，癌症特征数量平均值大约11，占癌症总特征的40%左右。并且癌症实例数既有占比较大的，也有较小的。例如表5中，Kde_SOPPM的top_100模式中，实例数高至2 032，低至104。反观PSSOPP_OA算法的top_100模式，癌症特征数量平均值大约6，占癌症总特征的20%左右。癌症实例数几乎都很小，几乎集中在数据集中实例数较为稀少的特征。原因主要是PSSOPP_OA算法在求模式影响率时，分母为癌症特征对应的实例总数，这就使得癌症实例数量最少的特征往往影响率最大，top_k模式后件就几乎都是实例数占比小的癌症。现实中癌症有频发的也有比较罕见的，PSSOPP_OA算法在挖掘频发癌症时表现却差强人意。本文提出的Kde_SOPPMA算法利用平滑因子改进了此问题，在癌症实例数量分布不均匀时表现更加稳定。

3.7 算法效率评估

本节对提出算法的效率进行评估，主要与PSSOPP_OA算法进行效率对比。对比实验在4个合成数据集上完成，分析了本文算法和PSSOPP_OA算法在不同数据密集程度下的执行时间差异。

3.7.1 距离阈值的影响

图14显示了在4个合成数据集上，算法1和算法PSSOPP_OA运行时间与距离阈值的关系。对于算法1，污染源影响半径梯度为500 m，癌症病例的活动半径固定1 km。对于PSSOPP_OA算法，通过控制算法输入变量alpha2的大小，可以使生成邻近关系的距离阈值为3个影响半径的平均值，其余参数不影响效率，设置合理即可。
图14 运行时间与距离阈值的关系

Fig. 14 The relationship between the running time and distance thresholds

从图14可看出，随着距离阈值的增加，2个算法的时间都呈现上升趋势，算法1在距离阈值较小时，耗时比PSSOPP_OA算法长，这是因为距离阈值较小时，具有邻近关系的实例对较少，PSSOPP_OA算法并不能生成频繁模式，根据剪枝算法不必再继续生成候选模式，而算法1要计算所有候选模式的影响度。随着距离阈值的增大，PSSOPP_OA算法要进行的表实例连接操作越来越多，所以耗时急剧增长，算法1可直接从星型影响实例中生成实例表，所以耗时趋于稳定，在效率方面比PSSOPP_OA算法更胜一筹。

3.7.2 影响度阈值的影响

2个算法运行时间与影响度阈值的关系如图15所示，算法1中，污染物影响半径 r m i n、 r m i d、 r m a x分别为8.0、8.5、9.0 km，癌症病例的活动半径 r c为 1 km，一类、二类、三类致癌系数分别取1.0、0.7、0.3，平滑指数取0.6。PSSOPP_OA算法同样通过设置alpha2的值，使得生成邻近关系的距离阈值为3个影响半径的平均值。
图15 运行时间与影响度阈值的关系

Fig. 15 The relationship between the running time and effect index thresholds

在影响度阈值较低时，算法1耗时远低于PSSOPP_OA算法，由于PSSOPP_OA算法具有剪枝策略，在影响度阈值较高时，生成候选模式较少，所以随着影响度阈值增大，PSSOPP_OA算法耗时会略微少于算法1，与之相比，算法1整体耗时趋于稳定。

3.7.3 特征数的影响

图16中，特征数和实例数为污染源和癌症特征数以及实例数的总数，算法1中，污染物影响半径 r m i n、 r m i d、 r m a x分别为4.0、4.5、5.0 km，癌症病例的活动半径 r c为1 km，一类、二类、三类致癌系数分别取1.0、0.7、0.3，平滑指数取0.6，影响度阈值取0.1。PSSOPP_OA算法同样通过设置alpha2的值，使得生成邻近关系的距离阈值为3个影响半径的平均值，影响度阈值取0.1。结果如图16所示。
图16 运行时间与特征数的关系

Fig. 16 The relationship between the running time and the number of features

2个算法在不同的特征数下，算法1效率比PSSOPP_OA算法更高，PSSOPP_OA算法随着特征数增加，耗时也逐渐增加，算法1随着特征数增加，耗时趋于稳定。

3.8 挖掘结果分析

3.8.1 模式分析

为了进一步分析影响各种癌症的污染源，在真实数据集上进行了多组实验，表6展示了污染物影响半径 r m i n、 r m i d、 r m a x分别为6.0、7.0、8.0 km，癌症病例的活动半径 r c为1 km，一类、二类、三类致癌系数分别取0.80、0.15、0.05，平滑指数取0.6时的挖掘结果，只列举了每种癌症对应的影响度最大的模式，并按照影响度大小排序，这些结果也多次出现在其他输入参数的频繁模式中。
表6 按影响度排序的部分挖掘结果

Tab. 6 Partial mining results sorted by influence degree

空间序偶模式 影响度
[{颗粒物}，TBL(气管、支气管和肺癌)] 0.966
[{颗粒物}，结直肠癌] 0.905
[{颗粒物，烟尘，酸雾，苯并芘}，骨癌] 0.903
[{颗粒物，铅及其化合物，烟尘，酸雾}，肝癌] 0.876
[{颗粒物，酸雾，苯并芘，二噁英类}，乳腺癌] 0.870
[{颗粒物}，子宫癌] 0.857
[{烟尘，酸雾，苯并芘，二噁英类}，头颈部癌] 0.830
[{颗粒物}，淋巴癌] 0.819
[{六价铬及其化合物，酸雾，镍及其化合物，二噁英类}，白血病] 0.808
[{颗粒物，烟尘，酸雾，苯并芘}，腹部恶性肿瘤] 0.763
[{颗粒物，烟尘，酸雾，二噁英类}，宫颈癌] 0.754
[{颗粒物，烟尘，酸雾}，胰腺癌] 0.751
[{颗粒物，酸雾，苯并芘，二噁英类}，胸部恶性肿瘤] 0.739
[{铅及其化合物，镉及其化合物，砷及其化合物，镍及其化合物}，盆腔癌] 0.716
[{铅及其化合物，镉及其化合物，砷及其化合物，六价铬及其化合物}，脑癌] 0.699
[{颗粒物，铅及其化合物，烟尘，酸雾}，肾癌] 0.670
[{烟尘，酸雾，苯并芘，二噁英类}，眼耳部恶性肿瘤] 0.669
[{烟尘，酸雾，苯并芘，二噁英类}，皮肤癌] 0.628
[{颗粒物，镉及其化合物，烟尘，酸雾}，胃癌] 0.626
[{颗粒物，烟尘，酸雾，镍及其化合物}，甲状腺癌] 0.618
[{铅及其化合物，酸雾，镍及其化合物，二噁英类}，肢体恶性肿瘤] 0.610
[{颗粒物，烟尘，酸雾}，胆部恶性肿瘤] 0.609
[{烟尘，酸雾，苯并芘，二噁英类}，卵巢癌] 0.517
[{颗粒物，二氧化硫}，前列腺癌] 0.488
[{颗粒物，酸雾，苯并芘，二噁英类}，食管癌] 0.453
[{颗粒物，二氧化硫，烟尘，苯并芘}，肛门癌] 0.440
[{颗粒物，二氧化硫}，膀胱癌] 0.415
[{颗粒物，石油类，烟尘，氯类致癌物}，垂体恶性肿瘤] 0.336
通过表6可发现，颗粒物与很多癌症在空间中存在关联，尤其是肺癌、消化道癌与颗粒物关系较为密切，说明空气中的颗粒物、烟尘、酸雾等空气中的大颗粒分子对人体危害非常大。还有一部分癌症的发生可能与室外空气中的重金属成分相关，例如对脑癌影响度较大的均为重金属离子。苯并芘，二噁英类物质属于危害较强的一类致癌物，也与很多癌症存在空间关联。除此之外，有一些污染物单独出现影响度较小，但是当它与其他污染物一块出现，模式的影响度就会大幅增加，其中似乎有些污染物发挥了“催化剂”的作用，比如污染物“酸雾”如果单独出现，模式影响度可以忽略不计，但是当“酸雾”与“烟尘”或“颗粒物”同时出现，模式影响度就会大幅提升，可能与很多癌症的发生存在空间关联。
通过改进的空间同位模式挖掘理论，从空间数据分布的角度挖掘工业污染与癌症的关联关系，对云南省癌症防治提出相关建议。首先，建议云南省排污企业选址在盛行风向的下风口处，至少15 km以内不能有人居住，尤其对于颗粒物排放较多的企业；其次，对于排放颗粒物、烟尘等大颗粒污染物以及苯并芘、二噁英较多的企业，周边居民定期进行肺癌、消化道癌等恶性肿瘤筛查，最后，本研究结果也可为癌症流行病学专家提供参考，进一步研究污染源和癌症的关系。

3.8.2 混杂因素分析

混杂通常是由于一个或多个外来因素的存在，掩盖或夸大了研究因素与疾病的联系，从而部分或全部地歪曲了两者间的真实联系。本文可以通过配比法实现混杂因素控制。配比法是指选择某些特征上与处理组一致的对照，排除这些因素的混杂作用，从而凸显出研究因素的效应。通过一个例子来解释本文如何利用配比法实现混杂控制。
肺癌的混杂因素主要包括吸烟、职业、肺部慢性疾病、遗传因素，在进行模式挖掘时，可以选择其中一个或多个因素配比，吸烟是最常见的肺癌元凶，所以此处选择吸烟进行配比。将真实数据集的肺癌患者中有吸烟经历的患者和没有吸烟经历的患者分开，分别与污染源进行空间序偶模式挖掘。输入参数为污染物影响半径 r m i n、 r m i d、 r m a x分别为6.0、7.0、8.0 km，癌症病例的活动半径 r c为1 km，一类、二类、三类致癌系数分别取0.80、0.15、0.05，平滑指数取0.6，未进行混杂控制与进行了混杂控制的结果对比如表7、表8所示。
表7 top_10模式影响度排序

Tab. 7 top_10 patterns influence degree sequence

模式 未进行混杂控制 进行混杂控制
全体肺癌病例 吸烟肺癌病例 未吸烟肺癌病例
[{颗粒物}，肺癌] 0.733 267 0.547 896 0.663 529
[{颗粒物，二氧化硫}，肺癌] 0.707 699 0.537 499 0.660 082
[{颗粒物，烟尘}，肺癌] 0.703 397 0.537 169 0.602 412
[{颗粒物，烟尘，酸雾}，肺癌] 0.698 457 0.470 928 0.659 817
[{颗粒物，二氧化硫，烟尘}，肺癌] 0.693 392 0.533 641 0.591 096
[{颗粒物，烟尘，苯并芘}，肺癌] 0.6899 48 0.451 520 0.646 803
[{颗粒物，二氧化硫，苯并芘}，肺癌] 0.674 282 0.408 540 0.641 783
[{颗粒物，苯并芘}，肺癌] 0.671 279 0.405 032 0.638 911
[{颗粒物，汞及其化合物，烟尘}，肺癌] 0.664 098 0.499 861 0.571 227
[{颗粒物，酸雾}，肺癌] 0.653 135 0.421 261 0.606 689
表8 进行混杂控制与未进行混杂控制时top_50、top_100模式中相同模式百分比

Tab. 8 Percentage of the same patterns in top_50 and top_100 patterns with or without confounding control (%)

模式 吸烟 未吸烟
Top_50 72 88
Top_100 69 90
从表7可看出，与未进行混杂控制的top_10模式相比，进行混杂控制时不论是吸烟还是未吸烟，都有70%的模式与未进行混杂控制的模式影响度变化顺序一致。进行混杂控制时，吸烟的影响度普遍低于未吸烟的，但是患肺癌的人数依然居高不下，从侧面表明了吸烟对肺癌有一定的影响，符合预期。
通过表8可知，进行混杂控制时与未进行混杂控制时模式基本保持一致，但部分模式存在一定的差异，吸烟情况差异较为明显，这种差异主要由吸烟患者的空间位置分布与混杂因素共同引起。我们在挖掘癌症与污染源的空间关联关系时，一般选择top_10、top_20影响度较大的模式进行分析，在结果中，这些模式几乎完全一致，所以是否控制混杂因素对于研究污染源与癌症的空间关联关系并无太大影响，但是控制混杂可以使得结果更精细。

4 结论

传统的空间同位模式挖掘算法在挖掘空间序偶模式时存在诸多限制，本文利用核密度估计(KDE)模型结合空间同位模式挖掘算法，提出了一种新的基于距离衰减效应和影响加权的频繁性度量方法-影响度，影响度的计算不仅能够有效地衡量污染源实例与癌症实例之间距离变化对模式频繁程度的影响，还结合现实条件将污染源对癌症的影响机制进行建模，尽可能地考虑风环境、污染物浓度对于污染物扩散的影响，提出“致癌系数”区分企业污染物中不同类别的致癌物，用“致癌系数”作为权重进行加权求和计算各种污染物对癌症的影响，解决了传统方法的局限性。此外，本文还利用平滑因子改进了因癌症实例数分布不均引起的挖掘异常，提高了方法的稳健性。实验结果表明，无论是宏观角度还是微观角度，影响度与参与度同样都可以体现模式的频繁程度，但影响度度量更能捕获在空间中距离更近且影响度更大的模式，更能反映污染源对癌症的影响规律。
但是，本文所提出的方法还有一些不确定性和局限性。首先，污染物在一个地区的分布受多种因素的影响，如污染物类型、释放浓度、天气条件（风、降水）、地形等，这些因素使得污染源的扩散具有不确定性，尽管本文给出了一个模型尽可能的模拟污染物在真实世界的扩散过程，仍然无法真实还原复杂的空气污染情况。其次，该方法的提出考虑了一些影响机制，主要集中在对污染源影响的建模上，这些机制的考虑可能会降低所提方法在一些实际应用中的普适性和可操作性。由于这些机制的设置比较独立，所以本文所提方法除了可以用于挖掘室外空气污染源对癌症的影响，也适用于发现其他疾病与其他多种因素的空间同位模式，例如距离沼泽区越近的人群越容易患血吸虫病。在未来的工作中，在尽量消除该方法的不确定性以及局限性的基础上，拟在挖掘到高影响模式后进一步考虑识别模式的高影响区域，以便提供更有针对性的癌症筛查区域以及提出城市规划的合理化建议。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Sung H, Ferlay J, Siegel R L, et al. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries[J]. CA: a Cancer Journal for Clinicians, 2021, 71(3):209-249. DOI: 10.3322/caac.21660

[2]
Stocks P. On the relations between atmospheric pollution in urban and rural localities and mortality from cancer, bronchitis and pneumonia, with particular reference to 3:4 benzopyrene, beryllium, molybdenum, vanadium and arsenic[J]. British Journal of Cancer, 1960, 14(3):397-418. DOI:10.1038/bjc.1960.45

PMID

[3]
Ramis R, Diggle P, Cambra K, et al. Prostate cancer and industrial pollution risk around putative focus in a multi-source scenario[J]. Environment International, 2011, 37(3):577-585. DOI:10.1016/j.envint.2010.12.001

PMID

[4]
Santos-Sanchez V, Córdoba-Doña J A, García-Pérez J, et al. Industrial pollution and mortality from digestive cancers at the small area level in a Spanish industrialized Province[J]. Geospatial Health, 2020, 15(1):147-155. DOI:10.4081/gh.2020.802

[5]
Hwang J, Bae H, Choi S, et al. Impact of air pollution on breast cancer incidence and mortality: A nationwide analysis in South Korea[J]. Scientific Reports, 2020, 10:5392. DOI:10.1038/s41598-020-62200-x

PMID

[6]
Lynge E, Holmsgaard H A, Holmager T L F, et al. Cancer incidence in Thyborøn-Harboøre, Denmark: A cohort study from an industrially contaminated site[J]. Scientific Reports, 2021, 11:13006. DOI:10.1038/s41598-021-92446-y

PMID

[7]
Lagunas-Rangel F A, Linnea-Niemi J V, Kudłak B, et al. Role of the synergistic interactions of environmental pollutants in the development of cancer[J]. GeoHealth, 2022, 6: e2021GH000552. DOI:10.1029/2021gh000552

[8]
Turner M C, Andersen Z J, Baccarelli A, et al. Outdoor air pollution and cancer: An overview of the current evidence and public health recommendations[J]. CA: a Cancer Journal for Clinicians, 2020, 70(6):460-479. DOI:10.3322/caac.21632

[9]
Hill W, Lim E L, Weeden C E, et al. Lung adenocarcinoma promotion by air pollutants[J]. Nature, 2023, 616(7955):159-167. DOI:10.1038/s41586-023-05874-3

[10]
Shekhar S, Huang Y. Discovering spatial co-location patterns: A summary of results[M]//Jensen C S, Schneider M, Seeger B, et al., Eds. Advances in Spatial and Temporal Databases. Heidelberg: Springer Berlin Heidelberg, 2001:236-256. DOI:10.1007/3-540-47724-1_13

[11]
Li J D, Adilmagambetov A, Jabbar M S M, et al. On discovering co-location patterns in datasets: A case study of pollutants and child cancers[J]. GeoInformatica, 2016, 20(4):651-692. DOI:10.1007/s10707-016-0254-1

[12]
Akbari M, Samadzadegan F, Weibel R. A generic regional spatio-temporal co-occurrence pattern mining model: A case study for air pollution[J]. Journal of Geographical Systems, 2015, 17(3):249-274. DOI:10.1007/s10109-015-0216-4

[13]
Huang Y, Shekhar S, Xiong H. Discovering colocation patterns from spatial data sets: A general approach[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(12):1472-1485. DOI:10.1109/TKDE.2004.90

[14]
Yoo J S, Shekhar S, Smith J, et al. A partial join approach for mining co-location patterns[C]// Proceedings of the 12th annual ACM international workshop on Geographic information systems. New York: ACM, 2004:241-249. DOI:10.1145/1032222.1032258

[15]
Yoo J S, Shekhar S, Celik M. A join-less approach for co-location pattern mining: A summary of results[C]// Fifth IEEE International Conference on Data Mining (ICDM'05). IEEE, 2005:813-816. DOI:10.1109/ICDM.2005.8

[16]
Wang L Z, Bao Y Z, Lu J, et al. A new join-less approach for co-location pattern mining[C]// 2008 8th IEEE International Conference on Computer and Information Technology. IEEE, 2008:197-202. DOI:10.1109/CIT.2008.4594673

[17]
Xiao X Y, Xie X, Luo Q, et al. Density based co-location pattern discovery[C]// Proceedings of the 16th ACM SIGSPATIAL international conference on Advances in geographic information systems. New York: ACM, 2008:1-10. DOI:10.1145/1463434.1463471

[18]
杨培忠, 王丽珍, 王晓璇, 等. 一种基于列计算的空间并置模式挖掘方法[J]. 中国科学:信息科学, 2022, 52(6):1053-1068.

[ Yang P Z, Wang L Z, Wang X X, et al. A spatial co-location pattern mining approach based on column calculation[J]. Scientia Sinica (Informationis), 2022, 52(6):1053-1068. ]

[19]
Xiong H, Shekhar S, Huang Y, et al. A framework for discovering co-location patterns in data sets with extended spatial objects[C]// Proceedings of the 2004 SIAM International Conference on Data Mining. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2004:78-89. DOI:10.1137/1.9781611972740.8

[20]
Liu Z, Huang Y. Mining co-locations under uncertainty[M]//Advances in Spatial and Temporal Databases. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013:429-446. DOI:10.1007/978-3-642-40235-7_25

[21]
Yao X J, Chen L J, Peng L, et al. A co-location pattern-mining algorithm with a density-weighted distance thresholding consideration[J]. Information Sciences, 2017, 396:144-161. DOI:10.1016/j.ins.2017.02.040

[22]
胡添, 刘涛, 杜萍, 等. 空间同位模式支持下城市服务业关联发现及特征分析[J]. 地球信息科学学报, 2021, 23(6):969-978.

DOI

[ Hu T, Liu T, Du P, et al. Correlation discovery and feature analysis of urban service industry supported by spatial co-location model[J]. Journal of Geo-information Science, 2021, 23(6):969-978. ] DOI:10.12082/dqxxkx.2021.200408

[23]
徐振, 荆耀栋, 毕如田, 等. 基于资源环境数据格网化表达的关联模式发现[J]. 地球信息科学学报, 2018, 20(1):28-36.

DOI

[ Xu Z, Jing Y D, Bi R T, et al. The discovery of spatial association patterns of resource and environment information based on grid data[J]. Journal of Geo-information Science, 2018, 20(1):28-36. ] DOI:10.12082/dqxxkx.2018.170266

[24]
谢旺, 王丽珍, 陈红梅, 等. 基于空间序偶模式挖掘污染源与癌症病例的关系[J]. 数据分析与知识发现, 2021, 5(2):14-31.

[ Xie W, Wang L Z, Chen H M, et al. Identifying relationship between pollution sources and cancer cases with spatial ordered pair patterns[J]. Data Analysis and Knowledge Discovery, 2021, 5(2):14-31. ] DOI:10.11925/infotech.2096-3467.2020.1026

[25]
邓星. 典型地域的风向特征研究[J]. 风能, 2017(8):46-51.

[ Deng X. Study on wind direction characteristics in typical areas[J]. Wind Energy, 2017(8):46-51. ]

[26]
Wang L Z, Fang Y, Zhou L H. Preference-based spatial co-location pattern mining[M]. Singapore: Springer Nature Singapore, 2022. DOI:10.1007/978-981-16-7566-9

Options
文章导航

/

〈 〉