EN中文

地球信息科学学报 >

2023 , Vol. 25 >Issue 12: 2361 - 2373

DOI: https://doi.org/10.12082/dqxxkx.2023.230425

2023年第十八届中国地理信息科学理论与方法学术年会优秀论文

遥感图像菱形三十面体六边形全球离散格网建模及存储

  • 梁启爽 ,
  • 陈艺航 ,
  • 贲进 ,
  • 周建彬 ,
  • 丁俊杰 ,
  • 代金池
展开
  • 信息工程大学地理空间信息学院，郑州 450001
*贲 进（1977— ），男，江苏海安人，博士，教授，主要从事摄影测量与遥感、全球离散格网、空间影像信息研究。 E-mail:

梁启爽（1999— ），男，河北衡水人，硕士生，主要从事全球离散格网等方面研究。E-mail:

收稿日期: 2023-07-21

  修回日期: 2023-11-15

  网络出版日期: 2023-12-05

基金资助

河南省重大科技专项国家超级计算郑州中心创新生态系统建设科技专项(201400210100)

收起

Modelling and Storage Method for Hexagonal Remote Sensing Images in Rhombic Triacontahedron Discrete Global Grid System

  • LIANG Qishuang ,
  • CHEN Yihang ,
  • BEN Jin ,
  • ZHOU Jianbin ,
  • DING Junjie ,
  • DAI Jinchi
Expand
  • Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, China
*BEN Jin, E-mail:

Received date: 2023-07-21

  Revised date: 2023-11-15

  Online published: 2023-12-05

Supported by

Foundation item: Special Science Fund for Innovation Ecosystem Construction of National Supercomputing Center in Zhengzhou(201400210100)

Fold

摘要

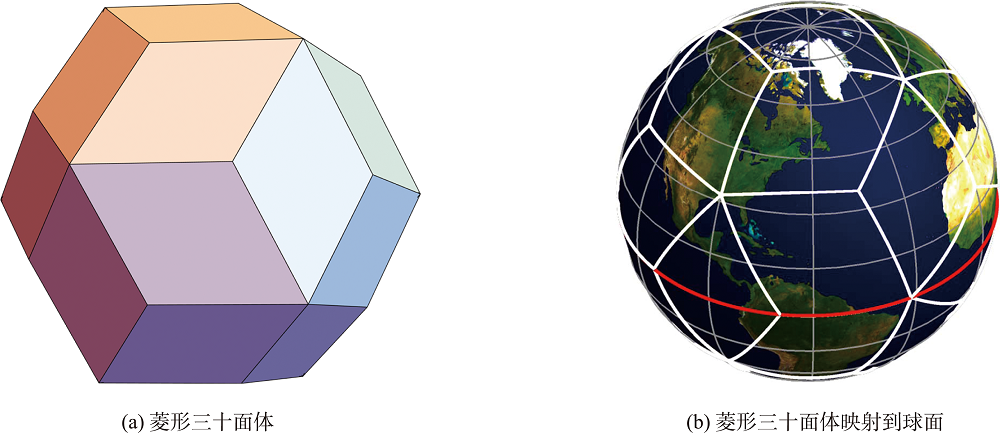
全球离散格网系统（Discrete Global Grid System，DGGS）是数字化的地球参考框架，在多源、多尺度地球空间数据集成分析方面优势明显。本文选择菱形三十面体六边形全球离散格网系统，提高格网与地球的整体拟合精度和空间采样率；建立遥感图像六边形像素数学模型，提出兼容开放标准格式的数据存储方案。① 根据地理位置将遥感图像格网化，完成遥感图像六边形DGGS建模；其次，建立六边形单元与矩形像素严密对应关系，等效保留六边形单元的邻域信息； ② 采用GeoTIFF开放标准格式精确存储六边形属性值以及投影、变换参数； ③ 设计依托六边形DGGS格网标准数据集为基础的多尺度六边形DGGS生成算法。实验结果表明：本文方案不仅能保证六边形像素遥感图像数据与标准文件格式兼容，而且能保证矩形像素与六边形单元逐一对应，较好地保留了六边形单元数据的图像信息和空间分布特征，相较于欧空局SMOS数据组织方案更具优势。本文方案打破了六边形单元与矩形像素遥感图像的数据组织壁垒，使用常见GIS/RS软件即可读取六边形像素的遥感图像，并可通过对矩形像素的操作等效实现对六边形单元的处理，有望推动六边形DGGS在遥感数据组织、处理、共享等方面的应用。

关键词： 菱形三十面体; 全球离散格网系统; 六边形; 数据建模; 双倍偏移坐标; 遥感图像; 数据存储; SMOS

本文引用格式

梁启爽 , 陈艺航 , 贲进 , 周建彬 , 丁俊杰 , 代金池 . 遥感图像菱形三十面体六边形全球离散格网建模及存储[J]. 地球信息科学学报, 2023 , 25(12) : 2361 -2373 . DOI: 10.12082/dqxxkx.2023.230425

Abstract

The explosive growth of multisource Remote Sensing (RS) data poses challenges to the application of fusion analysis. Discrete Global Grid System (DGGS) is a digital earth reference model supporting integration and analysis of multisource and multiscale geospatial data. In this study, a Rhombic Triacontahedron (RT) hexagonal DGGS is chosen as the basic digital framework to improve the overall fitting accuracy to the Earth and the spatial sampling efficiency of the grid which is conceptually equivalent to pixel. A mathematical model of hexagonal pixels of RS images is established, and the storage scheme of hexagonal pixels compatible with open-standard format is also proposed. First, the RS images are gridded according to the geographical location, and the hexagonal DGGS modeling of RS image was completed. Secondly, a rigorous correspondence between hexagon and rectangular pixels is established geometrically to preserve the neighborhood information of hexagon pixels by improving the way of double offset coordinates mapped to the rectangular array. Then, the GeoTIFF open-standard format is used to accurately store the hexagonal pixel values, projection and transformation parameters. Finally, a multiscale hexagonal DGGS generation algorithm based on the hexagonal DGGS standard dataset is designed. Experiment results show that using RT hexagonal equal area grid to organize global scale RS images can realize uniform sampling of global data, ensure the overall consistency of cells in different latitudes, avoid drastic changes of cells in high latitudes, and be more suitable for global scale data processing and analysis. The proposed storage scheme can not only ensure that the hexagon pixel RS image dataset is compatible with the standard file format, but also ensure that the rectangular pixels correspond to the hexagon pixels one by one. Hexagonal pixels could be stored in the open-standard format GeoTIFF with a fixed pattern in the form of rectangular arrays for data access, with transformation parameters and metadata used to reconstruct the hexagons. The image information and spatial distribution characteristics of hexagonal DGGS data are preserved well, which is more advantageous than the Soil Moisture and Ocean Salinity (SMOS) data organization scheme. This scheme break through the hexagonal with rectangular pixels in RS image data organization barriers, GIS/RS software that can be read using common hexagon pixels in RS image, and can complete the hexagonal pixels by the operation of the rectangular pixel equivalent processing, is expected to promote hexagon global discrete grid systems in RS data organization, processing, sharing, and other applications.

Key words： rhombic triacontahedron; Discrete Global Grid System; hexagon; data modelling; double offset coordinates; remote sensing image; data storage; SMOS

1 引言

随着遥感对地观测技术飞速发展，海量遥感数据的组织管理、分析处理、传输共享对数据建模的理论、方法和技术提出了更高要求。全球离散格网系统（Discrete Global Grid System，DGGS）递归剖分地球空间形成的多尺度离散层次结构有助于建立以位置为主键的新型地理空间数据模型[1]，在结构上有望实现多来源、多尺度、大区域遥感数据的集成、融合与分析。现有绝大多数成果均使用柏拉图多面体构造DGGS[2]，其中二十面体因面数最多成为首选[3⇓-5]。然而，二十面体不易与地球建立支持地理现象分布特征的定位方案[6]，且格网单元的均匀性仍有待提升。
部分学者选择面数更多的多面体，进一步提高DGGS与地球表面的拟合精度。Hall等[7]采用一 百二十面体，但面数过多易导致繁琐的跨面计算。Liang等[8]和王蕊等[6]采用菱形三十面体（Rhombic Triacontahedron，RT），无需像二十面体那样拼接三角面构造“逻辑菱形”（图1），可直接建立二维平面坐标系统并采用矩阵线性算法提高计算效率。
图1 菱形三十面体与地球的定位关系

Fig. 1 Location scheme for the rhombic triacontahedron and Earth

六边形具有排列一致相邻、采样效率和角分辨率最高[1]等优秀几何属性，有利于提高数据建模和处理精度[9]。不同孔径（3、4、7）的六边形剖分灵活组合，可获得最接近原数据分辨率的格网层次。其中，四孔六边形格网系统的单元方向固定，且层次结构易与四叉树编码、二进制位运算[5]等有效结合，有利于提高地理空间数据处理效率。
国内外学者在六边形DGGS数据组织处理方面展开了深入研究。贲进等[10]提出利用二十面体四孔六边形DGGS组织多源异构空间数据的基本思路。张继凯等[11]提出二十面体四孔六边形DGGS的四叉树结构，实现全球海洋温度场的可视化。Li等[12]采用二十面体三孔六边形DGGS集成加拿大异构地形数据，提高单一来源地形数据质量。Mahdavi-Amiri等[13]将小波变换算法与二十面体三孔六边形DGGS结合，实现了多尺度地理空间数据数据的累进传输。
尽管如此，六边形DGGS标准数据集的共享仍存在较大挑战，主要原因是缺少六边形格网数据存储和共享的相关扩展标准。部分学者采用私有文件格式存储[12,14]，但非标准格式无法直接被商业软件解析，不利于数据集的推广应用。欧空局（European Space Agency，ESA）发射的“土壤湿度和海洋盐分任务”（Soil Moisture and Ocean Salinity Mission，SMOS）卫星采用二十面体Snyder等积四孔六边形格网（Icosahedral Snyder Equal-area Aperture 4 Hexagonal Discrete Global Grid，ISEA4H DGG）采集辐射信息[15]，并以数十个矩形像素近似模拟一个六边形单元存储至NetCDF文件中。其不足主要体现在： ① 多个矩形像素模拟一个六边形单元，不仅增加了数据量，而且降低了数据精度； ② 模拟六边形单元的矩形像素集合的数量和形状不固定，不利于矩形与真实六边形快速转换； ③ 只能由矩形像素重采样得到多分辨率SMOS数据集，精度较低。
针对上述问题，本文选择菱形三十面体（下文简称三十面体）四孔六边形DGGS作为遥感图像载体，并将三十面体六边形DGGS数据与现有开放标准格式建立关联（生成的数据称为“六边形DGGS格网标准数据集”），实现数据的存储和共享。由于六边形单元无法精确映射为完整矩形栅格阵列，如何保留六边形DGGS数据良好的特性（如单元等积、一致相邻等）并减少信息损失，是提高数据建模精度的关键。

2 研究方法

全文研究思路设计如下：首先，采用间接法将传统矩形经纬遥感图像重采样至三十面体六边形DGGS，如图2（b）；其次，借助等积多面体投影将六边形格网化遥感图像精确映射至三十面体表面，此过程无信息损失且球面与多面体表面六边形单元等积，如图2（c）；然后，建立基于三十面体菱形面结构的六边形单元与矩形像素“一对一”严格映射关系，如图2（d）；最后，借助开放标准格式存储与六边形单元等效的矩形像素，封装属性值、投影变换参数等信息，便于数据集共享，如图2（e）。
图2 遥感图像三十面体六边形像素建模和存储技术路线

Fig. 2 Technology frame of modeling and storage of remote sensing images with RT hexagon pixels

2.1 遥感图像三十面体六边形格网建模

2.1.1 三十面体六边形离散格网系统设置

对于遥感信息采样和建模而言，DGGS单元形状均匀、面积相等是刚性需求[16-17]。王蕊等[6]提出三十面体Leeuwen等积投影，相较于Snyder等积投影可大幅度减小角度变形，且克服了迭代求解效率较低的不足。本文以三十面体Leeuwen等积投影的四孔六边形DGGS开展后续研究，并在菱形面边界设置不同的归属规则，I类菱形面保留格心（单元中心）位于i轴和j轴边界的单元，Ⅱ类菱形面保留格心位于j轴（不包括原点O）和i轴对面边界的单元。使用整数编码H[di, (i, j)n]标识球面上的每个六边形，其中di为菱形面索引，(i, j)为格网中心编码，n为格网层次，i, j∈Z+，如图3。该编码方案与规则矩形格网的一致，其优势体现在行列索引规则整齐、坐标运算简单，易与并行计算相关联等。
图3 三十面体四孔六边形格网系统

注:不同颜色表示不同类型的六边形单元。

Fig. 3 RT aperature-4 hexagonal grid system

2.1.2 遥感图像三十面体六边形格网采样量化

在地球信息科学领域，现实世界的栅格建模方法是将空间变量离散化为规则格网，每个格网单元被赋予地理位置信息和属性信息[14]，三十面体六边形DGGS即以等积六边形为基本单元对地球表面无缝无叠地均匀、高效采样。有两种方法可以获得六边形像素遥感图像：由传感器直接采集辐射信息而成[15]；由传统矩形像素遥感图像间接重采样得到[18-19]。直接法几乎没有信息损失，是获取数据的最理想途径，但需要传感器硬件支持。因为目前六边形像素成像器件尚未普及，所以这种方法只适用于特定应用场景。间接法纯粹通过算法实现，无需特殊硬件支持，是生成数据的最方便途径，适用于大多数的应用场景。遥感图像三十面体六边形DGGS数据间接采样量化步骤如下： ① 需要依据图像分辨率确定合适格网层次，为保证图像在格网上的表达精度，格网单元分辨率应当等于或优于原始数据分辨率，三十面体六边形DGGS不同层次单元分辨率如表1所示； ② 根据菱形面单元索引编码特征，遍历每个格网单元整数坐标H[di, (i, j)n]，并将其转换为地理坐标(Bi, Li)； ③ 将单元中心地理坐标反算至遥感图像所在的投影平面坐标系，插值计算对应点的属性值并赋予格网单元。
表1 三十面体六边形全球离散格网不同层次分辨率

Tab. 1 Resolution at different levels of the RT hexagonal DGGS

格网层次 … 9 10 11 12 13 14
单元平均面积/km2 … 65.100 80 16.275 20 4.066 24 1.019 35 0.254 88 0.063 72

2.2 遥感图像三十面体六边形像素数据存储

2.2.1 平面六边形单元位置描述

已有轴坐标系、偏移坐标系和双倍偏移坐标系等描述平面六边形单元位置的方法，如图4。这些方法的不同之处主要在于：① 六边形映射至矩形阵列是否高效；② 与笛卡尔坐标转换是否方便[20]。
图4 3种平面六边形索引坐标系统[20]

注: (u, v)表示在对应坐标系下的坐标。

Fig. 4 Three coordinate systems for plane hexagonal grid

轴坐标系通过2个线性无关的单位向量e1,e2描述平面上任意位置的六边形，其中e1,e2的夹角为60°，设平面六边形中心点集合为L，则有：
L = u e 1 + v e 2 ;   u ,   v ∈ Z
式中： u ,   v为六边形在轴坐标系下的坐标。
轴坐标系是描述二维平面六边形最方便的坐标系，但映射为矩形阵列时需要额外空间，且六边形的空间邻域关系也会发生改变，如图5（a）。偏移坐标和双倍偏移坐标均是基于正交轴建立的，奇数行在u方向偏移一个单位，二者的不同之处在于双倍偏移坐标的水平步长u是偏移坐标的2倍，设双倍偏移坐标水平和垂直方向的基向量分别为b1, b2，平面六边形中心点集合L可表示为：
图5 不同坐标系下六边形映射为矩形阵列

注:左图是六边形在对应(轴、偏移、双倍、优化双倍)坐标系下的样式，右图是六边形映射至矩形阵列时的样式。黑色箭头代表某一单元的邻域关系，灰色箭头表示像素填充。

Fig. 5 Rectangular arrays of hexagons stored in different coordinate systems

L = u b 1 + v b 2 u = 2 k ,   v = 2 h                                   ( v % 2 = 0 ) u = 2 k + 1 ,   v = 2 h + 1         ( v % 2 = 1 )   k ,   h ∈ Z
式中：u,v为六边形在双倍偏移坐标系下的坐标；%为取余运算。
相较于偏移坐标系，双倍偏移坐标系会使图像宽度增加一倍，该方案的优势是六边形映射至矩形阵列时，在空间位置上依然保持正确的邻域关系。但会造成一半的空间浪费（白色区域为空），且“棋盘阵列”排列样式不利于六边形像素遥感图像分析，如图5（c）。因此，本文改进六边形单元映射至矩形阵列的方法（下文简称优化双倍偏移坐标），将蓝色位置处像素值填充至右侧空白单元，两个正方形像素组合为一个矩形，利用规则排列的矩形等效替代六边形，如图5（d）。

2.2.2 六边形整数坐标映射至优化双倍偏移坐标

以三十面体菱形面中心为原点建立投影坐标系oxy，如图6（a）。该坐标系有2个作用：建立三十面体表面投影点坐标H[di, (xi, yi)]和地理坐标(Bi, Li)的相互转换；整数坐标H[di, (i, j)n]与六边形优化双倍偏移坐标H[di, (I, J)n]的过渡计算。为提高计算速度，选择构建与目标区域相关的外接多边形，多边形各边分别与菱形面各边平行。图6（b）展示了某研究区与多个菱形面相交构建的外接多边形ABCD，在此基础上可建立局部整数坐标并确定坐标搜索范围。设研究区域边界地理坐标点的数量为m，坐标点集合表示为 V = ( B i ,   L i ) 0 ≤ i ≤ m，主要计算过程如下：
图6 三十面体局部跨面区域处理

Fig. 6 Local area span processing of RT

（1）将研究区边界的地理坐标 ( B i ,   L i )利用Leeuwen等积多面体正投影转换为投影坐标H[di, (xi, yi)]；
（2）将H[di, (xi, yi)]投影坐标转换为整数编码H[di, (i, j)n]，并对其统计排序，确定外接多边形4个角点的整数坐标：A(imin, jmin)、B(imax, jmin)、C(imax, jmax)、 D(imin, jmax)；
（3）依次遍历四边形ABCD内六边形单元的整数坐标(i, j)(i∈(imin, imax), j⊆(jmin, jmax))，确定研究区最小外接矩形abcd的投影坐标：a(xmin, ymax)、b(xmin, ymin)、c(xmax, ymin)、d(xmax, ymax)，并依据基向量b1, b2的大小计算在投影坐标系下水平和垂直方向分辨率，如图6（c）；
（4）根据式(3)计算每个六边形单元位于优化双倍偏移坐标系下的坐标H[di, (I, J)n]，将六边形单元属性值赋予对应位置的矩形像素。
I = ( y i - y a ) b 1 + 0.5             y i ⊆ ( y m i n ,   y m a x )               J = ( x i - x a ) b 2 + 0.5             x i ⊆ ( x m i n ,   x m a x )
式中： 为向下取整。

2.2.3 多尺度六边形DGGS数据生成

传统的遥感图像金字塔是一种典型的多分辨率层次结构，可根据用户实际需求以不同的分辨率存储和显示，多用于图像降采样和压缩。本文采用的四孔六边形DGGS天然具有“树”层次属性，由此以生成的六边形DGGS格网标准数据集为基础，设计多尺度六边形格网数据生成方案。由于不同层次的六边形不能完全嵌套叠合，导致每个六边形父单元覆盖1个完整的子单元和6个相邻子单元的一半，如图7（a）。因此，本文定义六边形降采样核，将核中位于不同位置的单元赋予不同的权重，如图7（b）。最后，从分辨率为n的球面六边形格网对应的矩形像素数据开始，应用六边形降采样核，并保留分辨率为n-1下的子单元，重复迭代计算，直到所需分辨率数据。
图7 六边形多分辨率降采样数学模型

注:n为六边形格网层次。

Fig. 7 Multi-resolution hexagonal mathematical model

根据式(2)，六边形降采样核等效于多个矩形子核，即单个六边形卷积运算可由多个矩形卷积运算组合执行，且单个矩形卷积运算可以同时完成，有助于算法并行化加速。由矩形像素图像计算多尺度六边形格网过程可由图8描述，算法流程如下：
图8 六边形DGGS格网标准数据集转换至不同分辨率的六边形格网

Fig. 8 Conversion of Hexagonal DGGS grid standard datasets to grids with different resolutions

（1）读取优化双倍偏移坐标H[di, (I, J)n]，利用式(4)计算单元对应的投影坐标H[di, (xi, yi)]；
x = x a + J × b 1 y = y a + I × b 2
（2）根据投影坐标计算整数编码H[di, (i, j)n]，依据式(5)分别确定I、Ⅱ类六边形父单元整数编码 H[di, (i, j)n-1]，并根据图7（b）降采样核和相邻单元计算父单元的属性值；
( i ,   j ) n - 1 = i n 2 , j n 2                           Ⅰ 类 ( i ,   j ) n - 1 = i n 2 , j n - 1 2             Ⅱ 类
在计算机内部由于2的乘法和除法可以借助位运算快速执行，将式(5)改写为：
( i ,   j ) n - 1 = i n ≫ 1 ,   j n ≫ 1                           Ⅰ 类 ( i ,   j ) n - 1 = i n ≫ 1 ,   j n - 1 ≫ 1             Ⅱ 类
式中： ≫为右移运算符。
（3）根据父单元整数编码计算六边形父单元中心投影坐标H[di, (x, y)n-1]，并依据六边形方向向量计算格点（即六边形单元顶点）投影坐标，利用逆三十面体Leeuwen等积投影将其映射至球面。

2.2.4 标准文件格式扩展

目前有许多易于数据共享的标准栅格数据存储格式，主要包括GeoTIFF、HDF、NetCDF和ERDAS IMAGINE等。其中，GeoTIFF（Geographic Tagged Image File Format）是一种被广泛支持和使用的开放格式[21]，具有显著优势：支持嵌入与地理坐标系相关的空间参考信息；包含丰富的元数据信息，如坐标系、像元大小、投影参数等，这些元数据能帮助用户正确地解释和处理栅格数据；支持LZW、JPEG等多种压缩算法；支持多张图像在同一个文件存储等。
因此，本文利用GeoTIFF文件标准组织和管理六边形DGGS格网数据的空间投影、坐标变换等信息。GeoTIFF采用EPSG（European Petroleum Survey Group）数据库的参考信息设置地理键编码，其中未包含Leeuwen多面体投影坐标系。扩展定义表2中的地理键和编码，可完整记录Leeuwen多面体投影的元数据。
表2 部分地理键值的设置及含义

Tab. 2 Settings and meanings of some geographic key values

GeoTIFF格式标签 数值 标签说明
ModelPixelScaleTag （b1, b2, 0） 用于定义像素在地理坐标系统中的缩放比例
ModelTiepointTag （0, 0, xa, ya, 0） 用于定义图像像素和地理坐标之间的映射关系
GTCitationGeoKey “三十面体Leeuwen等积多面体投影相关信息描述” 提供所使用的坐标系、投影方法或其他详细信息
的描述
GTRasterTypeGeoKey 2 表示不同类型栅格数据（1：表示灰度栅格；2：表示彩色栅格；3：表示伪彩色图像；4：表示透明度掩码）
GeographicTypeGeoKey 投影坐标系 图像地理坐标系类型
ProjectedCSTypeGeoKey 自定义（例26917：UTM Zone 17N） 指定投影坐标系类型

3 实验与分析

3.1 遥感图像三十面体六边形量化建模

遥感图像六边形格网化建模是后续格网数据组织管理、分析处理、分发共享的首要前提。本文选择坐标基准WGS84，分辨率约为1.1 km、RGB 3波段、全球尺度的谷歌遥感图像为实验对象。图9为全球范围内遥感图像六边形像素建模结果，并添加全球大陆海岸线矢量数据验证建模结果在地理位置上的正确性。图9（a）—图9（d）分别主要显示了非洲、欧洲和亚洲、北美和南美洲、南极洲地区，该过程不仅可生成全球六边形像素遥感数据，还验证本文格网生成算法、采样量化算法以及整数编码坐标与地理坐标相互转换算法的正确性。
图9 谷歌图像三十面体六边形像素建模结果（全球不同视图）

Fig. 9 Results of RT hexagonal pixel modeling (different views of the globe)

由图9可知，本文递归剖分产生的六边形格网单元可以无缝无叠的覆盖全球，使用六边形等积格网组织全球尺度的遥感图像，可实现对全球大范围区域数据的均匀采样，能够保证不同纬度地区单元总体一致，避免了经纬格网在高纬度地区的单元剧烈变化，更适合全球范围数据的处理和分析。

3.2 六边形像素遥感图像存储

为验证六边形整数编码坐标映射至矩形阵列算法的正确性，将图9中球面六边形格网数据以菱形块为单位存储在GeoTIFF标准影像格式中，并使用基于TIFF格式的LZW无损压缩算法。全球六边形像素数据存储结果如图10所示，图11展示北京市图像的内部细节。
图10 三十面体六边形格网对应的GeoTIFF数据集

注:红色数字为三十面体面号。

Fig. 10 GeoTIFF image corresponding to RT hexagon grid

图11 北京市矩形像素图像细节（低分辨率）

注:红色箭头代表六边形的邻域关系。

Fig. 11 Details of rectangular pixel image of Beijing (low resolution)

本文借助三十面体和优化双倍偏移坐标系搭建了六边形DGGS格网数据与开放标准格式相互转换的“桥梁”，将全球范围内三十面体六边形DGGS数据均匀划分至30个大小相等的菱形块，且图10中每一菱形块与图9的球面菱形区域逐一对应。在无需恢复球面六边形单元的一般应用场景下，六边形DGGS格网标准数据集可当作普通遥感图像正常使用；在专业应用场景下，专用算法可根据存储的元数据信息将其精确恢复至球面。由图11（b）可知，六边形单元以规则排列的矩形存储在GeoTIFF文件中，正方形像素组合而成的矩形呈现出奇数、偶数行交错排列的特征。该结构不仅正确保留了六边形单元之间的空间相邻关系，且可将六边形单元的全部操作等价转换为更易于理解和实现的矩形栅格操作。

3.3 双倍偏移坐标对比

为验证优化双倍偏移坐标相较于一般双倍偏移坐标的优势，本文选择同一地区Sentinel-2遥感图像，在六边形量化完成后分别采用2种方案生成数据，结果如图12、图13。
图12 优化双倍偏移坐标数据

Fig. 12 Results of optimizing double offset coordinates

图13 双倍偏移坐标数据

Fig. 13 Results of double offset coordinates

分析实验结果，得出以下结论：
（1）本方案在物理空间上建立了六边形和矩形像素间的“一一对应”关系，保留了奇偶数行六边形交错排列的几何特点，如图12。而双倍偏移坐标仅在逻辑上保留六边形相邻单元的空间邻域关系，在栅格数据邻域分析等具体应用时需对其额外判断处理，理论上并不能完全发挥六边形在图像处理分析上的优势。
（2）相较于双倍偏移坐标，本方案生成的六边形GeoTIFF遥感图像色调均匀、纹理清晰、地物布局连续，较好地保留了六边形格网数据的图像特征和地物空间分布特征，为六边形像素遥感图像目视判读、智能解译和认知推理奠定了良好基础。以双倍偏移坐标为基础生成的图像整体色调偏暗，空值单元不仅会浪费存储空间，间断的地物表达也不利于在遥感图像中挖掘信息。

3.4 与SMOS方案对比

ESA提供的SNAP①(①https://earth.esa.int/eogateway/tools。)软件支持对SMOS数据的加载和处理，六边形单元在投影平面中被离散化为多个矩形（图14），并将像素值分配至相关的矩形像素处理。根据上文内容明显可知，本方案在数据处理和数据量方面具有明显优势，对比如表3。
图14 SMOS数据存储方案

Fig. 14 Storage scheme of SMOS

表3 SMOS与本文方案对比

Tab. 3 Comparison between SMOS and the proposed scheme

评价指标 方案对比
SMOS存储方案 本文方案
数据量 一个六边形单元与多个（约为40）矩形像素对应 一个六边形单元与一个矩形像素对应（图5（d））
模拟六边形形态 六边形的形态不固定（图14） 矩形奇偶数行交错排列，与六边形单元排列模式相同（图12）
数据处理 处理多个矩形等效处理一个六边形 处理一个矩形等效处理一个六边形
卷积运算模板 不固定 固定
矩形像素算法可用性 可直接使用 可直接使用
为进一步验证本文方案的优势，选择Sentinel-2遥感图像，根据图像分辨率将原始数据建模完成后存储至GeoTIFF中，并利用2.2.3节转换算法生成不同分辨率的六边形像素数据，如图15。图16分别为对应分辨率下的矩形像素图像。分析图16可发现，本文方案与SMOS方案相比具有以下特点：
图15 连续3个分辨率六边形像素Sentinel-2图像

Fig. 15 Hexagonal pixel Sentinel-2 images with three different resolutions

图16 连续3个分辨率矩形像素Sentinel-2图像

Fig. 16 Rectangular pixel Sentinel-2 images with three different resolutions

（1）在任何位置上均能保持矩形像素与六边形单元排列方式相同，便于在物理空间内快速确定某一单元相邻六边形单元。
（2）本文保证了六边形单元与矩形像素严格对应，使得在不同分辨率下六边形和矩形在空间位置上均能保持一致。由于六边形单元与矩形像素数量相等，该方案不仅没有产生数据冗余，而且无需转化到物理空间上的六边形，在处理矩形像素图像时等效地处理六边形单元，开放的文件存储标准使得常用的GIS和遥感软件可直接操作。
（3）本文建立了六边形单元与矩形像素“一对一”映射关系，与传统的图像金字塔相似，经过卷积运算后可抽取GeoTIFF图像的奇数行、偶数列，再结合封装的元数据信息，在获取多分辨率数据时无需重采样，经过少量计算即可获得不同分辨率格网数据，便于格网数据集与六边形DGGS两者间的相互转换。

4 结论

本文选择三十面体六边形DGGS作为大区域遥感数据均匀采样和数据量化的载体，进一步提高六边形像素遥感图像的建模精度，建立了六边形DGGS整数编码与优化双倍偏移坐标的双向映射关系，并提出兼容开放标准格式的六边形格网数据存储方案。与SMOS方案相比，不仅在任何位置和不同层次下均能够保证六边形单元和矩形像素相同的排列方式，而且较好保留了六边形DGGS数据的属性信息和几何特征，开放的文件标准格式使得六边形DGGS数据易于分发和共享。本文打破了六边形和矩形数据组织的壁垒，为在实际应用中充分发挥六边形像素遥感数据集采样效率高、存储空间小、几何特性好的独特优势提供了可行技术途径，具有较好的推广应用前景。下一步基于该方案继续研究特征提取、图像分割等处理算法，进而在三十面体六边形DGGS数据中发掘更多的信息。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Sahr K, White D, Kimerling A J. Geodesic discrete global grid systems[J]. Cartography and Geographic Information Science, 2003, 30(2):121-134. DOI:10.1559/152304003100011090

[2]
Kmoch A, Matsibora O, Vasilyev I, et al. Applied open-source discrete global grid systems[J]. AGILE: GIScience Series, 2022, 3:1-6. DOI:10.5194/agile-giss-3-41-2022

[3]
周良辰, 盛业华, 林冰仙, 等. 球面菱形离散格网正二十面体剖分法[J]. 测绘学报, 2014, 43(12):1293-1299.

[ Zhou L C, Sheng Y H, Lin B X, et al. Diamond discrete grid subdivision method for spherical surface with icosahedron[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12):1293-1299. ] DOI:10.13485/j.cnki.11-2089.2014.0192

[4]
林冰仙, 许德朋, 盛业华, 等. 正二十面体球面菱形离散格网的编码模型及其映射方法[J]. 测绘学报, 2016, 45(S1):23-31.

[ Lin B X, Xu D P, Sheng Y H, et al. Coding model and mapping method of spherical diamond discrete grids based on icosahedron[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1):23-31. ] DOI:10.11947/j.AGCS.2016.F003

[5]
周建彬, 贲进, 王蕊, 等. 四孔六边形全球离散格网一致瓦片层次结构编码运算[J]. 武汉大学学报·信息科学版, 2023, 48(4):639-646.

[ Zhou J B, Ben J, Wang R, et al. Encoding and operation for the aperture-4 hexagonal discrete global grids on uniform tiles[J]. Geomatics and Information Science of Wuhan University, 2023, 48(4):639-646. ] DOI:10.13203/j.whugis20200530

[6]
王蕊, 贲进, 梁晓宇, 等. 菱形三十面体格网系统构建的等积投影方法研究[J]. 武汉大学学报·信息科学版, 2023.

[ Wang R, Ben J, Liang X Y, et al. Research on the equal-area projection for the construction of the rhombic triacontahedron grid systems[J]. Geomatics and Information Science of Wuhan University. 2023. ] DOI:10.13203/j.whugis20220231

[7]
Hall J, Wecker L, Ulmer B, et al. Disdyakis triacontahedron DGGS[J]. ISPRS International Journal of Geo-Information, 2020, 9(5):315. DOI:10.3390/ijgi9050315

[8]
Liang X Y, Ben J, Wang R, et al. Construction of rhombic triacontahedron discrete global grid systems[J]. International Journal of Digital Earth, 2022, 15(1):1760-1783. DOI:10.1080/17538947.2022.2130459

[9]
郑明阳, 贲进, 周建彬, 等. 局部区域多孔径六边形格网系统快速生成算法[J]. 武汉大学学报·信息科学版, 2022, 47(9):1376-1382.

[ Zheng M Y, Ben J, Zhou J B, et al. Fast generation algorithm of multi-aperture hexagonal grid systems of regional-scale[J]. Geomatics and Information Science of Wuhan University, 2022, 47(9):1376-1382. ] DOI:10.13203/j.whugis20200342

[10]
贲进, 童晓冲, 汪磊, 等. 利用球面离散格网组织空间数据的关键技术[J]. 测绘科学技术学报, 2010, 27(5):382-386.

[ Ben J, Tong X C, Wang L, et al. Key technologies of geospatial data management based on discrete global grid system[J]. Journal of Geomatics Science and Technology, 2010, 27(5):382-386. ] DOI:10.3969/j.issn.1673-6338.2010.05.018

[11]
张继凯, 聂俊岚, 陈贺敏, 等. 基于菱形块四叉树的全球六边形网格实时绘制方法[J]. 计算机辅助设计与图形学学报, 2017, 29(10):1824-1834.

[ Zhang J K, Nie J L, Chen H M, et al. Real-time rendering method for global hexagon grid based on quad-tree of diamond blocks[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(10):1824-1834. ] DOI:10.7666/d.D01111246

[12]
Li M K, McGrath H, Stefanakis E. Integration of heterogeneous terrain data into Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2021, 48(6):546-564. DOI:10.1080/15230406.2021.1966648

[13]
Mahdavi Amiri A, Alderson T, Samavati F. Geospatial data organization methods with emphasis on aperture-3 hexagonal discrete global grid systems[J]. Cartographica: the International Journal for Geographic Information and Geovisualization, 2019, 54(1):30-50. DOI:10.3138/cart.54.1.2018-0010

[14]
de Sousa L M, Leitão J P. HexASCII: A file format for cartographical hexagonal rasters[J]. Transactions in GIS, 2018, 22(1):217-232. DOI:10.1111/tgis.12304

[15]
Suess M, Matos P, Gutierrez A, et al. Processing of SMOS level 1c data onto a discrete global grid[C]// IGARSS 2004.2004 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2004:1914-1917. DOI:10.1109/IGARSS.2004.1370716

[16]
梁晓宇, 贲进, 周建彬, 等. 菱形三十面体六边形全球离散格网系统构建算法[J]. 地理与地理信息科学, 2023, 39(2):8-16.

[ Liang X Y, Ben J, Zhou J B, et al. Construction of rhombic triacontahedron hexagonal discrete global grid system[J]. Geography and Geo-information Science, 2023, 39(2):8-16. ] DOI:10.3969/j.issn.1672-0504.2023.02.002

[17]
Purss M. Topic 21: Discrete global grid systems abstract specification[EB/OL]. [2023-11-14] http://www.opengis.net/doc/as/dggs/1.0

[18]
Ma Y, Li G Q, Yao X C, et al. A precision evaluation index system for remote sensing data sampling based on hexagonal discrete grids[J]. ISPRS International Journal of Geo-Information, 2021, 10(3): 194. DOI:10.3390/ijgi10030194

[19]
Teanby N A. An icosahedron-based method for even binning of globally distributed remote sensing data[J]. Computers & Geosciences, 2006, 32(9):1442-1450. DOI:10.1016/j.cageo.2006.01.007

[20]
Hoogeboom E, Peters J W T, Cohen T S, et al. HexaConv[EB/OL]. 2018: arXiv: 1803.02108. https://arxiv.org/abs/1803.02108.pdf

[21]
贲进, 张永生, 童晓冲. GeoTIFF解析及在遥感影像地理编码中的应用[J]. 信息工程大学学报, 2005, 6(1):94-98.

[ Ben J, Zhang Y S, Tong X C. Analysis of GeoTIFF and usage of LibGeoTIFF library[J]. Journal of Information Engineering University, 2005, 6(1):94-98. ] DOI:10.3969/j.issn.1671-0673.2005.01.028

Options
文章导航

/

〈 〉