EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 3: 591 - 603

DOI: https://doi.org/10.12082/dqxxkx.2024.230502

地球信息科学理论与方法

违背不相关性假设对Triple Collocation方法精度的影响

  • 谈松林 , 1, 2 ,
  • 王洁 , 1, 2, * ,
  • 季静静 1, 2 ,
  • 刘美丽 3 ,
  • 湛忠宇 3 ,
  • 刘淼 4 ,
  • 王丽荣 5 ,
  • 胡晓东 6
展开
  • 1.南京信息工程大学，南京 210044
  • 2.水利部水文气象灾害机理与预警重点实验室，南京 210044
  • 3.江苏省水文水资源勘测局南京分局，南京 210008
  • 4.江苏省水文水资源勘测局，南京 210029
  • 5.河北省气象灾害防御和环境气象中心，石家庄 050022
  • 6.江苏省水利科学研究院，南京 210017
*王洁（1984— ），男，山东诸城人，博士，副教授，主要从事水文水资源方面的研究。E-mail:

谈松林（2000— ），男，江苏南京人，硕士生，主要从事水文水资源方面与Collocation方法的研究。E-mail:

Copy editor: 蒋树芳

收稿日期: 2023-08-28

  修回日期: 2023-11-10

  网络出版日期: 2024-03-31

基金资助

国家自然科学基金项目(41877158)

河北省省级科技计划资助项目(19275408D)

江苏省水利科技项目(2020040)

收起

Investigating the Impact of Violations in Orthogonality and Zero Cross-Correlation Assumption upon the Accuracy of Triple Collocation Methods

  • TAN Songlin , 1, 2 ,
  • WANG Jie , 1, 2, * ,
  • JI Jingjing 1, 2 ,
  • LIU Meili 3 ,
  • ZHAN Zhongyu 3 ,
  • LIU Miao 4 ,
  • WANG Lirong 5 ,
  • HU Xiaodong 6
Expand
  • 1. School of Hydrology and Water Resources, Nanjing University of Information Science and Technology, Nanjing 210044, China
  • 2. Key Laboratory of Hydrometeorological Disaster Mechanism and Warning of Ministry of Water Resources, Nanjing University of Information Science and Technology, Nanjing 210044, China
  • 3. Nanjing Sub-Bureau of Hydrology and Water Resources Survey, Jiangsu Survey Bureau of Hydrology and Water Resources, Nanjing 210008, China
  • 4. Jiangsu Survey Bureau of Hydrology and Water Resources, Nanjing 210029, China
  • 5. Hebei Meteorological Disaster Defense and Environmental Meteorology Center, Shijiazhuang 050022, China
  • 6. Nanjing Hydraulic Research Institute, Nanjing 210017, China
*WANG Jie, E-mail:

Received date: 2023-08-28

  Revised date: 2023-11-10

  Online published: 2024-03-31

Supported by

National Natural Science Foundation of China(41877158)

S&T Program of Hebei(19275408D)

Jiangsu Water Conservancy Science and Technology Project(2020040)

Fold

摘要

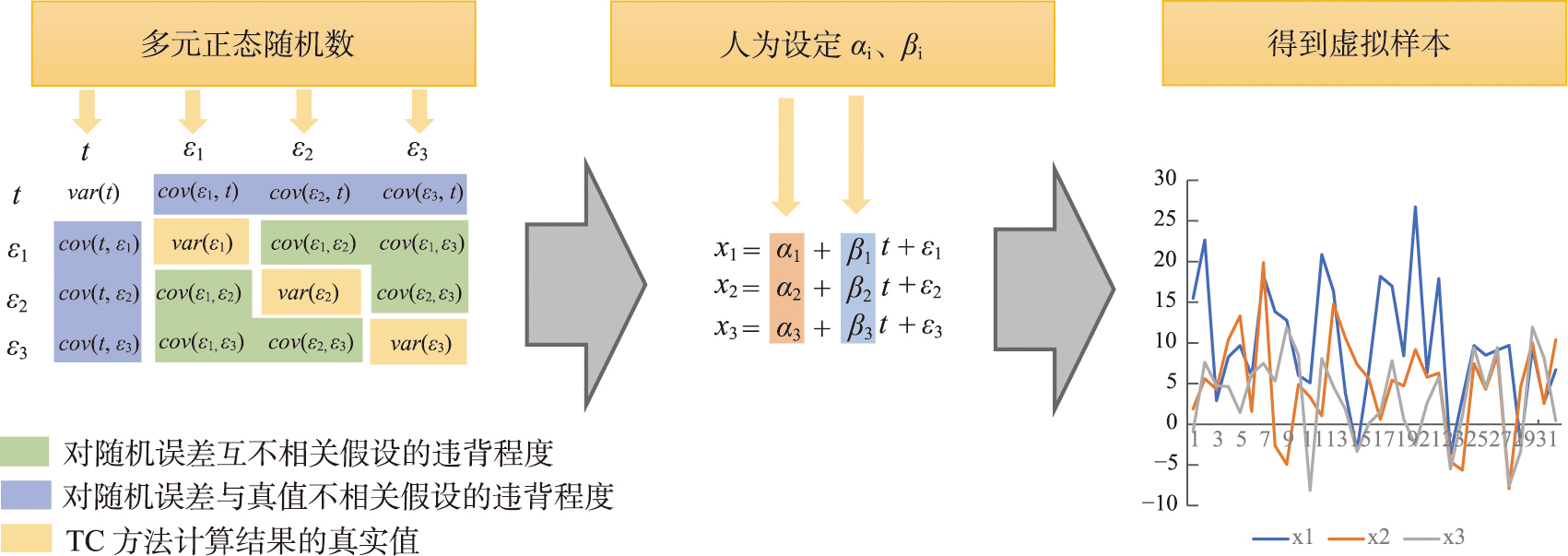
Triple Collocation（TC）方法是一种可以在未知真值情况下评估3个独立观测样本各自不确定性的方法，该方法使用的前提是误差形式假设与2组不相关性假设，但在实际使用中，这3条假设难以完全满足。其中2组不相关性假设经常面临较大的违背，并且无法得知这种假设违背对结果误差的影响。本文通过虚拟样本实验生成了多组不同程度违背不相关性假设的样本，以定量评估不同程度假设违背对结果误差的影响。结果表明，一般情况下，某一条不相关性假设的违背程度增加时，方法的结果误差会相应地呈线性或平方倍数增加；但当不相关性假设的违背处于某个特定关系时，TC方法结果的误差会突然大幅度增加，这种现象在以往的研究中并没有得到重视，后文将该现象简称为异常点。为了探求异常点出现的原因，本文从理论上推导出了违反不相关性假设与结果误差之间的关系，这种关系呈现为分式结构，而异常点的出现正是这种分式结构所致。异常点的存在影响了方法的稳定性。从差值形式的TC方法的角度来看，抑制异常点的关键在于如何更好地设计缩放系数。本文给出了2种抑制异常点的方法： ① 忽略加性偏差系数，使得缩放系数不受两组不相关性假设的影响； ② 限制缩放系数的上下限。根据实际数据分析，第2种改进方法优于第1种。第2种方法不仅保留了TC方法的准确性，而且有效地避免了异常点的出现。值得注意的是，在实际数据中，部分异常点会以负值形式出现并因计算结果不能为负而被剔除。在使用TC方法进行计算时，重复次数较少的情况下，可以不考虑异常点的影响。

关键词： Triple collocation; 假设违背; 异常点; 遥感; 数据同化; 数据评估; 数据不确定性分析; 无实测数据

本文引用格式

谈松林 , 王洁 , 季静静 , 刘美丽 , 湛忠宇 , 刘淼 , 王丽荣 , 胡晓东 . 违背不相关性假设对Triple Collocation方法精度的影响[J]. 地球信息科学学报, 2024 , 26(3) : 591 -603 . DOI: 10.12082/dqxxkx.2024.230502

Abstract

Triple Collocation (TC) is a technique for assessing the uncertainties of three samples individually without knowledge of the true values. This method is based on the assumptions of linearity, orthogonality, and zero cross-correlation. In practical use, these three assumptions are often difficult to achieve, particularly the orthogonality and zero cross-correlation assumptions, which often encounter significant violations. Moreover, we are uncertain about the impact of these assumption violations on the errors of the method's results. In this study, we simulated multiple sets of synthetic samples with varying degrees of two assumption violations to investigate the impact of assumption violations on the accuracy of the TC method. The results of synthetic samples experiment indicate that, in general, when there is an increase in the violation of orthogonality or zero cross-correlation assumptions, the error of the method's results increases linearly or quadratically. However, under certain specific conditions of assumption violation, there is a sudden and spike-like increase in the error of TC method results. This phenomenon is referred to as "outliers". To understand the origin of the outliers, we derived the complete mathematical relationship between the violation of assumptions and the errors of the results. This relationship exhibits a fractional structure rather than a linear one, contributing to the emergence of outliers. From the perspective of the difference notation, this fractional structure results from rescaling coefficients. Continuing to analyze this mathematical relationship, we can draw two conclusions. Firstly, merely ensuring the approximate independence of the three samples does not necessarily lead to improved method results. When the structural relationships among the three samples meet certain conditions, outliers emerge. Additionally, previous attempts at method improvement have aimed at overall reducing the sensitivity of this method to assumptions, neglecting the presence of outliers. Considering these factors, the key to suppressing outliers lies in better designing these rescaling coefficients. The paper presents two possible improvement methods:(1) Ignoring the additive bias, so that the rescaling coefficients are not affected by the orthogonality or zero cross-correlation assumptions. (2) Limiting the upper and lower bounds of the rescaling coefficients. We achieved favorable results in suppressing outliers by constraining the absolute values of the rescaling coefficients between 0.25 and 4. Both improvement methods can suppress the occurrence of outliers. However, when the additive bias is significant, the first improvement method generates substantial extreme errors due to its inherent structure, which is insufficient to eliminate outliers. The second method performs effectively even in complex scenarios. Lastly, we conducted a simple estimation of the probability of outliers occurring in practical usage, which was approximately 3.2%. In addition, we used SMOS, SMAP, and AMSR2 soil moisture data to validate the phenomenon of outliers and compared the two improved methods. According to real data, some outliers appear as negative values and are removed because the calculated results cannot be negative. Therefore, A portion of the outlier does not cause a significant deviation in the calculation result; instead, they simply prevent the calculation of meaningful results. Therefore, when employing the TC method with fewer repetitions for calculations (e.g., with fewer than 500 repetitions), the influence of outliers can be disregarded.

Key words： Triple Collocation; assumption violations; spike-like anomalous region; remote sensing; data assimilation; data calibration; data uncertainty analysis; absence of Gauge-Data

1 引言

Triple collocation（TC）方法是一种通过3个独立观测样本两两比对来估计3个样本各自不确定性的数据评估方法。与其他常见的评估方法不同，其他方法一般需要一组较为准确的实测数据作为参考数据，并将其他数据与这组参考数据进行对比。然而，获取这组参考数据通常需要较大的成本并且其自身也会存在一定的误差。TC方法通过假设了一个同时与3个样本线性相关的序列，并将其视为真值。将每个样本的误差分为对于“真值”的线性偏差与随机误差，从而在两组不相关性假设的前提下，使用严格的数学方法估算出每个样本各自的不确定性[1⇓-3]。受求解的限制，真值序列与线性偏差是不可直接解出的，一般使用随机误差的方差的大小来衡量各样本的不确定性。TC方法的计算结果可为其他数据同化或校准方法提供参考[4]，或独立地进行数据融合或校准工作[5]。这种方法在地球科学和遥感等领域具有广泛的应用。
从协方差形式TC方法视角出发，构造TC方法的关键在于如何设计误差形式来构造方程组，并且使用不同的假设来简化该方程组并使其可解。Stoffelen[1]首次提出了TC方法，针对风场数据的特点，提出了$x_{1}=t+\varepsilon_{1}, x_{2}=\beta_{2} t+\varepsilon_{2}, x_{3}=\beta_{3} t+\varepsilon_{3}$的误差形式假设（其中$x_{1}, x_{2}, x_{3}$分别为站点实测数据，遥感观测数据，模式再分析数据），并引入$<t \varepsilon_{i}>=0(i=1,2,3), \quad<\varepsilon_{1} \varepsilon_{3}>=<\varepsilon_{2} \varepsilon_{3}>=0$的不相关性假设。这为后续的研究奠定了两个基本的方向：使用线性（或可化为线性）的误差形式假设建立方程组与使用两组不相关性假设简化条件使方程组可解。在此基础上， Caires等[2]加入了加性偏差αi，使用了$x_{1}=t+\varepsilon_{1}, x_{2}=\alpha_{2}+\beta_{2} t+\varepsilon_{2}, x_{3}=\alpha_{3}+\beta_{3} t+\varepsilon_{3}$的误差形式假设，并对不相关性假设做出了相应的更改，使用了的不相关性假设。这一改进使得随机变量的分布不再局限于均值为0的分布。Scipal等[3]将TC方法从校准风场数据引入到校准土壤水数据中，考虑到土壤水的实测数据具有高度不确定性，无法作为参考序列的特点，进一步地改进了误差形式假设，使用了三组$x_{i}=\alpha_{i}+\beta_{i} t+\varepsilon_{i}(i=1,2,3)$的误差假设，这种假设搭配方案充分利用了各项假设条件，目前应用最为广泛。
TC方法的建立依赖于误差形式假设与两组不相关性假设，尤其是两组不相关性假设使得方程组的求解成为可能，但这两组不相关性假设在实际应用中难以得到满足。Yilmaz等[6]通过数学推导，分离出了以$x_{i}=\beta_{i} t+\varepsilon_{i}(i=1,2,3)$作为误差形式假设的TC方法中因违背不同假设所导致的误差，但这种形式的TC方法在当前研究中使用的不多。而常用的TC方法是以$x_{i}=\alpha_{i}+\beta_{i} t+\varepsilon_{i}(i=1,2,3)$作为误差形式假设的，对不相关性假设违背的响应要复杂很多。近年来，少有学者对其进行深入研究。
本文首先通过大量的虚拟样本实验，探求当2组不相关性假设不能得到完全满足时， TC方法结果误差的变化情况。然后通过数学推导给出了不相关性假设违背程度与结果误差的具体关系，模拟了上述虚拟样本实验的结果并给出了数学解释。借助上述两项研究，本文发现了导致结果误差激增的异常点，分析了其产生的原因与带来的影响，并试图提出了2种抑制异常点的改进方法。接着，从理论上初步估算了在实际使用中TC方法出现异常点的概率。使用实测数据，证实了异常点在实际使用中的存在，并对比了2种改进方法的效果

2 基本假设

Gruber等[7]系统总结了TC方法所需的5条基本假设，并被后续研究广泛引用：
（1） 误差形式假设
误差形式假设是TC方法的出发点。其假设1个与3个样本都线性相关的“真值”序列符合如下关系：
$x_{i}=\alpha_{i}+\beta_{i} t+\varepsilon_{i}$
式中：$\alpha_{i}, \beta_{i}$，为3个样本各自关于“真值t”的线性误差的系数；$\varepsilon_{i}$为3个样本各自的随机误差。
（2） 平稳性假设
平稳性假设并非是方法推导过程所必需的条件，其作用是使得方差等统计变量具有意义。Zwieback等[8]指出在不考虑对样本序列的子集仅进行二次计算的情况下，违反平稳性假设对方法结果并不会造成太大影响。在实际应用中，有研究使用滑动平均[9]、对数转换[10]、小波分析[11]等方法对样本进行预处理。这些做法不仅能使样本更好地满足平稳性要求，还能部分的消除样本与“真值”的非线性关系，使得误差形式假设得到更好地遵守。
（3） 随机误差与真值不相关
随机误差与真值不相关性假设，在差值形式的TC方法中表现为$<t \varepsilon_{i}>=0$；由于E($\varepsilon_{i}$)=0，也可写为$<(t-\bar{t}) \varepsilon_{i}>=0$，在协方差形式中表现为$\operatorname{cov}\left(t, \varepsilon_{i}\right)=0$，二者是等价的。共有3条：$\operatorname{cov}\left(t, \varepsilon_{1}\right)=0, \quad \operatorname{cov}\left(t, \varepsilon_{2}\right)=0, \quad \operatorname{cov}\left(t, \varepsilon_{3}\right)=0$。
（4） 随机误差互不相关
随机误差互不相关性假设，在差值形式的TC方法中表现为$<\varepsilon_{i} \varepsilon_{j}>=0$，在协方差形式中表现为$\operatorname{cov}\left(\varepsilon_{i}, \varepsilon_{j}\right)=0$，由于E($\varepsilon_{i}$)=0，两者是等价的。共有3条：$\operatorname{cov}\left(\varepsilon_{1}, \varepsilon_{2}\right)=0, \quad \operatorname{cov}\left(\varepsilon_{1}, \varepsilon_{3}\right)=0, \quad \operatorname{cov}\left(\varepsilon_{2}, \varepsilon_{3}\right)=0$。
（5） 代表性假设
由于观测方式、观测尺度的不同，3个样本中所包含的各自的真值是存在差异的。例如在土壤水分校准工作中，站点实测、主动微波遥感、被动微波遥感这3 种测量方式所得的土壤水分数据的观测尺度、采样间隔是不同的。代表性假设即假设这其中产生的所有误差均能被误差假设中的线性偏离所概括。
上述5条假设，从数学推导的角度来看，可以归结为误差形式假设、随机误差与真值不相关性假设、随机误差互不相关性假设这3条假设。

3 TC方法

TC方法通常有2种等价的形式：差值形式与协方差形式。差值形式的TC方法是通过3个样本之间的线性变换构造一个新的序列后，两两内积得出的；而协方差形式TC方法是通过求解协方差方程组得出的。两者在数学上是等价的[7]，其操作的核心都可看成同一种内积操作[12]。可通过协方差定义：$\operatorname{cov}\left(x_{1}, x_{2}\right)=<\left(x_{1}-\overline{x_{1}}\right)\left(x_{2}-\overline{x_{2}}>\right.$，得出二者之间的关系。值得指出的是，即使在不相关性假设不能得到满足时，这种等价关系也是成立的。差值形式的TC方法清晰地展现了针对3个样本的变换操作及相互比对的过程。本文重点介绍差值形式的TC方法的基本原理：
首先需要有3个符合上述基本假设的样本：x1，x2，x3。
根据误差形式假设（假设1）可得：
$\left\{\begin{array}{l} x_{1}=\alpha_{1}+\beta_{1} t+\varepsilon_{1} \\ x_{2}=\alpha_{2}+\beta_{2} t+\varepsilon_{2} \\ x_{3}=\alpha_{3}+\beta_{3} t+\varepsilon_{3} \end{array}\right.$
在x1，x2，x3中任选一个样本作为参考样本（本文选择x1样本作为参考样本），构建缩放系数β*2、β*3，与2个新序列x*2、x*3：
$\left\{\begin{array}{c} \beta_{2}^{*}=\frac{<\left(x_{1}-\overline{x_{1}}\right)\left(x_{3}-\overline{x_{3}}\right)>}{<\left(x_{2}-\overline{x_{2}}\right)\left(x_{3}-\overline{x_{3}}\right)>} \\ \beta_{3}^{*}=\frac{<\left(x_{1}-\overline{x_{1}}\right)\left(x_{2}-\overline{x_{2}}\right)>}{\left\langle\left(x_{2}-\overline{x_{2}}\right)\left(x_{3}-\overline{x_{3}}\right)>\right.} \end{array}\right.$
$\left\{\begin{array}{l} x_{2}^{*}=\beta_{2}^{*}\left(x_{2}-\overline{x_{2}}\right)+\overline{x_{1}} \\ x_{3}^{*}=\beta_{3}^{*}\left(x_{3}-\overline{x_{3}}\right)+\overline{x_{1}} \end{array}\right.$
式中：$\langle(*)(*)\rangle$为2组样本中对应元素两两相乘后计算均值，例如$x_{1}=\left(a_{1}, a_{2}, a_{3}, \cdots, a_{n}\right), x_{2}=\left(b_{1}, b_{2}, b_{3},\right.\left.\cdots, b_{n}\right) \text {; 则 }<\left(x_{1}\right)\left(x_{2}\right)>=\frac{1}{n} \sum_{i=1}^{n} a_{i} b_{i}$
缩放系数β*2、β*3的构建利用了2条不相关性假设（假设3与假设4），使其一方面可以通过2个样本之间的运算直接求出，为一个确定的值；另一方面其可以化简成2个样本线性乘法偏差系数βi, βj之比，以β2*为例:
根据E($\varepsilon_{i}$)=0得：
$x_{i}-\bar{x}_{i}=\left(\alpha_{i}+\beta_{i} t+\varepsilon_{i}\right)-\left(\alpha_{i}+\beta_{i} \bar{t}\right)=\beta_{i}(t-\bar{t})+\varepsilon_{i}$
将式(5)代入式(3)，并根据2条不相关性假设（假设3与假设4）消去为0的项得：
$\beta_{2}^{*}=\frac{<\left(x_{1}-\overline{x_{1}}\right)\left(x_{3}-\overline{x_{3}}\right)>}{<\left(x_{2}-\overline{x_{2}}\right)\left(x_{3}-\overline{x_{3}}\right)>} =\frac{\beta_{1} \beta_{3}<(t-\bar{t})^{2}>+\beta_{1}<(t-\bar{t}) \varepsilon_{3}>+\beta_{3}<(t-\bar{t}) \varepsilon_{1}>+<\varepsilon_{1} \varepsilon_{3}>}{\beta_{2} \beta_{3}<(t-\bar{t})^{2}>+\beta_{2}<(t-\bar{t}) \varepsilon_{3}>+\beta_{3}<(t-\bar{t}) \varepsilon_{2}>+<\varepsilon_{2} \varepsilon_{3}>} =\frac{\beta_{1} \beta_{3}<(t-\bar{t})^{2}>}{\beta_{2} \beta_{3}<(t-\bar{t})^{2}>}=\frac{\beta_{1}}{\beta_{2}}$
同理可得β3*：
$\beta_{3}^{*}=\frac{\left\langle\left(x_{1}-\overline{x_{1}}\right)\left(x_{2}-\overline{x_{2}}\right)>\right.}{\left\langle\left(x_{3}-\overline{x_{3}}\right)\left(x_{2}-\overline{x_{2}}\right)\right\rangle} =\frac{\beta_{1} \beta_{2}<(t-\bar{t})^{2}>+\beta_{1}<(t-\bar{t}) \varepsilon_{3}>+\beta_{2}<(t-\bar{t}) \varepsilon_{1}>+<\varepsilon_{1} \varepsilon_{2}>}{\beta_{2} \beta_{3}<(t-\bar{t})^{2}>+\beta_{2}<(t-\bar{t}) \varepsilon_{3}>+\beta_{3}<(t-\bar{t}) \varepsilon_{1}>+<\varepsilon_{1} \varepsilon_{3}>} =\frac{\beta_{1}}{\beta_{3}}$
由于式(6)、式(7)与假设3、4，新序列$x_{2}^{*}、 x_{3}^{*}$中的所有α2、α3、β2、β4被转化为α1、β1：
$ \left\{\begin{array}{l} x_{1}=\alpha_{1}+\beta_{1} t+\varepsilon_{1} \\ x_{2}^{*}=\alpha_{1}+\beta_{1} t+\beta_{2}^{*} \varepsilon_{2} \\ x_{3}^{*}=\alpha_{1}+\beta_{1} t+\beta_{3}^{*} \varepsilon_{3} \end{array}\right.$
由此，可通过两两相减，约去含有“真值t”的项：
$ \left\{\begin{array}{l} x_{1}-x_{2}^{*}=\varepsilon_{1}-\beta_{2}^{*} \varepsilon_{2} \\ x_{1}-x_{3}^{*}=\varepsilon_{1}-\beta_{3}^{*} \varepsilon_{3} \\ x_{3}^{*}-x_{2}^{*}=\beta_{3}^{*} \varepsilon_{3}-\beta_{2}^{*} \varepsilon_{2} \end{array}\right.$
再将式(9)中的式子，两两进行内积运算：
$ \left\{\begin{aligned} <\left(x_{1}-x_{2}^{*}\right)\left(x_{1}-x_{3}^{*}\right)>= & <\varepsilon_{1} \varepsilon_{1}>-\beta_{2}^{*}<\varepsilon_{1} \varepsilon_{2}> \\ & -\beta_{3}^{*}<\varepsilon_{1} \varepsilon_{3}>+\beta_{2}^{*} \beta_{3}^{*}<\varepsilon_{2} \varepsilon_{3}> \\ <\left(x_{1}-x_{2}^{*}\right)\left(x_{3}^{*}-x_{2}^{*}\right)>= & \beta_{3}^{*}<\varepsilon_{1} \varepsilon_{3}>-\beta_{2}^{*}<\varepsilon_{1} \varepsilon_{2}> \\ & -\beta_{2}^{*} \beta_{3}^{*}<\varepsilon_{2} \varepsilon_{3}>+\beta_{2}^{* 2}<\varepsilon_{2} \varepsilon_{2}> \\ <\left(x_{3}^{*}-x_{1}\right)\left(x_{3}^{*}-x_{2}^{*}\right)>= & \beta_{3}^{* 2}<\varepsilon_{3} \varepsilon_{3}>-\beta_{2}^{*} \beta_{3}^{*}<\varepsilon_{2} \varepsilon_{3}> \\ & -\beta_{2}^{*}<\varepsilon_{1} \varepsilon_{2}>+\beta_{2}^{*} \beta_{3}^{*}<\varepsilon_{2} \varepsilon_{3}> \end{aligned}\right.$
根据2条不相关性假设（假设3与假设4）可得：
$ \left\{\begin{array}{l} <\left(x_{1}-x_{2}^{*}\right)\left(x_{1}-x_{3}^{*}\right)>=<\varepsilon_{1} \varepsilon_{1}> \\ <\left(x_{1}-x_{2}^{*}\right)\left(x_{3}^{*}-x_{2}^{*}\right)>=\beta_{2}^{* 2}<\varepsilon_{2} \varepsilon_{2}> \\ <\left(x_{3}^{*}-x_{1}\right)\left(x_{3}^{*}-x_{2}^{*}\right)>=\beta_{3}^{* 2}<\varepsilon_{3} \varepsilon_{3}> \end{array}\right.$
式中：$ <\varepsilon_{i} \varepsilon_{i}>$即为随机变量$ \varepsilon_{i}$的方差，$ \sigma_{\varepsilon_{i}},x_{1}, x_{2}^{*}, x_{3}^{*}, \beta_{2}^{*}, \beta_{3}^{*}$均可通过样本$ x_{1}, x_{2}, x_{3}$求出，所以$ \sigma_{\varepsilon_{i}}$可以用$ x_{1}, x_{2}^{*}, x_{3}^{*}, \beta_{2}^{*}, \beta_{3}^{*}$表示：
$ \left\{\begin{aligned} \sigma_{\varepsilon_{1}}^{2} & <\left(x_{1}-x_{2}^{*}\right)\left(x_{1}-x_{3}^{*}\right)> \\ \sigma_{\varepsilon_{2}}^{2} & =\frac{<\left(x_{1}-x_{2}^{*}\right)\left(x_{3}^{*}-x_{2}^{*}\right)>}{\beta_{2}^{* 2}} \\ \sigma_{\varepsilon_{3}}^{2} & =\frac{<\left(x_{3}^{*}-x_{1}\right)\left(x_{3}^{*}-x_{2}^{*}\right)>}{\beta_{3}^{* 2}} \end{aligned}\right.$

4 虚拟样本实验

由于TC方法的特点是在未知真值的情况下对数据集的不确定性进行估计，而实际数据的真值部分难以确定，使用实际数据难以检验该方法结果的准确性，也无法得知其基本假设被遵守的程度。并且在TC方法的视角下，站点实测数据也存在一定的误差，是处于方法应当进行评估与校准的范围之内，使用站点实测数据作为真值的评估方式难以逻辑自洽。因此本文使用虚拟样本，通过人为制造“真值”与对不相关性假设违背程度已知的样本，探求不同假设违背下TC方法结果误差的变化情况。

4.1 虚拟样本

对两组不相关性假设的违背程度，可以使用$ \operatorname{cov}\left(\varepsilon_{i}, \varepsilon_{j}\right), \operatorname{cov}\left(t, \varepsilon_{i}\right)(i, j=1,2,3, \quad i \neq j)$这6个变量进行量化。当协方差为零时，即不相关，该条假设完全满足；当协方差大于（或小于）零时，即正相关（或负相关），假设不能得到满足；协方差与零的距离越大，表示相关性越强，对假设的违背程度就越大。为了下文论述方便，将2组共6条不相关性假设对应的协方差进行编号，见表1。
表1 两组不相关性假设违背程度及下文简称

Tab. 1 Quantification of deviation from orthogonality and zero cross-correlation assumption, and subsequent abbreviation

所属假设 量化违背程度的指标 下文简称
随机误差与真值不相关性假设 c o v t , ε 1 x
c o v t , ε 2 y
c o v t , ε 3 z
随机误差互不相关性假设 c o v ε 1 , ε 2 a
c o v ε 1 , ε 3 b
c o v ε 2 , ε 3 c
TC方法所估计的值为。使用多元正态分布随机数可以生成4组符合指定条件的序列：。将序列按照误差形式假设拼接，便可得出违背一定不相关性假设且结果真实值已知的样本（图1）。应用TC方法计算这些样本组的不确定性，并将TC方法计算所得结果与已知真实值进行比对，便可得到在该种违背情况下TC方法结果的误差。
图1 虚拟样本制造过程

Fig. 1 The production process of generate synthetic samples

4.2 实验设计

为了分析不同不相关性假设违背对结果误差的影响，本文利用控制变量法，每组实验保持5条不相关性假设得到遵守，其中1条不相关性假设由最大负违背逐渐变化至不违背，再逐渐变化至最大正违背。即5条假设的协方差为0，1个假设的协方差由最大负值变化至最大正值。为了下文论述方便，将唯一在变化的假设称为实验变量。由于也可能会影响结果误差与实验变量之间的关系，每组实验还需要在不同下进行多次重复。实验方案如下。经过多次实验验证，使用不同的衡量标准对下文结论并不会造成明显影响。下文中，结果误差采用对3个样本各自估计值的绝对误差和的形式进行衡量：
$\delta_{M A E}=\sum_{i=1}^{3}\left|\delta_{\varepsilon_{i}}\right|=\sum_{i=1}^{3}\left|\widehat{\sigma_{\varepsilon_{i}}^{2}}-\sigma_{\varepsilon_{i}}^{2}\right|$
式中：$\widehat{\sigma_{\varepsilon_{i}}^{2}}$为对第i条样本的随机误差方差的估计值，即TC方法对虚拟样本的计算结果；$\sigma_{\varepsilon_{i}}^{2}$为第i条样本真实的随机误差方差，在虚拟样本实验中即为前期人为设定的“真值”。
为了方便讨论，后文中将每次实验得到的结果误差与实验变量之间的关系连成的曲线简称为误差关系曲线。

4.3 虚拟样本实验结果

根据如表2所示的实验方案，得到虚拟样本实验结果，如图2所示。
表2 虚拟样本实验方案

Tab. 2 Synthetic samples experimental design

实验组 实验名称 实验变量 α i值 β i值 其他参数
A组 实验1 a α 1 = α 2 = α 3 = 1 β 1变化 β 2 = 0.5 β 3 = 0.7 t - = 10
v a r t = 50
v a r ε 1 = 30
v a r ε 2 = 30
v a r ε 3 = 30
每组实验中， a , b , c , x , y , z中的非实验变量设置为0.001，即假设满足不相关性假设。
为保证所设计的统计参数具有代表性，样本数量设计为200 000个
实验2 β 1 = 0.6 β 2变化 β 3 = 0.7
实验3 β 1 = 0.6 β 2 = 0.5 β 3变化
B组 实验4 b α 1 = α 2 = α 3 = 1 β 1变化 β 2 = 0.5 β 3 = 0.7
实验5 β 1 = 0.6 β 2变化 β 3 = 0.7
实验6 β 1 = 0.6 β 2 = 0.5 β 3变化
C组 实验7 c α 1 = α 2 = α 3 = 1 β 1变化 β 2 = 0.5 β 3 = 0.7
实验8 β 1 = 0.6 β 2变化 β 3 = 0.7
实验9 β 1 = 0.6 β 2 = 0.5 β 3变化
X组 实验10 x α 1 = α 2 = α 3 = 1 β 1变化 β 2 = 0.5 β 3 = 0.7
实验11 β 1 = 0.6 β 2变化 β 3 = 0.7
实验12 β 1 = 0.6 β 2 = 0.5 β 3变化
Y组 实验13 y α 1 = α 2 = α 3 = 1 β 1变化 β 2 = 0.5 β 3 = 0.7
实验14 β 1 = 0.6 β 2变化 β 3 = 0.7
实验15 β 1 = 0.6 β 2 = 0.5 β 3变化
Z组 实验16 z α 1 = α 2 = α 3 = 1 β 1变化 β 2 = 0.5 β 3 = 0.7
实验17 β 1 = 0.6 β 2变化 β 3 = 0.7
实验18 β 1 = 0.6 β 2 = 0.5 β 3变化

注：经大量实验验证，改变 α i值不会改变实验结果，故 α i值变化的情况在此不做讨论。

图2 不同实验条件下误差关系曲线

Fig. 2 Relationship between error and degree of assumption violation

由于方法的对称性，XYZ组、ABC组分别呈现出相似的实验结果。挑选X组、A组进行分析，见图2。在每幅子图中，误差关系曲线上的每一个点代表一种可能的假设违背的情况，纵坐标为在该种情况下的方法结果误差。
观察虚拟样本实验结果，可发现：在一些特定的组合下，误差关系曲线在某个特殊区间内会出现一个异常的突起，且这个突起的区间会随着的改变而变化。为了讨论的方便，后文将这个特殊区间简称为异常点。
在实验1、实验2 中，随着值由负到正的变化，异常点从x轴的正值区域逐渐向左移动至负值区域。当值取负时，异常点出现在x轴的正轴；当值取正时，异常点出现在x轴的负轴。当异常点移动到可能的最大违背外，便不再出现。与实验1实验2相比，实验3中异常点的位置变化呈现相反的规律。这说明，在同一实验组中，不同对异常点的影响并不都是相同的，不满足对称性。
在实验10、实验11、实验12中，误差关系曲线呈现不光滑的特征。在实验10中，异常点也呈现出实验3中的移动规律，但仅在值接近于0的时候出现。实验11，实验12中未出现异常点。假如不考虑异常点，在XYZ组实验中，误差关系曲线表现为直线，在ABC组实验中，误差关系曲线可近似为抛物线。

5 数学模拟及分析

5.1 结果误差与假设违背程度的关系

本文尝试推导出结果误差与假设违背程度的关系，从理论上对上文虚拟样本实验结果进行解释。Yilmaz等[6]通过数学推导将以为误差形式假设的TC方法的结果误差分为3类：真值泄漏误差，违背真值与随机误差不相关性假设的误差，违背随机误差互不相关性假设的误差。其中真值泄漏误差指：因缩放系数不能很好地削去“真值”项而导致的误差，即在式（8）、式（9）的过程而产生的误差。但常用的以为误差形式假设的TC方法，其缩放系数也会随假设违背而变化，无法作为一个常数存在于这3类误差之中，其中每一项都受对2组不相关性假设的违背的影响，无法使用这种分类方式。
下文使用每组中对3条样本各自的估计值与真实值的残差来衡量，不进行误差分类。
$\delta_{\varepsilon_{i}}=\widehat{\sigma_{\varepsilon_{i}}^{2}}-\sigma_{\varepsilon_{i}}^{2}$
式中：$\widehat{\sigma_{\varepsilon_{i}}^{2}}$为对第条样本的随机误差方差的估计值，即TC方法对虚拟样本的计算结果；$\sigma_{\varepsilon_{i}}^{2}$为第i条样本真实的随机误差方差。
将式（4）、式（5）及式（6）、式（7）的前半部分，代入式（12）中并减去$\sigma_{\varepsilon_{i}}^{2}$项，化简可得：
$\delta_{\varepsilon_{1}}=-\frac{p_{1}}{q_{1}}$
其中：
$\begin{aligned} p_{1}= & a b+\beta_{1}^{2} y z+a \beta_{3} x+b \beta_{2} x+a \beta_{1} z+ \\ & b \beta_{1} y-2 \beta_{1} c x-\beta_{1}^{2} c v t+\beta_{2} \beta_{3} x^{2}- \\ & \beta_{1} \beta_{3} x y-\beta_{1} \beta_{2} x z+a \beta_{1} \beta_{3} v t+b \beta_{1} \beta_{2} v t \end{aligned}$
$q_{1}=c+\beta_{3} y+\beta_{2} z+\beta_{2} \beta_{3} v t$
$\delta_{\varepsilon_{2}}=-\frac{p_{2}}{q_{2}}$
其中：
$\begin{aligned} p_{2}= & a c+\beta_{2}^{2} x z+a \beta_{3} y+a \beta_{2} z-2 b \beta_{2} y+\beta_{2} c x+ \\ & \beta_{1} c y-b \beta_{2}^{2} v t+\beta_{1} \beta_{3} y^{2}-\beta_{2} \beta_{3} x y-\beta_{1} \beta_{2} y z+ \\ & a \beta_{2} \beta_{3} v t+\beta_{1} \beta_{2} c v t \end{aligned}$
$q_{2}=b+\beta_{3} x+\beta_{1} z+\beta_{1} \beta_{3} v t$
$\delta_{\varepsilon_{3}}=-\frac{p_{3}}{q_{3}}$
其中：
$\begin{aligned} p_{3}= & b c+\beta_{3}^{2} x y-2 a \beta_{3} z+b \beta_{3} y+\beta_{3} c x+ \\ & b \beta_{2} z+\beta_{1} c z-a \beta_{3}{ }^{2} v t+\beta_{1} b t_{2} z^{2}-\beta_{2} \beta_{3} x z- \\ & \beta_{1} \beta_{3} y z+b \beta_{2} \beta_{3} v t+\beta_{1} \beta_{3} c v t \end{aligned}$
$q_{3}=a+\beta_{2} x+\beta_{1} y+\beta_{1} \beta_{2} v t$
经对比，通过数学推导所得出的结果与虚拟样本实验的结果完全一致（图3）。
图3 虚拟样本实验与数学模拟对比

Fig. 3 Comparison between synthetic sample experiment and mathematical simulation

5.2 异常点出现的原因

根据式（15）—式（23）可知，假设违背程度值对TC方法结果误差的影响呈现非线性关系。整体来看，可以将这种关系视为一个分式结构。当分母接近于0时，分子并不会随之接近于0，这导致结果误差会突然大幅度增加，这就是虚拟样本实验中的异常点出现的原因。
进一步观察式（15）—式（23）的分母部分，其中包括多个变量。根据上文中虚拟样本实验结果：改变值会影响异常点出现的位置，在此，这一实验结果就可以得到理论解释：在保证其中5条假设为0，为定值的条件下，改变就会使得原先接近于0的分母不再接近于0。这时调整实验变量，分母会再次接近于零，异常点就会再次出现。此外，由于中每项中的分母各不相同，这也解释了上文虚拟样本实验中，值的改变对异常点位置的影响不满足对称性的结论。并且，式（15）—式（23）中没有项，这解释了改变不会影响方法误差的结论。值得注意的是，在的分母中，并没有与自身相对应项，这说明当仅对第条样本进行估计时，第条样本不会因自身的误差组成结构而出现异常点。

6 讨论

6.1 异常点带来的影响

以往的研究通常默认对2组不相关性假设的违背程度与结果误差之间的关系是单调的；即认为随着假设违背程度的增加，结果误差是增加的。这种思想往往会体现在2个方面： ① 在选取样本时，通常认为只要样本能较好地满足独立性，TC方法的误差就能控制在合理的范围内。式（15）—式（23）说明了在某些特殊情况下，即使假设得到较好地遵守，当乘偏差系数、“真值”方差、对假设的违背程度处于某种特殊关系时，也有可能出现结果误差较大的情况。存在异常点说明方法的结果并不稳定，在实际应用中，使用TC方法还需要考虑更复杂的非线性关系； ② 以往的方法改进研究主要关注于如何整体降低方法对2组不相关性假设的敏感度[13]，或提高方法的适用范围[14-15]，从而忽视了假设违背与结果误差之间的非线性关系。因此，未来的方法改进可以更加关注如何弱化这种非线性关系、抑制异常点并提高方法的稳定性。在某些情况下，一些看似不精确的方法有可能因其对基本假设的违背不敏感，反而在实际使用中表现较好。

6.2 抑制异常点的方法

6.2.1 忽略加性偏差系数（改进1）

异常点的存在影响了TC方法的可靠性。消除异常点的方法，在于如何消除误差中的分母。这个分母是由缩放系数所产生的。例如：使用样本均值之比代替式（3）中的缩放系数，将其改为不受不相关性假设所影响的形式。
$\left\{\begin{array}{l} \beta_{2}^{*}=\frac{\overline{x_{1}}}{\overline{x_{2}}}=\frac{\alpha_{1}+\beta_{1} t}{\alpha_{2}+\beta_{2} t} \approx \frac{\beta_{1}}{\beta_{2}} \\ \beta_{3}^{*}=\frac{\overline{x_{1}}}{\overline{x_{3}}}=\frac{\alpha_{1}+\beta_{1} t}{\alpha_{3}+\beta_{3} t} \approx \frac{\beta_{1}}{\beta_{3}} \end{array}\right.$
便能消除不相关性假设对缩放系数的影响，避免异常点的出现。但强行忽略加法偏差系数，在一些加性偏差较大的样本中，会产生较大的误差。值得指出的是，这种改进方法与使用作为误差形式假设的TC方法，从最终结果上来看是等价的。

6.2.2 限制缩放系数的上下界（改进2）

缩放系数的分式结构带来了结果误差的分式结构，限制缩放系数的上下限，使其不出现异常增大或接近于0，也可抑制异常点的出现。
$\beta_{i}^{*}(i=2,3)=\left\{\begin{array}{lr} \operatorname{sgn}\left(\beta_{i}^{*}\right) \times b, & \left|\beta_{i}^{*}\right|>b \\ \beta_{i}^{*}, & a<\left|\beta_{i}^{*}\right|<b \\ \operatorname{sgn}\left(\beta_{i}^{*}\right) \times a, & \left|\beta_{i}^{*}\right|<a \end{array}\right.$
式中：sgn(*)为符号函数；b为上界，控制$\beta_{i}^{*}$不异常增大；a为下界，控制$\beta_{i}^{*}$不接近于0；根据缩放系数$\beta_{i}^{*}$的定义：$\beta_{i}^{*}$表示两组样本乘偏差系数的相对比例$\frac{\beta_{i}}{\beta_{j}}$。为了方便取值，可设置$b=\frac{1}{a}$，即的上下界与$\frac{\beta_{i}}{\beta_{j}}$的上下界相等。通常$\frac{\beta_{i}}{\beta_{j}}$的变化范围一般不会太大，故下文中取$b=\frac{1}{a}=4$。
这种改进方法，使得TC方法可以在绝大部分情况下保留其原先的数学结构及准确性，仅在异常点出现时进行强制修正，如图4所示。但也限制了3组样本两两之间的乘偏差系数相对比例的范围，通常来说，这个相对比例不会太大，不易超出所给的范围。但还需要在实际数据中进行检验。
图4 2种改进方法的误差关系曲线的对比

Fig. 4 Comparison of the relationship between error and degree of assumption violation for traditional algorithm and two improved algorithms

值得注意的是$\beta_{2}^{*}$、$\beta_{3}^{*}$当两者都接近于0且一正一负时，这种改进方法会强行将$\beta_{2}^{*}$、$\beta_{2}^{*}$变化到a，-a这个过程中会产生较大的误差。不过与在这一点传统方法出现的异常点相比，误差得到明显的抑制。并且这个误差可以通过调整参数a、b进行避免。
2种改进方法在GitHub上发布，网址为： https://github.com/muming-ing/Anomaly-Suppressed-Triple-Colloction。

6.3 出现异常点的概率

异常点是由多种参数共同作用了产生的一种特殊情况。在实际应用中，极端误差出现的概率决定了TC方法稳定性的强弱，也是衡量上述改进方法好坏的重要指标，值得进一步地讨论。本文对此仅做初步地估算，假设影响异常点出现的参数各自独立且符合正态分布，根据各参数的现实意义设置合理的正态分布参数，见表3。根据表3所假定的参数分布，随机生成10 000组样本，估算3种TC方法出现异常点的概率，见表4。
表3 影响异常点出现的各项参数的假定分布

Tab. 3 Assumed distributions of various parameters affecting the occurrence of outliers

参数 假定的分布或值
情景1 情景2 情景3
a , b , c , x , y , z N ( 0   ,   8 ) N ( 0   ,   8 ) N ( 0   ,   8 )
β i N ( 1,0.5 ) N ( 1,0.5 ) N ( 1,0.5 )
α i 0 N ( 0   ,   1 ) N ( 0   ,   3 )
v a r ( ε i ) 30
v a r ( t ) 50
t - 10
表4 各情景下误差概率分布

Tab. 4 Probability distribution of errors for different α iscenarios (%)

概率 情景1
 情景2 情景3
TC 改进1 改进2 TC 改进1 改进2 TC 改进1 改进2
P ( δ M A E > 30 ) 29.56 28.70 29.13 29.20 30.30 29.00 29.24 36.49 28.78
P ( δ M A E > 100 ) 6.76 5.00 5.53 6.50 7.60 5.40 6.88 10.38 5.41
P ( δ M A E > 200 ) 3.27 1.35 1.77 3.20 3.90 1.80 3.06 5.21 1.65
P ( δ M A E > 500 ) 1.25 0.18 0.12 1.70 1.70 0.50 1.19 2.21 0.20
P ( δ M A E > 800 ) 0.76 0.05 0.01 1.20 0.70 0.10 0.70 1.43 0.01
P ( δ M A E > 1   000 ) 0.56 0.03 0.01 1.00 0.70 0.00 0.49 1.22 0.00
由于因正常违背不相关性假设很难导致结果误差到达很高的程度，当结果误差超过$\delta_{M A E}>200$时，可认为此时的误差情况都是由异常点产生的。根据表4可知，TC方法出现异常点的概率为3.2%左右。
与传统的TC方法相比，在上述3个情景中，改进2都对异常点的出现具有明显的抑制作用，并且随着异常值大小的增加，抑制效果逐渐变得明显。在情景1下，改进1也对异常点具有明显地抑制作用，但随着αi项的加入（如表4中情景2、情景3），式中的近似关系逐渐无法成立，该改进方法的结构性误差逐渐增加，在情景3中产生极端误差的概率甚至比具有异常点的TC方法更大。

6.4 实测数据验证

选取SMOS, SMAP, AMSR2三套独立的遥感土壤水分数据作为TC方法的输入，使用2016—2022年ISMN站点数据进行验证。验证方式为假设地面站点数据为真值，通过最小二乘法分离出3个遥感数据集各自的系统偏差与随机误差，计算出随机误差的方差并与TC方法的结果进行对比。
经过质量控制，共选取1 465个站点与相对应的遥感数据，形成1 465组样本用于异常点的验证与改进方法的对比。其中分别有562、1 147、555组样本在传统TC方法、改进1、改进2的计算中出现计算结果不合理（计算结果为负）的情况，选取在3种方法同时可计算出非负结果的221组样本进行对比：
实测数据验证结果表明，异常点在实际应用中存在，且对方法整体的精度产生了较大的影响。但异常点出现的概率要小于上文所估计的概率，造成这个差异的主要原因是，在实际应用中异常点往往以负异常（结果为负值并较真值产生较大的偏差）的形式出现，由于计算结果不应为负，这些异常点被视为不合理的结果并据此被剔除。需要承认的是，由于负异常现象的影响，当使用次数较少时，例如在离散站点中使用TC方法，异常点出现的概率较低，可以考虑忽略异常点的影响。然而，当使用次数较多时，例如对于格点数据进行反复计算时，需要充分考虑异常点的影响。
观察图5可知，使用改进1、2都能有效地去除异常点。但改进1由于自身结构缺陷，在去除异常点的同时会造成计算结果的精度下降，并明显增加不合理结果出现的概率；相反，改进2在处理正常值时保留了TC方法结果的精确性，仅在出现异常点的时候进行干预，因此具有较好的结果精度。在改进2中，出现不合理结果的个数相较于TC方法减少了7个，有效地消除了负异常值，并在出现异常点时也能够进行有效地估计，提高了方法的稳定性。
图5 TC方法、改进1、改进2与参考值的相关性对比

Fig. 5 Comparing TCA, Improvement 1, Improvement 2 by assuming gauge data as the ‘truth’

7 结论与展望

（1）本文对Triple Collocation（TC）方法在其假设不能完全满足的情况下的表现进行了深入的探讨。通过虚拟样本实验与数学理论推导，发现了异常点现象。
（2）推导了违反不相关性假设程度与结果误差之间的复杂非线性关系。这项研究对后续规范TC方法的使用范围、改进方法结构具有重要意义。
（3）针对异常点问题，本文提出了两种可能的改进方法：忽略加性偏差系数和限制缩放系数的上下界。这两种方法都能不同程度地抑制异常点的出现，其中改进2在实际应用中取得了更好的结果。如何彻底地消除异常点，如何减少TC方法出现计算结果不合理（计算结果为负）的情况，还需要进一步的研究。
（4）TC方法对真值的衡量标准是建立在误差形式假设之上的，即与三组数据集同时线性相关的是“真值”，这种定义显然不够严谨。实际应用中，真值的标准是与数据的用途息息相关的。例如，不同尺度模型所需数据的尺度也是不同的。数据的准确性是在一定框架下进行衡量的产物。即使TC方法的数学假设完全成立，其关于真值的定义是否可靠?还需要进一步的研究。

感谢南京信息工程大学高性能计算中心为本研究提供的计算资源。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Stoffelen A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation[J]. Journal of Geophysical Research: Oceans, 1998, 103(C4):7755-7766. DOI:10.1029/97jc03180

[2]
Caires S, Sterl A. Validation of ocean wind and wave data using triple collocation[J]. Journal of Geophysical Research: Oceans, 2003, 108(C3):3098. DOI:10.1029/2002jc001491

[3]
Scipal K, Holmes T, de Jeu R, et al. A possible solution for the problem of estimating the error structure of global soil moisture data sets[J]. Geophysical Research Letters, 2008, 35(24):L24403. DOI:10.1029/2008gl035599

[4]
梁顺林, 李新, 谢先红, 等. 陆面观测、模拟与数据同化[M]. 北京: 高等教育出版社, 2013.

[ Liang S L, Li X, Xie X H. Land surface observation, modeling and data assimilation[M]. Beijing: Higher Education Press, 2013. ]

[5]
Yilmaz M T, Crow W T. The optimality of potential rescaling approaches in land data assimilation[J]. Journal of Hydrometeorology, 2013, 14(2):650-660. DOI:10.1175/jhm-d-12-052.1

[6]
Yilmaz M T, Crow W T. Evaluation of assumptions in soil moisture triple collocation analysis[J]. Journal of Hydrometeorology, 2014, 15(3):1293-1302. DOI:10.1175/jhm-d-13-0158.1

[7]
Gruber A, Su C H, Zwieback S, et al. Recent advances in (soil moisture) triple collocation analysis[J]. International Journal of Applied Earth Observation and Geoinformation, 2016, 45:200-211. DOI:10.1016/j.jag.2015.09.002

[8]
Zwieback S, Scipal K, Dorigo W, et al. Structural and statistical properties of the collocation technique for error characterization[J]. Nonlinear Processes in Geophysics, 2012, 19(1):69-80. DOI:10.5194/npg-19-69-2012

[9]
范悦, 邱建秀, 董建志, 等. 基于Triple Collocation方法的微波土壤水分产品不确定性分析与时空变化规律研究[J]. 遥感技术与应用, 2020, 35(1):85-96.

[ Fan Y, Qiu J X, Dong J Z, et al. Error characteristics of microwave soil moisture products based on triple collocation and its spatial-temporal pattern[J]. Remote Sensing Technology and Application, 2020, 35(1):85-96. ] DOI:10.11873/j.issn.1004-0323.2020.1.0085

[10]
Su C H, Ryu D. Multi-scale analysis of bias correction of soil moisture[J]. Hydrology and Earth System Sciences, 2015, 19(1):17-31. DOI:10.5194/hess-19-17-2015

[11]
Tsamalis C. Clarifications on the equations and the sample number in triple collocation analysis using SST observations[J]. Remote Sensing of Environment, 2022, 272:112936. DOI:10.1016/j.rse.2022.112936

[12]
Pan M, Fisher C K, Chaney N W, et al. Triple collocation: Beyond three estimates and separation of structural/non-structural errors[J]. Remote Sensing of Environment, 2015, 171:299-310. DOI:10.1016/j.rse.2015.10.028

[13]
Dong J Z, Wei L N, Chen X, et al. An instrument variable based algorithm for estimating cross-correlated hydrological remote sensing errors[J]. Journal of Hydrology, 2020, 581:124413. DOI:10.1016/j.jhydrol.2019.124413

[14]
Su C H, Ryu D, Crow W T, et al. Beyond triple collocation: Applications to soil moisture monitoring[J]. Journal of Geophysical Research: Atmospheres, 2014, 119(11):6419-6439. DOI:10.1002/2013jd021043

[15]
McColl K A, Vogelzang J, Konings A G, et al. Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target[J]. Geophysical Research Letters, 2014, 41(17):6229-6236. DOI:10.1002/2014gl061322

Options
文章导航

/

〈 〉