EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 3: 620 - 637

DOI: https://doi.org/10.12082/dqxxkx.2024.230427

地球信息科学理论与方法

耦合统计方法、机器学习模型和聚类算法的滑坡易发性评价方法

  • 王启盛 , 1 ,
  • 熊俊楠 , 1, 2, * ,
  • 程维明 2 ,
  • 崔兴洁 1 ,
  • 庞全 4, 5 ,
  • 刘俊 3 ,
  • 陈文杰 1 ,
  • 唐浩然 1 ,
  • 宋南霄 1
展开
  • 1.西南石油大学土木工程与测绘学院， 成都 610500
  • 2.中国科学院地理科学与资源研究所 资源与环境信息系统国家重点实验室，北京 100101
  • 3.中山大学地理科学与规划学院， 广州 510275
  • 4.四川省安全科学技术研究院，成都 610046
  • 5.四川安信科创有限公司， 成都 610041
*熊俊楠（1981— ），男，四川南充人，博士，教授，主要从事地理信息系统与灾害风险分析方面的研究。 E-mail:

王启盛（1999— ），男，四川广安人，硕士生，主要从事机器学习与灾害风险评估研究。 E-mail:

Copy editor: 蒋树芳

收稿日期: 2023-07-23

  修回日期: 2023-10-11

  网络出版日期: 2024-03-31

基金资助

四川省科技厅重点研发项目(2021YFQ0042)

西藏自治区科技计划项目(XZ201901-GA-07)

国家重点研发计划课题(2020YFD1100701)

中国科学院战略先导专项(A类)(XDA20030302)

四川省科研院所基本科研业务费项目(2023JDKY0039-01)

收起

Landslide Susceptibility Mapping Methods Coupling with Statistical Methods, Machine Learning Models and Clustering Algorithms

  • WANG Qisheng , 1 ,
  • XIONG Junnan , 1, 2, * ,
  • CHENG Weiming 2 ,
  • CUI Xingjie 1 ,
  • PANG Quan 4, 5 ,
  • LIU Jun 3 ,
  • CHEN Wenjie 1 ,
  • TANG Haoran 1 ,
  • SONG Nanxiao 1
Expand
  • 1. School of Civil Engineering and Geomatics, Southwest Petroleum University, Chengdu 610500, China
  • 2. State Key Laboratory of Resource and Environmental Information System, Institute of Geographic and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
  • 3. School of Geography and Planning, Sun Yat-Sen University, Guangzhou 510275, China
  • 4. Sichuan Academy of Safety Science and Technology, Chengdu 610046, China
  • 5. Sichuan Anxin Kechuang Technology Co., Ltd., Chengdu 610041, China
*XIONG Junnan, E-mail:

Received date: 2023-07-23

  Revised date: 2023-10-11

  Online published: 2024-03-31

Supported by

Key R&D project of Sichuan Science and Technology Department(2021YFQ0042)

The Science and Techno-logy Project of Xizang Autonomous Region(XZ201901-GA-07)

National Key R&D Program of China(2020YFD1100701)

Strategic Priority Research Program of the Chinese Academy of Sciences(XDA20030302)

Sichuan Provincial Research I-nstitutes Basic Scientific Research Operating Expenses Program(2023JDKY0039-01)

Fold

摘要

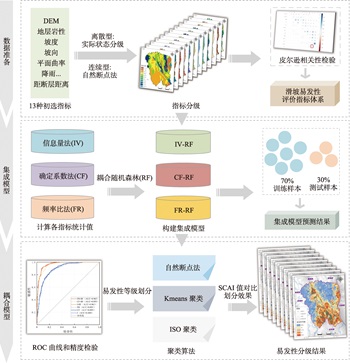
我国西部山区滑坡灾害频发，精确评估滑坡易发性对地质灾害防治至关重要。结合统计方法与机器学习模型的集成模型已广泛的应用于滑坡易发性评价，然而对其结果的进一步优化仍值得考虑。本文提出一种耦合统计方法、机器学习模型以及聚类算法的综合评价方法，以宁南县为例，研究其对滑坡易发性评价精度的提升效应。该方法首先将信息量法（Information Value, IV）、确定系数法（Certainty Factor, CF）和频率比法（Frequency Ratio, FR）分别与随机森林模型（Random Forest, RF）结合，得到三种集成模型（IV-RF、CF-RF、FR-RF）。此后，引入ISO聚类算法对三种集成模型的结果进行分级，得到三种耦合模型（IV-RF-ISO、CF-RF-ISO、FR-RF-ISO）。AUC值（Area Under the Curve）、准确率、F1分数和种子单元面积指数（Seed Cell Area Indexes，SCAI）被用于评估模型的精度。结果显示，集成模型性能均优于单一模型，其准确率和F1分数均大于0.85，AUC值均大于0.9。其中FR-RF模型表现最优，准确率（0.911）、F1分数（0.912）和AUC值（0.965）较FR模型分别提升了0.095、0.096和0.074。与自然断点法和Kmeans聚类法相比，引入ISO算法的耦合模型FR-RF-ISO分级效果最优，其高低易发区SCAI值的差异更为显著。本研究成果表明，耦合统计方法、机器学习与聚类算法的综合评价方法具有较高精度，为提高滑坡易发性评价精度提供思路。

关键词： 滑坡易发性; 信息量; 确定系数; 频率比; 随机森林; 聚类算法; 宁南县

本文引用格式

王启盛 , 熊俊楠 , 程维明 , 崔兴洁 , 庞全 , 刘俊 , 陈文杰 , 唐浩然 , 宋南霄 . 耦合统计方法、机器学习模型和聚类算法的滑坡易发性评价方法[J]. 地球信息科学学报, 2024 , 26(3) : 620 -637 . DOI: 10.12082/dqxxkx.2024.230427

Abstract

Landslides frequently occur in the mountainous areas of western China. Accurate mapping of landslide susceptibility is essential for geohazard management. Integrated models combining statistical methods and machine learning models have been widely applied to landslide susceptibility mapping. However, further optimization of their results is still worth investigation. This study proposes a comprehensive assessment method that couples statistical methods, machine learning models, and clustering algorithms. The effectiveness of the proposed method on improving the accuracy of landslide susceptibility mapping in Ningnan County is investigated. Firstly, the landslide influencing factors are selected from five aspects: geological environment, topography and geomorphology, meteorology and hydrology, vegetation and soil, and human engineering activities in the study area. Indicators are initially selected based on correlation analysis using the Pearson correlation coefficient method, and highly correlated factors are eliminated to establish the landslide susceptibility mapping index system. Next, the Information Value (IV), Certainty Factor (CF), and Frequency Ratio (FR) methods are combined with Random Forest (RF) model respectively to obtain three integrated models (IV-RF, CF-RF, and FR-RF). Then, the ISO clustering algorithm, Natural Breaks clustering, and Kmeans clustering algorithms are introduced to classify the results of the three integrated models, obtaining nine coupled assessment models (IV-RF-ISO, CF-RF-ISO, FR-RF-ISO, IV-RF-NBC, CF-RF-NBC, FR-RF-NBC, IV-RF- Kmeans, CF-RF- Kmeans, and FR-RF- Kmeans). Lastly, Area Under the Curve value (AUC), accuracy, F1 score, and Seed Cell Area Indexes (SCAI) are used to evaluate the accuracy of the models. The results demonstrate that all the integrated models outperform single models. The accuracy and F1 score of all integrated models both exceed 0.85, and their AUC values exceed 0.9. The integrated models effectively address the misclassification of non-landslide samples, which is especially prominent in single IV and CF models. Among the integrated models, the FR-RF model performs the best. The accuracy (0.911), F1 score (0.912), and AUC value (0.965) of FR-RF model improves by 0.095, 0.096, and 0.074, respectively, compared to the FR model. Compared with the natural break and Kmeans clustering methods, the coupled FR-RF-ISO model exhibits the optimal classification results, and the difference in SCAI values between its high and low susceptibility zones is more significant. The extremely high landslide susceptibility zones are primarily concentrated in the southern, eastern, and central parts of Ningnan County. The study demonstrates the high accuracy of the integrated assessment method that couples statistical methods, machine learning, and clustering algorithms, and provides insights for improving the accuracy of landslide susceptibility mapping.

Key words： landslide susceptibility; information value; certainty factor; frequency ratio; random forest; clustering algorithm; Ningnan County

1 引言

滑坡灾害突发性强、分布范围广，对当地基础设施、生态环境和居民生命财产安全造成了巨大威胁。我国西部山区地形起伏较大、地质构造活跃、季节性降雨集中，滑坡灾害频发[1]。国家减灾委员发布的《“十四五”国家综合防灾减灾规划》[2]中提到，我国亟需提高灾害风险管理水平，提升防灾减灾科技支撑能力。滑坡易发性评价是地质灾害风险防治的重要组成部分，通过准确、可靠的评价技术，识别滑坡高易发性区域，可为防灾减灾工作提供科学依据[3-4]。
目前，滑坡易发性评价理论方法主要分成知识驱动和数据驱动[5]。知识驱动法[6]是基于专家经验的主观判断和定性分析评价方法，评价结果缺乏客观性和可重复性，如层次分析法[7]、模糊综合评判法[8]等。数据驱动法[9]是基于统计分析和机器学习等技术，从大量数据中挖掘滑坡发生的规律和关联性的评价方法，具有客观性和可量化性。近年来，随着计算机技术的发展，数据驱动法的运用越来越广泛，涌现了众多使用统计模型和机器学习技术的滑坡易发性评价方法。常见的统计分析方法主要有信息量法（Information Value, IV）[10-11]、确定系数法（Certainty Factor, CF）[12]、频率比法（Frequency Ratio, FR）[13]、证据权法[14]等，但由于滑坡发生机理复杂，传统的统计方法评价精度较低[15]。故引入具有更高预测准确性的机器学习模型，如随机森林（Random Forest, RF）[16]、逻辑回归模型[17]、支持向量机[18]、卷积神经网络[19]等，机器学习具有强大的自适应学习能力，能较好的捕捉到因子与滑坡之间的非线性关系特征[20]。
尽管与统计方法相比，机器学习方法显著提高了滑坡易发性评价的准确性，但何种模型具有最佳评价效果，学术界尚未达成一致共识[21]。这是因为单一的评价模型或方法存在一定局限性，难以恰当地代表滑坡易发性的输入数据与实地情况相符，导致模型无法准确拟合最佳函数和样本集的真实分布[22]，集成模型则被认为是解决这个问题的有效技术。因此，将统计方法与机器学习模型结合，创建混合评价模型已成为近年来的研究趋势[23]。罗路广等[24]和徐胜华等[25]对九寨沟和陕西省开展滑坡易发性评价中，将确定系数和熵指数分别与逻辑回归模型和支持向量机结合，发现采用集成模型比单一模型评价结果更加合理。Chen等[23]利用二元统计指数、确定性因子、熵指数耦合随机森林模型，对太白县开展滑坡易发性评价，结果表明CF-RF有更好的预测精度。王世宝等[26]基于频率比与集成学习开展滑坡易发性评价，发现耦合频率比后的随机森林模型比梯度提升树表现更优。以上研究的共同结论是：统计方法与机器学习模型的结合提高了滑坡易发性的预测能力。统计方法利用数理统计深入分析滑坡影响因子，解决不同因子间的数据整合，机器学习模型能够学习到隐藏在数据中的规律，集成模型能很好的继承两者优点，提高滑坡易发性评价的准确性和可靠性。
在滑坡易发性建模过程中，将统计方法与机器学习模型耦合，具有较高的预测精度。但在计算出易发性结果后，还需对易发性等级进行划分。这方面，大多数的研究都采用自然断点法（Natural Break Classification, NBC）来确定分级阈值[27-28]。然而，不同的分级方法会直接影响易发性评价结果，以往的研究大都忽略了分级方法的选择。是否可以使用其余分级方法来代替自然断点法对易发性评价结果进行划分，进而提高集成建模评价效果，在现有研究中较少讨论。
综上所述，滑坡易发性评价是一项复杂而多样化的任务，需要综合考虑孕灾环境、致灾因子、承灾体的异质性和复杂性，有必要开发更多模型来满足复杂条件下滑坡易发性评价的需求。尽管统计方法与机器学习模型的耦合并不鲜见，然而对集成模型评价结果的优化仍值得研究。本文提出一种将统计方法、机器学习模型和聚类算法结合的滑坡易发性综合评价方法。选用众多学者使用较多的IV、CF和FR统计方法[21]，分别与RF进行结合，引入ISO聚类分级方法，得到3种耦合模型（IV-RF-ISO、CF-RF-ISO、FR-RF-ISO），并与自然断点法和Kmeans聚类进行对比，探究不同聚类方法对易发性评价结果的影响。研究结果丰富了滑坡易发性评价方法，为滑坡预测研究提供一种准确可靠的模型选择，同时为宁南县的滑坡防治提供重要的科学依据。

2 研究方法

本文技术路线如图 1所示，首先，在研究区内初选13种易发性评价指标并分级，通过皮尔逊相关性系数法对初选指标进行相关性检验，剔除强相关性因子，建立滑坡易发性评价指标体系。其次，将研究区376个滑坡点作为正样本，在滑坡点一公里缓冲区外选取376个随机点作为负样本，选取70%样本点作为训练样本，30%样本点作为验证样本，提取各影响因子的IV、CF和FR值，在R软件中构建RF滑坡易发性评价模型，对研究区1 865 178个格网进行预测，得到基于IV-RF、CF-RF和FR-RF 3种集成模型的宁南县滑坡易发性结果，再通过绘制ROC曲线使用准确率、精确率、召回率和F1分数对模型预测性能进行精度验证。最后，使用ISO聚类、自然断点法和Kmeans聚类对易发性进行分级，使用SCAI指数评估耦合模型的分级效果。
图1 耦合统计方法、机器学习模型与聚类算法的滑坡易发性评价技术路线

Fig. 1 Technical route for landslide susceptibility mapping methods coupling with statistical methods, machine learning models and clustering algorithms

2.1 统计方法

2.1.1 信息量法（IV）

信息量法（Information Value，IV）[29]以信息论为基础计算研究区内影响滑坡的各因子信息量值，反映滑坡的易发性，信息量值越大，越有利于滑坡的发生。利用式（1）计算评价因子的信息量值：
I V X i , K = l n N i / N S i / S
式中： I V X i , K表示评价因子Xi对滑坡事件K提供的信息量值； Ni表示分布在评价因子Xi区域内滑坡点个数； N表示研究区内总的滑坡点个数； Si表示评价因子Xi的面积； S表示研究区总面积。

2.1.2 确定性系数法（CF）

确定性系数法（Certainty Factor，CF）[30]是一种常用的概率分析方法，根据滑坡点数据计算不同指标因子状态下滑坡发生的先验概率。CF值的范围为-1~ 1，正值表示滑坡发生的确定性高，负值表示滑坡发生的确定性低。CF值的计算如式（2）所示。
C F = P P a - P P s P P s 1 - P P a ,               P P a < P P s P P a - P P s P P a 1 - P P s ,               P P a ≥ P P s
式中： CF表示滑坡灾害发生的确定性系数； PPa表示评价因子区域内滑坡点个数与面积的比值； PPs表示研究区内滑坡点总数与研究区面积的比值。

2.1.3 频率比法（FR）

频率比法（Frequency Ratio，FR）[31]是一种常见的数理统计方法，常用来计算评价因子对滑坡发生的相对影响程度。FR值越大表示该因子对滑坡发生的影响程度越大。FR值的计算如式（3）所示。
F R = N i / N S i / S
式中： FR表示频率比值； Ni表示评价因子区域内滑坡点个数； N表示研究区内滑坡总数； Si表示评价因子面积； S表示研究区总面积。

2.2 随机森林模型（RF）

随机森林模型（Random Forest， RF）[32-33]是一种集成学习模型，由多个分类与回归树（CART）组成，可以应对高维数据和大量特征的情况，能够评估特征的重要性，具有良好的泛化能力和鲁棒性。它具有两个随机过程，即样本的随机有放回抽样和特征变量子空间的随机选择。通过对原始数据集进行自助重采样，每个决策树都会基于不同的训练样本集进行建模，从而增加了模型的多样性，利用个体分类树之间的差异性，提高建模性能并避免模型过拟合。同时每棵决策树的节点分裂使用基尼系数（Gini Index）作为杂质函数来衡量节点的纯度，以最大程度地降低分类误差。基尼系数（Gini Index）计算如式（4）所示。
  G i n i   I n d e x = 1 - ∑ c p 2 ( c ∣ t )
式中： c表示分类子节点个数； t表示决策树的节点； p为c的相对频率。

2.3 聚类算法

K-means聚类算法[34-35]是一种无监督学习方法，用于将给定的数据集划分为K个不同的簇。算法的基本思想是先随机选择K个初始质心，然后通过迭代的方式不断调整质心的位置，直到达到收敛条件。在每一次迭代中，算法会根据每个数据点与质心的距离将其归类到最近的簇中。然后，根据簇内的数据点更新质心的位置，通常采用计算簇内数据点的均值来得到新的质心位置。这个过程将不断迭代，直到质心的位置不再发生显著变化，或达到预定的迭代次数。
ISO聚类（Iterative Self-Organizing）[36-37]，是一种基于自组织数据分析技术的聚类方法。ISO聚类算法通过迭代的方式不断调整聚类中心的位置，以实现数据点的聚类。该算法的基本思想是在每一次迭代中，根据数据点与聚类中心的距离将其分配到最近的簇中，并通过计算簇内数据点的均值来更新聚类中心的位置。这个过程将不断迭代，直到达到收敛条件。

2.4 精度评价

混淆矩阵（Confusion Matrix）[38]是一种用于衡量分类模型性能的矩阵表示形式。通过混淆矩阵计算出的准确率（Accuracy）、精确率（Precision）、召回率（Recall）和F1分数（F1 Score）可全面地评估分类模型的性能，其中F1分数是精确率和召回率的调和平均值，各精度指标的计算方法如式（5）—式（8）所示。
A c c u r a c y = T P + T N T P + T N + F P + F N
P r e c i s i o n = T P T P + F P
R e c a l l = T P T P + F N
F 1   S c o r e = 2 × T P 2 × T P + F P + F N
式中： TP和FN表示模型正确预测和错误预测的滑坡点数； FP和TN表示模型错误预测和正确预测的非滑坡点数。
ROC曲线（Receiver Operating Characteristic Curve）[39]常用来评价模型的分类性能，在滑坡灾害易发性评价中，横轴（特异性）表示正确预测的非滑坡样本比例，纵轴（敏感性）表示正确预测的滑坡样本比例。ROC曲线越接近左上角，ROC曲线下的面积越大，即AUC（Area Under the Curve）值越大，评价模型性能则越优秀，模型精度越高。
种子单元面积指数（Seed Cell Area Indexes，SCAI）[40]可以用于评估滑坡灾害易发性评价精度。它主要通过考虑易发性分区面积和历史滑坡所占比例来量化评估易发性分区效果。计算方法为：SCAI=分区面积占总面积比例/滑坡点数量占分区面积比例，高易发性等级区的SCAI值越低，低易发性等级区的SCAI值越高，两者比值越大，差异越明显，分区效果越好。

3 研究区概况及数据来源

3.1 研究区概况

如图2所示，宁南县地处于四川省西南部，位于102°27′44″E—102°55′09″E， 26°50′12″N—27°18′34″N之间，总面积为1 670 km²，地形以山地为主，海拔高度531~3 865 m。气候类型为亚热带季风气候，季节干湿明显，年均降雨量约为1 074 mm。宁南县地质环境十分复杂，地形地貌条件多变，地处于横断山东北部和青藏高原东南边缘，地势特点为两山夹一槽，地势西北高、东南低，沟壑纵横，崇山峻岭连绵不断。研究区内人口主要集中的河（沟）谷沟口、坡脚及半山斜坡地带，第四系松散堆积物十分丰富，极易形成滑坡灾害[41]。根据地质资料和现场调研，研究区内断裂带主要包括则木河断裂、宁南-会理断裂、大桥河断裂、迴龙弯断裂等。宁南县2022年地质灾害普适型项目调查结果显示，宁南县地质灾害以滑坡为主，自然和人为因素导致的滑坡地质灾害隐患点高达376处，易发生于区内奥陶系、志留系、三叠系、侏罗系的泥质白云岩、页岩、泥岩等易滑地层，对人民财产安全造成了严重的威胁。
图2 宁南县地理概况

Fig. 2 Geographical overview of Ningnan County

3.2 数据源

滑坡的演化过程复杂，通常是在自然和人为等多种因素耦合下所导致[42]。本文从研究区地质环境、地形地貌、气象水文、植被土壤、人类工程活动5个方面初选：数字高程模型DEM（Digital Elevation Model）、归一化植被指数NDVI（Normalized Difference Vegetation Index）、地层、年降水量、距道路距离、距水系距离、距断层距离、坡度、坡向、平面曲率、剖面曲率、土地利用、土壤质地13个滑坡影响因子，构建宁南县滑坡易发性评价数据库，数据来源如表 1所示。
表1 研究区数据源

Tab. 1 Data sources for the study area

数据名称 来源 类型 分辨率/比例尺 数据年份
滑坡灾害点 宁南县2022年地质灾害普适型项目 数据表 - 1976—2022
DEM 美国航空航天局 栅格 12.5 m 2015
地层 全国1:20万数字地质图[43] 矢量 1:20万 -
断裂带 全国1:20万数字地质图 矢量 1:20万 -
降水 中国气象局 站点 - 2015—2019
水系 全国基础地理数据库 矢量 1:25万 2015
道路 全国基础地理数据库 矢量 1:25万 2015
土壤质地 国家山洪灾害调查与评估项目 矢量 1:25万 -
NDVI Google Earth Engine 栅格 30 m 2013—2021
土地利用 GLOBELAND30 栅格 30 m 2020

3.3 指标分级

本文以30 m×30 m的栅格作为基础评价单元，以地层、距断层距离、DEM、坡度、坡向、剖面曲率、年均降雨量、距水系距离、NDVI、土壤类型、距道路距离、土地利用和平面曲率13个滑坡影响因子建立滑坡易发性评价指标体系，对于连续性因子距道路距离、距水系距离、距断层距离、高程按等间距进行分级，离散型因子按实际状态分级，其余因子按自然断点法分级[44]（图3）。
图3 评价指标分级

Fig. 3 Assessment index grading chat

3.3.1 地质环境

不同地层具有不同的岩石性质及其组合关系，直接制约滑坡灾害发育类型与规模[45]，区内地层信息分布如图3（a）所示，主要包含侏罗系、寒武系、奥陶系、震旦系等。断层运动影响地质体中节理、裂隙的发育，使岩石破碎，为滑坡发育提供条件[46]。如图3（b）所示，境内断裂构造发育以南北向构造为主，多展布于背斜近轴部，呈分支复合状。

3.3.2 地形地貌

地形地貌在滑坡的形成、分布和发展中起着重要的控制作用[47]。本文涉及的地形地貌因子高程、坡度、坡向、剖面曲率和平面曲率皆通过DEM提取。高程影响滑坡的势能变化[48]，如图3（c）所示，按400 m间隔将高程分成6类。较大的坡度增加了土壤或岩石受重力作用的程度。不同坡向受不同气候因素的影响，影响水分的累积和分布，导致土壤水分含量的空间分异[49]。剖面曲率影响水分的积聚和排水情况，进而影响土壤或岩石的稳定性。较大的平面曲率通常意味着地表存在明显的凸起或凹陷，这些地形特征可能会导致地表土壤的不稳定性，增加滑坡发生的风险。坡向按实际情况分成9个方向，坡度、剖面曲率和平面曲率按自然断点法分成5类（图3（d）、图3（e）、图3（f）、图3（m））。

3.3.3 气象水文

降雨是滑坡的主要诱发因素之一。降雨会导致土壤饱和度的增加，减小土壤的抗剪强度，引起地表径流增大、地下水位上升[50]。本文根据宁南县附近多个气象站点降水数据进行插值，得到宁南县多年平均降水量，如图3（g）所示，按自然断点法将其分成5类。宁南县境内水系丰富，主要有黑水河和金沙江以及龙洞河、三岔河、老木河等多条山溪。河流对两岸的边坡有冲刷和浸润，从而改变坡体形态结构，如图3（h）所示，以500 m为间隔将距水系距离划分成5类。

3.3.4 植被土壤

归一化植被指数（NDVI）可以反映植被的生长状况，NDVI值越高，通常表示植被茂盛、根系发达，能够有效固定土壤[51]。本文通过Google Earth Engine中Landsat8影像计算2013—2021年的年均NDVI值，如图3（i）所示，按自然断点法将其分成6类。不同土壤类型具有不同的颗粒组成、孔隙结构等物理和力学性质，如图3（j）所示，研究区内主要包含砂粘土、粘壤土、粘土等。

3.3.5 人类工程活动

道路的建设和使用会引起土地破坏、土壤移动和水文过程的改变，如图3（k）所示，以500 m为间隔，将其分成5类。不同的土地利用类型对滑坡的影响不同，如森林、草地等自然植被覆盖较好的土地类型能够增加土壤的抗剪强度，对坡体起稳定作用[52]，如图3（j）所示，研究区土地利用类型主要包括耕地、森林、草地等。

4 结果及分析

4.1 皮尔逊相关性分析

在进行滑坡易发性评价时，需考虑滑坡影响因子之间的相关性，影响因子的相关性过强时会造成数据的冗余，从而对评价模型的准确性造成影响[53]。本文使用皮尔逊相关性系数（r）确定影响因子之间的相关程度[54]，r的取值在-1~1之间，r的绝对值越接近1，影响因子的相关性越强；若 r的绝对值大于0.5，表明影响因子具有强相关性。相关系数计算结果如图4所示，平面曲率和坡度的相关性系数为0.54，具有较强相关性，故在后续滑坡易发性建模过程中剔除平面曲率。
图4 相关性系数矩阵

Fig. 4 Correlation coefficient matrix

4.2 IV、CF和FR值

如表2所示，不同指标的IV、CF和FR值取值范围不统一，但都表征对滑坡的影响程度，值越大影响越大。地层为志留系、距断层距离<500 m、高程1 000~1 400 m、坡度<14.8°、坡向为东北、剖面曲率0~7.9、年降水量<838 mm、距水系距离<500 m、NDVI值0.62~0.71、土壤类型为粉粘壤土、距道路距离1 500~2 000 m和土地利用类型为耕地区间内的IV、CF和FR值均最大。且各指标的IV、CF和FR值的大小排列均具有相似的趋势和顺序。
表2 各评价指标IV、CF和FR值

Tab. 2 Values of each assessment index IV, CF and FR

评价指标 指标分级 滑坡数 IV CF FR
地层 各侵入岩组 2 -1.04 -0.65 0.35
奥陶系 51 -0.53 -0.41 0.59
白垩系 6 0.40 0.33 1.49
第四系 31 0.71 0.51 2.03
二叠系 22 -0.40 -0.33 0.67
寒武系 17 -1.58 -0.79 0.21
泥盆系、三叠系 0 0.00 -1.00 0.00
元古界 3 0.07 0.07 1.08
震旦系 3 -2.52 -0.92 0.08
志留系 4 0.91 0.60 2.48
侏罗系 237 0.83 0.56 2.29
距断层距离/m <500 162 0.25 0.22 1.28
500~1 000 96 0.20 0.18 1.22
1 000~1 500 45 -0.10 -0.10 0.90
1 500~2 000 21 -0.53 -0.41 0.59
>2 000 52 -0.50 -0.40 0.60
高程/m <1 000 57 0.52 0.41 1.69
1 000~1 400 117 0.62 0.46 1.86
1 400~1 800 129 0.46 0.37 1.58
1 800~2 200 54 -0.22 -0.20 0.80
2 200~2 600 19 -1.15 -0.68 0.32
>2 600 0 0.00 -1.00 0.00
坡度/° <14.8 97 0.48 0.38 1.62
14.8~23.9 159 0.43 0.35 1.54
23.9~32.7 86 -0.18 -0.16 0.84
32.7~43.0 29 -1.03 -0.64 0.36
>43.0 5 -1.73 -0.82 0.18
坡向 平地 0 0.00 -1.00 0.00
北 37 -0.21 -0.19 0.81
东北 81 0.36 0.30 1.42
东 82 0.16 0.15 1.17
东南 63 0.13 0.12 1.13
南 32 -0.19 -0.17 0.83
西南 28 -0.39 -0.33 0.67
西 23 -0.37 -0.31 0.69
西北 30 -0.13 -0.13 0.87
剖面曲率 0~7.9 159 0.33 0.28 1.38
7.9~14.4 121 -0.04 -0.04 0.96
14.4~22.3 74 -0.12 -0.11 0.89
22.3~33.4 23 -0.56 -0.43 0.57
>33.4 0 0.00 -1.00 0.00
年降水量
/mm		 <838 94 0.72 0.51 2.05
838~872 154 0.65 0.48 1.91
872~902 65 -0.41 -0.33 0.67
902~935 28 -1.09 -0.67 0.33
>935 35 -0.67 -0.49 0.51
距水系距离/m <500 82 0.15 0.14 1.16
500~1 000 61 -0.05 -0.05 0.95
1 000~1500 55 -0.04 -0.04 0.96
1 500~2 000 48 -0.03 -0.03 0.97
>2 000 131 -0.03 -0.03 0.97
植被覆盖度 <0.45 5 0.27 0.24 1.31
0.45~0.62 10 0.14 0.13 1.15
0.62~0.71 73 0.77 0.54 2.15
0.71~0.78 101 0.25 0.22 1.29
0.78~0.84 130 0.04 0.04 1.04
>0.84 57 -0.80 -0.55 0.45
土壤类型 粉壤土 6 -0.43 -0.35 0.65
粉粘壤土 55 1.14 0.68 3.13
壤土 0 0.00 -1.00 0.00
砂粘壤土 6 -2.25 -0.89 0.11
砂粘土 135 0.04 0.04 1.04
粘壤土 121 0.22 0.20 1.24
粘土 53 -0.16 -0.15 0.85
距道路距离
（m）		 <500 136 0.28 0.24 1.32
500 ~1 000 79 0.01 0.01 1.01
1 000 ~1 500 45 -0.28 -0.24 0.76
1 500 ~2 000 62 0.32 0.27 1.38
>2 000 84 -0.07 -0.07 0.93
土地利用 耕地 292 0.94 0.61 2.56
森林 60 -1.37 -0.75 0.25
草地 9 -0.52 -0.41 0.59
灌木林 5 0.24 0.21 1.27
湿地 0 0.00 -1.00 0.00
水体 1 -0.93 -0.61 0.39
防渗区 9 0.70 0.50 2.01

4.3 精度验证

4.3.1 集成模型精度对比

将IV、CF和FR值叠加，经随机森林模型训练后，得到3种集成模型的易发性评价结果。对结果绘制ROC曲线并进行精度验证。如图5和表3所示，统计方法耦合随机森林后的评价精度各方面表现均优于单一模型，准确率和F1分数均大于0.85，AUC值均大于0.9，表明3种集成模型具有良好的拟合精度和预测性能，均有效的评价了宁南县滑坡易发性。且IV模型和CF模型的精确率明显小于召回率，即预测正确的非滑坡样本比例明显小于预测正确的滑坡样本比例，说明模型对非滑坡样本进行了较多的错误分类，此情况在耦合随机森林模型后，得到较好解决。3种集成模型的准确率、F1分数和AUC值的大小排序均为FR-RF>IV-RF>CF-RF，其中FR-RF模型表现最优，其准确率、F1分数和AUC值分别为0.911、0.912和0.965，较单一模型分别提升了0.095、0.096和0.074。
图5 ROC曲线

Fig. 5 ROC curve

表3 各模型精度评估结果

Tab. 3 Results of accuracy assessment of each model

模型 准确率 精确率 召回率 F1分数 AUC
IV 0.750 0.672 0.976 0.796 0.889
CF 0.778 0.705 0.955 0.811 0.895
FR 0.816 0.820 0.811 0.816 0.891
IV-RF 0.908 0.909 0.907 0.908 0.963
CF-RF 0.876 0.871 0.883 0.877 0.955
FR-RF 0.911 0.897 0.928 0.912 0.965

4.3.2 耦合模型精度对比

将IV-RF、CF-RF和FR-RF 3种集成模型计算结果经ISO聚类、自然断点法和Kmeans聚类分级，结果如图6和表4所示。IV-RF-ISO模型低易发区的SCAI值大于CF-RF-ISO模型和FR-RF-ISO模型，高易发区的SCAI值小于CF-RF-ISO模型和FR-RF-ISO模型，故IV-RF-ISO分级效果优于CF-RF-ISO、FR-RF-ISO。3种集成模型经ISO聚类分级后对比自然断点法，其高易发区SCAI值大小相似，但低易发区SCAI值均更大，可认定ISO聚类法分级效果优于自然断点法。ISO聚类法相较于Kmeans聚类法而言，虽然高易发区SCAI值和低易发区SCAI值都更大，但ISO聚类法的高低易发区SCAI值的比值更大，差异更为显著，故ISO聚类法分级效果优于Kmeans聚类法。综上，集成模型引入ISO聚类算法后，相比于自然断然法和Kmeans聚类可以提升精度，其中FR-RF-ISO耦合模型分级效果最好。
图6 基于ISO聚类、自然断点法和Kmeans聚类的滑坡易发性分级结果

Fig. 6 Results of landslide susceptibility classification based on ISO clustering, Natural Break Classification and Kmeans clustering

4.4 滑坡易发性空间分布

如图6所示，IV-RF-ISO、CF-RF-ISO和FR-RF-ISO 3种耦合模型的评价结果在空间分布上大体类似，极高和高易发性区域主要集中在宁南县南部、东部和中部部分区域，该区域地形起伏较大，断层分布密集，人类工程活动频繁，土壤抗剪能力较差，有利于滑坡的发育。极低和低易发性区域主要集中在宁南县西部和北部，该区域人口分布稀疏，较小受到人类工程活动影响、植被覆盖密集，土壤抗剪能力强。如表4所示，滑坡点数量和滑坡密度与易发性等级呈正相关，易发性等级越高，区域滑坡点个数越多，滑坡密度越大。
表4 各模型的滑坡易发性分级结果

Tab. 4 Results of landslide susceptibility grading for each model

模型 等级 面积/km2 滑坡数 滑坡密度/（个/km2） SCAI值
IV-RF-ISO 极低 538.80 0 0.00 **
低 376.95 8 0.02 10.58
中 296.81 25 0.08 2.10
高 257.83 79 0.31 0.50
极高 208.27 264 1.27 0.10
IV-RF-NBC 极低 567.15 0 0.00 **
低 368.83 10 0.03 8.10
中 287.21 23 0.08 2.14
高 248.71 77 0.31 0.48
极高 206.76 266 1.29 0.10
IV-RF-Kmeans 极低 981.23 10 0.01 57.36
低 232.67 22 0.09 1.47
中 240.66 72 0.30 0.48
高 118.88 102 0.86 0.08
极高 105.22 170 1.62 0.04
CF-RF-ISO 极低 571.99 0 0.00 **
低 358.22 9 0.03 8.49
中 290.09 30 0.10 1.67
高 244.21 82 0.34 0.43
极高 214.16 255 1.19 0.11
CF-RF- NBC 极低 607.33 0 0.00 **
低 345.28 12 0.03 5.92
中 292.78 33 0.11 1.55
高 230.92 85 0.37 0.37
极高 202.35 246 1.22 0.10
CF-RF-Kmeans 极低 1 027.36 16 0.02 39.30
低 226.44 34 0.15 0.90
中 214.91 74 0.34 0.37
高 94.95 84 0.88 0.06
极高 115.00 168 1.46 0.05
FR-RF-ISO 极低 557.62 0 0.00 **
低 353.14 5 0.01 14.86
中 298.64 20 0.07 2.66
高 253.18 78 0.31 0.49
极高 216.09 273 1.26 0.10
FR-RF-NBC 极低 594.16 0 0.00 **
低 341.42 6 0.02 11.57
中 290.11 25 0.09 2.01
高 243.90 76 0.31 0.47
极高 209.07 269 1.29 0.10
FR-RF-Kmeans 极低 1 004.94 9 0.01 66.85
低 232.31 27 0.12 1.19
中 215.31 62 0.29 0.45
高 124.31 117 0.94 0.08
极高 101.78 161 1.58 0.04

注：**表示极低等级滑坡点在易发性分区的面积占比为0，无法作为SCAI公式的分母。

5 结论与讨论

5.1 结论

滑坡是中国最危险的自然灾害之一，它会造成巨大的生命财产损失。本文以宁南县为研究区，将IV、CF和FR 3种统计方法分别和随机森林模型结合，并使用ISO聚类法对其进行分级，提出了一种滑坡易发性综合评估方法，并进行了精度对比分析，主要结论如下：
（1）IV-RF、CF-RF和FR-RF 3种集成模型性能均优于单一模型，其准确率和F1分数均大于0.85，AUC值均大于0.9，集成模型较好的解决了IV模型和CF模型对非滑坡样本进行了较多的错误分类问题。 3种集成模型的综合性能排序为FR-RF>IV-RF>CF-RF，FR-RF模型预测效果最优，其准确率、F1分数和AUC值分别为0.911、0.912和0.965，较单一模型分别提升了0.095、0.096和0.074。
（2）ISO聚类法的高低易发区SCAI值的比值更大，差异更为显著，综合分级效果优于自然断点法和Kmeans聚类法，其中FR-RF-ISO模型分级效果最好。
（3）IV-RF-ISO、CF-RF-ISO和FR-RF-ISO模型的评价结果在空间分布上大体类似，极高和高易发性区域主要集中在宁南县南部、东部和中部部分区域。评价结果可以为当地滑坡防治和灾害管理提供科学依据。

5.2 讨论

5.2.1 不确定性分析

集成模型由统计方法和机器学习模型耦合构成，统计方法能够定量计算影响因子对滑坡易发性的空间影响，将其作为机器学习模型的输入条件。不同统计方法中，CF比IV和FR预测精度更高（AUC=0.895），更能反映影响因子对滑坡发育的空间信息差异。FR法的计算方法简单直接，且具有较高的预测精度。IV法来评估不同影响因子对滑坡发生的预测能力，但未能充分体现各因子与滑坡的空间相关性。RF可以识别数据中的非线性规律，处理高维数据，适用于滑坡易发性建模。将IV、CF和FR耦合RF后，易发性评价精度得到较大提升，同时各精度评定指标均表现出一致的规律，集成模型的准确率、F1分数和AUC值的大小排序均为FR-RF>IV-RF>CF-RF，表明FR与RF的结合效果最好，综合表现最优。
自然断点法是使用最多的易发性分级方法，它基于数据的分布特点，将数据按照自然分界点分成不同的组，本研究中SCAI值结果显示，它的分级效果具有较好的精度。Kmeans聚类通过最小化数据点与其所属簇的质心之间的距离对易发性进行分级，本研究中其极低易发性等级面积显著大于另外两种聚类算法，导致极低易发性区也存在部分滑坡点，分级效果不如ISO聚类算法。ISO聚类算法表现出最优秀的分级能力， SCAI值的高低易发性等级差异最显著，它根据数据的距离和聚类数目进行迭代分组，然后根据各组的均值和标准差来合并或拆分群集，直到满足停止条件。研究结果表明， ISO聚类算法有可能代替自然断点法成为提高滑坡易发性精度的有效方式。
虽然本研究中引入的ISO聚类算法在易发性中表现出比自然断点法更好的精度，但不代表ISO聚类一定优于自然断点法。由于研究区和实验样本的限制，难以覆盖所有类型的集成建模，在不同的样本选取比例、不同的空间尺度、不同的指标体系等情况下，很难保证ISO聚类的表现一定优于自然断点法，这也是本研究的不确定性来源。但是，本文的意义主要在于提出统计方法、机器学习模型和聚类算法结合的滑坡易发性综合评价方法，并论证聚类算法在集成建模的有效性，通过引入ISO聚类算法，为提高滑坡易发性评价精度提供新的视角。

5.2.2 研究存在的问题及展望

由于滑坡的演化机制复杂，影响滑坡的因素众多，相关数据获取困难，本文所使用的易发性评价指标可能并不全面，后期可考虑气象、地下水、岩性、气温、地震等因子，建立更全面的指标体系，提高评价结果准确性。同时，本研究仅选用了信息量、确定系数和频率比3种统计方法，聚类方法仅选用ISO聚类、自然断点法和Kmeans聚类，对于其余的统计方法和聚类方法并没进行讨论。未来的研究可以考虑引入更多种类的统计方法、聚类方法和机器学习模型，如证据权法、信息熵、回归模型、支持向量机、深度学习、期望最大化（EM）聚类、高斯混合模型（GMM）聚类等，开展相关模型对比研究。
滑坡易发性评价是一项复杂而多样化的任务，需要综合应用多种方法和技术，复杂条件下的滑坡易发性评价不仅仅依赖于模型的性能，包括地质条件、气候特征、土地利用和人类活动等，这些因素的相互作用可能导致评价过程的挑战和复杂性，本文由于实验的侧重点是针对方法模型的研究，对于因子与滑坡的相关性分析，在本次研究中我们并未充分展开，在未来的研究中，我们需要更加关注因子与滑坡之间的相关性，避免无关因子对结果造成的污染。同时，本文按照5比5的正负样本选取方式进行实验设计，而正负样本不同的选取比例会造成不同的结果，后续研究可从此方面着手，完善滑坡易发性评价方法。
综上所述，我们还需不断探索更加全面、有效的评价方法，以更好地为滑坡预测和防治工作提供科学支持和指导。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
朱庆, 曾浩炜, 丁雨淋, 等. 重大滑坡隐患分析方法综述[J]. 测绘学报, 2019, 48(12):1551-1561.

DOI

[ Zhu Q, Zeng H W, Ding Y L, et al. A review of major potential landslide hazards analysis[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(12):1551-1561. ]

DOI

[2]
中华人民共和国应急管理部. 国家减灾委员会关于印发《“十四五”国家综合防灾减灾规划》的通知:国减发〔2022〕1号[EB/OL].(2022-06-19)[2023-09-23].

[ Ministry of Emergency Management of the People's Republic of China. The National Disaster Reduction Commission on the issuance of the "14th five year plan for national comprehensive disaster prevention and reduction": Guo Jian Fa [2022] No.1[EB/OL] (2022-06-19)[2023-09-23]https://www.mem.gov.cn/gk/zfxxgkpt/fdzdgknr/202207/t20220721_418698.shtm

[3]
周侯伯, 肖桂荣, 林炫歆, 等. 基于特征筛选与差分进化算法优化的滑坡危险性评估方法[J]. 地球信息科学学报, 2022, 24(12):2373-2388.

DOI

[ Zhou H B, Xiao G R, Lin X X, et al. Landslide hazard assessment method based on feature screening and differential evolution algorithm optimization[J]. Journal of Geo-Information Science, 2022, 24(12):2373-2388. ] DOI:10.13577/j.jnd.2021.0321

[4]
Fell R, Corominas J, Bonnard C, et al. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning[J]. Engineering Geology, 2008, 102(3/4):85-98. DOI:10.1016/j.enggeo.2008.03.022

[5]
Chen Y, Dong J L, Guo F, et al. Review of landslide susceptibility assessment based on knowledge mapping[J]. Stochastic Environmental Research and Risk Assessment, 2022, 36(9):2399-2417. DOI:10.1007/s00477-021-02165-z

[6]
E.A. Sezer, H.A. Nefeslioglu, T. Osna. An expert-based landslide susceptibility mapping (LSM) module developed for Netcad Architect Software[J]. Computers & Geosciences, 2017, 98:26-37. DOI:10.1016/j.cageo.2016.10.001

[7]
Lyu H, Shen J, Arulrajah A. Assessment of geohazards and preventative countermeasures using AHP incorporated with GIS in Lanzhou, China[J]. Sustainability, 2018, 10:304. DOI:10.3390/SU10020304

[8]
Shahabi H, Hashim M, Bin Ahmad B. Remote sensing and GIS-based landslide susceptibility mapping using frequency ratio, logistic regression, and fuzzy logic methods at the central Zab Basin, Iran[J]. Environmental Earth Sciences, 2015, 73(12):8647-8668. DOI:10.1007/s12665-015-4028-0

[9]
Hu Q, Zhou Y, Wang S, et al. Machine learning and fractal theory models for landslide susceptibility mapping: Case study from the Jinsha River Basin[J]. Geomorphology, 2020, 351:106975. DOI:10.1016/j.geomorph.2019.106975

[10]
熊俊楠, 朱吉龙, 苏鹏程, 等. 基于GIS与信息量模型的溪洛渡库区滑坡危险性评价[J]. 长江流域资源与环境, 2019, 28(3):700-711.

[ Xiong J N, Zhu J L, Su P C, et al. Risk assessment of landslide in the xiluodu reservoir area based on GIS and information value method[J]. Resources and Environment in the Yangtze Basin, 2019, 28(3):700-711. ] DOI:10.11870/cjlyzyyhj201903021

[11]
庄建琦, 崔鹏, 葛永刚, 等“5.12"汶川地崩塌滑坡危险性评价一一以都汶公路沿线为例[J]岩石力学与工程学报, 2010, 29(2):3736-3742.

[ Zhuang J Q, Cui P, Ge Y G, et al. Risk assessment of collapses and landslides caused by 5.12 Wenchuan earthquake: A case study of Dujiangyan-Wenchuan highway[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2):3736-3742.1 ]

[12]
冯杭建, 周爱国, 唐小明, 等. 基于确定性系数的降雨型滑坡影响因子敏感性分析[J]. 工程地质学报, 2017, 25(2):436-446.

[ Feng H J, Zhou A G, Tang X M, et al. Susceptibility analysis of factors controlling rainfall-triggered landslides using certainty factor method[J]. Journal of Engineering Geology, 2017, 25(2): 436-446. ] DOI: 10.13544/j.cnki.jeg.2017.02.022

[13]
Zhang Y X, Lan H X, Li L P, et al. Optimizing the frequency ratio method for landslide susceptibility assessment: A case study of the Caiyuan Basin in the southeast mountainous area of China[J]. Journal of Mountain Science, 2020, 17(2):340-357. DOI:10.1007/s11629-019-5702-6

[14]
刘璐瑶, 高惠瑛. 基于证据权与Logistic回归模型耦合的滑坡易发性评价[J]. 工程地质学报, 2023, 31(1):165-175.

[ Liu L Y, Gao H Y. Landslide susceptibility assessment based on coupling of woe model and logistic regression model[J]. Journal of Engineering Geology, 2023, 31(1): 165-175.]. DOI:10.13544/j.cnki.jeg.2020-482

[15]
张钟远, 邓明国, 徐世光, 等. 镇康县滑坡易发性评价模型对比研究[J]. 岩石力学与工程学报, 2022, 41(1):157-171.

[ Zhang Z Y, Deng M G, Xu S G, et al. Comparison of landslide susceptibility assessment models in Zhenkang County, Yunnan Province, China[J]. Chinese Journal of Rock Mechanics and Engineering, 2022, 41(1):157-171. ] DOI:10.13722/j.cnki.jrme.2021.0360

[16]
吴润泽, 胡旭东, 梅红波, 等. 基于随机森林的滑坡空间易发性评价:以三峡库区湖北段为例[J]. 地球科学, 2021(1):321-330.

[ Wu R Z, Hu X D, Mei H B, et al. Spatial susceptibility assessment of landslides based on random forest: A case study from Hubei section in the Three Gorges Reservoir area[J]. Earth Science, 2021(1):321-330. ]

[17]
Althuwaynee O F, Pradhan B, Park H J, et al. A novel ensemble decision tree-based CHi-squared Automatic Interaction Detection (CHAID) and multivariate logistic regression models in landslide susceptibility mapping[J]. Landslides, 2014, 11(6):1063-1078. DOI:10.1007/s10346-014-0466-0

[18]
刘纪平, 梁恩婕, 徐胜华, 等. 顾及样本优化选择的多核支持向量机滑坡灾害易发性分析评价[J]. 测绘学报, 2022, 51(10):2034-2045.

DOI

[ Liu J P, Liang E J, Xu S H, et al. Multi-kernel support vector machine considering sample optimization selection for analysis and evaluation of landslide disaster susceptibility[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(10): 2034-2045.] DOI: 10.16441/j.cnki.hdxb.20200247

[19]
黄武彪, 丁明涛, 王栋, 等. 基于层数自适应加权卷积神经网络的川藏交通廊道沿线滑坡易发性评价[J]. 地球科学, 2022, 47(6):2015-2030.

[ Huang W B, Ding M T, Wang D, et al. Evaluation of landslide susceptibility based on layer adaptive weighted convolutional neural network model along Sichuan-Tibet traffic corridor[J]. Earth Science, 2022, 47(6):2015-2030. ] DOI:10.3969/j.issn.1672-9528.2021.04.032

[20]
Huang F, Cao Z, Guo J, et al. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping[J]. CATENA, 2020, 191:104580. DOI:10.1016/j.catena.2020.104580

[21]
Reichenbach P, Rossi M, Malamud B D, et al. A review of statistically-based landslide susceptibility models[J]. Earth-Science Reviews, 2018, 180:60-91. DOI:10.1016/j.earscirev.2018.03.001

[22]
Umar Z, Pradhan B, Ahmad A, et al. Earthquake induced landslide susceptibility mapping using an integrated ensemble frequency ratio and logistic regression models in West Sumatera Province, Indonesia[J]. CATENA, 2014, 118:124-135. DOI:10.1016/j.catena.2014.02.005

[23]
Chen W, Xie X, Peng J, et al. GIS-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method[J]. CATENA, 2018, 164:135-149. DOI:10.1016/j.catena.2018.01.012

[24]
罗路广, 裴向军, 黄润秋, 等. GIS支持下CF与Logistic回归模型耦合的九寨沟景区滑坡易发性评价[J]. 工程地质学报, 2021, 29(2):526-535.

[ Luo L G, Pei X J, Huang R Q, et al. Landslide susceptibility assessment in Jiuzhaigou scenic area with GIS based on certainty factor and logistic regression model[J]. Journal of Engineering Geology, 2021, 29(2):526-535. ] DOI:10.13544/j.cnki.jeg.2019-202

[25]
徐胜华, 刘纪平, 王想红, 等. 熵指数融入支持向量机的滑坡灾害易发性评价方法——以陕西省为例[J]. 武汉大学学报(信息科学版), 2020, 45(8):1214-1222.

[ Xu S H, Liu J P, Wang X H, et al. Landslide susceptibility assessment method incorporating index of entropy based on support vector machine: A case study of Shaanxi Province[J]. Geomatics and Information Science of Wuhan University, 2020, 45(8):1214-1222. ] DOI:10.13203/j.whugis20200109

[26]
王世宝, 庄建琦, 樊宏宇, 等. 基于频率比与集成学习的滑坡易发性评价——以金沙江上游巴塘—德格河段为例[J]. 工程地质学报, 2022, 30(3):817-828.

[ Wang S B, Zhuang J Q, Fan H Y, et al. Evaluation of landslide susceptibility based on frequency ratio and ensemble learning—Taking the Batang-Dege section in the upstream of Jinsha River as an example[J]. Journal of Engineering Geology, 2022, 30(3):817-828. ] DOI:10.13544/j.cnki.jeg.2020-639

[27]
林炫歆, 肖桂荣, 周侯伯. 顾及土地利用动态变化的滑坡易发性评估方法[J]. 地球信息科学学报, 2023, 25(5):953-966.

DOI

[ Lin X X, Xiao G R, Zhou H B. Landslide susceptibility assessment method considering land use dynamic change[J]. Journal of Geo-Information Science, 2023, 25(5):953-966. ] DOI:10.5846/stxb202106201639

[28]
田乃满, 兰恒星, 伍宇明, 等. 人工神经网络和决策树模型在滑坡易发性分析中的性能对比[J]. 地球信息科学学报, 2020, 22(12):2304-2316.

DOI

[ Tian N M, Lan H X, Wu Y M, et al. Performance comparison of BP artificial neural network and CART decision tree model in landslide susceptibility prediction[J]. Journal of Geo-information Science, 2020, 22(12):2304-2316. ] DOI:10.13544/j.cnki.jeg.2014.06.029

[29]
谭玉敏, 郭栋, 白冰心, 等. 基于信息量模型的涪陵区地质灾害易发性评价[J]. 地球信息科学学报, 2015, 17(12):1554-1562.

DOI

[ Tan Y M, Guo D, Bai B X, et al. Geological hazard risk assessment based on information quantity model in Fuling district, Chongqing city, China[J]. Journal of Geo-Information Science, 2015, 17(12): 1554-1562.]. DOI:10.3724/SP.J.1047.2015.01554

[30]
张晓东. 基于遥感和GIS的宁夏盐池县地质灾害风险评价研究[D]. 北京: 中国地质大学(北京).

[ Zhang X D. Risk assessment of geological hazards in Yanchi County of Ningxia based on remote sensing and GIS[D]. Beijing: China University of Geosciences.]

[31]
Jaafari A, Najafi A, Pourghasemi H R, et al. GIS-based frequency ratio and index of entropy models for landslide susceptibility assessment in the Caspian forest, northern Iran[J]. International Journal of Environmental Science and Technology, 2014, 11(4):909-926. DOI:10.1007/s13762-013-0464-0

[32]
Breiman L. Random forests[J]. Machine Learning, 2001, 45(1):5-32. DOI:10.1023/A:1010933404324

[33]
Hong H, Miao Y, Liu J, et al. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping[J]. CATENA, 2019, 176:45-64. DOI:10.1016/j.catena.2018.12.035

[34]
Pokharel B, Althuwaynee O F, Aydda A, et al. Spatial clustering and modelling for landslide susceptibility mapping in the north of the Kathmandu Valley, Nepal[J]. Landslides, 2021, 18(4):1403-1419. DOI:10.1007/s10346-020-01558-5

[35]
吴宏阳, 周超, 梁鑫. 基于样本优化策略研究的滑坡易发性评价[J/OL]. 武汉大学学报(信息科学版), 2023. DOI:10.13203/J.whugis20220527.

[ Wu H Y, Zhou C, Liang X, et al. Evaluation of landslide susceptibility based on sample optimization strategy research[J]. Geomatics and Information Science of Wuhan University, 2023. DOI: 10.13203/J.whugis20220527]

[36]
Wang J, Cheng W M, Zhou C H, et al. Automatic mapping of lunar landforms using DEM-derived geomorphometric parameters[J]. Journal of Geographical Sciences, 2017, 27(11):1413-1427. DOI:10.1007/s11442-017-1443-z

[37]
Ariel N, Tal S, Eli A. Mapping areas prone to piping using random forest with key explanatory variables[J]. Geoderma, 2023, 431:116367. DOI:10.1016/j.geoderma.2023.116367

[38]
仉文岗, 何昱苇, 王鲁琦, 等. 基于水系分区的滑坡易发性机器学习分析方法:以重庆市奉节县为例[J]. 地球科学, 2023(5):2024-2038.

[ Zhang W G, He Y W, Wang L Q, et al. Machine learning solution for landslide susceptibility based on hydrographic division: Case study of Fengjie County in Chongqing[J]. Earth Science, 2023(5):2024-2038. ]

[39]
Swets J A. Measuring the accuracy of diagnostic systems[J]. Science, 1988, 240(4857):1285-1293. DOI:10.1126/science.3287615

PMID

[40]
Conforti M, Robustelli G, Muto F, et al. Application and validation of bivariate GIS-based landslide susceptibility assessment for the Vitravo River catchment (Calabria, south Italy)[J]. Natural Hazards, 2012, 61(1):127-141. DOI:10.1007/s11069-011-9781-0

[41]
程振全. 宁南县干田坝滑坡风险评价[D]. 西安: 长安大学.

[ Cheng Z Q. Risk assessment of gantianba landslide in Ningnan County[D]. Xi'an: Changan University. ]

[42]
Wang L Q, Zhang Z H, Huang B L, et al. Triggering mechanism and possible evolution process of the ancient Qingshi landslide in the Three Gorges Reservoir[J]. Geomatics, Natural Hazards and Risk, 2021, 12(1):3160-3174. DOI:10.1080/19475705.2021.1998230

[43]
李晨阳; 王新春; 何春珍; 等. 全国1∶200000数字地质图(公开版)空间数据库(V1).中国地质调查局发展研究中心;中国地质调查局[创建机构, 1957.全国地质资料馆[传播机构],2019-06-30.10.23650/data.A.2019.NGA120157.K1.1.1.V1;

[ Li C Y, Wang X C, He C Z, et al. Spatial database of national 1:200 000 digital geologic map (public version) (V1). China Geological Survey Development Research Center; China Geological Survey [Creating Agency], 1957.National Geological Data Library [Disseminating Agency],2019-06-30.10.23650/data.A.2019.NGA120157.K1.1.1.V1;

[44]
李文彬, 范宣梅, 黄发明, 等. 不同环境因子联接和预测模型的滑坡易发性建模不确定性[J]. 地球科学, 2021, 46(10):3777-3795.

[ Li W B, Fan X M, Huang F M, et al. Uncertainties of landslide susceptibility modeling under different environmental factor connections and prediction models[J]. Earth Science, 2021, 46(10):3777-3795. ] DOI: 10.16152/j.cnki.xdxbzr.2020-03-007

[45]
李松林, 许强, 汤明高. 三峡库区滑坡空间发育规律及其关键影响因子[J]. 地球科学, 2020, 45(1):341-354.

[ Li S L, XU Q, TANG M G. Study on spatial distribution and key influencing factors of landslides in Three Gorges reservoir area[J]. Earth Science, 2020, 45(1):341-354. ]

[46]
王世宝, 庄建琦, 郑佳, 等. 基于深度学习的CZ铁路康定—理塘段滑坡易发性评价[J]. 工程地质学报, 2022, 30(3):908-919.

[ Wang S B, Zhuang J Q, Zheng J, et al. Landslide susceptibility evaluation based on deep learning along Kangding-Litang section of cz railway[J]. Journal of Engineering Geology, 2022, 30(3):908-919. ] DOI: 10.13544/j.cnki.jeg.2021-0115

[47]
黄发明, 曹昱, 范宣梅, 等. 不同滑坡边界及其空间形状对滑坡易发性预测不确定性的影响规律[J]. 岩石力学与工程学报, 2021, 40(S02):3227-3240.

[ Huang F M, Cao Y, Fan X M, et al. Effects of different landslide boundaries and their spatial shapes on the uncertainty of landslide susceptibility prediction[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(S02):3227-3240. ]

[48]
刘佳, 伍宇明, 高星, 等. 基于GEE和U-net模型的同震滑坡识别方法[J]. 地球信息科学学报, 2022, 24(7):1275-1285.

DOI

[ Liu J, Wu Y M, Gao X, et al. Image recognition of Co-seismic landslide based on GEE and U-net neural network[J]. Journal of Geo-Information Science, 2022, 24(7):1275-1285. ] DOI:10.15961/j.jsuese.202000529

[49]
苏巧梅, 赵尚民, 郭建立. 霍西煤矿区地表滑坡灾害敏感性数值建模与等级划分[J]. 地球信息科学学报, 2017, 19(12):1613-1622.

DOI

[ Su Q M, Zhao S M, Guo J L. Numerical modeling and degree division to landslide susceptibility in the ground surface of huoxi coal mine area[J]. Journal of Geo-information Science, 2017, 19(12): 1613-1622.]

[50]
麦鉴锋, 冼宇阳, 刘桂林. 气候变化情景下广东省降雨诱发型滑坡灾害潜在分布及预测[J]. 地球信息科学学报, 2021, 23(11):2042-2054.

DOI

[ Mai J F, Xian Y Y, Liu G L. Predicting potential rainfall-triggered landslides sites in Guangdong Province (China)using MaxEnt model under climate changes scenarios[J]. Journal of Geo-Information Science, 2021, 23(11):2042-2054. ] DOI:10.13379/j.issn.1003-8825.202003037

[51]
黄发明, 殷坤龙, 蒋水华, 等. 基于聚类分析和支持向量机的滑坡易发性评价[J]. 岩石力学与工程学报, 2018, 37(1):156-167.

[ Huang F M, Yin K L, Jiang S H, et al. Landslide susceptibility assessment based on clustering analysis and support vector machine[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1):156-167. ] DOI:10.13722/j.cnki.jrme.2017.0824

[52]
Quevedo R P, Velastegui-Montoya A, Montalván-Burbano N, et al. Land use and land cover as a conditioning factor in landslide susceptibility: A literature review[J]. Landslides, 2023, 20(5):967-982. DOI:10.1007/s10346-022-02020-4

[53]
兰恒星, 伍法权, 周成虎, 等. 基于GIS的云南小江流域滑坡因子敏感性分析[J]. 岩石力学与工程学报, 2002, 21(10):1500-1506.

[ Lan H X, Wu F Q, Zhou C H, et al. Analysis on susceptibility of GIS based landslide triggering factors in Yunnan Xiaojiang watershed[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(10):1500-1506. ] DOI:10.3321/j.issn:1000-6915.2002.10.014

[54]
Chen W, Zhang S, Li R, et al. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling[J]. Science of the Total Environment, 2018, 644:1006-1018. DOI:10.1016/j.scitotenv.2018.06.389

Options
文章导航

/

〈 〉