EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 3: 693 - 708

DOI: https://doi.org/10.12082/dqxxkx.2024.230675

遥感科学与应用技术

考虑局部方差互信息和梯度一致性的改进SFIM遥感图像融合方法

  • 王淑香 ,
  • 金飞 , * ,
  • 林雨准 ,
  • 左溪冰 ,
  • 刘潇
展开
  • 信息工程大学 地理空间信息学院, 郑州 450001
*金飞（1984— ），男，河南临颍人，博士，副教授，主要从事遥感图像智能解译研究。E-mail:

王淑香（1982— ），女，河南汝州人，硕士，副教授，主要从事遥感图像处理研究。E-mail:

Copy editor: 蒋树芳

收稿日期: 2023-11-14

  修回日期: 2024-01-05

  网络出版日期: 2024-03-31

基金资助

河南省自然科学基金面上项目(222300420592)

收起

An Improved SFIM Remote Sensing Image Fusion Method Considering Local Variance Mutual Information and Gradient Consistency

  • WANG Shuxiang ,
  • JIN Fei , * ,
  • LIN Yuzhun ,
  • ZUO Xibing ,
  • LIU Xiao
Expand
  • Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, China
*JIN Fei, E-mail:

Received date: 2023-11-14

  Revised date: 2024-01-05

  Online published: 2024-03-31

Supported by

Natural Science Foundation of Henan Province(222300420592)

Fold

摘要

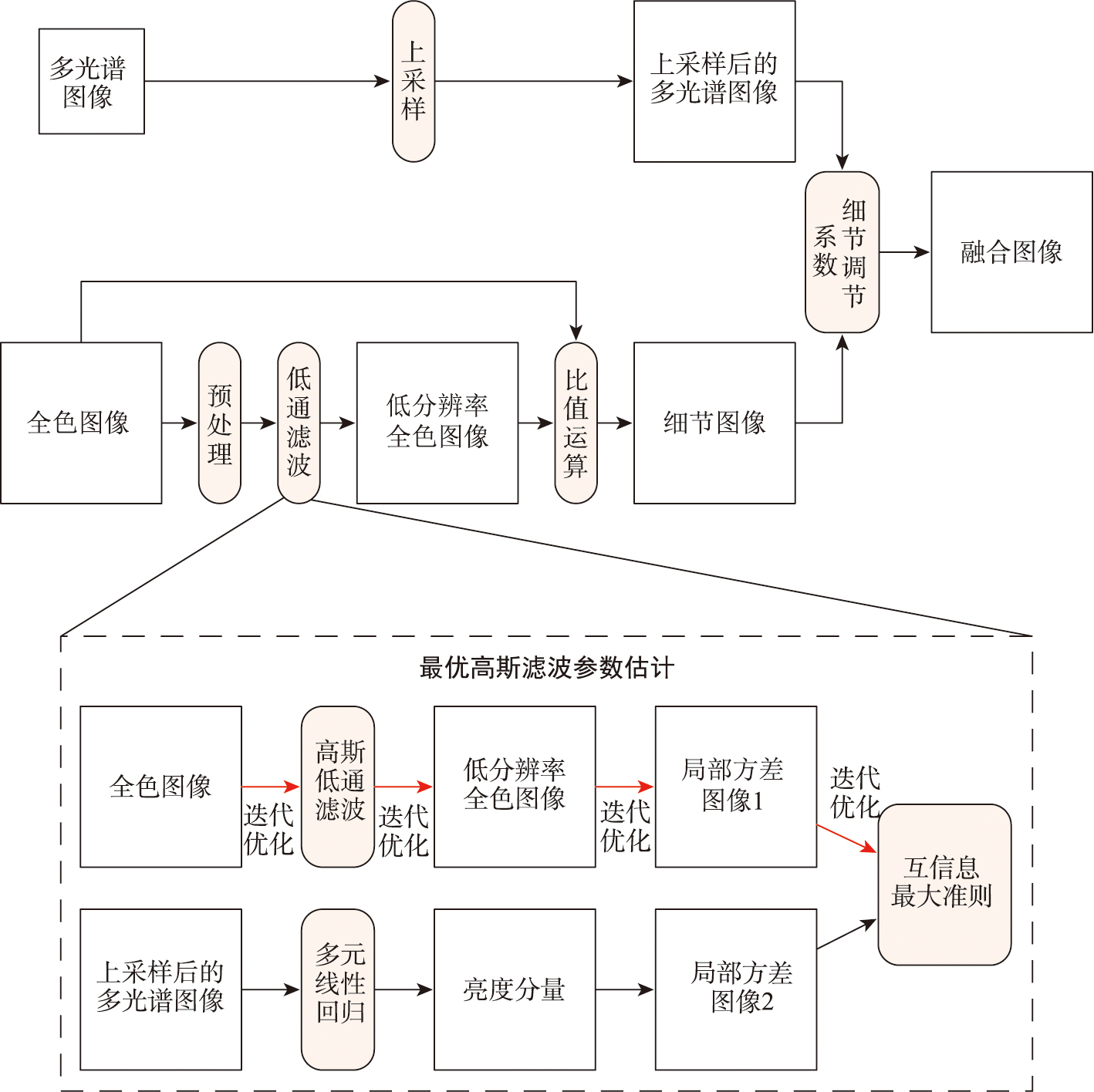
全色图像和多光谱图像由于光谱和空间尺度上的差异，融合结果容易出现光谱失真或空间失真。如何同时实现两个尺度上的对齐，是提高融合效果的关键。传统的SFIM（Smoothing Filter-based Intensity Modulation）遥感图像融合方法可以保证光谱尺度上的一致，但在衡量空间尺度一致上还不够精确。针对此问题，本文提出了一种基于局部方差互信息的空间尺度对齐方法，并在平均梯度一致性的约束下进一步改进SFIM方法。该方法首先对多光谱各波段线性拟合生成多光谱强度图像，并对高分辨率全色图像进行高斯低通滤波，改变滤波参数循环计算2幅图像的局部方差图像间的互信息，当互信息最大时，高斯滤波参数为最佳滤波估计参数；然后，用该高斯滤波器卷积高分辨率全色图像，得到与多光谱图像空间尺度一致的低分辨率全色图像；之后，高低分辨率全色图像间比值处理得到细节图像，以高分辨率全色图像平均梯度为基准，引入调节系数控制细节图像的注入量；最后，细节图像、调节系数与多光谱图像相乘得到融合图像。为验证本文方法的有效性，在IKONOS和Quickbird两种数据集的植被区、建筑区和混合区3个不同场景六组图像开展融合实验。实验结果表明，对于KONOS数据，本文方法3组实验在光谱保持指标SAM上均位于第二，信息量EN有2组第一，对于Quickbird数据，本文方法3组实验在SAM、EN和AG3个指标上均为最优，具有较好的光谱保持能力和信息丰富程度；空间信息保持指标SCC值虽非最佳，但与SCC值最佳的AGSFIM方法相比， 4组实验的SAM、EN和AG这3个指标整体明显优于对方，而与SCC值相近的GSA或SFIM方法对比，本文方法在6组实验中其他3个指标的也均优于对方，平均提升了13.39%、39.52%和34.03%。同时，本文方法在目视效果上也有较为不错的表现，融合真彩色图像与原始真图像彩色差异较小，图像清晰度基本近似全色图像。融合场景方面，本文方法对于植被为主或混合区域，光谱保持优势明显，图像信息量较为丰富；以建筑为主的场景，融合结果的光谱、 信息的丰富程度和清晰度也具有不错效果。

关键词： 局部方差图像; 互信息; 高斯滤波; 平均梯度; 细节注入; SFIM模型; 遥感; 图像融合

本文引用格式

王淑香 , 金飞 , 林雨准 , 左溪冰 , 刘潇 . 考虑局部方差互信息和梯度一致性的改进SFIM遥感图像融合方法[J]. 地球信息科学学报, 2024 , 26(3) : 693 -708 . DOI: 10.12082/dqxxkx.2024.230675

Abstract

Due to differences in spectral and spatial scales, the fusion results of panchromatic and multispectral images often have spectral or spatial distortion. How to achieve alignment on both scales simultaneously is crucial for enhancing fusion performance. The traditional Smoothing Filter-based Intensity Modulation (SFIM) remote sensing image fusion method can ensure consistency on the spectral scale but is not precise enough in measuring spatial scale consistency. To address this issue, this paper proposes a spatial scale alignment method considering local variance mutual information and further improves the SFIM method with the constraint of average gradient consistency. This method first linearly fits each band of the multispectral images to generate an intensity image and applies Gaussian low-pass filtering to high-resolution panchromatic images. By iteratively calculating the mutual information between the local variance images of the two images, the optimal filtering estimation parameters are determined when the mutual information is maximized. Then, the Gaussian filter is used to convolve the high-resolution panchromatic image, obtaining a low-resolution panchromatic image that matches the spatial scale of the multispectral images. The detail image is obtained by processing the ratio between the high-resolution and low-resolution panchromatic images. Based on the average gradient of high-resolution panchromatic images, an adjustment coefficient is introduced to control the amount of detail injection. Finally, the fusion image is obtained by multiplying the detail image, modulation factor, and multispectral image. To validate the effectiveness of this method, fusion experiments are conducted on six sets of images from three different scenes: vegetation area, building area, and mixed area of the IKONOS and Quickbird datasets. For the IKONOS data, the three experimental groups of our method all rank second in terms of spectral retention index SAM, and the information content EN ranks first in two groups. For the Quickbird data, the proposed method performs best in terms of SAM, EN, and AG indices in all three sets of experiments, demonstrating good spectral preservation and information richness. The proposed method outperforms the AGSFIM method in terms of SAM, EN, and AG in four sets of experiments, though the AGSFIM method obtains the highest spatial information preservation index SCC. Compared with the GSA or SFIM methods with similar SCC values, the proposed method shows an average improvement of 13.39%, 39.52%, and 34.03% for the other three indicators in the six experiments. In terms of fusion scenes, the proposed method performs well in scenes where vegetation or mixed areas dominate, while scenes dominated by buildings show the advantages of the proposed method in spectral methods. The abundance and clarity of image information also satisfactory, especially in fusion scenes with a higher proportion of vegetation. Moreover, the proposed method also exhibits good visual appearance. There is minimal color difference between the fused true-color image and the original true image and acomparable image clarity against the panchromatic image. In terms of fusion scenes, the method in this paper demonstrates a clear advantage in spectral preservation for vegetation-dominated or mixed areas, with a relatively rich amount of image information; for scenes dominated by buildings, the fusion results also show good performance in terms of spectral richness, information content, and clarity.

Key words： local variance image; mutual information; gaussian filtering; average gradient; detail injection; SFIM model; remote sensing; image fusion

1 引言

受限于衍射极限、调制传递函数、信噪比等因素的影响，遥感系统对地观测成像时难以同时兼顾理想的空间分辨率、光谱分辨率和时间分辨率，为了解决应用场景对光谱、空间、时相等多维丰富信息需求的矛盾，遥感图像融合技术应运而生。其中，全色图像与多光谱图像融合是最具代表性的应用之一，可以实现光谱信息与空间信息的优势互补，最终获取空间分辨率高、光谱信息丰富的融合图像。
传统的遥感图像融合方法分为三大类：基于分量替换（Component Substitution,CS）的融合方法、基于多分辨率分析（Multi-Resolution Analysis，MRA）的融合方法、基于模型优化（Model-Based，MB）的融合方法[1]。其中，最为经典和相对成熟的是分量替换法，包括颜色空间变换法[2]（Hue Intensity Saturation, HIS）、主成分变换法（Principal Component Analysis，PCA）和格拉姆—施密特施密特正交变换法[3]（Gram-Schmidt，GS）及其改进的将波段响应函数考虑在内的光谱细节注入的自适应法[4] (GS adaptive，GSA)等，这类方法首先利用多光谱图像线性拟合全色分量，确保空间尺度不发生变化，然后通过高分辨率全色图像替换抵消多光谱图像的空间信息，用以提升融合结果的清晰度。然而，由于受到全色图像和多光谱图像之间线性相关局限的影响，融合图像光谱失真的共性问题依然存在。
为了改善光谱失真的问题，一类方法是将每个原始数据都分解为不同分辨率的一系列影像，在不同的分辨率上进行融合，最后进行逆变换获得融合后的影像，这就是多分辨率分析方法。常用的有基于频率域的高通滤波[5](High-Pass Filtering，HPF)、小波变换[6]、曲波变换[7]等，但这些方法在空间细节方面存在较严重的失真。
基于模型优化的方法在低分辨率多光谱图像和全色图像分别是高分辨率多光谱的图像的空间和光谱的退化的假设条件下，建立源图像和高分辨率多光谱图像之间的能量函数，优化求解获得融合图像。代表性方法包括基于梯度细节纠正的自适应模型[8]、光谱增强与和细节注入联合的变分优化模型[9]等。该类方法对光谱和空间退化过程进行显式建模，模型严密，更贴近真实场景情况[10]，但需要人为设置合适的先验信息和约束条件，计算复杂度较高。
为了克服传统方法的不足，图像融合领域的学者开始了基于深度学习的图像融合方法研究。唐霖峰等[11]重点关注图像融合深度学习采用的监督范式和网络架构，主要有卷积神经网络（Convolutional Neural Network，CNN）和生成对抗网络（Generative Adversarial Network, GAN）2种；邓良剑等[12]在同一框架下对比分析了7种典型卷积神经网络图像融合方法，为进一步研究奠定了基础；杨勇等[13]立足深度学习的可解释性，从经典方式和协同方式2个方面对深度学习在全色图像锐化中的研究进行系统的总结。这些研究表明，基于深度学习的方法因其优秀的特征提取能力，在融合效果上比传统方法更有优势。然而，由于缺乏标准数据集、网络模型规模大和时间复杂度高等问题，深度学习图像融合在实际应用中受到了一定影响。
综上所述，传统方法只需一对全色图像和多光谱图像输入即可获得融合图像，数据泛化性较好，在实际应用场景尤其是应急保障任务中更具实用性。传统图像融合方法关键在于如何在光谱特征改变最小的情况下，最大限度地提高空间分辨率[14]。基于空间域平滑滤波的强度调制[15]（Smoothing Filter-based Intensity Modulation，SFIM）融合方法光谱保真效果较好，模型简单，计算量小，具有较大的实用价值。该方法首先将高分辨率全色图像退化为低分辨率全色图像，确保光谱尺度上的一致，然后使用两者之间的比值图像，作为高低空间分辨率图像间的空间细节差异注入到原始多光谱图像中，从而得到高分辨率多光谱图像。Chen等[16]认为图像融合结果下采样后近似于低分辨率多光谱图像以保持光谱先验信息， Fang等[17]认为下采样的融合结果在细节上也要近似于低分辨多光谱图像，即在图像域和梯度域上，融合结果下采样后尽可能等于原始多光谱图像。同理，如果存在理想的低分辨率全色影像，在空间尺度应与原始多光谱图像保持一致，在光谱尺度应与高分辨率全色图像一致。可见，大部分基于SFIM模型的相关方法重点在如何得到退化的全色图像。然而，现有空间滤波退化方法由于基于图像域使得缺乏对空间尺度差异的精确描述；另外，没有顾及不同图像场景对空间细节注入的需求，容易造成融合结果空间信息融入不足或过量的情况。
针对此问题，本文在弱化全色图像和多光谱图像之间线性影响的基础上，以SFIM模型为基础，提出一种以梯度域高斯滤波参数估计为核心的改进SFIM遥感图像融合方法（Local Variant Mutual Information SFIM，LVMI-SFIM）。主要工作包括： ① 在使高分辨率图像退化的滤波参数估计上，引入梯度域局部方差图像，结合互信息相似性评价准则，计算最优高斯滤波参数估计，将其作用于高分辨率全色图像，以得到与多光谱图像空间尺度更为相似的低分辨率全色图像；② 针对不同场景对空间细节注入的需求，引入自适应注入系数，调控细节注入量。实验表明，本文方法融合图像光谱失真小、空间结果清晰，评价指标优于对比方法。

2 研究方法

本文方法技术路线图如图1所示。首先，预处理，将多光谱图像上采样，全色图像波段复制和直方图匹配预处理。其次，高斯低通滤波参数估计，考虑多光谱上采样图像合成的亮度分量图像和全色图像高斯滤波退化图像的局部方差图像，计算两者间的互信息，依据相似度最大原则进行最优高斯滤波参数估计。再次，细节图像获取，将最优高斯滤波器作用于预处理后的全色图像，得到低分辨率图像，将各波段对应的高低分辨率图像比值处理得到细节图像。然后，迭代计算细节注入系数，在高分辨率全色图像平均梯度的约束下，得到最优细节注入系数。最后，基于SFIM模型，将多光谱图像、细节图像和最优细节注入系数联合，得到融合的高分辨率多光谱图像HMS。
图1 本文方法基本流程

Fig.1 Flowchart of the LVMI_SFIM

2.1 SFIM模型

图像融合过程中，基于波段间比例的空间细节注入可以较好地保持光谱信息[18]。SFIM模型通过多光谱图像和细节注入量的乘积计算融合图像，波段间比例保持不变，聚焦于解决空间信息的融入问题，确保了模型的光谱保持能力，是一种高保真的图像融合方法[19]。融合模型为：
H M S = M S u p ∘ P P L + e p s
式中： ∘表示哈达玛积； H M S为融合后高分辨率多光谱图像； M S u p为多光谱上采样图像 P为高分辨率全色图像； P L为全色图形退化后的低分辨率全色图像； e p s是确保分母不为零的规则化常量。
从式（1）可以看出，基于SFIM模型图像融合的核心有2个方面：
（1）低分辨率全色图像计算
理想的 P L光谱特征应与全色图像 P一致，空间分辨率应与多光谱上采样图像 M S u p一致。目前对于理想的低分辨率全色图像求取没有统一的标准，已有的研究方法存在不同差异。经典的SFIM方法采用的是3×3均值滤波，MTF_SFIM方法为匹配卫星遥感器MTF的高斯滤波，AGSFIM方法使用了梯度一致性的多项式拟合估计高斯滤波参数[20]。这些各具优势，也存在这一定的局限性。
（2）空间细节注入量控制
不同图像具有成像波段、纹理结构等方面的特征差异，理想的细节注入量应随之动态调整，单一比值 P / （ P L + e p s ）处理难以响应不同图像的具体需求，细节注入量不足容易出现融合图像模糊、过大则会导致图像过于锐化，现有的SFIM模型相关融合方法并没有考虑。
本文分别针对SFIM模型这2个核心要素进行理论分析，基于具体问题设计优化改进的融合算法，改进的SFIM融合方法为：
H M S = M S u p ∘ g ∘ P i P i , L + e p s
式中： g为细节注入调节系数； P i , L为与多光谱各波段直方图匹配的低分辨率全色图像。

2.2 局部方差互信息的高斯滤波参数估计

通常， P L可由全色图像 P经过低通滤波得到，但在低通滤波时将涉及2个关键问题： ① 使用何种低通滤波器； ② 如何衡量滤波后图像 P L与 M S u p在空间尺度上的一致性。
对于低通滤波器的选择问题上，理想的低通滤波应该匹配遥感器的调制传递函数MTF，但是卫星数据提供商提供的数据产品，绝大多数遥感成像系统的MTF补偿方法都没有公开。一些研究表明，高斯滤波器有着与MS传感器的MTF相似的形状，可以使用高斯滤波器匹配MS传感器的调制传输函数，且具有较强的鲁棒性。对于高斯滤波器的参数估计和使用上，Yin等[21]和杨勇等[22]使用了相关系数为准则，以低通滤波后低分辨率全色 P L和多光谱拟合强度 I L相关性最大时的滤波参数为最优高斯滤波器，但相关系数仅能表示变量间的线性相关性。遥感图像在成像过程中受到各种因素影响，不同传感器获得的图像不仅有线性关系，也存在着非线性关系。互信息（Mutual Information， MI）是信息论里一种有用的信息度量，反映了2幅图像之间信息的相互包含程度和信息冗余程度，当两幅图像相似度越高或重合部分越大时，其相关性越大，信息冗余越多，互信息越大[23]。Zhou等[24]利用互信息作为衡量特征冗余的指标，在图像融合时以此为目标函数取得了较好的效果。
Ruderman[25]发现自然图像的局部方差（或标准差）具有与原图像相似的自然场景统计特性，能够较好地描述灰度图像的结构信息， Sheikh等[26]的应用证明了这种自然场景统计特性的有效性。遥感图像是对自然场景的真实反映，因此，局部方差适用于刻画遥感图像的结构特征。
综上，局部方差图像之间的互信息可以衡量图像空间结构特征的相似度，更符合融合模型对 P L与 M S u p空间尺度一致性的要求。以得到与 M S u p空间尺度一致的 P L为目标，计算高斯滤波器窗口和方差，基本步骤为：
步骤（1）：对原始低分辨率多光谱图像 M S进行上采样得到与 P的尺寸一致的 M S u p；
步骤（2）：对 M S u p使用多元线性回归计算得到强度图像 I L；
步骤（3）：利用高斯低通滤波器对 P进行滤波处理得到 P G S F k , j；
步骤（4）：分别计算 P G S F k , j和 I L的局部方差，得到表征空间结构特征的局部方差图像 σ k , j和 σ I L；
步骤（5）：计算 σ k , j和 σ I L的互信息 M I σ k , j , σ I L；
步骤（6）：改变高斯滤波器窗口大小K和方差 σ，重复步骤（3）—步骤（5）；当 M I最大时，二者在空间特征上最相似，此时滤波器窗口大小K和方差 σ即为所估计的最优高斯滤波器参数；
步骤（7）：用最优高斯滤波器参数K和 σ，分别对 P i进行滤波处理得到 P i , L。

2.3 梯度一致性约束的最优注入系数计算

不同的图像有不同的空间结构特征和光谱信息，从而对细节注入量有不同的要求。细节注入越多，融合图像结构特征越清晰，但其光谱信息可能会失真；细节注入越少，融合图像光谱信息得以保持，但可能不够清晰。这说明融合图像光谱信息和空间信息的平衡可以通过控制细节注入量来实现。
平均梯度（Average Gradient，AG）反映了图像微小细节反差变化的速率，可以用来定量表征图像的纹理细节。图像的AG 越高，纹理细节越丰富，图像空间结构越清晰[27]。因此，细节注入量可以用平均梯度作为指标来量化计算。因全色图像和多光谱图像融合目的是要在空间尺度和全色图像对齐，故作为量化基准的平均梯度可以参照全色图像的平均梯度。
本文以平均梯度一致性为约束条件，计算最优注入系数来调节细节的注入量。假设图像为f，它的平均梯度定义为：
A G = 1 ( M - 1 ) ( N - 1 ) ∑ i = 1 M - 1 ∑ j = 1 N - 1 [ f ( i , j ) - f ( i + 1 , j ) ] 2 + [ f ( i , j ) - f ( i , j + 1 ) ] 2 2
式中： [M，N]为图像f的尺寸。
设定细节注入量系数 g的取值范围为 [ 0.5,1.5 ]，步长为0.1，依次根据式（2）迭代计算融合图像4个波段平均梯度的均值 A G H M S ¯，当其与高分辨率全色图像的平均梯度 A G P ¯差异最小时，此时 g的取值即为最优的注入量系数 g o p t。最终的融合公式为：
H M S = M S u p ∘ g o p t ∘ P i P i , L + e p s

3 实验及分析

3.1 实验数据

为验证本文方法的有效性，采用Meng等[28]制作的数据集，包括IKONOS、Quickbird 2种卫星数据类型，以验证方法对不同卫星数据类型的适应性。KONOS数据的多光谱图像空间分辨率为4 m、全色图像空间分辨率为1 m； Quickbird数据的多光谱图像空间分辨率为0.61 m、全色图像空间分辨率为2.44 m。2种卫星数据全色均为1个波段，尺寸为1 024×1 024；多光谱图像为4个波段，尺寸为512×512。此外，对于每种卫星数据类型，根据不同地物覆盖类型，分别选取了植被、建筑、不同地物混合的3类场景，以验证方法对包含不同内容的图像融合的有效性。依据文献中对数据集场景的描述，植被区场景位于郊区、山区和农村，植被是其主要组成部分；建筑区场景图像主要位于城市地区，以建筑物为重点，可能存在少量的树木、道路等；混合区有植被、建筑物、水或土壤等不同类型地物组成，且每类地物所占比例相差不大。

3.2 实验结果分析

在融合结果评价上，分别从定性和定量两方面进行分析。定性评价方面，将多光谱图像实验结果合成真彩色显示，便于从视觉角度直观的观察光谱信息的保留情况；在此基础上提取梯度信息，通过梯度图显示不同融合结果细节的差异。需要说明的是，结果图为原始尺寸按比例缩小图，红色框中为图中局部区域的实际比例。定量评价方面，从光谱保真度、空间信息保持度、图像清晰度和信息的丰富程度4个角度，选取了光谱角映射（Spectral Angle Mapper， SAM）[29]、空间相关系数（Spatial Correlation Coefficient， SCC）[30]、平均梯度和信息熵EN（Entropy， EN）作为评价指标，其中， SCC的理想值为1， SAM的理想值为0。同时将本方法与其他7种方法进行对比实验，这些方法分别为GSA方法[4]、BAGDC方法[8]、SFIM方法[15]、AGSFIM方 法[20]、BDSD方法[31]、AFHH[32]和MTF-SFIM方法。其中，MTF-SFIM方法以SFIM方法为基础模型，低分辨率全色图像由MTF匹配的高斯滤波获得[33]。

3.2.1 植被区图像融合结果及评价

图2和图3为包含植被多的IKONOS和QuickBird 的全色图像和多光谱图像8种不同融合方法的结果图像，图4和图5为对应的梯度图像。图2和图3目视发现， MTF-SFIM方法、 AGSFIM方法、 BAGDC和AHFF方法在两组实验中植被部分都存在不同程度的光谱失真，在QuickBird数据中建筑顶部同样存在此问题（图3红色框所示），原因在于注入了过量的空间信息，增加了其梯度（图4和图5绿色框所示）。其他融合方法在光谱信息的保持上表现较好，视觉上难以察觉到光谱的差异。空间细节方面，GSA方法和AHFF方法建筑物上有空间失真，BDSD方法因存在块状使建筑物具有不均匀的细节损失；本文方法梯度图像整体比较平滑，注入的空间信息介于全色图像和多光谱图像之间，保证了植被对于光谱信息的需要，也相对提升了空间信息。表1和表2为包含植被较为丰富的IKONOS数据和QuickBird数据不同方法融合结果的指标值。可以看出，BAGDC方法光谱指标SAM最佳，但目视观察植被存在明显的光谱失真，本文方法在两组实验中的SAM指标排在前两位，说明具有较好的光谱保持能力，这也和目视判读结果基本一致；同时本文方法在EN指标上也表现优秀，表明融合图像包含信息量较为丰富；对于AG指标，本文方法在IKONOS数据上低于MTF-SFIM、BDSD和AGSFIM，但也明显大于其他方法，在QuickBird数据上则表现最佳，略高于MTF-SFIM方法和AGSFIM方法，是其他方法的两倍；在空间信息保持指标SCC上，AGSFIM方法取值最大，本文方法的两组数据取值则处于中位数，与表现最差的相比，分别提高了10%和21.6%，与最优的AGSFIM和相近的GSA与SFIM相比， 3个指标整体表现更好。
图2 IKONOS数据植被区不同方法融合结果

Fig.2 The fusion results of different methods for IKONOS data in vegetation region

图3 Quickbird数据植被区不同方法融合结果

Fig. 3 The fusion results of different methods for Quickbird data in vegetation region

图4 IKONOS数据植被区不同方法融合结果梯度图像

Fig. 4 Gradient of different fusion image for IKONOS data in vegetation region

图5 QuickBird数据植被区不同方法融合结果梯度图像

Fig. 5 Gradient of different fusion image for Quickbird data in vegetation region

表1 IKONOS植被区融合结果客观评价指标

Tab. 1 Objective evaluation indicators for the fusion results of IKONOS vegetation region

方法
指标		 GSA BDSD SFIM MTF-SFIM AGSFIM BAGDC AFHH LVMI-SFIM
SAM↓ 1.164 1.461 0.883 1.000 1.166 0.820 0.878 0.855
EN ↑ 0.778 0.826 0.783 0.834 0.830 0.316 0.782 0.989
AG↑ 13.056 18.305 15.833 19.236 18.615 12.183 13.606 17.634
SCC↑ 0.663 0.647 0.713 0.854 0.877 0.755 0.688 0.715

注：表中加粗数值表示最佳， 表示最差。

表2 QuickBird植被区融合结果客观评价指标

Tab. 2 Objective evaluation indicators for the fusion results of QuickBird vegetation region

方法
指标		 GSA BDSD SFIM MTF-SFIM AGSFIM BAGDC AFHH LVMI-SFIM
SAM↓ 1.856 1.704 0.999 1.123 1.300 1.085 1.015 0.953
EN ↑ 0.367 0.479 0.433 0.519 0.534 0.159 0.391 0.772
AG↑ 12.275 13.530 13.951 22.249 22.616 10.324 10.474 24.360
SCC↑ 0.762 0.692 0.741 0.913 0.931 0.649 0.704 0.789

注：表中加粗数值表示最佳， 表示最差。

3.2.2 建筑区图像融合结果及评价

图6和图7为建筑或道路较多的IKONOS和QuickBird的全色图像和多光谱图像8种不同融合方法的结果图像，图8和图9为对应的梯度图像。从图6和图7融合结果可知，对于建筑场景（红色方框），没有明显的光谱失真，其差异主要是亮度和细节上的差异。结合梯度图像，除BDSD方法分块处理导致的细节提升不均匀、 AHFF方法略微模糊外，其他融合方法空间信息都得到了提升。对于植被区域， MTF-SFIM方法AGSFIM方法和BAGDC方法梯度过于突出，使其存在着明显的光谱失真。相较于这些方法，本文方法融合图像在光谱信息保持和空间信息提升方面均有较好的效果。
图6 IKONOS数据建筑区不同方法融合结果

Fig. 6 The fusion results of different methods for IKONOS data in building region

图7 Quickbird数据建筑区不同方法融合结果

Fig. 7 The fusion results of different methods for Quickbird data in building region

图8 IKONOS数据建筑区不同方法融合结果梯度图像

Fig. 8 Gradient of different fusion image for IKONOS data in building region

图9 Quickbird数据建筑区不同方法融合结果梯度图像

Fig. 9 Gradient of different fusion image for Quickbird data in building region

表3和表4为以建筑或道路为主的IKONOS数据和QuickBird数据不同方法融合结果指标值。从指标绝对量化值来看，对于IKONOS数据， BAGDC的SAM表现最优为1.060， BDSD最差，两者差2倍多，本文方法比最优的BAGDC低17.2%； BDSD在EN和AG上最优，但这与目视观察结果不完全一致；在SCC指标上， AGSFIM则表现最佳，本文方法与其只差0.016。对于QuickBird数据，除SCC位于第三外，其他3个指标则为最佳， SCC指标上 AGSFIM同样最佳，本文方法与其相差0.029，与表现最差的AHFF方法相比，提高了0.127。
表3 IKONOS建筑区融合结果客观评价指标

Tab.3 Objective evaluation indicators for the fusion results of IKONOS buiding region

方法
指标		 GSA BDSD SFIM MTF-SFIM AGSFIM BAGDC AHFF LVMI-SFIM
SAM↓ 1.289 2.252 1.216 1.235 1.396 1.060 1.210 1.212
EN ↑ 1.282 1.511 1.360 1.454 1.358 1.338 1.324 1.304
AG↑ 29.298 39.383 32.689 35.909 31.759 30.812 24.200 30.627
SCC↑ 0.944 0.871 0.933 0.954 0.955 0.893 0.779 0.938

注：表中加粗数值表示最佳， 表示最差。

表4 QuickBird 建筑区 融合结果客观评价指标

Tab.4 Objective evaluation indicators for the fusion results of IKONOS building region

方法
指标		 GSA BDSD SFIM MTF-SFIM AGSFIM BAGDC AHFF LVMI-SFIM
SAM↓ 1.075 1.572 0.807 0.893 1.041 0.858 0.825 0.793
EN ↑ 0.621 0.739 0.692 0.736 0.733 0.615 0.649 0.888
AG↑ 14.781 16.959 17.974 22.149 22.146 20.413 11.233 22.702
SCC↑ 0.937 0.845 0.901 0.954 0.961 0.874 0.805 0.932

注：表中加粗数值表示最佳， 表示最差。

3.2.3 混合区图像融合结果及评价

图10和图11为包含植被、建筑、道路、水系等多种地物混合的IKONOS和QuickBird的全色图像和多光谱图像8种不同融合方法的结果图像，图12和图13为对应的梯度图像。从视觉上可以直观地看出， MTF-SFIM方法、 AGSFIM方法和 BAGDC方法植被存在着明显的光谱失真现象，其他方法与多光谱图像相似。在细节保持方面，BDSD方法融合图像上建筑物（红色方框）边缘存在类似“叠影”现象，AHFF方法边缘不够清晰，其他几种方法建筑物边缘清晰度基本相似，视觉难以分辨优劣。
图10 IKONOS数据混合区不同方法融合结果

Fig. 10 The fusion results of different methods for IKONOS data in mixed region

图11 Quickbird数据混合区不同方法融合结果

Fig. 11 The fusion results of different methods for Quickbird data in mixed region

图12 IKONOS数据混合区不同方法融合结果梯度图像

Fig. 12 Gradient of different fusion image for IKONOS data in mixed region

图13 Quickbird数据混合区不同方法融合结果梯度图像

Fig. 13 Gradient of different fusion image for Quickbird data in mixed region

表5和表6为以植被和建筑为主的混合场景IKONOS数据和QuickBird数据不同方法融合结果指标值。本文方法SAM在两组实验中表现最优或次优，EN均最大，说明本文方法有不错的光谱保持能力、信息量也最多；在空间清晰度指标AG方面，本文方法在QuickBird数据上的表现最佳，在IKONOS数据上表现居中；在空间信息保持指标SCC上，与表现最差的AHFF方法相比，本文方法分别提高了10%和17.5%，与表现最优的AGSFIM方法和相近的GSA及SFIM方法相比，本文方法在其他3个指标上的整体表现优于对方。
表5 IKONOS混合区融合结果客观评价指标

Tab. 5 Objective evaluation indicators for the fusion results of IKONOS Mixed region

方法
指标		 GSA BDSD SFIM MTF-SFIM AGSFIM BAGDC AHFF LVMI-SFIM
SAM↓ 0.855 1.040 0.696 0.753 0.871 0.646 0.706 0.681
EN ↑ 0.800 0.834 0.821 0.854 0.842 0.838 0.817 0.910
AG↑ 11.622 15.800 12.565 15.858 15.234 12.994 10.293 13.681
SCC↑ 0.934 0.902 0.925 0.969 0.980 0.938 0.840 0.929

注：表中加粗数值表示最佳， 表示最差。

表6 QuickBird混合区融合结果客观评价指标

Tab. 6 Objective evaluation indicators for the fusion results of Quickbird mixed region

方法
指标		 GSA BDSD SFIM MTF-SFIM AGSFIM BAGDC AHFF LVMI-SFIM
SAM↓ 1.444 1.858 0.909 1.008 1.195 0.935 0.923 0.890
EN ↑ 0.408 0.521 0.428 0.466 0.477 0.294 0.421 0.724
AG↑ 9.006 10.287 9.970 12.632 13.217 9.681 7.856 13.620
SCC↑ 0.850 0.758 0.838 0.925 0.941 0.881 0.736 0.865

注：表中加粗数值表示最佳， 表示最差。

3.2.4 3组实验综合分析

由于不同地物对光谱保真和空间信息增强方面敏感度不同，绿色植被和水域场景相对于建筑场景更加敏感。在植被和水域场景较多的情况下，应以保持光谱为主，过多的细节注入，将使其光谱失真较为严重，影响着图像整体指标表现。从6组实验结果比较可以看出，不同的图像融合方法由于方法侧重点不同，在光谱保真度和空间信息增强方面有不同的特点，因而适用的融合场景和地物类型也有所不同（表7）。
表7 不同融合方法综合比较

Tab. 7 Comparison of different fusion methods

方法 方法重点 融合结果 适应场景
光谱保持 空间保持
GSA 多光谱图像线性拟合亮度分量 视觉效果较好
客观指标不佳		 客观指标不高 植被为主
BDSD 分块处理，局部共享权重 无明显光谱失真 块状明显
清晰度不稳定
SFIM 均值滤波获取低分辨率全色图像 视觉效果较好 客观指标不高 植被为主
混合场景
MTF-SFIM 与卫星传感器MTF匹配的高斯低通滤波获取低分辨率全色图像 光谱失真明显 边缘细节显著
清晰度较好		 建筑为主
AGSFIM 多项式表示平均梯度和高斯滤波参数方差间关系
BAGDC 自适应梯度、细节注入校正约束联合的变分优化
AHFF 多级高通滤波获取注入细节，结构相似度和均方根误差联合计算细节注入权重 视觉效果较好 边缘细节不足 植被为主
LVMI-SFIM 局部方差互信息的高斯滤波空间尺度对齐，梯度一致性约束细节注入系数 视觉效果较好 客观指标EN较好、SCC不高 植被为主
混合场景

3.3 最优高斯滤波参数估计分析

在IKONOS和QuickBird 2种不同传感器 P i , L遥感图像生成中，MTF-SFIM方法的高斯滤波器参数为[41×41, 0.17]和[41×41,0.15]；AGSFIM方法高斯滤波器的参数为[3×3，0.1]和[3×3，0.63]；本文提出的基于方差图像互信息的高斯滤波参数估计方法，计算出滤波器的参数为[9×9，0.7]和[11×11，0.3]。需要说明的是，本文的高斯滤波器采用了与MTF-SFIM方法中相同的kaiser窗和窗口系数处理方式，以加速参数的求解。
空间相关系数可以有效衡量融合图像与全色图像的空间信息相似性。将空间相关系数作为两幅图像空间相似性度量准则，计算不同低通滤波得到的各波段 P i , L和 M S u p的空间相关系数。空间相关系数公式为：
S C C = ∑ i = 1 M ∑ j = 1 N [ ∇ F A i , j - ∇ F A ¯ ] · [ ∇ F B i , j - ∇ F B ¯ ] ∑ i = 1 M ∑ j = 1 N [ ∇ F A i , j - ∇ F A ¯ ] 2 · [ ∇ F B i , j - ∇ F B ¯ ] 2
式中： A和B表示单波段图像； ∇表示使用sobel 算子提取的梯度图像； ∇ F A ¯ 和 ∇ F B ¯表示梯度图像的均值。
表8和表9记录了不同滤波器下 P i , L与 M S u p的空间相关系数，可以看出，本文提出的高斯滤波参数估计方法得到的 P i , L，其与 M S u p各波段空间相关系数除QuickBird数据在第3和4波段略低于MTF匹配高斯滤波外，其余均高于另外3种低通滤波方法，说明了本文高斯滤波器参数估计方法的可靠性。
表8 IKONOS混合区低分辨率全色与多光谱图像的空间相关系数SCC

Tab. 8 SCC for low resolution panchromatic and multispectral images in IKONOS mixed region

低通滤波方法
P i , L		 多光谱图像 M S u p
波段1 波段2 波段3 波段4
3×3
均值滤波		 0.921 0 0.883 7 0.834 6 0.822 4
MTF
高斯滤波		 0.931 2 0.951 4 0.921 2 0.886 7
梯度一致性
高斯滤波		 0.019 4 0.013 4 0.013 0 0.016 5
方差互信息
高斯滤波		 0.962 9 0.952 1 0.940 4 0.927 4
表9 QuickBird混合区低分辨率全色与多光谱图像的空间相关系数SCC

Tab. 9 SCC for low resolution panchromatic and multispectral images in QuickBird mixed region

低通滤波方法
P i , L		 多光谱图像 M S u p
波段1 波段2 波段3 波段4
均值滤波
3×3		 0.753 4 0.782 9 0.549 6 0.637 7
MTF
高斯滤波		 0.789 2 0.845 7 0.805 6 0.835 1
梯度一致性
高斯滤波		 -0.037 3 0.076 9 -0.102 8 -0.120 2
方差互信息
高斯滤波		 0.925 6 0.895 4 0.801 8 0.834 3

3.4 细节调节系数g与融合指标关系分析

在图像处理中，图像融合基本需求是保持原始多光谱图像光谱信息不丢失的情况下，提高增强图像的细节信息和纹理特征、保持边缘细节及能量。经过实验发现（图14、图15），对于IKONOS的3组实验数据，随着g的变化融合指标SAM和SCC基本不变， AG基本呈线性增加趋势，而信息熵EN的变化较为复杂，不同的g对应的EN可能相同。对于Quickbird数据，细节调节系数g与融合指标间关系存在同样的规律。因此，以融合结果的平均梯度AG与全色图像的平均梯度AG差异最小时的g为最优调节系数，在保证SAM和SCC 2个指标不受影响情况下，可避免平均梯度AG过大，导致图像过于锐化，或平均梯度AG过小，降低图像清晰度。
图14 IKONOS数据细节调节系数g与融合指标的关系

Fig. 14 The relationship between detail adjustment factor g and indicators for IKONOS dataset

图15 Quickbird数据细节调节系数g与融合指标的关系

Fig. 15 The relationship between detail adjustment factor g and indicators for Quickbird dataset

4 结论与讨论

针对多光谱图像和全色图像的融合问题，本文提出了一种改进的SFIM遥感图像融合方法，该方法结合了梯度域局部方差互信息的高斯滤波和梯度一致性的自适应细节注入。主要工作如下：
（1）本文提出了一种基于局部方差图像互信息的高斯低通滤波参数估计方法。该方法得到的低分辨率全色图像与原始低分辨率多光谱图像空间相关性SCC在大部分波段上大于其他低通滤波方法，提高了两者间的空间相似性，减少了因空间尺度差异造成的融合图像空间信息失真。
（2）在保留SFIM模型光谱保真的优点基础上，以全色图像的平均梯度为基准，引入细节调节系数，能够动态的调整细节注入量，有效地平衡了光谱信息和空间信息之间的关系。
（3）本文方法在光谱信息保持、图像清晰度和信息的丰富程度上具有一定的优势，尤其适用于植被所占比例较高的场景。
本文方法充分考虑了待融合图像的场景，依据场景内容动态确定高斯低通滤波的参数，进一步提高了SFIM模型的光谱保持能力。同时，在平均梯度和信息熵两个指标上，也取得了较为不错的结果。依据图像场景计算高斯滤波参数得到的图像提高了其与多光谱图像在空间尺度上的相关性，但这种全局处理方式导致同波段的不同区域都使用相同的注入系数，未能充分考虑不同区域对空谱信息需求的差异。下一步将考虑与基于图像分割和深度学习卷积网络的局部处理思想相结合，以进一步提升遥感图像空谱融合质量。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
李树涛, 李聪妤, 康旭东. 多源遥感图像融合发展现状与未来展望[J]. 遥感学报, 2021, 25(1):148-166.

[ Li S T, Li C Y, Kang X D. Development status and future prospects of multi-source remote sensing image fusion[J]. National Remote Sensing Bulletin, 2021, 25(1):148-166. ]

DOI

[2]
Carper W, Lillesand T, Kiefer P. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data[J]. Photogrammetric Engineering & Remote Sensing, 1990, 56(4):459-467.

[3]
Chavez P, Kwarteng A. Extracting spectral contrast in landsat thematic mapper image data using selective principal component analysis[J]. Photogrammetric Engineering and Remote Sensing, 1989, 55:339-348.

[4]
Aiazzi B, Baronti S, Selva M. Improving component substitution pansharpening through multivariate regression of MS Pan data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10):3230-3239. DOI:10.1109/TGRS.2007.901007

[5]
Chavez Jr P S, Sides S C, Anderson J A. Comparison of three different methods to merge multiresolution and multispectral data: LANDSAT TM and SPOT panchromatic: ABSTRACT[J]. AAPG Bulletin, 1990, 74:964-972. DOI:10.1306/44b4c288-170a-11d7-8645000102c1865d

[6]
Nunez J, Otazu X, Fors O, et al. Multiresolution-based image fusion with additive wavelet decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(3):1204-1211. DOI:10.1109/36.763274

[7]
Nencini F, Garzelli A, Baronti S, et al. Remote sensing image fusion using the curvelet transform[J]. Information Fusion, 2007, 8(2):143-156. DOI:10.1016/j.inffus.2006.02.001

[8]
刘红毅, 赵肖飞, 韩海波, 等. 基于光谱映射和细节注入的Pansharpening[J]. 电子学报, 2023, 51(6):1527-1540.

DOI

[ Liu H Y, Zhao X F, Han H B, et al. Pansharpening by jointing spectral mapping and detail injection[J]. Acta Electronica Sinica, 2023, 51(6):1527-1540. ] DOI:10.12263/DZXB.20210857

[9]
Lu H Y, Yang Y, Huang S Y, et al. A unified pansharpening model based on band-adaptive gradient and detail correction[J]. IEEE Transactions on Image Processing, 2021, 31:918-933. DOI:10.1109/TIP.2021.3137020

[10]
张兵, 高连如, 李嘉鑫, 等. 高/多光谱遥感图像超分辨率融合研究进展与展望[J]. 测绘学报, 2023, 52(7):1074-1089.

DOI

[ Zhang B, Gao L R, Li J X, et al. Advances and prospects in hyperspectral and multispectral remote sensing image super-resolution fusion[J]. Acta Geodaetica et Cartographica Sinica, 2023, 52(7):1074-1089. ] DOI:10.11947/j.AGCS.2023.20220499

[11]
唐霖峰, 张浩, 徐涵, 等. 基于深度学习的图像融合方法综述[J]. 中国图象图形学报, 2023, 28(1):3-36.

[ Tang L F, Zhang H, Xu H, et al. Deep learning-based image fusion: A survey[J]. Journal of Image and Graphics, 2023, 28(1):3-36. ]

[12]
邓良剑, 冉燃, 吴潇, 等. 遥感图像全色锐化的卷积神经网络方法研究进展[J]. 中国图象图形学报, 2023, 28(1):57-79.

[ Deng L J, Ran R, Wu X, et al. CNN-based remote sensing pan-sharpening: A critical review[J]. Journal of Image and Graphics, 2023, 28(1):57-79. ]

[13]
杨勇, 苏昭, 黄淑英, 等. 基于深度学习的像素级全色图像锐化研究综述[J]. 遥感学报, 2022, 26(12):2411-2432.

[ Yang Y, Su Z, Huang S Y, et al. Deep-learning approaches for pixel-level pansharpening[J]. National Remote Sensing Bulletin, 2022, 26(12):2411-2432. ]

DOI

[14]
杨景辉. 遥感影像像素级融合通用模型及其并行计算方法[J]. 测绘学报, 2015, 44(8):943.

DOI

[ Yang J H. The general ized model and paral lel computing methods for pixel-level remote sensing image fusion[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8):943. ] DOI:10.11947/j.AGCS.2015.20150059

[15]
Liu J G. Smoothing Filter-based Intensity Modulation: A spectral preserve image fusion technique for improving spatial details[J]. International Journal of Remote Sensing, 2000, 21(18):3461-3472. DOI:10.1080/014311600750037499

[16]
Chen C, Li Y Q, Liu W, et al. Image fusion with local spectral consistency and dynamic gradient sparsity[C]//2014 IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2014:2760-2765. DOI:10.1109/CVPR.2014.347

[17]
方帅, 潮蕾, 曹风云. 自适应权重注入机制遥感图像融合[J]. 中国图象图形学报, 2020, 25(3):546-557.

[ Fang S, Chao L, Cao F Y. New pan-sharpening method based on adaptive weight mechanism[J]. Journal of Image and Graphics, 2020, 25(3):546-557. ]

[18]
Vivone G, Restaino R, Chanussot J. Full scale regression-based injection coefficients for panchromatic sharpening[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 2018, 27(7):3418-3431. DOI:10.1109/TIP.2018.2819501

[19]
韩冰, 赵银娣. 一种改进的SFIM高光谱图像融合算法[J]. 遥感信息, 2012, 27(5):44-47,54.

[ Han B, Zhao Y D. An improved smoothing filter-based intensity modulation algorithm for hyperspectral image fusion[J]. Remote Sensing Information, 2012, 27(5):44-47,54. ] DOI:10.3969/j.issn.1000-3177.2012.05.008

[20]
王密, 何鲁晓, 程宇峰, 等. 自适应高斯滤波与SFIM模型相结合的全色多光谱影像融合方法[J]. 测绘学报, 2018, 47(1):82-90.

DOI

[ Wang M, He L X, Cheng Y F, et al. Panchromatic and multi-spectral fusion method combined with adaptive Gaussian filter and SFIM model[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(1):82-90. ] DOI:10.11947/j.AGCS.2018.20170421

[21]
Yin H T, Li S T. Pansharpening with multiscale normalized nonlocal means filter: A two-step approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(10):5734-5745. DOI:10.1109/TGRS.2015.2429691.

[22]
杨勇, 卢航远, 黄淑英, 等. 基于自适应注入模型的遥感图像融合方法[J]. 北京航空航天大学学报, 2019, 45(12):2351-2363.

[ Yang Y, Lu H Y, Huang S Y, et al. Remote sensing image fusion method based on adaptive injection model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(12):2351-2363. ] DOI:10.13700/j.bh.1001-5965.2019.0372

[23]
董宏平, 刘利雄. 互信息域中的无参考图像质量评价[J]. 中国图象图形学报, 2014, 19(3):484-492.

[ Dong H P, Liu L X. No-reference image quality assessment in mutual information domain[J]. Journal of Image and Graphics, 2014, 19(3):484-492. ] DOI:10.11834/jig.20140220

[24]
Zhou M, Yan K Y, Huang J, et al. Mutual information-driven pan-sharpening[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, 2022:1788-1798. DOI:10.1109/CVPR52688.2022.00184.[LinkOut]

[25]
Ruderman D L. The statistics of natural images[J]. Network: Computation in Neural Systems, 1994, 5(4):517-548. DOI:10.1088/0954-898x_5_4_006

[26]
Sheikh H R, Bovik A C. Image information and visual quality[J]. IEEE Transactions on Image Processing, 2006, 15(2):430-444. DOI:10.1109/TIP.2005.859378

PMID

[27]
Cui G M, Feng H J, Xu Z H, et al. Detail preserved fusion of visible and infrared images using regional saliency extraction and multi-scale image decomposition[J]. Optics Communications, 2015, 341:199-209. DOI:10.1016/j.optcom.2014.12.032

[28]
Meng X C, Xiong Y M, Shao F, et al. A large-scale benchmark data set for evaluating pansharpening performance: Overview and implementation[J]. IEEE Geoscience and Remote Sensing Magazine, 2021, 9(1):18-52. DOI:10.1109/MGRS.2020.2976696

[29]
Alparone L, Wald L, Chanussot J, et al. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S data-fusion contest[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10):3012-3021. DOI: 10.1109/TGRS.2007.904923

[30]
Zhou J, Civco D L, Silander J A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data[J]. International Journal of Remote Sensing, 1998, 19(4):743-757. DOI:10.1080/014311698215973

[31]
Meng X C, Shen H F, Li H F, et al. Review of the pansharpening methods for remote sensing images based on the idea of meta-analysis: Practical discussion and challenges[J]. Information Fusion, 2019, 46:102-113. DOI: 10.1016/j.inffus.2018.05.006

[32]
Yang Y, Wan C X, Huang S Y, et al. Pansharpening based on adaptive high-frequency fusion and injection coefficients optimization[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 16:799-811. DOI:10.1109/JSTARS.2022.3232145

[33]
Aiazzi B, Alparone L, Baronti S, et al. MTF-tailored multiscale fusion of high-resolution MS and pan imagery[J]. Photogrammetric Engineering & Remote Sensing, 2006, 72(5):591-596. DOI:10.14358/pers.72.5.591

Options
文章导航

/

〈 〉