EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 3: 709 - 724

DOI: https://doi.org/10.12082/dqxxkx.2024.230339

遥感科学与应用技术

缺失时段对黑河流域夏季FY-4A AGRI地表温度时间维重建的影响分析

  • 罗雨梅 ,
  • 祝善友 , * ,
  • 李悦丽 ,
  • 张桂欣 ,
  • 徐永明
展开
  • 1.南京信息工程大学遥感与测绘工程学院，南京 210044
  • 2. 南京信息工程大学地理科学学院，南京 210044
*祝善友（1977—），男，山东日照人，博士，教授，博导，硕导，研究方向为热红外遥感基础理论与应用、生态遥感。 E-mail：

罗雨梅（1999— ），女，四川乐山人，硕士生，研究方向为地表信息获取与遥感监测。E-mail:

Copy editor: 蒋树芳

收稿日期: 2023-06-19

  修回日期: 2023-09-21

  网络出版日期: 2024-03-31

基金资助

风云卫星应用先行计划项目(FY-APP-2022.0204)

国家自然科学基金项目(42171101)

国家自然科学基金项目(42271351)

收起

Analyzing the Influence of Missing Periods on the Time Dimensional Reconstruction of Summer Land Surface Temperature in the Heihe River Basin Using FY-4A AGRI Data

  • LUO Yumei ,
  • ZHU Shanyou , * ,
  • LI Yueli ,
  • ZHANG Guixin ,
  • XU Yongming
Expand
  • 1. School of Remote Sensing & Geomatics Engineering, Nanjing University of Information Science & Technology， Nanjing 210044, China
  • 2. School of Geographical Science, Nanjing University of Information Science & Technology, Nanjing 210044, China
*ZHU Shanyou, E-mail:

Received date: 2023-06-19

  Revised date: 2023-09-21

  Online published: 2024-03-31

Supported by

Fengyun Application Pioneering Project(FY-APP-2022.0204)

Natural Science Foundation of China(42171101)

Natural Science Foundation of China(42271351)

Fold

摘要

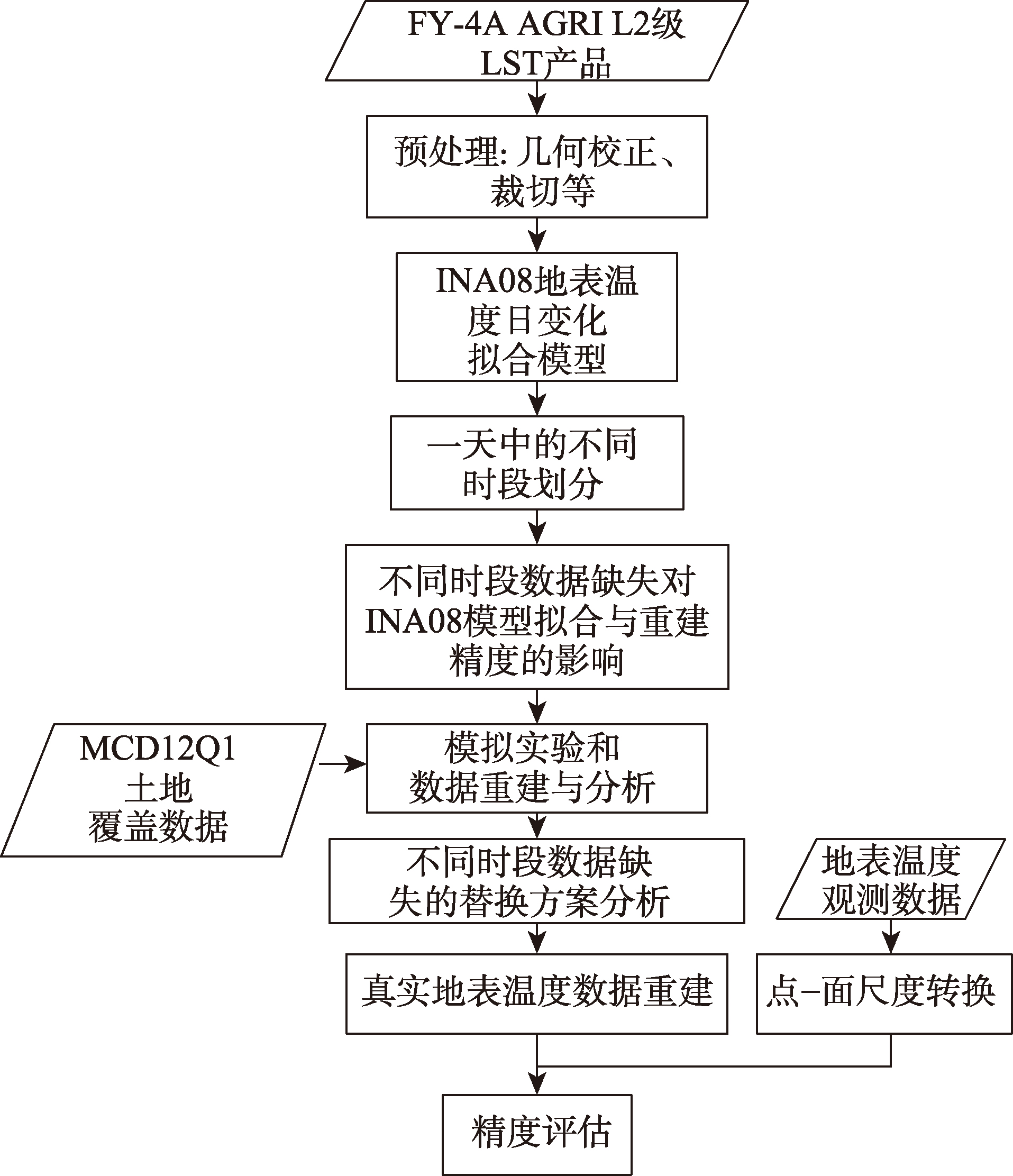
静止气象卫星产品在天气监测和气候变化应用中发挥着重要作用。受天气状况影响，静止气象卫星地表温度经常存在缺失现象，严重影响着地表温度产品的深入应用。在地表温度缺失值的时间维重建过程中，现有研究大多是比较了不同时间维重建方法的精度，而有关数据缺失时段对模型能否有效重建的影响研究较少。本文以黑河流域为例，基于INA08温度日循环模型，通过模拟实验分析夏季FY-4A（风云4号A星） AGRI（Advanced Geostationary orbit Radiation Imager，先进的静止轨道辐射成像仪） LST（Land Surface Temperature，陆地表面温度）数据缺失对重建结果精度的影响，提出了不同缺失时段的数值替换方案，并采用真实数据对理论实验分析结果进行验证。结果表明：① 缺失第二时段（13—15时）对重建结果的影响可忽略不计，缺失第五时段（次日0—6时）对重建结果影响最大；② 随着缺失时段的增多，参与INA08模型拟合的遥感反演原始值减少，精度也有所下降；③ 模拟实验总结的缺失时段数值替换方案对INA08模型重建FY-4A AGRI LST具有一定指导作用,缺失时段某个时刻被替换为其他时刻地表温度后，能够显著提高缺失数据重建精度。

关键词： FY-4A; AGRI; 地表温度; 时间维重建; 缺失时段; 日变化模型; 黑河流域

本文引用格式

罗雨梅 , 祝善友 , 李悦丽 , 张桂欣 , 徐永明 . 缺失时段对黑河流域夏季FY-4A AGRI地表温度时间维重建的影响分析[J]. 地球信息科学学报, 2024 , 26(3) : 709 -724 . DOI: 10.12082/dqxxkx.2024.230339

Abstract

Geostationary meteorological satellite products play a crucial role in various weather monitoring and climate change applications. Due to weather conditions such as cloud cover, precipitation, and atmospheric influence, the Land Surface Temperature (LST) data retrieved from geostationary meteorological satellites often exhibits missing values, which significantly limits the further applications of LST products. In the process of reconstructing missing values of LST using time series data, most of the existing studies focus on comparing the accuracy of different time dimensional reconstruction methods. There has been limited research on evaluating the impact of missing data on the effectiveness of different model reconstruction methods. Taking the Heihe River Basin as the case study area, this study adopts the INA08 Diurnal Temperature Cycle (DTC) model to analyze the impact of missing data on the reconstruction of summer LST data from the FY-4A (Fengyun 4A satellite) AGRI (Advanced Geostationary Orbit Radiation Imager). Then, a data replacement scheme is proposed for different missing time periods, and the LST reconstruction results are verified against field measurement data. Research results show that: (1) the absence of LST data during the second time period (local time of 13:00 to15:00) has a minimal impact on the reconstruction results, while the absence of LST data during the fifth time period (0:00 to 6:00 of the next day) has the most substantial impact on the reconstruction results; (2) with the increasing number of missing time periods, the available original AGRI LST data for fitting the INA08 model are reduced, leading to a decrease in the reconstruction accuracy; (3) the data replacement scheme with the simulation experiment provides valuable guidance for the reconstruction of FY-4A AGRI LST by using the INA08 model, and the reconstruction accuracy of missing data can be significantly improved by replacing certain missing time periods with other suitable time periods. In our study, different time periods are divided based on the daily temperature variation in the Heihe River Basin in the summer season. The time period division may vary depending on the geographical location and season. For a given region and season, appropriate time periods can be determined based on the local sunrise time, the time of maximum daily temperature, and the time of temperature attenuation, in conjunction with typical characteristics of temperature variation throughout the day.

Key words： FY-4A; AGRI; land surface temperatures; time dimension reconstruction; missing period; Diurnal Temperature Cycle (DTC); the Heihe River Basin

1 引言

陆地表面温度（Land Surface Temperature，LST）与地表、大气之间的相互作用以及能量交换密切相关[1⇓⇓⇓-5]，是区域和全球尺度陆表系统过程中的关键参数之一。高质量的LST作为地球表面最重要和最基本的物理参数[6]，被广泛应用于环境研究、水文研究、生态学研究、城市热岛研究等各个学科领域[7⇓⇓-10]。
获取LST的传统方法主要为气象站点测量，但是地面站点数据空间连续性较差。利用遥感技术反演LST能够克服传统方法的不足，获得长时间序列的地表温度空间连续分布数据。常用的地表温度遥感反演波段包括微波和热红外波段，其中微波遥感具有全天时、全天候的优势，但其空间分辨率相对于热红外波段非常低。热红外传感器，例如FY-4A/AGRI、NOAA/AVHRR、EOS/MODIS、Landsat-8/TIRS等，可提供不同空间分辨率的地表温度产品。
然而由于热红外波段无法穿透云层，热红外传感器只能获得云层上方的热辐射，而无法获取云下地表有关的热辐射信息。现有的地表温度产品都是对遥感影像进行云检测和云覆盖像元标识后，反演估算晴空环境下的地表温度，而将云覆盖像元的地表温度以缺省数值（如65533）进行表示。云覆盖像元地表温度信息缺失在一定程度上破坏了地表温度时空分布的全局性和连续性，严重阻碍和限制了地表温度产品的全天候应用[11-12]，需要采用合适方法对缺失值进行修补或重建。
云下地表温度缺失值重建的方法主要包括空间维重建、时间维重建以及时空融合重建。基于空间维的缺失值重建是根据LST在空间分布上的连续性特征，利用空间插值或统计回归方法，如规则样条函数、梯度距离平方反比、反距离加权、普通克里金和随机森林回归插值方法近似估算云覆盖像元LST[13⇓⇓⇓⇓-18]，或在传统空间插值方法基础上添加修正因子来提高重建精度[19]。然而空间维缺值重建方法通常用于极轨卫星，当区域内数据缺失较多时，重建精度会明显降低。基于时间维的缺失值重建是指基于当前像元相邻时相上的无云陆表温度信息，通过一定的时间插值方法对云覆盖区域缺失的陆表温度进行插补。较为简单的重建策略有线性插值法，但由于LST的时间变化复杂，且不能保证一天内有足够的有效图像，因此直接采用时序线性插值的误差相对较大。部分学者采用波谱分析与统计模型方法以提高时间序列LST重建精度，如Xu等[20]采用HANTS（Harmonic Analysis of Time Series）算法对MODIS地表温度数据进行了云影响观测数据的去除和重建，臧琳等[21]从时间序列角度建立地表温度与地表亮温之间的统计模型，实现大面积区域的数值重建。近年来，机器学习凭其稳健拟合模型的优势，被学者引入到时间序列遥感数据集重建当中，如Tian等[22]针对遥感图像分辨率低、视觉质量差的问题，提出了一种基于卷积神经网络的遥感图像超分辨率重建方法； Arslan和Sekertekin采用长短期记忆（Long Short-Term Memory，LSTM）网络对MODIS日LST数据进行重建[23]。基于机器学习的时间维重建方法适合于大量云覆盖区域的地表温度重建，不足是很难描述地表温度时序数据的突然变化情况[24]。利用地表温度日变化模型可以模拟一天中地表温度随时间的变化情况，因此国内外学者基于热传导方程和能量平衡方程发展了许多温度日循环（Diurnal Temperature Cycle，DTC）模型[25⇓⇓⇓-29]，通过数学形式和模型参数能够很好地描述LST日变化。基于时空融合的缺失值重建方法综合了LST的时间与空间信息，能够在一定程度上克服空间插补与时间插补存在的不足。如Weiss等[30]提出了Weiss法，通过从前后相邻的2幅影像中搜索有效的空间相邻像元，根据时空距离反加权进行重建，当有效像元数量不满足设定阈值时，使用所有年份平均LST、空间有效相邻像元LST与多年平均值之间的比率来插补。Li等[13]利用每日4次MODIS LST，提出了合并日观测值、利用时空相邻像元进行缺值估算的方法，最终得到全天候陆表温度数据。王爱辉等[11]提出了一种顾及时空特征的FY-4A LST重建模型，通过时间域、空间域的先后顺序对LST空值进行重建。时空融合的缺失值重建效果依赖于有效数据的数量与质量，当缺失区域不满足空间、时间重建方法的限定条件时，通常也无法得到高质量的重建产品数据。
静止气象卫星产品因其时间观测频率密集的特点，具有时间维重建优势。DTC模型以时间变化规律为前提，通过数学模型能够较好地表达高时间分辨率下地表温度的变化情况，适用于静止卫星温度产品缺值重建的研究。目前， DTC模型用于时序数据的重建取得了很大的进展，相关研究主要比较不同模型的重建精度，或者构建新的模型以提高重建精度。如Duan等[32]对6种DTC模型进行了晴空条件下模拟结果的分析与评估，并指出Inamdar提出的INA08模型采用的双曲线函数能够更准确地描述LST在夜间的衰减。刘紫涵等[33]利用多项式、傅里叶函数以及高斯函数构建DTC模型，实验结果说明该模型能有效修复风云2号F星扫描辐射计（Ⅱ型）地表温度空值数据。Hong等[34]在晴空条件下，利用参数缩减法对四参数地表温度DTC模型做出综合评价，指出INA08-ts模型用于静止卫星LST重建具有较高精度。然而DTC模型通常需要多个非空值时刻数据参与拟合，不同时段数据缺失是否能够准确拟合DTC模型并用于缺失值重建，以及哪些时段数据缺失对模型重建精度影响更大，都需要进一步开展研究。
本文从地表温度数据随时间的变化规律出发，选择重建精度较高的INA08模型，通过理论实验分析数据缺失对重建结果精度的影响，并提出缺失时段的空值替换方案，进而通过真实数据重建进行验证，为地表温度时间维重建提供指导作用。

2 研究方法

论文研究所采用的技术路线如图1所示，详细研究方法分别介绍如下。
图1 研究技术路线

Fig.1 The research flowchart

2.1 INA08地表温度日变化拟合模型

Inamdar在2008年提出了INA08模型[27]，使用余弦函数来表达LST的白天变化过程，使用双曲线函数表达夜间LST的自由衰减过程，具体公式如下：
T d a y t = T 0 + T a c o s π ω t - t m                             t < t s T n i g h t t = T 0 + δ T + T a c o s π ω t s - t m - δ T                                 × k k + t - t s                                                                 t ≥ t s
t s = t s s - 1
式中：式（1）公式左边分别表示白天和夜间时段t时刻的地表温度值； T 0表示日出前后的余温，其值等于24 h周期内的最低温度； T a表示地表温度日变化幅度，其值等于24 h周期内地表温度测量值的最高温度与最低温度之差； ω是余弦项半周期上的宽度，可以利用白天持续时间确定，通过计算地点的纬度值得到； t m是温度达到最大值的时间； t s是地表温度自由衰减的开始时间，可固定为常数[34]，并通过式（2）计算得到，其中 t s s表示日落时刻； δ T是 T 0和 T t → ∞之间的温差； k是衰减常数，可通过使式（1）的2个函数（ T d a y和 T n i g h t）在时间 t s上相等得到。
式（1）为非线性方程，本文采用Levenberg-Marquardt（LM）算法拟合LST的时间序列模型。LM算法是用于求解非线性方程的有效方法之一，通过迭代计算残差平方和，当残差平方和小于阈值时，视为拟合效果达到最佳，结束迭代并得出最优拟合公式。由于对大多数参数的初始估计值接近于它们的最终值，因此模型的收敛速度很快。

2.2 一天中的不同时段划分

由于天气状况的影响，FY-4A AGRI LST产品数据集通常存在着时间连续的缺值。为了分析一天内不同观测时刻的连续缺失对INA08模型重建FY-4A AGRI LST精度的影响，本文根据研究区夏季地表温度的日变化特点，将白天和夜间2个时段细分为图2所示的5个时段。图2中实线代表7月2日黑河流域某一晴空像元一天的温度变化曲线，虚线代表该像元AGRI反演地表温度拟合INA08模型得到的温度变化曲线。5个时段划分如下， 7—12时为第一时段，13—15时为第二时段，16—19时为第三时段，20时23时为第四时段，次日0—6时为第五时段。
图2 温度日变化时段划分示意

Fig. 2 Schematic diagram of the period division based on daily temperature change curve

经计算，黑河流域夏季的日出时刻大部分在6时和7时之间，因此将7时作为日变化周期的起始时刻。图2中，第一时段（7—12时）为温度迅速上升时段，平均每小时变化约5 K。第二时段（13—15时）为高温时段，该时段内温度变化幅度小，温度先缓慢上升，在达到一天最大值后，再缓慢下降，平均每小时温度变化约为1 K。第三时段（16—19时）为白天温度大幅下降时段，平均每小时变化约4 K。第四时段（20—23时）为夜间温度快速下降时段，平均每小时变化约2 K。经计算，黑河流域夏季地表温度的自由衰减时刻大部分在19—20时，因此将20时作为夜间自由衰减的起始时刻。第五时段（0—6时）为夜间地表温度平缓下降时段，该时段内温度变化小，部分位置存在小幅度波动，平均每小时变化小于1 K。

2.3 不同时段数据缺失及其替换对INA08模型拟合与重建精度的影响

FY-4A AGRI LST产品数据集的空间分辨率为4 km，与站点观测地表温度在空间尺度上差异较大，为了尽可能避免点、面尺度对不同地表温度对比结果的影响，本文选择黑河流域具有连续覆盖且面积较大的地表类型进行模拟实验与真实实验。
模拟实验包括3个方面，分别是单时段、2个时段以及3个时段地表温度数据缺失的模拟结果分析。通过将模拟实验数据的某一时段或多个时段人为赋值为缺失值，利用其余时段的遥感反演原始值基于INA08模型进行拟合，得到缺失时段的拟合值，在下文中称为直接拟合值。对缺失时段任意一个时刻进行补值，即空值数据替换，使该时刻的替换值参与INA08模型拟合，得到缺失时段新的拟合值，在下文中称为补值拟合值。分别计算直接拟合值、补值拟合值与原始遥感反演值之间的差异，分析不同时段数据缺失对重建精度的影响，并提出不同时段缺失数据的替换方案，为实际重建工作提供指导。
为了进一步验证模拟实验的分析结果，本文进行了真实数据重建与分析。将每个像元位置的LST缺失值重建分为如下3种情况： ①不满足INA08模型的重建条件，即AGRI时序地表温度中有效值数量少于模型参数个数，无法建立模型，则不进行重建；② 满足INA08模型的重建条件，且所有时段均有AGRI反演地表温度，则无需进行数据替换，直接利用遥感反演LST基于INA08模型进行拟合； ③ 满足INA08模型的重建条件，但存在着部分时段完全缺失的情况，利用其余时段的AGRI LST基于INA08模型得到直接拟合值，再根据数据替换方案进行空值替换，基于INA08模型得到补值拟合值。不同情况重建后的地表温度与地面站点实测值进行对比，分析重建结果误差。
常用的误差评价指标有决定系数R2、均方根误差（Root Mean Square Error，RMSE）[11,21,35-36]、平均绝对误差（Mean Absolute Error，MAE）[37-38]等。通常，对于较大的样本容量，决定系数的估计更可靠，较小的样本容量可能导致决定系数的估计不稳定。RMSE与MAE均反映了预测值与实际值之间的差异，前者对误差的平方进行了求和，它对较大误差的惩罚更重，对异常值更敏感；后者是对误差的绝对值进行求和，它对异常值的惩罚较小。本文选择了RMSE作为误差评价指标。

2.4 站点观测地表温度的点-面尺度转换

本文利用地面站点实测数据对FY-4A AGRI LST缺值重建结果进行验证。站点实测数据是一种点数据， FY-4A AGRI LST产品的空间分辨率为4 km，是像元尺度上的时间序列数据。通过INA08模型拟合，对缺失时刻的地表温度进行重建后，得到不同时刻的地表温度空间分布图，因此重建结果为面数据。在利用实测点进行精度验证时，存在尺度差异问题，从而影响验证结果。尽管黑河流域站点区域地表类型较为均一，但为了尽可能消除点、面尺度之间的地表温度差异，研究中将站点观测的地表温度进行点-面尺度转换，从而更准确地验证地表温度重建结果。
对于实测点的尺度转换已有学者做了相关研究，如周芳成等[12]利用地面站点验证云下遥感地表温度重构方法的精度，为了减小站点数据与遥感数据2种尺度间的误差，在验证前建立了地面实测数据与晴空遥感数据间的匹配关系，将站点实测值转换到像元尺度；刘艳等[39]利用地面点测量数据验证LAI产品之前，进行了尺度转换，将地面测量叶面积指数尺度上升到了遥感像元尺度。考虑到黑河流域地表覆盖类型在空间上没有复杂变化，本文利用晴空环境下的站点观测地表温度与FY-4A AGRI LST数据，建立两者之间的关系模型，进而将所有站点观测地表温度近似转换为像元尺度的观测。这种基于线性关系模型的尺度转换方法不能完全消除地面站点温度值与卫星遥感反演值之间的差异，但可在一定程度上缩小点-面尺度差异对真实实验结果精度分析的影响。地面站点实测数据与FY-4A AGRI LST数据关系模型如式（3）式、（4）所示。
F Y 晴 = a × L S T g r d + b
L S T g r d ' = a × L S T g r d + b
式中： F Y 晴为晴空环境下的FY-4A AGRI LST数据； L S T g r d为晴空环境下的站点观测地表温度， a 、 b为模型系数， L S T g r d '为像元尺度的地面站点实测数据近似值。

3 实验区概况与数据来源

3.1 实验区概况

本文以黑河流域为研究区。黑河流域是我国西北地区第二大内陆流域，位于河西走廊中部，流域面积约为14.29万km2。黑河流域气候干燥，降水稀少而集中，日照充足，太阳辐射强烈，昼夜温差大。地表覆盖类型变化不明显，主要覆盖类型为荒漠、草原、耕地，以及部分森林、湿地。黑河流域研究区边界数据来源于国家冰川冻土沙漠科学数据中心(http://www.ncdc.ac.cn)[40]。

3.2 数据来源

3.2.1 FY-4A AGRI地表温度数据

静止气象卫星风云四号A星FY-4A，于2016年12月11日成功发射，开启了我国新一代静止气象卫星时代。FY-4A装载了4个载荷，其中LST产品由先进的静止轨道辐射成像仪（AGRI）反演。FY-4A AGRI L2级LST产品数据集的空间分辨率为 4 km。本文获取了2021年6、7、8月的圆盘数据，根据风云卫星遥感数据服务网提供的经纬度查找表和数据行列号，对圆盘数据进行几何校正并裁剪出研究区，得到了FY-4A地表温度数据集。

3.2.2 地表温度观测数据

地面观测数据用于FY-4A地表温度重建结果的精度评价。气象台站观测数据是最为常用的数据源之一，可以提供高质量、高时间分辨率的地表温度数据。黑河流域共有13个地面气象站点，这些站点的地面温度观测在气象台站观测场内疏松平整的裸地上进行。所使用的站点观测地表温度都经过了严格质量控制。

3.2.3 MCD12Q1土地覆盖数据

MCD12Q1数据是一种MODIS全球范围内的土地覆盖类型产品，分辨率为500 m。该数据通过对MODIS的Terra和Aqua卫星的反射率数据进行监督分类，并采用辅助信息进行后处理进一步优化了特定类别。本文获取了2021年MCD12Q1数据（图3），采用第一个数据集Land cover type1（LC_Type1），并重采样至1 km。
图3 模拟实验数据点在研究区的位置分布

Fig. 3 Spatial distribution of the simulated experimental data points within the study area

4 实验结果与分析

4.1 模拟实验数据重建与分析

4.1.1 实验数据

实验数据点在研究区的位置如图3所示。图3反映了黑河流域的地表覆盖类型较为均一，空间均质性好，其中分布面积较广、范围较连续的地表覆盖类型为荒漠、草地和耕地。从2021年6、7、8月中的每个月份中分别选取晴空像元最多的一天，再从这三天中分别筛选出荒漠、草原、耕地3种不同地表覆盖类型的像元，要求这些像元AGRI反演的地表温度日变化曲线完整，不存在缺失值。

4.1.2 单时段地表温度数据缺失对重接结果影响的模拟分析

将5个时段中的任意单一时段人为赋值为空值，计算INA08模型拟合值与FY-4A AGRI LST原始值之间的RMSE，结果如图4所示。从图4中可以看出，缺失第二时段（高温时段）对模型拟合造成的影响最小， RMSE为2 K左右，这可能是因为高温时段地表温度变化较小的原因。影响模型拟合的参数 T a受一天中地表温度的最大、最小值影响，然而第二时段两端相邻的2个观测时刻（12时与16时）与一天中的温度最大值相差不大，因此参数 T a拟合误差相对较小。相比之下，缺失第五时段（夜间平缓下降时段）对模型拟合造成的影响最大，主要是因为夜间INA08模型的拟合方程为双曲线函数，若夜间温度平缓下降时段大量数值缺失，将导致拟合的双曲线模型渐进线斜率偏大，拟合值偏小。大部分实验结果显示，在白天时段中，缺失第三时段数据缺失造成的重建结果误差最大，第一时段次之，第二时段最小；在夜间时段中，缺失第四时段数据造成的重建结果误差小于第五时段。
图4 单一时段LST缺失情况下直接拟合值的RMSE

Fig. 4 RMSE of directly fitted LST for the condition of missing a single time period

在不同位置上，点7的实验结果与其他实验点差异较大，如缺失第一时段的RMSE偏高，缺失第五时段的RMSE相对较低。对于第一时段，一方面是遥感反演的该点地表温度在8时存在着温度下降的异常现象；另一方面，由于第一时段的数据缺失，缺少低温值参与INA08模型的拟合，导致直接拟合值偏高。也就是说， 8时的直接拟合值偏高、遥感反演原始值偏低，两者进行对比的误差较大，从而第一时段缺失重建的RMSE偏高。对于第五时段， 点7在第四时段的遥感反演LST下降速度相比其他实验点较为缓慢，当第四时段原始值参与INA08模型拟合时，第五时段直接拟合值呈缓慢下降趋势，减小了直接拟合值与遥感反演值之间的差异，因此第五时段缺失重建的RMSE偏低。
进一步地，补充模拟缺失时段内任意一个时刻的地表温度，使其参与模型拟合，计算补值拟合值与原始遥感反演值之间的RMSE'，结果如图5所示。对比图4和图5可以发现，当缺失时段有一个时刻的地表温度数据参与模拟后，整体RMSE'都在5 K以内，大多数实验点的第一时段RMSE'在1 K左右，第二时段RMSE'在2 K以内，第五时段RMSE'在3 K以内。实验结果均显示RMSE降低、精度提升，由此说明在缺失单时段的情况下，补充某一时刻的原始值使其参与模型拟合，能够有效提高INA08模型拟合与重建精度。
图5 单一时段LST缺失情况下补值拟合值的RMSE'

Fig. 5 RMSE' of the fitted LST based on complementary data for the condition of missing a single time period

4.1.3 2个时段地表温度数据缺失对重建结果影响的模拟分析

将5个时段中任意两时段人为赋值为空值，计算直接拟合值与原始值之间的RMSE；在模拟缺失的2个时段中，分别补充该时段内任意一个时刻的原始值，使其参与模型拟合，并计算补值拟合值与AGRI地表温度之间的RMSE'。由于夜间2个时段均缺失时，无法建立夜间拟合模型，因此这类模拟实验主要分析白天缺失2个时段、白天夜间各缺失一个时段的情况。图6和图7分别展示了不同缺失情况下拟合值与原始值之间的RMSE与RMSE'。
图6 不同两时段LST缺失情况下直接拟合值的RMSE

Fig. 6 RMSE of directly fitted LST for the condition of missing two different time periods

图7 不同两时段LST缺失情况下补值拟合值的RMSE'

Fig. 7 RMSE' of the fitted LST based on complementary data for the condition of missing two different time periods

从图6可以看出，缺失两时段的模拟数据重建误差整体上比缺失单时段数据大。除点7以外，其他实验点缺失包括第五时段在内的2个时段时，重建RMSE误差多在10 K以上，其余缺失情况的误差相对较小， RMSE大多在5 K左右。在单时段LST数据缺失的模拟实验中，分析了点7第一时段与第四时段存在遥感反演原始值的异常变化，造成第一时段数据缺失的RMSE偏高与第五时段数据缺失的RMSE偏低；然而，在2个时段数据缺失的模拟实验中， RMSE的计算同时受到2个缺失时段原始值的影响，因此缺失时段中包括第一、五时段的重建RMSE可能偏高或偏低。
比较图6和图7可以发现，在模拟缺失的时段中补充任意某个时刻的地表温度参与模型拟合，精度都有所提高，大部分模拟实验的RMSE'小于4 K，部分模拟实验的RMSE'小于1 K，个别模拟实验的RMSE'大于4 K。对比图5与图7可以发现，图5中RMSE'小于1 K、小于2 K与小于4 K的模拟实验分别占总实验的26.7%、55.6%和84.4%，图7分别为14.8%、 44.4%和93.8%，即图7的RMSE'更多集中在2 ~4 K。因此当缺失时段增加到2个时段后，精度的提升效果有所降低。

4.1.4 3个时段地表温度数据缺失对重建结果影响的模拟分析

将5个时段中任意三时段人为赋值为空值，计算直接拟合值与原始值之间的RMSE；在模拟缺失的3个时段中分别补充该时段内任一时刻的地表温度，使其参与模型拟合，并计算补值拟合值与原始值间的RMSE'。由于白天3个时段均缺失时无法建立白天拟合模型，夜间两个时段缺失时无法建立夜间的拟合模型，因此这类模拟实验为白天缺失2个时段和夜间缺失一个时段的情况。图8和图9分别展示了不同模拟实验下拟合值与原始值之间的RMES与RMSE'。
图8 不同三时段LST缺失情况下直接拟合值的RMSE

Fig. 8 RMSE of directly fitted LST for the condition of missing three different time periods

图9 不同三时段LST缺失情况下补值拟合值的RMSE'

Fig. 9 RMSE' of the fitted LST based on complementary data for the condition of missing three different time periods

从图8可以看出，大部分实验结果的RMSE大于5 K，占90.7%，而缺失单时段和两时段的重建RMSE大于5 K的分别约为53%和80.3%，因此，缺失三时段的重建误差要比缺失单时段、两时段的更大。由此可见，在大量数据缺失情况下，直接基于INA08模型拟合的结果误差较大。从图8不同的实验点来看，缺失的3个时段中包括第五时段的实验结果误差更大，其中点7与其他实验点的实验结果差异较大，特别是缺失第一、二、四时段时，再次说明了点7的异常温度日变化对实验结果的影响。根据图9， RMSE'小于2 K与小于4 K的模拟实验占总实验的40.7%和90.7%，与图5、图7相近。个别模拟实验的RMSE'在1 ~1.5 K，仅占总实验的5.6%，原因可能是随着缺失值不断增多，能够参与拟合的数据大量减少，模型拟合精度随之降低。

4.2 不同时段数据缺失的替换方案分析

INA08模型由白天的余弦函数以及夜间的双曲线函数构成。影响余弦函数曲线形状的关键参数有振幅与周期，即地表温度的高温值、低温值以及最高温度的时刻是影响INA08白天模型拟合的关键。影响双曲线函数形状的关键参数为渐近线的斜率，即夜间时段两个端点时刻的地表温度值是影响INA08夜间模型拟合的关键。根据研究区夏季地表温度日变化特点，以及前文不同时段地表温度缺失对重建精度的模拟分析结果，表1给出了不同时段数据缺失的替换方案。
表1 不同时段数据缺失的替换方案

Tab. 1 Replacement scheme for missing data at different time periods

缺失时段个数 缺失时段 替换方案
1 一 次日6时替换7时空值
二 不用替换
三 10时替换19时空值
四 白天模型计算20时拟合值替换该时刻空值
五 7时替换次日6时空值
2 一、二 次日6时替换7时空值
一、三 次日6时替换7时空值进行第一次拟合；10时拟合值替换19时空值进行第二次拟合
一、四 次日6时替换7时空值进行第一次拟合；白天模型计算20时拟合值替换该时刻空值进行第二次拟合
一、五 白天模型直接进行第一次拟合；白天模型计算7时拟合值替换次日6时进行第二次拟合
二、三 10时替换19时空值
二、四 白天模型计算20时拟合值替换该时刻空值
二、五 7时替换次日6时空值
三、四 10时替换19时空值进行第一次拟合；白天模型计算20时拟合值替换该时刻空值进行第二次拟合
三、五 10时替换19时空值，7时替换次日6时空值
3 一、二、四 次日6时替换7时空值进行第一次拟合；白天模型计算20时拟合值替换该时刻空值进行第二次拟合
一、二、五 白天模型直接进行第一次拟合；白天模型计算7时拟合值替换次日6时进行第二次拟合
一、三、四 次日6时替换7时空值进行第一次拟合；10时拟合值替换19时空值进行第二次拟合；白天模型计算20时拟合值替换该时刻空值进行第三次拟合
一、三、五 白天模型直接进行第一次拟合；10时拟合值替换19时空值，7时拟合值替换次日6时进行第二次拟合
二、三、四 10时替换19时空值进行第一次拟合；白天模型计算20时拟合值替换该时刻空值进行第二次拟合
二、三、五 10时替换19时空值，7时替换次日6时空值
在理论上，随着缺失时段数量的增多，部分时段缺失无法直接用其他时段遥感反演值进行空值替换时，可进行多次模型拟合，但这可能在一定程度上会降低模拟拟合与地表温度重建精度。
为了检验数据缺失的替换方案对提升重建精度是否具有有效性，本文利用以上替换方案对地表温度数据进行了缺失值重建与结果分析。

4.3 真实地表温度数据重建与分析

4.3.1 站点观测地表温度的点-面尺度转换的效果分析

图10为站点实测温度进行点-面尺度转换前后与FY-4A AGRI LST数据比较。可以看出，图10（b）中的数据更集中分布在1：1线上，且RMSE降低至1.48 K，说明尺度转换后的站点实测温度与FY-4A AGRI LST数据具有明显的线性相关性，因此点-面转换后的站点实测温度可以更为可靠地地验证地表温度重建结果。
图10 FY-4A AGRI LST与点-面转换前后的地面站点实测温度的散点图

Fig. 10 Scatter plot between FY-4A AGRI LST and the temperature measured at ground stations before and after point-to-surface conversion

4.3.2 真实地表温度缺失数据重建实验结果分析

利用黑河流域地面站点坐标位置提取出7月份的FY-4A AGRI LST，判断数据的缺失情况，将满足2.3部分所述缺失情况（3）的数据作为真实实验数据，通过INA08模型拟合，对缺失时刻的地表温度进行重建。计算直接重建结果与点-面尺度转换后的地面实测值之间误差RMSE，并计算基于表1对空值替换后的重建结果误差RMSE'，结果如表2所示。
表2 真实实验数据与结果

Tab. 2 Real experimental data and results

缺失时段 日期 站点 AGRI LST与实测值相关性R2 RMSE RMSE'
1 7月11日 酒泉 0.989 2 2.37 1.15
1 7月11日 张掖 0.983 2 4.48 2.14
1 7月11日 临泽 0.980 3 5.12 3.96
2 7月6日 临泽 0.951 3 1.80 -
2 7月17日 高台 0.985 7 0.77 -
3 7月4日 肃南 0.953 5 13.34 5.55
3 7月12日 托勒 0.989 6 6.88 3.50
3 7月18日 祁连 0.9711 7.17 2.09
4 7月22日 山丹 0.963 4 5.47 5.12
5 7月8日 酒泉 0.969 1 11.41 3.44
5 7月17日 民乐 0.986 0 62.07 0.88
5 7月23日 鼎新 0.968 5 60.41 1.80
1、2 7月11日 民乐 0.992 2 5.91 3.34
1、2 7月16日 高台 0.996 2 9.76 1.36
1、2 7月19日 额济纳旗 0.930 8 6.80 6.71
1、3 7月11日 托勒 0.983 7 7.25 4.64
2、3 7月3日 托勒 0.995 9 7.29 3.56
2、3 7月3日 肃南 0.872 8 11.11 5.92
2、3 7月3日 野牛沟 0.976 4 7.78 4.29
2、3 7月12日 野牛沟 0.925 7 4.30 3.93
2、4 7月12日 额济纳旗 0.982 4 3.17 2.58
3、4 7月17日 肃南 0.972 9 6.43 5.50
3、4 7月22日 祁连 0.981 4 15.26 6.04
3、4 7月27日 高台 0.953 6 3.49 2.32
2、3、4 7月19日 山丹 0.645 3 5.99 3.79
2、3、4 7月19日 祁连 0.964 9 3.89 8.14
由于天气状况的影响，云对地面造成的遮挡往往是时空连续的，卫星在获取地表温度数据时产生的缺值也是连续的，因此真实实验很少会出现模拟实验中跨时段缺值的情况。从表2的“缺失时段”也可以看出，在地面站点位置处，能够满足重建条件的7月份数据只有13天，并无法涵盖模拟实验中的所有缺失情况。
根据表2，空值替换后的重建结果与地面实测值之间的误差RMSE'总体呈现降低特点。部分日期与站点空值替换后的重建精度提高不大，通过分析站点实测数据发现，在FY-4A AGRI LST缺失的时间段里，对应的站点实测数据有明显的温度下降，而这种下降无法通过INA08模型准确拟合，因此空值替换后重建结果仍存在较大误差。
从缺失单一时段的实验结果来看，大部分真实实验的RMSE'降到4 K以内。缺失第二时段时，直接重建结果与实测值之间的误差RMSE在1 K左右，与其他缺失时段相比误差最小，且不需要其他时刻数据替换， RMSE'在表2中以斜线表示。缺失第五时段时，直接重建结果与实测值之间的误差RMSE相比于缺失其他时段较大，其中民乐与鼎新站点的RMSE高达60 K，这是由于第五时段为温度缓慢下降时段，该时段的缺失值重建采用INA08夜间模型进行拟合，在缺少夜间低温值的控制情况下，拟合的夜间双曲线斜率偏大，理论上应当缓慢降低的温度出现快速下降的趋势，从而造成拟合值异常偏低；在4.1.2部分的模拟实验中，不同的实验点在不同的数据拟合下，缺失第五时段的直接重建结果同样存在着RMSE的起伏变化。山丹站点FY-4A AGRI LST在7月22日的缺值率为72.5%，缺失率过高使得INA08模拟拟合精度较差，这是造成该站点缺失地表温度重建结果精度不高的主要原因。上述分析结果总体表明，真实数据得到的重建精度与模拟实验结论一致。
从缺失两时段的真实实验结果来看，空值替换后重建结果与站点实测值之间的误差RMSE'多为 2 K~5 K，比模拟实验中的误差要大一些。由于模拟实验中，在模拟个别时段缺失的情况下，保留了其他时段所有遥感反演值，而真实实验中，往往存在着一些时段全部缺失的情况，而且其余时段也有部分缺失值。因此，在真实实验中，参与模型拟合的地表温度数值比模拟实验少，模型拟合效果较差，误差更大。
缺失三时段的真实实验情况较少，往往是存在长时间、大区域缺值而不满足重建条件。表2中给出了第二、三、四时段连续缺值的两个真实实验结果，山丹站点的FY-4A AGRI LST在7月19日的缺值率为60%，缺值率较高，并且站点实测值与对应时刻的FY-4A原始值相关性为0.6453，相关性较其他真实实验更低，这也是空值替换后重建误差仍然较大的原因之一。祁连站点的FY-4A AGRI LST在7月19日的缺值率为55%，缺失数据空值替换后的重建精度反而降低，其主要原因是，当第二、三、四时段连续缺失时，INA08模型的拟合缺少了高温值输入，得到的白天时段余弦函数曲线对称轴向左偏移，夜间时段的双曲线函数曲线向下偏移，即直接拟合值偏低；缺失时段利用晴空时段的遥感反演原始值进行空值替换后，替换后的温度值比实际温度值要高，使得INA08模型拟合得到的补值拟合值偏高；由于该站点的地表温度实测值在第二时段开始下降，因此直接拟合值误差更小，补值拟合值误差反而更大。
在空间分布上，选取了真实试验中2021年7月5日18:00的重建前后数据进行对比，如图11所示。在7月5日，黑河流域南部地区受云遮挡的时间更长，FY-4A AGRI LST数据缺失更严重，参与拟合INA08模型的温度值较少，因此存在许多不满足重建条件的像元；相比之下，北部和中部地区可重建像元更多，并且重建后图像中的颜色过渡更为自然。从重建后的地表温度图像可以看出，黑河流域北部地区的温度高于中、南部地区的温度，符合黑河流域北部多为荒漠、中南部多为耕地与草原的实际情况；在中、南部地区，存在着西北-东南走向的条带状高温区，为黑河流域中、南部的荒漠覆盖地区，说明重建温度的空间分布合理，精度较好。总体而言，地表类型均一的自然地表的表面温度重建精度更高，异质性较大像元的地表温度重建效果相对较差。
图11 2021年7月5日18:00重建前后图像

Fig. 11 The LST images before and after reconstruction acquired at 18:00 on July 5,2021

5 结论与讨论

5.1 结论

针对FY-4A AGRI LST产品数据集的不同时段缺失情况，本文对黑河流域夏季地表温度日变化进行时段划分，采用INA08模型通过模拟数据分析数据缺失对重建精度的影响，并提出缺失时段替换方案，进而开展真实数据重建研究。在夏季地表温度缺失的模拟实验中，选取晴空条件下的9个实验点作为研究对象，模拟单时段、两时段、三时段地表温度缺失，将直接拟合值、补值拟合值分别与原始值进行比较。在夏季地表温度缺失的真实数据重建实验中，选择7月黑河流域地面实测站点所对应的FY-4A AGRI LST，对满足重建条件的实验点采取缺失时段的空值替换，并将直接重建结果、空值替换后重建结果分别与地面站点实测地表温度进行比较。结论如下：
（1）不同时段缺失以及不同缺失情况对INA08模型重建缺值的影响效果不同。单时段数据缺失的情况下，缺失第二时段（13~15时）的拟合误差最低，直接重建结果的RMSE为2 K左右，缺失第五时段（次日0时至6时）的拟合误差最大，直接重建结果的RMSE大于10 K。当缺失时段包括第五时段在内时，缺失两时段和三时段的重建RMSE多在10 K以上，其余缺失情况的误差相对较小，RMSE大多在5 K左右。
（2）随着缺失时段的增多，缺失时段数据替换后的重建结果误差逐渐增大。在模拟实验中，单时段缺失数据替换后重建结果的RMSE多为1 K左右，两时段缺失数据替换后的小部分重建结果RMSE小于1 K，而三时段缺失数据替换后重建结果的RMSE均大于1 K。
（3）真实实验与模拟实验结果的缺失时段与替换方案影响具有高度一致性。根据研究区夏季地表温度日变化特点，以及前文不同时段地表温度缺失对重建精度的模拟分析结果，提出的缺失时段替换方案，能够在一定程度上提高地表温度缺失数据重建精度。

5.2 讨论与展望

本文以黑河流域作为实验区，在深入分析缺失时段对地表温度重建精度影响的基础上，提出了缺失时段数据替换方案，对于FY-4A AGRI LST缺失数据的时间维重建具有一定的指导作用。但需要在以下方面深入开展后续研究工作。 ① 根据温度日变化规律进行的时段划分是针对黑河流域夏季时间的，由于时段划分节点与时间、地点、天气状况等因素有关，时段划分结果会随地理位置和季节变化而产生变化。但是，不同区域、不同日期的研究时段划分与替换重建方案原理在本质上是相同的，因此对于其他研究区域，可通过计算当地日出时刻、一天中温度最大值时刻、自由衰减时刻，结合该区域典型地物温度日变化规律，进行合适的时段划分。 ② 研究中开展的模拟实验是针对晴空条件下进行的，虽然在不同天气状况的真实实验中进行了检验，也取得了与模拟实验一致的较高重建精度，但晴空与非晴空环境下的地表温度日变化特征复杂多变，这将造成INA08地表温度日变化模型拟合具有一定程度的不确定性。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Anderson M C, Norman J M, Kustas W P, et al. A thermal-based remote sensing tech-nique for routine mapping of land-surface carbon, water and energy fluxes from field to regional scales[J]. Remote Sensing of Environment, 2008, 112(12). DOI:10.1016/j.rse.2008.07.009

[2]
Brunsell N A, Gillies R R. Length scale analysis of surface energy fluxes derived from remote sensing[J]. Journal of Hydrometeorology, 2003, 4(6):1212-1219. DOI:10.1175/1525-7541(2003)004<1212:LSAOSE>2.0.CO;2

[3]
Karnieli, Arnon, Agam, et al. Use of NDVI and land surface temperature for drought a-ssessment: merits and limitations[J]. Journal of Climate, 2010, 23(3). DOI:10.1175/2009JCLI2900.1

[4]
Kustas W, Anderson M. Advances in thermal infrared remote sensing for land surface modeling[J]. Agricultural and Forest Meteorology, 2009, 149(12). DOI:10.1016/j.agrformet.2009.05.016

[5]
Zhang R, Tian J, Su H, et al. Two improvements of an operational two-layer model for terrestrial surface heat flux retrieval[J]. Sensors, 2008, 8(10). DOI:10.3390/s8106165

[6]
Bai Y, Wong M S, Shi W-Z, et al. Advancing of land surface temperature retrieval usi-ng extreme learning machine and spatio-temporal adaptive data fusion algorithm[J]. Re-mote Sensing, 2015, 7(4). DOI:10.3390/rs70404424

[7]
Moosavi V, Talebi A, Mokhtari M H, et al. A wavelet-artificial intelligence fusion appr-oach (WAIFA) for blending Landsat and MODIS surface temperature[J]. Remote Sensing of Environment, 2015, 169. DOI:10.1016/j.rse.2015.08.015

[8]
Holmes T R H, Crow W T, Hain C, et al. Diurnal temperature cycle as observed by t-hermal infrared and microwave radiometers[J]. Remote Sensing of Environment, 2015, 158. DOI:10.1016/j.rse.2014.10.031

[9]
Grigsby S P, Hulley G C, Roberts D A, et al. Improved surface temperature estimates with MASTER/AVIRIS sensor fusion[J]. Remote Sensing of Environment, 2015, 167. DOI:10.1016/j.rse.2015.05.019

[10]
Weng Q, Fu P. Modeling annual parameters of clear-sky land surface temperature variat-ions and evaluating the impact of cloud cover using time series of Landsat TIR data[J]. Remote Sensing of Environment, 2014, 140:267-278. DOI:10.1016/j.rse.2013.09.002

[11]
王爱辉, 杨英宝, 潘鑫, 等. 顾及时空特征的FY-4A云覆盖像元地表温度重建模型[J]. 武汉大学学报(信息科学版), 2021, 46(06):852-862.

[ Wang A H, Yang Y B, Pan X, et al. Land s-urface temperature reconstruction model of FY-4A cloudy pixels considering spatial and temporal characteristics[J]. Geomatics and Information Science of Wuhan University, 2021, 46(6):852-862. ] DOI:10.13203/j.whugis20200039

[12]
周芳成, 唐世浩, 韩秀珍, 等. 云下遥感地表温度重构方法研究[J]. 国土资源遥感, 2021, 33(1):78-85.

[ Zhou F C, Tang S H, Han X Z, et al. Research on reconstructing missing rem-otely sensed land surface temperature data in cloudy sky[J]. Remote Sensing for Natural Resources, 2021, 33(1):78-85. ] DOI:10.6046/gtzyyg.2020113

[13]
张军, 覃志豪, 刘梅, 等. 利用空间插值法估算云覆盖像元地表温度的可行性研究[J]. 地理与地理信息科学, 2011, 27(6):45-49,115.

[ Zhang J, Qin Z H, Liu M, et al. Estimating of la-nd surface temperature under the cloud cover with spatial interpolation[J]. Geography a-nd Geo-Information Science, 2011, 27(6):45-49,115. ]

[14]
涂丽丽, 覃志豪, 张军, 等. 基于空间内插的云下地表温度估计及精度分析[J]. 遥感信息, 2011(4):59-63,106.

[ Tu L L, Qin Z H, Zhang J, et al. Surface temperature estimation and a-ccuracy analysis of clouds based on spatial interpolation[J]. Remote Sensing Information, 2011(4):59-63,106. ] DOI:10.3969/j.issn.1000-3177.2011.04.012

[15]
周义, 覃志豪, 包刚. GIDS空间插值法估算云下地表温度[J]. 遥感学报, 2012, 16(03):492-504.

[ Zhou Y, Qin Z H, Bao G. Land surface temperature estimation under cloud cover wi-th GIDS[J]. Journal of Remote Sensing, 2012, 16(3):492-504. ] DOI:10.11834/jrs.20121091.

[16]
Zhao W, Duan S B. Reconstruction of daytime land surface temperatures under cloud-c-overed conditions using integrated MODIS/Terra land products and MSG geostationary s-atellite data[J]. Remote Sensing of Environment, 2020, 247:111931. DOI:10.1016/j.rse.2020.111931.

[17]
鲍瑶, 杨英宝. 长时序无缝地表温度重建方法研究[J/OL]. 遥感技术与应用. https://kns.cnki.net/kcms/detail/62.1099.TP.20230327.1632.002.html.

[ Bao Y, Yang Y B. Research on long-term Gap-Free Land surface temperature reconst-ruction method[J/OL]. Remote Sensing Technology and Application,

[18]
Wu P, Yin Z, Yang H, et al. Reconstructing geostationary satellite land surface tempera-ture imagery based on a multiscale feature connected convolutional neural network[J]. R-emote Sensing, 2019, 11(3):300. DOI:10.3390/rs11030300

[19]
崔晓临, 程贇, 张露, 等. 基于DEM修正的MODIS地表温度产品空间插值[J]. 地球信息科学学报, 2018, 20(12):1768-1776.

DOI

[ Cui X L, Cheng Y, Zhang L, et al. Spatial interpolation of MODIS land surface temperature products based on DEM correction[J]. Journal of G-eo-Information Science, 2018, 20(12):1768-1776. ] DOI:10.12082/dqxxkx.2018.180340

[20]
Xu Y, Shen Y. Reconstruction of the land surface temperature time series using harmo-nic analysis[J]. Computers & Geosciences, 2013, 61:126-132. DOI:10.1016/j.cageo.2013.08.009

[21]
臧琳, 宋冬梅, 甘宇亮, 等. 统计模型与滤波算法的地表温度重建方法探讨[J]. 测绘科学, 2016, 41(7):11-17.

[ Zang L, Song D M, Gan Y L, et al. Study on reconstruction of LST ba-sed on the statistical model and filtering algorithm[J]. Science of Surveying and Mappi-ng, 2016, 41(7):11-17. ] DOI:10.16251/j.cnki.1009-2307.2016.07.003

[22]
Tian Y, Jia R S, Xu S H, et al. Super-resolution reconstruction of remote sensing imag-es based on convolutional neural network[J]. Journal of Applied Remote Sensing, 2019, 13(4):046502-046502. DOI:10.1117/1.JRS.13.4.046502

[23]
Arslan N, Sekertekin A. Application of Long Short-Term Memory neural network model for the reconstruction of MODIS Land Surface Temperature images[J]. Journal of Atm-ospheric and Solar-Terrestrial Physics, 2019, 194, 105100. DOI:10.1016/j.jastp.2019.105100

[24]
Mo Y, Xu Y, Chen H, et al. A review of reconstructing remotely sensed land surface t-emperature under cloudy conditions[J]. Remote Sensing, 2021, 13(14):2838. DOI:10.3390/rs13142838

[25]
Schädlich S, Göttsche F M, Olesen F-S. Influence of land surface parameters and atmo-sphere on METEOSAT brightness temperatures and generation of land surface temperat-ure maps by temporally and spatially interpolating atmospheric correction[J]. Remote Se-nsing of Environment, 2001, 75(1). DOI:10.1016/S0034-4257(00)00154-1

[26]
Feng G, Masek J, Schwaller M, et al. On the blending of the Landsat and MODIS sur-face reflectance: predicting daily Landsat surface reflectance[J]. IEEE Transactions on G-eoscience and Remote Sensing, 2006, 44(8):2207-2218. DOI:10.1109/TGRS.2006.872081

[27]
Inamdar A K, French A, Hook S, et al. Land surface temperature retrieval at high spat-ial and temporal resolutions over the southwestern United States[J]. Journal of Geophys-ical Research: Atmospheres, 2008, 113(D7). DOI:10.1029/2007JD009048

[28]
Göttsche F-M, Olesen F-S. Modelling the effect of optical thickness on diurnal cycles o-f land surface temperature[J]. Remote Sensing of Environment, 2009, 113(11):2306-2316. DOI:10.1016/j.rse.2009.06.006

[29]
Duan S B, Li Z L, Wu H, et al. Modeling of day-to-day temporal progression of clear-sky land surface temperature[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5):1050-1054. DOI:10.1109/LGRS.2012.2228465

[30]
Weiss D J, Atkinson P M, Bhatt S, et al. An effective approach for gap-filling contine-ntal scale remotely sensed time-series[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 98:106-118. DOI:10.1016/j.isprs jprs.2014.10.001

[31]
Li X, Zhou Y, Asrar G R, et al. Creating a seamless 1km resolution daily land surface temperature dataset for urban and surrounding areas in the conterminous United States[J]. Remote Sensing of Environment, 2018, 206:84-97. DOI:10.1016/j.rse.2017.12.010

[32]
Duan S-B, Li Z-L, Wang N, et al. Evaluation of six land-surface diurnal temperature c-ycle models using clear-sky in situ and satellite data[J]. Remote Sensing of Environme-nt, 2012, 124. DOI:10.1016/j.rse.2012.04.016

[33]
陈颖, 段四波, 冷佩, 等. 极轨卫星热红外地表温度日变化模拟[J]. 遥感信息, 2016, 31(6):7-14.

[ Chen Y, Duan S B, Leng P, et al. Modeling of diurnal cycle of land surface temper-ature based on polar orbiting satellite thermal infrared data[J]. Remote Sensing Informat-ion, 2016, 31(6):7-14. ] DOI:10.3969/j.issn.1000-3177.2016.06.

[34]
Hong F, Zhan W, Göttsche F-M, et al. Comprehensive assessment of four-parameter di-urnal land surface temperature cycle models under clear-sky[J]. ISPRS Journal of Photo-grammetry and Remote Sensing, 2018, 142:190-204. DOI:10.1016/j.isprsjprs.2018.06.008

[35]
张德军, 杨世琦, 王永前, 等. 基于FY3C地表温度重建的多云地区旱情监测评估[J]. 自然资源学报, 2021, 36(4):1047-1061.

DOI

[ Zhang D J, Yang S Q, Wang Y Q, et al. Assessing dro-ught conditions over cloudy regions based on reconstructed FY3C/VIRR LST[J]. Journal of Natural Resources, 2021, 36(4):1047-1061. ] DOI:10.31497/zrzyxb.20210418

[36]
刘紫涵, 吴鹏海, 吴艳兰, 等. 风云静止卫星地表温度产品空值数据稳健修复[J]. 遥感学报, 2017, 21(1):40-51.

[ Liu Z H, Wu P H, Wu Y L, et al. Robust reconstruction of missing d-ata in Feng Yun geostationary satellite land surface temperature products[J]. Journal of Remote Sensing, 2017, 21(1):40-51. ] DOI:10.11834/jrs.20176003

[37]
柯灵红, 王正兴, 宋春桥, 等. 青藏高原东北部MODIS LST时间序列重建及与台站地温比较[J]. 地理科学进展, 2011, 30(7):819-826.

[ Ke L H, Wang Z X, Song C Q, et al. Recons-truction of MODIS LST time series and comparison with land surface temperature(T) a-mong observation stations in the Northeast Qinghai-Tibet Plateau[J]. Progress in Geogra-phy, 2011, 30(7):819-826. ] DOI:10.11820/dlkxjz.2011.07.006

[38]
韩晓勇, 韩玲, 戚鹏程. 秦巴山区MODIS LST时序数据重建及特征分析[J]. 地理与地理信息科学, 2016, 32(1):71-77.

[ Han X Y, Han L, Qi P C. Reconstruction of MODIS LST ti-me series and features analysis in Qinling-Bashan Mountain area[J]. Geography and Geo-Information Science, 2016, 32(1):71-77. ] DOI:10.3969/j.issn.1672-0504.2016.01.014

[39]
刘艳, 王锦地, 周红敏, 等. 用地面点测量数据验证LAI产品中的尺度转换方法[J]. 遥感学报, 2014, 18(6):1189-1198.

[ Liu Y, Wang J D, Zhou H M, et al. Upscaling approach for v-alidation of LAI products derived from remote sensing observation[J]. Journal of Remot-e Sensing, 2014, 18(6):1189-1198. ] DOI:10.11834/jrs.20144084

[40]
吴立宗. 黑河流域研究区边界:国家冰川冻土沙漠科学数据中心(www.ncdc.ac.cn).

[ Wu L Z. The boundary of the Black River Basin study area: National Cryosphere Desert Data Center(www.ncdc.ac.cn) DOI:10.12072/ncdc.Westdc.db0013.2020]

Options
文章导航

/

〈 〉