EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 5: 1283 - 1295

DOI: https://doi.org/10.12082/dqxxkx.2024.230673

地球信息科学理论与方法

综合局部莫兰指数和PageRank算法的网络空间资源节点隐喻可视化表达

  • 齐凯 ,
  • 张衡 , * ,
  • 周杨 ,
  • 刘一帆 ,
  • 李庆祥
展开
  • 战略支援部队信息工程大学地理空间信息学院，郑州 450001
*张 衡（1976—），男，河南郑州，博士，副教授，主要从事摄影测量与遥感方向的研究。 E-mail:

齐 凯（1998—），男，河南周口人，硕士生，主要从事摄影测量与遥感方向的研究。E-mail:

收稿日期: 2023-11-13

  修回日期: 2024-01-11

  网络出版日期: 2024-05-21

基金资助

国家重点研发计划项目(2016YFB0801301-2)

国家重点研发计划项目(2016YFB0801303)

收起

Metaphor Representation of Resource Nodes in Cyberspace Based on Local Moran Index and PageRank Algorithm

  • QI Kai ,
  • ZHANG Heng , * ,
  • ZHOU Yang ,
  • LIU Yifan ,
  • LI Qingxiang
Expand
  • Institute of Geospatial Information,Information Engineering University, Zhengzhou 450001, China
*ZHANG Heng, E-mail:

Received date: 2023-11-13

  Revised date: 2024-01-11

  Online published: 2024-05-21

Supported by

National Key Research and Development Program of China(2016YFB0801301-2)

National Key Research and Development Program of China(2016YFB0801303)

Fold

摘要

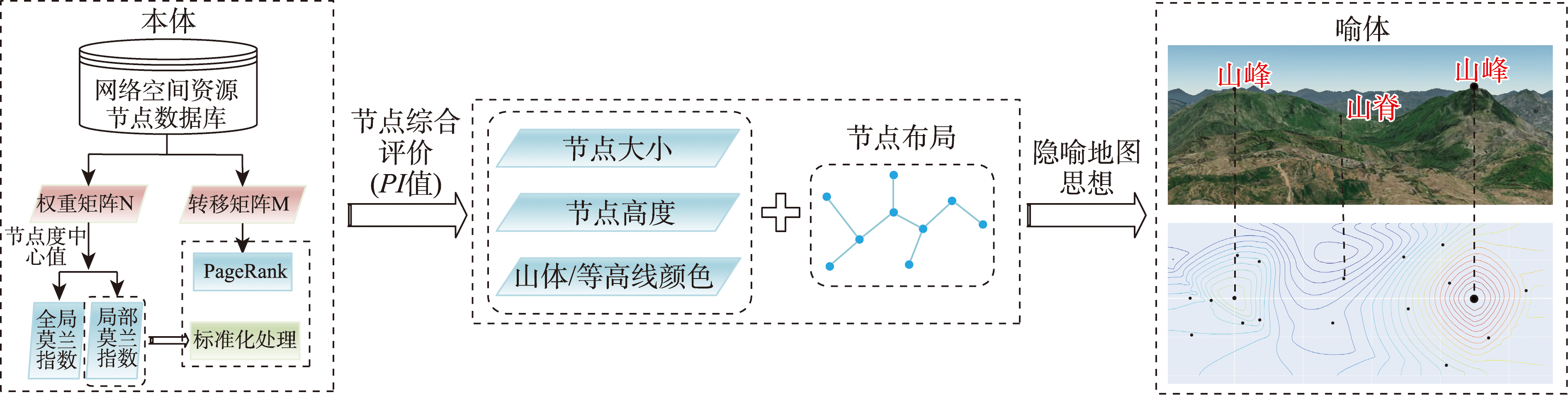
可视化是一种非常有效的网络空间资源分析方式，通过借助点线面、符号、地形等形象映射抽象数据，可以更好地管理、维护和优化网络空间。考虑到网络空间资源节点在网络中的空间相关性和重要性，本文借助隐喻地图思想，将网络空间中资源节点视为本体，传统地理空间中山峰和等高线作为喻体进行可视化表达。首先，通过节点之间的拓扑关系构建空间权重矩阵和转移矩阵，以此计算出节点的局部莫兰指数和PageRank值。为了更全面地综合考虑节点在局部和全局范围内的空间相关性和重要性，使局部莫兰指数进行标准化处理与PageRank值达到相同的取值范围后将二者结合得到综合评价指标（PI值）；然后，将网络空间资源节点根据FR算法围绕重要程度最高的节点进行布局，通过PI值赋予节点高度值和大小；最后，借助隐喻地图的思进行可视化表达。实验数据表明，相较于传统的节点评价方法，该方法将用于衡量地理空间数据中是否存在空间聚集现象的莫兰指数引入到网络空间，可以突出节点中属性值较高并且与其相连节点属性值也高的节点；同时，基于隐喻地图思想进行可视化表达可以直观表现出节点在网络空间中的所处地位以及与其他节点间的相互关系，并且在针对格式化数据进行渲染时，随着网络规模的扩大隐喻地图效率优于传统拓扑图。

关键词： 网络空间; 网络空间测绘; 莫兰指数; 莫兰散点图; PageRank算法; 综合评价; 隐喻地图; 可视化

本文引用格式

齐凯 , 张衡 , 周杨 , 刘一帆 , 李庆祥 . 综合局部莫兰指数和PageRank算法的网络空间资源节点隐喻可视化表达[J]. 地球信息科学学报, 2024 , 26(5) : 1283 -1295 . DOI: 10.12082/dqxxkx.2024.230673

Abstract

Visualization serves as an incredibly effective method for analyzing and understanding cyberspace resources. By leveraging elements such as points, lines, surfaces, symbols, and terrain, it offers valuable insights for the management, maintenance, and optimization of cyberspace by transforming abstract data into tangible and comprehensible forms. In this context, this paper recognizes the significance of spatial relationships and the importance of resource nodes in the network and adopts the concept of a metaphorical map as a means of visualization. It draws an analogy between the resource nodes in cyberspace and the metaphorical representation of peaks and contouring lines in traditional geographic space, facilitating visual expression and understanding. The methodology proposed in this paper involves constructing spatial weight matrices and transfer matrices based on the topological relationships among nodes in cyberspace. These matrices enable the computation of indices such as the Moreland index and PageRank value for each node, which are vital metrics for evaluating the local importance of nodes within the network. To comprehensively assess the spatial correlation and significance of nodes on both local and global scales, the local Moran index is standardized, and the PageRank values are transformed to a consistent range. These standardized indices are then combined to derive a comprehensive evaluation index called the PI value. Subsequently, the network space resource nodes are arranged around the most prominent node utilizing the FR algorithm. The PI value guides the assignment of height values and sizes to each node, facilitating their visual representation. Finally, the visualization is performed using a metaphorical map that allows for an intuitive depiction of the nodes' positions in the network space and their relationships with other nodes. Our experimental results demonstrate that this method effectively incorporates the Moreland index, commonly employed to measure spatial aggregation in geospatial data, into the network space analysis. As a result, the method effectively highlights nodes and their interconnected nodes with higher attribute values. Furthermore, the visual representation based on the metaphorical map provides a natural and intuitive understanding of the nodes' positions and their interconnections in network space. It offers a means of effectively communicating complex information about the network's structure and topology. Moreover, when rendering formatted data, the efficiency of the metaphorical map exceeds that of traditional topology maps, particularly as the scale of the network expands. The metaphorical map proves to be a powerful tool for visualizing and comprehending the intricate relationships within cyberspace resources.

Key words： cyberspace; cyberspace mapping; Moran index; Moran scatter plot; PageRank algorithm; comprehensive evaluation; metaphorical map; visualization

1 引言

网络空间中不存在距离和方向的概念，各种事件与过程均在零时间、零距离下完成，是一种完全区别于传统地理空间的虚拟空间，其中包含丰富的资源信息。网络空间资源通常是指在网络空间中存在、存储、传输和共享的各种实体化和虚拟化资源，如物理设备、传输介质、应用程序、数据集、多媒体内容等。如何在有效的空间内，合理、有效的将网络空间资源信息展示出来是亟待解决的问题[1-4]。隐喻地图作为非空间数据可视化的方式，可以赋予非空间数据以虚拟坐标，通过构造虚拟地图空间将抽象的非空间数据映射到人们所熟悉领域对象上，帮助用户以空间思维进行信息获取与知识发现[5-7]。将网络空间资源数据通过隐喻地图方式进行映射可以更加精准的分析网络结构、了解网络的变化规律、为决策者提供有价值的网络信息资源。
目前有很多学者针对网络空间资源可视化开展了一系列的研究，主要从图化简技术[8⇓⇓⇓⇓⇓-14]和可视化技术[15⇓⇓⇓⇓⇓⇓⇓⇓-24] 2个方面进行。针对于大规模的网络资源数据，通过图化简技术可以有效的避免视觉混乱造成的信息冗余现象。图化简技术主要包括边捆绑算法和节点聚类2类，Qu等[8]通过借助三角函数构造控制网格以此实现边捆绑的效果；Holten等[9]基于弹簧模型提出了力导向的FDEB(Force-Directed Edge Bundling)边捆绑方法；Hurter等[10]基于核密度估计的提出了KDEEB(Kernel Density Estimation Edge Bundling)边捆绑方法；Peysakhovich[11]等基于通用图的属性驱动提出了ADEB(Attribute Driven Edge Bundling)边捆绑方法。以上方法均是通过将边按照一定的规则进行捆绑，进而解决边过多造成的视觉混乱。Rosvall[12]和Harrison[13]等分别通过基于社区发现算法的节点聚类和通过属性合并创建要素的层级结构以此凸显网络中的关键节点，减少视觉混乱；王续盘等[14]通过将Blondel和k-核分解算法相结合，构建了点群要素多尺度表达模型，可以为数据分析提供不同尺度下的节点数据。
网络资源可视化技术主要分为地理强相关、弱相关和非空间相关3类。其中地理强相关的制图方法是以传统的地图作为底图进行资源绘制[15-16]；地理弱相关的制图方法强调地理单元属性之间的相对关联程度，而非精确的地理关联性[17⇓⇓-20]；非空间相关的地图制图方法不再以地理空间为核心，主要用于描述与网络空间中与空间不相关的资源要素[21⇓⇓-24]。隐喻地图被广泛的应用于各个领域的研究中，Gould等[25]通过隐喻地图研究了人们对城市中心地带的感知；Gronemann等[26]研究了网络数据内在关联的地图隐喻表达；CHEN等[27]通过隐喻地图方式提出 D-Map 可视化方法，模拟社交网络空间信息的传播过程；艾廷华等[28]等引入水流扩展的思想，绘制Voronoi图以此来隐喻各类地理对象；信睿等[29]基于Gosper曲线和隐喻地图思想研究非空间数据的空间隐喻表达与分析；高贞[30]以河流符号的长度、线型、线宽、颜色等视觉特征隐喻非空间层次信息，绘制了河系地图；Chen等[31]基于隐喻地图的思想根据信息之间的转发特征构建了R-Map的可视化地图；Chi等[32]基于玫瑰图的结构和特点构建了多维玫瑰图，以此隐喻出多维数据；Ma等[33]将社交媒体中紧急需求事件的关键词、相关主题和转发评论等转化为隐喻地图中相应的地图特征，以此构建了一种基于隐喻图的应急需求可视化方法。
考虑到网络空间并非传统的地理空间，如果仍然采用欧氏距离进行网络空间分析，难以满足抽象、复杂的网络空间资源信息的描述与表达需求。并且网络空间中资源数据呈指数级增长，以传统的文字、数字和图表等信息对网络空间资源数据进行分析难以发现其中的问题[6]。为了更好的感知和描述网络空间资源信息综合考虑节点在局部和全局范围内的空间相关性和重要性，本文基于局部莫兰指数[34]和PageRank[35]值借鉴隐喻地图的思想进行可视化表达。实验结果表明本文将用于衡量地理空间数据中是否存在空间聚集现象的莫兰指数引入到网络空间，可以突出节点中属性值较高并且与其相连节点属性值也高的节点；同时，基于隐喻地图思想进行可视化表达可以清晰的表现出节点在网络中所处的地位，以及与其他节点之间的关系。同时，本文方法针对大规模网络的格式化数据进行渲染时效率优于传统拓扑网络，可以更好地理解、分析和应对大规模网络中的威胁和安全问题。

2 研究思路

在地理空间中地形的高低起伏构成了山峰、洼地和山脊，通常采用等高线来表示地形起伏。通常情况下，人眼视觉映射的垂直方向与对象的重要程度呈正相关。为此本文考虑通过地理空间中的山峰和等高线的高度和位置隐喻网络空间中的资源，如图1所示。将网络空间资源视为本体，基于网络空间中拓扑数据构建权重矩阵N和转移矩阵M，分别计算出局部莫兰指数和PageRank值。其中，莫兰指数可以用来衡量网络空间资源之间的空间相关性，发现资源之间的空间集聚模式；而PageRank值可以衡量网络空间资源中的重要性和影响力，能够识别出关键资源和核心节点。为了综合考虑节点相关性和重要性，使局部莫兰指数进行标准化处理与PageRank值达到相同的取值范围后将二者结合得到综合评价指标，以此赋予节点大小、高度值和颜色。再通过传统的FR算法围绕重要程度最高的节点进行布局，最终在二维空间中隐喻出等高线图，在三维空间中隐喻出山峰图。
图1 网络空间资源节点隐喻地图可视化表达

Fig. 1 Visualization of metaphor map of resource nodes in cyberspace

通过综合评定指标可以将网络空间资源隐喻到等高线和山峰上，隐喻地图中关键要素及含义如表1所示。山峰和等高线的高度代表网络资源的在经过综合评价之后的重要程度，山峰上的节点表示高重要性，洼地上的节点表示低重要性；位置信息可以表示网络资源在网络中的相对位置；节点的大小可以反映出资源的综合影响力。通过山峰和等高线隐喻网络空间资源可以更直观地感受和理解网络空间中资源信息的数据特征以及网络中关键的节点，并从中挖掘出潜在的规律。
表1 隐喻地图关键要素及含义

Tab. 1 Key elements and implications of metaphor map

关键要素 隐喻地图含义
山峰 表示网络中重要程度较高的节点
山谷 表示网络中重要程度较低的节点
节点大小 与网络中节点重要程度成正相关
节点位置
 围绕网络中重要程度最高的节点进行布局，表示节点在拓扑空间中相对的位置关系
等高线 等高线的高度与网络中节点重要程度成正相关

3 研究方法

3.1 网络空间资源节点评价方法

3.1.1 网络空间权重矩阵

空间权重矩阵（Spatial Weight Matrix）是一种用于描述空间接近性或空间关系的矩阵。这个矩阵可以用来描述单元之间的空间依赖性，是空间统计、空间计量经济分析的重要基础[36]。本文将空间权重矩阵引入到网络空间中，通过网络空间资源间拓扑关系构建网络空间权重矩阵，若网络空间中有n个节点，则会构建出n×n的权重矩阵N：
N = w 11 w 12 ⋯ w 1 n w 21 w 22 ⋯ w 2 n ⋮ ⋮ ⋯ ⋮ w n 1 w n 2 ⋯ w n n
其中，网络空间权重矩阵中元素满足：
w i j = 1                             i 和 j 相 接                       0                           i 和 j 不 相 接 或 i = j
式中： i和 j代表网络空间中资源节点的编号，当网络空间资源中拓扑节点 i和节点 j相连接时，则在矩阵中对应的元素 w i j为1，否则元素 w i j为0。

3.1.2 莫兰指数

莫兰指数主要用于衡量空间数据中是否存在空间聚集的现象。莫兰指数又分为全局莫兰指数IG（global Moran's I）和局部莫兰指数IL（local Moran's I）。其中，全局莫兰指数用来分析空间整体上有没有自相关性存在，局部莫兰指数可以反映网络空间资源中某一节点 i附近的空间集聚状况，表达公式可表示为：
I G = n × ∑ i = 1 n ∑ j = 1 n w i j x i - x - x j - x - ∑ i = 1 n ∑ j = 1 n w i j × ∑ i = 1 n x i - x - 2
I L = n × x i - x - ∑ j = 1 n w i j x j - x - ∑ i = 1 n x i - x - 2
式中： n代表网络空间资源中拓扑节点的个数； w i j  代表权重矩阵N中的第 i行第 j列的值； x i和 x j分别代表网络空间资源中拓扑节点 i和节点 j的属性值； x -为所有网络空间资源中拓扑节点属性值的平均。考虑到网络空间中度中心值较大的节点通常被认为是社团中的核心节点，这些节点在传递信息资源时起到关键作用，所以本文将度中心值作为节点的属性值，表达公式可表示为：
D C i = k i n - 1
式中： k i表示现有的与节点 i相连的边的数量； n - 1表示节点 i与其他节点都相连的边的数量。
全局莫兰指数的取值范围是[-1，1]，当全局莫兰指数取值范围是（0，1]时空间正相关，取值范围是[-1,0）时空间负相关，当莫兰指数为0时，则说明呈空间随机分布。局部莫兰指数的取值范围并没有限制。局部莫兰指数会将网络空间资源节点划分到4个象限中，以此表示节点属性值与周围节点的属性值呈现不同的关系。

3.1.3 PageRank算法

PageRank算法将节点之间的连接关系表示为一个有向图G=(V, E)，其中V和E分别表示网络空间节点和节点之间有向边的集合，在其基础上引入随机游走模型，即一阶马尔可夫链，表示网络空间节点中信息传递的过程。可以用于评估网络空间中节点的重要性。一般的随机游走模型的转移矩阵由两部分的线性组合组成，一部分是有向图的基本转移矩阵M，表示从一个节点到其链出的所有节点的转移概率相等，另一部分是完全随机的转移矩阵，表示从任意一个节点到其它节点的转移概率都是1/n [35]。
M = m i j n × n
式中： m i j取值与节点和节点之间的有向边有关，如果节点 j有k个有向边链出，并且节点 i是其链出的一个节点，则 m i j的取值为1/k；否则 m i j为0，其中 i, j=1,2,…,n。
R = d × M × R + 1 - d n × 1
式中：第一项表示依照转移阵M访各个节点的概率，第二项表示完全随机访问各个节点的概率。d 为线性组合系数，当d接近1时，随机游走主要依照转移矩阵M进行，当d接近0时，随机游走主要以等概率随机访问各个节点。1代表n维列向量，其中所有元素都等于1。R的各个分量称为各个节点的PageRank值，则由式（7）可以计算出每个节点的PageRank值。
P R v i = d ∑ v j ∈ M v i P R v j L v j + 1 - d n             ( i = 1,2 , … , n )

3.2 网络空间资源节点综合度量

局部莫兰指数可以确定节点在拓扑网络中与其邻居节点之间的相互作用程度。节点的局部莫兰指数越高，表示该节点与其邻居节点之间的相关性越显著。PageRank值可以确定节点在整个网络中的影响力大小。节点的PageRank值越高，表示该节点在整个拓扑网络中就越重要。为了综合考虑节点在整个网络中的空间相关性和重要性，将局部莫兰指数与PageRank值相结合，如果局部莫兰指数较高且与节点的PageRank一致，那说明该节点不仅在空间上具有聚集性，并且在网络中具有较高的重要性。反之，如果莫兰指数较高但节点的PageRank较低，那可能说明该节点在网络中重要性较低，但在空间上具有一定的聚集性。考虑到局部莫兰指数的取值范围较大，而PageRank值的取值范围为[0,1]，为了消除局部莫兰指数在综合评价时的主导地位，考虑将局部莫兰指数的值进行标准化，达到与PageRank值相同的取值范围，以下是将局部莫兰指数标准化的伪代码：
算法1 网络空间资源节点局部莫兰指数标准化
输入：网络空间资源节点的局部莫兰指数
输出：标准化后的局部莫兰指数
# 计算局部莫兰指数绝对值之和
abs_sum_values = 计算局部莫兰指数绝对值之和
# 将数据绝对值调整到（0，1）范围内，且所有值之和为1
adjusted_data = 将数据调整到（0，1）范围内
# 保持数据原始的正负性
Until normalized_data
将标准化之后的局部莫兰指数和PageRank值进行综合得到PI值，该值可以对网络空间资源节点进行综合评价，表达式如下：
P I = α · R + 1 - α I L · 1
式中：α表示比例系数；1表示n维列向量。

3.3 网络空间资源节点布局算法

为了更直观地感受出网络空间资源节点之间的在非欧式空间中的布局，在隐喻地图中引入FR（Fruchterman-Reingold）布局算法，该布局算法将所有的节点看作电子，每个节点都会在斥力和引力的作用下达到平衡状态[37]。FR算法在布局时将根据式（9）计算出来的最大PI值作为中心节点，其余节点根据式（10）计算每个节点的斥力和引力，最终达到平衡状态。
F r = k 2 d F a = d 2 k
式中：d代表任意2个节点之间的实际距离；k代表网络中每个节点所占据的理想空间的大小。经过FR布局算法之后，可确定资源节点在山峰图和等高线中的位置。

4 实验与分析

4.1 实验数据

为了探究本文方法的可靠性，使用社交网络中经典网络进行实验验证，主要包括针对空手道俱乐部成员构成的Karate网络[38]、Lusseau等[39]在新西兰针对宽吻海豚的生活习性构造的Dolphin网络、根据维克多·雨果的小说《悲惨世界》中人物之间交往关系建立的Lesmis网络[40]和根据美国政治类书籍在亚马逊网上书店的销售情况分析购买者的政治倾向构造的Polbooks网络[41]。在验证了本文方法的可靠性之后，基于网络空间中真实的路由器拓扑数据进行实验分析，路由器网络主要由4 677个路由器节点和由路由器节点构成的6 123条边构成，这 5个网络的信息如表2所示。
表2 网络数据集特征

Tab. 2 Classic network set

网络名称 节点数/个 边数/条 平均度 图密度
Karate 34 78 4.588 0.139 0
Dolphin 62 159 5.129 0.084 0
Lesmis 77 254 6.597 0.087 0
Polbooks 105 441 8.400 0.081 0
路由器网络 4 677 6 123 2.618 0.000 6

4.2 网络实验分析验证

本文首先基于社交网络中经典网络进行实验分析，按照实验顺序分为计算莫兰指数、计算PageRank值、综合节点度量指标和构建网络空间隐喻地图4个阶段，再基于真实的路由器网络来验证构建的网络空间节点地图在大规模网络中的可行性。
图4 Karate网络资源节点地图

Fig. 4 Karate network resource node map

（1）根据经典网络节点之间的拓扑关系构建权重矩阵，根据式（5）计算出每个节点的度中心值，将度中心值和权重矩阵代入到式（3）中计算出Karate、Dolphin、Lesmis和Polbooks网络的全局莫兰指数，结果如表3所示。从计算出的全局莫兰指数，可看出这4个经典网络中的全局莫兰指数均为负值，表示在这4个网络中，节点之间的关系呈现出负相关，其中Karate网络的全局莫兰指数最小为-0.576，并且 Z I>2.58，说明针对Karate网络有99%的可能性相似的特征节点往往在网络中相对较远的位置出现，而相邻的节点之间的特征差异较大。
表3 经典网络在网络空间中的全局莫兰指标

Tab. 3 Global Moran indicators of classical networks in cyberspace

网络名称 全局莫兰指数I 期望值E(I) 标准差sd(I) 标准差z值 p值
Karate -0.576 -0.030 0.101 -5.393 0.000
Dolphin -0.098 -0.016 0.088 -0.922 0.178
Lesmis -0.275 -0.013 0.075 -3.510 0.000
Polbooks -0.102 -0.010 0.049 -1.892 0.029
为了更清楚的表现出每个节点与邻接节点的空间集聚状况，计算出每个网络的局部莫兰指数并得到局部莫兰散点图，如图2所示。在局部莫兰散点图中如果斜线的斜率为正，表示属性值在网络空间上呈现出正相关性，说明属性值高的节点周围节点的属性值也高；如果斜线的斜率为负，表示属性值在网络空间上呈现出负相关性，说明相邻节点的属性值不存在相似性。从图中可以看出Karate网络中斜线的斜率最高，表明在Karate网络中节点的空间负相关性最强，Lesmis网络和Polbooks网络次之，Dolphin网络的相关性最弱。
图2 经典网络局部莫兰散点图

Fig. 2 Local Moran scatter plot of classical networks

（2）根据经典网络节点之间的拓扑关系构建转移矩阵M。根据式（8）计算出Karate、Dolphin、Lesmis和Polbooks网络的PageRank值，结果如图3中绿色柱状图所示。其中每个网络中所有节点的PageRank值之和为1。
图3 经典网络节点指标对比分析

Fig. 3 Comparison and analysis diagram of classical network node indicators

（3）通过算法1可以将局部莫兰指数的数值控制在（-1，1）之间，且所有节点的局部莫兰指数的绝对值之和与PageRank值之和保持一致，均为1。同时，标准化之后的局部莫兰指数仍保留了正负性，仍然可以通过正负性判断节点的空间相关性。从图3中可以看出当节点的局部莫兰指数在x轴的上方时，则代表该节点在空间中呈现出正相关；当在x轴下方时，则代表该节点在空间中呈现出负相关。经过标准化之后可以将局部莫兰指数和PageRank值对网络空间资源进行综合评价。
在真实的网络空间中，通常更关注节点之间呈现出正相关的情况，特别是当网络中某个节点具有高属性值时，与其相连的周围节点的属性值也很高的情况。这些节点在整个网络中扮演着关键的角色。根据式（9）计算经典网络中节点的综合评价指标PI值（本实验中比例系数   α  取值为0.5，表示局部莫兰指数和PageRank值的重要程度相同）得到图3中折线图。
以Dolphin网络中的节点37和节点55为例，从图中可以看出如果仅从PageRank值考虑，节点37按照重要性排序为15，经过节点综合度量之后，该节点的次序上升到第二，因为该节点具有较高的重要性和空间正相关性，所以在综合度量之后该节点在整个网络中的排序会提升；而节点55按照重要性排序为2，经过节点综合度量之后，该节点的次序下降到15，因为该节点具有较高的重要性，但是在整个网络中的呈现出负相关，所以综合度量之后该节点在整个网络中排序有所下降。通过综合度量指标对资源节点进行评价时可以综合考虑节点在局部和全局范围内的空间相关性和重要性，以此可以突出节点中属性值较高并且与其相连节点属性值也高的节点。
（4）通过FR布局算法对经典网络中节点进行布局，可以确定资源节点在山峰图和等高线中的位置，同时根据步骤（3）中计算出的PI值赋予节点高度值，则可通过节点的位置和高度值在三维空间中隐喻表达出经典网络的山峰图和等高线图。以Karate网络为例从不同角度展示网络中山峰图，如图4所示。从图3可看出Karate网络中节点1的综合指标最高，因此在山峰图中节点所处的山峰也最高，同时该节点在等高线图中所处的位置坐标为（0，0），其余节点则以节点1为中心节点，根据公式（10）计算其余节点与中心节点之间的斥力和引力，最终达到一个平衡的状态，节点之间的位置关系可以看出节点与其他节点的关联程度，关联程度越高的两个节点之间的距离越近。并且在图中将PI值前三的节点以红色进行标记，可以突出在整个网络中经过综合度量之后的重要程度较高的节点。
通过同样的方式可以得到Dolphin、Lesmis、Polbooks网络的等高线图和山峰图，从图5可通过节点的大小和节点所处的位置对整个网络进行分析。相较于传统使用文字、图标和数字的表达方式，该方式在综合评价了节点在局部和全局范围内的空间相关性和重要性的基础上，以地理空间中常见的等高线和山峰图对节点进行隐喻表达，可以直观的感受出节点之间的相关性和在网络中的所处的地位。
图5 经典网络节点地图

Fig.5 Classic network resource node map

4.3 路由器网络可视化表达

在验证了本文方法的有效性之后，通过上述方法针对真实的路由器网络进行可视化，可视化效果如图6所示。由于路由器网络中资源节点过多，将节点的颜色根据PI值设为渐变色。从图6（a）中可以看出，id为11354921的节点在等高线图中所处的位置坐标为（0，0），说明该节点的PI值最高，路由器网络中其余节点以该节点为中心进行布局，若图中两个节点距离较近，则表示二者之间的关联强度较高。通过图中节点的大小和颜色可以直观的分析路由器节点在该网络中的地位，同时可以对节点地图进行缩放。当选中其中某个节点时，系统会显示该节点的坐标、路由器id、路由器在真实地理空间中的坐标和路由器所属的国家信息，这样可以更好地理解、分析和应对网络中的威胁和安全问题。
图6 真实路由器网络节点地图

Fig. 6 Node map of real router network

4.4 对比分析

为了突出本文方法的有效性，将隐喻地图与传统拓扑图从可视化效果和构建效率进行对比分析。如图7展示了传统拓扑图的可视化效果。从图中可以看出传统拓扑网络在针对小规模网络时表达效果较好，但当随着网络规模的扩大，会出现节点堆叠和节点之间连边交叉的现象，使得图形变得混乱不清，难以直观地理解网络的结构和关系。相较于传统的拓扑网络，隐喻地图将网络中的节点以颜色、大小、位置等视觉要素的方式隐喻到等高线图和山峰图中进行可视化表达，提供了更直观、易懂的视觉化表达效果，这种隐喻地图的表达方式可以帮助用户快速理解和分析大规模网络的结构、关系和特点，使得复杂的网络拓扑变得可视化和可交互，提供更好的人机交互体验。
图7 经典网络拓扑图

Fig. 7 Classic network topology

从构建效率上来看，在构建隐喻地图时使用了综合评价指标及更为复杂的视觉元素进行可视化表达，故在构建隐喻地图时首先要对拓扑数据进行处理。而传统拓扑图主要使用线段和节点来表示连接和关系，视觉表达较简单，故从整体的构建效率来看，传统拓扑图更加高效。但是当二者针对格式化数据进行渲染时，随着网络规模的扩大，隐喻地图效率会优于传统拓扑图。表4展示了隐喻地图和传统拓扑图针对格式化数据在运行效率的对比。
表4 隐喻地图和传统拓扑图针对格式化数据在运行效率的对比

Tab. 4 Comparison of operational efficiency of metaphor map and traditional topology map （s）

网络名称 Karate网络 Dolphin网络 Lesmis网络 Polbooks网络 路由器网络
传统拓扑图 0.144 0.149 0.177 0.192 62.220
隐喻地图 1.587 3.216 2.257 2.319 5.686

5 结论与展望

5.1 结论

本文考虑到网络空间是一种区别于传统地理空间的虚拟空间，因此在针对大规模网络空间资源数据进行可视化时引入了隐喻地图的思想构建节点地图。该模型首先通过网络中拓扑关系构建权重矩阵N和转移矩阵M，根据转移矩阵M计算出PageRank值，再根据权重矩阵N通过度中心值计算莫兰指数，将二者综合作为节点的评价指标。最后依据FR布局算法对节点进行布局，通过综合指标赋予节点高度值和大小，根据隐喻地图的思想将网络空间资源数据作为本体，山峰和等高线作为喻体构建网络空间资源节点地图。本文通过对经典的Karate、Dolphin、Lesmis、Polbooks网络和真实的网络空间路由器节点数据进行实验，主要结论如下：
（1）本研究将用于衡量地理空间数据中是否存在空间聚集的现象的莫兰指数引入到网络空间中，可以通过网络空间资源中的拓扑数据计算节点的全局莫兰指数和局部莫兰指数，以此来分析网络空间中资源节点的空间相关性。
（2）将PageRank算法与局部莫兰指数综合对网络空间资源节点进行综合评价，在考虑了节点在局部范围内的空间相关性的同时还考虑了节点在全局范围内的重要性。Dolphin网络中节点37和节点55的实验结果表明，该方式可以突出节点中属性值较高并且与其相连节点属性值也高的节点，能够较好地实现节点的综合评价，并且在针对格式化数据进行渲染时，随着网络规模的扩大隐喻地图效率优于传统拓扑图。
（3）通过将隐喻地图的思想引入到网络空间中构建网络空间资源节点地图，图中通过PageRank算法和局部莫兰指数综合评价，赋予节点大小和高度值，通过FR布局算法赋予节点位置，最终在二维空间中隐喻出等高线图，在三维空间中隐喻出山峰图。实验结果表明，相较于传统拓扑表达方式该方法能够直观的观察出资源节点在网络空间中所处的地位以及与其他节点之间的关系。

5.2 展望

本文初衷是通过隐喻地图的思想构建网络空间资源节点地图，以便于对大规模网络数据进行管理和分析。结果表明，本文方法相较于传统可视化方式，能够清楚的展示出节点在网络空间中的重要性程度以及与其他节点之间的关系，但本文方法相较于传统方法没有突出节点之间的连接关系。同时，考虑到网络空间中存在大规模的网络，因此同时对网络空间资源数据展示会造成冗余现象，因此在接下来的工作中将从以下2个方面进行：① 在隐喻地图中构建其他元素来隐喻网络空间中节点之间的连接关系，从而更直观地呈现数据结构和关联性，帮助用户理解和分析信息；② 将地理空间中的LOD（Level of Detail，细节层次）技术引入到网络空间资源节点地图中，以不同的细节层次模型进行层次化组织，供可视化时进行调用。
本文图文责任编辑：蒋树芳 黄光玉

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
李响, 杨飞, 王丽娜, 等. 网络空间地图制图方法研究综述[J]. 测绘科学技术学报, 2019, 36(6):620-626,631.

[Li X, Yang F, Wang L N, et al. A survey of mapping methods for cyberspace[J]. Journal of Geomatics Science and Technology, 2019, 36(6):620-626,631.] DOI:10.3969/j.issn.1673-6338.2019.06.013

[2]
陈云海, 江南, 曹一冰, 等. 地图学理论在网络空间地图制图中的应用[J]. 测绘科学技术学报, 2020, 37(3):301-306.

[Chen Y H, Jiang N, Cao Y B, et al. Application of cartography theory in cartography of cyberspace map[J]. Journal of Geomatics Science and Technology, 2020, 37(3):301-306.] DOI:10.3969/j.issn.1673-6338.2020.03.014

[3]
孙中伟, 路紫, 王杨. 网络信息空间的地理学研究回顾与展望[J]. 地球科学进展, 2007, 22(10):1005-1011.

DOI

[Sun Z W, Lu Z, Wang Y. The geography of cyberspace: Review and prospect[J]. Advances in Earth Science, 2007, 22(10):1005-1011.] DOI:10.3321/j.issn:1001-8166.2007.10.003

[4]
Kitchin R M. Towards geographies of cyberspace[J]. Progress in Human Geography, 1998, 22(3):385-406. DOI:10.1191/030913298668331585

[5]
Cook K S. Drawn for the mind’s eye: Map metaphors in early modern English literature[J]. The Cartographic Journal, 2018, 55(2):170-177. DOI: 10.1080/00087041.2018.1436734

[6]
艾廷华. 大数据驱动下的地图学发展[J]. 测绘地理信息, 2016, 41(2):1-7.

[Ai T H. Development of cartography driven by big data[J]. Journal of Geomatics, 2016, 41(2):1-7.] DOI:10.14188/j.2095-6045.2016.02.001

[7]
郭妍. 隐喻思维下的空间信息表达和可视化查询设计[D]. 武汉: 武汉大学, 2009.

[Guo Y. Spatial information expression and visual querying design in metaphor thinking[D]. Wuhan: Wuhan University, 2009.]

[8]
Qu H M, Zhou H, Wu Y C. Controllable and progressive edge clustering for large networks[C]// International Symposium on Graph Drawing. Berlin, Heidelberg: Springer, 2007:399-404.

[9]
Holten D, Van Wijk J J. Force-directed edge bundling for graph visualization[J]. Computer Graphics Forum, 2009, 28(3):983-990. DOI:10.1111/j.1467-8659.2009.01450.x

[10]
Hurter C, Ersoy O, Telea A. Graph bundling by kernel density estimation[J]. Computer Graphics Forum, 2012, 31(3pt1):865-874. DOI:10.1111/j.1467-8659.2012.03079.x

[11]
Peysakhovich V, Hurter C, Telea A. Attribute-driven edge bundling for general graphs with applications in trail analysis[C]// 2015 IEEE Pacific Visualization Symposium (PacificVis). IEEE, 2015:39-46. DOI:10.1109/PACIFICVIS.2015.7156354

[12]
Rosvall M, Bergstrom C T. Maps of random walks on complex networks reveal community structure[J]. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(4):1118-1123. DOI: 10.1073/pnas.0706851105

PMID

[13]
Harrison L, Lu A D. The future of security visualization: Lessons from network visualization[J]. IEEE Network, 2012, 26(6):6-11. DOI: 10.1109/MNET.2012.6375887

[14]
王续盘, 张衡, 周杨, 等. Blondel和k-核分解混合算法相结合的网络空间点群要素多尺度模型构建[J]. 地球信息科学学报, 2021, 23(12):2128-2138.

DOI

[Wang X P, Zhang H, Zhou Y, et al. Multi-scale model of point group elements in network space combined with blondel and k-shell decomposition hybrid algorithm[J]. Journal of Geo-Information Science, 2021, 23(12):2128-2138.] DOI:10.12082/dqxxkx.2021.210397

[15]
Batten P. Some principles for landscape mapping on the Internet[J]. Journal of Map & Geography Libraries, 2006, 2(1):99-110. DOI:10.1300/j230v02n01_05

[16]
张龙. 网络资源测绘数据表达与分析技术研究[D]. 郑州: 战略支援部队信息工程大学, 2018.

[Zhang L. Research on the technologies of expression and analysis for the cyberspace surveying and mapping[D]. Zhengzhou: Information Engineering University, 2018.]

[17]
Becker R A, Eick S G, Wilks A R. Visualizing network data[J]. IEEE Transactions on Visualization and Computer Graphics, 1995, 1(1):16-28. DOI:10.1109/2945.468391

[18]
Martin D. Understanding cyberspace cartographies: A critical analysis of Internet infrastructure mapping[D]. London, UK: University College London, 2008

[19]
张峥. 赛博地图构建理论研究[D]. 郑州: 解放军信息工程大学, 2012.

[ZHANG Z. Theoretical Research on Cybermap construction[D]. Zhengzhou: PLA Information Engineering University, 2012.]

[20]
王映雪. 网络空间关系及节点信息地图可视化方法与技术研究[D]. 郑州: 战略支援部队信息工程大学, 2020.

[Wang Y X. Research on the method and technology of cyberspace relation and node map information visualization[D]. Zhengzhou: Information Engineering University, 2020.] DOI:10.27188/d.cnki.gzjxu.2020.000213

[21]
Bray T. Measuring the web[J]. Computer Networks and ISDN Systems, 1996, 28(7/8/9/10/11):993-1005. DOI:10.1016/0169-7552(96)00061-X

[22]
Wise J A, Thomas J J, Pennock K, et al. Visualizing the non-visual: Spatial analysis and interaction with information from text documents[C]// Proceedings of Visualization 1995 Conference. IEEE, 2009:51-58. DOI:10.1109/INFVIS.1995.528686

[23]
蒋秉川, 万刚, 徐锐. 网络空间剖分机理与可视化方法研究[J]. 系统仿真学报, 2017, 29(S1):1-8.

[Jiang B C, Wan G, Xu R. Research on the mechanism of network spatial partition and visualization method[J]. Journal of System Simulation, 2017, 29(S1):1-8.] DOI:10.16182/j.issn1004731x.joss.2017S1001

[24]
岳香豆. 改进的标签传播社区发现算法及可视化展示[D]. 太原: 山西大学, 2020.

[Yue X D. Improved label propagation community discovery algorithm and visual display[D]. Taiyuan: Shanxi University, 2020.] DOI:10.27284/d.cnki.gsxiu.2020.000570

[25]
Gould P R, White R. Mental maps[M]. Harmondsworth: Penguin, 1974.

[26]
Gronemann M, Jünger M. Drawing clustered graphs as topographic maps[M]//Graph Drawing. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013:426-438. DOI: 10.1007/978-3-642-36763-2_38

[27]
Chen S M, Chen S, Wang Z H, et al. D-Map: Visual analysis of ego-centric information diffusion patterns in social media[C]// 2016 IEEE Conference on Visual Analytics Science and Technology (VAST). IEEE, 2016:41-50. DOI:10.1109/VAST.2016.7883510

[28]
艾廷华, 禹文豪. 水流扩展思想的网络空间Voronoi图生成[J]. 测绘学报, 2013, 42(5):760-766.

[Ai T H, Yu W H. Algorithm for constructing network voronoi diagram based on flow extension ideas[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5):760-766.]

[29]
信睿, 艾廷华, 何亚坤. Gosper地图的非空间层次数据隐喻表达与分析[J]. 测绘学报, 2017, 46(12):2006-2015.

DOI

[Xin R, Ai T H, He Y K. Visualisation and analysis of non-spatial hierarchical data of gosper map[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(12):2006-2015.] DOI:10.11947/j.AGCS.2017.20160596

[30]
高贞. 层次化语义信息的河系地图隐喻表达[D]. 武汉: 武汉大学, 2020.

[Gao Z. Metaphorical expression of hierarchical semantic information on river map[D]. Wuhan: Wuhan University, 2020.]

[31]
Chen S, Li S H, Chen S M, et al. R-map: A map metaphor for visualizing information reposting process in social media[J]. IEEE Transactions on Visualization and Computer Graphics, 2020, 26(1):1204-1214. DOI:10.1109/TVCG.2019.2934263

[32]
Chi X, Hua J, Ren X. A novel metaphor graph drawing method for multidimensional data visualisation and its case study on COVID-19 vaccination analysis[J]. International Journal of Environmental Research and Public Health, 2022, 19(23):15547. DOI:10.3390/ijerph192315547

[33]
Ma X Y, Cui K C, Ji C W, et al. Visualization of emergency needs posted on social media by metaphor map[J]. Data and Information Management, 2021, 5(1):1-10. DOI: 10.2478/dim-2020-0021

[34]
Anselin L. Local indicators of spatial association—LISA[J]. Geographical Analysis, 1995, 27(2):93-115. DOI: 10.1111/j.1538-4632.1995.tb00338.x

[35]
Brin S. The PageRank citation ranking: bringing order to the web[J]. Proceedings of ASIS, 1998,98:161-172. DOI: 10.1007/978-3-319-08789-4_10

[36]
孙婧. 长江经济带城市群旅游流时空演化与溢出效应研究[D]. 岳阳: 湖南理工学院, 2022.

[Sun J. Study on spatial and temporal evolution and spillover effect of tourism flow in urban agglomeration of Yangtze River economic belt[D]. Yueyang: Hunan Institute of Science and Technology, 2022.]

[37]
Fruchterman T M J, Reingold E M. Graph drawing by force-directed placement[J]. Software-Practice & Experience, 1991, 21(11):1129-1164. DOI:10.1002/spe.4380211102

[38]
Zachary W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977, 33(4):452-473. DOI:10.1086/jar.33.4.3629752

[39]
Lusseau D, Schneider K, Boisseau O J, et al. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations[J]. Behavioral Ecology and Sociobiology, 2003, 54(4):396-405. DOI: 10.1007/s00265-003-0651-y

[40]
Knuth D E. The Stanford GraphBase: a platform for combinatorial computing[M]. New York, N.Y.: ACM Press, 1993.

[41]
Adamic L A, Glance N. The political blogosphere and the 2004 U.S. election: Divided they blog[C]// Proceedings of the 3rd international workshop on Link discovery. ACM, 2005:36-43. DOI:10.1145/1134271.1134277

Options
文章导航

/

〈 〉