EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 9: 2106 - 2122

DOI: https://doi.org/10.12082/dqxxkx.2024.240238

地球信息科学理论与方法

顾及地理环境各向异性的PM2.5浓度时空预测模型

  • 王军杰 , 1 ,
  • 王达 1 ,
  • 丁晨 , 1, * ,
  • 唐建波 1, 2 ,
  • 石岩 1, 2 ,
  • 杨学习 1, 2
展开
  • 1.中南大学地理信息系，长沙 410083
  • 2.湖南省地理空间信息工程技术研究中心，长沙 410018
* 丁晨（1996— ），男，安徽合肥人，博士生，主要从事时空数据挖掘、地理场景建模与理论研究。 E-mail:

王军杰（1996— ），男，河南周口人，硕士生，主要从事时空数据挖掘研究。E-mail:

Editor: 蒋树芳

收稿日期: 2024-04-26

  修回日期: 2024-07-01

  网络出版日期: 2024-09-10

基金资助

国家自然科学基金面上项目(42271485)

湖南省自然科学基金项目(2022JJ40585)

湖南省自然科学基金项目(2024JJ8343)

中南大学中央高校基本科研业务费专项资金资助(2024ZZTS0638)

收起

A Spatiotemporal Prediction Model of PM2.5 Concentration Incorporating Geographic Environmental Anisotropy

  • WANG Junjie , 1 ,
  • WANG Da 1 ,
  • DING Chen , 1, * ,
  • TANG Jianbo 1, 2 ,
  • SHI Yan 1, 2 ,
  • YANG Xuexi 1, 2
Expand
  • 1. Department of Geo-Informatics, Central South University, Changsha 410083, China
  • 2. Hunan Geospatial Information Engineering and Technology Research Center, Changsha 410018, China
* DING Chen, E-mail:

Received date: 2024-04-26

  Revised date: 2024-07-01

  Online published: 2024-09-10

Supported by

National Natural Science Foundation of China(42271485)

Hunan Provincial Natural Science Foundation of China(2022JJ40585)

Hunan Provincial Natural Science Foundation of China(2024JJ8343)

Fundamental Research Funds for the Central Universities of Central South University(2024ZZTS0638)

Fold

摘要

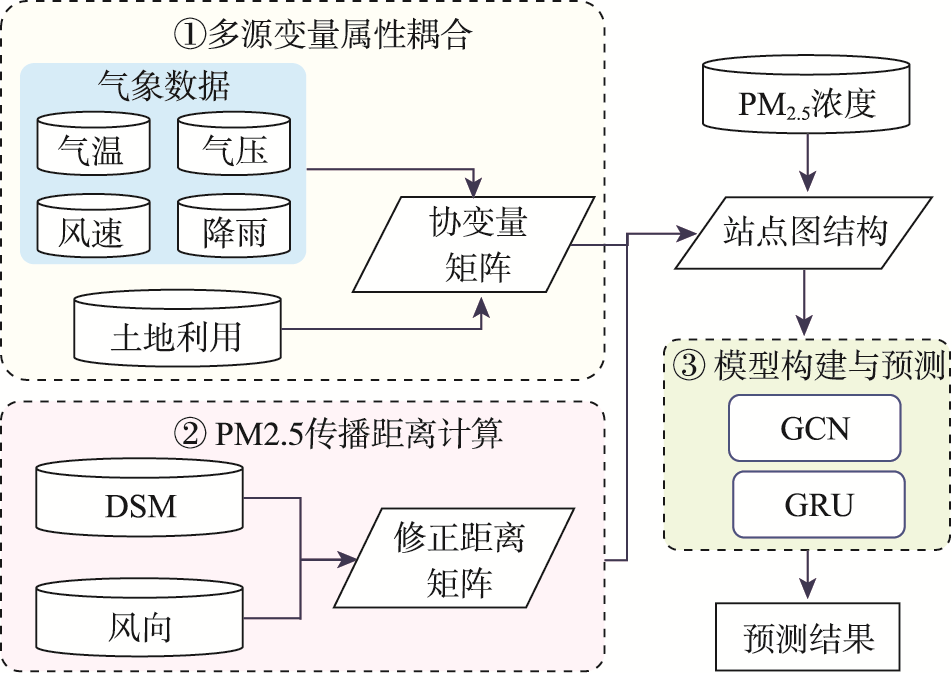
PM2.5浓度预测对于空气污染的防控和治理具有重要意义。传统图卷积神经网络（Graph Convolutional Network, GCN）等时空预测模型主要通过监测站点间的欧氏距离来度量PM2.5分布的空间相关性，未顾及地形和风向等因素对大气污染物传输过程的各向异性影响，导致地形复杂区域内的预测结果精度偏低。为此，本文提出了一种顾及地理环境各向异性的PM2.5浓度时空图卷积网络预测模型。首先，考虑地理环境的各向异性特征，利用地形和风向等对站点间PM2.5传播的各向异性影响构建GCN的边，将站点PM2.5浓度、土地利用和其他气象因子建模为GCN的节点特征。其次，通过GCN提取站点PM2.5浓度的空间特征。最后，通过门控循环单元（Gate Recurrent Unit, GRU）建模站点PM2.5浓度的时间特征并进行预测。本文以山地型省份贵州省2017年逐小时PM2.5浓度记录进行实验，并采用一系列时空预测基线模型（GTWR、STSVR和GCN+GRU）与本文模型进行对比。实验结果表明： ① 本文模型的PM2.5浓度预测结果的RMSE、MAE别为10.047、6.848，相比基线模型平均下降了11.29%和12.16%；R2为0.883，比基线平均提升了3.72%； ② 通过不同地形对站点PM2.5浓度相关性影响分析，论证了山脉沟谷等地形会显著影响站点间的PM2.5浓度的相关性，进而影响站点PM2.5浓度预测结果； ③ 充分考虑地形和风向对PM2.5传播产生的各向异性影响，能够显著提升存在山脉和沟谷地形区域内PM2.5预测精度。

关键词： PM2.5浓度预测; 时空图卷积网络; 空间相关性; 地理协变量; 地形距离; 风向; 各向异性; 地理环境特征

本文引用格式

王军杰 , 王达 , 丁晨 , 唐建波 , 石岩 , 杨学习 . 顾及地理环境各向异性的PM2.5浓度时空预测模型[J]. 地球信息科学学报, 2024 , 26(9) : 2106 -2122 . DOI: 10.12082/dqxxkx.2024.240238

Abstract

PM2.5 concentration prediction plays a pivotal role in the prevention and control of air pollution. Traditional forecasting models, such as the Graph Convolutional Network (GCN) and other spatial-temporal prediction models, measure the spatial correlation of PM2.5 distribution primarily by monitoring the Euclidean distance between monitoring stations. However, these models often fail to account for the anisotropy effects of terrain, wind direction, and other factors that significantly influence the transport process of air pollutants. This oversight can result in lower accuracy of prediction results, especially in areas with complex terrain. This paper proposes a novel spatiotemporal convolutional network prediction model for PM2.5 concentration that takes into account the anisotropy of the geographical environment. The model first constructs the edges of the GCN by incorporating the anisotropic effects of terrain and wind direction on PM2.5 propagation between stations. It then models the station PM2.5 concentration, land use, and other meteorological factors as node characteristics of the GCN. The model employs GCN to extract the spatial characteristics of PM2.5 concentration and subsequently uses a Gate Recurrent Unit (GRU) to model and predict the temporal characteristics of PM2.5 concentration at the station. The model's performance was evaluated using hourly PM2.5 concentration records from the mountainous Guizhou province in 2017. It was compared against several spatiotemporal prediction baseline models, including Geographically and Temporally Weighted Regression (GTWR), Spatio-Temporal Support Vector Regression (STSVR), and a combined GCN+GRU model. The experimental results demonstrate that the model proposed in this paper significantly outperforms the baseline models. The Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) ratios of PM2.5 concentration predicted by the model are 10.047 and 6.848, respectively, which represent decreases of 11.29% and 12.16% compared to the baseline models. The R-squared value of 0.883 indicates an average improvement of 3.72% from the baseline. Furthermore, the analysis of the influence of different terrains on the correlation of PM2.5 concentration at different stations reveals that mountainous, gully, and other terrain features can significantly affect the correlation of PM2.5 concentration between stations. This, in turn, impacts the prediction results of PM2.5 concentration at different stations. The study concludes that fully considering the anisotropic effects of terrain and wind direction on PM2.5 propagation can substantially enhance the prediction accuracy of PM2.5 in mountain and gully terrain areas. By integrating the anisotropic characteristics of the geographical environment into the prediction model, this research contributes to the development of more accurate forecasting tools for PM2.5 concentrations. This development is expected to ensure accurate prediction of PM2.5 concentrations in areas with complex terrain and support the development of effective air pollution control strategies.

Key words： PM2.5 concentration prediction; spatiotemporal graph convolutional network; spatial autocorrelation; geographic covariates; terrain distance; wind direction; anisotropy; geographical environment feature

1 引言

随着我国城镇化水平的不断提高与发展，空气污染问题在多个领域备受关注[1-2]。PM2.5是导致中国空气污染的主要原因之一[3]，长期暴露在高浓度的PM2.5环境中会严重危害人体健康，增加患肺癌和心脏病的风险[4-5]。近年来，随着中国生态文明建设的持续投入，空气质量有了明显改善[6]。但是，由于PM2.5的产生原因多样、传播过程复杂、监测手段有限[7-8]，要彻底解决PM2.5污染问题仍然存在较大难度，需要更精确地感知和预测手段。
目前的PM2.5浓度预测模型方法主要有数值模拟方法、统计建模方法、机器学习方法和深度学习方法[9-10]。数值模拟方法主要是基于大气污染物形成、扩散、沉降的原理和机制，通过数学或物理的方式构建大气污染物的稀释和扩散等模拟演化模型进行污染物浓度预测[11-12]。数值模拟方法充分考虑了大气污染物的物理和化学过程，具有可解释性强和预测趋势准确的优势，但也存在模型求解复杂、模型参数难以确定导致预测结果存在不确定性等局限性[13]。统计建模方法直接利用数学统计方法从PM2.5浓度观测数据中获取变化规律进行预测[14]。统计建模方法大多基于线性关系建模，简单高效且迁移性强，如时空地理加权回归（Geographically and Temporally Weighted Regression, GTWR）模型通过结合空间和时间维度的分析进行PM2.5浓度预测[15]。然而，PM2.5浓度时空演化过程通常涉及土地利用、气象等多因素表现为复杂的非线性关系[16]，统计建模方法难以有效提取非线性复杂关系，导致预测结果不理想[17]。机器学习方法主要基于统计学中的回归预测发展而来，结合PM2.5浓度的自身变化规律以及其他因素影响来预测浓度[18⇓-20]。机器学习方法通常模型结构简单易于训练，但是难以充分捕捉PM2.5浓度的时空相关性[21]。因此，有学者考虑站点空气污染物存在空间依赖性，如Yang等[22]结合风向提出时空支持向量回归（Space-Time Support Vector Regression, STSVR）来预测PM2.5浓度。但是地形对PM2.5传播的各向异性影响未被考虑，站点间的山脉等地形对站点可能存在分隔作用，进而影响站点间的空气污染物浓度相关性以及预测精度。
近几年，由于深度学习在挖掘高维数据的潜在非线性关系中表现出较强的优势，逐渐被专家学者们引入到PM2.5浓度预测中。白盛楠等[23]建立了基于多变量的长短期记忆神经网络（LSTM）PM2.5浓度预测模型实现了北京市2010—2017年PM2.5日值浓度的预测； Becerra-Rico等[24]基于门控循环单元（Gated Recurrent Unit, GRU）实现了空气污染物的浓度预测。这类方法能够对PM2.5浓度时序数据之间的相关性进行学习与建模，但忽视了PM2.5的空间传输作用，可能会导致预测效果表现不稳定[25]。因此，有学者在LSTM等循环神经网络的基础上，引入GCN构建深度学习模型进行预测，进而来捕获PM2.5浓度的空间相关性。如马俊文等[26]提出一种基于RNN与GCN的PM2.5浓度预测模型，降低了PM2.5浓度的预测误差； Gao等[10]将LSTM和GCN相结合提升了PM2.5浓度的预测效果。利用图结构建模站点空间相关性的方法被证实能够实现更准确的PM2.5浓度预测。但是，现有方法主要通过站点间空间位置的直线距离来度量空间邻近关系，忽视了地形等对PM2.5传播具有重要影响的地理环境特征。由于地理环境的复杂性，站点间空间相关性可能存在着各向异性，为此，需要融合多地理协变量来实现对PM2.5浓度的精准预测。
综上所述，现有方法在考虑监测站点间PM2.5浓度的空间相关性时，使用欧氏距离将监测站点间的空间相关性建模为各向同性，而使用风向来衡量站点间的空间相关性时，未考虑到山脉或沟谷等地形对站点间PM2.5传输的产生的各向异性影响，影响预测模型的精度和可解释性。鉴于此，本文引入地形距离并结合风向建模监测站点间PM2.5浓度的空间相关性，充分考虑地形和风向引起的站点PM2.5传输扩散的各向异性，提出了顾及地理环境各向异性的PM2.5浓度时空图卷积网络预测模型。该方法较现有的PM2.5浓度预测方法更符合PM2.5的传输扩散规律，能进一步提高站点PM2.5浓度预测精度，降低现有方法在山脉和沟谷较多地区的站点PM2.5浓度预测误差。

2 研究方法

时空图卷积方法为空气污染物浓度预测提供了较好的学习策略。然而，在建模站点之间的图结构时，现有研究大多采用最近邻或者欧氏距离来衡量站点间空气污染物浓度相关性，未考虑到地形和风向等因素对空气污染传播的影响。为了解决这个问题，本研究顾及了地形和风向对空气污染物传播的各向异性的影响，修正了站点间的空气污染物空间传播路径，并结合其他气象因素和土地利用信息作为图结构的节点属性，使用GCN充分捕捉站点间PM2.5的空间相关性，进而使用GRU捕获站点的时间相关性，得到预测结果，方法流程如图1所示。
图1 本文研究方法流程

Fig. 1 Flow chart of research methods

2.1 多源变量属性耦合

研究表明，气象属性（如气温、气压、降雨、风速）以及土地利用类型与PM2.5浓度之间存在着显著关联，其中PM2.5浓度与风速、气温、气压和降雨呈现负相关，与植被和水体等土地利用类型呈现负相关，与不透水面呈现正相关[27⇓⇓⇓-31]，因此，进行站点PM2.5浓度预测时，需要综合考虑站点所处的自然环境因素，包括气象属性和土地利用类型。为了综合考虑影响站点PM2.5浓度的因素，本研究将气象因素中的气温、气压、风速、降雨建模为站点的动态属性（D），将土地利用信息建模为站点的静态属性（L）。若时间序列长度为T的n个站点的PM2.5浓度表示为 X ( X ∈ R n × T )，站点的土地利用类型为 L ( L ∈ R n × 1 )，那么为了融合T个时刻中某一时刻t时站点的静态属性，取站点的PM2.5浓度矩阵的对应列为X t，与土地利用矩阵L融合。t时刻融合土地利用后的站点属性为：
E l t = [ X t ,   L ] ,   E l t ∈ R n × 2
式中： Xt为t时刻站点的PM2.5浓度； L = l 1 ⋮ l n， ln表示第n个站点的土地利用类型； E l t为t时刻融合土地利用后的站点属性。在本研究中，t时刻将站点所处的土地利用类型L作为站点的静态属性，并将站点的PM2.5浓度Xt与站点所处的土地利用类型属性L进行融合，得到t时刻融合土地利用后的站点属性 E l t。
为了建模站点的动态属性D，引入气温、气压、降雨和风速作为4个动态属性 D 1 ,   D 2 ,   D 3 ,   D 4，记为D∈ R n × ( 4 × T )。考虑到站点的空气污染物浓度会受到站点气温、气压、降雨和风速的累积影响，在耦合生成t时刻的站点属性时，设置了时间窗口（窗口长度为m），针对每一个动态属性取t时刻的前m个时刻的属性值 D i t - m , t = [ D i t - m , … ,   D i t - 1 ,   D i t ]进行融合。最终，通过耦合站点静态和动态属性后的t时刻的站点属性可以表示为：
E t = [ X t ,   L ,   D 1 t - m , t ,   D 2 t - m , t , … ,   D i t - m , t ] ,   E t ∈ R n × ( 2 + i × m )
式中： Xt为t时刻站点的PM2.5浓度； L = l 1 ⋮ l n， ln表示第n个站点的土地利用类型；   D i t - m , t为任意动态属性取t时刻的前m个时刻的属性值；i为站点的动态属性数目，且最大为4，表示站点的4种动态属性（气温、气压、降雨和风速）； Et表示t时刻耦合站点静态和动态属性后的站点属性。

2.2 PM2.5传播距离计算

地理学第一定律指出“一切事物都与其他事物相关，但近距离事物比远距离事物更相关”[31]。考虑到PM2.5污染物在不同监测站点间存在传输与扩散，所以距离越近的监测站点间的空气污染物的浓度特征越具有相似性。然而，山脉等高地形区域会对空气污染物的传播会产生阻隔作用[32]，导致污染物的各向异性传播，影响站点间的空气污染物相关性。如图2所示，对点A到点B的最短距离与地形距离路径分别进行可视化。黑色线条和红色线条分别表示A到B的最短距离与地形距离路径。由于A到B之间存在高地势区域，这些高地势区域阻碍PM2.5在A到B之间的传播，使得PM2.5传播路径并非是最短距离（黑色直线），而应该是地形距离约束下的点A到点B的PM2.5地形距离路径（红色曲线）更符合实际传播路径。因此，需要根据地形对站点间的PM2.5传播距离进行量化计算。
图2 PM2.5传播路径对比示意图

Fig. 2 Comparison of PM2.5 transmission paths

（1）地形距离计算定义。本研究通过计算地形约束下的PM2.5传播路径来近似表征地形对PM2.5空间传输的影响。A*算法是一种能够在有障碍物或者约束情况下快速找到一条到达目的节点的最短路径的方法[33]，本文采用A*算法在DSM数据中计算PM2.5的空间传输路径。具体而言，本文考虑到高地势区域站点的空气污染物更容易传播扩散到低地势区域站点，通过计算DSM网格节点与其八邻域网格节点之间的高度差以修正预估代价，获得符合实际的PM2.5传播路径，进而计算各站点间的地形距离，构建地形距离矩阵。DSM网格节点 R ( i , j )与对应邻居 R ( w , v )的空间位置如图3所示。
图3 节点与邻居节点空间位置关系

Fig. 3 Spatial position relationship between a node and its neighbor node

节点 R ( i , j )与邻居节点 R ( w , v )的高差计算公式如下：
△ d R ( i , j ) , R ( w , v ) = H R ( w , v ) - H R ( i , j )
式中：(i, j)和(w, v)均为节点在DSM网格对应行列号所在的网格位置； R ( i , j )为DSM第i行j列的网格， R ( w , v )是 R ( i , j )的某个邻居； H R ( i , j )和 H R ( w , v )均是对应网格位置的高程值； △ d R i , j , R w , v是2个节点之间的高差。
节点 R ( i , j )与对应邻居节点 R ( w , v )的地形距离计算公式如下：
C = S × ( Δ x ) 2 + ( Δ y ) 2 + Δ d
式中： S为格网边长； Δd、Δx和Δy分别代表 R ( w , v )和 R ( i , j )之间的高差以及x方向和y方向的格网序数差。
通过修正A*算法，可以得到任意2个站点间的地形距离。若从站点p到站点q经过k个节点，那么站点p到站点q的地形距离mpq，可由式（5）计算得到。若站点数目为n，那么将得到n个站点中任意 2个站点间的地形距离矩阵 m 11 ⋯ m 1 n ⋮ ⋮ ⋮ m n 1 ⋯ m n n，其中对角线元素为0，表示站点到自身的地形距离。
m p q = ∑ i = 1 k C i
式中： Ci表示从站点p到站点q经过的第i个节点与第i-1个节点间的地形距离。
（2）站点风向约束定义。站点间的空气污染物的传输作用会受到风向的影响[22]。如图4所示，某一时刻，站点p3、p4的风向v3、v4存在朝向站点p0的风向分量，站点p0的PM2.5浓度将受到站点p3和p4的PM2.5传输影响，而可能不受到站点p1和p2站点的PM2.5传输影响，且受影响程度与角度以及距离有关（角度由站点之间连线与风向来定义，距离由站点间的地形距离来定义）。因此，为了进一步解决站点间PM2.5浓度相关性的各向异性问题，将风向和地形距离相结合，计算任意时刻站点间的PM2.5传播修正距离。具体而言，对于任意时刻t，以任意站点vi为研究对象，根据其它任意站点vj与站点vi的位置坐标，生成指向站点vi的方向向量 v → i j，然后将站点vj在t时刻的风向向量与向量 v → i j计算夹角，得到t时刻站点vj与站点vi的风向夹角 θ i j t，若t时刻站点vj到站点vi的地形距离为mij，则可以得到站点vi与站点vj在t时刻PM2.5传播距离wij。那么任意t时刻站点间的PM2.5传播距离可以表示为 w 11 ⋯ w 1 n ⋮ ⋮ w n 1 ⋯ w n n，记为W t。PM2.5在空间上的传播过程不仅受到路径的影响，而且也与风向等因素具有显著关联。对于相同的传播路径，但完全不同的风向可能会导致PM2.5传播的路径方向相反（图4）。为此，本文进一步结合风向对PM2.5传播距离进行加权，具体计算公式如下：
w i j m i j , θ i j t | α = 0 ,                                                 90 ° < θ i j t ≤ 180 ° e ( - m i j 2 × s i n θ i j t ) / 2 α 2 ,     0 ° ≤ θ i j t ≤ 90 °
式中： mij和θij(t)分别为第i和j个站点间的地形距离以及t时刻站点j风向关于站点i连线的夹角；α为站点i的最近邻距离。当风向与PM2.5的地形传播路径一致（即其角度θij(t)≤90°）时，风向对于PM2.5在该路径上的传播具有促进作用；而当风向与PM2.5的地形传播路径相反（即其角度θij(t)>90°）时，风向对于PM2.5在该路径上的传播具有阻碍作用，此时PM2.5可能不会沿着该路径进行传播，为此本文将其设置为0（即不考虑当前PM2.5站点与其邻近PM2.5站点之间的传播）。
图4 风向对空气污染物传播路径影响的示意图

Fig. 4 Diagram of the influence of wind direction on the path of air pollutants

2.3 模型构建与预测

图5展示了本研究所提出模型的整体框架，模型在顾及地形和风向对站点污染物的各向异性影响的基础之上，通过捕获站点空气污染物的时空特征来预测站点的PM2.5浓度。
图5 本文预测模型整体框架

Fig. 5 The framework of the proposed prediction model

将研究区域内的空气质量监测站点以及站点间的关系看作一个图G=(V, W)。 V = v 1 ,   v 2 ,   … ,   v n表示图中所有的节点的集合，即空气质量监测站点的集合，n是空气质量监测站点的数目，W表示图中节点的边，即站点间的距离，任意2个节点vi ， vj之间的边为wij∈W。将各个空气质量监测站点的PM2.5浓度视为其固有属性，用矩阵X表示。把影响站点PM2.5浓度的外部因素，包括动态属性（D）和静态属性（L）视为站点的协变量属性，通过多源变量属性耦合得到站点属性矩阵E。因此，站点PM2.5浓度预测问题可以视为基于站点的图结构G、站点多源变量属性E来学习函数f，并预测站点未来的PM2.5浓度 y ^，如式（7）所示。
y ^ = f ( G ,   E )
式中： G和E分别为研究区域内的空气质量监测站点以及站点间的关系； f表示函数； y ^为站点未来的PM2.5浓度预测结果。
GCN的主要目的是考虑相邻节点的影响，获取图中每个节点的表示，因其能够建模非线性复杂关系以及相互依赖关系而备受相关研究学者的关注[34-35]。GCN将邻接矩阵和特征矩阵作为输入，建模过程如式（8）所示。对于t时刻，本文将耦合后的站点属性变量Et作为GCN特征矩阵的输入，同时将前m个时刻站点间PM2.5传播距离矩阵对应位置上的均值形成的矩阵 W t _ m e a n作为GCN邻接矩阵的输入，利用GCN提取站点间PM2.5浓度的空间相关性，得到包含空间特征的站点空气污染物浓度的时变序列。
y l + 1 = σ ( D ˜ -   1 2 A ˜ D ˜ -   1 2 y l W l )
式中： σ表示sigmoid激活函数； A ˜ = A + I是自环邻接矩阵； D ˜为度矩阵；Wl为第l卷积层的权值矩阵； yl为第l卷积层输出表示。
GRU具备记忆时间序列历史信息，能够捕获到时间序列的时间依赖特征[36-37]。由于PM2.5浓度预测属于时间序列回归分析问题，所以本文使用GRU模型建模PM2.5浓度时间特征，对于给定的时刻t，将通过GCN得到包含空间特征的站点空气污染物浓度的时变序列作为GRU的输入，利用GRU单元来提取时变特征序列中所蕴含的时间特征，学习PM2.5浓度序列在时间上的相关性，进而训练预测得到PM2.5浓度逐小时预测结果。GRU建模过程如下：
R t = σ ( W r · [ g c ( E t , W t _ m e a n ) ,   H t - 1 ] + b r )
Z t = σ ( W z · [ g c ( E t , W t _ m e a n ) ,   H t - 1 ] + b z )
H t ~ = t a n h ( W h · [ g c ( E t , W t _ m e a n ) ,   R t ⊙ h t - 1 ] + b h )
h t = ( 1 - Z t ) ⊙ H t - 1 + Z t ⊙ H t ~ )
式中： R t ∈ R n ∙ h和 Z t ∈ R n ∙ h分别表示重置门和更新门（h为隐藏单元个数)； H t ~和Ht分别是t时刻的候选隐状态和隐状态； H t - 1 ∈ R n ∙ h表示上一个时刻的隐状态； Wr和Wz分别是重置门和更新门的权重矩阵； br、bz和bh分别是重置门、更新门和候选隐状态的偏置项； σ表示sigmoid激活函数； []表示连接操作； ☉表示Hadamard积（按元素乘积）运算符； gc(·)表示卷积操作。

3 实验及结果分析

3.1 实验设计

3.1.1 研究区域与数据集介绍

本文选择位于中国西南地区的贵州省（24°37'N—29°13'N，103°36'E—109°35'E）作为研究区域。贵州省位于云贵高原，地势西高东低，自中部向北、东、南三面倾斜，其中92.5%的面积为山地和丘陵。贵州北部有大娄山，自西向东北斜贯北境；中南部苗岭横亘东北境有武陵山，由湘蜿蜒入黔；西部有乌蒙山，地势险峻。由于大气环流和地形的影响，西部地区易受到东部等地区污染物的输送影响，同时由于研究区域东部地区地势相对低洼，易造成局部区域污染物聚集，复杂的地形对该地区空气污染物预测造成了巨大挑战。因此，本文选取贵州省为研究区域，验证所提出PM2.5浓度预测模型的有效性。图6为贵州省空气质量监测站点位置，图中站点颜色表示2017年的PM2.5小时平均浓度的不同数值范围。
图6 贵州省空气质量监测站点空间分布

Fig. 6 Spatial distribution of air quality monitoring stations in Guizhou Province

本研究收集了研究区域2017年1月1日至2017年12月31日的数据，包括PM2.5浓度数据、气象数据、土地利用数据和DSM数据。PM2.5浓度数据来源于中国环境监测总站（https://air.cnemc.cn），监测站点分布如图6所示。气象数据来源于欧洲中期天气预报中心（ECMWF），风速和风向由U、V型风分量计算得到[38]。土地利用数据来源于武汉大学黄昕团队公开的中国土地覆盖数据集[39]，包括田地、森林、水系等9种类型。DSM数据来源于ALOS（Advanced Land Observing Satellite）。本文所使用的实验数据及其特征描述如表1所示。为了获得各空间质量监测站点的气象和土地利用等属性信息，本文采用最近邻插值法获得各PM2.5监测站点位置处的各协变量值，以此作为输入数据，构建PM2.5时空预测模型。
表1 本文实验数据及其特征描述

Tab. 1 The experimental data and their characteristics

数据类型 数据来源 数据年份 取值范围 时间分辨率 空间分辨率 均值 标准差
PM2.5 /(µg/m³ ) 中国环境监测总站 2017 [1.00, 863] 小时 站点 31.13 593.94
气温/℃ ECMWF 2017 [-4.26, 39.92] 小时 0.1°×0.1° 15.42 55.15
气压/KPa ECMWF 2017 [79.81, 97.99] 小时 0.1°×0.1° 87.38 13.74
U型风分量/(m/s) ECMWF 2017 [-6.91, 7.20] 小时 0.1°×0.1° -0.67 1.47
V型风分量/(m/s) ECMWF 2017 [-7.97, 10.23] 小时 0.1°×0.1° 0.30 6.03
降雨量/(mm/h) ECMWF 2017 [0.0, 12.66] 小时 0.1°×0.1° 0.17 0.28
土地利用数据(NA) 中国土地覆盖数据集 2017 [1, 9] - 30 m - -
DSM/m ALOS 2017 [254, 2 606] - 30 m 1 114.69 445.78

注：U型风分量和V型风分量分别为纬向风速和经向风速。

3.1.2 实验参数设置及模型评价指标

模型的最大训练次数为2 000次，并采用早停策略（Early Stopping)，早停参数设置为10；学习率设置为0.01； Batch Size为128； GCN层数为2； GRU单元数为16；权重衰减率设置为0.000 5；损失函数为平均绝对误差（Mean Absolute Error， MAE）；优化器采用自适应矩估计（Adaptive moment estimation，Adam)；根据文献[38,40]采用最大信息系数（Maximal Information Coefficient， MIC）测量所有站点的时间相关性。当时滞为4时，站点的平均PM2.5浓度时间相关性在0.3以上，表明时滞为4时站点间PM2.5浓度存在不可忽略的相关性。因此，选择历史输入时长为4，进行逐小时预测。实验数据按照8:2分别划分为训练集和测试集，数据量分别为7 008和 1 752。为了评估模型的有效性，本文采用均方根误差（Root Mean Square Error， RMSE）、MAE和R2作为评价指标。评价指标计算公式如下：
R M S E = 1 N p N q ∑ i = 1 N p ∑ j = 1 N q y p , t - y ^ p , t 2
M A E = 1 N p N q ∑ i = 1 N p ∑ j = 1 N q | y p , t - y ^ p , t |
R 2 = 1 - ∑ t = 1 ( y t - y ^ t ) 2 ∑ t = 1 ( y t - y - t ) 2
式中： Np和Nq分别为站点个数和预测时间序列的长度； yp,t和 y ^ p , t分别为t时刻站点p的PM2.5观测值和预测值； y、 y ^和 y - t分别为站点的PM2.5观测值、预测值和均值。R2值越接近于1，表明模型的预测结果越好。

3.2 模型预测结果分析

3.2.1 不同预测模型结果对比

基于贵州省2017年数据集，完成逐小时的PM2.5浓度预测与评估，并与现有时空模型预测结果进行对比来验证所提出模型的性能。对比模型包括Huang等[41]提出的GTWR模型、Yang等[22]提出的考虑风向的STSVR模型、以及兼顾时空特征的GCN+GRU模型[42]。对比模型方法对于站点PM2.5浓度的空间相关性采用欧氏距离度量。GTWR模型和GCN+GRU模型不考虑站点间风向夹角，将风向作为站点PM2.5浓度的属性变量，STSVR模型将站点间风向夹角作为输入变量。对比模型的其它输入变量与本研究模型方法保持一致，使用欧氏距离度量站点PM2.5浓度相关性时，本文方法则退化为GCN+GRU方法。如表2所示，本文设置了消融实验来分析地形和风向的影响。由表2可知，在时空相关性模型中考虑将风向建模到站点间距离来衡量站点间PM2.5浓度相关性的STSVR模型相比于直接将风向作为站点属性变量的GTWR模型有更优的预测性能，表明风向对于站点的时空相关性是具有显著影响的，考虑风向对PM2.5的传输扩散影响可以提高模型的预测性能。由于GCN+GRU模型能够更好地捕捉数据之间的复杂关系，因此在预测空气污染物浓度时比STSVR表现更好。本文方法使用地形距离时相比于对比模型RMSE降低3.76%，同时顾及地形和风向因素引起的站点PM2.5传输扩散的各向异性时，相比于最优对比模型的的RMSE和MAE分别降低了11.29%和12.16%， R2提升了3.72%。
表2 不同方法在测试集上的性能比较

Tab. 2 Performance comparison of different methods on a test set

方法 输入特征 RMSE MAE R2
GTWR PM2.5浓度、欧氏距离、气象因素、土地利用 19.125 0 15.599 5 0.683 8
STSVR PM2.5浓度、欧氏距离、气象因素、土地利用 14.265 6 10.315 7 0.763 8
GCN+GRU PM2.5浓度、欧氏距离、气象因素、土地利用 11.325 3 7.796 0 0.851 1
本文方法 PM2.5浓度、地形距离、气象因素、土地利用 10.900 0 7.398 4 0.862 1
本文方法 PM2.5浓度、（风向约束）地形距离、气象因素、土地利用 10.046 6 6.848 0 0.882 8
提升/% - +11.29 -12.16 +3.72
为了评估本文模型方法对所有站点的PM2.5浓度预测效果，针对所有站点，使用RMSE指标对比了不同模型方法在不同站点的PM2.5浓度预测效果，对比结果如图7所示。由图7可知，相比之下，本研究所提出的模型方法在大部分站点PM2.5浓度预测结果的RMSE均为最小，说明本文所提模型方法能够有效提升站点PM2.5浓度预测效果。
图7 不同方法在不同站点的PM2.5浓度RMSE预测结果

Fig. 7 PM2.5 concentration prediction results RMSE by different methods at different stations

3.2.2 不同时间范围模型预测性能

为了评估本文所提模型在不同输入时长（1、2、3、4、5和6 h）和预测时长（1、2、3和4 h）的性能，进行了不同输入时长和预测时长的实验，实验结果如图8所示。由图8可知，模型的预测性能随着预测时长的增加而降低，在多个输入时长和预测时长中，输入时长为4，预测时长为1时，模型能够取得较好的效果。因此，本文模型方法能够捕获站点PM2.5浓度的时间相关性，并进行逐小时的PM2.5预测。
图8 不同输入时长和预测时长的RMSE预测结果

Fig. 8 Prediction result RMSE for different input duration and prediction duration

另外，为了分析本文模型方法捕捉时间序列的能力，在时间上进行分季节建模并通过在季节上的真值和预测值的散点回归图进行定量评估本文模型方法，实验结果如图9所示。由图9可知，PM2.5浓度具有明显的时间特征，本研究所提模型在4个时段的预测效果整体表现良好，其中9—11月、1—2月和12月的R2在0.86以上。本文模型的预测能力随时间变化，根据6—8月的回归图来看模型在 6—8月的预测结果存在明显的PM2.5浓度低值高估现象，R2仅有0.71。
图9 PM2.5浓度预测值和观测值的回归图

Fig. 9 Regression graph of predicted and observed PM2.5 concentration

3.2.3 模型预测结果空间化分析

为了体现本研究所提模型对所有站点同时预测结果的优势，随机选取测试集中连续5 h的预测结果与真实结果进行对比，并以克里金插值结果图的形式进行可视化。结果如图10所示。图10的前5张图片是PM2.5的真实变化情况，后5张图片是模型的预测结果情况。由图10可知，上午6时到10时是人们出行的高峰期之一，更多的车辆排放更多的尾气造成更严重的空气污染，因此整体区域的PM2.5的浓度逐渐升高。
图10 本文模型预测结果空间连续插值结果

Fig. 10 The model in this paper predicts the results of spatial continuous interpolation

贵州在北部大娄山、东北部武陵山、西北部乌蒙山、西南部老王山和中部苗岭的包围之下，地势大致呈西高东低，从中部向北、东、南3个方向倾斜。贵州省的西北部海拔较高，东部存在河谷低洼带，因此，在西部地区PM2.5容易向周围扩散而不容易聚集，使得西部整体的PM2.5浓度较低，而东部地区低洼区域不利于PM2.5浓度扩散，容易导致PM2.5浓度聚集。贵州高原山地居多，属于北亚热带季风湿润气候区，受低纬度高海拔的影响，冬季省中部以上地区以偏北风为主，其余地区以偏南风为主。贵州省在西南部地区存在山脉，限制了东部PM2.5浓度向西南部地区的扩散，受到风向和地形的影响，在选取的12月16日（冬季）的连续5 h内PM2.5浓度呈现出由东南区域向西北区域逐渐扩散的现象。根据结果可以看出，所提出模型在贵州省的PM2.5预测结果整体变化与真实情况非常接近。

3.3 地形因素影响分析与讨论

（1）地形修正距离与站点PM2.5浓度相关性
在保持风向基本相同时，分析站点间存在与不存在山脉等高地势地形时站点相关性。首先选取3个站点A、站点B、站点C，且站点A与站点B之间存在较高地形阻隔，站点B与站点C之间没有较高地形区域，如图11（a）所示。在站点的风向时间序列数据中，选取连续24 h内平均风向在0 ~90 °范围内的时间区间，计算站点间的PM2.5浓度相关性，相关性结果如图11（b）所示。
图11 地形对PM2.5浓度相关性影响

Fig. 11 Correlation effect of terrain on PM2.5 concentration

由图11（b）可知，站点的PM2.5浓度相关性在时间段3~5 h时逐渐增大，在时间段5~15 h内大致保持稳定，15 h后相关性整体相关性出现下降，即PM2.5在中短时间内的传输使得站点间的PM2.5浓度相近，而在长时间后PM2.5主要受到站点本身属性的影响，传输作用对站点间PM2.5浓度的相关性贡献较小。站点A与站点B之间存在高地势区域阻隔时，即使站点B与站点C的距离大于站点A与站点B的距离，站点B与站点C的PM2.5浓度相关性在多个时间段内都大于站点A与站点B的PM2.5浓度相关性。
作为对照，本文选取地形平缓区域的3个站点进行地形对站点间PM2.5浓度相关性影响分析，站点位置和相关性分析结果分别如图11（c）、图11（d）所示。由图11（d）可以看出，站点D与站点E、站点E与站点F的PM2.5浓度相关性变化趋势基本相同，整体站点间PM2.5浓度相关性呈现先基本不变，随后逐渐下降的趋势，距离更近的站点E和站点F的PM2.5浓度相关性整体大于相距较远的站点D和站点E的PM2.5浓度相关性，地形平缓导致地形对站点间的PM2.5浓度相关性影响不显著。实验验证高地势区域的地形对PM2.5传播是有阻碍作用的，进而影响站点之间PM2.5浓度的相关性。因此，将地形特征嵌入站点间距离度量，用以表征地形对于站点间PM2.5浓度相关性的影响是有必要的。
（2）地形距离的有效性评估
由于地形距离作用的影响与气象因素的作用大小（风速大小）是紧密相关的，为了进一步说明考虑地形因素的有效性，本文限定气象条件来对地形因素进行讨论。钟雨桐等指出不利气象条件为风速较低，本地PM2.5无法迅速消散的情况，即不利扩散条件[43]。根据有利气象条件和不利气象条件的定义，分别在有利气象条件和不利气象条件情况下，就地形影响进行讨论。首先，选取4个处于不同地形的站点，如图12所示。其中，站点2579A处于高地势区域，且处于山脉包围之中；站点2583A处于西北部山脉的山麓附近；站点1441A西北部和东部区域为山脉，且位于西北部和东部区域山脉形成的沟谷区域；站点1914A位于地势相对平缓的区域，但是西南部和北部存在山脉。然后，按照有利气象和不利气象筛选条件筛选出2017年12月28日17:00为有利气象条件时间，2017年10月25日16:00为不利气象条件时间。最后，分别在有利气象条件和不利气象条件下，对比本文方法以及GCN+GRU方法在选取站点上的PM2.5浓度预测情况，对比结果如表3所示。
图12 部分站点分布与地形可视化结果

Fig 12 Partial station distribution and terrain visualization results

由表3可知，在不利气象条件下，本研究所提模型相比于GCN+GRU模型在站点1441A、1914A、2579A和2583A的预测结果RMSE分别降低了4%、2%、1%和0.8%；在有利气象条件时，本文方法相比于对比模型在这些站点的预测结果RMSE分别降低了22.19%、8.11%、10.76%和13.97%。
表3 不同站点PM2.5浓度预测结果RMSE对比分析表

Tab. 3 RMSE comparison of the PM2.5 concentration prediction results at different stations

站点 RMSE
不利气象条件 有利气象条件
本文方法(r1) GCN+GRU(r2) (r1-r2)/r2×100% 本文方法(r1) GCN+GRU(r2) (r1-r2)/r2×100%
1441A 7.217 7 7.547 3 4 11.491 3 14.768 2 22.19
1914A 3.668 7 3.764 5 2 14.697 0 15.994 2 8.11
2579A 16.014 0 16.308 8 1 17.190 0 19.263 0 10.76
2583A 8.240 7 8.312 6 0.8 8.580 2 9.973 3 13.97

注： r1和r2分别为本文方法和GCN+GRU方法的RMSE。

在不利气象条件下，2579A完全被山脉包裹，由于缺乏强风，地形对PM2.5的传输扩散影响不显著。站点1914A和站点2583A处于地势相对平缓区域，不利气象条件下地形对PM2.5的传输扩散影响不明显。由于1441A处于沟谷地形，不利气象条件下沟谷地形可能会导致空气污染物在该区域的滞留和累积，考虑地形能够更好地捕捉到沟谷地形对PM2.5浓度的影响，使得在不利气象条件时站点1441A的预测结果RMSE降低效果在选取的4个站点中表现最优。
在有利气象条件下，由于1441A处于沟谷地形，有利气象条件导致PM2.5容易沿着沟谷快速扩散，而站点1441A在4个站点中表现出最大的RMSE降低比例，表明有利气象条件下沟谷地形对PM2.5传输扩散具有显著影响。站点2579A被山脉包裹，站点2583A西部存在高大山脉，本文方法更好地考虑了山脉地形对PM2.5传输扩散的阻挡效应，减少了预测误差。因此，相比于不利气象条件时，站点2579A和站点2583A在有利气象条件时的RMSE降低比例仅次于1441A，达到10%以上。在有利气象条件下，由于站点1914A处于地势平缓区域，地形对PM2.5的传输扩散影响有限，在4个站点中的RMSE降低比例最小，仅有8.11%。
综上所述，在有利和不利气象条件下，本文方法在降低站点PM2.5浓度预测误差上均能够起到良好的效果。在有利气象条件和不利气象条件下，本文方法相比于对比模型对处于沟谷地形的站点1441A上的RMSE降低比例是选取的4个站点中降低最大的，说明本文方法能够很好地捕捉到沟谷地形对PM2.5传输扩散的影响，从而提高预测准确性。在有利气象条件时，选取的4个站点上的PM2.5浓度预测结果的RMSE降低比例会有更大提升，且处于不同地形的站点的PM2.5浓度预测效果提升不同，在存在山脉或沟谷的地区会有较大的预测效果提升，说明在有利气象条件下考虑地形因素能够使得预测结果更准确。
（3）不同DSM分辨率对模型预测结果分析
DSM是数字地表模型，涵盖了地表建筑物、桥梁和树木等高度。为了分析不同DSM分辨率对模型预测结果的影响，对30 m分辨率DSM数据进行重采样分别得到300、3 000、30 000 m分辨率的DSM数据，并按照本研究所提模型进行实验，实验结果如表4所示。由表4可知，模型使用高分辨率的DSM能够取得更好的预测效果。高分辨率的DSM数据能够提供更详细的地形情况，通过地形距离计算能够得到更真实的PM2.5传输情况，进而能够得到更好的站点PM2.5浓度预测效果。因此，考虑地形因素对于提升站点PM2.5浓度预测结果是有效的。
表4 不同分辨率DSM下的模型预测结果

Tab. 4 Model prediction results under different resolution DSM

不同分辨率/m RMSE MAE R2
30 10.900 0 7.398 4 0.862 1
300 11.390 2 7.684 8 0.849 4
3 000 11.685 8 8.180 7 0.841 4
30 000 11.737 3 8.047 7 0.840 0

3.4 土地利用类型影响分析与讨论

现有研究表明，草地和水体与PM2.5浓度呈现负相关，而建成区等不透水面与PM2.5浓度呈现正相关，且植被相比水体能更有效降低PM2.5浓度[44]。为了分析不同土地利用类型对站点PM2.5浓度预测结果的影响，本文选取了地形较为平坦区域且具有不同土地利用类型的3个站点（1911A、2578A和2581A）进行分析。其中，站点1911A周围的土地利用类型为水体，站点2578A周围的土地利用类型为不透水面（建成区），站点2581A周围的土地利用类型为植被，站点的PM2.5浓度预测结果的评估指标对比结果如表5所示。由表5可知，周围土地利用类型为植被类型的站点2581A的PM2.5浓度预测误差最小，而土地利用类型为建成区的站点2578A的PM2.5浓度预测误差最大，土地利用类型为水域的站点1911A的PM2.5浓度预测误差处于二者之间，实验结果与土地利用和PM2.5浓度相关性研究结论一致。
表5 不同土地利用类型上站点的PM2.5浓度预测结果

Tab. 5 Prediction results of PM2.5 concentration on different land use types

预测结果 站点
1911A 2578A 2581A
RMSE 9.076 1 15.687 9 8.521 4
MAE 6.340 1 11.370 1 6.084 6
R2 0.884 2 0.827 6 0.927 9

4 结论

为了解决站点间PM2.5传输过程同时受到地形和风向因素的而产生的各向异性影响，引入站点间地形距离并结合风向来建模PM2.5在地形和风向约束下的空间传输过程，进而提出了一种顾及地理环境各向异性的PM2.5浓度时空图卷积网络预测模型。以地形距离和风向来衡量站点PM2.5传输扩散的各向异性，并结合站点的其它气象因素和土地利用类型特征，采用GCN模型计算空间特征，并通过GRU建模PM2.5浓度的时间序列特征，构建顾及地理环境各向异性的时空图卷积网络预测模型，为PM2.5浓度的精准预测提供了一种新的思路。通过在中国贵州省的PM2.5浓度预测实验表明，地理环境中各向异性的因素（地形、风向）对PM2.5浓度预测效果具有重要影响。本文顾及地形距离和风向改进的预测模型相比于现有方法在不同地形均能有效降低站点PM2.5浓度预测误差，尤其是在沟谷地形本文方法相比于最优对比模型的RMSE降低约为22%，有效提升了PM2.5浓度预测的精度，对空气污染预测和防治具有重要参考价值。
本文研究仍然存在一些局限性。如在考虑PM2.5的空间传输时，本文主要从自然地理环境特征角度出发考虑了地形因素、气象因素的影响。由于大范围人类活动数据获取较困难，因此本文对于人类活动对于PM2.5传播的影响未进行建模，而人类活动也是影响PM2.5聚集与传播的一个重要因素。因此，需要进一步探索其他因素（如人类活动特征）的影响以提高PM2.5浓度预测精度。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Liu B, Yan S, Li J Q, et al. A spatiotemporal recurrent neural network for prediction of atmospheric PM2.5: A case study of Beijing[J]. IEEE Transactions on Computational Social Systems, 2021, 8(3):578-588. DOI:10.1109/TCSS.2021.3056410

[2]
贺灿飞, 张腾, 杨晟朗. 环境规制效果与中国城市空气污染[J]. 自然资源学报, 2013, 28(10):1651-1663.

DOI

[He C F, Zhang T, Yang S L. Air pollution in Chinese cities: Does enforcement of environmental regulations matter?[J]. Journal of Natural Resources, 2013, 28(10):1651-1663.] DOI:10.11849/zrzyxb.2013.10.001

[3]
中华人民共和国生态环境部. 2020中国生态环境状况公报[R]. 2021.

[Ministry of Ecology and Environment of the People's Republic of China. 2020 report on the state of the ecology and environment in China[R]. 2021.]

[4]
Shang Y, Sun Z W, Cao J J, et al. Systematic review of Chinese studies of short-term exposure to air pollution and daily mortality[J]. Environment International, 2013, 54:100-111.] DOI:10.1016/j.envint.2013.01.010

PMID

[5]
Xing Y F, Xu Y H, Shi M H, et al. The impact of PM2.5 on the human respiratory system[J]. Journal of Thoracic Disease, 2016, 8(1):E69-E74. DOI:10.3978/j.issn.2072-1439.2016.01.19

[6]
Li C, Hammer M S, Zheng B, et al. Accelerated reduction of air pollutants in China, 2017-2020[J]. Science of the Total Environment, 2022, 803:150011 DOI:10.1016/j.scitotenv.2021.150011

[7]
Yang M L, Zhu Z J. Simulation analysis of spatial distribution of PM2.5 concentration based on LUR model[J]. Journal of Atmospheric and Environmental Optics, 2022, 17(3):347-359. DOI:10.3969/j.issn.1673-6141.2022.03.007

[8]
Jin H Y, Chen X H, Zhong R D, et al. Influence and prediction of PM2.5 through multiple environmental variables in China[J]. Science of the Total Environment, 2022, 849:157910 DOI:10.1016/j.scitotenv.2022.157910

[9]
Fu H Y, Zhang Y T. Improving the EEMD-GRNN model for PM2.5 prediction based on time scale reconstruction[J]. Journal of Geo-information Science, 2019, 21(7):1132-1142. DOI:10.12082/dqxxkx.2019.180598

[10]
Gao X, Li W. A graph-based LSTM model for PM2.5 forecasting[J]. Atmospheric Pollution Research, 2021, 12(9):101150. DOI:10.1016/j.apr.2021.101150

[11]
Wu Q Z, Xu W S, Shi A J, et a1. Air quality forecast of PMl0 in Beijing with Community Multi-scale Air Quality Modeling(CMAQ) system: Emission and improvement[J]. Geoscientific Model Development, 2014, 7(5):2243-2259. DOI:10.5194/gmd-7-2243-2014

[12]
邓涛, 吴兑, 邓雪娇, 等. 珠三角空气质量暨光化学烟雾数值预报系统[J]. 环境科学与技术, 2013, 36(4):62-68.

[Deng T, Wu D, Deng X J, et al. Numerical forecast system of air quality photochemical smog over Pearl River Delta Region[J]. Environmental Science & Technology, 2013, 36(4):62-68.] DOI:10.3969/j.issn.1003-6504.2013.04.013

[13]
Wang T J, Jiang F, Deng J J, et al. Urban air quality and regional haze weather forecast for Yangtze River Delta Region[J]. Atmospheric Environment, 2012, 58:70-83. DOI:10.1016/j.atmosenv.2012.01.014

[14]
王德冬, 秦聪. 区域PM2.5时空回归建模与预测[J]. 中国环境监测, 2019, 35(5):107-113.

[Wang D D, Qin C. Modeling and prediction of PM2.5 distribution using spatiotemporal Kriging with trend model[J]. Environmental Monitoring in China, 2019, 35(5):107-113.] DOI:10.19316/j.issn.1002-6002.2019.05.13

[15]
Bai Y, Wu L X, Qin K, et al. A geographically and temporally weighted regression model for ground-level PM2.5 estimation from satellite-derived 500 m resolution AOD[J]. Remote Sensing, 2016, 8(3):262. DOI:10.3390/rs8030262

[16]
Ma Z W, Hu X F, Sayer A M, et al. Satellite-based spatiotemporal trends in PM2.5 concentrations: China, 2004-2013[J]. Environmental Health Perspectives, 2016, 124(2):184-192. DOI:10.1289/ehp.1409481

[17]
杨亚莉, 李智伟, 钟卫军. 基于二向注意力循环神经网络的PM2.5浓度预测[J]. 空军工程大学学报(自然科学版), 2020, 21(6):101-106.

[Yang Y L, Li Z W, Zhong W J. A prediction of PM2.5 concentration based on a two-direction attention-based recurrent neural network[J]. Journal of Air Force Engineering University (Natural Science Edition), 2020, 21(6):101-106.] DOI:10.3969/j.issn.1009-3516.2020.06.016

[18]
李龙, 马磊, 贺建峰, 等. 基于特征向量的最小二乘支持向量机PM2.5浓度预测模型[J]. 计算机应用, 2014, 34(8):2212-2216.

DOI

[Li L, Ma L, He J F, et al. PM2.5 concentration prediction model of least squares support vector machine based on feature vector[J]. Journal of Computer Applications, 2014, 34(8):2212-2216.] DOI:10.11772/j.issn.1001-9081.2014.08.2212

[19]
戴李杰, 张长江, 马雷鸣. 基于机器学习的PM2.5短期浓度动态预报模型[J]. 计算机应用, 2017, 37(11):3057-3063.

DOI

[Dai L J, Zhang C J, Ma L M. Dynamic forecasting model of short-term PM2.5 concentration based on machine learning[J]. Journal of Computer Applications, 2017, 37(11):3057-3063.] DOI:10.11772/j.issn.1001-9081.2017.11.3057

[20]
李祥, 彭玲, 邵静, 等. 基于小波分解和ARMA模型的空气污染预报研究[J]. 环境工程, 2016, 34(8):110-113,134.

[Li X, Peng L, Shao J, et al. Air pollution forecast based on wavelet decomposition and ARMA model[J]. Environmental Engineering, 2016, 34(8):110-113,134.] DOI: 10.13205/j.hjgc.201608023

[21]
秦东明, 丁志军, 金玉鹏, 等. 基于自编码网络的空气污染物浓度预测[J]. 同济大学学报(自然科学版), 2019, 47(5):681-687.

[Qin D M, Ding Z J, Jin Y P, et al. An air pollutant prediction model based on auto-encoder network[J]. Journal of Tongji University (Natural Science), 2019, 47(5):681-687.] DOI:10.11908/j.issn.0253-374x.2019.05.013

[22]
Yang W T, Deng M, Xu F, et al. Prediction of hourly PM2.5 using a space-time support vector regression model[J]. Atmospheric Environment, 2018, 181:12-19. DOI: 10.1016/j.atmosenv.2018.03.015

[23]
白盛楠, 申晓留. 基于LSTM循环神经网络的PM2.5预测[J]. 计算机应用与软件, 2019, 36(1):67-70,104.

[Bai S N, Shen X L. PM2.5 prediction based on LSTM recurrent neural network[J]. Computer Applications and Software, 2019, 36(1):67-70,104.] DOI:10.3969/j.issn.1000-386x.2019.01.012

[24]
Becerra-Rico J, Aceves-Fernández M A, Esquivel-Escalante K, et al. Airborne particle pollution predictive model using Gated Recurrent Unit (GRU) deep neural networks[J]. Earth Science Informatics, 2020, 13(3):821-834. DOI:10.1007/s12145-020-00462-9

[25]
黄婕, 张丰, 杜震洪, 等. 基于RNN-CNN集成深度学习模型的PM2.5小时浓度预测[J]. 浙江大学学报(理学版), 2019, 46(3):370-379.

[Huang J, Zhang F, Du Z H, et al. Hourly concentration prediction of PM2.5 based on RNN-CNN ensemble deep learning model[J]. Journal of Zhejiang University (Science Edition), 2019, 46(3):370-379.] DOI:10.3785/j.issn.1008-9497.2019.03.016

[26]
马俊文, 严京海, 孙瑞雯, 等. 基于LSTM-GCN的PM2.5浓度预测模型[J]. 中国环境监测, 2022, 38(5):153-160.

[Ma J W, Yan J H, Sun R W, et al. Prediction model of PM2.5 concentration based on LSTM-GCN[J]. Environmental Monitoring in China, 2022, 38(5):153-160.] DOI: 10.19316/j.issn.1002-6002.2022.05.17

[27]
张云伟, 王晴茹, 陈嘉, 等. 城市街谷内PM2.5浓度时空变化及影响因素分析[J]. 中国环境科学, 2016, 36(10):2944-2949.

[Zhang Y W, Wang Q R, Chen J, et al. Temporal and spatial characteristics of PM2.5 concentration in urban street canyons and analysis on the affecting factors[J]. China Environmental Science, 2016, 36(10):2944-2949.] DOI:10.3969/j.issn.1000-6923.2016.10.012

[28]
贺祥, 林振山. 基于GAM模型分析影响因素交互作用对PM2.5浓度变化的影响[J]. 环境科学, 2017, 38(1):22-32.

[He X, Lin Z S. Interactive effects of the influencing factors on the changes of PM2.5 concentration based on GAM model[J]. Environmental Science, 2017, 38(1):22-32.] DOI:10.13227/j.hjkx.201606061

[29]
Han L J, Zhou W Q, Li W F. City as a major source area of fine particulate (PM2.5) in China[J]. Environmental Pollution, 2015, 206:183-187. DOI:10.1016/j.envpol.2015.06.038

PMID

[30]
许珊, 邹滨, 蒲强, 等. 土地利用/覆盖的空气污染效应分析[J]. 地球信息科学学报, 2015, 17(3):290-299.

DOI

[Xu S, Zou B, Pu Q, et al. Impact analysis of land use/cover on air pollution[J]. Journal of Geo-information Science, 2015, 17(3):290-299.] DOI:10.3724/SP.J.1047.2015.00290

[31]
Tobler W R. A computer movie simulating urban growth in the Detroit Region[J]. Economic Geography, 1970, 46:234 DOI:10.2307/143141

[32]
黄小刚, 赵景波, 孙从建, 等. 汾渭平原PM2.5空间分布的地形效应[J]. 环境科学, 2021, 42(10):4582-4592.

[Huang X G, Zhao J B, Sun C J, et al. Orographic influences on the spatial distribution of PM2.5 on the Fen-Wei Plain[J]. Environmental Science, 2021, 42(10):4582-4592.] DOI: 10.13227/j.hjkx.202102024

[33]
Hart P E, Nilsson N J, Raphael B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2):100-107. DOI:10.1109/TSSC.1968.300136

[34]
Lin Y J, Mago N, Gao Y, et al. Exploiting spatiotemporal patterns for accurate air quality forecasting using deep learning[C]// Proceedings of the 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. ACM, 2018:359-368. DOI:10.1145/3274895.3274907

[35]
徐冰冰, 岑科廷, 黄俊杰, 等. 图卷积神经网络综述[J]. 计算机学报, 2020, 43(5):755-780.

[Xu B B, Cen K T, Huang J J, et al. A survey on graph convolutional neural network[J]. Chinese Journal of Computers, 2020, 43(5):755-780.] DOI:10.11897/SP.J.1016.2020.00755

[36]
Dey R, Salem F M. Gate-variants of Gated Recurrent Unit (GRU) neural networks[C]// 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS). IEEE, 2017:1597-1600. DOI:10.1109/MWSCAS.2017.8053243

[37]
黎煜昭, 刘启亮, 邓敏, 等. 基于物理约束GRU神经网络的河流水质预测模型[J]. 地球信息科学学报, 2023, 25(1):102-114.

DOI

[Li Y Z, Liu Q L, Deng M, et al. A physics-constrained GRU neural network for river water quality prediction[J]. Journal of Geo-information Science, 2023, 25(1):102-114.] DOI:10.12082/dqxxkx.2023.220331

[38]
Xiao F, Yang M, Fan H, et al. An improved deep learning model for predicting daily PM2.5 concentration[J]. Scientific Reports, 2020, 10(1):20988. DOI:10.1038/s41598-020-77757-w

PMID

[39]
Yang J, Huang X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019[J]. Earth System Science Data, 2021, 13(8):3907-3925. DOI:10.5194/essd-13-3907-2021

[40]
毛文婧, 王卫林, 焦利民, 等. 基于深度学习的中国连续空间覆盖PM2.5浓度预报[J]. 测绘学报, 2022, 51(3):361-372.

DOI

[Mao W J, Wang W L, Jiao L M, et al. Continuous spatial coverage PM2.5 concentration forecast in China based on deep learning[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(3):361-372.] DOI:10.11947/j.AGCS.202.20200385

[41]
Huang B, Wu B, Barry M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices[J]. International Journal of Geographical Information Science, 2010, 24(3):383-401. DOI: 10.1080/13658810802672469

[42]
Kim D Y, Jin D Y, Suk H I. Spatiotemporal graph neural networks for predicting mid-to-long-term PM2.5 concentrations[J]. Journal of Cleaner Production, 2023, 425:138880 DOI:10.1016/j.jclepro.2023.138880

[43]
钟雨桐, 韦晶, 郑月明, 等. 基于静风期污染物的PM2.5排放清单空间精细化方法[J]. 地球信息科学学报, 2021, 23(11):1971-1983.

DOI

[Zhong Y T, Wei J, Zheng Y M, et al. Spatial refinement method of the PM2.5 emission inventory based on the quiescent period pollutant[J]. Journal of Geo-information Science, 2021, 23(11):1971-1983.] DOI: 10.12082/dqxxkx.2021.210290

[44]
邹雨轩, 吴志峰, 曹峥. 耦合土地利用回归与人口加权模型的PM2.5暴露风险评估[J]. 地球信息科学学报, 2019, 21(7):1018-1028.

DOI

[Zou Y X, Wu Z F, Cao Z. Assessing PM2.5 exposure risk by coupling land use regression model and population weighted model[J]. Journal of Geo-information Science, 2019, 21(7):1018-1028.] DOI:10.12082/dqxxkx.2019.180695

Options
文章导航

/

〈 〉