EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 10: 2254 - 2267

DOI: https://doi.org/10.12082/dqxxkx.2024.230665

专栏：“GIS 与未来城市交通”

基于边折叠的实景三维模型简化算法

  • 金河 , 1, 2, 3 ,
  • 刘涛 , 1, 2, 3, * ,
  • 杜萍 1, 2, 3 ,
  • 张钊 1, 2, 3 ,
  • 丁楠楠 1, 2, 3 ,
  • 陈忱 4 ,
  • 贾彦党 4 ,
  • 刘昌新 4
展开
  • 1.兰州交通大学测绘与地理信息学院，兰州 730070
  • 2.地理国情监测技术应用国家地方联合工程研究中心，兰州 730070
  • 3.甘肃省地理国情监测工程实验室，兰州 730070
  • 4.甘肃省交通规划勘察设计院股份有限公司，兰州 730030
* 刘 涛（1981— ），男，湖北随州人，博士，教授博导，主要研究方向为空间关系理论、GIS与遥感一体化、GIS和 RS应用与开发。E-mail:

金 河（1997— ），男，宁夏中卫人，硕士生，主要研究方向为实景三维研究。E-mail:

Copy editor: 蒋树芳 , 黄光玉

收稿日期: 2023-11-08

  修回日期: 2024-01-20

  网络出版日期: 2024-10-09

基金资助

甘肃省科技重大专项(22ZD6GA010)

国家自然科学基金项目(42261076)

国家自然科学基金项目(42061060)

兰州交通大学重点研发项目资助(LZJTU-ZDYF2301)

收起

Mesh Simplification Algorithm for Photorealistic 3D Models Based on Edge Collapse

  • JIN He , 1, 2, 3 ,
  • LIU Tao , 1, 2, 3, * ,
  • DU Ping 1, 2, 3 ,
  • ZHANG Zhao 1, 2, 3 ,
  • DING Nannan 1, 2, 3 ,
  • CHEN Chen 4 ,
  • JIA Yandang 4 ,
  • LIU Changxin 4
Expand
  • 1. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China
  • 2. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, Lanzhou 730070, China
  • 3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China
  • 4. Gansu Provincial Transportation Planning Survey and Design Institute Co., Ltd., Lanzhou 730030, China
* LIU Tao, E-mail:

Received date: 2023-11-08

  Revised date: 2024-01-20

  Online published: 2024-10-09

Supported by

Major Science and Technology Special Project of Gansu Province(22ZD6GA010)

National Natural Science Foundation of China(42261076)

National Natural Science Foundation of China(42061060)

Key Research and Development Project of Lanzhou Jiaotong University(LZJTU-ZDYF2301)

Fold

摘要

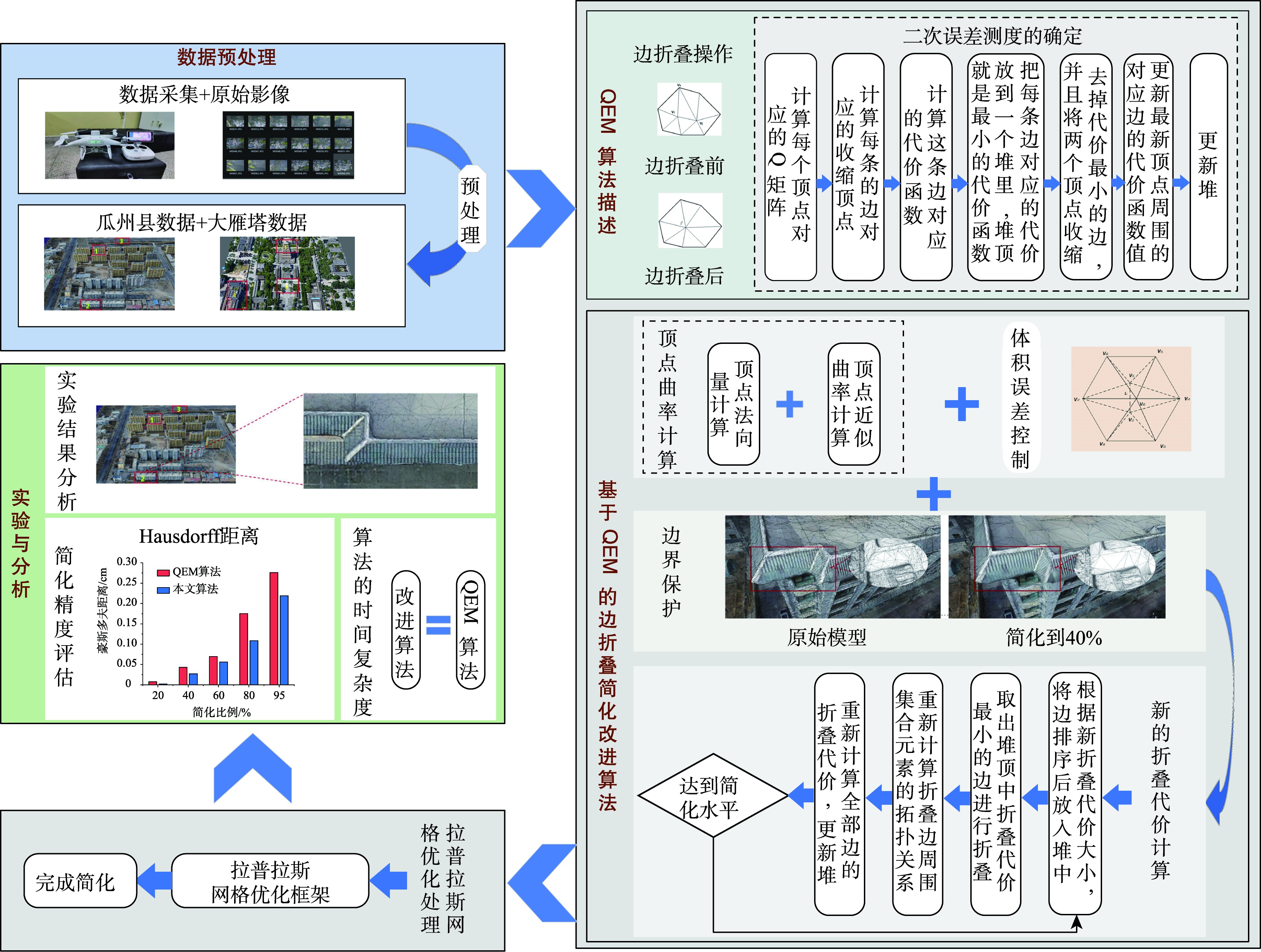
三维模型轻量化是实景三维中国建设的当务之急，对三维模型进行一定简化是较为合适的途径。在模型简化算法中，二次误差测度QEM(Quadric Error Metrics)算法是较为经典的算法。但传统的QEM算法在简化过程中没有专门的机制来保护重要细节，并且简化后模型网格质量有待进一步优化。为此，本文提出了一种基于边折叠的实景三维模型简化与优化方法，该方法中的简化算法引入了顶点近似曲率及体积误差作为约束条件，以改变边折叠代价从而使三维模型在简化的同时能够保持模型的重要细节，达到较好的简化效果。在改变边折叠代价的同时加入边界保护条件，有效保护了模型边界。最后针对简化后的网格进行了拉普拉斯网格优化处理，用于三角形形状优化和特征保持。本文使用的数据源是采用倾斜摄影测量方式采集影像并使smart3D三维重建得到的格式为OSGB的实景三维网格模型数据，使用这一数据源进行实验研究，并和经典的QEM算法进行对比。研究结果表明，本文算法很好地保留了三维模型的细节特征，同时提高了简化模型的网格质量。该算法适用于实景三维模型的轻量化。

关键词： 二次误差测度; 拉普拉斯网格优化; 模型简化; 实景三维; 边折叠; 误差度量; 特征保持; 边界保护

本文引用格式

金河 , 刘涛 , 杜萍 , 张钊 , 丁楠楠 , 陈忱 , 贾彦党 , 刘昌新 . 基于边折叠的实景三维模型简化算法[J]. 地球信息科学学报, 2024 , 26(10) : 2254 -2267 . DOI: 10.12082/dqxxkx.2024.230665

Abstract

The lightweighting of three-dimensional models is a pressing need in the construction of realistic three-dimensional environments in China. Simplifying three-dimensional models to a certain extent is a suitable approach. In the realm of model simplification algorithms, the Quadric Error Metrics (QEM) algorithm is considered a classic method. However, traditional QEM algorithms lack a dedicated mechanism to preserve crucial details during the simplification process, and the post-simplification mesh quality needs further optimization. To address these challenges, this paper proposes a real-world three-dimensional model simplification algorithm based on edge collapsing. The aim is to better preserve key details and enhance the mesh quality of the simplified model in the process of three-dimensional model lightweighting. The simplification algorithm in this method introduces vertex approximation curvature and volume error as constraints, altering the edge collapsing cost to maintain important details while achieving effective simplification. By incorporating boundary preservation conditions while modifying edge collapsing costs, the algorithm effectively safeguards the model's boundaries. Finally, post-simplification mesh optimization is performed using the Laplacian mesh optimization method to optimize triangle shapes and preserve features. Experiments were conducted to verify the proposed algorithm and compare it with the traditional QEM algorithm. The research results indicate that our proposed method retains regions with rich details better than the traditional QEM algorithm, significantly reducing the number of elongated triangles and improving mesh quality. This algorithm is applicable to the lightweighting of real-world three-dimensional models, contributing to enhanced model performance and visualization effects.

Key words： Quadric Error Metrics; Laplacian mesh optimization; model simplification; real-world 3D; edge collapsing; error metrics; feature preservation; boundary protection

1 引言

实景三维是对一定范围内人类生产、生活和生态空间构建真实、立体、时序化反映和表达的数字空间[1]。实景三维模型是实景三维中国建设中的数据底座，当前的实景三维模型一般采用倾斜摄影采集技术、LiDAR激光雷达扫描技术、人工建模技术等方法创建接近实际场景的三维模型[2]。然而，实景三维模型具有结构复杂、数据量大等特点，给数据存储、处理和渲染都带来了巨大的挑战。为确保在复杂网络环境下，实景三维模型数据在三维可视化场景中进行复杂而高效的可视化与分析任务，对于满足不同应用需求的可视化效率与效果进行优化的研究也日渐丰富[3]。所以在现有计算机硬件的条件下如何渲染大数据体量的实景三维建筑模型来保证三维可视化的效率与效果是最关键的问题[4]。因此，对实景三维模型进行简化变得尤为必要。实景三维模型通过简化，可以降低模型的复杂度，在保持模型主要形状和特征的同时，消除冗余的几何信息，使得实景三维模型更加轻量化，以达到减少模型数据量和提高渲染效率的目标。
目前，被国内国外广泛采纳的三维模型简化技术主要涵盖几何删除法和顶点重采样法等多种方法。在这些技术中，顶点重采样法存在一些弊端，比如多次对模型进行采样可能引起失真，造成视觉效果较差，而且实现的难度较大。相较之下，几何删除法因其清晰的思路、对计算机硬件要求相对较低以及简化后模型能够保持良好视觉效果等诸多优势，已经成为广泛应用的简化技术。几何删除法根据删除元素的不同，可分为顶点删除法[5]、边折叠法[6-7]、三角面片塌陷法[8-9]等多种方法。在这些方法中，边折叠法因其简化速度快、效率高，同时还能维持原模型的拓扑结构，因此成为目前应用最广泛的简化技术之一[10]。
一些国内外研究者在二次误差测度（QEM）的基础上进行了算法的改进，特别关注细节的保留和模型质量的提升方面。Garland等[11]是一种经典的网格简化算法，它在边折叠算法的基础上，引入二次误差测度（Quadric Error Metrics，QEM）来控制简化过程，但是经该算法简化后的模型过于均匀，无法适用于对细节要求较高的区域。张韵等[12]通过考虑曲线近似曲率和待折叠边邻域三角形的平均面积作为惩罚因子，成功减少了模型表面的三角面片数量，有效降低了模型在内存中的占用，从而获得了更优质的模型。然而，这一优化手段导致了较长的处理时间。Li等[13]将二次误差测度与顶点绝对曲率结合，处理后的模型较好地保持了细节特征，但网格质量较差。Tseng等[14]在文献[11]的基础上进行了改进，较好地保持了细节特征，但是简化后狭长三角形较多，导致模型几何不稳定，影响网格的可视化效果和渲染质量。Ozaki等[15]基于QEM提出一个适用于大规模实景三维模型复杂网格的简化算法，但对细节特征的保持欠佳。栾婉娜等[16]在简化的同时能够有效保持网格特征，得到视觉上更加均匀的网格模型，但该算法需要先进行分割再拼接，步骤繁琐。
以上算法难以在保留细节特征和网格质量之间取得平衡，有些专注于提升网格质量，但却忽略了细节特征，有些保留了细节特征，却忽略了网格质量。为此，本文提出一种新的实景三维模型简化算法。对基于边折叠的二次误差测度算法进行改进，通过引入顶点近似曲率和体积误差控制来影响边折叠的代价，从而更好地保留模型的细节特征。同时，消除简化过程中可能产生的狭长三角形，确保模型在保留细节特征的同时，具有更高的模型质量。

2 研究方法

如图1所示，本文研究方法包括数据预处理、QEM算法描述、基于QEM的边折叠简化改进算法、拉普来是网格优化处理4个重要过程。在网格简化的过程中，每次都选择具有最小折叠代价的边进行折叠操作。目前，通常通过逐一搜索和对比的方式来寻找具有最小折叠代价的边。然而，一种更加精细的方法是利用二叉堆来存储边的折叠误差队列，并借助堆排序的原理将边的折叠代价进行排序，使得每次迭代简化时，更易于提取具有最小折叠代价的边。考虑到实景三维模型在不同区域有不同的细节特征保持需求，本文在折叠代价中引入顶点曲率及体积误差控制，以实现更为灵活的简化操作。
图1 技术流程

Fig. 1 Technical flow chart

2.1 数据预处理

本文采用无人机航拍得到甘肃省酒泉市瓜州县倾斜摄影影像数据，然后使用smart3D对采集数据进行内业处理，内业处理包括空三测量、构建TIN模型（三角网模型）等过程。在本文中，smart3D软件处理后输出OSGB格式的Mesh模型。

2.2 QEM算法描述

2.2.1 边折叠操作

边折叠算法是Hoppe[17]最早提出的一种三角网格方法，该算法通过不断迭代进行边折叠操作达到简化的目的。迭代进行边折叠过程中，每次选择折叠误差最小的边，删除与该边所有相邻的顶点与面，然后对边折叠后所产生的空洞重新进行三角化。边折叠操作如图2所示，将Vi与Vj两个顶点合并至新顶点V，与Vi、Vj相连的所有的点都与新的顶点V相连，同时对边折叠产生的空洞重新进行三角化。
图2 边折叠算法

Fig. 2 Edge collapse operatpor

2.2.2 二次误差测度的确定

一条边是否需要折叠是由其折叠代价决定的，本文使用二次误差测度（QEM）来计算折叠边的代价。定义网格中顶点 V = [ V x   V y   V z   1 ] T，所有初始误差矩阵为Q。原始网格中顶点V具有n个相邻面，其每个平面的平面方程为ax+by+cz+d=0， P = [ a   b   c   d ] T为平面方程的系数。其中平面法向量为单位向量。顶点V的顶点误差ΔV为顶点V 到其所有一阶邻域三角形面片距离的平方和，如 式（1）所示。
Δ V = Δ V x , V y , V z , 1 T = ∑ P ∈ P V P T V 2 = V T ( ∑ P ∈ P ( V ) K p ) V
式中：Kp是求网格中任意点到平面P距离平方和矩阵，如式（2）所示。矩阵Q如式（3）所示，Q为顶点V的二次误差矩阵，为4×4的对称矩阵，这样每点都有属于自己的代价矩阵Q。
K P = P P T = a 2 a b a c a d a b b 2 b c b d a c b c c 2 c d a d b d c d d 2
Q = ∑ p ∈ P V K p
定义一条边ViVj，边ViVj折叠到一个新的顶点V，新顶点V的二次误差测度矩阵表示为 Q n e w = Q i + Q j，折叠代价为 Δ ( V ¯ ) = V ¯   T Q n e w V ¯，具体展开折叠代价为：
Δ ( V - ) = q 11 x 2 + 2 q 12 x y + 2 q 13 x z + 2 q 14 x + q 22 y 2 +                                         2 q 23 y z + 2 q 24 y + q 33 z 2 + 2 q 34 z + q 44
分别对x、y、z求偏导，通过 ∂ △ / ∂ x = ∂ △ / ∂ y = ∂ △ / ∂ z = 0确定V的位置，具体操作如下：
V -   = q 11 q 12 q 13 q 14 q 12 q 22 q 23 q 24 q 13 q 23 q 33 q 34 0 0 0 1 - 1 ×   0 0 0 1
如果式（5）中左侧矩阵是可逆的，则可以直接求出；如果不可逆，则折叠边的中点和2个端点中选择使折叠代价最小的点作为新顶点。

2.3 基于QEM的边折叠简化改进算法

2.3.1 顶点曲率计算

在微分曲面中，曲率是一种用于量化曲面细节特征信息的度量指标，它能够描述曲面上折痕、拐点和尖角等特征变化明显的区域[18]。由于三维模型由众多三角网格构成，通常使用网格顶点的离散曲率来衡量顶点位置的凹凸程度[19]。在三维模型的平坦区域，曲率较小，而在具有折痕、拐点等特征的区域，曲率则较大[20]。为了更好地保留模型的局部细节特征，本文将顶点近似曲率引入二次误差测度中。这里所指的顶点近似曲率是指顶点的法向量与其一环邻域内各个三角面单位法向量之间的夹角，用于表示顶点的法线方向的变化程度。顶点曲率计算包括顶点法向量计算和顶点近似曲率计算2个步骤。
（1） 顶点法向量计算
本文将顶点一环邻域内全部三角形的平面法向量的平均值作为该顶点的法向量。由于顶点一环邻域内的所有三角形都共享该顶点，因此其法向量的平均值可被视为该顶点的整体法向量，如图3所示。在光滑表面上，邻近三角形的法向量通常趋向一致，因此平均法向量可以更好地代表该点的法向量。对于顶点v，其相邻三角形集合T(v)，每个三角形 t ∈ T ( v )。为了在法向量计算中赋予不同三角形不同的重要性，对顶点一阶邻域三角形面的内角αi进行加权计算，以适应不同区域的几何特征。顶点法向量计算公式如式（6）所示。
n v = ∑ t ∈ T ( v ) n t α i / C o u n t ( T ( v ) )
式中：nv为顶点v的法向量；Count(T(v))表示一环邻域所有三角形数量；nt为三角形平面的法向量。
图3 相邻三角形法向量及内角

Fig. 3 Adjacent triangle normals and interior angles

（2） 顶点近似曲率计算
顶点近似曲率计算公式如（8）所示，其中三角面T中3个顶点分别记作Vi、Vj、Vk，则T的单位法向量 n t i表示为：
n t i = V j - V i × V k - V j V j - V i × V k - V j
得到三角面T的单位法向量后，可得出该顶点的曲率kv，即：
k v = ∑ C o u n t ( T ( v ) ) θ n v , n t i C o u n t ( T ( v ) )
式中： θ ( n v , n t i )是顶点法向量与其一环邻域内三角面T的夹角，即 θ ( n v , n t i ) = a r c c o s n v ∙ n t i ∣ n v ∣ ∙ ∣ n t i ∣。

2.3.2 体积误差控制

在对一些细节要求较高的实景三维模型中，仅仅依靠顶点近似曲率无法充分捕捉局部细节特征。为了更准确地度量模型表面的细节特征，本文引入体积误差控制，以确保模型的细节特征区域在简化过程中得到有效保留。体积误差是指在进行某次边折叠操作后，简化模型与初始模型之间的体积变化量。通过控制体积误差，能够更加有效地把握原始模型的体积变化，使得简化结果能够在满足细节需求的同时，获得适当的轻量化处理。体积误差计算过程如图4所示。
图4 体积误差分析

Fig. 4 Volume error analysis

图4中，当边Li折叠为点vi0时（其中Li表示折叠边），体积误差Cv表示以vi0为顶点，以边Li其一阶邻域三角形为底面的所有锥体的体积之和。其中Li的一阶邻域三角形指边Li各个顶点的一阶邻域三角形，如图中Li的一阶邻域三角形(ΔVi1Vi2Vi4)、(ΔVi1Vi2Vi7)、(ΔVi1Vi6Vi7)、(ΔVi1Vi5Vi6)、(ΔVi1Vi4Vi5)、(ΔVi2Vi3Vi8)、(ΔVi2Vi7Vi8)、(ΔVi2Vi3Vi4)。边Li全部一阶邻域三角形的集合记为 { f o t } T i。即得：
C v = ∑ T j ∈ f o t T i 1 3 ( v i 0 ∙ P T j T ) ∙ S T j
式中：vi0表示边Li的折叠点，折叠点vi0的坐标记为(xi, yi, zi, 1)，设三角形Tj的平面方程为ajx+bjy+cjz+dj=0，其中 a j 2 + b j 2 + c j 2 = 1， P T i为顶点vi0在三角形 Tj所在平面投影点。令 P T i = ( a j ,   b j ,   c j ,   d j )，三角形Tj的面积为 S T j。
式（9）的正负取值反映了简化前后模型的凹凸特性。在模型简化的过程中，体积误差可能呈正值或负值，甚至可能出现网格模型发生变化而体积误差仍然为零的情况。因此，为了更加准确地评估简化模型体积的变化，本文采用平方体积累加的方法[21]来计算体积误差，如式（10）所示。
C v 2 = ∑ T j ∈ f o t T i 1 9 ( v i 0 ∙ P T j T P T j ∙ v i 0 T ) ∙ S T j 2

2.3.3 边界保护

在很多情况下，保持模型的边界形状至关重要，特别是对于边界具有特殊语义和功能的模型，如建筑物、汽车等。使用QEM算法简化后模型出现以下结构，如图5所示。
图5 三维模型边界QEM算法简化效果

Fig. 5 Simplification of 3D model boundaries

为使边界变化最小，本文引入边界约束，有针对性地保护模型的边界形状，确保简化后的模型在边界处更好地与原始模型保持一致。
边界保护操作步骤如下： ① 用V表示简化前顶点集合，用B表示原始边界顶点的集合，B={b1, b2, …, bi}，其中i是边界顶点的数量； ② 将这些边界点用作参照，以确保简化后的模型 V ˙中的顶点集合包含原始边界点集B； ③在简化过程中，计算每个简化后的顶点与其最近边界顶点之间的欧氏距离，并将这个距离的平方作为边界约束，即边界约束项Bv，如式（11）所示。
B v = ∑ ( d ( v ,   b ) 2 )  
式中：d(v, b)表示简化后的顶点v与原始边界点b之间的欧氏距离，其中 v ∈ V ˙   ,   b ∈ B；   V ˙为简化后的顶点集合；B为原始边界点的集合。

2.3.4 新的折叠代价计算

新折叠代价综合考虑了顶点曲率、边界约束项和体积误差，能够更加精确地控制折叠过程，保留重要细节的同时，确保简化后的模型与原始模型在边界处保持良好的对应关系，现对模型重要细节进行约束。新折叠代价计算公式如式（12）所示。
Δ V = V T ( k v B v ∑ P ∈ P ( V ) K p ) V / C v 2
式中： Q = k v B v ∑ P ∈ P ( V ) K p / C v 2为新顶点的二次误差矩阵。

2.4 拉普拉斯网格优化处理

三角形的形状对曲率的影响远比三角形的大小对曲率的影响更加显著[22]。经本文改进简化算法处理后的模型保留了更多细节特征，但仍然存在一些狭长三角形，因此有必要对简化后的网格进行优化处理。
拉普拉斯网格优化算法是当前常用的优化方法。截至目前，已有众多保留特征的拉普拉斯网格优化算法[23⇓-25]。为了在优化过程中保留细节特征，本文采用Nealen等[26]中提出的拉普拉斯网格优化框架，用于三角形形状优化和特征保持。拉普拉斯网格优化处理的具体步骤如下：
（1） 用 G = ( V , E )来表示简化后的一个网格，其中 V = [ v 1 T ,   v 2 T , … ,   v n T ] T ,   v i = [ v i x ,   v i y ,   v i z ] T ∈ R 3是顶点， E是边，拉普拉斯坐标定义为：
δ i = ∑ { i , j } ∈ E w i j ( v j - v i ) = ∑ { i , j } ∈ E w i j v j - v i
其中 ∑ { i , j } ∈ E   w i j = 1且权重的选择如式（14）。
w i j = ω i j ∑ { i , k } ∈ E ω i k
本文权重选择定义了δi的性质。一些常见的选择包括式（15）和式（16）。
ω i j = 1
ω i j = c o t α + c o t β
式（15）代表均匀权重，而式（16）代表余切权重。这些方程中使用的角度如图6所示。
图6 拉普拉斯算子几何形式

Fig. 6 Laplace operator geometric form

对于 V d = [ v 1 d ,   v 2 d ,   … ,   v n d ] T，其中 d ∈ { x ,   y ,   z }，表示包含n个顶点的x、y或z坐标的n×1向量，可以分别计算拉普拉斯矩阵 Δ d = [ δ 1 d ,   δ 2 d ,   … ,   δ n d ] T，其中 d ∈ { x ,   y ,   z }的x、y和z坐标，如式（17）所示。
Δ d = L V d
式中：L是m×n的拉普拉斯矩阵。
（2） 拉普拉斯网格优化求解。
L u I m × m | 0 V d ' = Δ d , c V ( 1 . . . m ) d
式中：Lu为利用均匀权值构建的拉普拉斯矩阵； V d '为要求解的平滑后的网格顶点。本文用m个顶点作为约束。这样等式左边是一个 ( m + n ) × n的矩阵乘以一个 n × 1的向量，右边是一个 ( m + n ) × 1的向量。

3 实验与分析

本文在硬件配置为2.20 GHz的Intel(R) Xeon(R) Silver 4214 CPU和16 GB内存的环境下，采用C++语言，结合OSG（OpenSceneGraph）、OpenMesh库以及MeshLab工具，实现了改进的QEM算法。本文使用的场景模型数据源为甘肃省酒泉市瓜州县城区（部分）和陕西省西安市大雁塔通过倾斜摄影测量方式采集航摄影像，经过三维重建技术得到的实景三维模型，然后进行简化实验。在相同简化程度下，对比分析了本文改进算法与传统QEM算法的简化结果，以验证本文方法的有效性和可行性。

3.1 实验结果分析

本文选取2组实验数据各3个典型实验区，如图7所示，包括建筑物和道路，它们通常在地图制作、城市规划、导航和地理信息系统（GIS）中起到关键作用。建筑物和道路是城市和乡村地理空间中的2个主要要素，它们在各种应用中都扮演着关键角色。保留这些区域细节可以提供更准确的地理信息，从而改善城市规划、导航、紧急情况响应和地理分析等方面的应用。
图7 实验数据

Fig. 7 Experimental data

采用改进算法和QEM算法分别对3个实验区进行40%和80%程度的模型简化，结果如表1、表2图8所示。由图8可知，简化程度为40%时， 2种算法都具有良好的简化效果，但经本文算法简化后的三角网格显然更加规则，说明网格质量更高；当简化程度达到80%时，在细节丰富的窗户等区域（如图8（a）和图8（b），图9（a）和图9（b）），改进算法生成的网格数量明显多于QEM算法，且保留了大量的细节。
表1 瓜州县模型简化统计

Tab. 1 Statistical simplification of Guazhou County Model

对比项 本文算法 QEM算法
区域1 区域2 区域3 区域1 区域2 区域3
面片数/个 209 041 69 680 181 429 60 476 92 329 30 776 167 232 55 744 145 143 48 381 73 863 5 090
简化程度/% 40 80 40 80 40 80 40 80 40 80 40 80
表2 大雁塔模型简化统计

Tab. 2 Statistical simplification of Big Wild Goose Pagoda Model

对比项 本文算法 QEM算法
区域1 区域2 区域3 区域1 区域2 区域3
面片数/个 537 645 179 215 299 388 99 796 526 355 175 452 430 116 143 372 239 511 79 837 421 085 140 302
简化程度/% 40 80 40 80 40 80 40 80 40 80 40 80
图8 瓜州县数据本文算法与QEM算法简化后效果

Fig. 8 Schematic comparison of the algorithm in this paper and the simplified QEM Algorithm with Guazhou County data

图9 大雁塔数据本文算法与QEM算法简化后效果

Fig. 9 Schematic comparison of the algorithm in this paper and the simplified QEM algorithm with Big Wild Goose Pagoda

对采用改进算法简化后的模型进行优化处理，优化结果如图10、图11所示。由图可知，优化前的模型明显存在一定数量的狭长三角形，经过优化后狭长三角形的数量明显减少。同时，优化后的三角形大多与正三角形类似，极大地提升了模型质量，视觉效果较好。
图10 瓜州县数据本文算法优化后效果

Fig. 10 Effect diagrams of algorithm optimization in Guazhou County data in this paper

图11 大雁塔数据本文算法优化后效果

Fig. 11 Effect diagrams of algorithm optimization in Big Wild Goose Pagoda data in this paper

图12为瓜州县数据实验区2边界实景图。由于本文加入了边界保护，有效地保护了边界，使 得边界呈现更接近于原始模型的效果。通过对比图13(a)和图13(c)，图13(b)和图13(d)，相对于QEM算法，本文算法通过边界保护效果更好。
图12 瓜州县数据实验区2边界实景图

Fig. 12 Realistic scene images of the experimental area 2 boundaries in Guazhou County data

图13 瓜州县数据实验区2边界简化效果对比

Fig. 13 Comparative analysis of boundary simplification effects in experimental area 2 of Guazhou County data

3.2 简化精度评估

本文使用Hausdorff距离[27]来量化简化后的模型与原始模型之间的差异，在简化实景三维模型的情境中， Hausdorff距离可以用来评价简化前后模型之间的形状差异，即简化效果。较小的Hausdorff距离表示简化后的模型保留了更多的细节和形状信息，与原始模型更为接近。反之，如果Hausdorff距离较大，则意味着简化过程可能丢失了重要的细节特征或产生了较大的形状变化。
运用MeshLab计算2组数据3个实验区域的简化误差（图14），得出以下结论：在较低的简化程度条件下，本文改进算法与QEM算法的简化误差接近，但本文算法在细节保留方面仍具有一定优势；随着简化程度不断增大，特别是达到80%及以上的简化程度时，本文算法的优势十分显著，说明它不仅能够较好地保留细节特征，而且还极大地降低了简化误差。
图14 2组数据不同区域简化误差对比

Fig. 14 Comparative analysis of simplification errors in different regions for two sets of data

3.3 算法的时间复杂度

本文方法的实现分为3个阶段：
（1）阶段1包括确定折叠顶点的位置、计算折叠代价以及对需要折叠的边进行堆排序；假设本文原始模型有L条边，简化后的模型有L'条：
① 折叠顶点位置的时间复杂度为O(L)；
② 确定边折叠代价的时间复杂度为O(L)；
③ 堆排序的时间复杂度为O(L logL)。
因此，得出初始化阶段的总时间复杂度为 O(L logL)。
（2） 阶段2对折叠边进行迭代简化。
① 迭代简化的时间复杂度为 O l o g L - i，其中i表示迭代次数。
② 在简化阶段总的时间复杂度为： O L   l o g L - ( L ' - 1 )   l o g   L ' - 1
（3）阶段3通过拉普拉斯优化模型中的狭长三角形。
拉普拉斯网格优化阶段的时间复杂度为 O i | M |，其中i代表迭代次数， | M |是顶点的数量。
本文算法的总体时间复杂度为O(L logL)，与QEM算法的时间复杂度O(L logL)相同。因此在同样的时间复杂度下本文较好地保持了模型的细节特征，同时模型的质量进一步增加强。

4 结论

实景三维模型作为当前智慧城市、数字孪生以及实景三维中国建设等多个领域的基座，凸显出其在地理信息领域的重要作用。在构建实景三维模型时，需要构建海量的三角网格和纹理，随着实景三维模型数据的真实性以及精确度增强，数据量也在不断的攀升，对计算机性能要求也越高，那么在有限的计算机性能以及内存限制下，如何高效的进行实景三维可视化成为当下更迫切的需求。虽然目前已有研究也在保留细节及网格质量上有了一些研究成果，但难以在保留细节特征和网格质量之间取得平衡。因此，本文提出一种基于边折叠实景三维模型简化算法。首先基于QEM边折叠算法，通过将顶点曲率和体积误差控制与简化时的边折叠代价结合实现模型简化。实验结果表明，随着简化程度的不断提高，当简化程度达到80%时，在细节丰富的窗户等区域，本文算法生成的网格数量明显多于QEM算法，且在细节丰富的区域网格越密集。同时，随着简化程度提高本文简化误差相较于QEM算法更低，简化误差越高意味着简化过程可能丢失了重要的细节特征或产生了较大的形状变化。因此本文方法处理后的模型相较于传统QEM算法能够更好地保留细节丰富的区域，极大地减少狭长三角形的数量，提升网格质量。但是，本文方法较为耗时，因此下一步将探索利用GPU技术提升方法的性能，使之更加适用于实景三维数据的处理。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
史与正, 陈梦华, 黄煜, 等. 实景三维模型的建筑物单体模型框架搭建[J]. 测绘通报, 2023(6):161-166.

DOI

[Shi Y Z, Chen M H, Huang Y, et al. The construction of building monomer model framework based on real scene 3D model[J]. Bulletin of Surveying and Mapping, 2023(6):161-166.] DOI:10.13474/j.cnki.112246.2023.0187

[2]
王师. 基于实景三维模型创建可量测实景图片研究[J]. 测绘与空间地理信息, 2023, 46(11):81-83.

[Wang S. Research on creating measurable real-world images based on real-world 3D models[J]. Geomatics & Spatial Information Technology, 2023, 46(11):81-83.]

[3]
陈曦. 顾及多层次几何细节特征的实景三维模型轻量化可视化方法[D]. 成都: 西南交通大学, 2021.

[Chen X. Lightweight visualization method of real 3D model considering multi-level geometric details[D]. Chengdu: Southwest Jiaotong University, 2021.]

[4]
王振娟, 花卫华, 刘修国, 等. 一种消除三维地质模型边界裂缝的锁边LOD方法[J]. 地球信息科学学报, 2023, 25(5):967-981.

DOI

[Wang Z J, Hua W H, Liu X G, et al. An edge-locking LOD method for eliminating boundary cracks in 3D geological models[J]. Journal of Geo-information Science, 2023, 25(5):967-981.] DOI:10.12082/dqxxkx.2023.220589

[5]
张春森, 张会, 郭丙轩, 等. 城市场景结构感知的网格模型简化算法[J]. 测绘学报, 2020, 49(3):334-342.

DOI

[Zhang C S, Zhang H, Guo B X, et al. Structure-aware simplified algorithm of mesh model for urban scene[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(3):334-342.]

DOI

[6]
李少卿, 霍亮, 沈涛, 等. 顾及角度误差的三维建筑模型边折叠简化算法[J]. 武汉大学学报(信息科学版), 2021, 46(8):1209-1215.

[Li S Q, Huo L, Shen T, et al. A simplification algorithm for edge collapse of 3D building model considering angle error[J]. Geomatics and Information Science of Wuhan University, 2021, 46(8):1209-1215.] DOI:10.13203/j.whugis20190269

[7]
Huang J, Wang X H, Wang J. Mesh simplification algorithm based on edge curvature metrics and local opti-mization[J]. International Journal of Modeling, Simulation, and Scientific Computing, 2020, 11(1):1950042. DOI:10.1142/s1793962319500429

[8]
袁泽平, 徐益冰, 缪钢烽, 等. 融合边折叠与平面约束的建筑物模型简化方法[J]. 测绘科学, 2023, 48(5):191-196.

[Yuan Z P, Xu Y B, Miao G F, et al. Simplification method of building model combining edge folding and plane constraints[J]. Science of Surveying and Mapping, 2023, 48(5):191-196.] DOI:10.16251/j.cnk-i.1009-2307.2023.05.022

[9]
李鹏, 颜青松, 曲英杰, 等. 融合纹理信息的实景三维模型简化算法[J]. 测绘科学, 2021, 46(10):151-158,166.

[Li P, Yan Q S, Qu Y J, et al. Mesh simplified algorithm considering texture information[J]. Science of Surveying and Mapping, 2021, 46(10):151-158,166.] DOI:10.16251/j.cnki.1009-2307.2021.10.020

[10]
陈博, 佘江峰, 谈俊忠, 等. 三维场景中建筑物模型简化研究进展[J]. 武汉大学学报(信息科学版), 2020, 45(9):1429-1437.

[Chen B, She J F, Tan J Z, et al. Research progress on simplification of building models in 3D scenes[J]. Geomatics and Information Science of Wuhan University, 202 0, 45(9):1429-1437.] DOI:10.13203/j.whugis20190470

[11]
Garland M, Heckbert P S. Surface simplification using quadric error metrics[C]// Proceedings of the 24th annual conference on Computer graphics and interactive techniques. ACM, 1997:209-216. DOI:10.1145/-258734.258849

[12]
张韵, 王淑营, 郑庆, 等. 保持细节几何特征的三维网格模型轻量化算法[J]. 计算机应用, 2023, 43(4):1226-1232.

DOI

[Zhang Y, Wang S Y, Zheng Q, et al. Lightweight algorithm of 3D mesh model for preserving detailed geometric features[J]. Journal of Computer Applications, 2023, 43(4):1226-1232.] DOI:10.11772-/j.issn.1001-9081.2022030434

[13]
Li L, He M Y, Wang P. Mesh simplification algorithm based on absolute curvature-weighted quadric error metrics[C]// 2010 5th IEEE Conference on Industrial Electronics and Applications. IEEE, 2010:399-403. DOI:10.1109/ICIEA.2010.5516908

[14]
Tseng J L, Lin Y H. 3D surface simplification based on extended shape operator[J]. WSEAS Transactions on Computers, 2013, 12(8):320-330.

[15]
Ozaki H, Kyota F, Kanai T. Out-of-Core Framework for QEM-based Mesh Simplification[C]// EGPGV@EuroVis. 2015:87-96. DOI:10.5555/2853213.2853227

[16]
栾婉娜, 刘成明. 基于逆Loop细分的半正则网格简化算法[J]. 图学学报, 2020, 41(6):980-986.

[Luan W N, Liu C M. A semi-regular mesh simplification algorithm based on inverse Loop subdivision[J]. Journal of Graphics, 2020, 41(6):980-986.] DOI:10.11996/JG.j.2095-302X.2020060980

[17]
Hoppe H. Progressive meshes[M]// Seminal Graphics Papers:Pushing the Boundaries, Volume 2. New York, USA: ACM, 2023:111-120. DOI:10.1145/3596711.3596725

[18]
刘峻, 范豪, 孙宇, 等. 结合边折叠和局部优化的网格简化算法[J]. 计算机应用, 2016, 36(2):535-540.

DOI

[Liu J, Fan H, Sun Y, et al. Mesh simplification algorithm combined with edge collapse and local optimization[J]. Journal of Computer Applications, 2016, 36(2):535-540.] DOI:10.11772/j.issn.10019081.2016.02.0535

[19]
Dutta K, Bhattacharjee D, Nasipuri M, et al. 3D face recognition based on volumetric representation of range image[M]// Advanced Computing and Systems for Security. Singapore: Springer, 2019.

[20]
张文新, 温佩芝, 黄佳, 等. 一种改进的二次误差测度简化算法[J]. 桂林电子科技大学学报, 2015, 35(1):59-63.

[Zhang W X, Wen P Z, Huang J, et al. An improved quadric error metric mesh simplification algorithm[J]. Journal of Guilin University of Electronic Technology, 2015, 35(1):59-63.] DOI:10.16725/j.c nki.cn45-1351/tn.2015.01.014

[21]
张霞, 段黎明, 刘璐. 保持特征的高质量三角网格简化方法[J]. 计算机集成制造系统, 2014, 20(3):486-493.

DOI

[Zhang X, Duan L M, Liu L. High quality triangular mesh simplification with feature-preserving[J]. Computer Integrated Manufacturing Systems, 2014, 20(3):486-493.] DOI:10. 13196/j.cims.2014.03.zhang xia.0486.8.2014034

[22]
彭育辉, 高诚辉, 何炳蔚. 三角形品质对离散点曲率的影响关系研究[J]. 中国机械工程, 2008, 19(20):2459-2462,2468.

[Peng Y H, Gao C H, He B W. Research on the relationship between triangle quality and discrete curvature[J]. China Mechanical Engineering, 2008, 19(20):2459-2462,2468.] DOI:10.3321/j.issn:1004-132X.2008.20.016

[23]
Zhang H, Yuan X, Han Q, et al. 3D mesh optimiza- tion based on contour recovery and least-squares vert- ex movement allocation[C]// Proc SPIE 12551, Fourth International Conference on Geoscience and Remote Sensing Mapping (GRSM 2022), 2023,12551:721-725. DOI:10.1117/12.2668219

[24]
Liu Y, Yan D M, Cheng X B, et al. Surface deformation technology of large-scale complex components based on Laplace[C]// Proc SPIE 12507, Advanced Optical Manufacturing Technologies and Applications 2022; and 2nd International Forum of Young Scientists on Advanced Optical Manufacturing (AOMTA and YSAOM 2022), 2023,12507:378-383. DOI:10.1117/12.2655822

[25]
Chartrand G, Cresson T, Chav R, et al. Liver segmentation on CT and MR using Laplacian mesh optimization[J]. IEEE Transactions on Bio-Medical Engineering, 2017, 64(9):2110-2121. DOI:10.1109/T-BME.2016.2631139

PMID

[26]
Nealen A, Igarashi T, Sorkine O, et al. Laplacian mesh optimization[C]// Proceedings of the 4th international conference on Computer graphics and interactive techniques in Australasia and Southeast Asia. ACM, 2006:381-389. DOI:10.1145/1174429.1174494

[27]
Jungeblut P, Kleist L, Miltzow T. The complexity of the Hausdorff distance[J]. Discrete & Computational Geometry, 2024, 71(1):177-213. DOI:10.1007/s00454-023-00562-5

Options
文章导航

/

〈 〉