EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 10: 2282 - 2299

DOI: https://doi.org/10.12082/dqxxkx.2024.240079

专栏：“GIS 与未来城市交通”

基于轨迹数据的出租车潜在充电需求估计及时空特征分解

  • 马瑞晨 , 1, 2 ,
  • 王聘玺 3, 4 ,
  • 黄爱玲 , 1, * ,
  • 奇格奇 1 ,
  • 徐笑涵 1
展开
  • 1.北京交通大学交通运输学院，北京 100044
  • 2.香港理工大学土地测量及地理资讯学系，香港 999077
  • 3.清华大学车辆与运载学院汽车安全与节能国家重点实验室，北京 100084
  • 4.北京交通发展研究院 城市交通节能减排检测与评估北京市重点实验室，北京 100161
* 黄爱玲（1977— ），女，广西大新人，教授，博士，主要从事交通运输系统工程、大数据挖掘研究。E-mail:

马瑞晨（1998— ），男，内蒙古乌兰察布人，博士生，主要从事交通时空大数据挖掘研究。E-mail:

Copy editor: 蒋树芳 , 黄光玉

收稿日期: 2024-02-04

  修回日期: 2024-05-22

  网络出版日期: 2024-10-09

基金资助

国家重点研发计划项目(2023YFB4301901)

国家自然科学基金项目(52472336)

国家自然科学基金项目(72371021)

收起

Estimation of Potential Charging Demand for Taxis and Spatiotemporal Feature Decomposition Based on Trajectory Data

  • MA Ruichen , 1, 2 ,
  • WANG Pinxi 3, 4 ,
  • HUANG Ailing , 1, * ,
  • QI Geqi 1 ,
  • XU Xiaohan 1
Expand
  • 1. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China
  • 2. Department of Land Surveying and Geo-informatics, The Hong Kong Polytechnic University, Hongkong 999077, China
  • 3. State Key Laboratory of Automotive Safety and Energy, School of Vehicle and Mobility, Tsinghua University, Beijing 100084, China
  • 4. Beijing Key Laboratory of Energy Conservation and Emission Reduction in Urban Transportation, Beijing Transport Institute, Beijing 100161, China
* HUANG Ailing, E-mail:

Received date: 2024-02-04

  Revised date: 2024-05-22

  Online published: 2024-10-09

Supported by

National Key Research and Development Program of China(2023YFB4301901)

National Natural Science Foundation of China(52472336)

National Natural Science Foundation of China(72371021)

Fold

摘要

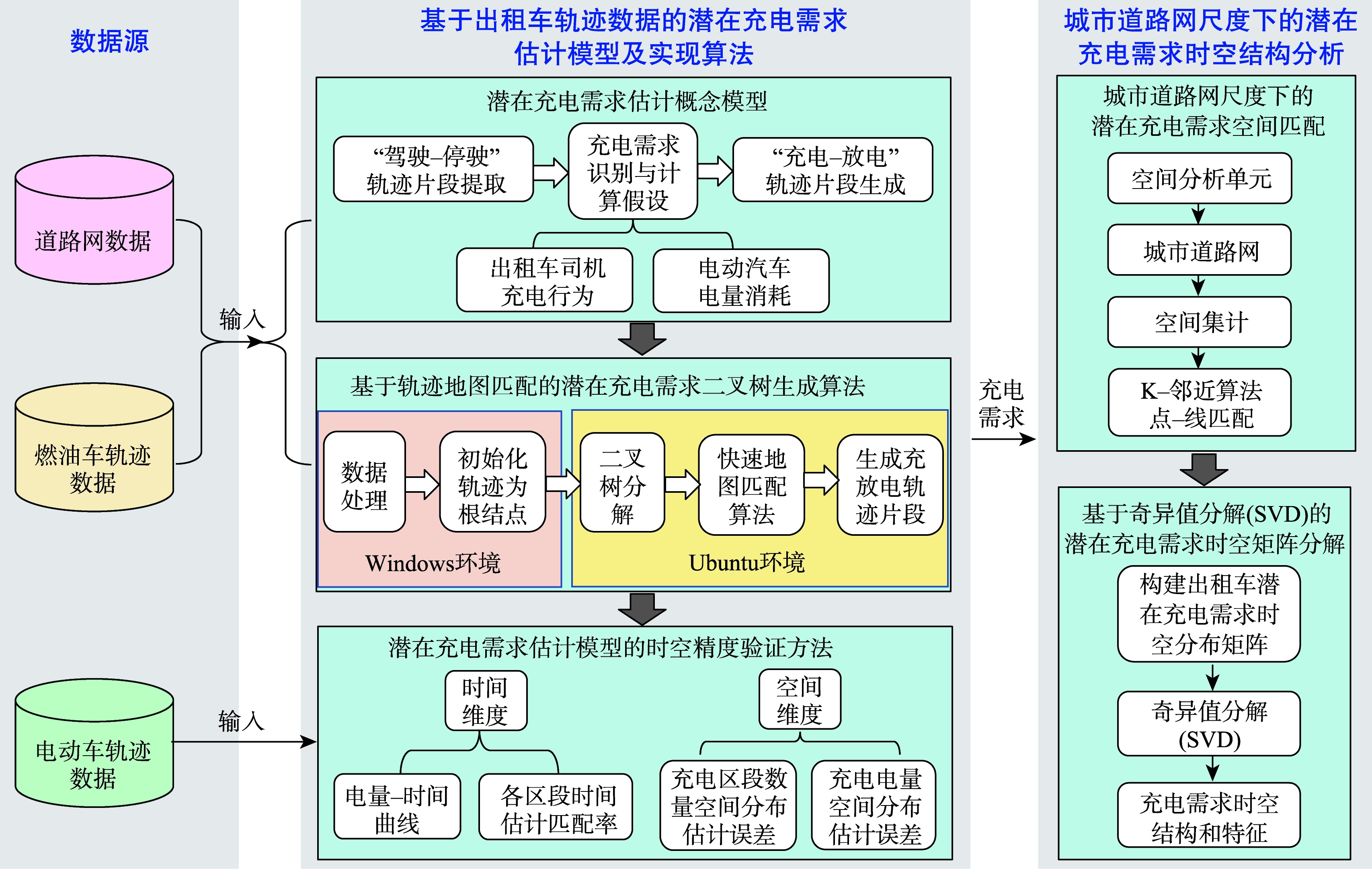
在大城市出租车队电动化转型过程中，出租车充电需求呈现出充电负荷高、时空分布随机性强的特征。为精确估计出租车队完全电动化转型后的充电需求，本文提出了一种仅基于燃油出租车轨迹数据的潜在充电需求识别概念模型以及基于轨迹地图匹配的二叉树实现算法，为电动化转型滞后地区提供了新的充电需求估计范式。本文使用890辆带有电池状态字段的电动出租车轨迹数据对模型和算法进行验证，结果表明，充电区段数量、充电需求电量等指标的估计误差小于6.5%。此外，模型和算法在不同电池电量消耗阈值θ和不同空间尺度（500、1 000和10 000 m栅格）下具有较高的时空分布估计精度。在此基础上，本文提出以北京市六环内真实道路网为空间分析单元，运用奇异值分解算法对潜在充电需求时空矩阵进行分解降维，以挖掘潜在充电需求的时空特征模式。最后，运用北京市连续3 d共1 913辆出租车轨迹数据进行案例研究，结果表明，北京市出租车潜在充电需求的空间分布呈现出明显的重点区域、关键通道聚集性特征，与该区域的高出行活动强度以及长途出行相关的高密度充电需求高度吻合。分解后的充电需求呈现出常态化充电需求为主导、上下午异质性充电需求以及工作时段和非工作时段异质性充电需求为辅的时空结构特征。该分析方法有助于挖掘潜在充电需求的空间分布结构特征及时空耦合关系，为出租车队电动化转型下的充电基础设施中长期规划、电网负荷调度调节和充电需求管理等提供决策参考。

关键词： 城市交通; 交通电动化; 充电需求; 二叉树; 地图匹配; 奇异值分解; 时空特征; 轨迹数据

本文引用格式

马瑞晨 , 王聘玺 , 黄爱玲 , 奇格奇 , 徐笑涵 . 基于轨迹数据的出租车潜在充电需求估计及时空特征分解[J]. 地球信息科学学报, 2024 , 26(10) : 2282 -2299 . DOI: 10.12082/dqxxkx.2024.240079

Abstract

In the transition of urban taxi fleets toward electrification in large cities, the charging demand of taxis exhibits characteristics of high charging load and strong spatiotemporal randomness, with a noticeable mismatch between charging supply and demand in time and space. To accurately estimate the potential charging demand post- the full electrification of the taxi fleet, this study introduces a bottom-up conceptual framework and a binary tree algorithm based on trajectory map matching, leveraging fuel taxi trajectory data exclusively. This approach provides a new paradigm for estimating charging demands in regions lagging behind in the electrification transition. The model and algorithm are validated using trajectory data from 890 electric taxis with battery status fields (State of Charge, SOC). Results show that the estimation errors of indicators such as the number of charging segments and charging amount are less than 6.5%. Moreover, the model also exhibits high spatiotemporal distribution estimation accuracy under different parameter settings (battery depletion threshold θ) and spatial scales (with grid sizes of 500 m, 1 000 m, and 10 000 m), ensuring their applicability in real-world scenarios. Specifically, the temporal distribution error of charging amount is less than 8.5% in the best-case scenario, and over half of the charging amount within 500 m grids has a spatial distribution error less than 0.3, with 59% of the 500 m grids having an estimated error of charging segment count less than 0.3. Building upon this, the Singular Value Decomposition (SVD) algorithm is used to decompose and reduce the dimensionality of the spatiotemporal matrix of charging demands, identifying spatiotemporal patterns of potential charging demands within the real road network of Beijing's Sixth Ring Road at road level. Finally, a case study is conducted using trajectory data from 1 913 taxis in Beijing over three consecutive days from March 9th (Monday) to March 11th (Wednesday) in 2019, and the results indicate that the spatial distribution of potential charging demands for taxis in Beijing exhibits prominent clustering features in key areas and critical corridors, corresponding to high-density charging demands associated with residents' high activity levels and long-distance travel. The decomposed charging demands reveal a spatiotemporal structural pattern dominated by regular charging demands, with supplementary heterogeneity in charging demands between morning and afternoon, as well as during working and non-working hours. This analysis method assists in uncovering the spatial distribution structural characteristics of potential charging demand and spatiotemporal coupling relationships, providing decision-making references for long-term planning of charging infrastructure, grid load scheduling, and charging demand management in the electrification transformation of taxi fleets.

Key words： urban traffic; traffic electrification; charging demand; binary tree; map matching; singular value decomposition; spatiotemporal characteristics; trajectory data

1 引言

随着社会经济的不断发展、居民出行活动的不断增加，传统燃油车的高碳排放成为城市环境污染的关键因素之一。随着中国“双碳”目标的提出，以及政府对交通充电、补能行业的大量政策支持，中国已经成为全球新能源车辆推广和充换电基础设施建设的领先国家。中国2022年电动汽车销量占全球销量的60%[1]，占国内所有新乘用车注册量的四分之一[2]，成功实现了“十四五”节能减排工作计划中20%的电动汽车份额目标。在出租车电动化领域，《北京市“十四五”时期交通发展建设规划》[3]提出“十四五”时期巡游出租车100%新能源化的政策目标。截至2022年底，中国电动汽车公用充电桩保有量达到100万根，占全球充电桩总量的51%[4]。
然而，由于充电基础设施建设初期缺乏电动车实际运营数据的支撑，部分充电站点在选址和容量规划上不尽合理[5]。加之出租车充电负荷高、时空分布随机性强的特点，其充电供需时空错配现象明显[6]，表现为充电热点地区“一桩难求”，而其他地区利用率低下，造成资源浪费。对比来看，荷兰阿姆斯特丹的公用充电桩平均时间利用率为34%，而我国32个主要城市的利用率平均值仅为11%，远低于该水平[4]。此外，据估算北京市电动汽车入网的充电负荷与原有用电负荷的同时率可达85%，电网面临过载风险[7]。因此，仅依赖现有燃油车数据对其潜在充电需求进行精确估计，并挖掘其充电需求的时空耦合关系，可以为交通电动化转型起步地区的政府部门、充电运营企业和电力部门进行决策、规划、投资和调度提供关键支撑。一方面，有助于供给侧资源优化配置[8]、配电网安全稳定运行[9]以及“车-桩-路-网”协同规划[5]；另一方面，有助于需求端进行充电需求管理，引导潜在充电需求再分配，提升资源利用效率，真正实现电动化转型带来的经济和环境效益。
充电需求估计需要解决2大问题： ① 充电电量估计； ② 充电需求空间位置分布估计。针对第一类问题，已有研究有自上而下方法和自下而上方法2种。自上而下方法以整个区域为研究对象，依次估算研究区域电动汽车保有量、各类车辆使用强度，进而结合电池容量、充电类型（家用、工作、公共等） 等静态数据估算快充和慢充千瓦时充电需求[10-11]。这类方法多基于调查数据或年鉴数据，缺乏实时性和车辆充放电规律的考虑。自下而上方法多以个体活动为分析单元，从充电桩端或者车辆端入手，由于详细的桩端动态数据难以获取且只能反映某一时段已满足的充电需求[12]，故多数研究从车端进行。车端轨迹数据驱动结合数理统计模型在充电需求估计中应用较多，常见的有蒙特卡罗仿真方法[9]、智能体仿真方法[13]等，即通过设定电池状态（State of Charge, SOC）与行车、驻车行为间的关联规则，来推演电池消耗同车辆活动链间的动态变化。近期研究在此基础上加入了驾驶员行为的考虑，如效用最大化模型[14]等；然而并非每次充电决策均是理性的，有研究纳入了充电需求与地点不确定性的考虑，即驾驶员通过有限理性决策来捕捉充电机遇[15]。但是上述基于车端轨迹数据的方法对于缺失SOC字段的燃油车轨迹数据不适用，而且占用大量计算资源，亟需高效的模型设计和算法结构，如二叉树结构。与此同时，Lazzeroni等[16]提出了一种自上而下和自下而上相结合的办法，应用浮动车数据和Bass模型估计出了2030年和2035年意大利都灵市166个区域在电池电量消耗阈值在40%、60%和80%情况下的充电电量的空间分布，但是缺乏对方法准确性的验证和阈值敏感性的探讨。
针对第二类问题，充电需求分布的空间尺度包括区域、路网和具体点位，大部分研究仅以区域为尺度估计充电需求，进而引发2大问题。① 充电需求点分布受可变面状单元问题（Modifiable Areal Unit Problem，MAUP）影响而以不同的集计结果呈现[17]。② 现阶段常使用覆盖模型和截流模型进行充电桩布局[18]，这2种模型对充电需求的空间估计精度提出了更高的要求，因此具体到实际地点的需求更具实践价值[5]。He等[19]直接将区域几何中心点作为充电需求空间代理位置，而Wang等[20]通过0~1整数规划模型将充电需求进行分配到精确位置。国际清洁交通委员会最新的一项研究通过交通流量与路段长度的乘积集计为车队电驱动行驶里程（Vehicle Kilometer Traveled, VKT），然后乘以车辆能源消耗密度，将中、重型电动货车车队的能源消耗投射至路网上来估算2030年路网充电需求[21]。该方法提供了路网能源消耗分布的精确方法，但并没有将充电需求点落实到精确地理位置，缺乏精细化分析充电需求时空分布的能力。因此，亟需一种基于燃油车轨迹数据的自下而上的充电需求估计范式，且具备算法高效性、时空精确性和可迁移扩展性。
充电需求分布的时空特征与城市空间结构和城市兴趣点（Point of Interest, POI）分布紧密相关。一类研究侧重通过空间计量的方法研究充电需求的影响因素及作用关系[8]，如Kang等[6]基于车辆位置服务大数据和充电桩位置数据考察了充电供需的空间错配现象，并用空间回归模型证明了商场、交通站点、居民区等地面服务设施对充电需求的显著影响。另一类研究则聚焦于不同土地利用类型下充电需求的逐小时变化规律，如Li等[22]基于出租车轨迹数据，通过时间序列仿真的方法选择了4个地点来探究不同土地利用类型下充电桩利用率的时间变化规律，包括国贸（商业区域）、中关村（科研区域）、天通苑（居住区域）以及玉泉营（开发不充分区域），表明不同土地利用类型下的充电需求高峰各异，且开发强度低的地区充电需求低。Straub等[23]构建了基于居民活动链的仿真模型用于估算德国柏林448个交通小区在居住、购物和工作3种出行目的下的充电需求空间分布，以及工作充电、家用充电和机会充电①(①机会充电指的是在车主在进行休息、吃饭等活动时，电动汽车利用停驶时间进行的“随时充电”，区别于等待电池完全放电，或者等待工作周期或工作班次结束后再进行充电的行为（https://assets.discoverbattery.com/documents/02_dry_cell/885_product_literature/dry-cell-opportunity-charging-guide.pdf）。) 3种类型下的充电需求时间变化规律。周椿奇等[24]基于动态能耗理论构建的模型分别对私家车、运营车的充电需求时空分布进行描述，其对于空间位置的刻画仅限于8个充电节点，缺乏对城市宏观区域内充电需求时空分布特征的精细分析。因此，已有研究或选取典型小区域作为土地利用样本，未结合地理位置、区域功能和社会经济属性分析，或只呈现某区域充电需求随时间变化的整体情况，缺少分解方法等的应用（如张量分解等）来提取充电时空分布的主要特征，也缺少将真实空间区域作为研究对象，导致对充电需求与城市空间结构的时空耦合关系挖掘不充分。
综上所述，本文旨在提出一种仅利用传统燃油车轨迹数据的出租车队潜在充电需求的精确估计范式，并对其时空结构进行探究。这里的潜在充电需求指出租车队完全电动化后产生的充电需求，包括充电电量、充电时间和充电空间位置分布。本文创新点有以下3点。① 提出了一种基于真实场景下出租车轨迹数据的潜在充电需求识别概念模型和基于轨迹地图匹配的潜在充电需求二叉树生成算法，用于精确识别出租车潜在充电地点、充电时间并估计充电电量，且使用真实电车数据对所提方法估计时空准确度进行验证。其中，潜在充电需求识别概念模型构建了一种区别于仿真方法而是基于数模驱动的需求估计方法；而二叉树生成算法则是对概念模型的快速实现。② 提出以道路网作为空间单元的量化分析视角，规避网格单元可能出现的可变面状单元问题。③ 应用奇异值分解的方法对高维时空矩阵压缩，以北京市六环内真实空间区域为研究对象，探索城市道路网尺度下的潜在充电需求的时空结构，为大城市出租车队电动化转型过程中城市电力配置、充电需求管理等提供参考建议。

2 基于出租车轨迹数据的潜在充电 需求估计及时空结构分析方法

2.1 研究设计

本文提出的出租车潜在充电需求估计及时空结构分析方法的技术路线图如图1所示，具体研究流程如下： ① 构建潜在充电需求估计概念模型，即结合电动出租车充电行为特征，基于轨迹数据提出辨识轨迹片段转换、识别充电需求的理论方法； ② 提出基于轨迹地图匹配的潜在充电需求二叉树生成算法，旨在结合真实数据条件下快速实现概念模型，得到包括充电电量、充电时间和充电空间位置分布在内的充电需求； ③ 分别从时空2个维度设计2项指标，依托真实电动车轨迹数据对本文所提模型和算法进行时空精度验证； ④ 将充电需求集计于道路网空间分析单元； ⑤ 构建充电需求时空分布矩阵，通过奇异值分解得到城市道路网尺度下的充电需求时空结构和特征。
图1 出租车潜在充电需求估计及时空特征分解技术路线

Fig. 1 Technical roadmap for potential charging demand estimation of taxis and spatiotemporal feature decomposition

2.2 基于出租车轨迹数据的潜在充电需求估计模型及实现算法

2.2.1 潜在充电需求估计概念模型

对于一个拥有稳定人口和成熟经济规模的城市而言，其出行模式较为稳定，以燃油车或电动出租车驾驶行为来估计出租车平均行驶距离具有合理性[20]。在城市交通电动化转型初期，真实环境下电动汽车充放电数据缺失为充电需求管理带来挑战。因此，本文旨在以燃油出租车轨迹数据为代理，对充电需求的时空分布进行估计。Cai等[13]的研究较早将车辆轨迹引入到交通电动化领域的研究中，其将车辆轨迹划分为驾驶片段和停驶片段，通过智能体仿真方法估算PHEV（Plug-in Hybrid Electric Vehicles）取代传统燃油车的进程中可节省的碳排放。随着电动化步伐进入纯电时代，利用车辆轨迹数据感知充放电规律仍然具有极大潜力。
本节提出了一种区别于该研究[13]中仿真方法的基于轨迹数据的潜在充电需求识别概念模型。该概念模型以出租车是否停留为标准将轨迹划分为驾驶区段（Driving Segment）drivej和停留区段（Resting Segment）restj，如出租车时空轨迹示意图图2左侧时间轴划分的阴影片段和非阴影片段所示。停留状态的判别需提前指定阈值δ1，本文设定δ1=5分钟。当停留时间tj>δ1时该区段被识别为restj，restj和restj+1间的区段被识别为drivej。对于如何识别司机是否在某停留区段充电，考虑到充电需求的影响因素包括电池容量（续航里程）以及电量消耗速率[20]等，本文根据已有文献对出租车司机充电行为[25]、电动汽车电量消耗[26]的研究，对充电需求识别与计算做出以下假设：
图2 出租车潜在充电需求估计概念模型示意图

Fig. 2 Schematic diagram of the conceptual model for estimating the potential charging demand of taxis

（1） 出租车司机倾向于在长时间停留的时间和地点进行充电；
（2） 出租车电池电量消耗达到θ（% SOC）时一定会产生充电需求。
出租车辆电池电量消耗阈值θ（% SOC）的物理意义为电车在两次充电行为间被允许运行的最大放电消耗SOC，可以根据电池容量换算为放电行驶里程阈值threshold。在图2中，假定出租车在长时间驻车点p1、p2和p3停留充电（p1、p2、p3停留时 间>δ1）。在p1充电后的行驶轨迹为traj1（轨迹长度小于threshold），对应第i段放电区段dischargei；然后出租车行驶至下一个驻车点p2进行接续充电，对应第i段充电区段chargei，依此规律交替进行完成充放电的循环。该概念模型用于充电需求识别具有一定的灵活性，充电行驶阈值threshold的设置能够反映出电池性能、群体驾驶行为的差异，因此在异质性的时空场景下，通过阈值设置可以提取出不同城市、不同电池技术进步条件下的潜在充放电行为。阈值threshold可以设置为一个固定估计值，在现实场景下其可能是一个分布[26]。

2.2.2 基于轨迹地图匹配的潜在充电需求二叉树

生成算法
2.2.1节构建的潜在充电需求识别概念模型可以进一步抽象为3种替代关系： ① 能源消耗替代充电需求； ② 长驻车时间段替代充电需求产生时间段； ③ 长时间驻车所在地点替代充电需求产生地点。基于此，本文设计一套实现算法把以“驾驶-停驶”为循环单元的轨迹转换为以“充电-放电”为循环单元的轨迹。转换过程中需要保证所有放电区段均在放电行驶里程阈值内，线性遍历会导致重复计算而占用计算资源。二叉树是一种节点二分的树形结构，其递归遍历可以为该场景提供一种高效处理方式。
本节融合二叉树结构和快速地图匹配算法（Fast Map Matching, FMM）[27]，设计了潜在充电需求二叉树生成算法，旨在利用真实环境下的出租车轨迹数据识别充电地点、充电时间以及充电量。算法示意图如图3所示，首先，算法将某车辆连续行驶轨迹初始化为根节点。其次，判断当前轨迹长度是否小于一次充电行驶阈值threshold。放电区段轨迹长度直接影响耗电量的估计和算法准确性，以往基于出租车轨迹的研究在计算行驶距离时往往简化为计算轨迹点或OD间的欧式距离[28]或球面距离[29]，而没有考虑轨迹与路网的匹配。现实中，出租车GPS设备在受建筑物遮挡或电磁干扰时会存在大量噪声而偏离路网，使得计算结果存在不同程度的偏差。本文使用基于C++语言开发的FMM[27]在Ubuntu环境下对轨迹数据和北京市道路网进行匹配计算，将轨迹点匹配到路段后，累计经过的路段长度获得真实轨迹长度traji。
图3 基于出租车轨迹地图匹配的充电需求二叉树生成算法示意图

Fig. 3 Schematic diagram of charging demand binary tree generation algorithm based on taxi trajectory map matching

在获取到精确的轨迹长度traji后，若轨迹长度traji在续航里程threshold之内则无需充电，否则依据2.2.1节假设（1）寻找车辆最大停留区段作为充电区段，即 c h a r g e i = m a x ( r e s t j ) ,   j = 0 ,   1 ,   … ,   n，其中n为该轨迹停留区段数量。轨迹从该充电区段chargei将原始轨迹划分为左右两支子轨迹片段，形成包含左子树和右子树的二叉树结构如图3（b）所示。将左子树和右子树作为中间结点，依次递归进行轨迹长度与阈值关系的判断及子树划分，直到所有叶子结点的轨迹长度均小于阈值。最终，输出二叉树叶子结点作为放电区段集合{…, d i s c h a r g e i - 1 ,   d i s c h a r g e i , d i s c h a r g e i + 1 ,   …}，每一放电区段的起始驻车点为充电地点，停留时间为充电时段，于是充电时段依次表示为{…, c h a r g e i - 1 ,   c h a r g e i ,   c h a r g e i + 1 , …}。注意到图3（b）中放电区段 d i s c h a r g e i - 2受研究时段边界约束而无法分配至前序充电区段，故不计入研究时段内充电需求。于是，该算法提取到的任一车辆v的充电区段i描述为 c h a r g e i ( v ) = { t s t a r t , i ( v ) ,   t e n d , i ( v ) , W i ( v ) ,   l o n i ( v ) ,   l a t i ( v ) }。其中， t s t a r t , i ( v ) 、 t e n d , i ( v )分别为充电开始时间和结束时间，具体而言充电区段时间长度 t e n d , i ( v ) - t s t a r t , i ( v )是车辆停留时间的近似，其值大于实际充电时间，相对接近于充电枪接入时间。Wi（kWh）为充电电量，计算方法为所属放电区段轨迹长度traji与百公里能耗δ（kWh/100 km）的乘积，loni(v)、lati(v)为充电地点经度和纬度。
总结来看，本文所提的二叉树生成算法展现出2点优势。① 二叉树的数据结构符合概念模型提供的充电需求估计思路。二叉树根节点为车辆轨迹输入，叶子结点为充电片段输出，左右子树分枝过程对应放电区段和车辆电池驱动范围的对比判断； ② 概念模型的实现需要循环判断所有放电区段同驱动阈值的关系，二叉树结构可以规避重复计算和搜索。主要因为二叉树算法利用了局部性原理，其在搜索过程中，通常会沿着一条路径从根节点向下搜索而集中在局部区域，减少了访问节点的次数，提高了算法效率。值得注意的是，尽管FMM提前计算并存储了路网中给定路长阈值下的所有OD路段的最短路长，将轨迹匹配中的在线运算替换为从最短路表格中进行哈希搜索，但其仍然是算法效率制约瓶颈。

2.2.3 潜在充电需求估计模型的时空精度验证方法

利用同一套电动出租车轨迹数据得到充电需求的真实值和估计值，分别从时间、空间维度对模型估计精度进行验证。真实充电需求的提取方法如下，若车辆v的某轨迹片段同时满足： ① 车辆处于停驶状态； ② ∀ t v ∈ t s t a r t , i ' v , t e n d , i ' v - 1， S O C t ( v ) + 1 ≥ S O C t ( v )，则认为 [ t s t a r t , i ' v , t e n d , i ' v ]为真实充电需求时段。其中， S O C t ( v ) + 1和 S O C t ( v )分别为车辆v在t+1时刻和t时刻的电池状态， t s t a r t , i ' v和 t e n d , i ' v分别为电动出租车轨迹考察片段始末时刻， l o n i ' ( v ) , l a t i ' ( v )为充电地点真实经纬度，真实充电电量的计算见式（1），记作 W i ' v。于是，车辆v的 第i个真实充电区段和和估计充电区段分别 记作 c h a r g e i ' ( v ) = { t s t a r t , i ' ( v ) ,   e n d , i ' ( v ) ,   W i ' ( v ) ,   l o n i ' ( v ) ,   t l a t i '   ( v ) }   和   c h a r g e i   ( v ) = { t s t a r t , i v ,   t e n d , i v ,   W i ( v ) , l o n i ( v ) ,   l a t i ( v ) }，关于 c h a r g e i ( v )中各变量的阐释见2.2.2节。
从2方面验证潜在充电需求估计的时间准确性： ① 电量-时间曲线，用于反应区域总体的充电电量波动； ② 定义各区段时间估计匹配率A，考察真实充电区段 c h a r g e i ' ( v )被其估计时间区段 c h a r g e i ( v )所覆盖的比率，即两时间区段的交集百分比。各区段时间估计匹配率A的计算公式如 式（2）所示，分子L表示估计和真实时间区段的交集时间长度，计算式如式（3）所示；分母表示出租车真实充电需求时段的长度。
W i ' v = S O C t e n d , i ' v - S O C t s t a r t , i ' v
A = L / ( t e n d , i ' v - t s t a r t , i ' v )               L > 0 0                                                                                               L ≤ 0
L = m i n { t e n d , i ( v ) ,   t e n d , i ' ( v ) } - m a x { t s t a r t , i ( v ) ,   t s t a r t , i ' ( v ) }    
验证潜在充电需求估计的空间准确性，首先需要将充电地点空间位置的真实值和估计值进行集计，以网格作为空间分析单元进行误差度量。本文设计了 P s l o t ( E ≤ ε )和 P p o w e r ( E ≤ ε )指标来度量出租车辆潜在充电需求的空间分布估计误差，分别表示各网格充电区段数量和充电电量估计值同真实值的相对误差②(②相对误差的计算方法：相对误差 =|估计值-真实值|/真实值。)小于等于ε的网格数量N(E≤ε)占全北京网格数量 N t o t a l的比例，如式（4）、式（5）所示。
P s l o t ( E ≤ ε ) = N ( E ≤ ε ) / N t o t a l
P p o w e r ( E ≤ ε ) = N ( E ≤ ε ) / N t o t a l

2.3 城市道路网尺度下的潜在充电需求时空结构分析

2.3.1 城市道路网尺度下的潜在充电需求空间匹配

在进行出租车潜在充电需求时空结构挖掘之前，需要将潜在需求点进行空间集计。然而不同尺度的平面二维区域划分系统如行政区、泰森多边形、方格渔网等均会受MAUP的影响而出现偏误。由于城市空间内的物理移动受道路网约束，以道路网作为基本分析单元来理解城市分异格局可以减弱MAUP的影响，成为城市量化研究的新角度[30]。本文以北京市六环内道路网为空间对象，采用K-邻近算法将充电地点经纬度匹配至道路网，并将该点充电需求电量、充电区段起止时间赋值给道路网路段属性。包含r个路段的北京市道路网可以表达为 N E T = { N e t r } , r ∈ R，Netr为第r条路段，R为北京市道路网中有充电行为请求的路段集合；而 N e t r = { c h a r g e i ( v ) } , v ∈ V ,   i ∈ I， c h a r g e i ( v )为车辆v的第i个估计充电区段，V和I分别为路段r上有充电需求的车辆集合、该车辆充电次数集合。

2.3.2 基于奇异值分解（SVD）的潜在充电需求时空矩阵分解

在将充电地点进行路网匹配后，每条道路集计了不同时间分布的潜在充电需求。本文构建了出租车潜在充电需求时空分布矩阵M(m×n)对信息进 行集计表示，矩阵的行数m表示一天内的24 h，即 m=24；矩阵的列数n表示充电需求匹配到路段后有充电行为发生的路段数目，其数值为路段集合R中元素的数目，本文中n=2 186。针对每个路段Netr，将所有车辆的充电时段 c h a r g e i ( v ) = { t s t a r t , i ( v ) , t e n d , i ( v ) , W i ( v ) , l o n i ( v ) , l a t i ( v ) }中的充电电量 W i ( v )离散化为小时，记作向量 W i → ( v ) m × 1，其第 t s t a r t , i ( v )个元素至第 t e n d , i ( v )个元素的值为 W i ( v )，其余元素为0。将路段Netr中所有充电需求电量逐小时累积，可得针对每个路段的m×1的列向量dr， d r = ∑ v ∑   i W i → ( v ) m × 1。该列向量单独编码了对应路段全天充电电量的 逐小时分布状况。n个dr列向量组成了包含高 维时空信息的潜在充电需求矩阵 M ( m × n )，实例化后为 M ( 24 × 2   186 )。
为有效提取潜在充电需求矩阵 M ( m × n )包含 的时空结构，可以对矩阵进行分解降维，将高维时空信息映射至低维空间[31]。奇异值分解（Singular Value Decomposition, SVD）的方法通过只保留最重要的奇异值和向量来降低维数，可以减少数据中噪声的影响；且SVD分解后的矩阵正交，保留了原矩阵行与列之间的对应关系[32]，可以得到充电需求时空耦合模式。因此，本文应用SVD将潜在充电需求时空矩阵 M ( 24 × 2186 )分解为3个矩阵的乘积，如式（6）所示。若矩阵M秩为r，分解得到的S为对角矩阵，左、右奇异矩阵分别为 U m × r和 V n × r，且满足 U T U = V T V = E， E为对角矩阵。进一步拆解来看，奇异值分解将M分解为r个秩一矩阵的和， δ p u p v p T即为一种矩阵分布模式。其中， δ p是矩阵S的第p个对角线元素，被称作奇异值； δ p也是第p个矩阵 u p v p T的权重，表示第p种充电需求分布模式的重要性，且 δ 1 ≥ δ 2 ≥ … ≥ δ r。up和vp均为单位向量，是矩阵U和V的第p列，分别表示第p种充电需求的时间分布和空间分布。在由高维空间向低维空间映射过程中，保留奇异值较大的k项（1≤k≤r）可提取并表达潜在充电需求时空特征。因此，充电需求时空结构指城市内充电需求的整体时空耦合模式和规律，它是多种因素作用、多特征复合的复杂状态。而SVD分解得到的每种模式对应一个时间向量和空间向量，表征对应空间位置在24 h内充电需求的具体时空特征。
M = U S V T = ∑ i = 1 r δ p u p v p T

3 北京市充电需求估计及时空结构识别实例验证

3.1 数据来源及研究区域

3.1.1 数据来源及处理

本文使用的数据包括北京市传统出租车轨迹数据、北京市小规模电动出租车轨迹数据、以及北京市道路网数据。① 传统燃油出租车轨迹数据来源于高德公司，脱敏处理后的字段包括出租车车辆ID、GPS信号经纬度、秒级时间、行驶速度以及载客状态。由于出租车一次充放电行为可能跨越多日，为避免受单日时间内出租车充电需求随机性的影响，本文选取2019年3月9日—11日连续3 d数据为研究对象。数据清洗环节包括位置准则和速度准则：剔除经纬度在北京市辖区（115.83°E—116.73°E，39.64°N—40.60°N）外的数据；剔除瞬时速度超过100 km/h（北京市最高限速）的数据。 ② 北京市小规模电动出租车轨迹包含890辆采用固定充电桩进行充电的出租车，采集日期为2020年8月8日—11日共4 d，数据字段除增 加电池SOC数据外，同传统燃油出租车轨迹数据完全相同，处理后共提取4 022段有效充电区段。③ 北京市道路网数据来源于OpenStreetMap，并分2份处理：其一保留上述经纬度范围内的数据，构造有向拓扑道路网用于轨迹地图匹配，网络包含边235 321条，节点96 667个；其二保留北京市六环内的快速路、主干路、次干路和支路数据，用于地理空间结构挖掘及可视化。

3.1.2 研究区域

本文以北京市六环内道路网路段为空间分析的基本单元，北京市六环内主要路网如图4所示。本文标注出11个重点考察区域，如以回龙观、天通苑和望京为代表的超大型社区；以望京、国贸为代表的商业区域；以北京城市副中心、亦庄、大兴新城核心区和良乡大学城为代表的重点规划发展区域，以及北京奥运村、首钢工业园等城市文旅重点区域，以及位于六环东北侧的北京首都国际机场。
图4 北京市六环内主要道路网络及部分重点区域

Fig. 4 Major road network and key areas within Beijing's Sixth Ring Road

3.2 基于电动车轨迹数据的潜在充电需求估计模型验证

为验证本文所提出的概念模型和算法对潜在充电需求估计的准确性，并考察不同电池电量消耗阈值θ（% SOC）下模型的适用性，本节利用北京市890辆电动出租车连续4日轨迹数据得到真实充电需求和不同θ下的估计值，并对二者进行对比。3.2.1节—3.2.3节分别从统计学指标、时间和空间准确性3个方面进行模型验证。

3.2.1 潜在充电需求估计的统计学指标验证

不同θ参数下本文所提模型对充电区段数量、充电需求电量等指标的估计精度存在差异，其估计值和真实值对比如表1所示。具体来看，θ值为50%意味着电车在2次充电行为间被允许运行的最大放电消耗为50%SOC，即电池电量消耗大于50%SOC时才一定会产生充电需求，θ值为100%意味着允许电池电量接近耗尽再产生充电需求。结果表明，不同θ值下能使不同指标达到误差最小， θ值为50%的模型在充电总时长估计上表现最好； θ值为90%的模型在充电区段数量误差最小；θ值为100%的模型能够同时获得最好的充电需求电量估计和充电总能量估计。此外，不同θ参数下的模型对充电需求电量的估计误差均在3.5%以内。随着θ值的增加，本文所提出的二叉树生成算法趋向于提取长时间驻车区段，并将前期消耗电量分配至该区段作为充电需求，因而忽略短时间驻车区段。这使得高θ值参数下估计得到的充电区段数量更少、充电总时长更短、平均每个充电区段需求电量更高。
表1 不同 θ参数下模型估计值和真实值的对比

Tab. 1 Comparison of performance between estimated and real values for various θ

模型参数 真实值 θ=50% θ=60% θ=70% θ=80% θ=90% θ=100%
充电区段数量/个 4 022 7 822
[94.48%]		 6 525
[62.23%]		 5 470
[36.00%]		 4 627
[15.04%]		 3 894*
[3.18%]		 3 276
[18.55%]
充电需求电量/(% SOC) 202 942 205 761
[1.39%]		 209 045
[3.01%]		 209 028
[3.00%]		 210 026
[3.49%]		 209 008
[2.99%]		 205 177*
[1.10%]
平均每个充电区段需求电量/(% SOC/个) 50.46 26.31
[47.87%]		 32.04
[36.51%]		 38.21
[24.27%]		 45.39
[10.04%]		 53.67*
[6.37%]		 62.63
[24.12%]
充电总时长/h 34 085 33 986*
[0.29%]		 33 818
[0.78%]		 33 026
[3.11%]		 32 238
[5.42%]		 31 138
[8.65%]		 29 734
[12.77%]
充电总能量/(% SOC·h) 2 002 338 959 193
[52.10%]		 1 164 961
[21.45%]		 1 350 381
[15.92%]		 1 562 989
[15.74%]		 1 767 116
[13.06%]		 1 912 669*
[8.24%]

注：[ ]中的数字表示各估计指标同真实值间的相对误差ε， *表示各指标表现最好的估计值。

3.2.2 潜在充电需求估计的时间验证

潜在充电需求估计的时间维度准确性验证从电量-时间波动和各区段时间估计匹配率两方面进行考察。首先，本文将各充电时段需要的电量在时间维度上进行累加，得到不同θ参数下估计和真实充电需求电量的逐小时变化图如图5所示。为解释图5中估计分布同真实分布间的巨大差异，本文在表1中增加了充电总能量（% SOC·h）指标，由各充电区段时间长度（h）同充电电量（%SOC）的乘积累加得到。值得注意的是，当θ参数值较小时，潜在充电时间分布估计值被严重低估，这是因为算法将部分充电需求电量分配给较短驻车时段，致使乘积变小、充电总能量变小、同真实值偏离较大；当θ参数值增加，算法倾向于将充电需求电量分配给长时间驻车时段，致使乘积变大、充电总能量变大、进而接近真实值。
图5 不同θ参数下潜在充电时间分布估计同真实分布的对比

Fig. 5 Comparison of estimated distribution of potential charging time under different θ parameters with true distribution

图6展示了不同θ参数下各真实充电需求区段在不同时间估计匹配率A上的频数和频率分布，最突出的是第一个柱子（ 0 ≤ A < 0.1）和最后一个柱子 ( 0.9 ≤ A < 1)的分布变化，二者分别表示没有估计到的充电区段分布和几乎完全估计准确的充电区段分布。当θ=50%时，模型能够准确提取到60.4%的充电区段，17%的区段没有提取到，而剩余22.6%的估计区段存在不同程度的偏误。随着θ值的增加，由于模型倾向于提取2次充电间隔较长的驻车区段为潜在充电区段，而忽略一部分充电区段，因此没有估计到的充电区段增加而高精度提取的充电区段数量减少。
图6 不同θ参数下各真实充电需求区段在不同时间估计匹配率A上的频数和频率分布

Fig. 6 Frequency and distribution of matching rates for actual charging demand segments at different time estimates A under various θ parameters

因此，不同θ参数使得本文所提模型和算法对提取不同指标产生不同适应性。较小θ参数值能够捕捉短时间充电需求，从而提高充电总时长估计准确率和各区段时间估计匹配率A，如θ=50%时充电总时长估计误差仅0.29%；而较大θ参数值能够提升对充电区段数量、充电总能量等指标的准确率，如θ=90%时充电区段数量估计误差仅3.18%， θ=100%时充电总能量估计误差为8.24%、充电需求电量估计误差为1.10%。

3.2.3 潜在充电需求估计的空间验证

本节将北京市空间区域栅格化为500、1000和10 000 m边长的网格，随后将真实充电地点的空间位置和不同θ参数下的估计充电位置进行集计，得到不同尺度下的充电区段数量和充电电量分布。不同空间尺度和不同θ参数下充电需求估计量的误差累积分布曲线如图7所示，随着相对误差ε取值增加，估计误差 P s l o t ( E ≤ ε )和 P p o w e r ( E ≤ ε )趋近于1；且曲线越靠近左上方，模型估计量的空间分布误差越小。总的来说，随着空间尺度增加，空间栅格对估计量的容错能力增大。当使用参数θ=90%时的模型估计充电区段数量的空间分布时，45.92%的500 m栅格误差小于0.2，而10 000 m栅格误差小于0.2的占比达到78.79%。此外，不同θ参数对充电需求估计量误差的影响较大，参数θ值越高，模型估计的空间分布误差越小。这一结论同3.2.1节时间验证的结论相一致，如表1所示。当参数θ为90%和100%时，充电区段数量估计和充电需求电量估计误差最小，分别为3.18%和1.10%，从总量上保证了相比于模型在其他θ值下更高的估计精度。
图7 不同空间尺度和θ值下的充电区段数量和充电电量估计误差累积分布

Fig. 7 Accumulated distributions of estimated errors in number and quantity of charging events across different spatial scales and θ values

事实上，出租车司机个体的充电行为具有极大的随机特征，仅根据电池SOC外的轨迹数据估计这些车辆完全电动化后的充电需求具有极大难度。本文所提出的潜在充电需求估计模型和算法能够保证充电区段数量、充电需求电量、平均每个充电区段需求电量和充电总时长的估计相对误差小于6.5%，并具有较高的时空分布估计精度，保证其在现实场景下的适用性。其中，充电需求电量的时间分布误差小于8.5%，一半以上充电需求电量在500 m栅格下的空间分布误差小于0.3，59%的500 m栅格的充电区段数量估计误差小于0.3。相比之下，Jin等[33]研究构建了高斯混合模型对充电需求空间分布进行估计，最好可实现不同空间尺度下的平均绝对百分比误差小于1；与此同时，其使用的自回归移动平均模型对时间分布估计的均方根误差最低为9.975。但其方法组合复杂，除利用电车轨迹数据外还需使用充电桩端订单数据，不利于方法的推广和拓展。而本文所提出的方法适用于电车和充电桩数据缺失的情况下，仅利用燃油车为代理的轨迹数据实现包括充电电量、充电时间和充电地点等多维度信息的较高精度估计。

3.3 基于燃油车轨迹数据的北京市充电需求估计及时空结构识别

3.3.1 北京市潜在充电需求的估计结果

根据《中国纯电动乘用车实际行驶性能:能耗、续驶里程和充电模式》[26]，选取中型车作为现阶段北京市出租车的代表车型，其百公里能耗δ和续驶里程为型式核准认证标称值，分别为12.6 kWh/100 km和468 km。为有效估计充电需求及其时空分布，本文需要保证时间匹配率不为0的区段不少于70%，在此基础上，尽可能提升充电电量和空间位置估计精度，于是折中假设电动出租车在电池电量消耗θ为90%SOC时产生充电需求，即一次充电行驶阈值threshold为468 km的90%（420 km）。本文应用基于轨迹地图匹配的潜在充电需求二叉树生成算法从2019年3月9日—11日连续3 d的出租车轨迹数据中提取出北京市六环范围内发生充电请求的出租车 1 913辆，有效充电区段4009段，充电总量达107 434 kWh，日均35 811 kWh。
选取2019年3月10日为本文考察的典型日，出租车充电需求的一阶空间分布图如图8所示。出租车潜在充电需求量呈现出明显的重点区域、关键通道聚集性特征。从区域上来看，需求量集中于北京市五环内核心区，尤其是四环至五环的东北部区域，以及四环到六环路的东中部地区，其中，机场（C）、望京（F）、国贸（D）区域充电需求旺盛，大部分路段单日充电需求量超过90 kWh。相比之下，五环至六环路的西南和西北地区充电需求活力较低，以良乡大学城（I）和首钢园（G）为例，单日路段充电需求量不超过60 kWh。从主要通道上来看，北京五环内城区通往东北方向机场（C）通道、正东方向通州城市副中心（H）通道和东南部亦庄地区（K）主通道表现出与长途出行相关的高密度充电需求，单日充电需求量在90 kWh以上。
图8 城市道路网尺度下的典型工作日北京市六环内出租车充电需求空间分布

Fig. 8 Spatial distribution of taxi charging demand within Beijing's Sixth Ring Road on typical workdays at urban road network scale

3.3.2 北京市潜在充电需求的时空结构

本节通过奇异值分解对2019年3月10日北京市六环内出租车充电需求时空分布一阶矩阵进行分解降维，识别充电需求中存在的时空结构。奇异值是衡量不同矩阵分布模式重要性的指标，奇异值越大表示该模式特征包含原矩阵信息越多。从奇异值分布碎石图来看（图9），前3项奇异值便能表示69%原矩阵的时空信息，第4项后的奇异值变化幅度极小。因此可以从出租车充电需求时空分布矩阵 M ( 24 × 2   186 )中提取出3种典型的时空关联结构特征。
图9 出租车充电需求时空分布一阶矩阵标准化奇异值分布

Fig. 9 Taxi charging demand spatiotemporal distribution first-order matrix standardized singular value distribution

图10（a）、图10（c）和图10（e）分别表示时间单位向量的变化趋势，时间单位向量的正负对应出租车充电需求在时间维度上的波动方向，而向量数值的绝对值则对应不同时刻充电需求波动的显著程度。图10（b）、图10（d）和图10（f）分别表示空间单位向量的分布特征，暖色调表示该道路充电需求出现正向波动，冷色调表示负向波动，颜色的深浅表示对应方向上波动的显著程度。同时结合时间和空间单位向量来看，若某条道路的时空单位向量同时出现正向波动，表明该种类型充电需求在对应空间范围和时间段内出现了显著增长；相反，如果时空单位向量出现异向波动，则表明对应时空条件下出租车充电需求降低。
图10 典型日北京市六环内出租车充电需求时空特征奇异值分解结果

Fig. 10 Taxi charging demand spatiotemporal characteristic singular value decomposition result within Beijing Sixth Ring Road on one typical day

如图10（a）所示，出租车充电需求特征I的标准化奇异值为51.2%，时间分布全部为正且时变较小；而图10（b）中需求特征I的空间分布值均为正，且和图8中的充电需求空间分布高度一致，因此出租车充电需求特征I代表北京市常态化充电需求。出租车充电需求特征II的标准化奇异值为11%，该特征表示上下午充电需求异质性。其时间分布见图10（c），在中午12时前均为负值，12时后均为正值。对应图10（d）中的空间分布特征，大型居住社区如回龙观（A）、天通苑（B），以及新型开发区如亦庄（K）、城市副中心（H）的空间向量以负向波动为主导，表明凌晨0时至中午12时出租车充电需求旺盛，这部分需求通常为单班出租车司机在居住地附近的夜间充电需求。而国贸地区（D）、北京奥运村（E）、国贸到城市副中心通道（D-H）的空间向量以正向波动为主导，表明12时后该地区充电需求旺盛。这部分需求通常为发生在订单繁忙区域的机遇充电，出租车司机在完成上午的订单任务后，利用午餐间隙进行快速补电。值得注意的是，首都机场西侧道路空间向量为负，而南侧道路空间向量为正，这是因为道路西侧多居住小区，而道路南侧为机场入口处，多物流公司，用地性质的不同影响了出租车司机的充电行为。基于城市道路网的时空规律挖掘能准确体现出区域边界的特征差异，这是基于栅格的挖掘方法所不具备的优势。
出租车充电需求特征III的标准化奇异值为6.8%，该特征表示工作时段和非工作时段充电需求异质性。其时间分布见图10（e），在0—8时、19—24时的非工作时间为负值，早上8—19时之间的工作时段均为正值。国际清洁交通委员会对电动出租车电池数据分析表示，在8—19时的充电时段中，又以14—17时为高峰，因为两班倒的出租车运营经常在下午17—18时换班，换班前发生充电行为[26]。对应图10（f）中的空间分布特征，北京城市副中心（H）和良乡大学城（I）的空间向量以负向波动为主导，表明该区域出租车多为单一型夜间充电。而本文所标注的其他重点研究区域均包含正向及负向波动的空间向量，表明这些地区的出租车均有日间和夜间充电需求。这可能是由于这些地区为混合功能区、职住相对均匀，所以同时包含节律性夜间充电和接送客间隙的机遇充电。值得注意的是亦庄高新技术开发区，在政策支持下亦庄修建了大量的充电基础设施，充电服务半径率先达到0.9 km，成为全市首个建成的充电服务半径达标的重点区域[34]。然而其潜在充电需求分布多集中于区内的 2条主干道，其他区域充电需求并不明显，且呈现出工作时段和非工作时段利用差异，这提示充电桩部署要分重点、分批次，避免均质化部署带来的资源浪费。

4 结论与讨论

4.1 结论

本文提出的充电需求估计模型和算法是一种基于燃油车轨迹大数据的自下而上的方法框架。所提的概念模型通过3种替代关系阐述了将以“驾驶-停驶”为循环的轨迹转换为以 “充电-放电”为循环的轨迹的技术方法；而二叉树算法在Ubuntu环境下通过递归遍历对上述概念模型进行实现，将叶子节点输出为充电需求，包括充电电量、充电时间和充电空间位置分布。该模型和算法具备算法高效性、时空精确性和可迁移扩展性，为电动化转型滞后地区提供了精确、可靠的充电需求估计范式。同现有研究相比，本文所提方法创新性地解决了真实电动汽车轨迹数据缺乏环境下的充电需求估计难题，并将潜在充电需求点落实到精确地理位置，进而具备了精准量化分析潜在充电需求时空分布的能力。此外，本文还提出了以道路网作为基本分析单元，并通过奇异值分解来挖掘潜在充电需求的时空结构，进而挖掘充电需求与真实城市空间结构的时空耦合关系。
本文使用890辆带有电池状态字段的电动出租车轨迹数据对模型和算法进行验证，估计模型的实验结果表明，其在不同电池电量消耗阈值θ和空间尺度下具有较高的时空分布估计精度。具体来看，不同θ参数使得本文所提方法对提取不同指标产生不同适应性，较小θ参数设置能够提高充电总时长估计准确率和各区段时间估计匹配率A；较大θ参数值能够提升对充电需求电量、充电区段数量和充电地点空间分布的估计准确率。此外，随着空间尺度增加，空间栅格对估计量的容错能力增大。
此外，本文以北京市六环内区域为实证案例，利用利用连续3 d部分出租车轨迹数据，分析北京市出租车潜在充电需求分布的地理空间格局，研究发现出租车潜在充电需求量呈现明显的分区域、分通道的空间聚集特征。具体来看，机场、望京、国贸等区域充电需求旺盛，北京五环内城区通往首都机场、通州城市副中心和亦庄地区的3条主通道表现出与长途出行相关的高密度充电需求，单日充电需求量在90 kWh以上。随后基于奇异值分解对潜在充电需求的时空结构进行分析，得到3种类型的充电需求：常态化充电需求、上下午异质性充电需求以及工作时段和非工作时段异质性充电需求。进一步结合城市土地利用和区域功能可挖掘出租车司机充电行为，如北京城市副中心和良乡大学城区域出租车多为节律性夜间充电，国贸等订单繁忙区域出租车常在接送客间隙进行机遇充电，而城市混合功能区两种充电行为往往同时存在。

4.2 讨论

随着出租车队电动化的推进、电池技术的进步以及居民活动强度的变化，出租车充电需求与供给的互动关系不断演化。相比于研究已经满足的充电需求，挖掘潜在的充电需求及其时空变化模式有助于解析出租车主真正的充电需求响应规律。随着车辆轨迹数据的爆发式增长，该方法还可推广至电动化转型过程中的其他城市、其他类型的车辆，用以指导充电基础设施的增量优化和存量更新[36]，如充电供需匹配研究、车队电动化转型后时代充电桩更新策略研究、针对充电需求时空拥挤的充电基础设施共享研究、V2G应用等。
值得注意的是，使用本文所提模型和算法来估计出租车潜在充电需求的结果受电池容量、电量消耗速率和驾驶行为异质性影响，充电需求时空分布存在不确定性。此外，本文所提方法在充电需求估计精度、求解算法效率和模型迭代发展等方面仍有改进空间。如应用驾驶过程动态能耗模型代替百公里能耗，融合多源数据进行高精度时空充电需求估计[5]，模型层面可以融入更丰富的地理位置信息提升模型估计精度，减少燃油车同电动汽车驾驶行为差异造成的估计误差；算法层面融合机器学习算法解决FMM计算瓶颈，实现在多场景、多阶段任务中的快速估计能力。随着补能方式的多样化发展，还有待探索换电行为和驾驶轨迹特征的关联关系，不断迭代该模型用来协同估计充电需求和换电需求。最后，本文使用SVD方法对时空矩阵降维，提取较大时空范围内充电需求的内在结构，但其存在计算复杂度高、可解释性差的缺点。开发计算高效、强表征能力的充电需求时空结构挖掘方法也是未来研究方向之一。

4.3 建议

基于上述结论，从支撑中长期规划、优化资源分配、保证电网安全和实施充电需求管理4个角度得到相关启发和建议：
（1） 政府规划部门以潜在充电需求估计为支撑制定出台近中长期的电动汽车充电基础设施规划。通过车辆轨迹大数据驱动需求估计模型来估计不同电动汽车渗透率下的充电需求及其空间分布，可以提供分批次、分阶段的需求基础数据，避免铺张建设导致的资源浪费。
（2） 充电桩服务建设、运营商等要以充电需求时空分布为参考有效部署充电基础设施。充电设备的供给要避免均质化与随机化，而是要以提升充电桩利用率为导向优化选址流程和定容策略，如在机场、望京、国贸等充电热点地区提供大功率充电桩、增加站均充电枪数目等；在北京城区正东、东北和东南方向的主要通道上增加路侧充电桩设置，在电池能量密度技术突破前极力缓解电动出租车司机的“里程焦虑”。
（3） 电力部门要对电网负荷实施调度调节，提升电网的安全性、经济性。城市电力系统是电动出租车队的动力源头，其具有实时平衡性和不易存储性[5]。电力部门预计要为北京市待电动化的3万辆电车③(③北京市交通委员会“出租汽车”行业概况指出，北京市巡游出租汽车运营约6万辆，其中电动车31 622辆（https://jtw.beijing.gov.cn/czqc/hygk/202110/t20211021_2517443.html?eqid=c267f529000cf7c700000003648fc1ab）。)入网新增日均561 MWh的充电供给。与此同时，其时空耦合关系为负荷聚合商提供了更为精确的充放电调节参考[7]，如回龙观、天通苑地区具有高夜间充电需求、国贸地区具有高午间充电需求等。有助于电动汽车集群参与电网需求响应条件下的电网配置策略优化，避免无序、大功率集中充电对电网的冲击。
（4） 电力部门和交通运行管理部门要以高精度的充电需求估计为有力工具研究充电需求管理策略。其包括： ① 被动管理策略如对不同区域实施峰谷电价调节机制，以期将持续增长的充电需求合理引导至利用率较低的充电设施[35]； ② 主动管理策略如充电服务导航系统引导出租车有序充电，通过用户侧优化充电需求再分配、助力电网系统削峰填谷和清洁能源消纳。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
IEA. Global EV Outlook 2023[EB/OL]. ( April 2023) [2023-06-04]. https://www.iea.org/reports/global-ev-outlook-2023/executive-summary.

[2]
Pet Mock P, Yang Z. A 2022 update on electric car sales: China taking the lead, the U.S. catching up, and Europe falling behind[R]. ICCT: The International Council on Clean Transportation. 2022. https://theicct.org/2022-update-ev-sales-us-eu-ch-aug22/.

[3]
北京市人民政府. 关于印发《北京市“十四五”时期交通发展建设规划》的通知[EB/OL]. ( 2022-05-07) [2023-06-04].

[Beijing Municipal People's Government. Notice on Issuing the "Transportation Development and Construction Plan for the 14th Five Year Plan Period in Beijing"[EB/OL]. ( 2022-05-07) [2023-06-04].] https://www.beijing.gov.cn/zhengce/gfxwj/202205/t20220507_2704320.html

[4]
Cui H Y, Ma R C, Liu Y N, et al. Charging up China's transition to electric vehicles: A dive into China's public charging infrastructure deployment and comparison with Europe and the United States[R]. ICCT: The International Council on Clean Transportation. 2024. https://theicct.org/publication/charging-up-china-transition-to-ev-jan24/.

[5]
王震坡, 张瑾, 刘鹏, 等. 电动汽车充电站规划研究综述[J]. 中国公路学报, 2022, 35(12):230-252.

[Wang Z P, Zhang J, Liu P, et al. Overview of planning of electric vehicle charging stations[J]. China Journal of Highway and Transport, 2022, 35(12):230-252.] DOI:10.19721/j.cnki.1001-7372.2022.12.019

[6]
Kang J, Kong H, Lin Z J, et al. Mapping the dynamics of electric vehicle charging demand within Beijing's spatial structure[J]. Sustainable Cities and Society, 2022,76:103507. DOI:10.1016/j.scs.2021.103507

[7]
赵轩, 张元星, 李斌, 等. 国内外车网互动试点成效分析与发展建议[J]. 电力自动化设备, 2022, 42(10):280-292.

[Zhao X, Zhang Y X, Li B, et al. Effect analysis and development suggestion of domestic and foreign vehicle grid integration pilots[J]. Electric Power Automation Equipment, 2022, 42(10):280-292.] DOI:10.16081/j.epae.202208017

[8]
Ma R C, Huang A L, Cui H Y, et al. Spatial heterogeneity analysis on distribution of intra-city public electric vehicle charging points based on multi-scale geographically weighted regression[J]. Travel Behaviour and Society, 2024,35:100725. DOI:10.1016/j.tbs.2023.100725

[9]
张毅, 朱攀. 电动出租车专用充电场站选址模型研究[J]. 地球信息科学学报, 2021, 23(5):802-811.

[Zhang Y, Zhu P. Research on site selection model of special charging stations for taxis[J]. Journal of Geo-Information Science, 2021, 23(5):802-811.] DOI:10.12082/dqxxkx.2021.200360

[10]
Bernard M R, Dall H. Assessing charging infrastructure needs in Québec[R]. ICCT: The International Council on Clean Transportation. 2022. https://theicct.org/publication/lvs-ci-quebec-can-EN-feb22/.

[11]
Zhang Y, Zhang Q, Farnoosh A, et al. GIS-Based Multi-Objective Particle Swarm Optimization of charging stations for electric vehicles[J]. Energy, 2019, 169:844-853. DOI: 10.1016/j.energy.2018.12.062.

[12]
Hüttel F B, Rodrigues F, Pereira F C. Mind the gap: Modelling difference between censored and uncensored electric vehicle charging demand[J]. Transportation Research Part C: Emerging Technologies, 2023,153:104189. DOI: 10.1016/j.trc.2023.104189

[13]
Cai H, Xu M. Greenhouse gas implications of fleet electrification based on big data-informed individual travel patterns[J]. Environmental Science & Technology, 2013, 47(16):9035-9043. DOI:10.1021/es401008f

[14]
Sica L, Deflorio F. Estimation of charging demand for electric vehicles by discrete choice models and numerical simulations: Application to a case study in Turin[J]. Green Energy and Intelligent Transportation, 2023, 2(2):100069. DOI:10.1016/j.geits.2023.100069

[15]
Li Y J, Su S, Liu B, et al. Trajectory-driven planning of electric taxi charging stations based on cumulative prospect theory. Sustainable Cities and Society. 2022, 86. DOI:10.1016/j.scs.2022.104125.

[16]
Lazzeroni P, Caroleo B, Arnone M, et al. A simplified approach to estimate EV charging demand in urban area: An Italian case study[J]. Energies, 2021, 14(20):6697. DOI: 10.3390/en14206697

[17]
Yang X, Peng Z H, Wang P X, et al. Seasonal variance in electric vehicle charging demand and its impacts on infrastructure deployment: A big data approach[J]. Energy, 2023,280:128230. DOI:10.1016/j.energy.2023.128230

[18]
Metais M O, Jouini O, Perez Y, et al. Too much or not enough? Planning electric vehicle charging infrastructure: Areview of modeling options[J]. Renewable and Sustainable Energy Reviews, 2022,153:111719. DOI:10.1016/j.r ser.2021.111719

[19]
He S Y, Kuo Y H, Wu D. Incorporating institutional and spatial factors in the selection of the optimal locations of public electric vehicle charging facilities: A case study of Beijing, China[J]. Transportation Research Part C: Emerging Technologies, 2016, 67:131-148. DOI:10.1016/j.trc.2016.02.003

[20]
Wang H, Zhao D, Cai Y T, et al. Taxi trajectory data based fast-charging facility planning for urban electric taxi systems[J]. Applied Energy, 2021,286:116515. DOI: 10.1016/j.apenergy.2021.116515

[21]
Ragon P L, Kelly S, Egerstrom N, et al. Near-term infrastructure deployment to support zero-emission medium- and heavy-duty vehicles in the United States[R]. ICCT: The International Council on Clean Transportation. 2023. https://theicct.org/publication/infrastructure-deployment-mhdv-may23/

[22]
Li M, Jia Y H, Shen Z J, et al. Improving the electrification rate of the vehicle Miles traveled in Beijing: A data-driven approach[J]. Transportation Research Part A: Policy and Practice, 2017, 97:106-120. DOI:10.1016/j.tra.2017.01.005

[23]
Straub F, Maier O, Göhlich D, et al. Forecasting the spatial and temporal charging demand of fully electrified urban private car transportation based on large-scale traffic simulation[J]. Green Energy and Intelligent Transportation, 2023, 2(1):100039. DOI:10.1016/j.geits.2022.100039

[24]
周椿奇, 向月, 童话, 等. 轨迹数据驱动的电动汽车充电需求及V2G可调控容量估计[J]. 电力系统自动化, 2022, 46(12):46-55.

[Zhou C Q, Xiang Y, Tong H, et al. Trajectory-data-driven estimation of electric vehicle charging demand and vechicle-to-grid regulable capacity[J]. Automation of Electric Power Systems, 2022, 46(12):46-55.] DOI:10.7500/AEPS20211227005

[25]
Tian Z Y, Wang Y, Tian C, et al. Understanding operational and charging patterns of Electric Vehicle taxis using GPS records[C]// 17th International IEEE Conference on Intelligent Transportation Systems (ITSC). IEEE, 2014:2472-2479. DOI:10.1109/itsc.2014.6958086

[26]
金伶芝, 王硕, 何卉, 等. 中国纯电动乘用车实际行驶性能: 能耗、续驶里程和充电模式[R]. 国际清洁交通委员会. 2023. https://theicct.org/wp-content/uploads/2023/06/中国纯电动乘用车实际行驶性能_FINAL.pdf.

[Jin L Z, Wang S, He H, et al. Real-world performance of battery electric passenger cars in China: Energy consumption, range, and charging patterns[R]. ICCT: The International Council on Clean Transportation. 2023. https://theicct.org/publication/pv-china-real-world-performance-apr23/.]

[27]
Yang C, Gidófalvi G. Fast map matching, an algorithm integrating hidden Markov model with precomputation[J]. International Journal of Geographical Information Science, 2018, 32(3):547-570. DOI:10.1080/13658816.2017.1400548

[28]
Deng Y J, Li M Y, Tang Q, et al. Heterogenous trip distance-based route choice behavior analysis using real-world large-scale taxi trajectory data[J]. Journal of Advanced Transportation, 2020,2020:8836511. DOI:10.1155/2020/8836511

[29]
Zhang S H, Wang Z Y. Inferring passenger denial behavior of taxi drivers from large-scale taxi traces[J]. PLoS One, 2016, 11(11):e0165597. DOI:10.1371/journal.pone.0165597

[30]
Zhu D, Wang N H, Wu L, et al. Street as a big geo-data assembly and analysis unit in urban studies: A case study using Beijing taxi data[J]. Applied Geography, 2017, 86:152-164. DOI:10.1016/j.apgeog.2017.07.001

[31]
何凌晖, 余庆, 李玮峰, 等. 新冠肺炎疫情影响下的城际交通运输需求分析[J]. 城市交通, 2020, 18(3):51-61.

[He L H, Yu Q, Li W F, et al. Inter-city transportation demand under the COVID-19 pandemic[J]. Urban Transport of China, 2020, 18(3):51-61.] DOI:10.13813/j.cn11-5141/u.2020.0024

[32]
Falini A. A review on the selection criteria for the truncated SVD in Data Science applications[J]. Journal of Computational Mathematics and Data Science, 2022,5:10006 4. DOI:10.1016/j.jcmds.2022.100064

[33]
Jin B F, Wang J J, Xu P, et al. Accurate charging demand estimation of electric vehicle via multi-data sources[C]. 2020 IEEE 3rd International Conference on Information Systems and Computer Aided Education (ICISCAE). IEEE, 2020:124-131. DOI:10.1109/ICISCAE51034.2020.9236795

[34]
北京经济技术开发区. 北京亦庄创新发布第66次网络发布:北京经开区成全市首个充电服务半径达标区域[EB/OL].( 2020-06-08) [2023-10-04].

[Beijing Economic-Technological Development Area. Beijing Yizhuang Innovation Release 66th Online Release: Beijing Economic and Technological Development Area Becomes the First Charging Service radius Standard Area in the City[EB/OL]. ( 2020-06-08) [2023-10-04].] https://kfqgw.beijing.gov.cn/zwgkkfq/yzttkfq/202103/t20210330_2332894.html.

[35]
Azin B, Yang X F, Marković N, et al. An incentivized scheme for electric vehicle charging demand management[J]. Transportation Research Part C: Emerging Technologies, 2023,155:104288. DOI:10.1016/j.trc.2023.104288

[36]
Li Y J, Pei W H, Zhang Q, et al. Optimal layout of electric vehicle charging station locations considering dynamic charging demand[J]. Electronics, 2023, 12(8):1818. DOI:10.3390/electronics12081818

Options
文章导航

/

〈 〉