EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 10: 2335 - 2351

DOI: https://doi.org/10.12082/dqxxkx.2024.240005

专栏：“GIS 与未来城市交通”

基于改进邻域聚合的路网图嵌入匹配方法

  • 杨铭 , 1, 2 ,
  • 杨剑 , 3, * ,
  • 侯洋 4, 2 ,
  • 方立 2 ,
  • 张猛 5 ,
  • 张变英 6 ,
  • 张静茹 2
展开
  • 1.福州大学先进制造学院，泉州 362200
  • 2.中国科学院海西研究院泉州装备制造研究中心，泉州 362216
  • 3.信息工程大学 地理空间信息学院，郑州 450052
  • 4.中国科学院福建物质结构研究所，福州 350002
  • 5.西安交通大学人居环境与建筑工程学院，西安 712000
  • 6.中国资源卫星应用中心，北京 100094
* 杨 剑（1985— ），男，广东高州人，博士，讲师，主要从事地理空间智能、众源地理信息服务研究。 E-mail:

杨 铭（1996— ），男，黑龙江五常人，硕士生，主要从事地理信息工程、计算机视觉研究。E-mail:

Copy editor: 蒋树芳 , 黄光玉

收稿日期: 2024-01-04

  修回日期: 2024-02-13

  网络出版日期: 2024-10-09

基金资助

国家自然科学基金项目(42130112)

国家自然科学基金项目(42371479)

国家自然科学基金项目(41901335)

智慧地球重点实验室基金资助项目(KF2023ZD04-02)

收起

A Method of Road Network Matching Using Graph Embedding via Improved Neighbor Aggregations

  • YANG Ming , 1, 2 ,
  • YANG Jian , 3, * ,
  • HOU Yang 4, 2 ,
  • FANG Li 2 ,
  • ZHANG Meng 5 ,
  • ZHANG Bianying 6 ,
  • ZHANG Jingru 2
Expand
  • 1. School of Advanced Manufacturing, Fuzhou University, Quanzhou 362200, China
  • 2. Quanzhou Institute of Equipment Manufacturing, Haixi Institute, Chinese Academy of Sciences, Quanzhou 362216, China
  • 3. School of Geospatial Information, Information Engineering University, Zhengzhou 450052, China
  • 4. Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou 350002, China
  • 5. School of Human Settlements and Civil Engineering, Xi'an Jiaotong University, Xi'an 712000, China
  • 6. China Centre for Resources Satellite Data and Application, Beijing 100094, China
* YANG Jian, E-mail:

Received date: 2024-01-04

  Revised date: 2024-02-13

  Online published: 2024-10-09

Supported by

National Natural Science Foundation of China(42130112)

National Natural Science Foundation of China(42371479)

National Natural Science Foundation of China(41901335)

Key Laboratory of Smart Earth(KF2023ZD04-02)

Fold

摘要

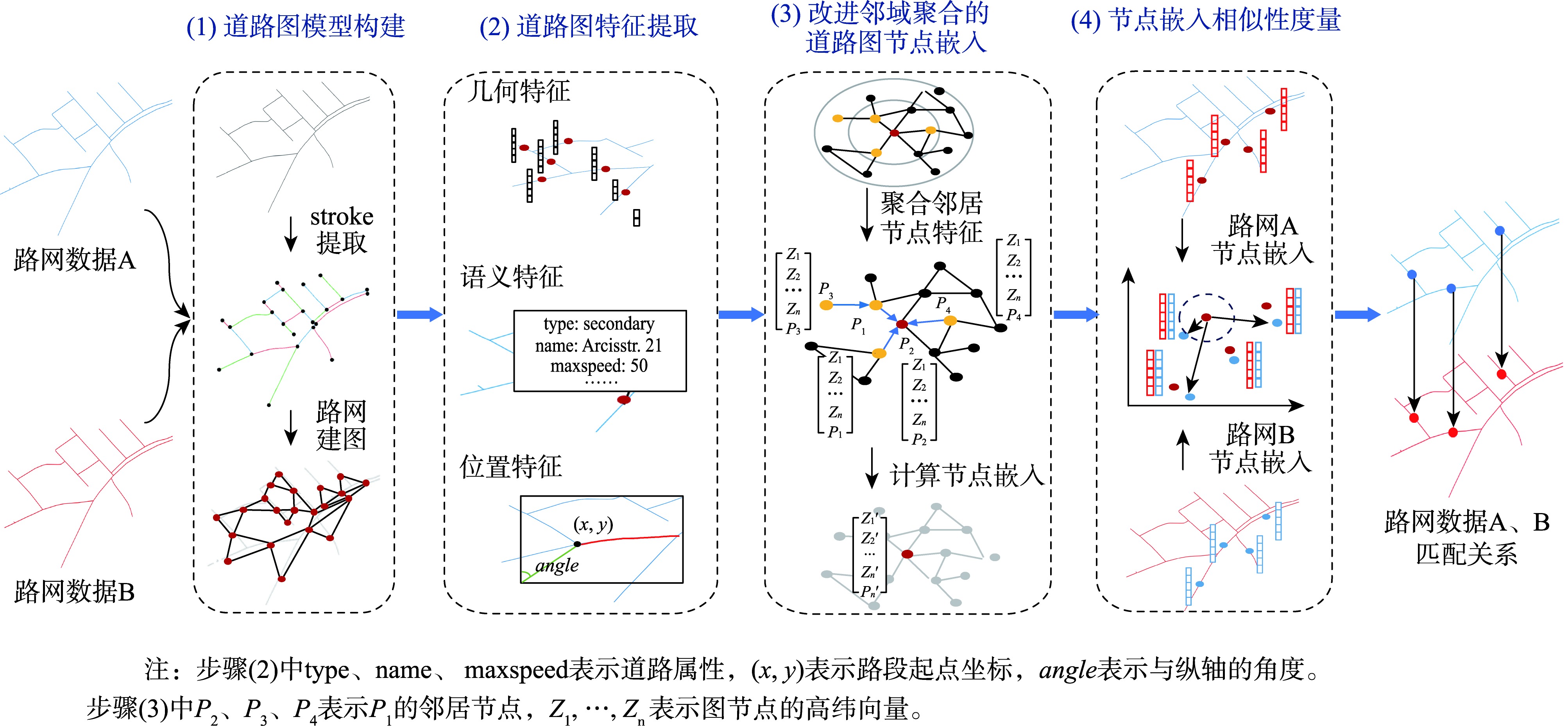
道路网作为一种重要的交通基础设施，路网数据的及时更新对交通管理、应急救援和城市规划等领域有重要应用意义。通过路网匹配来确定不同来源的路网数据中要素间的对应关系，既是实现路网更新的重要技术途径，也为众源路网数据质量评估等任务提供技术支撑，因而备受地理信息领域学者的关注。传统的路网匹配方法主要通过路网数据的几何和拓扑属性来度量路网结构的相似性，以此确定路网要素的匹配关系。但人工设计的特征和阈值易受专家经验局限，使其在复杂路网结构下性能下降。近年来，基于图神经网络的路网数据建模成为研究热点，已在多个路网建模任务中取得优异性能。但现有方法多采用在图拓扑结构上直接进行邻域聚合的方式，学习路网结构的嵌入表示，未在这一关键步骤中考虑路网要素的空间关系，没能充分利用图神经网络的表示学习能力。为此，本研究面向路网匹配任务，采用空间显式建模的思想，提出一种基于改进的邻域聚合图嵌入学习方法。首先，构建路网数据的道路图模型并提取几何、语义和位置特征。然后，基于GraphSAGE框架，提出空间、分类和混合3种邻域聚合算子，在邻域聚合操作中引入路网要素空间关系、属性类型的计算。最后，利用图节点嵌入的相似度确定路网要素的匹配关系。为验证本文方法的有效性，利用真实路网数据开展了充分实验，本文方法在实验区数据上的各项指标取得最优表现，比基线图神经网络方法的匹配正确率提升11%以上、召回率提升6.8%以上。并对路网图嵌入特征进行分析，从图嵌入结构和嵌入路网结构两方面，探讨了改进邻域聚合对图嵌入表示能力的作用，为进一步提升图神经网络路网建模提供了新视角。

关键词： 路网匹配; 邻域聚合; 图神经网络; 空间卷积; 空间显式; GNN表示能力; 路网结构模式

本文引用格式

杨铭 , 杨剑 , 侯洋 , 方立 , 张猛 , 张变英 , 张静茹 . 基于改进邻域聚合的路网图嵌入匹配方法[J]. 地球信息科学学报, 2024 , 26(10) : 2335 -2351 . DOI: 10.12082/dqxxkx.2024.240005

Abstract

As an important transportation infrastructure, the timely updating of road network data is of great significance in the fields of traffic management, emergency response, and urban planning. Road network matching that determines the correspondence between the features of road network data from different sources serves this purpose. It also provides technical support for tasks such as the quality assessment of crowdsourced road network data, which has attracted a lot of attention in the field of geographic information. However, traditional road network matching methods mainly measure the similarity of road network structure through the geometric and topological attributes of road network data to determine the matching relationship of road network elements. Such methods with manually designed features and thresholds are easily limited by experts' experience, which degrades their performance under complex road network structures. In recent years, road network data modeling based on graph neural networks has become a research hotspot and has achieved excellent performance in several road network modeling tasks. However, most of the existing methods use direct neighborhood aggregation on the graph topology to learn the embedded representation of the road network structure, without considering the spatial relationship of road network features in this key step, and failing to make full use of the representation learning capability of graph neural networks. For this reason, this study proposes an improved neighborhood aggregation that performs a spatially explicit graph-based embedding learning method for road network matching. First, a road graph model of the road network data is constructed, and geometric, semantic, and location features are extracted. Then, based on the GraphSAGE framework, three kinds of neighborhood aggregation operators (i.e., spatial, classified, and hybrid) are proposed, and the computation of spatial relationships and attribute types of road network features is introduced in the neighborhood aggregation operations. Finally, the similarity of graph node embedding is utilized to determine the matching relationship of road network features. To verify the effectiveness of the proposed method, extensive experiments are carried out using real-world road network data. The proposed method achieves the optimal performance in all metrics on the test data of the study region, which improves the matching correctness rate by more than 11% and the recall rate by more than 6.8% compared to the baseline graph neural network method. Furthermore, the road network graph embedding features are analyzed from the aspects of graph embedding structure and embedded road network structure, which helps explore the role of improved neighborhood aggregation on the graph embedding representation capability and provides a new perspective for further improving the graph neural network road network modeling.

Key words： road network matching; neighbor aggregation; graph neural network; spatial convolution; spatially explicit; GNN expressive power; structural pattern of road network

1 引言

道路网作为一种重要的城市基础设施，路网数据在城市规划、交通管理和应急救援等多个领域都有重要应用。为保证路网数据能及时反映城市发展变化，不同部门围绕自身应用需求采集生产了不同时间、不同规格的路网数据。受此影响，同一地区不同来源的路网数据间会存在较大差异，无法满足使用者的实际需求。为此，需要对不同来源或不同版本的路网数据进行路网匹配[1]，即在不同来源的路网数据中找到路段的对应关系。作为地理信息科学领域的重要问题之一，路网匹配在多源路网数据集成融合、路网变化监测与更新、路网数据质量评估中起到重要作用。
经典的路网匹配主要分为基于几何、语义相似性的匹配算法和高级匹配算法。基于几何的匹配算法是通过比较路段的空间坐标、长度、方向的相似度来实现路网匹配[2-3]。该类匹配算法易于实现，适用于稀疏、结构简单的路网数据，但在复杂路网结构下匹配精度的鲁棒性较差。基于语义的匹配算法主要分析不同道路属性数据之间的语义关联性，进而建立匹配关系[4-5]，包括道路名称、等级、类型等信息。但不同来源的路网数据存在属性不全的问题，导致道路的语义信息难以获取利用。高级匹配算法包括Buffer Growing(BG)算法[6]、Iterative Closest Points(ICP)算法[7]和限定笔划算法[8]等。这些算法综合考虑道路的几何以及拓扑等信息，并设计了更为复杂的优化匹配策略，提高了匹配的准确性，但依旧受道路复杂度、采样率等因素影响[9-10]。其中，BG和ICP是基于“线要素”和“点要素”比对的匹配算法，只能实现局部最优匹配，在道路复杂区域难以得到最优匹配结果[11-12]。限定笔划算法结合以上两种算法的优点，更多的考虑道路拓扑和上下文信息，实现了整体最优化匹配。Almotairi等[9]提出一种综合利用几何、拓扑、语义特征的路网匹配算法，综合局部和全局的角度来确认候选道路是否相似，提升了匹配的正确率，但对道路数据属性完整性要求较高。秦育罗等[10]提出一种顾及几何特征和拓扑连续性的由粗匹配到精匹配的分层匹配策略，但当漏匹配和误匹配位于匹配对象的一侧时，该算法无法进行探测和修正。总体而言，传统算法大都是通过人工提取路网结构特征，再度量不同来源的路网结构的相似性，然后按照一定的规则得到最佳匹配道路[13-14]。算法设计重在形式化人对路网结构的理解，但常常受限于经验和小样本确定的模型参数阈值，这使得在应对复杂路网结构时性能受限。而且传统方法过度依赖人工设计的相似性特征，对数据质量要求较高。随着技术的发展，路网匹配方法从主要依赖道路的局部形态特征变为综合考虑局部与全局特征，发展出更先进的相似性度量方法，但并没完全解决以上问题。
近年来，利用深度神经网络进行路网建模成为研究关注的热点，而路网的拓扑组织结构使得图神经网络（Graph Neural Network，GNN）成为路网建模的直接选择[15-16]，尤其在路网结构模式识别[17]、路段属性预测[18]等任务上展现出优异性能。相比传统特征工程方法，基于GNN的路网建模能更有效地捕捉路网结构的几何和语义信息，获得对下游任务更为相关的计算表征。王米琪等[17]基于图卷积网络（Graph Convolution Network，GCN）构建路网数据的无向图模型，通过道路线性剖分的方式获取道路的图节点特征，实现了对道路格网模式的识别。Yang等[19]提出一种基于GCN的方法用于立交桥检测，利用有限的标签和半监督学习方式进行训练，并采用自适应聚类方法实现了对立交桥的精确检测，克服了传统方法对复杂结构立交桥检测精度较低的问题。Guo等[18]提出一种优化的GCN模型，用于提取交通网络的时间和空间特征以进行交通预测，采用数据驱动的方式学习路网的优化图，从交通数据中揭示了路段之间的潜在关系。得益于对网络结构的表示能力，GNN也被用于排水系统、分子结构等空间网络的建模。Yu等[20]基于图自编码器网络（Graph Autoencoder Network，GAE）提出了一种用于尺度变换下水网相似性度量的无监督表示学习框架，提高了水网相似性度量的客观性和准确性。类似地，Yu等[21]基于GraphSAGE框架设计了水网模式分割方法，从拓扑连通性、蜿蜒平衡和方向统一性3个角度提取水网特征，成功将GCN应用于水网模式识别问题。在分子结构预测任务上，Danel等[22]提出了空间图卷积网络，在邻域聚合中引入分子的空间位置关系计算，让模型更加有效地学习图的全局特征，提高了GNN的空间结构预测精度和泛化能力。
图神经网络在路网等空间网络的建模上表现优异，为其在路网匹配任务上的应用带来启发。Soni等[23]面向包含点、线要素的车道级路网数据，利用基于图拓扑邻域采样和聚合的GNN框架GraphSAGE，提出了一种基于异构地理空间图嵌入相似度的路网匹配方法。该方法首先利用路网数据中POI点要素、车道线等线要素构建异构要素关系图，然后分别提取点、线要素对应的图节点特征，并通过路网表示学习得到图节点嵌入表示。对于不同来源的路网数据，分别计算路网数据的图节点嵌入表示，然后度量图节点嵌入相似性，作为路网匹配的判别依据。齐杰等[15]提出了一种结合GCN的道路网匹配方法，通过监督学习自动确定了道路网匹配方法中特征权重和匹配阈值，避免了专家经验赋值存在的主观偏差。包括Soni等人研究在内的空间网络建模多通过图拓扑邻域聚合获得图节点的嵌入表示，并未考虑图拓扑邻域内各邻居节点所表示要素的空间位置关系，使得路网空间关系无法被图神经网络充分学习表示，导致路网嵌入难以有效表征复杂路网结构而影响任务性能。为改善这种GNN建模上的缺陷，一些研究选择通过人工设计节点或边的特征来增强图节点嵌入的空间关系表示能力[17]，但这种延续特征工程的做法并没有充分利用GNN的学习能力，限制了模型泛化能力的提升。
针对以上不足之处，本文采用空间显式建模思想，设计了新的GNN邻域聚合函数，在路网嵌入学习中引入空间关系运算，增强图嵌入对路网数据的学习表示，提升GNN在路网匹配上的应用水平，并利用真实路网数据测试验证了本文方法的有效性。在此基础上，对图嵌入表示性能进行了实验分析，从图嵌入结构和路网嵌入效果上探讨了图嵌入表示能力差异。论文贡献主要包括：
（1） 提出一种基于改进邻域聚合的路网图嵌入方法，通过构建道路图并学习图节点嵌入，实现基于图节点嵌入的路网匹配。设计了空间、分类和混合3种邻域聚合函数，以提升图神经网络对路网空间结构的表示能力；
（2） 利用真实路网数据开展了路网匹配实验，对比研究了经典路网匹配算法、多个图神经网络路网匹配算法的性能，实验验证了基于改进邻域聚合的路网图嵌入方法的有效性。相比基线图神经网络方法，本文方法在实验区数据上的匹配正确率提升11%以上，召回率提升6.8%以上；
（3） 利用降维可视化技术对路网图嵌入性能进行评价，从图嵌入结构和嵌入样本道路两方面，分析了采用不同架构、不同邻域聚合函数的图神经网络的表示性能，为改进图神经网络的路网建模提供了新视角。

2 基于改进邻域聚合的路网图嵌入匹配

2.1 方法框架

本文利用图神经网络对路网数据进行表示学习，基于图节点嵌入计算路段相似性，推断不同来源路网数据的路段匹配关系，从而实现整体路网的匹配。本文方法受Soni等[23]的地理空间图嵌入方法的启发，不仅针对多源路网数据的差异对道路图构建方法进行改进，包括在道路图构建中引入stroke提取、道路图特征提取中增加了位置特征，还提出了基于改进邻域聚合的图节点嵌入方法，能更好的捕获路网结构信息，显著提升了路网匹配任务表现性能。本文方法的基本流程如图1所示，包括4个步骤：
图1 改进邻域聚合的路网图嵌入匹配方法框架

Fig. 1 The framework of road network matching using graph embedding with improved neighborhood aggregations

（1） 道路图模型构建。对路网数据进行预处理及stroke提取[24]，用路网数据构建描述路段关系的图模型，用图的节点表示stroke路段，图的边表示相邻路段的连接关系。
（2） 道路图特征提取。对路段的几何要素进行自动编码作为路段几何特征，采用路段的属性数据作为路段的语义特征，并使用路段的坐标和方位作为路段位置特征，综合几何、语义、位置3类特征作为道路图节点的初始特征描述。
（3） 改进邻域聚合的道路图节点嵌入。提出了空间、分类、混合3种邻域聚合函数学习路段的图节点嵌入，能够更好地捕获路网的复杂邻域关系，为路网匹配提供更有效的路段嵌入表示。
（4） 节点嵌入相似性度量。对不同来源的路网数据，分别学习路网数据的图节点嵌入，并利用图节点嵌入计算不同数据源之间的路段相似度，确定路段匹配关系，实现路网匹配。

2.2 道路图模型构建

路网数据通常采用图模型表示，通过描述路网拓扑关系，为路径规划、交通预测等分析任务提供基础数据结构。考虑不同来源的路网数据并不都包含道路行驶方向信息，本文采用无向图构建路网数据的道路图。常用道路图构建方式有2种：① 将路段视为图节点，路段间连接关系作为图的边[23]；② 也可将路段的连接点与交叉口作为图节点，路段作为图的边[17]。本文以路网数据预处理后的路段为单位，使用图节点嵌入的方式表征路段自身和邻域特征，以此计算不同路网数据中路段相似性，从而确定路网匹配关系，故选取以路段作为图节点的建图方法。道路图的构建过程如图2所示。对给定的路网数据R，本文通过路网数据预处理与stroke提取、道路图节点提取与邻域节点连接，构建相应的道路图 G R = V , E，其中V，E分别是道路图的节点集合和边集合。
图2 道路图构建流程

Fig. 2 Construction process of road network graph

首先，对路网数据进行预处理。滤除路网数据中的噪声数据，例如长度过小、无法建立拓扑连接的路段，并对路网数据进行stroke提取操作[24]。stroke提取旨在统一不同来源路网数据在路段分割建模上的差异，提高路网匹配的成功率。例如，不同来源路网数据对同一道路实体会给出路段数量不同的数据表示，导致因路段表示差异而无法建立路段匹配关系。因此，需对路网数据的原始路段进行处理，根据路网要素的长度、交叉口和转角的拓扑关系对路段进行断开操作，将结果作为后续图模型构建的路段数据输入，以消除不同数据源之间拓扑关系描述上的不一致，增加找到道路匹配对的可能性[8]。
然后，基于处理的路网数据确定图的节点和边，构建道路图。选取stroke路段的中点作为道路图节点（图2（c）），提取路段的几何、语义、位置特征作为图节点的初始特征输入。具体的节点特征的提取将在下一节讨论。在提取图节点之后，根据路段间的距离关系确定每个节点的邻域节点，连接相邻节点来构建图的边。路段节点的邻域可直接根据路段拓扑邻接关系来确定，也可通过搜索路段节点在地理空间中满足某种距离关系的邻居路段来确定。本文采用后者这种更具一般性的方法[23]，设置一个邻域搜索半径，然后对每个路段节点搜索邻域中Hausdorff距离高于一定阈值的路段节点。例如，在图2（d）中路段a、b、c（分别映射为道路图节点va、vb、vc）之间的Hausdorff距离都在设定的阈值内，因此va、vb和vc应按照va-vb-vc-va连接以形成道路图的边eab、ebc、eac。这种方法为路网匹配任务中处理平行道路及复杂路段带来灵活性。
随着路网数据规模（尤其是路段数量）的增加，会导致邻域节点搜索的计算开销快速增加。在具体实现中，可考虑对路网建立KD-Tree[25]等空间索引，提高路段节点邻域搜索的效率。

2.3 道路图特征提取

道路图构建后，需为图节点提取路网数据特征作为图嵌入学习的输入。对路网匹配而言，往往需要利用道路的几何和语义特征来综合判断路网之间的匹配关系[8]。道路的几何特征包括道路中心线的形状、长度、宽度等属性，而语义特征则包括道路的类型、等级、限行速度等。此外，本文还增加了道路位置特征用来表示路段的空间关系，最后得到每个图节点的特征输入，如图3所示。
图3 图节点路段的特征

Fig. 3 Graph node features of road segments

2.3.1 几何特征

本文采用线要素自动编码来表示路段的几何特征，相比于传统人工特征设计方法，能够更好地捕捉路段的几何形表示，提供更加灵活、通用的表示方式。但是，不同于轨迹数据根据移动对象的位移时间顺序排列，道路线要素不一定具备明确或唯一的方向信息（如行驶方向缺失、双向行驶道路），而不同路网数据源也可能对同一路段采用相反的方向表示。这将导致需指定数据顺序的序列数据编码器计算得到不同的嵌入向量。因此，通过比较道路要素两个端点的经纬度来确定道路要素的坐标顺序，确保它们在多个路网数据中保持一致，从而使序列编码器的嵌入结果具有可比性。为此，遍历路网数据的每条路段，比较路段端点的经纬度，取经度或纬度较小者作为路段起点。
本文采用LSTM自动编码器[26]对路段进行编码，可以避免不同路网数据的采样率不同而导致编码器关于几何形状与结构的编码知识存在差异。通过训练，编码器能获取路段线要素的固定维度向量，而不受数据长度、结构和坐标点数量的影响。选取2 000条道路要素，以1、10、15、20、25 m的间隔重新采集共5组数据作为训练数据输入，并生成相应标签。为确保生成的嵌入向量更接近原始数据，在原始输入中添加了随机噪声。本文使用编码器对所有图节点的路段线要素进行编码，将不定长的线要素编码成定长的128维向量。在损失函数选取上，本文采用对比损失函数[27]以适应数据相似性建模的需要。对比损失函数定义为：
L c o n t r a s t = 1 / N ∑ n = 1 N T D 2 + 1 - T m a x R - D , 0 2          
式中： N ≤ n ≤ 1； L c o n t r a s t为对比损失函数，用于训练模型；N为样本数量；T是样本匹配指标函数（2个样本匹配时取值为1，否则为0）； D = a n - b n 2，代表2个样本嵌入向量的欧氏距离；R是预先设定的阈值，代表样本嵌入空间周围的半径。

2.3.2 语义特征

不同来源路网数据的同一道路属性数据可能存在差异。这与路网数据的属性字段定义、采集时间甚至数据质量等因素有关。在选择语义特征时，可通过比较参与匹配的路网数据的属性数据，从属性的通用性、一致性和可比性等角度来选取道路属性作为语义特征输入。本文根据研究对象OSM和TeleAtlas的数据特点，选取了道路类型和道路名称，将其归一化，得到相应的枚举值作为节点路段的语义特征。

2.3.3 位置特征

为表示路段之间的位置、方向等空间关系，使用路段坐标、方位角度作为位置特征。对大规模路网数据，可对路网进行瓦片剖分（如，HERE的瓦片剖分）以提高计算效率、降低计算复杂度。路段坐标表示为路网瓦片地理范围内归一化的起始点坐标(x, y)。而路段方位角度可通过起始点位置到路网瓦片边界的夹角来确定，如图4所示。
图4 图节点路段的位置特征示意图

Fig. 4 An illustration of location features of a road segment for a graph node

2.4 改进邻域聚合的道路图节点嵌入

道路图构建与特征提取将路网数据转化为图神经网络的有效输入数据。为获得有效的路网数据嵌入表示，还需选择图嵌入学习框架，并围绕路网匹配任务设计嵌入生成算法。根据图模型对模型训练时未见过的图数据的适用性，可将图嵌入学习框架分为直推型（transductive）和归纳型（inductive）。直推型图模型无法直接适用新的图拓扑结构，而以GraphSAGE为代表的归纳型图模型能够将提取的模式泛化到训练时未见过的图数据结构。对于路网匹配任务而言，模型需适用于不同地区、不同拓扑结构的路网数据，那么归纳型框架更具实用性。因此，本文选择GraphSAGE作为图神经网络的基础架构，并通过改进邻域聚合函数提升图神经网络对路网数据的表示性能。

2.4.1 GraphSAGE框架

GraphSAGE框架的主要目标是学习一个图节点嵌入的生成函数，这个函数通过采样和聚合节点的邻域特征信息来生成图节点的嵌入向量[28]。其中，采样通过随机游走算法从目标节点的邻域节点中随机抽取一定数量的节点，而聚合则利用预先定义的函数对节点的邻域样本的特征进行计算，逐步更新目标节点的嵌入向量，直到达到指定聚合深度（网络层数）。总体而言，GraphSAGE中的聚合操作允许模型从局部邻域中汇聚信息，提高对整个图结构的理解，从而更好地捕捉节点之间的复杂关系。
GraphSAGE图节点嵌入更新的公式可定义为：
h v k = f k W k ∙ A G G u ∈ N v h u k - 1 , h v k - 1
式中： h v 0是节点v的嵌入向量； h v k是节点v第k层的嵌入向量； N v是节点v的邻居节点集合； f k是激活函数； W k是可学习参数；k是网络层数（也可表示聚合器数量和权重矩阵的数量）；AGG是聚合函数，包括Mean、GCN、Pooling和LSTM共4种基本实现。经分析与实验，发现选用Mean聚合更有利于相邻道路信息的融合，这是因为路网匹配关系的判别受相邻道路共同特征的影响。不影响一般性，不同网络层采用同样的激活函数，即 f k = σ，其中 σ是sigmod激活函数。使用Mean聚合的节点嵌入更新公式为：
h v k = σ W k ∙ h v k - 1 + ∑ u ∈ N v h u k - 1 / 1 + N v
式中： N v表示节点v的邻居节点个数。
GraphSAGE支持无监督训练和有监督训练 2种方式。在进行训练前需要构建一个道路图，并根据任务确定训练集和验证集。然后进行邻居节点采样与特征聚合操作，更新节点信息。在训练过程中，还需要计算损失函数来衡量模型的性能。之后通过反向传播算法，根据损失函数的梯度更新模型参数。最后对模型进行评估并进行迭代，逐步接近最优结果。
GraphSAGE的无监督学习基于以下假设，节点v与其邻居u具有类似的嵌入，而与没有交集的节点n不相似，损失函数为：
L α e v   =   - l o g σ e v T e u - N ∙ E u n ~ P n u l o g σ - e v T e u n      
式中：ev是节点v生成的嵌入；节点u是节点v的邻居节点； u n ~ p n u表示负采样，意思是节点un是从节点u的负采样分布Pn采样得到的；N为采样样本数。

2.4.2 邻域聚合函数的改进

邻域聚合作为GraphSAGE框架计算目标节点嵌入向量的关键步骤，是改进GraphSAGE算法、提升其下游任务表现的重要方向[28]。对路网数据而言，路段的空间布局、道路等级等特征也为节点路段邻域聚合提供了重要参考。而传统的邻域聚合函数无法有效利用以上特征，导致路网结构要素的空间关系无法被GNN充分学习而导致匹配任务性能难以提升。为此，本文通过改进GNN邻域聚合函数，增强聚合函数对图节点及其邻居节点的空间关系和类型关系的刻画，实现路网结构图表示性能的提升。为此，本文通过改进邻域聚合函数，提高聚合操作对目标节点和邻居节点的空间关系、类型关系的刻画，实现路段表示性能的提升。
（1） 空间聚合
空间聚合是在邻域聚合函数中显式考虑目标节点路段和邻居路段的空间位置关系，以提升路段嵌入对其邻域空间布局的表示性能。由于GraphSAGE在处理空间数据时并不考虑数据的空间位置顺序[22]，部分学者通过人工设计空间特征作为图节点特征输入来弥补模型在描述这类结构特征上的不足[20]。这种建模方式需要获取相关的专家知识，也存在数据依赖性高、模型泛化能力弱的问题。在分子结构分析上，有学者提出空间图卷积（SGCN）[22]方法，让模型直接学习节点之间的空间权重来调整图卷积操作。受此类工作启发，本文在GraphSAGE邻域聚合（式（2））基础上，引入目标节点和邻居节点的空间位置关系描述，以更好地捕捉节点之间的空间关系。空间聚合函数可写为：
h v s k = σ W k ∙ h v s k - 1 + ∑ u ∈ N v h u s k - 1 p u - p v / 1 + N v
式中：pu和pv分别是节点u和v表示的路段中点的坐标；pu-pv表示节点间的空间关系，由节点位置欧式距离计算得到。
（2） 分类聚合
分类聚合是在邻域聚合函数根据目标节点和邻居节点对应路段的道路类型关系，来选取相同类型的邻居节点更新目标节点的嵌入表示。考虑到不同来源的路网数据的道路分类分级并不一定相同，本文将道路类型分为I型道路、II型道路与III型道路3类，以此提高分类聚合函数的适用性[29]。其中，I型道路包括高速公路、主要道路、次要道路以及三级道路等；II型道路包括住宅区道路、生活性街道、服务道路等；III型道路包括步行道路、人行道、自行车道等。本文在GraphSAGE邻域聚合（式（2））基础上，根据这3类道路类型过滤节点邻域中相同类型的路段用于目标节点嵌入的更新。分类聚合可写为：
h v p k = σ W k ∙ h v p k - 1 + ∑ u ∈ N v h ¯ u p k - 1 / 1 + N v
式中： h ¯ u p k - 1是与节点v具有相同道路类型的邻居节点u的第k-1层的嵌入向量；W（k）是可以被训练的参数。
（3） 混合聚合
混合聚合综合了空间聚合和分类聚合操作。首先在邻域聚合函数中显式考虑目标节点路段和邻居路段的空间位置关系，然后根据道路类型关系选取相同类型的邻居节点来更新节点的嵌入表示。混合聚合可写为：
h v s p k = σ W k ∙ h v s p k - 1 + ∑ u ∈ N v h ¯ u s p k - 1 p u - p v / 1 + N v

2.5 节点嵌入相似性度量

对参与路网匹配的路网数据，分别构建各自的道路图并提取特征，然后进行道路图节点嵌入学习。路段嵌入向量用于计算不同来源路网数据的路段相似性，通过比较路段相似性来寻找匹配路段。首先，计算不同来源路网数据的节点嵌入高维向量的距离dve。因嵌入向量维度较大，因此使用临近加权曼哈顿距离计算。然后，利用节点的连接距离d（如Hausdorff距离）计算节点权重系数w（式（8）），并对其进行归一化，得到w'。这是因为空间上距离较近的路段可能具有更强相关性，反之相关性则较低。经过对比，采用线性归一化能够获得较好的结果。最后得到节点对应路段的相似性度量（式（9））。
w = d / d 1 / d
s c o r e = 1 / 1 + d v e w '
式中：d为道路之间的Hausdorff距离。得到节点间的相似性后，可以通过比较相似性度量与预先设定的阈值，来确定路段匹配关系。若2个不同来源路网数据的节点相似度高于设定的匹配阈值，则2个节点对应的路段视为匹配，否则不匹配。对整个路网数据而言，遍历其所有路段进行相似性分析，以完成路网匹配任务。

3 实验及结果

3.1 实验数据及实验设置

3.1.1 实验数据

路网匹配实验选取德国安斯巴赫地区作为测试区域，测试地区面积约99.92 km2。路网数据源包括开放街道地图（OpenStreetMap，OSM）、TeleAtlas商业电子导航数据。其中，OSM是一个开源、可编辑的全球地理信息数据库[30]，包含道路、河流、建筑物等要素的矢量数据。测试区内，OSM包含6 258条道路，对原始数据进行预处理后共有12 785条 道路；TeleAtlas包含5 024条道路，经过预处理后有7 523条道路。为评估不同算法完成路网匹配的性能，本文通过人工比对矢量数据、对比参考高分辨率卫星遥感影像相结合的方式，构建了安斯巴赫OSM-TeleAtlas路网匹配真值。图5展示了测试区域OSM、TeleAtlas的数据。将2个路网数据叠置在一起，可见OSM数据比TeleAtlas数据包含更多的路段要素。
图5 测试区安斯巴赫的OSM和TeleAtlas路网数据对比

Fig. 5 Comparison of OSM and TeleAtlas road network data in the test area of Ansbach

3.1.2 实验设置

本文采用Python和TensorFlow实现了道路图构建与图嵌入算法，并在配置AMD EPYC 7352 24核处理器以及英伟达RTX A6000图形处理单元的计算机平台下完成了路网匹配实验。在道路图构建中，设置图节点邻域查询阈值为100 m。在特 征提取中，经多次实验比较，选择设置LSTM的批 次大小BS=128，序列长度SL=256，隐藏层尺寸HS=128和学习率LR=0.001。在图嵌入学习中，使用GraphSAGE无监督训练方法，采用随机游走算法生成训练数据样本，用于图嵌入模型训练[23]。经多次实验比较，选择设置GraphSAGE的隐藏层通道数HS=256，小批量大小MBS=512，学习率LR=0.000 01，邻域采样深度NSD=3，随机游走的步长WL=3和随机游走的步数NW=7。

3.2 实验结果

为验证本文方法的有效性，选取路网匹配经典算法限定笔划算法（DSO）[8]、直接应用图神经网络的图卷积网络方法（GCN）、本文参考的地理空间图嵌入方法（GraphSAGE，GS）[23]、和本文提出的改进邻域聚合图嵌入方法GS+S、GS+P、GS+SP（分别表示在GS框架上使用空间聚合函数、分类聚合函数、混合聚合函数）进行实验对比。实验中，图神经网络方法（包括基线方法GS、GCN）和本文方法都使用相同图节点初始特征。

3.2.1 实验评估指标

实验指标采用匹配正确率（accuracy）、召回率（recall）和匹配成功率（match），计算方法为：
a c c u r a c y = 1 - b / a - c
r e c a l l = a - b - c / d
m a t c h = a - c / a
式中：a代表实验区域总路段要素数量；b代表错误匹配的路段要素数量；c代表匹配失败（即找不到匹配路段）的路段要素数量；d代表实际应匹配的路段要素数量。

3.2.2 模型参数选择

在进行路网嵌入匹配时，判别路段相似性的匹配阈值参数会影响最终的路网匹配结果。为此，首先通过实验比较选取最佳匹配阈值设置。如图6所示，提高匹配阈值，模型匹配正确率会随之上升，但召回率会降低；反之亦然。根据不同阈值下的计算指标综合考量，将节点匹配相似度的阈值设为0.6，此时不但具有较高的正确率和召回率，而且性能全面优于DSO方法。
图6 不同阈值下不同方法的匹配正确率及召回率

Fig. 6 Matching accuracy and recall of different methods using varying thresholds

此外，道路图构建中节点邻域的搜索范围、图嵌入学习的邻域采样深度也会影响模型性能，本文对这2个参数设置进行了比较分析。实验结果如 图7所示。对邻域的搜索范围而言，过大或过小都不利于节点特征的获取，会使匹配结果的正确率降低。邻域的搜索范围的设定受数据中道路长度影响，在测试区域的实验数据上设置邻域的搜索范围为100 m可以获得最优性能。对邻域采样深度而言，采样深度的增加虽然会扩大表示学习的范围与信息传递的深度，但会增加运算时间。因此要做好它们2个之间的平衡，过大或过小都不利于性能的提升。可以看到，在测试区域的实验数据上设置邻域采样深度为3时性能最好。
图7 不同邻域的搜索范围和邻域采样深度设置下的混合聚合方法(GS+SP)匹配正确率

Fig. 7 Matching accuracy of the hybrid aggregation method (GS+SP) under different neighborhood ranges and sampling depths

3.2.3 实验结果分析

GS+SP方法经过1 153个训练周期后，训练集和验证集的损失和精度趋于收敛。训练集和测试集的正确率分别为93.63%和87.27%，召回率为92.02%和84.37%，其混淆矩阵如表1所示。可看出，训练得到的网络具有较强的泛化能力和良好的实用性。
表1 基于混合聚合方法（GS+SP）的路网匹配混淆矩阵

Tab. 1 Confusion matrix for road network matching based on the hybrid aggregation method (GS+SP)

实际匹配道路 实际未匹配道路
预测匹配道路 2 928（58.28） 426（8.48）
预测未匹配道路 542（10.78） 1 128（22.46）

注： 括号外数字是符合行标题和列标题的结果数目/个，括号内是这个数字在全部结果中对应的占比/%。

表2给出了本文方法（GS+S、GS+P、GS+SP）与DSO、GCN、GS3种基线方法的实验对比。可以看出，相比GS以及GCN方法，DSO方法不管是正确率还是召回率性能都是最优的，因此直接应用图神经网络算法无法取得最优结果。本文提出的GS+S以及GS+P方法的性能相比GS有很大的提升，而且正确率超过DSO方法，但召回率和匹配成功率略有不足。而GS+SP方法各项指标全面超过3种基线方法，充分证明了方法的有效性。通过比较GS+S、GS+P和GS+SP共3种改进邻域聚合的路网嵌入匹配方法，可以看出不同聚合方式对实验结果的贡献并不相同。其中，GS+S相比GS方法正确率有很大提升，但召回率并无明显变化，因此验证了加入路段空间关系的空间聚合能够有效提升匹配正确率。而GS+P相比GS方法虽然正确率有提升，但对召回率的贡献更大，有效验证了分类聚合对性能的提升，尤其是对召回率的贡献。GS+SP方法的正确率与召回率相比其他方法都有提升，综合了前2种方法，充分证明了混合聚合对性能提升的贡献。
表2 本文路网嵌入匹配算法与基线算法的性能比较

Tab. 2 Performance comparison between the proposed methods and the baseline methods (%)

指标 DSO GCN GS GS+S GS+P GS+SP
匹配正确率 81.25 76.21 75.66 87.21 82.87 87.27
召回率 82.60 76.24 77.51 77.87 81.46 84.37
匹配成功率 73.87 68.21 69.31 69.67 72.89 75.26
为理解GS+SP的有效性，本文对路网匹配结果进行了可视化。如图8所示，本文算法可以有效匹配不同来源的路网数据。其中，在交叉路口、网格路段等较为复杂的路段，算法都能成功实现路网匹配，如图8（a）和图8（b）所示。其中不同颜色路网之间的黑色箭头为本文方法计算得到的路段间的匹配关系。但对于路网结构差异大的路段，算法未能有效匹配，如图8（c）中圆圈所示。
图8 测试区域OSM和TeleAtlas路网匹配结果可视化

Fig. 8 Visualization of the matching results between OSM and TeleAtlas road networks in the test area

为分析本文路网嵌入匹配方法对比基线方法的优势特点，本文比较了典型路网结构下的路网匹配结果差异。表3展示了不同匹配算法下路网间匹配关系的可视化结果，不同颜色路网间的黑色箭头代表了对应方法找到的正确的路段匹配关系，绿色箭头代表的是错误的匹配关系，用红色圆圈进行了标注。可以看到，样本道路1是高速公路，存在较多的平行路段，除了GS+SP和GS+S，其他方法都存在错误匹配，这是因为平行路段距离较近，导致错误的把不同数据中距离近的路段认定为匹配路段，没有完全考虑路段的空间关系。样本道路2和样本道路3是乡镇道路，存在较多的交叉路段，其中DSO、GCN和GS方法存在较多问题，不仅出现错误匹配路段，还存在漏匹配情况，而本文提出的3种方法在这个样本路段下均具有较好的结果。样本道路4和样本道路5是社区街坊道路，存在不同程度的格网结构，除了GS+SP和GS+S，其他方法均存在一定数量的错误匹配结果，这是由于不同数据中存在距离较近的非匹配路段，影响匹配结果的判断。综上所述，DSO、GCN、GS以及GS+P方法在复杂路段下易发生错误匹配问题，尤其当存在一对距离很近的路段时，易将其误判为匹配道路。GCN、GS和GS+S方法会错误判定距离较远的路段无法匹配。GS+S和GS+SP方法能够很好地区分复杂路段下的匹配关系，而且GS+SP方法也能够成功匹配一些距离较远的路段。
表3 本文路网嵌入匹配算法与基线算法在典型路段下的路网匹配结果比较

Tab. 3 Comparison of the road network matching results between the proposed embedding-based road network matching algorithms and the baseline algorithms on the typical road segments

综上所述，本文方法能够在乡镇道路、社区街坊道路等呈现复杂路网结构的路段上找到不同数据源的同名道路，在匹配准确率和召回率上表现更优。相比传统路网匹配方法，本文方法仅使用路网数据的基础属性信息，并通过GNN自动学习的路网结构特征，实现了路网匹配任务的性能提升；相比GNN路网匹配方法，本文方法在GNN初始特征相同的条件下，通过改进邻域聚合函数，实现了匹配准确率的显著提升。

4 讨论

4.1 特征消融实验

本文在路网匹配GNN建模（包括基线GCN、GS方法和本文提出的GS+S、GS+P、GS+SP方法）中，都使用了路段的几何、语义及位置特征。为理解这3类特征对GNN路网匹配算法表现的影响，进行了特征消融实验，即依次移除位置、语义、几何特征，比较GNN路网匹配算法的匹配正确率和召回率，如图9所示。
图9 道路网3类特征的消融实验结果

Fig. 9 Results of the ablation study on the three types of road network features

实验表明，所有GNN方法在不使用全部特征的情况下，匹配正确率以及召回率均有不同程度的下降。GCN、GS和GS+P共3种方法，在只使用“几何+语义”特征时，正确率降幅最小；使用“语义+位置”特征时，正确率降幅最大。因此，可以看出道路的位置特征对于GNN匹配性能影响较小，而几何特征影响较大。而GS+S和GS+SP方法在只使用“几何+位置”特征的情况下，正确率降幅最小，可见位置特征在这2种方法中的作用有明显提高。这是因为这两种方法都使用了空间邻域聚合，在节点嵌入计算过程中利用了道路的空间关系。从特征对召回率的影响可以看出，几种方法有大致相同的性能变化趋势，但GS+P以及GS+SP方法在只使用“几何+语义”特征与只使用“语义+位置”特征时的性能相对另外几种方法有明显提升，这是因为这 2种方法使用了分类邻域聚合，在节点嵌入计算过程中利用了道路的语义特征。

4.2 路网嵌入可视分析

为深入理解不同图嵌入算法的嵌入质量，本文利用高维数据降维算法t-SNE[31]对路网数据的路段嵌入向量进行可视化，并实现了路段嵌入可视化与路网数据的联动可视分析，用于分析路段嵌入向量分布与路网数据特征之间的联系。
如表4所示，GCN、GS以及本文提出的改进邻域聚合的GS+S、GS+P、GS+SP算法的路段嵌入结构及其嵌入样本效果存在明显差异。在路段嵌入结构上，GCN和本文方法都表现出多中心聚集结构，但在聚集的中心数量、聚集程度和空间分布上存在差异。GCN和GS+P表现出较强的聚集结构（蓝色较深的聚集块），而GS+S和GS+SP则表现出相对平均的聚集程度，但聚集范围内存在明显的带状间隔。GS的路段嵌入结果表现出和GS+方法完全不同的嵌入结构，GS嵌入结果呈现条带状的均匀分布。
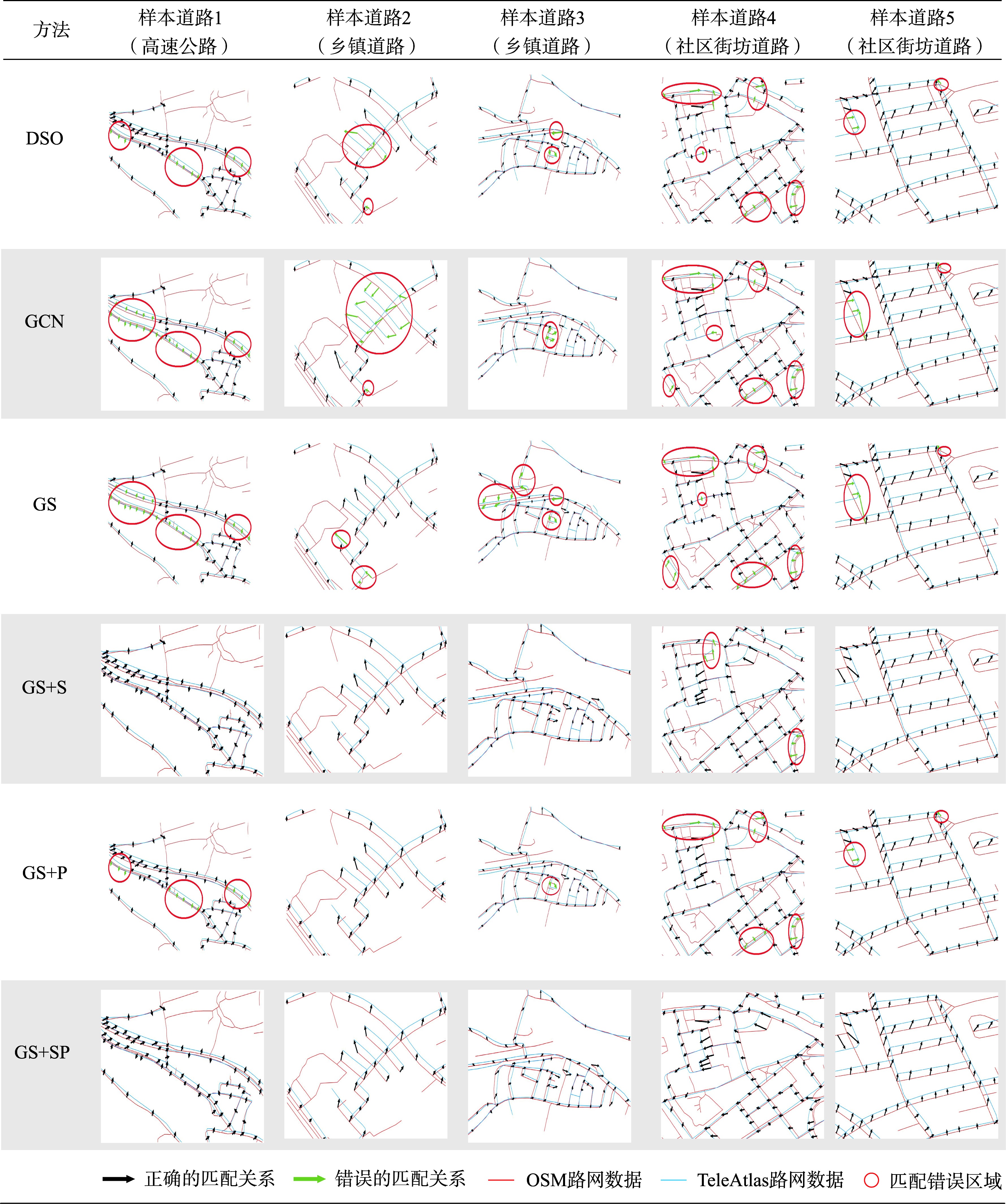表4 本文方法及图神经网络基线方法的典型路网结构嵌入比较

Tab. 4 Comparison of the typical road network structure embeddings between the proposed methods and the baseline methods using graph neural network

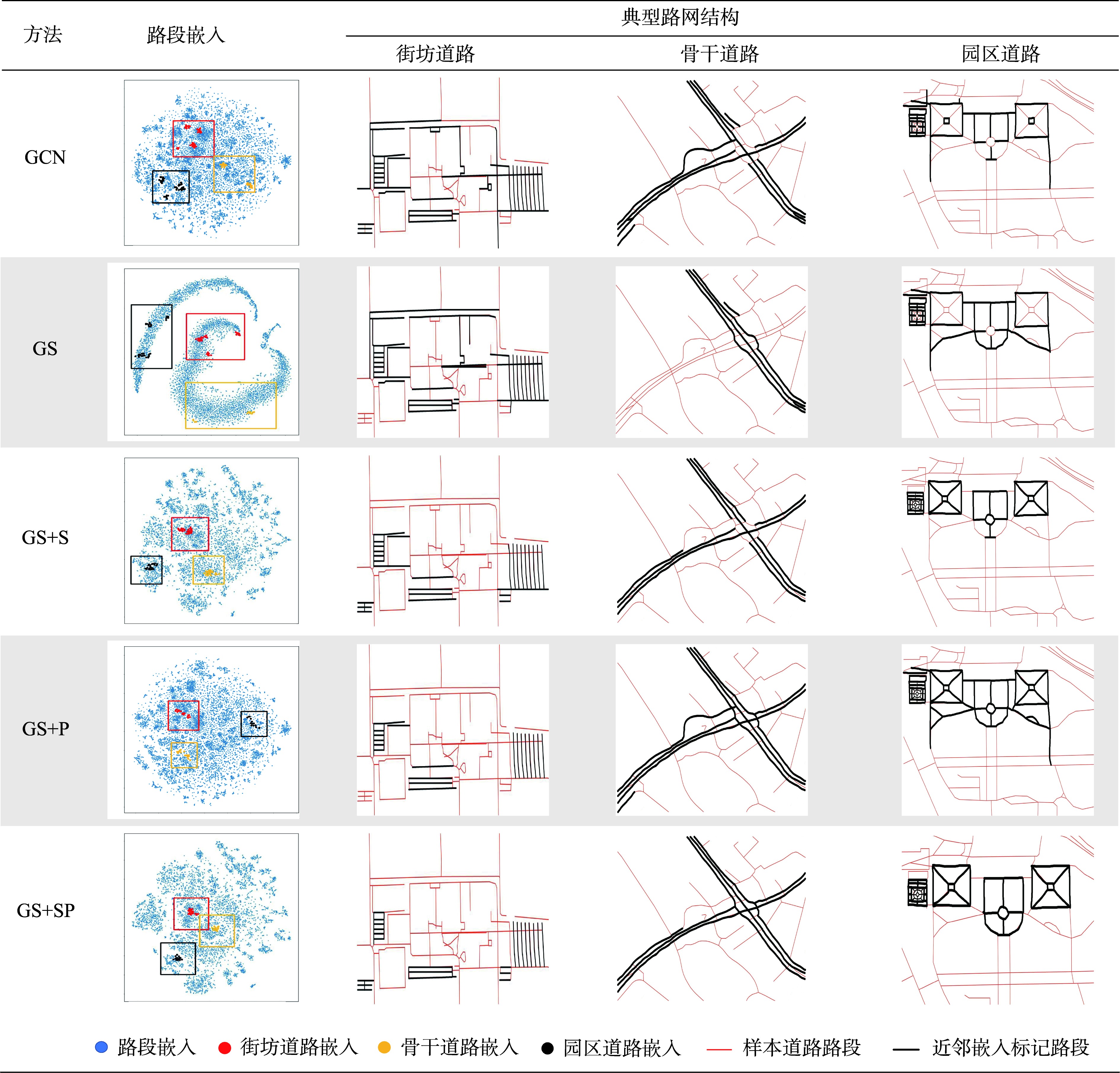注：在嵌入可视化中，通过K近邻方法检索典型路网结构的路段嵌入点（街坊道路、骨干道路、园区道路分别用红、黄、黑色高亮显示，并用相应颜色的线框表示该类路段嵌入分布范围）。在路网地图中，检索结果在原始路网数据（红色线段）上进行高亮标记（黑色线段）。

在典型路网结构嵌入效果上，本文选取了街坊道路、骨干道路（及交叉口）以及园区道路3种样本路网结构，来考察其中包含的梳形道路、骨干道路和对称结构道路等模式道路的嵌入邻近性。模式道路的嵌入邻近性一定程度上刻画了图神经网络对路网结构模式的表示能力。换句话说，每个路段在道路图拓扑结构上通过邻域聚合获得邻域特征信息时，能否学习到其与邻居路段共同表达的路网结构模式，并在路段嵌入中获得相比其他路网结构模式更为邻近的嵌入表征。为此，本文设计了一个路网结构K近邻嵌入检索方法。首先，在路段嵌入中定位样本路网结构的全部路段（每个路段对应一个蓝色点），标记路段嵌入对应的样本道路类型，并绘制每类样本路网结构的路段嵌入点的最小外接矩形框，以标识其路段嵌入分布范围。然后，检索路段嵌入的K近邻（K=5）节点嵌入，从中查找含有相同样本路网结构标记的嵌入点，标记为样本路网的近邻嵌入。其中，街坊道路、骨干道路和园区道路分别用红、黄、黑色表示。最后，将标记为近邻嵌入节点对应的路段在样本路网中标记为黑色。可以看到，GCN和GS方法的图节点嵌入存在2个以上的聚集结构，且聚簇分布较为分散。而在样本路网中被（黑色）标记的路段中，3类典型路网结构均出现模式道路结构在近邻嵌入中无法完整表达或表达出现混杂的情况（即检索结果出现非模式道路）。相比之下，本文提出的3种方法的路段嵌入呈现单一聚集结构。在样本路网中（黑色）标记的路段中，GS+S和GS+P在模式道路表达上有所提升，但仍存在局部表达不完整和混杂的情况，而GS+SP对模式道路的表达最为完整且混杂道路较少。GS+SP也存在部分路段表示不完整的情况，这种情况在GS+P得以避免却在GS+S存在，这是因为空间聚合操作较好保持了路段要素的几何形态，却未对其空间连续关系进行直接表达，导致形态变化较大的路段未得到近邻嵌入表示。不同方法计算的路网嵌入对路网结构表示能力总结如 表5所示。
表5 不同方法计算的路网嵌入的路网结构表示能力比较

Tab. 5 Comparison of the structural expressive power of road network embeddings computed using different methods

路网嵌入 路段嵌入降维
分布结构		 模式道路结构表示能力
街坊道路 骨干道路 园区道路
GCN 多中心聚集，局部聚集性强，簇集间隔小 聚簇分散
表示不完整、混杂		 聚簇分散
表示不完整、混杂		 聚簇分散
表示不完整、混杂
GS 条带均匀分布 聚簇分散
表示不完整、混杂		 聚簇分散
表示不完整、混杂		 聚簇分散
表示不完整、混杂
GS+S 多中心聚集，簇集间隔大 聚簇集中
表示较完整、局部混杂		 聚簇集中
表示局部不完整
 聚簇集中
表示局部不完整
GS+P 多中心聚集，局部聚集性强，簇集间隔小 聚簇较集中
表示局部不完整、局部混杂		 聚簇较集中
表示完整、局部混杂		 聚簇较集中
表示完整、局部混杂
GS+SP 多中心聚集，簇集间隔大 聚簇集中
表示完整
 聚簇集中
表示局部不完整
 聚簇集中
表示完整

注：颜色越深意味着路网嵌入的结构表示能力越强。 弱 中 强

综上所述，通过特征消融实验以及嵌入可视化分析，从特征作用和嵌入质量2个方面，探讨了本文提出的改进邻域聚合方法对GNN路网结构表示性能提升的作用，验证了本文方法的有效性。

5 结论

本文面向路网匹配，提出了一种基于GraphSAGE图嵌入学习框架的路网建模与匹配方法。该方法采用空间显式的建模思想，提出利用道路空间、类型信息的图节点嵌入更新方式，通过改进图神经网络的邻域聚合函数，在图嵌入学习阶段增强聚合运算对空间关系和道路类型的处理利用，提高图神经网络对路网复杂结构的表示能力，进而提升基于图神经网络进行路网匹配的性能。利用真实路网数据开展了多源路网匹配实验，结果表明本文方法在匹配正确率、召回率和匹配成功率指标上优于经典的限定笔划路网匹配算法、基线图神经网络（GCN和GraphSAGE）路网匹配算法。相比基线图神经网络方法，本文方法在实验区数据上，匹配正确率提升11%以上，召回率提升6.8%以上。本文方法在网格路段、平行路段等较为复杂的环境下均有良好的表现。通过对图神经网络方法的路网图嵌入结构和嵌入样本道路进行对比分析，发现性能较好的图神经网络模型能够将具有类似特征的道路生成的嵌入聚集在一起。本文研究为路网匹配任务提供了一种有效的图嵌入学习框架方法，验证了空间显式模型可显著提升路网匹配性能；也从图嵌入结构分析的角度，为图神经网络的路网数据建模与表示以及路网匹配以外的下游任务提供了新的研究视角。
考虑到路网匹配算法的表现受实验区、数据源等实验设置的影响，本文方法在实验区以外地区的算法性能有待检验。后续研究将构建大规模道路网匹配测试数据集，为提高本文在典型道路网数据场景下的适用性开展实验研究。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
王玉竹, 闫浩文, 禄小敏. 面向路网匹配的层次化语义相似性度量模型[J]. 地球信息科学学报, 2023, 25(4):714-725.

DOI

[Wang Y Z, Yan H W, Lu X M. Hierarchical semantic similarity metric model oriented to road network matching[J]. Journal of Geo-information Science, 2023, 25(4):714-725.] DOI:10.12082/dqxxkx.2023.220901

[2]
陈万鹏, 崔虎平. 基于相似性度量的城市路网实体匹配算法[J]. 测绘与空间地理信息, 2018, 41(12):39-42,46.

[Chen W P, Cui H P. Urban road network entity matching algorithm based on similarity measurement[J]. Geomatics & Spatial Information Technology, 2018, 41(12):39-42,46.] DOI:10.3969/j.issn.1672-5867.2018.12.011

[3]
刘闯, 钱海忠, 王骁, 等. 顾及上下级空间关系相似性的道路网联动匹配方法[J]. 测绘学报, 2016, 45(11):1371-1383.

DOI

[Liu C, Qian H Z, Wang X, et al. A linkage matching method for road networks considering the similarity of upper and lower spatial relation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11):1371-1383.] DOI:10.11947/j.AGCS.2016.20160062

[4]
吴冰娇, 王中辉, 杨飞. 用于多尺度道路网匹配的语义相似性计算模型[J]. 测绘科学, 2022, 47(3):166-173.

[Wu B J, Wang Z H, Yang F. A semantic similarity computational model for multi-scale road network matching[J]. Science of Surveying and Mapping, 2022, 47(3):166-173.] DOI:10.16251/j.cnki.1009-2307.2022.03.022

[5]
赵云鹏, 孙群, 刘新贵, 等. 面向地理实体的语义相似性度量方法及其在道路匹配中的应用[J]. 武汉大学学报(信息科学版), 2020, 45(5):728-735.

[Zhao Y P, Sun Q, Liu X G, et al. Geographical entity-oriented semantic similarity measurement method and its application in road matching[J]. Geomatics and Information Science of Wuhan University, 2020, 45(5):728-735.] DOI:10.13203/j.whugis20190039

[6]
Zhang M, Shi W, Meng L. A generic matching algorithm for line networks of different resolutions[C]// Workshop of ICA Commission on Generalization and Multiple Representation Computering Faculty of a Coruña University-Campus de Elviña, Spain. 2005,9:101-110.

[7]
王昊, 翟仁健, 周明辉, 等. 一种基于复杂网络的道路匹配方法[J]. 测绘科学技术学报, 2016, 33(1):88-93.

[Wang H, Zhai R J, Zhou M H, et al. A road matching method based on complex networks[J]. Journal of Geomatics Science and Technology, 2016, 33(1):88-93.] DOI:10.3969/j.issn.1673-6338.2015.06.017

[8]
张猛, 吴巧丽, 钱海忠. 一种适用于多源道路网自动匹配的通用算法[J]. 测绘科学技术学报, 2018, 35(1):82-86.

[Zhang M, Wu Q L, Qian H Z. A generic algorithm for automatic road-network matching between different datasets[J]. Journal of Geomatics Science and Technology, 2018, 35(1):82-86.] DOI:10.3969/j.issn.1673-6338.2018.01.016

[9]
Almotairi M, Alsahfi T, Elmasri R. Using local and global divergence measures to identify road similarity in different road network datasets[C]// Proceedings of the 11th ACM SIGSPATIAL International Workshop on Computational Transportation Science. ACM, 2018:21-28. DOI:10.1145/3283207.3283214

[10]
秦育罗, 宋伟东, 张在岩, 等. 顾及几何特征和拓扑连续性的道路网匹配方法[J]. 测绘通报, 2021(8):55-60.

DOI

[Qin Y L, Song W D, Zhang Z Y, et al. Matching method for road networks considering geometric features and topological continuity[J]. Bulletin of Surveying and Mapping, 2021(8):55-60.] DOI:10.13474/j.cnki.11-2246.2021.0240

[11]
Li L N, Goodchild M F. An optimisation model for linear feature matching in geographical data conflation[J]. International Journal of Image and Data Fusion, 2011, 2(4):309-328. DOI:10.1080/19479832.2011.577458

[12]
黄智深, 钱海忠, 王骁, 等. 基于降维技术的面状居民地匹配方法[J]. 测绘科学技术学报, 2012, 29(1):75-78.

[Huang Z S, Qian H Z, Wang X, et al. Dimension decrease-oriented habitation matching method[J]. Journal of Geomatics Science and Technology, 2012, 29(1):75-78.] DOI:10.3969/j.issn.1673-6338.2012.01.018

[13]
杨东凯, 寇艳红, 吴今培, 等. 智能交通系统中的地图匹配定位方法[J]. 交通运输系统工程与信息, 2003, 3(3):38-43.

[Yang D K, Kou Y H, Wu J P, et al. A Map-matching method in Intelligent Transport Systems[J]. Journal of Transportation Systems Engineering and Information, 2003, 3(3):38-43.] DOI:10.16097/j.cnki.1009-6744.2003.03.008

[14]
Sun Y, Lu Y F, Ding Z Q, et al. Multi-scale road matching based on the summation product of orientation and distance and shape descriptors[J]. ISPRS International Journal of Geo-Information, 2023, 12(11):457. DOI:10.3390/ijgi12110457

[15]
齐杰, 王中辉, 李驿言. 基于图卷积神经网络的道路网匹配[J]. 测绘通报, 2023(12):19-24,44.

DOI

[Qi J, Wang Z H, Li Y Y. Road network matching based on graph convolutional neural network[J]. Bulletin of Surveying and Mapping, 2023(12):19-24,44.] DOI:10.13474/j.cnki.11-2246.2023.0353

[16]
艾廷华. 深度学习赋能地图制图的若干思考[J]. 测绘学报, 2021, 50(9):1170-1182.

DOI

[Ai T H. Some thoughts on deep learning enabling cartography[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(9):1170-1182.] DOI: 10.11947/j.AGCS.2021.20210091

[17]
王米琪, 艾廷华, 晏雄锋, 等. 图卷积网络模型识别道路正交网格模式[J]. 武汉大学学报(信息科学版), 2020, 45(12):1960-1969.

[Wang M Q, Ai T H, Yan X F, et al. Grid pattern recognition in road networks based on graph convolution network model[J]. Geomatics and Information Science of Wuhan University, 2020, 45(12):1960-1969.] DOI:10.13203/j.whugis20200022

[18]
Guo K, Hu Y L, Qian Z, et al. Optimized graph convolution recurrent neural network for traffic prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(2):1138-1149. DOI:10.1109/TITS.2019.2963722

[19]
Yang M, Jiang C J, Yan X F, et al. Detecting interchanges in road networks using a graph convolutional network approach[J]. International Journal of Geographical Information Science, 2022, 36(6):1119-1139. DOI:10.1080/13658816.2021.2024195

[20]
Yu H F, Ai T H, Yang M, et al. A graph autoencoder network to measure the geometric similarity of drainage networks in scaling transformation[J]. International Journal of Digital Earth, 2023, 16(1):1828-1852. DOI:10.1080/17538947.2023.2212920

[21]
Yu H F, Ai T H, Yang M, et al. Automatic segmentation of parallel drainage patterns supported by a graph convolution neural network[J]. Expert Systems with Applications, 2023,211:118639. DOI:10.1016/j.eswa.2022.118639

[22]
Danel T, Spurek P, Tabor J, et al. Spatial graph convolutional networks[C]// International Conference on Neural Information Processing. Cham: Springer, 2020:668-675. DOI:10.1007/978-3-030-63823-8_76

[23]
Soni A, Boddhu S. Finding map feature correspondences in heterogeneous geospatial datasets[C]// Proceedings of the 1st ACM SIGSPATIAL International Workshop on Geospatial Knowledge Graphs. ACM, 2022:7-16. DOI:10.1145/3557990.3567590

[24]
黄博华, 钟巍, 翟仁健, 等. 城市道路网匹配的层次化面域剖分模型[J]. 测绘学报, 2018, 47(11):1526-1536.

DOI

[Huang B H, Zhong W, Zhai R J, et al. Hierarchical area partitioning method of urban road networks matching[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(11):1526-1536.] DOI:10.11947/j.AGCS.2018.20170699

[25]
Bentley J L. Multidimensional binary search trees used for associative searching[J]. Communications of the ACM, 1975, 18(9):509-517. DOI:10.1145/361002.361007

[26]
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8):1735-1780. DOI:10.1162/neco.1997.9.8.1735

PMID

[27]
Wu Z R, Xiong Y J, Yu S X, et al. Unsupervised feature learning via non-parametric instance discrimination[C]// 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. IEEE, 2018:3733-3742. DOI:10.1109/CVPR.2018.00393

[28]
Hamilton W L, Ying R, Leskovec J. Inductive representation learning on large graphs[C]// Proceedings of the 31st International Conference on Neural Information Processing Systems. ACM, 2017:1025-1035. DOI:10.5555/3294771.3294869

[29]
Zuo Z J, Yang L, An X Y, et al. A hierarchical matching method for vectorial road networks using delaunay triangulation[J]. ISPRS International Journal of Geo-Information, 2020, 9(9):509. DOI:10.3390/ijgi9090509

[30]
Goodchild M F. Citizens as sensors: The world of volunteered geography[J]. GeoJournal, 2007, 69(4):211-221. DOI:10.1007/s10708-007-9111-y

[31]
Van Der Maaten L, Hinton G E. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008,9:2579-2605.

Options
文章导航

/

〈 〉