EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 10: 2364 - 2383

DOI: https://doi.org/10.12082/dqxxkx.2024.240423

专栏：“GIS 与未来城市交通”

结合路段和网眼结构的路网模式识别方法

  • 张志义 , 1, 2, 3 ,
  • 禄小敏 , 1, 2, 3, * ,
  • 宋浩然 1, 2, 3 ,
  • 闫浩文 1, 2, 3 ,
  • 王利娟 1, 2, 3
展开
  • 1.兰州交通大学测绘与地理信息学院，兰州 730070
  • 2.地理国情监测技术应用国家地方联合工程研究中心，兰州 730070
  • 3.甘肃省测绘科学与技术重点实验室，兰州 730070
* 禄小敏（1982— ），女，甘肃陇西县人，博士，副教授，研究方向为空间关系及地图制图综合。E-mail:

张志义（2000— ），男，甘肃甘南藏族自治州人，硕士生，研究方向为模式识别。E-mail:

Copy editor: 蒋树芳 , 黄光玉

收稿日期: 2024-07-29

  修回日期: 2024-09-03

  网络出版日期: 2024-10-09

基金资助

国家自然科学基金项目(42161066)

国家自然科学基金青年基金项目(41801395)

国家自然科学基金重点项目(41930101)

自然资源部城市国土资源监测与仿真重点实验室开放基金资助课题(KF-2022-07-015)

收起

A Pattern Recognition Method for Road Network Combining Road Sections and Mesh Structures

  • ZHANG Zhiyi , 1, 2, 3 ,
  • LU Xiaomin , 1, 2, 3, * ,
  • SONG Haoran 1, 2, 3 ,
  • YAN Haowen 1, 2, 3 ,
  • WANG Lijuan 1, 2, 3
Expand
  • 1. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China
  • 2. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, Lanzhou 730070, China
  • 3. Key Laboratory of Science and Technology in Surveying & Mapping, Gansu Province, Lanzhou 730070, China
* LU Xiaomin, E-mail:

Received date: 2024-07-29

  Revised date: 2024-09-03

  Online published: 2024-10-09

Supported by

National Natural Science Foundation of China(42161066)

National Natural Science Foundation of China - Youth Fund(41801395)

Key Program of Natural Science Foundation of China(41930101)

Open Fund of Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Natural Resources(KF-2022-07-015)

Fold

摘要

道路网具有鲜明的空间分布模式，其模式识别在地图制图、地图匹配及空间查询等诸多领域均发挥着至关重要的作用。当前的路网模式识别方法多基于网眼结构与路段结构两种模型，取得了较好的识别效果，但亦存在一定局限。已有的基于网眼的识别算法往往局限于最小单元的格网模式，无法对整体规则、局部破碎的网眼群组进行模式识别；而基于路段结构的模式识别则涉及复杂的预处理与识别过程，并且仅能识别单一的路网模式。方向熵作为信息熵的一个分支，可以较好地描述地理数据的空间分布特征和规律。为此，本文结合了网眼结构在网眼规整情况下的识别优势和路段结构在分析路段排列方式方面的优势，在此基础上引入方向熵、矩形度和凹凸度等特征参量，构建了一种有效的路网模式识别算法。本文选取多个城市路网作为实验对象，通过计算出不同路网模式相对应的参量分类阈值，实现了格网模式和不规则模式路网的模式识别，且根据格网模式路网中网眼群组排列方式的不同，构建网眼质心最小生成树并使用方向熵将其细分为直线型网眼群组和格网型网眼群组。实验结果表明，结合路段和网眼结构的路网模式识别算法的模式分类精度达到了97%以上，能够有效完成典型路网模式的识别并较好地根据网眼群组的排列方式完成了格网模式的细分。与现有路网模式识别方法比较，本文构建了一种简单快速且较为精准的路网模式识别算法，为地图综合、模式识别和城市规划等领域的后续研究和应用提供了一种新的思路。

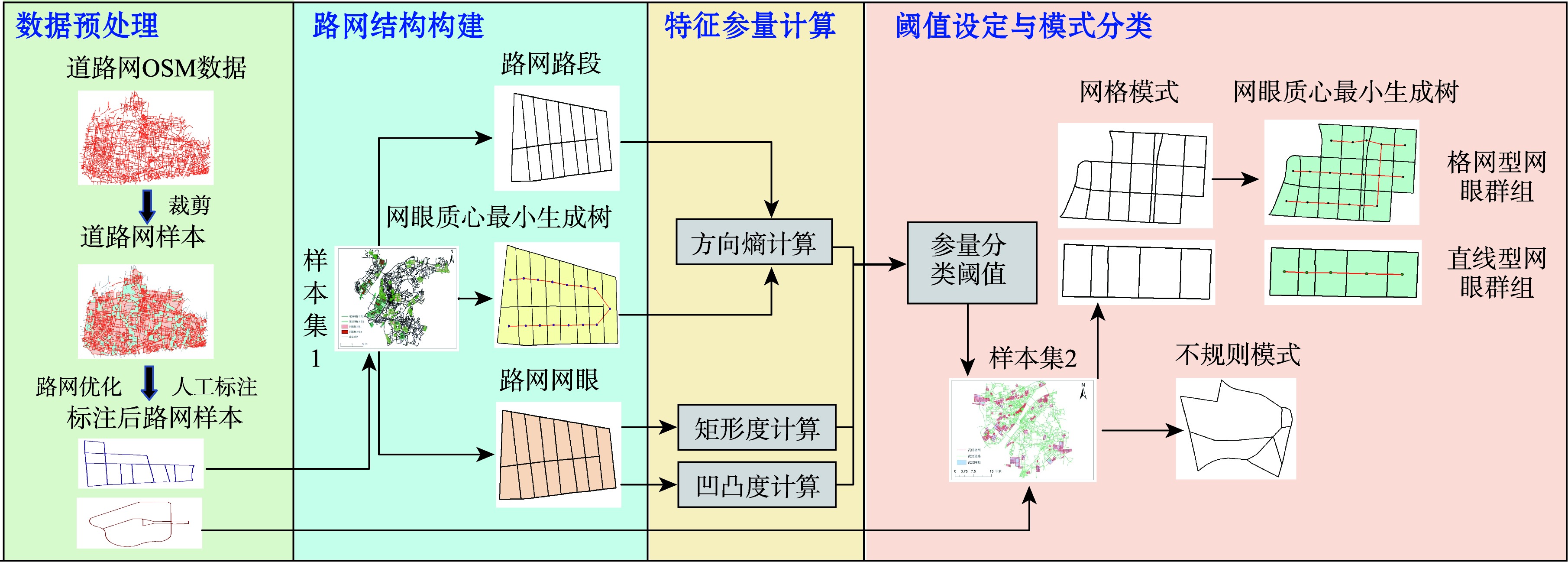
关键词： 模式识别; 方向熵; 格网路网; 不规则路网; 直线型网眼群组; 格网型网眼群组

本文引用格式

张志义 , 禄小敏 , 宋浩然 , 闫浩文 , 王利娟 . 结合路段和网眼结构的路网模式识别方法[J]. 地球信息科学学报, 2024 , 26(10) : 2364 -2383 . DOI: 10.12082/dqxxkx.2024.240423

Abstract

The road network has a distinct spatial distribution pattern, and its pattern recognition plays a crucial role in many fields such as mapping, map matching, and spatial queries. The current road network pattern recognition methods are mostly based on two models: mesh structure and road segment structure, which have achieved good recognition results, but also have certain limitations. Existing mesh based recognition algorithms are often limited to the grid pattern of the smallest unit, and cannot recognize patterns of globally regular and locally fragmented mesh groups; Pattern recognition based on road segment structure involves complex preprocessing and recognition processes, and can only recognize a single road network pattern. As a branch of information entropy, directional entropy can effectively describe the spatial distribution characteristics and patterns of geographic data. Therefore, this article combines the recognition advantages of mesh structure in the case of regular mesh and the advantages of road section structure in analyzing the arrangement of road sections. Based on this, feature parameters such as directional entropy, rectangularity, and concavity are introduced to construct an effective road network pattern recognition algorithm. This article selects the road networks of Wuhan, Shanghai, Nanjing, and Xi'an as experimental objects for sample construction. The sample sets of Nanjing and Xi'an are used to calculate the parameter classification thresholds corresponding to different road network modes and determine the road network pattern recognition rules. The sample sets of Wuhan and Shanghai are used to verify the feasibility and transferability of the algorithm proposed in this article. This method not only completes the pattern recognition of grid networks and irregular road networks, but also divides them into linear mesh groups and grid mesh groups based on the different arrangement of mesh groups in grid networks by constructing a minimum mesh centroid spanning tree and using directional entropy. The experimental results show that the pattern classification accuracy of the road network pattern recognition algorithm combining road segments and mesh structures reaches over 97%, which can effectively complete the pattern recognition of grid networks and irregular road networks, and can well subdivide grid patterns according to the arrangement of mesh groups in the grid network. The algorithm in this paper has good transferability and the recognition results are consistent with human cognition. Compared with existing road network pattern recognition methods, this paper constructs a simple, fast, and relatively accurate road network pattern recognition algorithm, providing a new approach for subsequent research in fields such as map synthesis, pattern recognition, and urban planning.

Key words： pattern recognition; directional entropy; grid road networks; irregular road networks; linear grid groups; grid-based grid groups

1 引言

道路网作为城市地理要素中必不可少的部分，其结构模式反映了城市的空间布局和规划风格、城市的地形地貌和功能结构[1⇓⇓-4]。道路网模式的挖掘与识别一直是相关学者研究的重要方向之一，路网模式的识别在地图制图、地图匹配、城市规划与发展等相关领域均有诸多应用[5⇓⇓⇓-9]。相关学者从不同角度出发，将道路网划分为不同的模式，典型的路网模式有辐射型路网模式[10]、格网型路网模式[11⇓⇓⇓-15]、环形路网模式[16⇓⇓⇓-20]以及不规则型路网模式等，格网模式和不规则模式的路网在宏观、中观、微观等多个层次的道路网中均为最常见的路网模式[21-22]。道路网闭合路段构成的网眼群组同样具备明显的空间分布模式，对网眼群组的模式识别有助于判别路网规整或混乱程度，根据网眼排列方式的不同，格网路网的网眼群组模式又可以分为直线型网眼群组和格网型网眼群组[23]。
纵观已有的路网研究，对于道路网格模式的识别主要分为基于路段和基于网眼2种方法。① 基于路段结构的路网模式识别。此类方法在构建路网图结构的基础上通过提取特征参量构建相关算法完成路网模式识别，如He[12]利用场的思想将道路网划分为一个个小的栅格单元，通过计算每个栅格单元的特征参量完成对道路网网格模式的识别；Heinzle等[18]利用霍夫变换方法完成道路网格网路段识别；He[24]通过对道路网进行线性剖分，使用支持向量机（Support Vector Machine, SVM）完成道路网格网模式识别；Wang等[13]通过计算路网节点之间的连接特征、形状特征和邻域特征，将这些特征参量带入图卷积网络（Graph Convolutional Network，GCN）中，以此完成道路网正交网格模式的识别。该类方法能够实现较高精度的路网模式识别，但是算法的预处理过程以及识别规则往往比较复杂，且已有的路段结构的模式识别算法无法顾及路网网眼的空间排列分布。② 基于网眼结构的路网模式识别。该类方法主要基于指标统计分类，如Yang等[25]根据道路网网眼的形状指标以及路网的方向特征完成了路网网格模式的识别，虽然该方法对形状不规则网眼的路网格网模式进行了识别，但是只能识别最小单元的网格；Tian[10-11,14-15]等基于道路网格式塔原则在道路网模式识别当中引入了机器学习，通过计算网眼的矩形度、凹凸度、方向一致性等参量指标，利用C4.5算法和主成分分析等方法完成了道路网格网模式的识别；Wang[23]通过设定多层次网眼的识别规则，完成了直线型网眼群组和格网型网眼群组的模式识别。此类方法往往只能识别最小单元下的格网模式，对整体规整、局部破碎的路网无法识别，且已有的网眼模式识别算法很少对网眼群组的排列方式进行研究。
综上所述，基于路段结构和网眼结构的方法均在一定程度上实现了道路网模式的识别，但仍然存在不足。而基于路段结构的识别方法针对整齐排列的路网识别效果较好，基于网眼结构的识别方法可较好地描述路网中任一网眼的规整情况以及网眼群组的空间分布规律。将以上两种结构结合，有望在充分考虑路网路段整体空间分布和网眼规整的情况下，完成从道路网整体模式到网眼群组排列模式的识别。
同时，方向熵作为信息熵的一种扩展[26]，常用于度量随机变量的“定向性”，是一种评价数据分布状况的指标，能够有效反映目标的空间分布规律，尤其对于结构化区域的识别效果更为明显[27]。与其他方法相比，方向熵的计算不需要事先设定阈值，因此也更加方便和灵活。它已经被应用于城市规划与分析等领域当中，如Peng[28⇓-30]将方向熵作为主要特征参量，通过判断聚落道路整体的混乱程度，进而反映出聚落道路网的空间秩序。将该指标应用到道路网模式识别中，通过对路网路段以及网眼群组几何模型结构进行方向熵计算，根据方向熵值的大小，可定量化描述路网路段及网眼群组的分布混乱和规整情况。
为此，本文将分别从道路网路段和网眼出发，引入方向熵作为路网的路段重要的参量描述，同时结合矩形度和凹凸度这2个关键指标来评价路网网眼的特性，构建一种结合路段和网眼结构的路网模式识别方法，完成对道路网的网格模式、不规则模式识别，以及路网中网眼群组的直线模式和格网模式识别。

2 研究方法

2.1 技术路线

本文旨在结合网眼结构和路网路段结构的优势，以实现路网和网眼群组模式的识别。由于城市路网中格网型、不规则型路网[10-11,13⇓-15]以及直线型、格网型网眼群组[23]最为常见，因此本文选取以上常见的路网模式进行识别。
算法流程如图1所示，其中包含道路网数据预处理、路网结构构建、特征参量计算、阈值设定与模式分类等步骤。
图1 融合路段和网眼的路网模式识别算法流程

Fig. 1 Algorithm flow for road network pattern recognition integrating road segments and grid networks

（1）数据预处理：从OpenStreetMap中获取道路网数据，并对其进行优化，包括道路网的删减和曲线化简，以提升路网模式识别的效率和数据的准确性。其次，对优化后的路网进行人工标注，将其划分为格网样本和不规则样本，而后根据网眼排列方式的不同将格网样本细化分为网眼格网模式和网眼直线模式，为后续路网特征的提取和计算奠定基础。
（2）路网结构构建：提取标注后样本的路段结构和网眼结构，在此基础上提取路网网眼的质心，根据Prim算法完成网眼质心最小生成树的构建。
（3）特征参量计算：根据提取的路段结构、网眼结构、网眼最小生成树结构，进行相对应的特征参量计算。对路段结构和网眼最小生成树结构进行方向熵计算，对网眼结构进行矩形度和凹凸度 计算。
（4）分类阈值设定和模式分类：将已构建好的样本划分为2个样本集：样本集1中的样本用于特征参量阈值统计，样本集2用于验证样本集1中所得的分类阈值是否能完成路网网格模式和不规则模式以及网眼群组的直线模式和格网模式分类。最后将分类结果与之前人工标注的结果进行对比，验证所得特征参量阈值进行模式分类是否能达到预期效果。

2.2 数据预处理

由于OpenStreetMap下载的道路网原始数据内部不仅包含了城市主干道路网，还包含了许多琐碎道路，诸如人行道和自行车道等。同时，道路网自身具有一定的曲线性，因此在实验开始前，先对道路网进行数据预处理，具体过程如下：
（1）将路网数据按照交叉点分割为多条路段；
（2）遍历整个道路网，将所有包含节点度为1的首尾节点的路段进行删除；
（3）遍历删减后的道路网，利用Douglas-Peucker算法对每条路段进行化简；
（4）优化结束。
图2（b）为路网优化过程中分割路段过程， 图2（c）为道路网多余路段删减过程，图2（d）为道路网道格拉斯普克算法优化过程。
图2 道路网样本集数据优化过程

Fig. 2 Data optimization process for road network sample set

2.3 网眼最小生成树构建

根据不同的路网模式，路网所包含的网眼群组的空间分布模式也不尽相同，其中格网路网的直线模式和网格模式是最常见的网眼群组的2种分布模式[23]，如图3（a）和图3（c）所示。
图3 直线型和格网型网眼群组及其最小生成树

Fig. 3 Linear and grid mesh groups and their minimum spanning trees

最小生成树（Minimal Spanning Tree）是将N个顶点通过N-1条边连接而成的权值最小无闭合连通子图。对于道路网眼模式识别而言，对网眼群组构建最小生成树具有以下优势： ① 将相邻的道路网眼相互连接起来，方便聚类描述； ② 通过构建网眼最小生成树可以较为直观地得出网眼群组的排列方式； ③ 通过构建网眼最小生成树将网眼群组原本的面状结构转换为边-节点结构，方便使用基于路段的模式识别方法快速高效地完成网眼群组的模式识别。
为将格网模式路网按照网眼群组的排列方式细分为直线型和格网型网眼群组，本文针对已标注为格网模式的路网构建网眼最小生成树，图4是基于Prim算法生成的直线模式和网格模式的道路网眼最小生成树，分析得出：① 直线型的网眼群组的最小生成树是一条直线，最小生成树每条边的方向集中（图3（b））；② 网格型的网眼群组的最小生成树是多条直线平行或正交斜交而成的，方向大都分布在2个方向上（图3（d））。
图4 路网网眼特征参量计算

Fig. 4 Calculation of feature parameters for the road network grid

2.4 特征参量计算

分别构建路网的路段结构、网眼结构和网眼最小生成树，并根据结构的不同提取对应的特征参量。其优势在于通过网眼结构可以顾及到每一个网眼的规整情况，通过路段结构和网眼最小生成树结构能够顾及到路网的整体排列方式。

2.4.1 针对网眼的特征参量提取与计算

格网路网和不规则路网的网眼结构的最大区别在于格网路网的网眼多为近似矩形和平行四边形，而不规则路网的网眼大都为形状混乱的多边形。为在网眼结构下区分路网网格模式和不规则模式，本次实验选择路网识别中最常见的矩形度和凹凸度2个网眼特征参量进行计算。
（1）矩形度。矩形度（Rectangularity, R）是指物体外形与矩形外形的相似程度，用于描述一个物体的形状规则程度。在路网中，矩形度通常是指道路网眼面积和网眼最小外接矩形面积的比值[29]，取值范围为(0,1]。如图4所示矩形度的计算方法，网眼矩形度越接近1，表示网眼越规则，越接近矩形形状；矩形度越趋于0，表示网眼越不规则，网眼无法趋近于矩形。
（2）凹凸度（Convexity, C）。凹凸度是一种描述多边形凹凸程度的特征参量，也用于描述事物趋近于四边形的程度。在道路网中，凹凸度通常是指道路网网眼面积与网眼所形成的凸壳面积的比值[30]，比值取值范围为(0,1]。如图4所示凹凸度的计算方法，凹凸度越接近于1就代表网眼的形状越规整，越趋近于四边形形状；反之，凹凸度越小，网眼形状越不规则。
对图5所示的格网路网和不规则路网提取 网眼并分别计算网眼的矩形度和凹凸度，发现 图5（a）的网眼的矩形度和凹凸度均趋近于1，而 图5（b）中的网眼的矩形度都小于0.75，有个别网眼凹凸度在0.5以下。
图5 格网网眼和不规则网眼

Fig. 5 Grid network and irregular network

2.4.2 针对边-节点结构的特征参量计算

从路段结构来看，不规则路网和格网路网最明显的区别在于，格网路网的路段排列规整，整体路网具有明显的方向性（理想情况下，格网路网的路段可划分为2个方向）；而不规则路网的路段排列混乱，路网中路段方向不一致。从网眼最小生成树结构来看，直线模式的网眼群组的最小生成树近似一条直线，而格网模式的网眼群组的最小生成树则由n个直线模式构成，均具有明确的方向关系。本文引入方向熵作为边-节点结构特征参量，借助其在描述数据空间分布方面的优势，对路网模式进行快速划分。
方向熵是一种用来反映数据方向分布情况的熵值。假设在空间中存在n个数据点，在使用经纬度或是xyz坐标表示这些空间点的方位时，若发现这些点呈现出特定的分布方向，则可以用方向熵来定量化描述这种方向性。将所有数据点排序之后按顺序计算所有相邻数据点之间的夹角，每一个夹角做为一个变量，以此得出变量的均衡分布程度，进而得出方向熵值。公式如下所示：
E N T R O P Y = - ∑ ( P i ) l o g 2 ( P i )
式中：Pi表示每个变量与所有变量之和的比值，如 式（2）所示。
P i = Y i Y s u m
当方向熵作用于路网模式识别时，对路网的路段结构和网眼质心最小生成树结构中的每条边分别确定一个相对的顺序，变量Yi表示每条路段通过首尾节点计算出的角度值，Ysum表示路网中所有路段角度的总和。如果所有变量Yi均匀分布，即在规定好相对坐标系以后，每一个角度均处于不同的划分区间中，方向熵就为最大值log2(Pi)，表示道路网中边的方向处于完全随机的状态，反之方向熵值越小，则表明道路网中存在明显的方向性，如图6所示。
图6 方向熵计算流程

Fig. 6 Directional entropy calculation process

道路网方向熵计算步骤如下：
（1）提取路网路段和网眼，并根据路网网眼构建网眼质心最小生成树模型；
（2）建立相对坐标系，选择一个道路路段作为起始边，将道路路网的首尾节点代入向量的点积公式计算得到每条道路路段的相对角度值；
θ = a r c t a n ( ( Y 2 - Y 1 ) / ( X 2 - X 1 ) ) · 180 ° π
式中：Y2和Y1是路段和最小生成树每条边的首尾节点处的纵坐标；X2和X1则表示横坐标；θ表示边的角度。
（3）遍历整个道路网，根据式（3）分别计算路网中每条路段以及网眼质心最小生成树每条边的角度值θ，并根据角度值之间的差异将其划分为多个Pi，在此基础上利用式（1）进行道路网方向熵值计算。
如图7（a）所示为网格模式道路网，首先提取路网路段并根据道路网眼的质心构建最小生成树，如图7（b）和图7（d）所示，其次统计路段和网眼最小生成树每条边的方向分布，如图7（c）和图7（e）所示，并根据式（1）来计算方向熵熵值，上图7中路网基于路段的方向熵熵值为1.153 1，而基于网眼质心最小生成树的方向熵熵值为0.991 0。
图7 道路网路段和网眼质心最小生成树分布

Fig. 7 Distribution map of minimum spanning tree of road network segments and grid centroids

2.5 道路网模式识别

在道路网的模式识别中，矩形度和凹凸度可用来描述路网中每一个网眼的规整情况，方向熵则可以用来描述路网中每条路段以及网眼质心最小生成树每条边的朝向和空间分布规律。

2.5.1 路网模式识别

不规则路网中路段的排列和空间分布较为随意。而格网型路网一般是由n条近似笔直的路段平行、垂直或斜交构建而成。以上两种路网模式从特征参量角度分析，具备以下特征：
（1） 由于不规则路网中路段排列混乱且方向分布复杂（图8（b）和图8（c）），因此不规则路网的方向熵熵值一般偏大，如图8（a）所示的不规则路网方向熵熵值为4.13；理想情况下的格网路网中所有路段的方向集中在2个方向上（图8（f）），方向熵熵值较小。若路网中相互垂直或斜交的路段数量相等，则方向熵值为1，如图8（d）所示，同时方向熵也可以应用于较大范围的路网格网模式识别中，如图8（g）所示，方向熵熵值为1.25；
图8 格网路网和不规则路网路段图和方向分布

Fig. 8 Grid network and irregular path network segment diagram and directional distribution

（2） 从网眼角度来看，不规则路网中网眼大多都为不规则的面状多边形结构，因此其矩形度和凹凸度数值偏小，如图8（a）所示路网网眼的矩形度最小值为0.45，凹凸度最小值为0.65；而格网路网中网眼形状大都为规整的四边形，因此格网路网中，每一个网眼的矩形度和凹凸度数值均趋近于1。图8（d）和图8（g）所示的2个格网路网包含的所有网眼的矩形度和凹凸度数值均在0.94以上。

2.5.2 网眼群组模式识别

根据格网模式路网包含的网眼群组排列方式的不同，又可将格网路网细分为由直线型排列（图9（a））或网格型排列(图9（c）)的网眼群组构成的格网路网。
图9 直线型和格网型网眼群组网眼质心最小生成树及方向分布

Fig. 9 Grid-type centroid minimum spanning tree and directional distribution map

（1） 在路网路段的约束下，直线型网眼群组包含网眼沿着一条明显的直线排列，并且通过对网眼提取质心构建的网眼最小生成树直接呈现出一条直线（图9（a））；格网型网眼群组模式最大的特点在于网眼按照相对固定的方向进行排列，通过网眼最小生成树可以明显看到其网眼最小生成树是由n条直线或平行或垂直和斜交构成的（图9（c）），具有明显的方向分布特征，理想情况下，格网模式网眼的最小生成树的边方向集中在2个方向上（图9（d））；
（2） 直线型网眼群组的网眼最小生成树方向熵值为0，根据方向熵计算理论所得，当网眼最小生成树所有边的方向均集中在一起时（图9（b）），熵值为0，意味着网眼群组的空间排列具有明显的规律；而格网型网眼群组方向熵熵值偏小。对格网模式的网眼最小生成树进行方向熵计算时，理想情况下，方向熵熵值在0~1之间，但由于最小生成树中个别边方向存在偏差，方向熵值会略微偏大，如图9（c）所示的格网网眼最小生成树的方向熵值为0.845。

3 实验结果与分析

实验选取南京市、武汉市、上海市和西安市作为对象。首先，分别对城市路网构建格网样本和不规则样本并进行标注，同时对路网格网样本根据网眼排列方式的不同进行网眼直线型和网眼格网型标注；其次，使用南京市和西安市路网样本数据集完成特征参量的阈值统计；最后，使用武汉市和上海市路网样本验证所得特征参量阈值是否能够完成路网的格网模式、不规则模式以及网眼群组的直线模式和格网模式的划分。下面从阈值设定、路网模式识别、实验对比及心理问卷等方面展开分析。

3.1 参量阈值设定

为完成特征参量阈值统计，本次实验将从优化后的南京市和西安市路网中选取出300个网格模式路网和50个不规则模式路网图10（a）和图10（b）），并将网格模式路网进一步细分为150个直线型网眼群组（图10（c））和150个格网型网眼群组（图10（d）），其中不规则模式路网中共包含1 537个网眼，格网路网中共包含2 398个网眼。之后对构建好样本集中的每一个路网样本进行标注，不规则型路网标注为0，格网型标注为1，直线型网眼群组标注为2，格网型网眼群组标注为3。最后对网眼群组构建网眼质心最小生成树（图10（c）和图10（d））。
图10 南京市和西安市路网样本

Fig. 10 Nanjing and Xi'an road network sample map

3.1.1 网眼特征参量阈值确定

通过对网眼的矩形度和凹凸度的计算可以快速判别出路网中每一个网眼的规整情况。选取的南京市和西安市路网样本共包含3 935个网眼，分别计算每一个网眼的矩形度和凹凸度并统计所有网眼的特征参量数值。如图11所示，蓝点表示已标注为格网路网所包含的网眼，红点表示标注为不规则路网所包含的网眼，图中可以明显看出格网路网网眼的矩形度和凹凸度数值集中，均趋近于1；而不规则路网网眼的矩形度和凹凸度数值分布散乱，大都偏低。因此为了将规整网眼和不规整网眼区分开，本次实验将矩形度大于0.75且凹凸度大于0.9的路网网眼视为规整网眼，反之则为不规整网眼。
图11 路网样本集矩形度和凹凸度散点统计

Fig. 11 Scatter plot of rectilinearity and concavity of road network sample set

3.1.2 方向熵阈值确定

通过分析图11，发现有部分不规则路网的网眼矩形度大于0.75且凹凸度大于0.9，为完成对路网格网模式和不规则模式的精确识别，通过判别方向熵值的大小进一步完成路网模式的判别。如图12所示为南京市构建的350个路网样本的方向熵熵值计算统计的散点图，图中方向熵明显将格网路网和不规则路网进行了划分，格网路网的方向熵值小于0.25，不规则路网的方向熵值大于0.25。
图12 路网样本方向熵散点统计

Fig. 12 Scatter plot of directional entropy of road network sample

路网中不仅路段存在着空间排列模式，路网构成的网眼同样也存在着明显的空间排列方式，通过提取网眼质心点构建最小生成树后计算方向熵也能够完成网眼群组直线型模式和格网型模式的准确划分。如图13所示，对南京和西安市已构建好的150个直线型网眼群组样本和150个格网型网眼群组样本进行了方向熵值计算，得出直线型网眼群组的方向熵值为0，格网型网眼群组的方向熵值在0~2.5之间。
图13 路网网眼最小生成树方向熵散点统计

Fig. 13 Scatter plot of directional entropy of road network grid minimum spanning tree

3.1.3 路网模式识别规则

本文通过结合不同路网结构使用矩形度、凹凸度以及方向熵等特征参量完成格网路网、不规则路网、直线型网眼群组和格网型网眼群组等路网的多模式识别。以上3种特征参量交相呼应，若只使用方向熵进行路网格网模式和不规则模式识别时，该特征参量只能用于判断路网样本路段排列的混乱程度，无法检测路网样本中是否存在网眼以及网眼是否规整等情况，因此只使用方向熵无法做到格网路网和不规则路网模式识别，同时也将不满足网眼群组模式识别的前提。而只使用矩形度和凹凸度特征参量计算只能用于判断路网样本中单一网眼的规整情况，无法做到对路网整体分布模式进行识别。如 图14为图15中人眼标注不规则的路网样本，若对该样本只计算方向熵，其熵值为2.367，属于格网路网方向熵阈值范围内，将会导致误判，但如果搭配矩形度和凹凸度等网眼特征参量，发现路网中7个网眼只有2个网眼形状规整，不属于格网路网。故为提高算法的精确率，将以上3个特征参量配合使用。
图14 方向熵识别错误路网

Fig. 14 Direction entropy identification error road network

图15 结合路段和网眼结构的路网多模式识别算法流程

Fig. 15 Flow of multi-pattern recognition algorithm for road network combining road section and mesh structure

综上所述，从路网路段方向、道路网眼、网眼质心最小生成树等多角度出发，分别计算统计出不同结构相应的特征参量阈值，将路网的格网模式和不规则模式以及网眼群组的直线模式和格网模式区分开来，具体算法流程如图15所示。

3.2 路网模式识别

为验证所得特征参量的阈值划分是否合理以及算法是否具备可迁移能力，本次实验将选用武汉市和上海市道路网（图16（a）和图16（b））进行验证。本次实验共构建450个道路网样本（400个网格模式、50个不规则模式）并分别提取和构建了路段结构、网眼结构、网眼质心最小生成树结构，其中400个网格模式路网又细分为200个直线型网眼群组(图16（c）)和200个格网型网眼群组（图16（d）），共包含4 693个道路网网眼。
图16 上海市和武汉市路网样本

Fig. 16 Shanghai and Wuhan road network sample map

首先对构建好后的路网样本进行网眼的矩形度和凹凸度计算，如图17所示，使用上述所得的矩形度和凹凸度的特征参量阈值可粗略完成路网的格网模式和不规则模式的划分，图中格网路网样本中网眼矩形度大于0.75且凹凸度大于0.9的网眼数量为 3 257个，有97个网眼在此阈值以下。不规则路网中有243个网眼矩形度大于0.75且凹凸度大于0.9，其余1 096个网眼均在此阈值之下，如表1所示。
图17 路网样本矩形度凹凸度散点分布

Fig. 17 Scatter distribution map of rectilinearity and concavity of road network sample

表1 路网样本网眼矩形度凹凸度统计

Tab.1 Statistics of rectilinearity and concavity of Wuhan road network sample (个)

路网网眼样本 格网路网网眼 不规则路网网眼
识别出格网路网网眼 3 257 243
识别出不规则路网网眼 97 1 096
网眼总数 3 354 1 339
完成矩形度和凹凸度计算以后，提取路网的路段进行方向熵熵值计算，如图18和表2所示，400个已标注好的格网路网样本中397个样本方向熵熵值均在0~ 2.5之间，3个路网样本方向熵值大于2.5，而50个不规则路网样本其方向熵熵值均在在2.5以上，因此通过方向熵较为精准地完成了路网格网模式和不规则路网模式的划分。之后对构建好的网眼质心最小生成树进行方向熵计算，所得结果如 图19和表3所示，发现200个标注为直线模式的网眼群组中有194个符合方向熵为0的特性，有6个识别错误，方向熵值大于0，而200个标注为格网模式的网眼群组其识别结果与方向熵阈值设定符合，熵值在0~2.5之间。
图18 路网样本方向熵散点分布

Fig. 18 Scatter distribution map of directional entropy of road network

表2 武汉路网模式划分

Tab. 2 Classification of Wuhan road network patterns (个)

路网样本 标注的格网路网 标注的不规则路网
格网路网 397 0
不规则路网 3 50
图19 样本网眼最小生成树方向熵散点分布

Fig. 19 Scatter distribution map of directional entropy of sample grid minimum spanning tree

表3 武汉网眼模式划分

Tab. 3 Classification of Wuhan grid patterns (个)

网眼群组样本 标注的直线型网眼 标注的格网型网眼
直线型网眼群组 194 0
格网型网眼群组 6 200
通过对方向熵识别错误的格网路网进行 分析，发现其熵值大于设定阈值的主要原因如 图20（a）所示，由于路网中包含近似圆的弧形路 段导致线性剖分后其整体路网方向分布错乱 （图20（b）），方向熵值为2.98。对直线型网眼群组的网眼最小生成树出现不为0的情况进行分析，发现方向熵识别错误主要原因如图20（c）所示，由于路网自身存在一定的弧段，导致生成的网眼的质心点位置产生偏移，因此根据网眼质心点构建的网眼最小生成树是一条曲线(图20（d）)，图20（c）中路网样本的方向熵值为0.72。
图20 算法识别错误样本

Fig. 20 Algorithm recognition error sample graph

如表4所示，可以看出，本文使用算法均展示出不错的性能，模式分类的准确率、精确度、召回率和F1值均在97%以上，说明该算法具有良好的泛化性能。
表4 模式分类的准确率、精确度、召回率和F1值

Tab. 4 Accuracy, precision, recall, and F1 values for pattern classification (%)

类型 准确率 精确度 召回率 F1
格网路网 99.33 100.00 99.25 99.62
不规则路网 99.33 94.33 100.00 97.08
直线型网眼群组 98.50 100.00 97.00 98.48
格网型网眼群组 98.50 97.08 100.00 98.52
综上所述，对武汉市路网模式识别中，使用以上所构建的算法流程进行模式识别时，除一个网眼直线型模式识别错误以外，其余样本的识别结果与人眼标注结果相符，同时也验证了方向熵在进行路网格网模式、不规则模式识别以及网眼群组直线型模式和格网模式识别时的可行性。

3.3 对比试验

为验证本文方法的有效性，从南京市样本集中选取了80个已标注好的格网路网样本（可细分为40个直线型网眼群组和40个格网型网眼群组）（共包含1 104个网眼）和20个不规则路网样本（共包含188个网眼），分别与Yang等[25]和Tian等[11]提出的基于网眼结构或路段结构的路网格模式识别方法进行对比实验。
对比实验1选取主方向差异值，网眼重叠面积比以及矩形度等特征参量，通过比较相邻网眼的相似程度完成路网的网格模式识别，如图21（b）所示，该算法可有效提取和识别出由形状相似的矩形网眼组成的网格路网，但无法对路网样本整体进行识别，若相邻网眼的重叠面积比过小，或存在形状非矩形的网眼时，将无法完成识别，如图22（a）和图22（b）所示。对比实验2通过根据路网路段拓扑关系构建关系图，后根据关系图中路段的角度相似关系提取路网的2个极大完全子图，根据对2个极大完全子图进行相联或相交操作完成网格模式路网的识别和提取，如图21（c）所示，该算法对排列规整的路网识别效果较好，但若格网路网中路段存在不平行的情况发生，将无法完成识别，如图23（a）所示。
图21 对比实验结果

Fig. 21 Comparison of experimental results

图22 对比实验1识别结果

Fig. 22 Comparison of experimental 1 identification results

图23 对比实验2识别结果

Fig. 23 Comparison of experimental 2 identification results

而本文采用的结合网眼和路段结构的路网模式识别算法较好地顾及了格式塔应用准则，不仅使用方向熵描述了道路路段整体的分布情况，同时使用矩形度和凹凸度描述了道路网中网眼的规整情况，在简单有效地完成路网模式识别的同时避免了网眼无法识别的情况的发生，如图22（c）、图22（d）、图23（b）所示。结合网眼和路段结构的路网模式识别算法有效识别了所选取的南京格网路网样本和不规则路网样本(图21（d）)，并且相较于以上2种对比算法，本文使用方法可有效将格网模式路网细分为直线型网眼群组或格网型网眼群组。
为验证本文算法的有效性，将从标注样本模式分类正确情况以及样本包含的网眼识别完整程度两方面进行定量评价和对比，如表5—表9所示，结果表明，本文算法可有效识别路网的格网模式和不规则模式并将格网路网细分为直线型网眼群组和格网型网眼群组。
表5 对比试验格网样本识别网眼数量

Tab. 5 Comparison of Experimental Results for Identifying the Number of Grids (个)

实验方法 识别出网眼数量 未识别出网眼数量 样本网眼数量
对比实验1 992 112 1 104
对比实验2 1 038 66 1 104
本文算法 1 104 0 1 104
表6 对比实验识别结果

Tab. 6 Comparative experimental identification results (个)

类型 对比实验1 对比实验2
标注的格网路网 标注的不规则路网 标注的格网路网 标注的不规则路网
格网路网 75 5 77 3
不规则路网 0 20 0 20
表7 本文算法识别结果

Tab. 7 Algorithm identification results in this paper (个)

类型 标注的格网路网 标注的不规则路网 标注的直线型网眼群组 标注的格网型网眼群组
格网路网 80 0 - -
不规则路网 0 20 - -
直线型网眼群组 - - 38 2
格网型网眼群组 - - 0 40
表8 对比试验模式分类的准确率、精确度、召回率和F1值

Tab. 8 Accuracy, precision, recall, and F1 values for the classification of comparative test modes (%)

类型 对比实验1
准确率 精确度 召回率 F1
格网路网 95.00 93.75 100.00 96.77
不规则路网 95.00 100.00 80.00 88.89
类型 对比实验2
准确率 精确度 召回率 F1
格网路网 97.00 96.25 100.00 98.09
不规则路网 97.00 100.00 86.96 93.03
表9 本文算法模式分类的准确率、精确度、召回率和F1值

Tab. 9 Accuracy, precision, recall, and F1 sore of the algorithm pattern classification in this article (%)

类型 准确率 精确度 召回率 F1
格网路网 100.00 100.00 100.00 100.00
不规则路网 100.00 100.00 100.00 100.00
直线型网眼群组 97.50 95.00 100.00 97.44
格网型网眼群组 97.50 100.00 95.24 97.56

3.4 问卷分析

为验证以上所得算法是否符合人类视觉认知，从武汉市和南京市道路网样本集中随机选取了10个格网型路网（5个直线型网眼、5个格网型网眼）样本和5个不规则型路网样本作为问卷研究对象，选择了80位地图专业相关的老师和学生进行问卷调查，在问卷中首先讲明格网型道路网、不规则型道路网已经直线型网眼和格网型网眼的定义，并以图示形式说明各个路网模式，为以上15个道路网提供格网型和不规则型2个选项，并对10格网型路网又提供了直线型网眼和格网型网眼2个选项，让调查者根据认知选择他们认为正确的路网模式。调查结果如表10所示，可以看出以上算法所得结果与人类认知基本符合。
表10 问卷调查结果

Tab. 10 Survey results

标号 标注 识别结果 符合认知程度/% 是否匹配
1 不规则路网 不规则路网 100 是
2 不规则路网 97.5 是
3 不规则路网 90 是
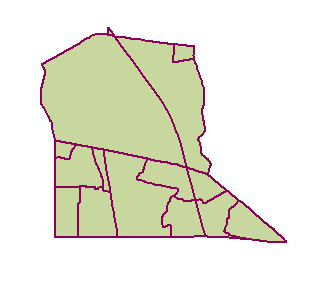4 不规则路网 100 是
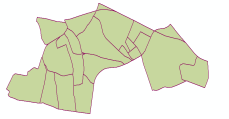5 不规则路网 92.5 是
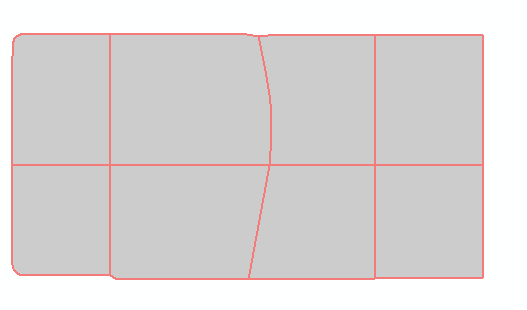6 格网路网
格网型网眼群组		 格网路网
格网型网眼群组		 100 是
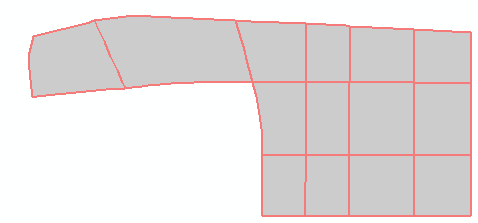7 格网路网
格网型网眼群组		 100 是
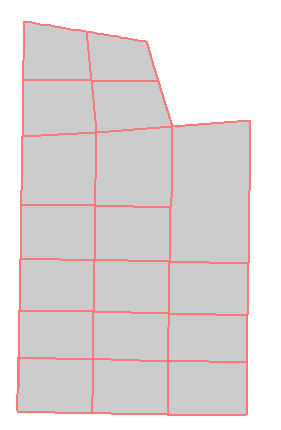8 格网路网
格网型网眼群组		 100 是
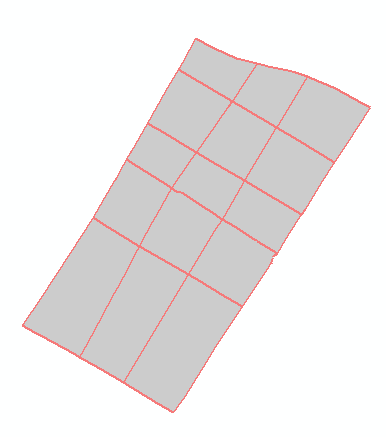9 格网路网
格网型网眼群组		 100 是
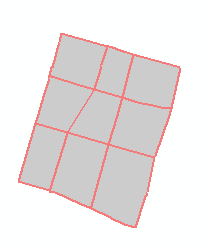10 格网路网
格网型网眼群组		 100 是
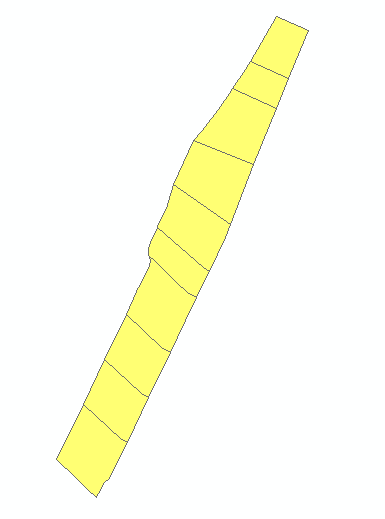11 格网路网
直线型网眼群组		 格网路网
直线型网眼群组		 100 是
12 格网路网
直线型网眼群组		 100 是
13 格网路网
直线型网眼群组		 100 是
14 格网路网
直线型网眼群组		 100 是
15 格网路网
直线型网眼群组		 100 是
对表10问卷调查所用的路网样本进行分析，发现3号不规则路网样本由于该路网样本中部分网眼和路网路段排列规整，导致有8名被调查人员错误认为该路网样本为格网路网。通过本文算法对3号不规则路网样本进行识别分析，发现该样本路网路段中存在多条曲线，导致路网整体方向分布混乱（图24（d）），路段方向熵值为2.79，且路网包含的30个网眼中仅有18个为规整网眼（图24（b）），故通过图18所示的本文路网模式识别规则，该路网样本为不规则路网。
图24 三号不规则路网样本识别结果

Fig. 24 Recognition results of sample 3 irregular road network

4 结论

路网的模式识别研究在地图制图、地图匹配、城市规划与发展等领域均有诸多应用。为克服已有算法预处理复杂、模式识别单一、网眼群组模式研究较少、算法难度大且迁移能力弱等问题，本文通过结合路网网眼结构和道路路段结构，利用方向熵、矩形度和凹凸度等特征参量，提出了一种简单有效的路网模式识别方法，完成了道路网模式以及路网包含网眼群组模式的识别。本文经实证分析，得出以下研究结果： ① 方向熵在描述空间现象方向的分布特征和规律方面具有很大的优势，在路网模式识别中，可定量化描述道路路段和道路网眼群组的排列规整程度，如格网路网的方向熵值在2.5以下，不规则路网的方向熵值在2.5以上，格网路网包含的直线型网眼群组最小生成树方向熵值为0，格网型网眼群组最小生成树方向熵值为0~2.5之间； ② 本文提取和构建了路网路段结构、网眼结构以及网眼最小生成树模型，通过计算相应的特征参量阈值完成了格网路网、不规则路网的模式识别，并根据格网路网所包含网眼排列方式的不同将其划分为直线型网眼群组和格网型网眼群组； ③ 本文将武汉市、上海市、南京市和西安市路网作为实验对象构建样本集，其中南京市和西安市样本集用于确定参量阈值和制定路网模式识别规则，武汉市和上海市样本集用于验证本文算法的可行性和可迁移能力，结果表明，本文算法具有较好的可迁移能力且模式识别精度均达到了97%以上； ④ 通过视觉认知对比和心理问卷调查，发现本文识别的路网模式和网眼群组模式识别结果符合人类认知。
本文算法亦存在些许不足，当规整路网中存在近似圆的弧形路段时，将出现错误识别的情况。究其原因，当路网进行线性剖分时，弧形路段会被分割为多条方向不同的直线，导致方向熵计算时，熵值过大，误判为不规则模式路网。该问题有望通过路网预处理的改进或引入新的路网图结构加以解决，这也是我们下一步的研究方向。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Louf R, Barthelemy M. A typology of street patterns[J]. Journal of the Royal Society, Interface, 2014, 11(101):20140924. DOI:10.1098/rsif.2014.0924

[2]
武芳, 巩现勇, 杜佳威. 地图制图综合回顾与前望[J]. 测绘学报, 2017, 46(10):1645-1664.

DOI

[Wu F, Gong X Y, Du J W. Overview of the research progress in automated map generalization[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10):1645-1664.] DOI:10.11947/j.AGCS.2017.20170287

[3]
Heinzle F, Anders K H, Sester M. Pattern recognition in road networks on the example of circular road detection[M]//Lecture Notes in Computer Science. Berlin, Heidelberg: Springer Berlin Heidelberg, 2006:153-167. DOI:10.1007/11863939_11

[4]
Yang B S, Zhang Y F. Pattern-mining approach for conflating crowdsourcing road networks with POIs[J]. International Journal of Geographical Information Science, 2015, 29(5):786-805. DOI:10.1080/13658816.2014.997238

[5]
Zhang X, Stoter J, Ai T H, et al. Automated evaluation of building alignments in generalized maps[J]. International Journal of Geographical Information Science, 2013, 27(8):1550-1571. DOI: 10.1080/13658816.2012.758264

[6]
Lüscher P. Characterising urban space from topographic databases : Cartographic pattern recognition based on semantic modelling[D]. Zurich: University of Zurich, 2011. DOI:10.5167/UZH-164120

[7]
Zhu J, Sun Y Z. Building an urban spatial structure from urban land use data: An example using automated recognition of the city centre[J]. ISPRS International Journal of Geo-Information, 2017, 6(4):122. DOI:10.3390/ijgi6040122

[8]
Yu B L, Shu S, Liu H X, et al. Object-based spatial cluster analysis of urban landscape pattern using nighttime light satellite images: A case study of China[J]. International Journal of Geographical Information Science, 2014, 28(11):2328-2355. DOI:10.1080/13658816.2014.922186

[9]
Tian J, Yu M T, Ren C, et al. Network-scape metric analysis: A new approach for the pattern analysis of urban road networks[J]. International Journal of Geographical Information Science, 2019, 33(3):537-566. DOI:10.1080/13658816.2018.1545234

[10]
田晶, 张泊宇, 吴荡. 一种矢量道路网辐射模式识别新方法[J]. 武汉大学学报(信息科学版), 2013, 38(10):1234-1238.

[Tian J, Zhang B Y, Wu D. A new method for identifying radial pattern in vector road networks[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10):1234-1238.] DOI:10.13203/j.whugis2013.10.008

[11]
田晶, 宋子寒, 艾廷华. 运用图论进行道路网网格模式提取[J]. 武汉大学学报(信息科学版), 2012, 37(6):724-727.

[Tian J, Song Z H, Ai T H. Grid pattern extraction in road networks with graph[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6):724-727.] DOI:10.13203/j.whugis2012.06.007

[12]
何亚坤, 艾廷华, 杜欣, 等. 网络空间向量剖分法识别城市路网网格模式[J]. 武汉大学学报(信息科学版), 2018, 43(1):138-144.

[He Y K, Ai T H, Du X, et al. Grid pattern recognition in street network space by vector tessellation method[J]. Geomatics and Information Science of Wuhan University, 2018, 43(1):138-144.] DOI:10.13203/j.whugis20150757

[13]
王米琪, 艾廷华, 晏雄锋, 等. 图卷积网络模型识别道路正交网格模式[J]. 武汉大学学报(信息科学版), 2020, 45(12):1960-1969.

[Wang M Q, Ai T H, Yan X F, et al. Grid pattern recognition in road networks based on graph convolution network model[J]. Geomatics and Information Science of Wuhan University, 2020, 45(12):1960-1969.] DOI:10.13203/j.whugis20200022

[14]
田晶, 何遒, 周梦杰. 运用主成分分析识别道路网中的网格模式[J]. 武汉大学学报(信息科学版), 2013, 38(5):604-607,630.

[Tian J, He Q, Zhou M J. Gird pattern recognition in road network using principal component analysis[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5):604-607,630.] DOI:10.13203/j.whugis2013.05.012

[15]
田晶, 张泊宇, 杨雯雨. 对自组织映射聚类实现道路网网格模式识别[J]. 武汉大学学报(信息科学版), 2013, 38(11):1330-1334.

[Tian J, Zhang B Y, Yang W Y. Gird pattern recognition based on clustering of self-organizing maps[J]. Geomatics and Information Science of Wuhan University, 2013, 38(11):1330-1334.] DOI:10.13203/j.whugis2013.11.007

[16]
Wang X S, You S K, Wang L. Classifying road network patterns using multinomial logit model[J]. Journal of Transport Geography, 2017, 58:104-112. DOI:10.1016/j.jtrangeo.2016.11.013

[17]
Xie F, Levinson D. Measuring the structure of road networks[J]. Geographical Analysis, 2007, 39(3):336-356. DOI:0.1111/j.1538-4632.2007.00707.x

[18]
Heinzle F, Anders K H, Sester M. Graph based approaches for recognition of patterns and implicit information in road networks[C]// Proc. 22nd International Cartographic Conference, A Coruna. 2005. DOI:http://dx.doi.org/

[19]
Heinzle F, Anders K H. Characterising space via pattern recognition techniques[M]// Generalisation of Geographic Information. Amsterdam: Elsevier, 2007:233-253. DOI: 10.1016/b978-008045374-3/50014-4

[20]
崔晓杰, 王家耀, 巩现勇, 等. 基于改进霍夫变换的环形交叉口识别方法[J]. 测绘学报, 2018, 47(12):1670-1679.

DOI

[Cui X J, Wang J Y, Gong X Y, et al. Round about recognition method based on improved Hough transform in road networks[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(12):1670-1679.]

[21]
崔晓杰. 城市道路网典型空间分布模式的识别方法研究[D]. 郑州: 战略支援部队信息工程大学, 2019.

[Cui X J. Research on identification method of typical spatial distribution patterns of urban road network[D]. Zhengzhou: Information Engineering University, 2019.]

[22]
王米琪. 基于图卷积神经网络的道路网模式识别[D]. 武汉: 武汉大学, 2021.

[Wang M Q. Road network pattern recognition based on graph convolution neural network[D]. Wuhan: Wuhan University, 2021.]

[23]
王安东, 武芳, 巩现勇, 等. 一种城市路网多层次复合网格模式识别方法[J]. 测绘学报, 2023, 52(11):1994-2006.

DOI

[Wang A D, Wu F, Gong X Y, et al. A recognition approach for compound grid pattern of urban road networks[J]. Acta Geodaetica et Cartographica Sinica, 2023, 52(11):1994-2006.] DOI:10.11947/j.AGCS.2023.20220528

[24]
He Y K, Ai T H, Yu W H, et al. A linear tessellation model to identify spatial pattern in urban street networks[J]. International Journal of Geographical Information Science, 2017, 31(8):1541-1561. DOI:10.1080/13658816.2017.1298768

[25]
杨必胜, 栾学晨. 城市道路网几何结构模式的自动识别方法[J]. 中国图象图形学报, 2009, 14(7):1251-1255.

[Yang B S, Luan X C. An automated method for structural pattern recognition of road networks[J]. Journal of Image and Graphics, 2009, 14(7):1251-1255.] DOI:10.11834/jig.20090705

[26]
杨亚琦, 李博雄, 杨东霞, 等. 基于信息熵的异常数据判别方法[J]. 科学技术创新, 2023(24):194-199.

[Yang Y Q, Li B X, Yang D X, et al. A method of discriminating abnormal data based on information entropy[J]. Scientific and Technological Innovation, 2023(24):194-199.] DOI: 10.3969/j.issn.1673-1328.2023.24.049

[27]
赵夫群, 温静. 基于信息熵和改进KMC的点云简化算法[J]. 测绘工程, 2023, 32(5):7-12.

[Zhao F Q, Wen J. Point cloud simplification algorithm based on information entropy and improved KMC[J]. Engineering of Surveying and Mapping, 2023, 32(5):7-12.] DOI:10.19349/j.cnki.issn1006-7949.2023.05.002

[28]
彭鹏, 栗坤, 王玲玲, 等. 基于极坐标直方图及方向熵的聚落街网研究——以河北鹿泉水峪村为例[J]. 重庆建筑, 2023, 22(11):23-27.

[Peng P, Li K, Wang L L, et al. Research on settlement street networks based on polar coordinate histogram and directional entropy: A case study of Shuiyu Village in Luquan, Hebei Province[J]. Chongqing Architecture, 2023, 22(11):23-27.]

[29]
彭鹏, 王玲玲, 栗坤, 等. 街道极坐标直方图及方向熵在传统聚落中的应用研究——以河北井陉当泉村为例[J]. 重庆建筑, 2023, 22(10):5-9.

[ Peng P, Wang L L, Li K, et al. Application of street polar histogram and direction entropy in traditional settlements: A case study of Dangquan Village in Jingxing, Hebei Province[J]. Chongqing Architecture, 2023, 22(10):5-9.]

[30]
彭鹏, 王玲玲, 栗坤. 基于街道极坐标直方图及方向熵的聚落研究——以河北井陉当泉村为例[J]. 北京建筑大学学报, 2023, 39(4):9-16.

[Peng P, Wang L L, Li K. Study on traditional settlements based on street polar histogram and direction entropy: A case study of Dangquan Village in Jingxing[J]. Journal of Beijing University of Civil Engineering and Architecture, 2023, 39(4):9-16.] DOI:10.19740/j.2096-9872.2023.04.02

Options
文章导航

/

〈 〉