EN中文

地球信息科学学报 >

2024 , Vol. 26 >Issue 12: 2759 - 2771

DOI: https://doi.org/10.12082/dqxxkx.2024.240505

遥感科学与应用技术

基于中心轴正交旋转的点云数据隧道断面提取方法

  • 王铁星 , 1, 2, 3 ,
  • 魏冠军 , 1, 2, 3, * ,
  • 王永鑫 4
展开
  • 1.兰州交通大学 测绘与地理信息学院，兰州 730070
  • 2.地理国情监测技术应用国家地方联合工程研究中心，兰州 730070
  • 3.甘肃省地理国情监测工程实验室，兰州 730070
  • 4.中国铁路兰州局集团有限公司科研技术监督所，兰州 730099
* 魏冠军（1976— ），男，甘肃庄浪人，博士，教授，主要研究方向为误差理论与测量数据处理研究。E-mail:

王铁星（1999— ），男，江西丰城人，硕士生，主要研究方向为隧道点云断面提取及三维重建研究。E-mail:

Office editor: 黄光玉

收稿日期: 2024-09-09

  修回日期: 2024-10-18

  网络出版日期: 2024-11-28

基金资助

国家自然科学基金项目(42364003)

国家自然科学基金项目(41964008)

收起

Tunnel Point Cloud Section Extraction Method Based on Orthogonal Rotation of the Central Axis

  • WANG Tiexing , 1, 2, 3 ,
  • WEI Guanjun , 1, 2, 3, * ,
  • WANG Yongxin 4
Expand
  • 1. Faculty of Geomatics Lanzhou Jiaotong University, Lanzhou 730070, China
  • 2. National Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, Lanzhou 730070, China
  • 3. Gansu Provincial Engineering Laboratory of Geographical Monitoring, Lanzhou 730070, China
  • 4. Research Technical Supervision Office of China Railway Lanzhou Bureau Group Co., Ltd., Lanzhou 730099, China
* WEI Guanjun, E-mail:

Received date: 2024-09-09

  Revised date: 2024-10-18

  Online published: 2024-11-28

Supported by

National Natural Science Foundation of China(42364003)

National Natural Science Foundation of China(41964008)

Fold

摘要

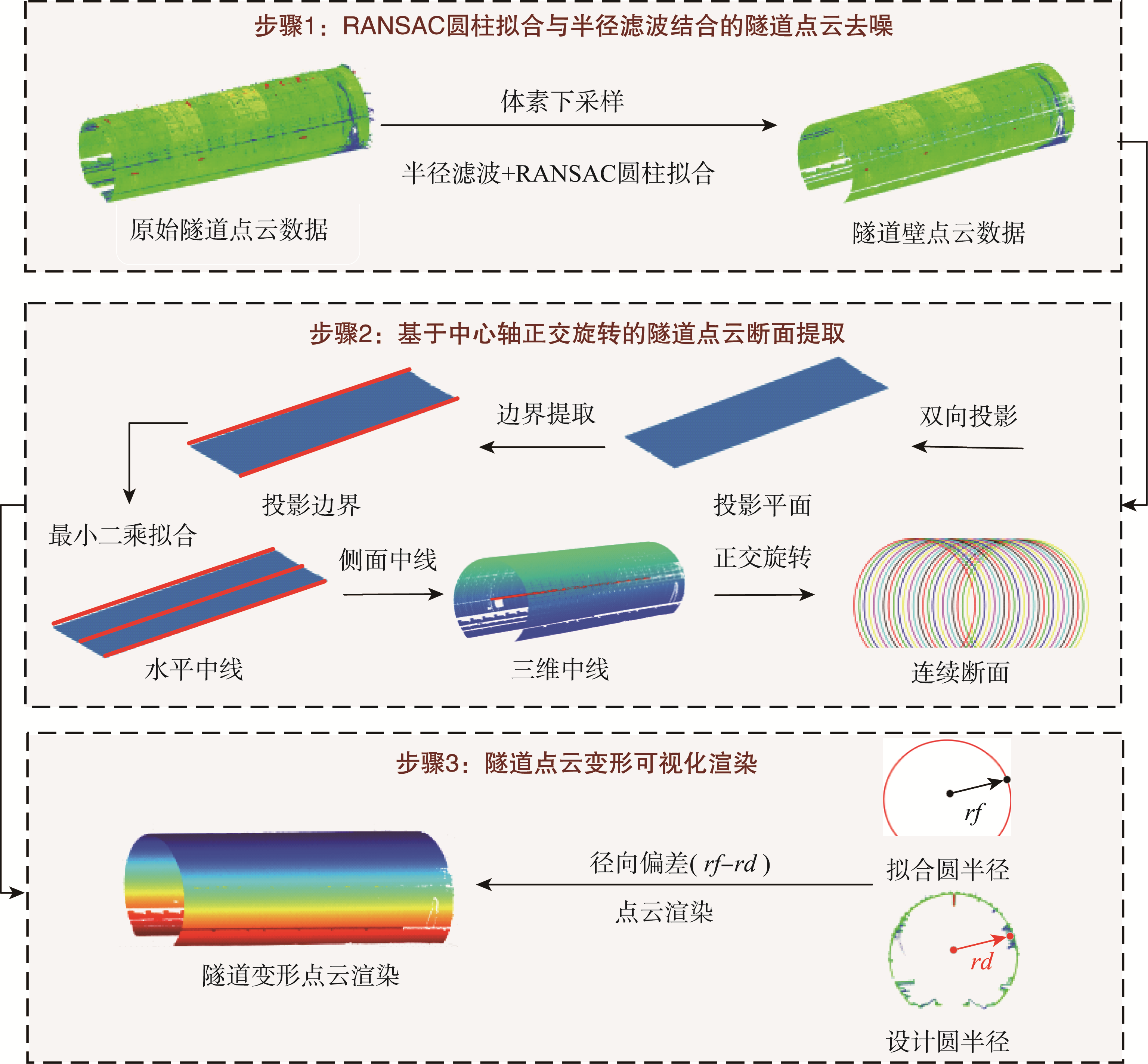
隧道断面的精确提取是隧道形变分析中的一个关键环节，然而，隧道内部复杂的形状和环境使得点云处理算法变得复杂，传统的断面提取与变形分析算法已经不适用于点云数据，因此亟需更高效和更鲁棒的算法。针对这一问题，本文提出了一种基于点云数据的隧道断面连续提取方法。首先，引入结合随机样本一致性（Random Sample Consensus，RANSAC）圆柱拟合与半径滤波的方法，以有效滤除离群点及附着在隧道壁上的噪声点；接着，通过双向投影获取隧道中轴线，并根据“与隧道中轴线正交旋转的直线相交于隧道壁”建立数学模型，从而实现对隧道点云断面的连续提取；最后，以断面点的拟合圆心坐标和设计半径为参数计算隧道的形变量，并通过可视化渲染直观展示隧道整体变形情况。为证明本文方法的有效性，实验选取了成都市某地铁线路三段地铁隧道的激光点云数据，结果表明，该方法滤除噪声时I类误差、II类误差和总误差均值分别为1.48%、1.03%和1.21%，Kappa系数达到97.45%。相比传统的最小二乘法、密度聚类法以及法向偏差法，本方法的3类误差之和分别降低了9.34%、10.61%和4.41%，Kappa系数则提高了5.36%、6.38%和3.65%。这充分展现出本方法更优越的鲁棒性和准确性；此外，该方法所提取出的隧道断面拟合半径与设计半径的偏差均值低至1.36 mm。相比目前的1.60 mm方法及6.00 mm方法，本文方法的偏差均值分别降低了2.5 mm和2.7 mm。而求得隧道形变量范围在0~18 mm之间，同时通过点云渲染方式直观展示了隧道整体变形情况。本研究的方法为隧道安全监测工作提供了可靠依据和基础支持。

关键词： 隧道工程; 断面提取; 形变可视化分析; 中心轴正交旋转; 激光点云数据; RANSAC圆柱拟合; 半径滤波; 双向投影

本文引用格式

王铁星 , 魏冠军 , 王永鑫 . 基于中心轴正交旋转的点云数据隧道断面提取方法[J]. 地球信息科学学报, 2024 , 26(12) : 2759 -2771 . DOI: 10.12082/dqxxkx.2024.240505

Abstract

The accurate extraction of tunnel sections is a pivotal step in tunnel deformation analysis. However, due to inadequate illumination, the reflection and occlusion caused by dust and structural elements generate noise and erroneous points in the point cloud data, complicating data processing. Additionally, the intricate geometry of tunnel features, such as curved surfaces, corners, and cracks, renders traditional section extraction algorithms ineffective for point cloud data. Consequently, there is an urgent need for more efficient and robust algorithms. To address this issue, this paper proposes a method for continuous tunnel section extraction based on laser point cloud data. First, a combination filtering method is introduced, integrating Random Sample Consensus (RANSAC) cylindrical fitting and radius filtering to effectively remove scattered outliers and noise points adhering to the tunnel walls with sparse density. Next, the tunnel central axis is obtained via bidirectional projection, and a mathematical function model is established in line with the principle that ‘a straight line intersecting the tunnel central axis intersects the tunnel wall’, enabling the continuous extraction of tunnel section point clouds. Finally, the fitting center coordinates of the section points and the tunnel design radius are used as parameters to calculate the radial deviation of the tunnel points, representing the shape variables. The tunnel point cloud is visually rendered using these shape variables to display the overall deformation of the tunnel. In this paper, laser point cloud data from three sections of a subway tunnel in Chengdu are used as the experimental data. The results show that the mean values of Class I error, Class II error, and total error are 1.48%, 1.03%, and 1.21%, respectively, with the Kappa coefficient reaching 97.45% when using this method for noise filtering. Compared to traditional methods such as least squares, density clustering, and normal deviation algorithms, this method reduces cumulative errors by 9.34%, 10.61%, and 4.41%, respectively, while increasing the Kappa coefficient by 5.36%, 6.38%, and 3.65%. This demonstrates the enhanced robustness and accuracy of the proposed method. Moreover, the mean deviation between the tunnel section fitting radius obtained through this method and the design radius is merely 1.36 mm, compared to deviations of 1.60 mm and 6.00 mm with existing methods, achieving reductions of 2.5 mm and 2.7 mm, respectively. The range of the tunnel shape variable is between 0 and 18 mm, and the overall deformation of the tunnel is visually displayed through point cloud rendering. The method provides a reliable foundation and essential support for tunnel safety monitoring.

Key words： tunnel engineering; section extraction; visualization analysis of deformation; orthogonal rotation of the central axis; laser point cloud data; RANSAC cylindrical fitting; radius filtering; bidirectional projection

1 引言

隧道工程的质量是交通运营安全的基础保障，构建数字化隧道模型对进行安全监测具有重要意义和价值[1-2]。三维激光扫描技术以其高精度、高效率、自动化、无接触等优点，已被证明是监测工程结构变形的有效手段[3⇓-5]，能够满足隧道变形监测的精度要求[6⇓-8]。受周围地质、施工及自身结构等因素的影响，隧道不可避免地会发生一定的变形，这可能直接影响到隧道后续的安全运营。因此，定期对隧道进行变形评估以确保工程在竣工后的安全性是十分必要的[9-10]。
断面测量是隧道变形监测的主要任务之一，比较不同时期的测量结果可以明确变形轮廓及其随时间的变化趋势[5]。随着地铁的不断建设，对地铁隧道进行形变检测变得尤为重要[11]。由于三维激光扫描技术具备便捷性及信息量大[12⇓-14]等特点，能够为隧道工程提供快速有效的测量结果[15-16]，因此如何从海量的隧道点云数据中准确提取隧道断面[17]已成为当前的研究热点。近年来，学者们提出了许多适用于隧道点云断面提取的方法。其中，基于点云的投影方法获取隧道断面[18⇓⇓-21]这一方法较为常见。该方法主要将隧道点云旋转至与某一坐标轴平行，然后将隧道点云投影至平面并提取中线，从而反映隧道的基本走向，然而，在较长隧道的情况下，该方法需要对点云进行分段处理，效率相对较低。程效军等[18]通过双向投影获取隧道在水平和竖直方向的边界线并插值中轴线控制点，从而获得隧道断面；Shi等[19]建立了隧道断面的原始点云圆柱投影，并采用最小二乘法基于椭圆模型拟合隧道断面曲线；Cheng等[20]提出一种从地面激光扫描点云中自动提取隧道断面的方法，使用最小二乘法和Rodrigues旋转公式调整初始断面方向，进而通过投影生成高精度的隧道断面，为隧道建模提供了有效的支持；杜黎明等[21]采用k邻近法对断面进行分块，并利用投影法构建断面点集；Sun等[5]采用双向投影法确定中心轴，并提出基于局部点密度的自适应断面提取算法，采用三次b样条曲线对断面点进行拟合。基于椭圆拟合的隧道断面提取[22⇓-24]也是一种常见方法，主要是将隧道形状视为圆柱或椭圆柱，通过拟合获取隧道断面。Zhang等[9]以隧道轴线为切片对点云进行处理，采用椭圆拟合方式获取隧道断面，并对断面变形进行评估；吴廷等[22]提出基于椭圆拟合的隧道中轴线及断面连续提取算法，并利用全站仪测量数据验证其可靠性；Yasuda等[23]提出了一种椭圆傅里叶分析的变形估计方法，通过变形前后隧道轮廓的傅里叶级数表示的差值来估计隧道变形情况；冯阳等[24]对点云进行切片，再通过空间圆拟合获取隧道断面，实现隧道壁点的准确提取。其他学者也提出了不同的隧道断面提取方法。Wang等[25]提出一种基于三维不变矩提取隧道中心轴的新方法，通过将隧道点云旋转使其中心轴与坐标轴平行，基于中心轴线切割隧道点云获取断面；Jia等[26]利用改进的移动最小二乘法确定隧道中心线，然后基于点云切片分析隧道断面的收敛情况，从而判定其安全状态；方俊杰[27]通过格网化内插的方式获得隧道任意位置的断面变形情况； Cao等[4]通过切片方式获取初始中心轴，并采用随机样本一致性隧道轴分割算法将其划分为线性段和非线性段，通过其法截面与局部拟合的二次曲面相交获取断面，证明了其算法对缺失数据和点密度的不敏感。Kang等[28]通过单向投影获取平面点云，并采用RANSAC曲线拟合算法提取隧道中心轴，通过其横截面平面与隧道面相交来提取断面，证明了其算法的可行性。
上述方法从海量三维点云数据中提取出隧道断面，能有效反映隧道基本走向和变形情况，提供了较好的建模支持。但仍存在以下问题：对异常值敏感，易受到少数噪声数据干扰，降低提取精度；在高噪声环境下处理隧道复杂结构时不够鲁棒，对噪声抑制能力不足、抵抗力较弱；部分技术在处理隧道点云时需进行分段或采用复杂的拟合算法，导致计算效率低下。因此，基于点云数据实现隧道变形可视化分析的断面提取仍然值得深入探索。为进一步探讨和改进，提高断面提取的准确性，并更有效地进行隧道变形可视化分析，本文在双向投影的基础上，提出了一种基于中心轴正交旋转的隧道断面提取及变形可视化分析方法。不同于传统的单一滤波方式，该方法首先引入结合RANSAC圆柱拟合与半径滤波的机制，对下采样后的隧道点云数据进行噪声去除；随后，通过双向投影获取隧道中轴线，并基于与中轴线正交旋转的直线与隧道壁相交以提取断面点；最后，利用这些断面点的拟合圆心坐标、隧道设计半径计算隧道变形量，并通过变形量对点云进行渲染，从而直观反映隧道整体变形情况。

2 隧道断面提取及形变可视化分析方法

本文主要对隧道断面提取及形变可视化分析方法进行研究，首先引入结合RANSAC圆柱拟合[29]与半径滤波[30]的方法对隧道点云进行噪声去除，获取隧道壁点云；再以双向投影方式获取中轴线，并提出基于中心轴正交旋转的方法连续提取隧道断面；最后根据断面点拟合圆圆心坐标与隧道设计半径求取隧道形变量，通过点云渲染展示隧道整体变形情况。本文技术路线如图1所示。
图1 隧道断面提取及形变可视化分析技术路线

Fig. 1 Technical route of tunnel section extraction and deformation visualization analysis

2.1 基于RANSAC圆柱拟合与半径滤波结合的去噪算法

本文通过提出的基于RANSAC圆柱拟合算法与半径滤波结合去噪算法对隧道场景中存在的离群点和噪声点进行滤除，如图2所示。首先对原始隧道点云数据进行体素下采样处理，适当减少数据量，提高处理效率；然后通过半径滤波去除一些离群点；最后对隧道壁点云进行RANSAC圆柱拟合，设定阈值并确定模型参数，筛选出最优的圆柱模型，去除附着在隧道壁上的外点，得到滤波后的隧道壁点云。
图2 基于RANSAC圆柱拟合与半径滤波结合的去噪算法流程

Fig. 2 Denoising algorithm flow based on combination of RANSAC cylinder fitting and radius filtering

本研究选用的隧道几何形状规则，未有大面积的凹陷等缺陷且中轴线总体上呈现为直线，因此采用RANSAC圆柱模型对隧道点云进行曲面拟合去噪，把隧道壁点作为内点保留，非隧道壁点作为外点去除，以此达到点云滤波的目的。圆柱模型公式为：
                x - x 1 2 + y - y 1 2 + z - z 1 2 - r 2 = a x - x 1 + b y - y 1 + c z - z 1 a 2 + b 2 + c 2
式中： x、y、z是圆柱面上点的坐标值； x1、y1、z1是圆柱轴线上一点；r是圆柱的半径； a、b、c是圆柱轴线的方向向量。
为实现RANSAC算法的自适应性，对初始数据点进行均匀随机采样，称不包含外点的样本为好样本，否则为差样本，记p为在K次抽样中所有样本均为差样本的概率。
p = 1 - q n K
K = l o g p l o g 1 - q n
式中：n为样本包含的点数，即确定模型参数所需要的最小数目；K为抽样次数。
自适应算法过程如下： ① 对内点占比作最保守估计 q = q 0，应用式（3）得到抽样次数初始值K0；② 抽样更新q0和K0分别为q1和K1，若 q 1 > q 0，则更新 q 0 = q 1，且应用式（3）更新抽样次数为 K 0 = K 1，否则，保持原来的q0、K1； ③ 对抽样次数进行判定，若抽样次数达到或已超过K0，则终止抽样；否则，返回第② 步。

2.2 基于二维投影的隧道中线估计

以隧道进口作为原点；定义隧道行进方向为X轴；定义垂直于X轴的横向方向为Y轴；定义隧道的垂直方向为Z轴，如图3中隧道双向投影所示。当隧道较短且为直线段或小弯曲段时，双向投影效果良好，而本研究所选用的为短直线型隧道，通过双向投影的方式将去噪后的隧道点云分别投影到XOY平面和XOZ平面，如图3中竖直投影和水平投影所示，利用边界函数boundary提取边界点云的向量索引，根据向量索引从投影后的平面点云中搜索边界点，从而获取边界点；然后采用最小二乘的方式对其进行直线拟合，得到两侧边界线，分别取两侧边界线的中线作为隧道在XOY平面和XOZ平面的水平中线和侧面中线，如图3中边界提取、XOY平面中线估计和XOZ平面中线估计所示；最后分别将水平中线正射投影至侧面中线所在的水平曲面，侧面中线正射投影至水平中线所在的竖直曲面，并将投影后水平中线在竖直曲面内移动直至与投影后侧面中线相交于一点P，两直线产生夹角P，如图3中隧道双向投影所示，将其中任一条直线绕交点往直线相向的方向旋转θ/2即为隧道中轴线，如图3中隧道三维中轴线所示。
图3 基于二维投影的隧道中轴线提取方法示意图

Fig. 3 Extraction of tunnel axis based on 2D projection

2.3 基于中心轴正交旋转的隧道断面连续提取

获取隧道中轴线后，提出一种基于中心轴正交旋转的隧道断面连续提取方法，利用与中心轴垂直的直线在其法截面内绕中心轴正交旋转与隧道壁相交得到断面点，主要过程为：如图4所示在中心轴上任取一初始点o，并另取一点n，作向量 o n →，令过o点且垂直于中心轴的平面为μ，在平面μ内任取一点p，作向量 o p →，求解垂直于向量 o n →与 o p →的向量 o q →，将 o p →与 o q →的线性表示定义为 o k →，延伸或缩短 o k →至 o k 1 →，使其向量长度略微大于半径，将 o k 1 →绕中心轴正交旋转与隧道壁相交，由于点云离散性的特征，可能存在某处没有交点的情况，此时对断面点进行估计，取其在X轴方向距离最近的点为此处断面点，再对其进行最小二乘空间圆拟合，并在圆上以设定圆弧距离均匀地提取断面点，从而获取单个隧道断面点集，设定断面间距，对整个隧道点云数据进行隧道断面的连续提取。
图4 基于中心轴正交旋转的隧道断面连续提取方法示意图

Fig. 4 Schematic diagram of tunnel section extraction method based on orthogonal rotation of central axis

2.4 隧道变形值求取

在对隧道壁点进行滤波及拟合断面点之后，需对断面点进行径向偏差提取以表征形变量，作为一种变形分析参考方式。通过对断面点进行最小二乘空间圆拟合获取圆心坐标，并以圆心坐标、隧道设计半径为参数，求取隧道径向偏差如式（5）所示。
L i = X i - X 0 2 + Y i - Y 0 2 + Z i - Z 0 2
Δ L i = L i - R d
式中：X0、Y0、Z0为横断面圆心O的坐标值； Δ L i为断面点的径向偏移量；Li表示断面点到横断面圆心O的距离；Rd为隧道设计半径值。

3 实验结果及分析

3.1 实验数据

为验证本文滤波算法的有效性及断面提取效果，利用Rigel VZ-400三维激光扫描仪在成都某地铁站区获取的部分地铁隧道点云数据进行相关实验，该段隧道全长58 m，设计半径为2.75 m，共包含55 783 119个扫描数据点，分别选取前、中、后三段隧道点云作为实验样本，如图5所示，其中数据1前段隧道长15.46 m，包含15 391 802个数据点；数据2中段隧道长15.55 m，包含14 049 500个数据点；而数据3后段隧道长15.82 m，含15 176 826个数据点。本文算法通过MATLAB语言实现，并在配置为Inter（R）Core（TM）i5-8265U @1.60GHZ 1.80 GHZ，8.0 GB RAM的计算机上运行。
图5 实验数据示意图

Fig. 5 Schematic diagram of experimental data

3.2 隧道点云滤波结果对比与分析

为证明本文滤波算法的可行性与精确度，对数据1、数据2、数据3这3段隧道点云进行了实验验证。首先对其进行体素下采样，经试验，确定体素间隔为0.01 m，以保持隧道特征完整，同时避免数据过于稀疏，从而得到滤波前的数据量分别为2 052 191、 1 881 242、2 054 173个点。然后对3段隧道分别提取12个断面，得到数据量分别为31 828、28 901、 30 577。为较好地去除离群点并保持隧道壁特征，对其进行半径滤波，通过试验设置搜索半径为0.1 m，并将邻域内最小点数设定为15时效果较佳，滤波后各自点数分别为30 385、27 065、28 866。最后利用RANSAC鲁棒估计来获取隧道圆柱模型参数，按最小整数递增的原则选取经验值1 mm作为初始距离阈值，终止距离阈值为10 mm。通过实验证明，当阈值设置分别为2、4、6 mm时，对比效果最佳，结果如表1所示。根据圆柱模型对隧道点进一步滤波,得到结果如图6所示。
表1 不同断面对应不同阈值的圆柱模型7个参数及滤波后点数

Tab. 1 Seven parameters and filtered points of cylindrical model with different cross-sections corresponding to different thresholds

数据 阈值/mm 轴线上一点(x, y, z)/m 方向向量(a, b, c) 半径r/m 滤波后点数/个
数据1 2 (112.045, 0.018, 1.856) (1.001, 0.026, 0.001) 2.754 18 712
4 (112.041, 0.017, 1.858) (1.004, 0.024, 0.002) 2.751 19 572
6 (112.042, 0.018, 1.856) (1.003, 0.027, 0.007) 2.753 20 604
数据2 2 (131.066, -0.068, 1.859) (1.006, 0.019, 0.005) 2.745 16 589
4 (131.069, -0.065, 1.864) (1.002, 0.014, 0.001) 2.752 17 303
6 (131.061,- 0.068, 1.866) (1.004, 0.022, 0.002) 2.743 18 500
数据3 2 (150.514, 0.054, 1.854) (1.005, 0.006, 0.007) 2.746 17 910
4 (150.507, 0.059, 1.857) (1.001, 0.003, 0.010) 2.749 18 804
6 (150.511, 0.063, 1.852) (0.998, 0.002, 0.003) 2.744 19 801
图6 RANSAC圆柱拟合滤波结果

Fig. 6 Results of RANSAC cylindrical fitting filtering

从图6中可看出，对于3段隧道，当阈值设置为2 mm时位置1、2、3处出现过度滤波的现象，将应保留的一些隧道壁点误判成噪声剔除，使得隧道轮廓特征未能完整保留；当阈值调整至4 mm时，则达到了最佳滤波效果，不仅完好保留了隧道壁轮廓特征，还有效去除了附着噪声；而当阈值提升到6 mm时虽然能够较好地保留隧道壁特征信息，但仍有一些附着噪声未能剔除干净，如位置4处所示。3组数据获得的圆柱模型7个参数（x, y, z，a, b, c，r）和滤波后点数如表1所示，从表1可看出，当阈值设置为4 mm时3个断面的拟合圆柱半径最为接近设计半径2.75 m，滤波效果最好。因此，以接近设计半径的先验值程度确定距离阈值为4 mm。
为评估本文算法对于提高滤波精度的贡献，将其与最小二乘法[31]、密度聚类法[32]、法向偏差法[33]进行了对比分析，结果如图7所示。从图7可以看出，最小二乘算法与密度聚类算法在位置1、2处出现欠滤波的现象，未能将隧道壁上的噪声点剔除干净，而法向偏差法在位置3、4、5、6处则存在过度滤波的现象，将隧道壁点错当作噪声点剔除。相比较之下，本研究提出的算法在保留隧道壁点的情况下最大程度剔除了噪声点，效果最佳。
图7 不同滤波算法对比结果

Fig. 7 Comparison results of different filtering algorithms

为进一步评价本文滤波算法的性能，采用标准的滤波精度3类误差评价和Kappa系数[1]评价对不同的滤波算法进行定量分析。3类误差主要通过对非隧道壁点与隧道壁点的错误分类进行精度评价，其中Ⅰ类误差为将非隧道壁点错误分类为隧道壁点的百分比，如式（6）所示；Ⅱ类误差为将隧道壁点错误分类为非隧道壁点的百分比，如式（7）所示；Ⅲ类误差为错误分类的点占样本隧道点云数据的百分比，即为总误差，如式（8）所示。其中，Ⅰ类和Ⅱ类误差能够反映出算法的适用性，总误差则体现了滤波的效果，即总误差越小，滤波效果越好。而Kappa系数作为统计学中度量一致性的指标，可以衡量分类准确率并显示算法的鲁棒性强弱，其表达式如式（9）所示。
T y p e I = b 0 a 0 + b 0 × 100 %
T y p e I I = c 0 c 0 + d 0 × 100 %
T o t a l = b 0 + c 0 a 0 + b 0 + c 0 + d 0 × 100 %
e = a 0 + b 0 + c 0 + d 0 P 0 = a 0 + d 0 e P c = a 0 + b 0 a 0 + c 0 + c 0 + d 0 b 0 + d 0 e 2
                                                      K a p p a = P 0 - P c 1 - P c
式中： a0表示正确分类的非隧道壁点的点数； b0表示将非隧道壁点错分类为隧道壁点的点数； c0表示将隧道壁点错分类为非隧道壁点的点数； d0表示正确分类的隧道壁点的点数。
为验证本文滤波算法的有效性，本文对3个隧道断面点云数据分别采用不同的滤波算法进行对比实验，将各分类点数手工标注出来，并通过3类误差、分类准确率和时间效率来验证不同滤波算法的性能，结果如表2和表3所示。
表2 用于不同断面的滤波算法参数

Tab. 2 Parameters of filtering algorithm for different sections

数据 滤波算法 a0 b0 c0 d0
数据1 最小二乘法 11 047 1 122 132 19 527
密度聚类法 10 989 1 180 257 19 402
法向偏差法 12 041 128 903 18 756
本文算法 11 973 196 269 19 390
数据2 最小二乘法 10 577 1 064 62 17 198
密度聚类法 10 441 1 200 98 17 162
法向偏差法 11 547 94 546 16 714
本文算法 11 483 158 115 17 145
数据3 最小二乘法 10 664 945 84 18 884
密度聚类法 10 712 897 169 18 799
法向偏差法 11 528 81 981 17 987
本文算法 11 437 172 201 18 767
表3 用于不同断面的滤波算法评估指标

Tab. 3 Evaluation index of filtering algorithm for different sections

数据 去噪算法 TypeI/% TypeII/% Total/% Kappa/% 时间/s
数据1 最小二乘法 9.22 0.67 3.94 91.53 15.78
密度聚类法 9.70 1.31 4.51 90.31 6.67
法向偏差法 1.05 4.60 3.24 93.22 9.13
本文算法 1.61 1.37 1.46 96.91 8.32
数据2 最小二乘法 9.14 0.36 3.90 92.00 11.49
密度聚类法 10.31 0.57 4.49 90.40 4.31
法向偏差法 0.81 3.16 2.21 95.43 6.99
本文算法 1.36 0.67 0.94 98.04 5.72
数据3 最小二乘法 8.14 0.44 3.37 92.74 12.62
密度聚类法 7.73 0.89 3.49 92.50 3.98
法向偏差法 0.70 5.17 3.47 92.74 7.18
本文算法 1.48 1.06 1.22 97.41 5.69
从算法适用性的角度出发，本文所提出的算法在3段隧道的Ⅰ类误差与Ⅱ类误差之和分别为2.98%、2.03%、2.54%，相较于最小二乘法、密度聚类法及法向偏差法，其适用性表现最佳；就滤波效果与算法鲁棒性而言，本文算法在3段隧道中的总误差最小，并且Kappa系数最高，表明其滤波效果优于其他3种算法，鲁棒性也更强；而从时间效率来看，本文算法相比于最小二乘法和法向偏差法具有更好的性能，仅次于密度聚类法，但后者在适用性、鲁棒性及滤波效果方面表现不佳。综上所述，本文的滤波算法在隧道场景中展现出良好的适用性，并具备较佳的滤波效果。采用该方法对下采样后的隧道点云数据进行滤波，其结果如图8所示。
图8 滤波结果示意图

Fig. 8 Schematic diagram of filtering results

3.3 隧道断面提取结果与分析

采用双向投影方式将去噪后获取的隧道壁点云分别投影至XOY、XOZ平面，根据2.2节所提出的方法从中提取投影边界点并拟合边界线，然后分别估计水平面和侧面所在的投影中线，最终得到隧道的三维中线，为更加清晰直观地观察投影后的点云，将其中一个投影结果局部放大，如图9所示。
图9 隧道中轴线提取

Fig. 9 Schematic drawing of tunnel central axis

根据2.3节提出的方法连续提取隧道断面点，设定断面间距为0.5 m，对数据1、数据2、数据3分别提取24个断面，如图10所示。为测试断面提取的精度，计算原始数据点与拟合断面的距离偏差，采用均方根误差值作为评价指标，得到如图11所示。
图10 隧道断面连续提取示意图

Fig. 10 Schematic diagram of tunnel section

图11 断面拟合均方根误差

Fig. 11 Sectional fitting root mean square error

数据1、数据2和数据3断面拟合的最大均方根误差分别为9.2、7.3、9.4 mm，而最小均方根误差分别为3.7、3.3、3.5 mm，各自的均方根误差均值分别为6.2、5.2、6.5 mm，这些结果证明了此次断面拟合的高准确度；由于隧道断面的标准形状为圆形，因此将拟合得到的圆形半径与设计半径2.75 m进行比较，如图12所示，其中数据1、数据2及数据3的拟合半径与设计半径之间最大差值分别为4.0、3.9、3.1 mm，而最小都为0 mm，其平均标准偏差分别为1.4、1.2、1.5 mm，表明了本文方法提取隧道断面的可行性。为进一步评估本文方法的有效性，我们使用相同的数据集，即成都某地铁线路的另一段隧道，将本文算法与Cao等[4]方法和Kang等[28]方法进行比较，如表4所示，相较于另外2种方法，本文方法在均方根误差均值与径向偏差均值上分别降低了2.5 mm、2.7 mm与2.0 mm、2.1 mm，效果更佳，验证了本文方法提取隧道断面的有效性及准确性。
图12 拟合半径与设计半径的偏差

Fig. 12 Deviation between fitting radius and design radius

表4 断面提取方法对比评估指标

Tab. 4 Comparative evaluation index of cross-section extraction methods

断面提取方法 均方根误差/mm 径向偏差/mm
最大值 最小值 均值 最大值 最小值 均值
文献[4]方法 14.8 5.5 8.7 9.0 1.0 4.2
文献[33]方法 15.3 5.2 8.9 9.0 0 4.3
本文方法 9.2 3.6 6.2 6.0 0 2.2

3.4 隧道点云变形可视化分析

本研究以圆形隧道为例，根据式（5）计算变形值，为直观展示隧道整体变形情况，对点云进行渲染，从而获得3段隧道的径向位移点云渲染图，如 图13所示，其变形值范围介于0~18 mm之间。当点处于向外突出部分时，径向偏差呈正值，以红色表示，当点处于向内凹陷部分时，则呈负值，以蓝色表示。图13中正负变形值的不对称分布表明了隧道整体变形向外突出和向内凹陷的不等效特征。其中，隧道顶部主要显示负值，而两侧主要显示正值，这说明整个隧道呈现出顶部下沉，两侧扩张的发展趋势。这一现象归因于隧道在竖直方向受到压力大于水平方向，使得结构趋近椭圆化，这是合理变形的一种体现。
图13 隧道点云整体变形渲染

Fig. 13 Overall deformation rendering of tunnel point cloud

4 结论与讨论

4.1 结论

本研究提出了一种基于激光点云的隧道断面提取及形变可视化分析方法，以成都市某地铁线路3段地铁隧道的激光点云为实验数据，实现了对隧道断面的高效提取及形变可视化分析，主要结论如下：
（1）提出了一种结合RANSAC圆柱拟合与半径滤波的组合滤波方法，有效剔除了离群点及附着在隧道壁上的噪声点，从而获得干净的隧道壁点云，相较于传统的最小二乘法、密度聚类法和法向偏差法，该方法展现出更强的鲁棒性和准确性。
（2）提出了一种基于中心轴正交旋转的隧道断面提取方法，以双向投影为基础获取中轴线，通过与其正交旋转的直线与隧道壁相交提取断面点，并将所提取的断面点与原始点云进行误差分析，同时参考已有方法验证该技术在取隧道断面提取方面的可行性和准确性。
本研究的方法能够精确地提取隧道断面，并有效反应出隧道变形情况，其算法具有良好的鲁棒性，为隧道安全监测工作提供了可靠依据。

4.2 讨论

本文在设计实验时，优先考虑了隧道的圆柱形特征，并采用组合滤波的方式提高了噪声去除的精度，但实际上并非所有隧道都类似于圆柱形，不能兼顾解决拱形（马蹄形）隧道、矩形隧道等的噪声去除问题是本文的不足之处。当隧道点云缺失较为严重时，提取的断面点较少，会导致拟合的精度降低，从而使得变形分析不准确。上述情况是影响本文实验结果的主要因素，后续会对其展开进一步研究，尝试将深度学习模块引入隧道点云去噪，使得去噪方法的适用性更强，并针对点云缺失的问题提出合适的上采样方法，降低上述因素对实验结果造成的影响。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
李勇, 罗尹政, 濮启鹏, 等. 一种适用于隧道场景的激光点云地面滤波和隧道壁及标靶球提取方法[J]. 中国激光, 2023, 50(13):3788/CJL220845.

[Li Y, Luo Y Z, Pu Q P, et al. A method for ground filtering of laser point cloud and extraction of tunnel wall and target sphere[J]. China Journal of Lasers, 2023, 50(13):3788/CJL220845.] DOI:10.3788/CJL220845

[2]
Cao Z, Chen D, Peethambaran J J, et al. Tunnel reconstruction with block level precision by combining data-driven segmentation and model-driven assembly[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(10):8853-8872. DOI:10.1109/TGRS.2020.3046624

[3]
毛庆洲, 徐浩轩, 朱璟, 等. 利用高密度点云现场检测在建隧道超欠挖[J/OL]. 武汉大学学报(信息科学版):1-12[2024-05-21].

[Mao Q Z, Xu H X, Zhu J, et al. On-site detection of over-excavation and under-excavation of tunnels under construction using high-density point clouds[J/OL]. Journal of Wuhan University (Information Science Edition):1-12[2024-05-21].] DOI:10.13203/j.whugis20220601

[4]
Cao Z, Chen D, Shi Y F, et al. A flexible architecture for extracting metro tunnel cross sections from terrestrial laser scanning point clouds[J]. Remote Sensing, 2019, 11(3):297. DOI:10.3390/rs11030297

[5]
Sun W X, Wang J, Jin F X, et al. An adaptive cross-section extraction algorithm for deformation analysis[J]. Tunnelling and Underground Space Technology, 2022, 121:104332. DOI:10.1016/j.tust.2021.104332

[6]
Lam S Y W. Application of terrestrial laser scanning methodology in geometric tolerances analysis of tunnel structures[J]. Tunnelling and Underground Space Technology, 2006, 21(3/4):410. DOI:10.1016/j.tust.2005.12.057

[7]
Gordon S J, Lichti D D. Modeling terrestrial laser scanner data for precise structural deformation measurement[J]. Journal of Surveying Engineering, 2007, 133(2):72-80. DOI:10.1061/(asce)0733-9453(2007)133:2(72)

[8]
Riveiro B, Morer P, Arias P, et al. Terrestrial laser scanning and limit analysis of masonry arch bridges[J]. Construction and Building Materials, 2011, 25(4):1726-1735. DOI:10.1016/j.conbuildmat.2010.11.094

[9]
Zhang Y X, Ren X H, Zhang J X, et al. A method for deformation detection and reconstruction of shield tunnel based on point cloud[J]. Journal of Construction Engineering and Management, 2024, 150(3):04024006. DOI:10.1061/JCEMD4.COENG-14225

[10]
卞政, 石波, 吴凡, 等. 基于PointNet++进行附属设施语义分割的隧道收敛变形分析[J/OL]. 铁道科学与工程学报:1-13[2024-05-21].

[Bian Z, Shi B, Wu F, et al. Analysis of tunnel convergence deformation based on PointNet++ semantic segmentation of ancillary facilities[J/OL]. Journal of Railway Science and Engineering: 1-13[2024-05-21].] DOI:10.19713/j.cnki.43-1423/u.T20240179

[11]
王耀东, 苏广思, 方恩权, 等. 基于激光雷达的隧道轮廓三维点云重构与形变检测研究[J]. 中南大学学报(自然科学版), 2024, 55(6):2393-2403.

[Wang Y D, Su G S, Fang E Q, et al. Research on three-dimensional point cloud reconstruction and deformation detection of tunnel contours based on LIDAR[J]. Journal of Central South University (Science and Technology), 2024, 55(6):2393-2403.] DOI: 10.11817/j.issn.1672-7207.2024.06.029

[12]
程云建, 王辉, 仇文革. 基于三维激光点云的隧道掌子面挤出位移场高精度监测方法[J]. 中国公路学报, 2024, 37(7):46-57.

DOI

[Cheng Y J, Wang H, Qiu W G. High-precision monitoring method for extrusion displacement field of tunnel face based on 3D laser point cloud[J]. China Journal of Highway and Transport, 2024, 37(7):46-57.] DOI:10.19721/j.cnki.1001-7372.2024.07.004

[13]
钱禹航, 王竞雪, 郑雪涛. 结合谱聚类和粒子群改进K-means聚类的机载LiDAR点云单木分割方法[J]. 地球信息科学学报, 2024, 26(9):2177-2191.

DOI

[Qian Y H, Wang J X, Zheng X T. Improved K-means clustering method based on spectral clustering and particle swarm optimization for individual tree segmentation of airborne LIDAR point clouds[J]. Journal of Geo-information Science, 2024, 26(9):2177-2191.] DOI:10.12082/dqxxkx.2024.240243

[14]
关宇忻, 王竞雪, 许峥辉. 顾及分层动态区域增长的车载LiDAR点云行道树提取方法[J]. 地球信息科学学报, 2024, 26(8):1975-1990.

DOI

[Guan Y X, Wang J X, Xu Z H. A hierarchical dynamic region growing method for extracting street trees from vehicle LIDAR point cloud data[J]. Journal of Geo-information Science, 2024, 26(8):1975-1990.] DOI:10.12082/dqxxkx.2024.240117

[15]
韦征, 周臻, 俞旻韬, 等. 基于三维激光扫描点云整体分析的铁路隧道超欠挖检测方法[J]. 铁道学报, 2023, 45(1):135-140.

[Wei Z, Zhou Z, Yu M T, et al. Research on detection method for tunnel underbreak and overbreak based on 3D laser scanning point cloud integral analysis[J]. Journal of the China Railway Society, 2023, 45(1):135-140.] DOI:10.3969/j.issn.1001-8360.2023.01.017

[16]
韦征, 曾庆谊, 周建强, 等. 基于概率密度的隧道三维激光扫描监测方法[J]. 铁道工程学报, 2023, 40(2):66-72.

[Wei Z, Zeng Q Y, Zhou J Q, et al. Tunnel 3D laser scanning monitoring method based on probability density[J]. Journal of Railway Engineering Society, 2023, 40(2):66-72.]

[17]
刘新根, 陈莹莹, 刘学增. 激光扫描盾构隧道断面变形快速检测[J]. 交通运输工程学报, 2021, 21(2):107-116.

[Liu X G, Chen Y Y, Liu X Z. Laser scanning-based rapid detection of deformation of shield tunnel section[J]. Journal of Traffic and Transportation Engineering, 2021, 21(2):107-116.] DOI:10.19818/j.cnki.1671-1637.2021.02.009

[18]
程效军, 贾东峰, 刘燕萍, 等. 基于中轴线的隧道点云去噪算法[J]. 同济大学学报(自然科学版), 2015, 43(8):1239-1245.

[Cheng X J, Jia D F, Liu Y P, et al. Tunnel point cloud denoising algorithm based on centerline[J]. Journal of Tongji University (Natural Science Edition), 2015, 43(8):1239-1245.] DOI:10.11908/j.issn.0253-374x.2015.08.018

[19]
Shi B, Yang M, Liu J, et al. Rail transit shield tunnel deformation detection method based on cloth simulation filtering with point cloud cylindrical projection[J]. Tunnelling and Underground Space Technology, 2023, 135:105031. DOI:10.1016/j.tust.2023.105031

[20]
Cheng Y J, Qiu W G, Lei J. Automatic extraction of tunnel lining cross-sections from terrestrial laser scanning point clouds[J]. Sensors, 2016, 16(10):1648. DOI:10.3390/s16101648

[21]
杜黎明, 钟若飞, 孙海丽, 等. 移动激光扫描技术下的隧道横断面提取及变形分析[J]. 测绘通报, 2018,(6):61-67.

DOI

[Du L M, Zhong R F, Sun H L, et al. Tunnel cross section extraction and deformation analysis based on mobile laser scanning technology[J]. Bulletin of Surveying and Mapping, 2018,(6):61-67.] DOI:10.13474/j.cnki.11-2246.2018.0177

[22]
吴廷, 侯阳飞, 鲍金. 基于三维激光点云的隧道中轴线及断面连续提取[J]. 测绘与空间地理信息, 2018, 41(11):85-87.

[Wu T, Hou Y F, Bao J. Continuous extraction of axis and section in tunnel based on 3D laser point cloud[J]. Geomatics & Spatial Information Technology, 2018, 41(11):85-87.] DOI:10.3969/j.issn.1672-5867.2018.11.024

[23]
Yasuda N, Cui Y. Deformation estimation of a circular tunnel from a point cloud using elliptic Fourier analysis[J]. Tunnelling and Underground Space Technology, 2022, 125:104523. DOI:10.1016/j.tust.2022.104523

[24]
冯阳, 陈长军, 闫利, 等. 一种基于半圆柱模型的隧道点云中轴线提取与滤波方法[J]. 测绘地理信息, 2021, 46(3):55-59.

[Feng Y, Chen C J, Yan L, et al. A method of central axis extraction and tunnel point cloud filtering by a semi-cylindrical model[J]. Journal of Geomatics, 2021, 46(3):55-59.] DOI:10.14188/j.2095-6045.2018490

[25]
Wang W X, Chen W W, Kevin W, et al. Extraction of tunnel center line and cross-sections on fractional calculus, 3D invariant moments and best-fit ellipse[J]. Optics & Laser Technology, 2020, 128:106220. DOI:10.1016/j.optlastec.2020.106220

[26]
Jia D F, Zhang W P, Liu Y P. Systematic approach for tunnel deformation monitoring with terrestrial laser scanning[J]. Remote Sensing, 2021, 13(17):3519. DOI:10.3390/rs13173519

[27]
方俊杰. 基于地面激光扫描仪的隧道断面提取研究[J]. 测绘与空间地理信息, 2021, 44(2):212-214,217.

[Fang J J. Research on extraction of tunnel section based on ground laser scanner[J]. Geomatics & Spatial Information Technology, 2021, 44(2):212-214,217.] DOI:10.3969/j.issn.1672-5867.2021.02.057

[28]
Kang Z Z, Zhang L Q, Tuo L, et al. Continuous extraction of subway tunnel cross sections based on terrestrial point clouds[J]. Remote Sensing, 2014, 6(1):857-879. DOI:10.3390/rs6010857

[29]
李先帅, 武斌. 基于椭圆拟合的隧道点云数据去噪方法[J]. 铁道科学与工程学报, 2021, 18(3):713-719.

[Li X S, Wu B. Denoising method of tunnel point cloud data based on ellipse fitting[J]. Journal of Railway Science and Engineering, 2021, 18(3):713-719.] DOI:10.19713/j.cnki.43-1423/u.T20200403

[30]
柳斌, 李雪梅. 一种基于激光雷达点云的自适应双半径滤波算法[J]. 兵工学报, 2023, 44(9):2768-2777.

DOI

[Liu B, Li X M. A self-adaptive dual radius filtering algorithm based on LIDAR point cloud[J]. Acta Armamentarii, 2023, 44(9):2768-2777.] DOI:10.12382/bgxb.2022.1093

[31]
Yu C Z, Ji F, Xue J P. Cutting plane based cylinder fitting method with incomplete point cloud data for digital fringe projection[J]. IEEE Access, 2020, 8:149385-149401. DOI:10.1109/ACCESS.2020.3016424

[32]
曹桂萍, 刘行思, 刘念, 等. 基于激光三维点云分割地铁隧道壁表面物体[J]. 光学学报, 2020, 40(21):38-46.

[Cao G P, Liu X S, Liu N, et al. Segmentation of subway tunnel wall surface objects based on laser 3D point cloud[J]. Acta Optica Sinica, 2020, 40(21):38-46.] DOI:10.3788/AOS202040.2110001

[33]
邓辉, 蓝秋萍, 廖威, 等. 基于法向偏差的隧道点云去噪算法[J]. 测绘工程, 2018, 27(1):59-63.

[Deng H, Lan Q P, Liao W, et al. Tunnel point clouds denoising algorithm based on normal deviation[J]. Engineering of Surveying and Mapping, 2018, 27(1):59-63.] DOI:10.19349/j.cnki.issn1006-7949.2018.01.012

Options
文章导航

/

〈 〉