EN中文

地球信息科学学报 >

2025 , Vol. 27 >Issue 1: 60 - 82

DOI: https://doi.org/10.12082/dqxxkx.2025.240718

地球信息科学理论与方法

地理空间智能预测研究进展与发展趋势

  • 王培晓 , 1 ,
  • 张恒才 , 1, 2, * ,
  • 张岩 3 ,
  • 程诗奋 1, 2 ,
  • 张彤 4 ,
  • 陆锋 1, 2, 5
展开
  • 1.中国科学院地理科学与资源研究所 地理信息科学与技术全国重点实验室，北京 100101
  • 2.中国科学院大学资源与环境学院，北京 100049
  • 3.香港中文大学太空与地球信息科学研究所，香港 999077
  • 4.武汉大学 测绘遥感信息工程国家重点实验室，武汉 430079
  • 5.政务大数据应用省部共建协同创新中心，福州 350003
*张恒才（1985— ），男，山东济南人，博士，副研究员，研究方向为三维时空智能、城市计算、人类活动大数据分析等。E-mail:

作者贡献：Author Contributions

王培晓、张恒才和陆锋综述了地理空间智能预测的研究现状，是“地理空间智能预测基础算子”的主要提出者；张岩和程诗奋参与了初稿的写作和修改；张彤提供了必要的平台支持，为基础算子的代码实现与实验提供帮助。所有作者均阅读并同意最终稿件的修改。

WANG Peixiao, ZHANG Hengcai, and LU Feng reviewed the current status of geospatial intelligent prediction and are the primary authors of Geospatial Intelligent Prediction Basic Operator. ZHANG Yan and CHENG Shifen contributed to drafting and revising the manuscript, while ZHANG Tong provided crucial platform support for the implementation of the basic operator. All authors have read and approved the final manuscript.

王培晓（1994— ）， 男，山东济南人，博士，博士后，研究方向为时空数据分析、时空预测、轨迹分析等。E-mail:

收稿日期: 2024-11-30

  修回日期: 2025-01-01

  网络出版日期: 2025-01-23

基金资助

国家重点研发计划项目(2022YFB3904102)

收起

GeoAI-driven Spatiotemporal Prediction: Progress and Prospects

  • WANG Peixiao , 1 ,
  • ZHANG Hengcai , 1, 2 ,
  • ZHANG Yan 3 ,
  • CHENG Shifen 1, 2 ,
  • ZHANG Tong 4 ,
  • LU Feng 1, 2, 5
Expand
  • 1. State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
  • 2. College of Resources and Environment, University of Chinese Academy of Sciences, Beijing 100049, China
  • 3. Institute of Space and Earth Information Science, the Chinese University of Hong Kong, Hong Kong 999077, China
  • 4. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing Science, Wuhan University, Wuhan 430079, China
  • 5. Fujian Collaborative Innovation Center for Big Data Applications in Governments, Fuzhou 350003, China
*ZHANG Hengcai, E-mail:

Received date: 2024-11-30

  Revised date: 2025-01-01

  Online published: 2025-01-23

Supported by

National Key Research and Development Program of China(2022YFB3904102)

Fold

摘要

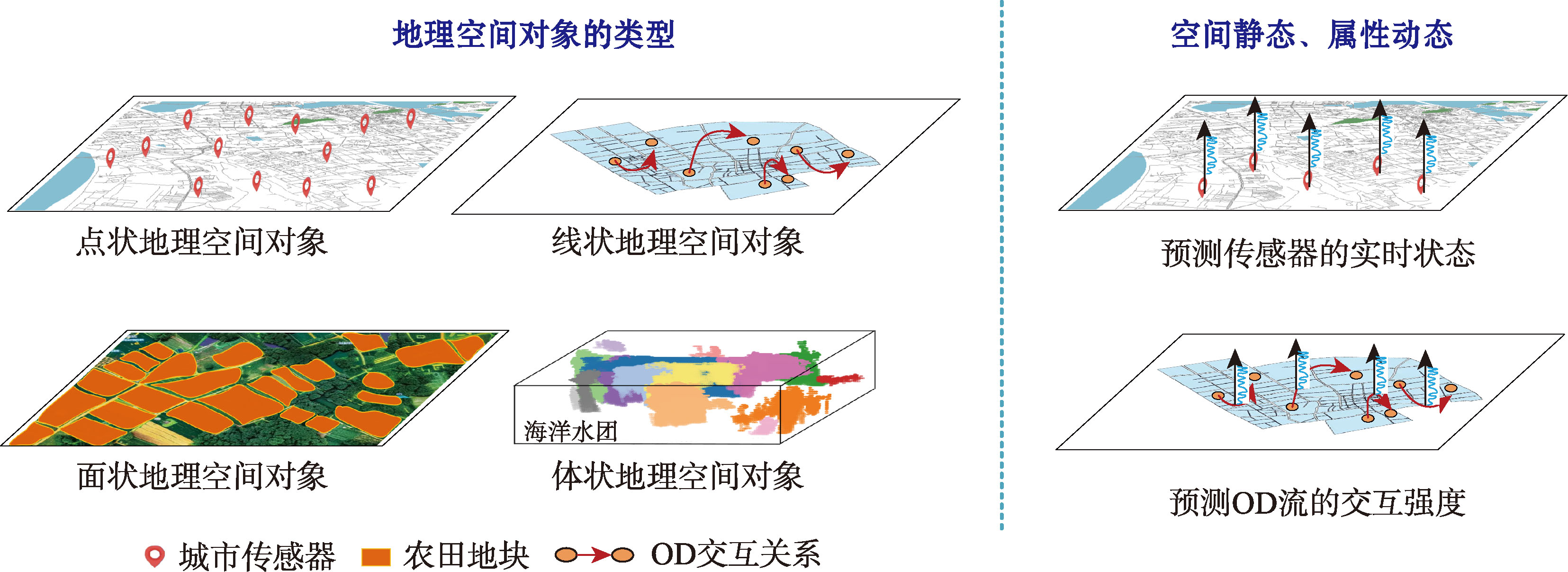
【意义】预测是地理空间人工智能（Geospatial Artificaial Intelligence, GeoAI）重要研究方向，也是测绘地理信息技术与人工智能技术深度融合、智能化创新的关键，支撑空间智能技术走向广域多样化应用场景落地应用。【进展】本文回顾了地理空间智能预测的技术发展历史，综述了基于统计学习、深度学习及生成式大模型的智能预测模型，阐述了智能预测模型中的时空依赖关系嵌入机制，解耦了时间关系建模、空间关系建模及时空关系建模等通用计算算子。【挑战与展望】本文总结归纳了智能预测模型在标注数据稀疏、可解释性缺失、泛化能力匮乏、模型压缩轻量化及模型高可靠性不足等挑战，思考并提出了地理空间智能预测技术未来4个发展趋势与研究方向：耦合多算子的可配置通用空间智能预测平台、融合多模态知识的生成式预测模型、先验指导的深度学习智能预测模型，以及地理空间智能预测模型拓展地球系统深度预测应用领域。

关键词： 地理空间人工智能; 时空预测; 时空建模; 深度学习; 生成模型

本文引用格式

王培晓 , 张恒才 , 张岩 , 程诗奋 , 张彤 , 陆锋 . 地理空间智能预测研究进展与发展趋势[J]. 地球信息科学学报, 2025 , 27(1) : 60 -82 . DOI: 10.12082/dqxxkx.2025.240718

Abstract

[Objectives] Forecasting is a key research direction in Geospatial Artificial Intelligence (GeoAI), playing a central role in integrating surveying, mapping, geographic information technologies, and artificial intelligence. It drives intelligent innovation and facilitates the application of spatial intelligence technologies across diverse real-world scenarios. [Progress] This study reviews the historical development of GeoAI-driven spatiotemporal forecasting, providing an overview of prediction models based on statistical learning, deep learning, and generative large models. In addition, it explores the mechanisms of spatiotemporal dependence embedding within these models and decouples general computational operators used for modeling temporal, spatial, and spatiotemporal relationships. [Prospect] The challenges faced by intelligent prediction models include sparse labeled data, lack of explainability, limited generalizability, insufficient model compression and lightweight design, and low model reliability. Furthermore, we discuss and propose four future trends and research directions for advancing geospatial intelligent prediction technologies: a generalized spatial intelligent prediction platform incorporating multiple operators, generative prediction models integrating multimodal knowledge, prior-guided deep learning-based intelligent prediction models, and the expansion of geospatial intelligent prediction models into deep predictive applications for Earth system analysis.

Key words： geospatial artificial intelligence; spatiotemporal forecasting; spatiotemporal modeling; deep learning; generative models

1 引言

地理空间智能预测基于空间对象的历史高维属性，预测其在未来的属性或状态值[1⇓-3]。作为地理信息科学与人工智能深度融合的典型技术，地理空间智能预测目前已成为地理空间人工智能（Geospatial Artificial Intelligence， GeoAI）的前沿研究主题[4⇓-6]。同时，在泛在地理信息时代，交通[7⇓-9]、空气质量[10⇓-12]、气象[13⇓-15]等高动态非结构化地理空间数据的爆发式增长，也为智能预测模型的实际应用提供了丰富的时空数据源和宝贵的发展机遇。
目前地理空间智能预测已在多个领域取得重要进展，如图1所示，根据地理空间对象的类型，预测任务可分为面向点状、线状、面状和体状要素的智能预测。顾名思义，点状地理空间对象指的是其空间形态可抽象为零维点的对象[16⇓-18]，而线状、面状和体状对象则分别指其空间形态可抽象为一维线、二维面和三维体的对象[19⇓-21]。在粗粒度预测任务中，线状、面状和体状地理空间对象通常不考虑其内部结构，而是将其抽象为点状对象，如预测农田地块的整体土壤状态[22]。但在细粒度建模中，为了更准确地捕捉对象的内部结构、空间关系和演变过程，可能需要保留原有的对象形态及其拓扑结构，如预测海洋水团内部的温度分布[23-24]。根据预测结果时间尺度的不同，地理空间智能预测又可以分为： ① 近临短时预测，特点是预测结果涵盖较短时间跨度，如预测未来几分钟或未来几小时的交通流量[25⇓-27]、空气质量[28]等； ② 中期预测，特点是预测结果涵盖中等时间范围，如预测未来几个月的气象变化[29-30]； ③ 长时预测，特点是预测结果涵盖较长时间跨度，如预测多年的气候变化趋势[31-32]。
图1 地理空间智能预测技术

Fig. 1 GeoAI-driven spatiotemporal prediction

除上述分类体系外，基于算法原理的分类体系也是国内外学者广泛采用的常见分类方式[33-34]。究其原因，地理空间智能预测的核心任务是建模地理空间数据中的复杂时空依赖关系，面向算法原理的分类体系则有助于剖析预测任务中的全过程协同作用机制，理解地球系统的运行模式与规律。在地理空间智能预测迅速发展的当下，从内在原理层面清晰梳理复杂的地理空间智能预测尤为重要，这不仅有助于全面把握当前的研究脉络，还为后续研究提供坚实的理论基础和方法指导。鉴于此，本文综述了基于统计学习、深度学习和深度生成模型的3类智能预测模型，系统梳理了智能预测模型中时空依赖的建模机制，提出了“地理空间智能预测基础算子”的概念，厘清了复杂模型的内在结构与功能关系，分析了地理空间智能预测模型面临挑战与未来发展趋势。

2 地理空间智能预测技术研究进展

2.1 基于统计学习的空间智能预测

基于统计学习的空间智能预测可分为2类：一类是基于经典统计学的预测，另一类是基于浅层机器学习的智能预测。需要注意的是，浅层机器学习同样依赖于概率论和统计推断，因此实际上也是统计学习的一种扩展。
基于经典统计学的预测是一种较早的预测技术，旨在通过建立特定的参数模型来预测地理空间对象的未知属性信息[35]。具体而言，这类方法可大致分为3类：仅考虑空间依赖的预测方法、仅考虑时间依赖的预测方法、以及结合空间依赖和时间依赖的预测方法。仅考虑空间依赖的预测方法假设观测数据在空间维度上遵循特定的数学法则，从而对不同位置上的未知数据进行预测，例如最近邻插值、克里金插值（Kriging）[35]、反距离权重（Inverse Distance Weighting， IDW）[36]和地理加权回归模型等（Geographically Weighted Regression， GWR）[37]。与之相对，仅考虑时间依赖的预测方法则假设观测数据在时间维度上遵循特定的数学法则，从而对不同时间窗口的未知数据进行预测，例如自回归模型（Autoregression，AR）[38]、历史平均模型（Historical Average， HA）[39]和自回归积分滑动平均模型（Autoregressive Integrated Moving Average Model， ARIMA）[40]等。此外，结合空间和时间依赖的预测方法则通过同时约束观测数据在时间维度和空间维度上的数学法则，实现不同位置或不同时间窗口未知数据的综合预测，例如时空克里金插值（Spatio-Temporal Kriging，ST-Kriging）[41]、时空反距离权重（Spatio-Temporal Inverse Distance Weighting， ST-IDW）[42]和时空自回归积分滑动平均模型（Spatio-Temporal Autoregressive Integrated Moving Average Model，ST-ARIMA）[43]等。鉴于统计学习模型具有明确的数学表达式，这类智能预测方法在计算效率和泛化能力等方面往往表现出一定的优势，但也面临着预测精度较低的挑战[44]。究其原因，统计学习模型遵循严格的数学法则，而实际的时空环境往往难以满足这些前提假设；此外，统计学习模型是一种参数模型，参数模型难以有效捕捉地理要素状态中蕴含的复杂非线性时空关系[45]。
随着大数据的蓬勃发展，浅层机器学习模型，如支持向量机（Support Vector Machine， SVM）[46]、随机森林（Random Forest， RF）、梯度提升机（Gradient Boosting Machines， GBM）[47]和K近邻（K-Nearest Neighbors， KNN）[48]等，因其数据驱动特性、计算效率高且能够揭示非线性关系，广泛应用于各种预测任务。然而，在地理空间智能预测任务中，经典的浅层机器学习模型往往表现不佳[49⇓-51]。究其原因，地理空间数据蕴含着复杂的空间自相关性和时间依赖性，但经典浅层机器学习模型的样本独立同分布假设违背了这一特性，限制了其在地理空间智能预测中的应用效果[52-53]。为了解决这一问题，很多学者在浅层机器学习模型中扩展空间关系和时间关系，以提升模型对地理空间数据的预测能力。在扩展空间关系方面，往往考虑的是空间依赖性，即观测数据在空间位置上的临近性或相似性[54-55]。引入空间依赖性的常见方法是在浅层机器学习模型中加入空间邻域[45,52]，例如，在城市交通流预测中，可以将目标交通路段及其相邻路段的交通流量作为输入去提升预测准确性[56-57]。在扩展时间关系方面，往往考虑的是时间依赖性，即观测数据在相邻时间窗口中的相似性[26,58]。与引入空间关系类似，引入时间依赖性的常见方法则是加入时间邻域，例如，在空气质量预测中，可以将当前时间窗口及过去时间窗口的PM2.5浓度值作为输入去提升预测结果的准确性和可靠性[27]。相较基于统计学习模型的智能预测方法，基于浅层机器学习模型的智能预测方法尽管能够捕捉非线性关系，但也存在一定的局限[59-60]。具体而言，此类模型难以捕捉深层次的非线性关系，且时空关系的扩展主要局限于输入特征的修改，未能深入挖掘时空数据中的复杂交互，限制了模型的预测精度[3,61]。此外，在此类模型中，空间邻域的地理要素选择、时间邻域的时间窗口设置等都需要依赖人工经验，不仅耗时且容易导致模型在面对新数据时表现不稳定[62-63]。

2.2 基于深度学习的空间智能预测

随着计算架构的革命性进展和并行计算能力的突破，深度学习模型呈现出前所未有的精度和广泛的跨领域应用潜力[28,64⇓-66]。与经典统计学习和浅层机器学习相比，深度学习模型凭借其卓越的复杂非线性关系捕捉能力、自动特征学习能力和多层次数据抽象能力，已成为当前地理空间智能预测领域的主流方法[67⇓-69]。近年来，国内外相关学者提出了各式各样的地理空间智能预测模型，并且从不同的研究视角出发，衍生出多种分类方式。
从空间视角来看，地理空间智能预测模型可分为基于格网的智能预测模型[70⇓-72]和基于图的智能预测模型[73⇓-75]。基于格网的智能预测模型将研究区域划分为规则排列的均匀网格单元，采用二维卷积神经网络建模数据中的空间依赖关系。由于规则格网结构具备覆盖范围广和计算便捷等优势，基于格网的智能预测模型非常适用于大尺度场景的预测任务[76⇓⇓-79]，例如时空三维多尺度膨胀密集网络模型（Spatio-Temporal 3D Multiscale Dilated Dense Network， ST-3DMDDN）用于预测城市尺度格网中的居民出行需求[72]、参数共享时空膨胀卷积网络（Parameter-Shared Spatio-Temporal Dilation Convolution Network， STP-DCN）[80]模型用于预测全国尺度格网中的空气质量。与之相较，基于图的智能预测模型则将研究区域中的空间对象抽象为图节点与边，采用图神经网络建模数据中的空间依赖关系。由于图结构可以更精准的刻画地理要素之间的复杂空间关系和拓扑结构，基于图的智能预测模型更适用于高精度的细粒度预测任务[81⇓-83]，例如，因果图神经网络（Causal Graph Convolutional Network，Causal-GCN）模型用于预测每个监测站点的空气质量[16]、双向时空图神经网络（Bidirectional Spatio-Temporal Graph Networks， BiSTGN）用于预测城市路网中每条路段的交通速度[7]。
从时间视角来看，地理空间智能预测模型可分为迭代型智能预测模型和非迭代型智能预测模型[84]。迭代型智能预测模型通常将当前时刻的预测结果作为下一时刻预测的输入，通过多次迭代更新预测真实值[7]；而非迭代型智能预测模型不依赖于先前的预测结果，而是基于独立的输入特征进行一次性预测[85]。典型的迭代型智能预测模型主要为循环神经网络的变种模型[74]，优点在于能够处理长度不固定的时间序列，无需提前知道序列的总长度，具有较强的适应性；缺点则在于迭代顺序计算难以实现并行化，计算开销较大，且训练过程中易产生梯度消失或梯度弥散现象。典型的非迭代型智能预测模型主要为一维卷积网络或基于注意力的变种模型[73,75]，例如时间卷积神经网络模型（Temporal Convolutional Network，TCN）[84]、变压器（Transformer）模型[86⇓-88]等。非迭代型智能预测模型克服了顺序计算的限制，可以在时间维度上并行处理数据，大幅提高了计算效率，但也大幅增加了模型的参数规模，易引发过拟合问题。
上述分类方式虽然包含了大多数地理空间智能预测模型，但依旧聚焦变量的时间自相关或空间自相关。与此同时，许多学者引入了协变量，通过挖掘协变量与目标变量之间的关系进一步提升智能预测模型的预测精度和适应性[70]。常见的协变量包括天气、兴趣点、土地利用、人口密度和交通基础设施等。例如，天气因素对交通流量有显著影响，结合实时气象数据与交通流量数据，可以提升交通流预测模型的准确性和鲁棒性[89]；兴趣点数据对居民出行需求有重要影响，结合兴趣点数据与出行需求数据，可以提高出行需求预测模型的精度和稳定性[90]；交通基础设施数据，包括道路网密度和交通信号位置，能够帮助识别交通瓶颈，优化交通调度和路线规划，增强交通流预测模型的实用性；土地利用数据能够揭示区域功能分布，结合土地利用与环境变化数据，可以优化城市规划和环境变化预测；人口密度在社会经济分析中具有重要作用，将其与公共卫生或资源分配数据结合，有助于提高疾病传播或资源需求的预测精度。此外，近年来，集成先验知识的深度学习也逐渐应用到智能预测模型去改善模型的预测精度、鲁棒性和可解释性[91]，如将流体个别变化方程集成至暴雨预测可以约束降雨的生成过程，增强模型对降雨分布和强度变化的理解[13]；将波动方程集成至地震预测可以约束震动波的传播过程，增强模型对地震波的传播特性的理解[92]；将克里金方程集成至深度学习模型中，可以有效增强模型的可解释性[93]。随着协变量的引入和先验知识的集成，智能预测模型能够有效融合多种数据源和物理规律，显著了提升模型的准确性和鲁棒性，增强了模型在复杂、动态环境中的适应性和可解释性。
总体而言，基于深度学习的智能预测方法正在不断发展，预测精度持续提升，其在各个领域中的表现也愈加卓越，逐渐主导了大多数地理空间智能预测任务的研究和应用，尤其在复杂环境下的高精度预测和动态建模方面展现出显著优势。

2.3 基于深度生成式模型的空间智能预测

基于深度生成式模型的空间智能预测主要通过学习数据的概率分布来输出预测值的潜在范围，而非单纯的数据拟合输出单一的估计值[94]。因此，这种方法也可称为概率性智能预测或不确定性智能预测[95⇓-97]。凭借在概率预测方面的优势，基于深度生成式模型的空间智能预测能够有效应对复杂场景中的不确定性，为决策者提供更加全面和丰富的信息支持。
常见的深度生成式模型包括变分自编码器（Variational AutoEncoder，VAE）[98]、生成对抗网络（Generative Adversarial Network，GAN）[99]、扩散模型（Diffusion Models）[100]和归一化流模型（Normalizing Flows）[101]等。其中，VAE通过引入潜在变量并结合变分推断方法，能够高效地逼近数据的后验分布，特别适用于高维和时序数据的生成[98]。GAN则通过生成器和判别器之间的对抗学习，能够逼真地生成数据样本，从而捕捉数据的分布特征[99]。扩散模型通过逐步向数据中添加噪声并反向去噪的过程生成数据，具有生成过程可控、生成质量高且稳定的特点[100]。流模型则利用一系列可逆变换将简单分布（如高斯分布）映射到复杂数据的真实分布，优势在于其精确的概率建模能力，能够计算数据的对数似然，从而有效建模数据的密度[101]。在地理空间智能预测任务中，深度生成式模型通常与经典深度学习模型相结合去实现高精度的概率预测任务，例如变分递归自编码器（Variational Recurrent AutoEncoder， VRAE）[102]、门控注意力生成对抗网络模型（Gated attentional Generative Adversarial Network，GaGAN）[103]、扩散时空图网络模型（Diffusion Spatio-Temporal Graph Network，DiffSTG）[95]和时空图归一化流模型（Spatio-Temporal Graph Normalizing Flow，STGNF）[104]等。
总的来说，基于深度生成式模型的智能预测具备较强的灵活性与可扩展性，能够提供多样化的预测结果，更好地揭示数据中的变动性与不确定性[94]。在面对高度复杂且动态变化的现实问题时，深度生成模型通过生成多种可能的预测分布，为决策者提供更为全面的决策依据，从而降低了单一预测值可能带来的风险。随着技术的不断进步，此类方法有望在更多领域得到广泛应用，进一步提高预测的准确性与可靠性，为复杂决策提供更加科学、全面的支持。

3 地理空间智能预测时空依赖建模机制

正如前文所述，深度学习模型已经成为当前地理空间智能预测的主流方法。在复杂多样的深度学习智能预测模型中，建模数据中的时间依赖关系和空间依赖关系是不可或缺的关键环节。因此，本小节深入探讨了地理空间智能预测时空依赖建模机制，并提出了“地理空间智能预测基础算子”的概念。具体而言，本小节将智能预测模型解耦为基础算子的组合，旨在厘清复杂模型的内在结构与功能关系。如图2所示，本小节总结了时间关系建模、空间关系建模和时空关系建模三类基础算子。
图2 地理空间智能预测基础算子的分类

Fig. 2 Classification of basic operators in GeoAI-driven spatiotemporal prediction

3.1 地理空间数据组织结构及问题定义

“地理空间智能预测基础算子”依赖于地理空间数据的组织形式。因此，本小节首先介绍了深度学习中常用的2种数据组织结构——格网结构和图结构，并在此基础上给出了不同数学结构下智能预测任务的数学定义。
图3展示了格网数据结构表征气温数据的一个示例。在规则格网结构中，研究区域被划分为均匀的网格单元，每个单元代表一个固定的空间区域，并存储该区域的温度值。一般而言，所有网格单元在所有时间窗口下采集的地理空间数据通常表现为一个三维张量[105-106]： X ˘ = X ˘ t t = 1 T ∈ R P × Q × T，其中 X ˘ t ∈ R P × Q表示第t个时间窗口的地理空间数据，P和Q表示格网数据结构的空间尺寸，T表示格网结构的时间尺寸（地理空间数据的时间窗口总数）。
图3 格网数据结构示意图

Fig. 3 Illustrations of grid data structures

图4展示了图数据结构表征传感器数据的一个示例。相较于气温数据的空间连续分布，传感器数据往往呈现离散不规则分布，而图结构在表征这种离散不规则分布具有天然的优势[107⇓-109]。在图结构 G = V ,   A = v i i = 1 N ,   A中，每个传感器可抽象为图节点vi∈V，节点vi与节点vj之间的关系可抽象为边Aij∈A。一般而言，所有图节点在所有时间窗口下采集的地理空间数据可表示为一个二维矩阵X∈RN×T，其中N表示图节点的总数，T表示时间窗口总数。其中， x t = x i t i = 1 N ∈ R N × 1表示所有图节点在特定时间窗口下采集的地理空间数据， x i = x i t t = 1 T ∈ R T × 1表示特定地理空间对象在所有时间窗口下采集的地理空间数据， x i t ∈ R 1 × 1表示特定地理空间对象在特定时间窗口下采集的地理空间数据。
图4 图数据结构示意图

Fig. 4 Illustrations of graph data structures

如图5所示，地理空间智能预测的目标就是建立一个基于格网结构的预测模型MGrid或基于图结构的预测模型MGraph。前者从三维张量 X ˘中挖掘时空依赖关系去预测未来的地理空间数据[70]，后者从二维矩阵X和图结构G中挖掘时空依赖关系去预测未来的地理空间数据[85]。式（1）和式（2）分别给出了两类模型的数学定义。
X ˘ ^ t + F ,   … ,   X ˘ ^ t + 2 ,   X ˘ ^ t + 1 = M G r i d ← X ˘ t - B + 1 ,   X ˘ t - B ,   … ,   X ˘ t - 1 ,   X ˘ t W
x ^ t + F ,   … ,   x ^ t + 2 ,   x ^ t + 1 = M G r a p h ← x t - B + 1 ,   x t - B ,   … ,   x t - 1 ,   x t G ,   W
式中：MGrid表示基于格网结构的智能预测模型； X ˘ t - B + 1 ,   X ˘ t - B ,   … ,   X ˘ t - 1 ,   X ˘ t ∈ R P × Q × B表示格网结构下历史采集的地理空间数据； X ˘ ^ t + F ,   … ,   X ˘ ^ t + 2 ,   X ˘ ^ t + 1 ∈ R P × Q × F表示格网结构下预测的地理空间数据；P和Q表示格网数据结构的空间尺寸；MGraph表示基于图结构的智能预测模型； x t - B + 1 ,   x t - B ,   … ,   x t - 1 ,   x t ∈ R N × B表示图结构下历史采集的地理空间数据； x ^ t + F ,   … ,   x ^ t + 2 ,   x ^ t + 1 ∈ R N × T表示未来/预测的地理空间数据； N表示图节点的总个数； B表示历史依赖步长； F表示预测步长； W表示地理空间智能预测模型中需要训练的参数。
图5 地理空间智能预测的数学定义

Fig. 5 Mathematical definition of GeoAI-driven spatiotemporal prediction

3.2 时间关系建模算子

时间关系建模基础算子主要面向“单个”地理空间对象的时间序列数据，捕捉时间序列数据的时间依赖关系，揭示数据在不同时间窗口之间的内在关联性。在复杂多样的地理空间智能预测模型中，时间关系建模基础算子通常分为迭代型算子和非迭代型算子2大类。
迭代型算子主要通过递归机制在多个时间窗口之间进行信息传递和状态更新，从而能够捕捉时间序列中的动态变化与依赖关系。常用的迭代型算子包括循环神经网络（Recurrent Neural Network，RNN）算子、长短时记忆网络（Long Short-Term Memory， LSTM）算子[110]、门控循环单元（Gated Recurrent Unit， GRU）算子[111]和神经常微分方程（Neural Ordinary Differential Equations， NODE）算子[112]等。如图6所示，RNN算子通过全连接操作实现信息在不同时间窗口之间的迭代传递，从而处理时序依赖任务； LSTM算子[110]和GRU算子[111]是经典RNN算子的变种，通过引入门控机制来解决经典RNN在长序列数据处理中的梯度消失或梯度爆炸问题，增强了模型对长时依赖关系的捕捉能力。图7展示了NODE算子的运算机制，相较于RNN算子及其变种，NODE算子是一种面向连续时间域的算子，通过常微分方程实现信息在“任意时刻”之间的迭代传递[112⇓-114]。总的来说，迭代型算子的优势在于能够处理长度不固定的时间序列，无需提前知道序列的总长度，具有较强的适应性。然而，它们也面临顺序计算的限制，例如每个时间窗口的输入都依赖于前一个时间窗口的输出，这种递归依赖使得无法在时间维度上实现并行计算。
图6 循环神经网络算子及其变种

Fig. 6 Recurrent neural network operator and its variants

图7 神经常微分方程算子

Fig. 7 Neural ordinal differential equation operator

非迭代型算子与迭代型算子不同，它们不依赖递归机制在时间维度上传递信息或更新状态，而是通过一次性的处理或变换来更新系统状态。常见的非迭代型算子包括一维卷积网络算子（One-Dimensional Convolutional Neural Network， 1D-CNN）[73]、因果卷积网络算子（Causal Convolutional Neural Network，Causal-CNN）、因果膨胀卷积网络算子（Causal Dilation Convolutional Neural Network，Causal-DCNN）[16,84,115]、以及时间注意力算子（Temporal Attention， TA）[82]等。如图8所示， 1D-CNN算子通过在时间维度上滑动卷积核去建立不同时间窗口之间的依赖关系[73]； Causal-CNN算子在1D-CNN算子的基础上严格遵循时间顺序，确保了每个时间窗口的预测仅依赖于过去和当前的输入；Causal-DCNN算子则在Causal-CNN的基础上引入膨胀卷积，通过扩大感受野来捕捉更长时间跨度的依赖关系[16,84,115]。图9展示了TA算子的运算机制，相较于1D-CNN算子及其变种，TA算子能够灵活地调整各个时间窗口的权重，从而更精准地捕捉时间序列数据中的时间依赖关系[82]。相较于迭代型算子，非迭代型算子克服了顺序计算的限制，可以在时间维度上并行处理数据，从而大幅提高计算效率。
图8 一维卷积网络算子及其变种

Fig. 8 One-dimensional convolutional network operator and its variants

图9 时间注意力算子

Fig. 9 Temporal attention operator

3.3 空间关系建模算子

空间关系建模基础算子主要面向所有地理空间对象在“单个时间窗口”下采集的地理空间数据，捕捉地理空间对象之间的空间依赖关系，揭示数据在不同空间位置之间的内在关联性。在复杂多样的地理空间智能预测模型中，空间关系建模基础算子通常分为基于格网结构的算子和基于图结构的算子。
基于格网结构的基础算子通过相邻格网单元之间的邻接关系实现信息在空间维度上的传递，从而捕捉地理实体之间的空间依赖模式[70]。常用的基于格网结构的基础算子包括二维卷积网络算子（Two-Dimensional Convolutional Neural Network，2D-CNN）算子[116]、二维膨胀卷积网络算子（Two-Dimensional Dilation Convolutional Neural Network，2D-DCNN）算子[80]等。如图10所示， 2D-CNN算子通过在二维空间维度上滑动卷积核去建立不同区域之间的空间依赖[116]； 2D-DCNN算子是在2D-CNN算子的基础上引入膨胀卷积，通过扩大感受野来捕捉更大范围的空间依赖。基于格网结构的基础算子具有明显的优缺点[80]。优点是结构简洁、计算效率高，易于并行处理，并且具有较好的灵活性和可扩展性，能够适应不同的空间分辨率和数据需求。缺点则在于它难以有效处理不规则地理空间数据，无法捕捉复杂拓扑或不规则分布的空间特征，同时在处理高分辨率数据时，具有较大的存储开销。
图10 二维卷积网络算子及其变种

Fig. 10 Two-dimensional convolutional network operator and its variants

基于图结构的基础算子利用图结构来表示地理实体的连接关系或依赖关系，从而完成地理实体之间的信息传递。常用的基于图结构的基础算子包括谱图卷积网络算子（Spectral Graph Convolutional Neural Network， Spectral-GCN）算子[117-118]、空间图卷积网络算子（Spatial Graph Convolutional Neural Network， Spatial-GCN）算子[119]、图注意力（Graph Attention Neural Network， GAT）算子[120]、以及空间注意力（Spatial Attention， SA）算子[82]等。其中，Spectral-GCN算子通过特征分解图拉普拉斯矩阵，将卷积操作转化为频谱域的矩阵乘法，从而捕捉不同图节点间的空间依赖[117-118]；Spatial-GCN算子则通过聚合邻居节点的特征，在空间域中提取空间依赖模式[119]；GAT算子在Spatial-GCN算子基础上，自适应调整节点间的相对重要性，进而在空间域中完成邻居节点的特征加权[120]。如图11所示，Spatial-GCN算子和GAT算子的主要区别在于邻居图节点对目标图节点的权重分配。前者假设邻居节点对目标节点具有相同的权重，而后者则根据节点间的相对重要性自适应调整权重。此外，SA算子也可以看成一种特殊的基于图结构的基础算子[82]。如图12所示，经典SA算子可以视为全连接图的GAT算子，两者的数学机制高度相似，均是加权聚合地理空间对象的特征信息。相较于基于格网结构的基础算子，基于图结构的基础算子能够很好地处理不规则、稀疏或异构的地理空间数据，灵活地刻画地理空间对象之间的复杂交互关系。然而，基于图结构的算子也面临着一些挑战，其中最为突出的是计算复杂度较高，尤其是在大规模图数据的处理中，图的遍历、卷积和聚合等操作需要大量计算资源。因此，尽管图结构在灵活性和适应性方面有显著优势，但其在计算和实现上的难度依然是其主要的短板。
图11 空间图卷积算子与图注意力算子的区别

Fig. 11 Difference between spatial graph convolution operator and graph attention operator

图12 空间注意力算子

Fig. 12 Spatial attention operator

3.4 时空关系建模算子

时空关系建模基础算子主要面向所有地理空间对象在“所有时间窗口”下采集的地理空间数据，旨在捕捉地理空间对象在时间和空间2个维度上的动态依赖关系，揭示数据在不同时间点和空间位置之间的内在演变规律。在复杂多样的地理空间智能预测模型中，时空关系建模基础算子可粗略分为时空一体化算子和非时空一体化算子两大类。
时空一体化算子是指能够统一处理空间和时间特征的基础算子，可以连贯和高效地捕捉到数据中的时空依赖关系。常见的时空一体化算子包括三维卷积神经网络算子（Three-Dimensional Convolutional Neural Network，3D-CNN）[71,77]、卷积长短期记忆网络算子（Convolutional Long Short-Term Memory，ConvLSTM）[106]、卷积门控循环单元算子（Convolutional Gated Recurrent Unit，ConvGRU）[105]和扩散卷积循环网络算子（Diffusion Convolutional Recurrent Neural Network，DCRNN）[121]等。如图13所示，3D-CNN算子通过在空间和时间维度上同时进行卷积操作，实现了时空特征的统一建模[71,77]。如图14所示，ConvLSTM[106]、ConvGRU[105]和DCRNN算子[121]分别利用二维卷积运算和图卷积运算替换LSTM、GRU中的全连接运算，实现了时空特征的统一建模。时空一体化算子避免了空间和时间特征的割裂，可以更好的捕捉时空依赖关系，尤其在处理复杂的时空模式时表现优异。然而，时空一体化算子也存在一定的缺点。具体而言，时空一体化算子的结构较复杂，可解释性较差，且难以直观理解空间特征和时间特征的交互作用。
图13 三维卷积网络算子

Fig. 13 Three-dimensional convolutional network operator

图14 基于长短时记忆网络和门控循环单元的时空一体化算子

Fig. 14 Spatiotemporal integration operators based on LSTM and GRU

如图15所示，非时空一体化算子往往将空间特征和时间特征分开建模，然后通过连接、加权或拼接等方式融合中间结果，从而捕捉数据中的时空依赖关系。常见的非时空一体化算子包括基础算子串联块和基础算子并联块。目前，许多智能预测建模任务仍主要依赖于非时空一体化算子，例如时间图卷积网络（Temporal Graph Convolutional Network, T-GCN）[74]通过串联Spectral-GCN算子与GRU算子来实现，而双向时空图网络（Bidirectional Spatiotemporal Graph Network, BiSTGN）[7]则通过并联GAT算子与GRU算子来实现。相比时空一体化算子，非时空一体化算子结构更简化，计算开销较低。但由于空间和时间特征独立处理，可能导致信息割裂，限制了模型对时空交互的捕捉能力。
图15 非时空一体化算子

Fig. 15 Basic operator of non-spatiotemporal integration

4 地理空间智能预测面临的挑战

4.1 预测模型标注数据稀缺挑战

智能预测模型核心是模型训练，标注数据质量高低直接影响预测模型的精度与准确率[122-123]。同时，标注数据与模型训练也是整个智能预测任务中最为耗时的步骤，但当下语义标注数据的通用性较差。因此，为了满足不同类型的预测需求，需要针对预测主题进行单独数据标注与处理。标注数据自身的时空分布特征，所蕴含的时空周期特征等也会影响模型参数选择，因此也需要在标注数据模式与分布特征基础之上设计最优的模型组件搭接策略[124]。此外，突发事件在标注数据中缺失较为严重，造成模型陷入零膨胀问题，模型往往会因为突发事件扰动出现性能下降或失效的风险[125-126]。
为应对该挑战，将强化学习理论与深度学习理论相结合，采用混合专家模型MoE、迁移学习[127-128]、多视图学习[7,57]手段相结合，深度挖掘数据缺失模式，挖掘周期性移动规律会弥补标注数据稀疏方面的不足[57,129-130]。基准数据集的构建对于智能预测模型的精度评测具有重要作用，如加州性能测量系统数据集（Caltrans Performance Measurement System，PeMS）[74]、洛杉矶交通数据集（Los Angeles traffic data、Metr-La）[107]、广州交通速度数据集（Guangzhou Urban Traffic Speed，GUTS）[26]、中国空气质量监测数据集（China Air Quality data，CAQ）[80]和哥白尼气候数据库（Copernicus Climate Data Store, CDS）[131]等。但为适应多种类型的空间智能预测，如何为基准数据集确定合理的数据规模与类型，制定合理的评价指标仍面临挑战。

4.2 预测模型可解释性缺失挑战

深度学习模型是当下流行的地理空间智能预测模型，缺乏可解释性是所有深度学习共同面临的挑战[132-133]。由于参数多、多层网络之间信息传递的非线性等黑盒特征多次引发领域专家对模型预测准确度与可信度的担忧，尤其是模型内部表征学习复杂多样。此外，缺乏有效的神经元隐语义解释等问题，使得模型更深层次的作用原理仍是不清晰的，且目前对于空间智能预测模型可解释性评估指标也极度缺乏[134-135]。
为了应对挑战，透明设计策略可以提高空间智能预测模型可解释性，但提升可解释性可能会增加模型的训练的时间和空间复杂度，可能增加模型的训练时间和空间复杂度，同时影响模型性能。在推进可解释性和透明设计的过程中，如何不出现大的性能衰减、不带来过大的计算开销是新的挑战[113]。地理空间智能预测模型的可解释性约束也是一种有效方法，通过和细粒度语义标注比对获得先验知识，但细粒度语义标注昂贵且可能不全面[136]。此外，学者可以通过敏感性SHAP分析[52,137]、消融实验[138]、可视分析[11,113]等手段验证模块是否发挥作用，也可以从因果推理[139]、解耦表征、辨识因子等角度深入探索预测模型的可解释性，但明确预测模型决策思路与内部语义，使得模型更加可信赖仍面临挑战。

4.3 预测模型泛化迁移能力匮乏挑战

地理空间智能预测模型泛化能力是目前面临的挑战，空间智能预测模型下游任务众多，在特定领域训练好的模型难以在其他领域进行快速部署，需要重新进行模型训练，大大影响了智能预测模型的真正落地[140]。一方面是有多模态数据的高动态空异质性造成。同一位置观测数据往往表现出周期性、邻近性等不同的规律模式[7,141]，时空依赖关系建模具有多样性，且多模态数据具有稀疏不平衡、分布有偏等特征[49]，给智能预测模型的泛化带来挑战。另一方面目前的空间智能预测模型大多属于强依赖数据标注的监督学习，导致计算资源和模型参数的过度冗余使用。当不被告知数据分布特征时，智能预测模型的仅通过自感知与泛化能力来实现新领域目标数据就显得异常困难。
为了应对挑战，亟需通过融合跨领域知识，来提高模型预测能力与鲁棒性，使得模型能够快速获取知识经验，加快知识迁移学习，提高预测任务的优化迭代能力，提高模型训练效率和性能[19,142]。深度元学习（Meta Learning）框架[143-144]也是实现空间智能预测模型的快速学习手段，通过专家知识的辅助实现预测模型的辅助学习与知识推理，利用学习时空数据相关的元知识来提高模型的泛化能力，空间智能预测模型架构自动化设计也是重要的研究命题，可以实现针对特定的下游任务完成模型的架构搜索设计，从繁重的重复试错调优中解放出来。

4.4 预测模型压缩轻量化挑战

模型轻量化目标是尽量减少模型参数量和计算量的同时保持模型的高准确率，目前地理空间智能预测模型动辄上亿的巨量参数，大量堆叠卷积层来捕获较大范围内的时空依赖关系，过多的神经网络层数造成模型的应用场景部署困难，较深的网络结构会加剧空间智能预测模型过平滑和过拟合的风险，损害模型的性能并增加模型的复杂性[145]。模型参数越来越大，所需的训练数据体量也随之暴增，有可能导致维数灾难的发生，而且模型参数使得模型计算量呈指数增长。
为了应对挑战，一些轻量化网络架构设计方案被提出[115,145]，例如膨胀卷积，通过减少神经网络的前向传播次数，提升模型的计算效率或参数规模。网络量化算法从网络参数存储视角降低模型存储空间，通过利用低精度数据格式来表征模型参数，实现模型压缩率与性能的平衡。也有学者通过知识蒸馏方式[142]来训练空间智能预测模型，通过预先训练好的大模型得到预测结果，借鉴生成式对抗网络中对抗学习的原理，来提高模型预测精度。

4.5 预测模型高可靠性不足挑战

目前空间智能预测模型大多以提升预测精度为目标，忽略了模型的高可靠性。在实际场景中，智能预测模型不仅要提高预测结果的准确性，也要保证预测结果的稳健可靠可信赖[[146-147]。空间智能预测模型深入各个领域应用场景进行重要决策时，模型可靠性是亟需解决的问题。评估预测模型对训练样本的学习程度，辨识模型参数中噪声至关重要。实现对预测模型样本多样性与拟合能力的有效量化，提高智能预测模型的安全性也是重要的挑战。面向不同的领域应用，如何实现涉密数据的不交换，但模型又能够快速捕捉非涉密信息是一个重要挑战[148-149]。
为了应对挑战，联邦学习[150-151]是一种有效的提高模型可靠性的方法，通过将预测模型训练过程分散到多设备中，每个设备只需使用其本地数据进行训练，然后将本地训练结果进行汇总，构建一个全局的智能预测模型，在一定程度上提高了模型的鲁棒性。预测模型的迭代进化能力也进一步提升模型可靠性，通过在线学习[152-153]、增量学习[154]等技术，使模型具备自动学习和持续更新的能力，从而在接收到新数据时及时调整，而不需要重新训练整个模型，实现保证长期稳定的预测效果。

5 地理空间智能预测未来发展趋势

（1）耦合多算子的可配置通用空间智能预测平台
目前地理空间智能预测模型的门槛比较高，难以满足广泛的时空预测需求，且预测模型的构建还是需要大量依赖专业领域知识，例如实景三维时空预测，仍然需要大量自然资源领域的专业知识。引入构建耦合多时空建模算子的可配置空间智能预测模型是未来的发展趋势之一，无代码/低代码通用地理空间智能预测平台的构建，一方面需要空间智能预测算子更加模块化，低代码平台通常包含了一系列预先构建好的模块和组件，用户可以通过拖拽这些模块和组件来快速构建应用程序，Cursor都时刻影响着人类深度学习能力。另一方面是通过LLM等，如ChatGPT、Gemin、KIMI等，提高人工智能语言的进化能力，通过自然语言创建基于自己知识库的GeoAI智能体（Agent），可以更容易创建地理空间智能预测模型。
（2）融合多模态知识生成式地理空间智能预测模型
需要构建具有任务普适性的空间智能预测“预训练模型”，从而实现新数据微调快速构建新预测模型适应新任务，解决领域自适应与迁移学习中冷启动问题。因此就需要在大量异构异质数据中学习智能预测任务的共性特点，实现对多模态数据的高效管理，构建跨任务跨领域的空间智能学习框架。此外，还需要捕捉数据潜在的分布偏移特征，挖掘多模态数据的关联特性，学习多模态数据的时空关系，挖掘不变性，构建更加精细化的泛化预测模型。目前生成式大模型为地理空间智能预测提供了新的机遇，且取得了比传统机器学习模型更好的性能，但是大模型的训练预测成本过高，也有学者通过Transformer、协同预测或自动化深度学习结构设计来不断优化，充分利用多模态数据、上下文信息、时空依赖建模、互补学习等技术手段，在降低成本的同时不过度降低模型的性能。
（3）PINN与深度学习融合的地理空间智能预测模型
大量新颖的人工智能与机器学习技术如常微分方程，先验指导的神经网络（Physics-informed Neural Network，PINN）等不断出现，将地理知识与规律直接嵌入地理空间智能预测模型，一方面减少地学领域样本稀疏、时空异质性等所带来的问题，用更少的数据样本学习到更具泛化能力的模型，另一方面提高地理模型的可解释性与可信任度。实现从地理经验约束到地理知识嵌入的跨越，实现具备AIGC大型人工智能模型特征的地理空间智能。
（4）地理空间智能预测模型拓展地球系统深度预测应用领域
目前已有的地理空间智能预测模型大多集中在城市时空数据，如交通流、空气质量、人流位置预测等，该类数据具有典型的时空特征，属于时空预测范畴。近年来，随着我国空天地海对地观测技术手段不断丰富，透视地球技术不断进步，地球系统数据爆发式增长，山林田湖草，水土气生人等各类自然资源要素都亟需地理空间智能预测能力，例如华为云盘古大模型实现气象的高精度预测，琅琊海洋大模型实现了全球海洋状态变量的中短期高精度预测。地理空间智能预测能力不仅提高城市计算能力，随着在自然资源深度应用，也能为国土空间规划、用途管制、耕地保护和生态修复、城市体检评估等自然资源业务领域带来深远的影响，为实现地球系统自然资源全要素的数字化和虚拟化、全状态的实时化和可视化、自然资源管理决策的协同化和智能化提供强有力的支撑。
代码可用性声明：“地理空间智能预测时空依赖嵌入机制”的代码实现地址为： https://github.com/GISerWang/GeoAI-driven-spatiotemporal-forecasting。
■ 本文图文责任编辑： 蒋树芳 黄光玉

利益冲突：Conflicts of Interest 所有作者声明不存在利益冲突。

All authors disclose no relevant conflicts of interest.

本文的数值计算得到了武汉大学超级计算中心的计算支持和帮助。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
郑宇. 城市计算概述[J]. 武汉大学学报(信息科学版), 2015, 40(1):1-13.

[ Zheng Y. Introduction to urban computing[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1):1-13. ] DOI:10.13203/j.whugis20140718

[2]
裴韬, 刘亚溪, 郭思慧, 等. 地理大数据挖掘的本质[J]. 地理学报, 2019, 74(3):586-598.

[ Pei T, Liu Y X, Guo S H, et al. Principle of big geodata mining[J]. Acta Geographica Sinica, 2019, 74(3):586-598. ] DOI:10.11821/dlxb201903014

[3]
Xu L, Chen N C, Chen Z Q, et al. Spatiotemporal forecasting in earth system science: Methods, uncertainties, predictability and future directions[J]. Earth-Science Reviews, 2021,222:103828. DOI:10.1016/j.earscirev.2021.103828

[4]
高松. 地理空间人工智能的近期研究总结与思考[J]. 武汉大学学报(信息科学版), 2020, 45(12):1865-1874.

[ Gao S. A review of recent researches and reflections on geospatial artificial intelligence[J]. Geomatics and Information Science of Wuhan University, 2020, 45(12):1865-1874. ] DOI:10.13203/j.whugis20200597

[5]
张永生, 张振超, 童晓冲, 等. 地理空间智能研究进展和面临的若干挑战[J]. 测绘学报, 2021, 50(9):1137-1146.

[ Zhang Y S, Zhang Z C, Tong X C, et al. Progress and challenges of geospatial artificial intelligence[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(9):1137-1146. ] DOI:10.11947/j.AGCS.2021.20200420

[6]
Janowicz K, Gao S, McKenzie G, et al. GeoAI: Spatially explicit artificial intelligence techniques for geographic knowledge discovery and beyond[J]. International Journal of Geographical Information Science, 2020, 34(4):625-636. DOI:10.1080/13658816.2019.1684500

[7]
Wang P X, Zhang T, Zheng Y M, et al. A multi-view bidirectional spatiotemporal graph network for urban traffic flow imputation[J]. International Journal of Geographical Information Science, 2022, 36(6):1231-1257. DOI:10.1080/13658816.2022.2032081

[8]
彭锦辉, 张功凯, 王彤, 等. 轨迹驱动的多层时空图神经网络交通路况短期预测[J]. 地球信息科学学报, 2024, 26(10):2300-2315.

[ Peng J H, Zhang G K, Wang T, et al. A trajectory-driven multi-layer spatiotemporal graph neural network for predicting short-term urban traffic state[J]. Journal of Geo-Information Science, 2024, 26(10):2300-2315. ] DOI:10.12082/dqxxkx.2024.240175

[9]
李欣, 孟德友. 基于路网相关性的分布式增量交通流大数据预测方法[J]. 地理科学, 2017, 37(2):209-216.

[ Li X, Meng D Y. Distributed incremental traffic flow big data forecasting method based on road network correlation[J]. Scientia Geographica Sinica, 2017, 37(2):209-216. ] DOI:10.13249/j.cnki.sgs.2017.02.006

[10]
魏勤谨, 谢品华, Khayyam J, 等. 基于随机森林的O3和NO2近地面质量浓度预测研究[J]. 大气与环境光学学报. 2024.

[ Wei Q J, Xie P H, Khayyam J, et al. Prediction of O3 and NO2 near ground concentrations based on random forest[J]. Journal of Atmospheric and Environmental Optics, 2024. ]

[11]
王培晓, 张恒才, 张彤, 等. 基于注意力常微分方程的PM2.5浓度预测及其可解释性分析[J]. 地球信息科学学报, 2024, 26(6):1363-1373.

[ Wang P X, Zhang H C, Zhang T, et al. An attentional ordinary differential equation for predicting PM2.5 concentration and its interpretability analysis[J]. Journal of Geo-Information Science, 2024, 26(6):1363-1373. ] DOI:10.12082/dqxxkx.2024.230678

[12]
Guan Q F, Wang J Y, Ren S L, et al. Predicting short-term PM2.5 concentrations at fine temporal resolutions using a multi-branch temporal graph convolutional neural network[J]. International Journal of Geographical Information Science, 2024, 38(4):778-801. DOI:10.1080/13658816.2024.2310737

[13]
Zhang T, Liu J, Gao C L, et al. Prior-Guided gated convolutional networks for rainstorm forecasting[J]. Journal of Hydrology, 2024,633:130962. DOI:10.1016/j.jhydrol.2024.130962

[14]
Zhang T, Liu J, Wang J L. Rainstorm prediction via a deep spatio-temporal-attributed affinity network[J]. Geocarto International, 2022, 37(26):13079-13097. DOI:10.1080/10106049.2022.2076914

[15]
Zhao Z W, Dong X C, Wang Y P, et al. Advancing realistic precipitation nowcasting with a spatiotemporal transformer-based denoising diffusion model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024,62:4102115. DOI:10.1109/TGRS.2024.3355755

[16]
王培晓, 张彤, 聂士超, 等. 顾及缺失值的因果图时空预测网络[J]. 测绘学报, 2023, 52(5):818-830.

[ Wang P X, Zhang T, Nie S C, et al. A causal graph convolutional network considering missing values for spatio-temporal prediction[J]. Acta Geodaetica et Cartographica Sinica, 2023, 52(5):818-830. ] DOI:10.11947/j.AGCS.2023.20220021

[17]
Zhou T, Huang B, Li R R, et al. An attention-based deep learning model for citywide traffic flow forecasting[J]. International Journal of Digital Earth, 2022, 15(1):323-344. DOI:10.1080/17538947.2022.2028912

[18]
Yu J J Q. Citywide traffic speed prediction: A geometric deep learning approach[J]. Knowledge-Based Systems, 2021,212:106592. DOI:10.1016/j.knosys.2020.106592

[19]
张雨松, 胥帅, 严兴宇, 等. 跨城市人类移动行为预测研究综述[J]. 计算机科学, 2024.

[ Zhang Y S, Xu S, Yan X Y, et al. A survey on cross-city human mobility prediction[J]. Computer Science, 2024. ]

[20]
Zhao Y B, Cheng S F, Gao S, et al. Predicting origin-destination flows by considering heterogeneous mobility patterns[J]. Sustainable Cities and Society, 2025,118:106015. DOI:10.1016/j.scs.2024.106015

[21]
Rong C, Ding J T, Li Y. An interdisciplinary survey on origin-destination flows modeling: Theory and techniques[J]. ACM Computing Surveys, 2024, 57(1):1-49. DOI:10.1145/3682058

[22]
Jiang L, Zhang X H, Zuo W J, et al. A neural network method for the reconstruction of winter wheat yield series based on spatio-temporal heterogeneity[J]. Computers and Electronics in Agriculture, 2018, 154:46-53. DOI:10.1016/j.compag.2018.08.047

[23]
Cheng L J, Abraham J, Trenberth K E, et al. Upper ocean temperatures hit record high in 2020[J]. Advances in Atmospheric Sciences, 2021, 38(4):523-530. DOI:10.1007/s00376-021-0447-x

[24]
Li G C, Cheng L J, Zhu J, et al. Increasing ocean stratification over the past half-century[J]. Nature Climate Change, 2020,10:1116-1123. DOI:10.1038/s41558-020-00918-2

[25]
Liu Y, Wang X K, Hou W H, et al. A novel hybrid model combining a fuzzy inference system and a deep learning method for short-term traffic flow prediction[J]. Knowledge-Based Systems, 2022,255:109760. DOI:10.1016/j.knosys.2022.109760

[26]
Chen X Y, Sun L J. Bayesian temporal factorization for multidimensional time series prediction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(9):4659-4673. DOI:10.1109/TPAMI.2021.3066551

[27]
祁朵, 毛政元. 基于自适应时序剖分与KNN的短时交通流量预测[J]. 地球信息科学学报, 2022, 24(2):339-351.

[ Qi D, Mao Z Y. Short-term traffic flow prediction based on adaptive time slice and KNN[J]. Journal of Geo-Information Science, 2022, 24(2):339-351. ] DOI:10.12082/dqxxkx.2022.210392

[28]
毛文婧, 王卫林, 焦利民, 等. 基于深度学习的中国连续空间覆盖PM2.5浓度预报[J]. 测绘学报, 2022, 51(3):361-372.

[ Mao W J, Wang W L, Jiao L M, et al. Continuous spatial coverage PM2.5 concentration forecast in China based on deep learning[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(3):361-372. ] DOI:10.11947/j.AGCS.2022.20200385

[29]
胡家敏, 潘岑, 于飞, 等. 气候条件对黔北地区辣椒产量的影响与气象产量预测模型研究[J]. 西南农业学报, 2024, 37(6):1322-1328.

[ Hu J M, Pan C, Yu F, et al. Effects of climate conditions on hot pepper yield in northern Guizhou and prediction model of meteorological yield[J]. Southwest China Journal of Agricultural Sciences, 2024, 37(6):1322-1328. ] DOI:10.16213/j.cnki.scjas.2024.6.022

[30]
王嫄, 霍鹏, 韩毅, 等. 基于深度学习的气象预报模型研究综述[J]. 计算机科学, 2024.

[ Wang Y, Huo P, Han Y, et al. Survey on deep learning-based meteorological forecasting models 2024. ]

[31]
Hofman J M, Watts D J, Athey S, et al. Integrating explanation and prediction in computational social science[J]. Nature, 2021, 595(7866):181-188. DOI:10.1038/s41586-021-03659-0

[32]
Kadow C, Hall D M, Ulbrich U. Artificial intelligence reconstructs missing climate information[J]. Nature Geoscience, 2020,13:408-413. DOI:10.1038/s41561-020-0582-5

[33]
Zheng G, Chai W K, Duanmu J L, et al. Hybrid deep learning models for traffic prediction in large-scale road networks[J]. Information Fusion, 2023, 92:93-114. DOI:10.1016/j.inffus.2022.11.019

[34]
Jin G Y, Liang Y X, Fang Y C, et al. Spatio-temporal graph neural networks for predictive learning in urban computing: A survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 36(10):5388-5408. DOI:10.1109/TKDE.2023.3333824

[35]
Campbell J Y, Thompson S B. Predicting excess stock returns out of sample: Can anything beat the historical average?[J]. The Review of Financial Studies, 2008, 21(4):1509-1531. DOI:10.1093/rfs/hhm055

[36]
Bartier P M, Keller C P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW)[J]. Computers & Geosciences, 1996, 22(7):795-799. DOI:10.1016/0098-3004(96)00021-0

[37]
Huang B, Wu B, Barry M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices[J]. International Journal of Geographical Information Science, 2010, 24(3):383-401. DOI:10.1080/13658810802672469

[38]
邓巧玲. 基于改进自回归理论的非平稳气温变化预测模型研究[J]. 科技资讯, 2024, 22(14):241-244.

[ Deng Q L. Research on non-stationary temperature change prediction model based on improved autoregressive theory[J]. Science & Technology Information, 2024, 22(14):241-244. ] DOI:10.16661/j.cnki.1672-3791.2405-5042-5996

[39]
徐齐利. 移动平均法智能预测系统设计与实现[J]. 信息与管理研究, 2021, 6(1):81-90.

[ Xu Q L. Design and implementation of intelligent prediction system based on moving average method[J]. Journal of Information and Management, 2021, 6(1):81-90. ]

[40]
Zhang X, Ren X. Short-term Prediction of Ionospheric TEC Based on ARIMA Model[J]. Journal of Geodesy and Geoinformation Science, 2020, 2(1):9-16. DOI:10.11947/j.JGGS.2019.0102

[41]
Aryaputera A W, Yang D Z, Zhao L, et al. Very short-term irradiance forecasting at unobserved locations using spatio-temporal Kriging[J]. Solar Energy, 2015, 122:1266-1278. DOI:10.1016/j.solener.2015.10.023

[42]
Li L X, Losser T, Yorke C, et al. Fast inverse distance weighting-based spatiotemporal interpolation: A web-based application of interpolating daily fine particulate matter PM2: 5 in the contiguous U.S. using parallel programming and k-d tree[J]. International Journal of Environmental Research and Public Health, 2014, 11(9):9101-9141. DOI:10.3390/ijerph110909101

[43]
Duan P B, Mao G Q, Zhang C S, et al. STARIMA-based traffic prediction with time-varying lags[C]//2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC). IEEE, 2016:1610-1615. DOI:10.1109/ITSC.2016.7795773

[44]
Cheng S F, Peng P, Lu F. A lightweight ensemble spatiotemporal interpolation model for geospatial data[J]. International Journal of Geographical Information Science, 2020, 34(9):1849-1872. DOI:10.1080/13658816.2020.1725016

[45]
Cheng S F, Lu F, Peng P, et al. Short-term traffic forecasting: An adaptive ST-KNN model that considers spatial heterogeneity[J]. Computers, Environment and Urban Systems, 2018, 71:186-198. DOI:10.1016/j.compenvurbsys.2018.05.009

[46]
袁从贵, 张新政. 时序峰值预测的最小二乘支持向量回归模型[J]. 控制与决策, 2012, 27(11):1745-1750.

[ Yuan C G, Zhang X Z. Least squares support vector regression for prediction of peak samples in time series[J]. Control and Decision, 2012, 27(11):1745-1750. ] DOI:10.13195/j.cd.2012.11.148.yuancg.027

[47]
朱珈莹, 安俊琳, 冯悦政, 等. 基于轻量级梯度提升机的南京大气臭氧浓度预测[J]. 环境科学, 2023, 44(7):3685-3694.

[ Zhu J Y, An J L, Feng Y Z, et al. Atmospheric ozone concentration prediction in Nanjing based on LightGBM[J]. Environmental Science, 2023, 44(7):3685-3694. ] DOI:10.13227/j.hjkx.202208095

[48]
周鑫, 张旗. 基于机器学习的分类模型预测对比[J]. 信息记录材料, 2024, 25(6):235-238.

[ Zhou X, Zhang Q. Prediction and comparison of classification models based on machine learning[J]. Information Recording Materials, 2024, 25(6):235-238. ] DOI:10.16009/j.cnki.cn13-1295/tq.2024.06.007

[49]
程诗奋, 彭澎, 张恒才, 等. 异质稀疏分布时空数据插值、重构与预测方法探讨[J]. 武汉大学学报(信息科学版), 2020, 45(12):1919-1929.

[ Cheng S F, Peng P, Zhang H C, et al. Review of interpolation, reconstruction and prediction methods for heterogeneous and sparsely distributed geospatial data[J]. Geomatics and Information Science of Wuhan University, 2020, 45(12):1919-1929. ] DOI:10.13203/j.whugis20200488

[50]
李静, 刘海砚, 郭文月, 等. 基于深度学习的人群活动流量时空预测模型[J]. 测绘学报, 2021, 50(4):522-531.

[ Li J, Liu H Y, Guo W Y, et al. A spatio-temporal network for human activity prediction based on deep learning[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(4):522-531. ] DOI:10.11947/j.AGCS.2021.20200230

[51]
樊子德. 异质时空数据插值方法研究[J]. 测绘学报, 2017, 46(5):668.

[ Fan Z D. Spatio-temporal interpolation methods for heterogeneous spatio-temporal data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5):668. ] DOI:10.11947/j.AGCS.2017.20170003

[52]
Wang P X, Zhang H C, Cheng S F, et al. Understanding human mobility and trip demand through sparse trajectories of private e-bikes[J]. Journal of Cleaner Production, 2024,471:143444. DOI:10.1016/j.jclepro.2024.143444

[53]
Zhang B B, Cheng S F, Wang P X, et al. Inferring freeway traffic volume with spatial interaction enhanced betweenness centrality[J]. International Journal of Applied Earth Observation and Geoinformation, 2024,129:103818. DOI:10.1016/j.jag.2024.103818

[54]
高俊, 曹雪峰. 空间认知推动地图学学科发展的新方向[J]. 测绘学报, 2021, 50(6):711-725.

[ Gao J, Cao X F. The new development direction of cartography promoted by spatial cognition[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(6):711-725. ] DOI:10.11947/j.AGCS.2021.20210043

[55]
赵斌, 韩晶晶, 史覃覃, 等. 语义轨迹建模与挖掘研究进展[J]. 地球信息科学学报, 2020, 22(4):842-856.

[ Zhao B, Han J J, Shi Q Q, et al. Advancements in semantic trajectory modelling and mining[J]. Journal of Geo-Information Science, 2020, 22(4):842-856. ] DOI:10.12082/dqxxkx.2020.190257

[56]
Cheng S F, Lu F, Peng P. Short-term traffic forecasting by mining the non-stationarity of spatiotemporal patterns[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(10):6365-6383. DOI:10.1109/TITS.2020.2991781

[57]
Cheng S F, Lu F, Peng P, et al. Multi-task and multi-view learning based on particle swarm optimization for short-term traffic forecasting[J]. Knowledge-Based Systems, 2019, 180:116-132. DOI:10.1016/j.knosys.2019.05.023

[58]
Yu H F, Rao N, Dhillon I S, et al. Temporal regularized matrix factorization for high-dimensional time series prediction[C]// Proceedings of the 30th International Conference on Neural Information Processing Systems. ACM, 2016:847-855. DOI:10.5555/3157096.3157191

[59]
Mosavi A, Ozturk P, Chau K W. Flood prediction using machine learning models: Literature review[J]. Water, 2018, 10(11):1536. DOI:10.3390/w10111536

[60]
Wang X X, Bouzembrak Y, Lansink A O, et al. Application of machine learning to the monitoring and prediction of food safety: A review[J]. Comprehensive Reviews in Food Science and Food Safety, 2022, 21(1):416-434. DOI:10.1111/1541-4337.12868

[61]
Liu J, Li T R, Xie P, et al. Urban big data fusion based on deep learning: An overview[J]. Information Fusion, 2020, 53:123-133. DOI:10.1016/j.inffus.2019.06.016

[62]
Manibardo E L, Laña I, Del Ser J. Deep learning for road traffic forecasting: Does it make a difference?[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(7):6164-6188. DOI:10.1109/TITS.2021.3083957

[63]
Xie P, Li T R, Liu J, et al. Urban flow prediction from spatiotemporal data using machine learning: A survey[J]. Information Fusion, 2020, 59:1-12. DOI:10.1016/j.inffus.2020.01.002

[64]
Rossi E, Chamberlain B, Frasca F, et al. Temporal graph networks for deep learning on dynamic graphs[EB/OL]. 2020: 2006.10637.

[65]
刘青豪, 张永红, 邓敏, 等. 大范围地表沉降时序深度学习预测法[J]. 测绘学报, 2021, 50(3):396-404.

[ Liu Q H, Zhang Y H, Deng M, et al. Time series prediction method of large-scale surface subsidence based on deep learning[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(3):396-404. ] DOI:10.11947/j.AGCS.2021.20200038

[66]
裴韬, 舒华, 郭思慧, 等. 地理流的空间模式:概念与分类[J]. 地球信息科学学报, 2020, 22(1):30-40.

[ Pei T, Shu H, Guo S H, et al. The concept and classification of spatial patterns of geographical flow[J]. Journal of Geo-Information Science, 2020, 22(1):30-40. ] DOI:10.12082/dqxxkx.2020.190736

[67]
Wang H L, Xu S L, Xu H S, et al. Rapid prediction of urban flood based on disaster-breeding environment clustering and Bayesian optimized deep learning model in the coastal city[J]. Sustainable Cities and Society, 2023,99:104898. DOI:10.1016/j.scs.2023.104898

[68]
Zhang Y C, Long M S, Chen K Y, et al. Skilful nowcasting of extreme precipitation with NowcastNet[J]. Nature, 2023, 619(7970):526-532. DOI:10.1038/s41586-023-06184-4

[69]
Zheng Q H, Tian X Y, Yu Z G, et al. Application of wavelet-packet transform driven deep learning method in PM2.5 concentration prediction: A case study of Qingdao, China[J]. Sustainable Cities and Society, 2023,92:104486. DOI:10.1016/j.scs.2023.104486

[70]
Zhang J B, Zheng Y, Qi D K, et al. Deep spatio-temporal residual networks for citywide crowd flows prediction[C]// Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence. ACM, 2017:1655-1661. DOI:10.5555/3298239.3298479

[71]
Guo S N, Lin Y F, Li S J, et al. Deep spatial-temporal 3D convolutional neural networks for traffic data forecasting[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(10):3913-3926. DOI:10.1109/TITS.2019.2906365

[72]
He R, Zhang C J, Xiao Y P, et al. Deep spatio-temporal 3D dilated dense neural network for traffic flow prediction[J]. Expert Systems with Applications, 2024,237:121394. DOI:10.1016/j.eswa.2023.121394

[73]
Yu B, Yin H T, Zhu Z X, et al. Spatio-temporal graph convolutional networks[C]// Proceedings of the 27th International Joint Conference on Artificial Intelligence. ACM, 2018:3634-3640. DOI:10.5555/3304222.3304273

[74]
Zhao L, Song Y J, Zhang C, et al. T-GCN: A temporal graph convolutional network for traffic prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(9):3848-3858. DOI:10.1109/TITS.2019.2935152

[75]
Guo S N, Lin Y F, Feng N, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[C]// Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence. ACM, 2019:922-929. DOI:10.1609/aaai.v33i01.3301922

[76]
Huang G, Ge C J, Xiong T Y, et al. Large scale air pollution prediction with deep convolutional networks[J]. Science China Information Sciences, 2021, 64(9):192107. DOI:10.1007/s11432-020-2951-1

[77]
Zhang S C, Zhou L X, Chen X Q, et al. Network-wide traffic speed forecasting: 3D convolutional neural network with ensemble empirical mode decomposition[J]. Computer-Aided Civil and Infrastructure Engineering, 2020, 35(10):1132-1147. DOI:10.1111/mice.12575

[78]
Le V D, Bui T C, Cha S K. Spatiotemporal deep learning model for citywide air pollution interpolation and prediction[C]//2020 IEEE International Conference on Big Data and Smart Computing (BigComp). IEEE, 2020. DOI:10.1109/bigcomp48618.2020.00-99

[79]
Jia T, Yan P G. Predicting citywide road traffic flow using deep spatiotemporal neural networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(5):3101-3111. DOI:10.1109/TITS.2020.2979634

[80]
Wang P X, Zhang H C, Liu J, et al. Efficient inference of large-scale air quality using a lightweight ensemble predictor[J]. International Journal of Geographical Information Science, 2024. DOI:10.1080/13658816.2024.2437044

[81]
Liu S, He M, Wu Z Q, et al. Spatial-temporal graph neural network traffic prediction based load balancing with reinforcement learning in cellular networks[J]. Information Fusion, 2024,103:102079. DOI:10.1016/j.inffus.2023.102079

[82]
Xu Y, Han L Z, Zhu T Y, et al. Generic dynamic graph convolutional network for traffic flow forecasting[J]. Information Fusion, 2023,100:101946. DOI:10.1016/j.inffus.2023.101946

[83]
Li G Y, Zhao Z L, Guo X G, et al. Towards integrated and fine-grained traffic forecasting: A Spatio-Temporal Heterogeneous Graph Transformer approach[J]. Information Fusion, 2024,102:102063. DOI:10.1016/j.inffus.2023.102063

[84]
Bai S J, Kolter J Z, Koltun V, et al. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[EB/OL]. 2018: 1803.01271.

[85]
Wang P X, Zhang H C, Cheng S F, et al. Quickly forecasting the future state of urban sensors by the missing-data-tolerant deep learning approach[J]. Sustainable Cities and Society, 2025,118:106044. DOI:10.1016/j.scs.2024.106044

[86]
Liang Y X, Xia Y T, Ke S Y, et al. AirFormer: Predicting nationwide air quality in China with transformers[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2023, 37(12):14329-14337. DOI:10.1609/aaai.v37i12.26676

[87]
Cai L, Janowicz K, Mai G C, et al. Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting[J]. Transactions in GIS, 2020, 24(3):736-755. DOI:10.1111/tgis.12644

[88]
Xu M X, Dai W R, Liu C M, et al. Spatial-temporal transformer networks for traffic flow forecasting[EB/OL]. 2020: 2001.02908.

[89]
Ren Y B, Chen H F, Han Y, et al. A hybrid integrated deep learning model for the prediction of citywide spatio-temporal flow volumes[J]. International Journal of Geographical Information Science, 2020, 34(4):802-823. DOI:10.1080/13658816.2019.1652303

[90]
Li M X, Gao S, Lu F, et al. Prediction of human activity intensity using the interactions in physical and social spaces through graph convolutional networks[J]. International Journal of Geographical Information Science, 2021, 35(12):2489-2516. DOI:10.1080/13658816.2021.1912347

[91]
张彤, 刘仁宇, 王培晓, 等. 感知物理先验的机器学习及其在地理空间智能中的研究前景[J]. 地球信息科学学报, 2023, 25(7):1297-1311.

[ Zhang T, Liu R Y, Wang P X, et al. Physics-informed machine learning and its research prospects in GeoAI[J]. Journal of Geo-Information Science, 2023, 25(7):1297-1311. ] DOI:10.12082/dqxxkx.2023.220795

[92]
Liu J, Zhang T, Gao C L, et al. Forecasting earthquake magnitude and epicenter by incorporating spatiotemporal priors into deep neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023,61:5911413. DOI:10.1109/TGRS.2023.3281784

[93]
Chen K Q, Liu E B, Deng M, et al. DKNN: Deep Kriging neural network for interpretable geospatial interpolation[J]. International Journal of Geographical Information Science, 2024, 38(8):1486-1530. DOI:10.1080/13658816.2024.2347316

[94]
Bond-Taylor S, Leach A, Long Y, et al. Deep generative modelling: A comparative review of VAEs, GANs, normalizing flows, energy-based and autoregressive models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(11):7327-7347. DOI:10.1109/TPAMI.2021.3116668

[95]
Wen H M, Lin Y F, Xia Y T, et al. DiffSTG: Probabilistic spatio-temporal graph forecasting with denoising diffusion models[C]// Proceedings of the 31st ACM International Conference on Advances in Geographic Information Systems. ACM, 2023:1-12. DOI:10.1145/3589132.3625614

[96]
Wang Q Y, Wang S H, Zhuang D Y, et al. Uncertainty quantification of spatiotemporal travel demand with probabilistic graph neural networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(8):8770-8781. DOI:10.1109/TITS.2024.3367779

[97]
Rasul K, Seward C, Schuster I, et al. Autoregressive denoising diffusion models for multivariate probabilistic time series forecasting[EB/OL]. 2021: 2101.12072.

[98]
Islam Z, Abdel-Aty M, Cai Q, et al. Crash data augmentation using variational autoencoder[J]. Accident Analysis & Prevention, 2021,151:105950. DOI:10.1016/j.aap.2020.105950

[99]
王力, 李敏, 闫佳庆, 等. 基于生成式对抗网络的路网交通流数据补全方法[J]. 交通运输系统工程与信息, 2018, 18(6):63-71.

[ Wang L, Li M, Yan J Q, et al. Urban traffic flow data recovery method based on generative adversarial network[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(6):63-71. ] DOI:10.16097/j.cnki.1009-6744.2018.06.010

[100]
Ho J, Jain A, Abbeel P, et al. Denoising diffusion probabilistic models[C]// Proceedings of the 34th International Conference on Neural Information Processing Systems. ACM, 2020:6840-6851. DOI:10.5555/3495724.3496298

[101]
Kobyzev I, Prince S J D, Brubaker M A. Normalizing flows: An introduction and review of current methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(11):3964-3979. DOI:10.1109/TPAMI.2020.2992934

[102]
Zheng Z, Wang L, Yang L X, et al. Generative probabilistic wind speed forecasting: A variational recurrent autoencoder based method[J]. IEEE Transactions on Power Systems, 2022, 37(2):1386-1398. DOI:10.1109/TPWRS.2021.3105101

[103]
Zhang T, Wang J L, Liu J. A gated generative adversarial imputation approach for signalized road networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(8):12144-12160. DOI:10.1109/TITS.2021.3110268

[104]
An Y, Li Z B, Liu W, et al. Spatio-temporal graph normalizing flow for probabilistic traffic prediction[C]// Proceedings of the 33rd ACM International Conference on Information and Knowledge Management. ACM, 2024:45-55. DOI:10.1145/3627673.3679705

[105]
Shi X J, Gao Z H, Lausen L, et al. Deep learning for precipitation nowcasting: A benchmark and A new model[EB/OL]. 2017: 1706.03458.

[106]
Shi X, Chen Z, Wang H, et al. Convolutional LSTM network: a machine learning approach for precipitation nowcasting[EB/OL]. 2015: 1506.04214.

[107]
Liu Y T, Rasouli S, Wong M, et al. RT-GCN: Gaussian-based spatiotemporal graph convolutional network for robust traffic prediction[J]. Information Fusion, 2024,102:102078. DOI:10.1016/j.inffus.2023.102078

[108]
Cui Z Y, Lin L F, Pu Z Y, et al. Graph Markov network for traffic forecasting with missing data[J]. Transportation Research Part C: Emerging Technologies, 2020,117:102671. DOI:10.1016/j.trc.2020.102671

[109]
Diao Z L, Wang X, Zhang D F, et al. Dynamic spatial-temporal graph convolutional neural networks for traffic forecasting[C]// Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence. ACM, 2019:890-897. DOI:10.1609/aaai.v33i01.3301890

[110]
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8):1735-1780. DOI:10.1162/neco.1997.9.8.1735

[111]
Chung J, Gulcehre C, Cho K, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[EB/OL]. 2014: 1412.3555.

[112]
Chen R T Q, Rubanova Y, Bettencourt J, et al. Neural ordinary differential equations[C]// Proceedings of the 32nd International Conference on Neural Information Processing Systems. ACM, 2018:6572-6583. DOI:10.5555/3327757.3327764

[113]
Wang P X, Zhang T, Zhang H C, et al. Adding attention to the neural ordinary differential equation for spatio-temporal prediction[J]. International Journal of Geographical Information Science, 2024, 38(1):156-181. DOI:10.1080/13658816.2023.2275160

[114]
Poli M, Massaroli S, Park J, et al. Graph neural ordinary differential equations[EB/OL]. 2019: 1911.07532.

[115]
Wang P X, Zhang H C, Cheng S F, et al. A lightweight spatiotemporal graph dilated convolutional network for urban sensor state prediction[J]. Sustainable Cities and Society, 2024,101:105105. DOI:10.1016/j.scs.2023.105105

[116]
Li Q, Wang Q, Li X L. Exploring the relationship between 2D/3D convolution for hyperspectral image super-resolution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(10):8693-8703. DOI:10.1109/TGRS.2020.3047363

[117]
Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[EB/OL]. 2016: 1606.09375.

[118]
Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[EB/OL]. 2016: 1609.02907.

[119]
Gilmer J, Schoenholz S S, Riley P F, et al. Neural message passing for quantum chemistry[EB/OL]. 2017: 1704.01212.

[120]
Veličković P, Cucurull G, Casanova A, et al. Graph attention networks[EB/OL]. 2017: 1710.10903.

[121]
Li Y G, Yu R, Shahabi C, et al. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting[EB/OL]. 2017: 1707.01926.

[122]
李自强, 杨薇, 杨先凤, 等. 基于弱标签争议的半自动分类数据标注方法[J]. 电子学报, 2024, 52(8):2891-2899.

[ Li Z Q, Yang W, Yang X F, et al. The semi-automatic classification data labeling method based on dispute about weak label[J]. Acta Electronica Sinica, 2024, 52(8):2891-2899. ] DOI:10.12263/DZXB.20230648

[123]
蔡莉, 王淑婷, 刘俊晖, 等. 数据标注研究综述[J]. 软件学报, 2020, 31(2):302-320.

[ Cai L, Wang S T, Liu J H, et al. Survey of data annotation[J]. Journal of Software, 2020, 31(2):302-320. ] DOI:10.13328/j.cnki.jos.005977

[124]
Cheng S F, Wang L Z, Wang P X, et al. An ensemble spatial prediction method considering geospatial heterogeneity[J]. International Journal of Geographical Information Science, 2024, 38(9):1856-1880. DOI:10.1080/13658816.2024.2358052

[125]
卢瑶. 基于联合时空注意图网络的城市稀疏异常预测方法研究[D]. 合肥: 中国科学技术大学, 2023.

[ Lu Y. Research on prediction method of urban sparse anomaly based on joint spatio-temporal attention graph network[D]. Hefei: University of Science and Technology of China, 2023. ] DOI: 10.27517/d.cnki.gzkju.2023.002057

[126]
叶绮霖, 蒲英霞, 叶翠. 应用时空滤波模型的亚洲内部国际人口迁移流影响因素分析及短期预测[J]. 地球信息科学学报, 2024, 26(6):1374-1389.

[ Ye Q L, Pu Y X, Ye C. Analysis of influential factors and short-term forecast of international migration flows in Asia using eigenvector space-time filtering models[J]. Journal of Geo-Information Science, 2024, 26(6):1374-1389. ] DOI:10.12082/dqxxkx.2024.240003

[127]
吕梦雨. 基于深度学习和迁移学习的河流水质时空分析预测研究[D]. 广州: 华南理工大学, 2023.

[ Lv M Y. Study on temporal and spatial analysis and prediction of river water quality based on deep learning and transfer learning[D]. Guangzhou: South China University of Technology, 2023. ] DOI:10.27151/d.cnki.ghnlu.2023.000398

[128]
李可汉. 面向城市时空数据的预测与知识迁移研究[D]. 杭州: 浙江大学, 2022.

[ Li K H. Research on prediction and knowledge transfer for urban spatio-temporal data[D]. Hangzhou: Zhejiang University, 2022. ] DOI: 10.27461/d.cnki.gzjdx.2022.001663

[129]
Gong Y S, Li Z B, Zhang J, et al. Missing value imputation for multi-view urban statistical data via spatial correlation learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(1):686-698. DOI:10.1109/TKDE.2021.3072642

[130]
Cheng S F, Lu F, Peng P, et al. A spatiotemporal multi-view-based learning method for short-term traffic forecasting[J]. ISPRS International Journal of Geo-Information, 2018, 7(6):218. DOI:10.3390/ijgi7060218

[131]
Hersbach H, Bell B, Berrisford P, et al. ERA5 hourly data on single levels from 1979 to present[DB/OL]. Copernicus Climate Change Service (C3S) Climate Data Store (CDS), 2018. DOI:10.24381/cds.adbb2d47

[132]
Salih A, Boscolo Galazzo I, Gkontra P, et al. Explainable artificial intelligence and cardiac imaging: Toward more interpretable models[J]. Circulation Cardiovascular Imaging, 2023, 16(4):e014519. DOI:10.1161/CIRCIMAGING.122.014519

[133]
Samek W, Montavon G, Lapuschkin S, et al. Explaining deep neural networks and beyond: A review of methods and applications[J]. Proceedings of the IEEE, 2021, 109(3):247-278. DOI:10.1109/JPROC.2021.3060483

[134]
陈冲, 陈杰, 张慧, 等. 深度学习可解释性综述[J]. 计算机科学, 2023, 50(5):52-63.

[ Chen C, Chen J, Zhang H, et al. Review on interpretability of deep learning[J]. Computer Science, 2023, 50(5):52-63. ] DOI:10.11896/jsjkx.221000044

[135]
Tang J B, Xia L H, Huang C, et al. Explainable spatio-temporal graph neural networks[C]// Proceedings of the 32nd ACM International Conference on Information and Knowledge Management. ACM, 2023:2432-2441. DOI:10.1145/3583780.3614871

[136]
田承涛. 面向社交媒体中文翻译文本的地名识别方法研究[D]. 南昌: 南昌大学, 2024.

[ Tian C T. Research on the method of place Name recognition for social media-oriented Chinese translation text[D]. Nanchang: Nanchang University, 2024.] DOI:10.27232/d.cnki.gnchu.2024.003045

[137]
Zhang B B, Cheng S F, Zhao Y B, et al. Inferring intercity freeway truck volume from the perspective of the potential destination city attractiveness[J]. Sustainable Cities and Society, 2023,98:104834. DOI:10.1016/j.scs.2023.104834

[138]
Chu C, Zhang H C, Wang P X, et al. DeepIndoorCrowd: Predicting crowd flow in indoor shopping malls with an interpretable transformer network[J]. Transactions in GIS, 2023, 27(6):1699-1723. DOI:10.1111/tgis.13095

[139]
曾春艳, 严康, 王志锋, 等. 深度学习模型可解释性研究综述[J]. 计算机工程与应用, 2021, 57(8):1-9.

[ Zeng C Y, Yan K, Wang Z F, et al. Survey of interpretability research on deep learning models[J]. Computer Engineering and Applications, 2021, 57(8):1-9. ] DOI:10.3778/j.issn.1002-8331.2012-0357

[140]
Dai X R, Liu G P, Hu W S. An online-learning-enabled self-attention-based model for ultra-short-term wind power forecasting[J]. Energy, 2023,272:127173. DOI:10.1016/j.energy.2023.127173

[141]
Liu Y, Zheng Y, Liang Y X, et al. Urban water quality prediction based on multi-task multi-view learning[C]// Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence. ACM, 2016:2576-2582. DOI:10.5555/3060832.3060981

[142]
邵仁荣, 刘宇昂, 张伟, 等. 深度学习中知识蒸馏研究综述[J]. 计算机学报, 2022, 45(8):1638-1673.

[ Shao R R, Liu Y A, Zhang W, et al. A survey of knowledge distillation in deep learning[J]. Chinese Journal of Computers, 2022, 45(8):1638-1673. ] DOI:10.11897/SP.J.1016.2022.01638

[143]
罗思涵, 杨燕. 一种基于深度学习和元学习的出行时间预测方法[J]. 南京大学学报(自然科学), 2022, 58(4):561-569.

[ Luo S H, Yang Y. A travel time estimation method based on deep learning and meta-learning[J]. Journal of Nanjing University (Natural Science), 2022, 58(4):561-569. ] DOI:10.13232/j.cnki.jnju.2022.04.001

[144]
李凡长, 刘洋, 吴鹏翔, 等. 元学习研究综述[J]. 计算机学报, 2021, 44(2):422-446.

[ Li F C, Liu Y, Wu P X, et al. A survey on recent advances in meta-learning[J]. Chinese Journal of Computers, 2021, 44(2):422-446. ] DOI:10.11897/SP.J.1016.2021.00422

[145]
Li G Y, Zhong S H, Deng X D, et al. A lightweight and accurate spatial-temporal transformer for traffic forecasting[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(11):10967-10980. DOI:10.1109/TKDE.2022.3233086

[146]
Liu J M, Lin H, Wang X D, et al. Reliable trajectory prediction in scene fusion based on spatio-temporal Structure Causal Model[J]. Information Fusion, 2024,107:102309. DOI:10.1016/j.inffus.2024.102309

[147]
Yang Y Y, Jin M, Wen H M, et al. A survey on diffusion models for time series and spatio-temporal data[EB/OL]. 2024: 2404.18886.

[148]
Rao J M, Gao S, Zhu S J. CATS: Conditional Adversarial Trajectory Synthesis for privacy-preserving trajectory data publication using deep learning approaches[J]. International Journal of Geographical Information Science, 2023, 37(12):2538-2574. DOI:10.1080/13658816.2023.2262550

[149]
Alrayes F S, Abdelmoty A I, El-Geresy W B, et al. Modelling perceived risks to personal privacy from location disclosure on online social networks[J]. International Journal of Geographical Information Science, 2020, 34(1):150-176. DOI:10.1080/13658816.2019.1654109

[150]
Kaur G, Grewal S K, Jain A. Federated learning based spatio-temporal framework for real-time traffic prediction[J]. Wireless Personal Communications, 2024, 136(2):849-865. DOI:10.1007/s11277-024-11292-z

[151]
Liu Q X, Sun S, Liang Y X, et al. Personalized federated learning for spatio-temporal forecasting: A dual semantic alignment-based contrastive approach[EB/OL]. 2024: 2404.03702.

[152]
Miao H, Zhao Y, Guo C J, et al. A unified replay-based continuous learning framework for spatio-temporal prediction on streaming data[EB/OL]. 2024: 2404.14999.

[153]
Yang L, Luo Z P, Zhang S M, et al. Continual learning for smart city: A survey[EB/OL]. 2024: 2404.00983.

[154]
Zhang W J, Han J D, Xu Z, et al. Urban foundation models: A survey[C]// Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. ACM, 2024:6633-6643. DOI:10.1145/3637528.3671453

Options
文章导航

/

〈 〉