EN中文

地球信息科学学报 >

2025 , Vol. 27 >Issue 6: 1275 - 1288

DOI: https://doi.org/10.12082/dqxxkx.2025.240705

第十九届中国地理信息科学理论与方法学术年会优秀论文

矢量线全球离散格网系统高精度建模方法

  • 丁俊杰 , 1 ,
  • 贲进 , 1, * ,
  • 代金池 1 ,
  • 王蕊 2
展开
  • 1.信息工程大学地理空间信息学院，郑州 450001
  • 2.北京市遥感信息研究所，北京 100080
*贲 进（1977—），男，江苏海安人，博士，教授，主要从事摄影测量与遥感、全球离散格网、空间影像信息研究。 E-mail:

作者贡献：Author Contributions

丁俊杰和贲进参与实验设计；丁俊杰、代金池和王蕊完成实验操作；丁俊杰、贲进参与论文的写作和修改。所有作者均阅读并同意最终稿件的提交。

The study was designed by DING Junjie and BEN Jin. The experimental operation was completed by DING Junjie, DAI Jinchi and WANG Rui. The manuscript was drafted and revised by DING Junjie and BEN Jin. All the authors have read the last version of paper and consented for submission.

丁俊杰（2000—）,男，湖南常德人，博士生，主要从事全球离散格网系统研究。E-mail:

收稿日期: 2024-12-23

  修回日期: 2025-03-17

  网络出版日期: 2025-06-06

基金资助

网信“十四五”规划项目(145BWX023009000X)

收起

Methods of High-Precision Vector Line Modeling in Discrete Global Grid Systems

  • DING Junjie , 1 ,
  • BEN Jin , 1, * ,
  • DAI Jinchi 1 ,
  • WANG Rui 2
Expand
  • 1. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, China
  • 2. Beijing Remote Sensing Information Research Institute, Beijing 100080, China
*BEN Jin, E-mail:

Received date: 2024-12-23

  Revised date: 2025-03-17

  Online published: 2025-06-06

Supported by

The “14th Five-Year” Plan Project for National Informatization(145BWX023009000X)

Fold

摘要

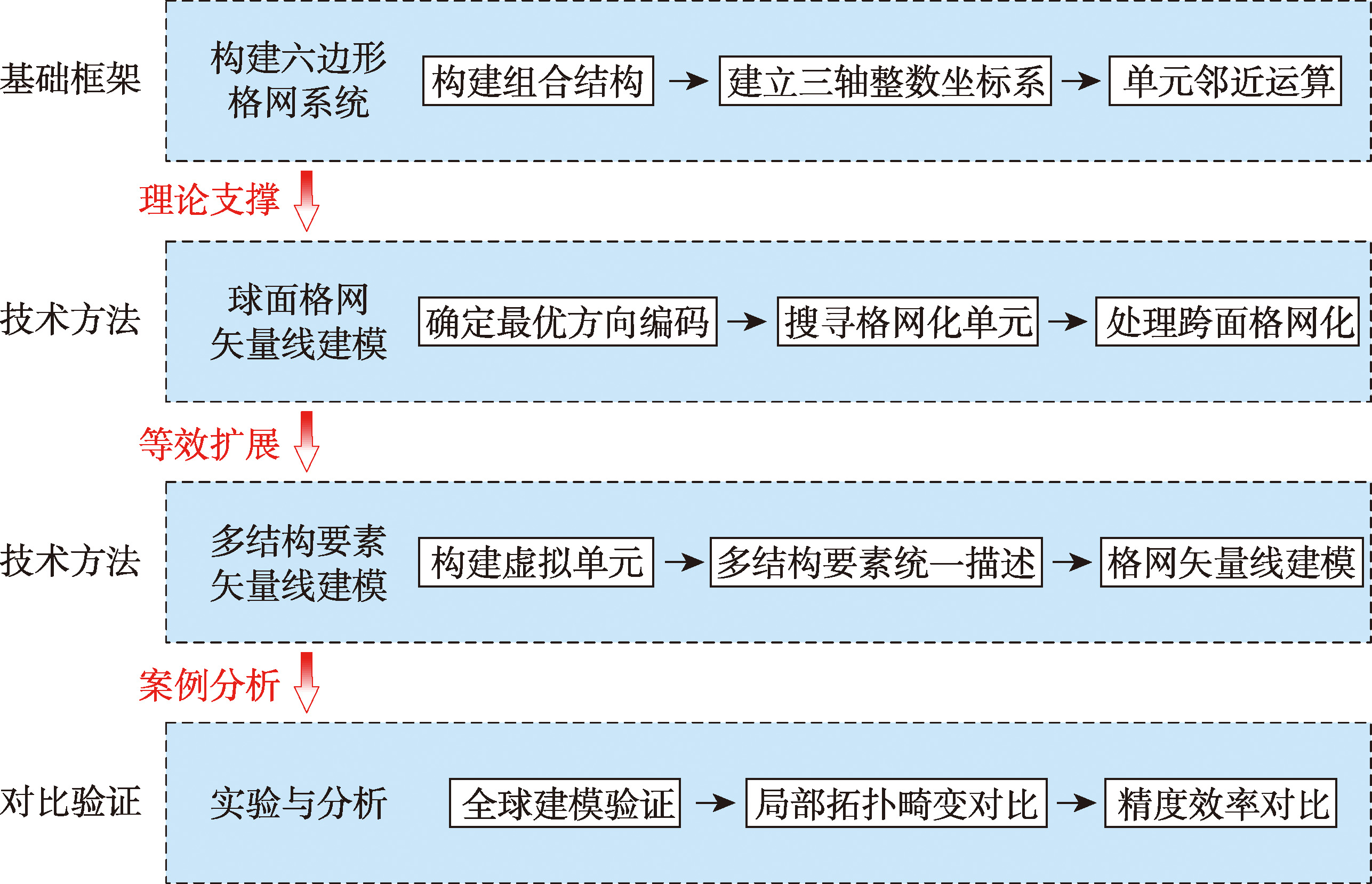
【目的】全球离散格网系统（Discrete Global Grid Systems，DGGS）本质上是多尺度栅格结构，地理空间矢量与格网的集成是难点，矢量线格网化是其中的基本问题。现有方案多以平面格网单元中心（格心）连线为矢量线建模结果，但扩展到球面后建模精度降低，本文针对这一缺陷提出矢量线全球离散格网系统高精度建模方法。【方法】首先选择与地球拟合程度更高的菱形三十面体构建六边形格网系统，以3个相邻菱形面构成组合结构并建立三轴整数坐标系描述单元空间位置；然后根据矢量线首尾端点所在单元确定最优方向编码以减少搜索范围，通过编码邻近运算搜索矢量线经过的球面单元，以球面格心连线为建模结果并提出跨面矢量线处理方法；最后增加单元顶点（格点）作为结构要素，实现多结构要素矢量线建模，进一步提高建模精度。【结果】实验结果表明：本文方案能正确实现全球各个大洲海岸线格网化建模，确保格网化单元与矢量线拓扑相交，且相较平面格网建模结果兼具精度和效率优势。【结论】针对传统矢量数据格网建模方法的几何精度损失和拓扑畸变问题，本文提出高精度球面格网化建模方法，为矢量数据转换至格网同构处理提供有力支撑。

关键词： 矢量线; 菱形三十面体; 全球离散格网系统; 多结构要素; 数据建模; 高精度; 六边形; 编码运算

本文引用格式

丁俊杰 , 贲进 , 代金池 , 王蕊 . 矢量线全球离散格网系统高精度建模方法[J]. 地球信息科学学报, 2025 , 27(6) : 1275 -1288 . DOI: 10.12082/dqxxkx.2025.240705

Abstract

[Objectives] Discrete Global Grid System (DGGS) is a hierarchical structure with seamless global coverage. It functions similarly to an electronic table covering the Earth, supporting the processing and analysis of heterogeneous geospatial data. However, the grid is essentially a multi-scale raster structure, and integrating geographic vector data into it remains a challenge in both research and application. Vector data includes points, lines, and polygons, among which vector line gridding is a fundamental problem. Most existing solutions express vector lines using the center lines of grid cells on a planar grid. However, when extended to spherical surfaces, the accuracy of vector data modeling decreases, making it difficult to meet application requirements. [Methods] This paper proposes a high-precision modeling method for vector lines in DGGS. First, a hexagonal global discrete grid is constructed based on the rhombic triacontahedron, which offers a higher degree of conformity to the sphere. Three adjacent rhombic faces are combined to form a composite structure, and a three-axis integer coordinate system is established to describe the spatial positions of hexagonal elements. Based on the grid cells corresponding to the start and end points of the vector line, optimal direction codes are determined to reduce the search range. The great arc of the vector line passing through the cells is identified using a neighborhood encoding operation. The resulting model is constructed based on the connecting line between grid centers, and a method for processing cross-surface vector lines is proposed. Finally, grid vertices are introduced as structural elements to enable vector line modeling using multiple structural elements, further improving the accuracy of hexagonal grid-based vector line modeling. Experiments show that the proposed method successfully models the grid representation of major coastlines across different continents. The results ensure that the grid model intersects with the original vector line topology, avoiding topological errors where original vector lines do not intersect with any grid cells.[Results] Compared with planar grid modeling, the proposed method achieves significantly higher accuracy in vector line gridding across various coastal regions worldwide. The modeling results demonstrate strong stability and are nearly unaffected by the resolution of the original vector data. Moreover, the method maintains an efficiency advantage, even after complex geometric operations on the spherical surface. [Conclusions] To address the geometric accuracy loss and topological distortion issues in traditional vector data grid modeling, this paper proposes a high-precision spherical grid modeling method. The approach shows strong potential to support the conversion of vector data to grid-based isomorphic representations.

Key words： vector lines; rhombic triacontahedron; Discrete Global Grid System; multi-structural elements; data modeling; high precision; hexagon; encoding operations

1 引言

地理空间矢量数据由离散的点、线、面组成，采用地理坐标记录位置，采用地图分幅组织管理。不同比例尺的矢量数据存在不易分割重组、数据拼接困难、容易产生断裂等问题[1]，因此构建全球、多尺度、开放空间数据管理框架是广受关注的问题。全球离散格网系统（Discrete Global Grid Systems，DGGS）将地球空间剖分为无缝无叠的多尺度层次结构，采用格网单元编码替代传统地理坐标进行数据操作，是极具潜力的多源异构时空数据统一组织、处理和挖掘框架[2-4]。
多面体全球离散格网系统使用特定方法递归剖分多面体表面，再将其映射到地球表面，形成全球连续、近似均匀的格网层次结构，有效避免传统经纬度格网在表示、存储高纬度地区数据的冗余问题[5-6]。格网剖分单元类型一般分为三角形、四边形和六边形，其中六边形具有更加理想的几何性质：邻接一致性、最高空间采样率和角分辨率[5,7-8]。六边形全球离散格网系统已成为当前研究热点，广泛应用于影像组织管理[9-10]、地理环境建模[7,11-12]、事件模拟分析[13-15]等领域。
矢量数据在格网系统中被离散化为一系列格网单元集合，即依据特定准则将其量化到对应尺度的层次单元上，这一过程称为“格网化建模”，是全球离散格网系统核心功能之一[16]。利用格网系统的多尺度特性，通过格网层次动态调节矢量数据的离散化程度；利用单元编码代替矢量位置信息，比浮点坐标更简单高效[17]。但由于数据模型本身的差异，矢量数据格网化类似于计算机图形学领域的栅格化，本质上是一个有损的过程，主要包括几何精度损失和拓扑畸变。Zhou等[18]归纳总结了矢量数据格网化的各类拓扑畸变，并通过提高局部地区格网分辨率修复拓扑畸变； Li等[19]介绍了点、线、面的矢量线格网化建模方法，并针对不同类型矢量数据定量统计了格网化过程中的几何精度损失，并分析了拓扑关系的变化；练文杰[20]设计了表达和存储矢量数据的格网化对象模型，通过格网系统多分辨率特性实现单元集合的编码压缩表示，一定程度上同时兼顾了存储空间与计算效率。
矢量点格网化最简单，直接根据其位置找到对应单元；矢量线格网化是核心问题，也是矢量面格网化的基础。Bresenham[21]首次提出直线栅格扫描算法，此后出现的各种改进算法大多针对平面矩形栅格，六边形格网的相关研究较少。Vince[22]针对Voronoi格网（矩形、六边形、立方体等）设计矢量线通用格网化算法，严格证明2维平面矢量线格网化问题等价于1维直线上的漫游路径问题，即直线上偏离原点距离的最小化问题。Tong等[17]设计平面六边形格网直线扫描算法，采用整数计算和避免除法操作以优化传统Bresenham算法。于文率等[23]对矢量线进行加密插值处理以逼近球面，但内插节点数目与矢量线精度之间的平衡很难掌握，且内插节点严重降低运算效率。杜灵瑀[24]在多面体表面的六边形格网上将Vince降维算法与“贪心”算法结合以实现矢量线格网化，其与同类算法相比具有显著的效率优势，因此本文在后续实验中选择该方法进行对比分析。Amiri等[25]将矢量线投影到多面体表面并构建最小外接菱形，遍历菱形内每个六边形并保留与矢量线拓扑相交的单元，但外接菱形内只有极少数有效单元，故造成巨大计算资源浪费，尤其是当格网层次高、研究区域大时，耗时呈指数级别增长。
上述研究仅关注局部地区，均采用平面格网化方法近似处理矢量线，但通过平面数据模型处理大范围乃至全球尺度数据时，会导致距离、方位的计算具有一定的变形与误差[6]。真实矢量线是球面测地线，因此上述方法存在以下问题： ① 矢量线在等积投影到多面体表面后并不是严格的直线，或只在一定精度允许范围内是直线，以平代曲的处理方法存在较大的误差[24]； ② 当矢量数据空间覆盖范围较广时（例如国境线），容易跨越多面体的多个面，不可避免导致矢量断裂，跨面处理始终是研究和应用难点； ③ 常见格网化算法一般将矢量线起止端点强制改正到相应格网单元中心（格心），导致其与原始矢量线存在一定偏移，导致单元搜寻易出现偏差[24]； ④ 矢量转换为栅格过程不可避免存在精度损失，因为仅考虑格心，格网化结果实际上是格心连线[19]，忽略了单元顶点（格点）和单元的边（格边）等多类型结构要素[14,26-28]的作用。
针对以上问题，本文提出了一种矢量线球面六边形格网高精度建模方法，将矢量线看作球面测地线进行格网化处理，并设计了跨面格网化方法，在此基础上等效扩展至包含格心和格点的多结构要素矢量线建模方法，进一步提高建模精度。

2 研究方法

2.1 研究框架

全文研究框架如图1所示，首先选择菱形三十面体构建几何变形更小、更利于跨面处理的六边形全球离散格网系统；在该格网系统下提出球面格网矢量线建模方法，计算最优方向编码、利用单元编码的邻近运算简化搜索矢量线对应格网单元的过程，通过求解多面体边界与矢量线交点并分面处理实现跨面格网化；然后通过构建虚拟单元，实现格点、格边的多结构要素统一描述，从而将球面格网化方法等效扩展到多结构要素；最后，利用全球海岸线数据广泛验证本文方法的可行性，在局部区域展示不同矢量线建模方法的拓扑畸变，并定量对比不同方法的建模精度和效率，证明本文方法的优越性。
图1 矢量线格网系统高精度建模研究框架

Fig. 1 Research framework for high-precision vector line modeling in grid systems

2.2 构建六边形格网系统

柏拉图多面体通常被选为构建全球离散格网系统的基础多面体，因为其每个表面都是相同大小的正多边形，适合规则单元的格网剖分；多面体面数越多，投影到球面时的变形就越小，因此大多数学者和机构选用柏拉图多面体中面数最多的正二十面体。然而，正二十面体仍存在与球面差异大、单元变形较大的问题；且其表面为三角形，与常用的行列索引和矩形数据组织方式不兼容，增加了格网数据处理的复杂度。因此，本文选择面数更多、表面为菱形的菱形三十面体（Rhombic Triacontahedron，RT）构建全球离散格网系统，在此基础上研究矢量线的高精度建模方法。
菱形三十面体单个面的空间覆盖范围较小，导致处理大范围地理空间数据时容易跨越多个菱形面，而跨面计算复杂且效率低。为减少跨面次数，本文将相邻的上、中、下3个菱形面组合，如图2所示，菱形三十面体可由10个完全相同的“组合结构”组成，实线为组合结构的边界线，虚线为组合结构内3个相邻菱形面间的连接线[29]。
图2 菱形三十面体组合结构

Fig. 2 Combined structures of the rhombic triacontahedron

以图2中的2号组合结构为例，以3个菱形面的公共顶点为原点，沿着菱形面的边建立三轴整数坐标系IJK，如图3所示。统一描述组合结构内所有单元的空间位置，无需考虑同一组合结构内3个菱形面的跨面问题，并将位于负坐标轴的单元对应坐标分量统一改正为0，以简化处理。采用四孔径六边形层次格网剖分方法，图3（a）和图3（b）分别为菱形三十面体组合结构第1层和第2层六边形格网，因此其他组合结构上的格网以及三轴整数坐标与图3所示完全相同。从而将RT中30个菱形面频繁的跨面运算简化为10个组合结构间的运算，且同一组合结构内的单元通过简单高效的整数坐标加减就可实现邻近运算，可有效提高对大区域地理空间数据的处理能力。
图3 六边形格网三轴整数坐标

Fig. 3 Three-axis integer coordinates of hexagonal grids

2.3 球面格网矢量线建模

2.3.1 确定最优方向编码

在平面六边形格网中，某一单元中心指向其相邻单元中心的一组向量称为方向向量，矢量线起始单元到结尾单元的格网化结果可由与矢量线夹角最小的2个方向向量的有序排列表示[24]，这2个最优方向向量可对搜索方向进行约束以减小搜索范围、提高格网化效率。然而球面是非欧氏曲面，其固有特性导致每个球面单元的形状都不一样，因此各个方向向量的长度、方向均不同，平面格网中通过方向向量的平移搜寻格网化单元的方法已经不再适用。
本文借助单元的编码邻近运算等效实现平面格网的向量平移法，不仅保留了单元间的拓扑关系，而且简化矢量线球面格网化的距离和方位量算。某一球面单元编码到其相邻单元编码的邻近运算码元称为方向编码，当矢量线较长或格网层次较高时，若仍采用2个最优方向编码，极易出现搜索路径不收敛、无法找到矢量线结尾端点对应单元的情况，因此采用3个最优方向编码约束球面单元搜索方向。
如图4所示，确定最优方向编码的过程如下：首先，分别计算矢量线起点和终点的格网化单元，例如起点A对应单元G1、终点B对应单元Gn；然后，根据首尾单元编码确定3个最优方向编码v1, v2, v3，使其方向最接近矢量线，其中v1,v2恰好位于矢量线的两侧，称为最邻近最优方向编码，而v3与矢量线方向密切相关，称为第三最优方向编码。
图4 球面最优方向编码

Fig. 4 Optimal direction codes on the sphere

其中，根据矢量线首尾单元整数坐标确定最优方向编码的规则如下。设起始单元编码为(i1, j1, k1)，结尾单元编码为(i2, j2, k2)，其坐标之差为di =i1-i2, dj =j1-j2, dk =k1-k2。本节假定首尾单元位于同一组合结构内，跨组合结构矢量线的处理方法见2.3.3节。以首尾单元位于组合结构上、中菱形面为例，如图5所示，起始单元为中心的蓝色单元，则dj=0，故可通过首尾单元整数坐标的差值直接判断得到3个最优方向编码，表1列举了最优方向编码及其对应的判断条件。
图5 最优方向编码判断规则

Fig. 5 Judgment rules of optimal direction codes

表1 单元坐标与最优方向编码的关系

Tab. 1 Correspondence between the coordinates of cells and optimal direction codes

判断条件1 最邻近最优方向编码 判断条件2 第三最优方向编码
di <0, dk ≥0 v1=（-1, 0, 0）, v2=（0, 0, 1） di<-dk v3=（-1, 0, -1）
di≥-dk v3=（1, 0, 1）
di ≥0, dk >di v1=（0, 0, 1）, v2=（1, 0, 1） d i 1 2 d k v3=（-1, 0, 0）
d i ≥ 1 2 d k v3=（1, 0, 0）
di ≥dk，dk >0 v1=（1, 0, 1）, v2=（1, 0, 0） di<2dk v3=（0, 0, 1）
di≥2dk v3=（0, 0, -1）
di >0, dk ≤0 v1=（1, 0, 0）, v2=（0, 0, -1） di>-dk v3=（1, 0, 1）
di≤-dk v3=（-1, 0, -1）
di ≥0, di >dk v1=（0, 0, -1）, v2=（-1, 0, -1） d i 1 2 d k v3=（1, 0, 0）
d i ≤ 1 2 d k v3=（-1, 0, 0）
di ≤ dk, dk <0 v1=（-1, 0, -1）, v2=（-1, 0, 0） di>2dk v3=（0, 0, -1）
di≤2dk v3=（0, 0, 1）

2.3.2 搜寻格网化单元

平面六边形格网化降维算法需将矢量线的首尾端点强制改正到对应单元中心，这会造成格网化单元搜寻的参考线与原始矢量线之间存在偏差，导致格网化结果也存在偏移误差。尤其是当矢量线较长或格网层次较高时，这种偏移误差严重降低建模精度。
本文以矢量测地线为参考线搜寻球面格网化单元，从原理上解决上述问题。如图4所示，首先从矢量线起始点对应单元G1开始，根据3个最优方向编码搜寻格网化单元，分别得到G1+v1, G1+v2, G1+v3，并将这3个邻近单元格心编码转换为地理坐标；分别计算3个格心与矢量线的球面距离，取距离最小的作为格网化单元。然后从单元G2开始，重复上述过程，逐单元进行格网化，如图6所示，直到刚好搜寻到矢量线结尾点对应单元。
图6 矢量线格网化示意图

Fig. 6 Grids converting of vector lines

格心到矢量线的球面距离计算相对复杂，而本文方法无需求解具体数值，只需要对比相对值大小。为提高搜寻效率，以矢量线起止端点A、B与地球球心O组成平面OAB，用格心Gi至平面OAB的距离|GiS|代替表示球面距离，作为格心与矢量线距离大小的衡量指标。该距离可通过空间内点到平面的距离公式计算，避免了复杂球面三角函数计算，从而提高搜寻球面格网化单元的效率。
本文三轴整数坐标系的建立方法导致组合结构上中菱形面单元与下菱形面单元的最优方向编码及其判断条件均不同。因此当矢量线经过I轴时，需要从起始单元出发，根据其最优方向编码先搜索至I轴上的格网化单元，然后再从I轴上的单元出发，重新计算最优方向编码，继续搜索至结尾单元。

2.3.3 处理跨面矢量线

当矢量线跨越菱形三十面体相邻2个组合结构时，在组合结构边界两侧的单元位于不同的三轴整数坐标系中，无法直接通过单元邻近运算实现格网化。本文计算菱形三十面体组合结构边界与矢量线的球面交点，将跨面矢量线分解到邻近的2个组合结构中分别进行格网化。
图7为第2层六边形格网，矢量线AB跨越0号组合结构和1号组合结构，且与组合结构边界的交点为P。由于点A和P对应的六边形单元均位于0号组合结构内，因此可通过2.3.1节和2.3.2节方法实现矢量线 A P ̑的格网化；而对于矢量线 P B ̑，由于点B对应的六边形单元位于1号组合结构内，即矢量线首尾单元在不同的三轴整数坐标系中，需要对点P对应单元（0, 0, 2）进行跨组合结构坐标变换，将其变换为相邻组合结构内的单元（6, 0, 4），然后在1号组合结构内实现 P B ̑的格网化建模。
图7 跨面处理方法

Fig. 7 Crossing-structure processing method

将编号为0—4的组合结构作为第一类，记为S1，相应地将编号为5—9的组合结构记为S2，用（0）、（1）、（2）分别表示上、中、下菱形面。相邻组合结构间单元的坐标变换由旋转变换和平移变换组合而成，设原始单元坐标为(i, j, k)，变换后的单元坐标为(i', j', k')，格网层次为n，菱形边上单元的个数为num=2n，则变换公式如式（1）所示。不同组合结构间的旋转矩阵R和平移矩阵T如表2所示。因此图7中点P采用序号为2的旋转平移矩阵实现跨组合结构坐标变换。
i ' j ' k ' = R i j k + T
表2 跨组合结构单元坐标变换

Tab. 2 Coordinate transformation for cells of crossing combined structures

序号 变换前
单元位置		 变换后
单元位置		 旋转矩阵R 平移矩阵T
1 S1(0) S1(0) 0 0 0 0 0 0 0 0 1 2   n u m 0 0
2 S1(0) S1(1) 0 0 - 1 0 0 0 0 0 0 2   n u m 0 n u m
3 S1(1) S2(0) 0 0 0 0 0 0 0 0 0 n u m 0 2   n u m
4 S1(2) S2(0) 0 0 0 0 0 0 - 1 0 0 n u m 0 2   n u m
5 S1(2) S2(1) 1 0 0 0 0 0 0 1 0 0 0 0
6 S2(0) S1(1) 0 0 1 0 0 0 1 0 0 0 0 0
7 S2(0) S1(2) 0 0 - 1 0 0 - 1 0 0 0 2   n u m n u m 0
8 S2(1) S1(2) 0 0 0 0 0 0 0 0 0 2   n u m 0 n u m
9 S2(2) S2(2) 1 0 0 1 0 0 0 0 0 0 - n u m 0
10 S2(2) S2(1) - 1 0 0 0 0 0 - 1 0 0 2   n u m 0 n u m

2.4 多结构要素矢量线建模

现有全球离散格网系统在数据建模时通常只考虑格心，即以单元中心的位置表示矢量线格网化六边形单元的位置，不可避免地造成了几何精度损失。六边形单元的6个格点和六条格边同样十分重要，格点不仅是单元覆盖区域的边界点，同样也能与位置相关数据建立关联，而一般来说格边常用作战场环境建模时障碍类要素的辅助表示[14-15]。因此为提高矢量数据格网建模精度，本文将上述球面格网矢量线建模方法扩展到格心和格点的多结构要素格网中。
为在三轴整数坐标系下统一表达格心和格点，首先在当前层次单元的基础上构建虚拟单元，如图8所示，所有的格心和格点均位于虚拟单元中心。设任意原始单元坐标为（i， j， k），则在格网多结构要素三轴整数坐标系下，可计算得到虚拟单元的坐标，原始单元格心对应的虚拟单元坐标为(3i, 3j,3k)，而其格点对应虚拟单元坐标可根据整数坐标邻近查询得到。因此以虚拟单元代替格心和格点，便可参考2.3节建立类似的格网多结构要素矢量线建模方法，且仅需对虚拟单元的最优方向编码判断规则以及跨组合结构单元坐标变换矩阵稍作改变。
图8 多结构要素格网

Fig. 8 Multi-structural elements grids

由于本文在菱形三十面体表面构建六边形格网，先计算得到单元要素的菱形面投影坐标，然后将其投影到球面上。因此需要推导格点的投影坐标，如图9所示，菱形面边长为L，内角分别为α=116.57°，β=63.43°，投影坐标系xy以菱形面中心为原点。设某一格心的投影坐标为(x0, y0)，则六个格点的投影坐标可由式（2）计算得到，其中 d x = L c o s α 2 / n u m ,   d y = 1 3 L s i n α 2 / n u m。最后，将投影坐标通过逆投影公式转换为经纬度坐标。
x 1 = x 0 + d x ,   y 1 = y 0 + d y x 2 = x 0 ,   y 2 = y 0 + 2 d y x 3 = x 0 - d x ,   y 3 = y 0 + d y x 4 = x 0 - d x ,   y 4 = y 0 - d y x 5 = x 0 ,   y 5 = y 0 - 2 d y x 6 = x 0 + d x ,   y 6 = y 0 - d y
图9 多结构要素几何关系

Fig. 9 Geometric relationships of multi-structural elements

3 实验与分析

3.1 全球建模验证

为检验上述矢量线球面六边形格网建模方法的可行性，选取从全球高分辨率海岸数据集GSHHG下载的非洲、美洲、大洋洲和南极洲的主要海岸线作为实验数据，在不同层次格网中分别实现矢量线建模。为便于整体观察，仅展示了第4层和第5层矢量线球面建模结果，如图10、图11和图12所示，其中红色线为海岸线数据，白色六边形为格网化建模结果，黑色实线为菱形三十面体组合结构边界，黑色虚线为组合结构内部三个菱形面间的连接线。
由上述结果可知，本文方案能够实现全球不同区域大范围矢量线的球面格网化，格网化单元均与原始矢量线空间相交。不管是菱形三十面体单个菱形面内还是组合结构内3个菱形面间连接线处，单元都连续排布且彼此邻近；同时组合结构边界处格网化正确、未出现单元空缺的现象。当格网层次较低时，例如图10（a）、图11（a）和图12（a），矢量线密集区域的格网化单元过于聚集，且存在多条矢量线位于同一个单元中的现象，故较难用格网化结果代替表示矢量线；而当格网层次较高时，例如图10（b）、图11（b）、图12（b），矢量线密集区域的格网化单元彼此分开，能够较为清晰地区分其所对应的矢量线。因此，根据全球离散格网无限剖分的特性，当格网层次足够高时，矢量线能够得到充分的格网化，从而可利用格网单元近似替代原始矢量线进行空间分析。
图10 非洲主要海岸线建模结果

Fig. 10 Modeling results of major coastlines in Africa

图11 美洲主要海岸线建模结果

Fig. 11 Modeling results of major coastlines in Americas

图12 大洋洲和南极洲主要海岸线建模结果

Fig. 12 Modeling results of major coastlines in Oceania and Antarctica

3.2 局部拓扑畸变对比

当矢量线较长或格网层次较高时，以平代曲的处理方法将导致不可容忍的误差。本文选取文献[24]的平面建模方法进行对比，为便于直观对比不同格网化建模方法，选择美国与加拿大平整的陆上交界国境线为实验数据，如图13所示，选取局部区域观察不同格网化建模方法的拓扑畸变，图14列举了平面建模方法、球面建模方法和多结构要素建模方法在同一实验区域的结果。
图13 实验区域示意图

Fig. 13 Schematic diagram of experimental area

图14 局部地区矢量线建模结果

Fig. 14 Modeling results of vector lines in local area

格网本质上是多尺度栅格数据结构，与矢量数据不兼容，基于格网的矢量数据建模不可避免存在一定精度损失。如图14（a）所示，平面格网化建模结果实际上是格心的连线，但存在与矢量线完全不相交的单元，这些单元被错误地判断为格网化结果，导致格心的连线严重偏离矢量线；如图14（b）所示，本文提出的球面格网化建模方法避免了上述拓扑错误，虽然建模结果仍然是格心的连线，但可确保每一个格网化单元均与矢量线相交，且与矢量线距离相对最近；如图14（c）所示，格网多结构要素建模的结果为格心和格点的连线，更加接近于矢量线。

3.3 建模精度对比

为定量对比不同格网化方法的建模精度，选择图13中美国本土东部狭长而蜿蜒的海岸线为实验数据，以保证实验的公正性。选取13—17层的高分辨率格网，统计3种格网化建模结果偏离原始矢量线球面距离的平均值，作为衡量建模精度的指标。同时为测试建模结果与原始矢量线数据精度的关系，首先对原始矢量线进行加密插值处理，每2个相邻矢量线端点间内插15个地理坐标点；然后利用不同的格网化方法分别对原始矢量线数据和加密矢量线数据进行格网化建模，并以加密矢量线为计算偏离距离的参考数据，统计建模结果与加密矢量线的距离平均值并分别计算本文两种方法相对于平面格心建模方法的精度比（平面格心建模结果偏离距离除以球面格心建模结果偏离距离或多结构要素建模结构偏离距离），结果如表3、表4和图15所示。
表3 原始矢量线建模结果

Tab. 3 Modeling results of the original vector lines

格网
层次		 平面格心
建模/m		 球面格心
建模/m		 球面格心建模精度比 多结构要
素建模/m		 多结构要素建模精度比
13 166.330 130.199 1.278 76.772 2.167
14 91.935 66.797 1.376 39.910 2.304
15 54.960 34.713 1.583 21.487 2.558
16 37.499 19.094 1.964 12.582 2.980
17 29.055 11.407 2.547 8.411 3.454
表4 加密矢量线建模结果

Tab. 4 Modeling results of the vector lines with increased density

格网
层次		 平面格心
建模/m		 球面格心
建模/m		 球面格心建模精度比 多结构要
素建模/m		 多结构要素建模精度比
13 145.557 130.138 1.118 75.856 1.919
14 76.381 65.868 1.160 38.992 1.959
15 40.278 33.910 1.188 20.844 1.932
16 22.072 18.475 1.195 11.745 1.863
17 12.751 10.621 1.200 7.330 1.739
图15 建模精度比较

Fig. 15 Comparison of modeling accuracy

分析以上实验结果，可得到以下结论：
（1）在同一格网层次下，平面格心建模的精度均最低，球面格心建模次之，多结构要素建模精度最高。且本文所提出的2种方法建模结果几乎不受矢量线数据精度的影响，原始矢量线建模结果精度只比加密矢量线建模结果精度低不到1 m，具有较强的稳定性。这是因为平面格心建模存在图14（a）所示的拓扑畸变单元，导致建模结果严重偏离，而本文的2种方法根据矢量测地线搜寻格网化单元，因此只要矢量线数据精度足够高，由不同精度矢量线建模得到的结果几乎完全相同。
（2）当矢量线数据精度较低时，如图15（a）所示，平面格心建模结果精度损失非常大，且随着格网层次增加，本文方案相对于平面格心建模的精度优势逐渐提升，第17层格网时本文方案的精度比达到了3倍左右。这是因为矢量线两相邻节点间实际距离太远，将其视为直线进行处理存在很大的误差，且当格网层次增加时，平面格心建模结果中出现拓扑错误单元数量增加，其建模精度提升变慢；而本文方案随格网层次升高，建模精度能够较为稳定地提升，因此精度比越来越大。
（3）当矢量线数据精度较高时，如图15（b）所示，以平代曲的影响较小，因此平面格心建模结果的精度略低于球面格心建模，且随着格网层次的增加，本文方法建模结果的精度比变化小，但多结构要素建模方法仍然具有明显的精度优势，在17层格网下建模结果偏离矢量线的平均距离小于10 m。

3.4 建模效率对比

进一步测试3种方法建模效率，实验数据同样选择美国本土东部狭长而蜿蜒的海岸线，选取13—17层的高分辨率格网，统计海岸线格网化建模的耗时，每种建模方法在同一格网层次下分别运行10次并取平均值，耗时单位为秒（s）。全部程序均编译为Release版本，在一台兼容机（硬件配置：Inter Core i5-10400F CPU@2.90GHz，16G RAM，KIOXIA-EXCERIA 480G SSD；操作系统：Windows 10 x64 Enterprise LTSC；开发工具：Microsoft Visual C++ Enterprise 2022）进行测试，耗时结果如表5所示，效率对比如图16所示。
表5 建模耗时结果

Tab. 5 Results of modeling time

格网层次 格网化建模耗时/s
平面格心建模 球面格心建模 多结构要素建模
13 0.289 0.173 0.586
14 0.686 0.381 1.872
15 4.157 3.000 6.561
16 9.849 7.243 14.599
17 20.778 14.912 30.817
图16 建模效率比较

Fig. 16 Comparison of modeling efficiency

分析以上实验结果，可得到以下结论：
（1）在同一格网层次下，球面格心矢量线建模方法效率最高，传统平面格心建模方法次之，多结构要素矢量线建模方法效率最低。这是因为球面格心建模方法采用单元整数编码运算搜索格网化单元，远比传统平面格心建模方法采用的浮点数坐标计算更加高效；格网多结构要素建模方法增加了格点作为单元结构要素，且每个格点的编码均需由其附属的格心编码计算得到，在显著提升建模精度的同时也导致效率有一定降低。
（2）本文提出的2种矢量线建模方法均充分考虑球面因素，得到更真实准确的建模结果，但必然导致计算量增加。球面格心建模方法克服了球面几何计算造成的效率降低，仍然具有最快的建模效率，建模效率平均约为平面格心建模方法的1.52倍；多结构要素建模方法计算量最大，但由此造成的建模效率降低仍在可接受范围内，其建模效率平均约为平面格心建模方法的0.57倍。
（3）理论上格网层次越高，矢量线建模精度越高，第n层格网多结构要素建模不仅效率高于第n+1层平面格心建模，而且精度更高，有力证明了所提出方法的优越性；第n层格网多结构要素建模效率高于第n+1层球面格心建模效率，但精度稍低，然而在实际应用时构建第n+1层球面格网系统需开辟成倍的内存空间，造成巨大的计算压力。因此，相比于直接增加格网层次以提高矢量建模精度，多结构要素建模是兼顾精度与效率的更优方法。

4 结论与展望

本研究的主要贡献包括以下3个方面： ① 选取菱形三十面体构建六边形全球离散格网系统，不仅减小了单元变形，而且有利于大范围数据的跨面处理； ② 提出了球面六边形格网矢量线建模方法，根据矢量线端点对应单元的高效整数编码邻近运算搜索格网化单元，实现矢量线球面格网高精度建模； ③ 将上述方法扩展到了格心和格点上，实现更高精度的球面多结构要素矢量线建模。与传统平面格网矢量线建模方法相比，本文提出的球面格网建模方法和多结构要素建模方法能正确实现全球范围矢量线格网化建模，不仅从原理上避免了矢量线与格网化单元无空间相交关系的拓扑错误，而且建模精度分别提升了约1.2倍和2倍、建模效率分别为其1.52倍和0.57倍。
综上所述，针对传统矢量数据格网化方法的严重几何精度损失和拓扑畸变问题，本文提出矢量数据高精度球面格网化建模方法，为利用全球离散格网系统组织管理矢量数据提供了精度损失小、处理效率高的技术途径。然而本研究的不足之处在于格网多结构要素矢量建模效率较低，后续研究将尝试对格心、格点一致编码，从算法出发全面提升矢量线格网化效率，最终实现实时格网化，满足高效处理海量矢量数据的应用需求。
AI使用说明：本文没有使用AI技术。
■ 本文图文责任编辑：黄光玉 蒋树芳

利益冲突：Conflicts of Interest 所有作者声明不存在利益冲突。

All authors disclose no relevant conflicts of interest.

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
关丽, 程承旗, 吕雪锋. 基于球面剖分格网的矢量数据组织模型研究[J]. 地理与地理信息科学, 2009, 25(3):23-27.

[Guan L, Cheng C Q, Lv X F. Study on the organization model for vector data based on global subdivision grid[J]. Geography and Geo-information Science, 2009, 25(3):23-27.]

[2]
赵学胜, 贲进, 孙文彬, 等. 地球剖分格网研究进展综述[J]. 测绘学报, 2016, 45(S1):1-14.

DOI

[Zhao X S, Ben J, Sun W B, et al. Overview of the research progress in the Earth tessellation grid[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1):1-14.] DOI:10.11947/j.AGCS.2016.F001

[3]
周成虎, 欧阳, 马廷. 地理格网模型研究进展[J]. 地理科学进展, 2009, 28(5):657-662.

[Zhou C H, Ou Y, Ma T. Progresses of geographical grid systems researches[J]. Progress in Geography, 2009, 28(5):657-662.]

DOI

[4]
Zhou L C, Lian W J, Lv G N, et al. Efficient encoding and decoding algorithm for triangular discrete global grid based on Hybrid Transformation Strategy[J]. Computers, Environment and Urban Systems, 2018, 68:110-120. DOI:10.1016/j.compenvurbsys.2017.11.005

[5]
Mahdavi-Amiri A, Alderson T, Samavati F. A survey of digital earth[J]. Computers & Graphics, 2015, 53:95-117. DOI:10.1016/j.cag.2015.08.005

[6]
赵学胜, 王磊, 王洪彬, 等. 全球离散格网的建模方法及基本问题[J]. 地理与地理信息科学, 2012, 28(1):29-34.

[Zhao X S, Wang L, Wang H B, et al. Modeling methods and basic problems of discrete global grids[J]. Geography and Geo-Information Science, 2012, 28(1):29-34.]

[7]
Bousquin J. Discrete Global Grid Systems as scalable geospatial frameworks for characterizing coastal environments[J]. Environmental Modelling & Software, 2021,146:105210. DOI:10.1016/j.envsoft.2021.105210

[8]
Mechenich M F, Žliobaitė I. Eco-ISEA3H, a machine learning ready spatial database for ecometric and species distribution modeling[J]. Scientific Data, 2023, 10(1):77. DOI:10.1038/s41597-023-01966-x

PMID

[9]
Gong P, Wang J, Yu L, et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data[J]. International Journal of Remote Sensing, 2013, 34(7):2607-2654. DOI:10.1080/01431161.2012.748992

[10]
Liang Q S, Zhou J B, Ben J, et al. Precise hexagonal pixel modeling and an easy-sharing storage scheme for remote sensing images based on discrete global grid system[J]. International Journal of Digital Earth, 2024, 17(1):2328824. DOI:10.1080/17538947.2024.2328824

[11]
Li M K, McGrath H, Stefanakis E. Integration of heterogeneous terrain data into discrete global grid systems[J]. Cartography and Geographic Information Science, 2021, 48(6):546-564. DOI:10.1080/15230406.2021.1966648

[12]
Robertson C, Chaudhuri C, Hojati M, et al. An integrated environmental analytics system (IDEAS) based on a DGGS[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 162:214-228. DOI:10.1016/j.isprsjprs.2020.02.009

[13]
Fichtner F, Mandery N, Wieland M, et al. Time-series analysis of Sentinel-1/2 data for flood detection using a discrete global grid system and seasonal decomposition[J]. International Journal of Applied Earth Observation and Geoinformation, 2023,119:103329. DOI:10.1016/j.jag.2023.103329

[14]
周建彬, 贲进, 丁俊杰, 等. 多结构要素六边形全球离散格网系统构建方法及应用[J]. 地球信息科学学报, 2023, 25(11):2107-2119.

DOI

[Zhou J B, Ben J, Ding J J, et al. Construction methods and applications of a hexagonal discrete global grid system considering multiple structural elements[J]. Journal of Geo-information Science, 2023, 25(11):2107-2119.] DOI:10.12082/dqxxkx.2023.220952

[15]
周建彬, 贲进, 黄心海, 等. 广域六角格兵棋地图构建方法与机动推演应用[J]. 系统工程与电子技术, 2023, 45(3):769-776.

DOI

[Zhou J B, Ben J, Huang X H, et al. Construction method of extensive hexagonal wargame map and application for marching deduction[J]. Systems Engineering and Electronics, 2023, 45(3):769-776.] DOI:10.12305/j.is sn.1001-506X.2023.03.18

[16]
Purss M B J, Gibb R, Samavati F, et al. The OGC® Discrete Global Grid System core standard: A framework for rapid geospatial integration[C]//2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). IEEE, 2016:3610-3613. DOI:10.1109/IGARSS.2016.7729935

[17]
Tong X C, Ben J, Liu Y Y, et al. Modeling and expression of vector data in the hexagonal discrete global grid system[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013,XL-4/W2:15-25. DOI:10.5194/isprsarchives-xl-4-w2-15-2013

[18]
Zhou L C, Lian W J, Zhang Y D, et al. A topology preserving gridding method for vector features in discrete global grid systems[J]. ISPRS International Journal of Geo-Information, 2020, 9(3):168. DOI:10.3390/ijgi9030168

[19]
Li M K, Stefanakis E. Geo-feature modeling uncertainties in discrete global grids: A case study of downtown Calgary, Canada[J]. Geomatica, 2020, 74(4):175-195. DOI:10.1139/geomat-2020-0011

[20]
练文杰. 基于全球离散格网的地理对象模型及关键技术研究[D]. 南京: 南京师范大学, 2019.

[Lian W J. Research on geographic object model and key technologies based on discrete global grid system[D]. Nanjing: Nanjing Normal University, 2019.]

[21]
Bresenham J E. Algorithm for computer control of a digital plotter[J]. IBM Systems Journal, 1965, 4(1):25-30. DOI:10.1147/sj.41.0025

[22]
Vince A. Discrete lines and wandering paths[J]. SIAM Journal on Discrete Mathematics, 2007, 21(3):647-661. DOI:10.1137/050642009

[23]
于文率, 童晓冲, 贲进, 等. 全球六边形离散格网的矢量线数据绘制精度控制[J]. 地球信息科学学报, 2015, 17(7):804-809.

DOI

[Yu W S, Tong X C, Ben J, et al. The accuracy control in the process of vector line data drawing in the hexagon discrete global grid system[J]. Journal of Geo-Information Science, 2015, 17(7):804-809.] DOI:10.3724/S P.J.1047.2015.00804

[24]
杜灵瑀. 矢量线六边形全球离散格网表达的理论与方法[D]. 郑州: 战略支援部队信息工程大学, 2019.

[Du L Y. Theory and method of vector line representation on hexagonal discrete global grid[D]. Zhengzhou: PLA Strategic Support Force Information Engineering University, 2019.]

[25]
Mahdavi Amiri A, Alderson T, Samavati F. Geospatial data organization methods with emphasis on aperture-3 hexagonal discrete global grid systems[J]. Cartographica, 2019, 54(1):30-50. DOI:10.3138/cart.54.1.2018-0010

[26]
陈艺航, 王金鑫, 曹泽宁, 等. 全球离散格网系统结构要素一体化编码与生成方法[J]. 地球信息科学学报, 2021, 23(8):1382-1390.

DOI

[Chen Y H, Wang J X, Cao Z N, et al. The uniform encoding and generation method of structure elements of discrete global grid systems[J]. Journal of Geo-Information Science, 2021, 23(8):1382-1390.] DOI:10.12082/dqxxkx.2021.200672

[27]
Huang X H, Ding J J, Ben J, et al. Advancing digital earth modeling: Hexagonal multi-structural elements in icosahedral DGGS for enhanced geospatial data processing[J]. Environmental Modelling & Software, 2024,172:105922. DOI:10.1016/j.envsoft.2023.105922

[28]
Lin B X, Zhou L C, Xu D P, et al. A discrete global grid system for earth system modeling[J]. International Journal of Geographical Information Science, 2018, 32(4):711-737. DOI:10.1080/13658816.2017.1391389

[29]
Ding J J, Huang X H, Ben J, et al. Encoding and operation scheme for the rhombic triacontahedron aperture 4 hexagonal discrete global grid system[J]. International Journal of Digital Earth, 2024, 17(1): 2316112. DOI:10.1080/17538947.2024.2316112

Options
文章导航

/

〈 〉